Unlocking the Potential of Cable-Driven Continuum Robots: A Comprehensive Review and Future Directions
Abstract
:1. Introduction
1.1. Origins of Continuum Robots
1.2. Classification of Continuum Robots
- Pneumatic continuum robots rely on air pressure as their driving force [24]. They are known for their high flexibility, simple structures, smooth movement, and lightweight construction [25]. Typically, these robots consist of multiple pneumatic chambers, with robot movement achieved by controlling changes in air pressure [26,27]. Nevertheless, pneumatic continuum robots have limitations, including restricted precision, noise generation, and high maintenance costs.
- SMA-driven continuum robots use shape memory alloys, special metal alloys known for their memory shape and superelasticity [28], as their driving mechanism. They exploit the SMA’s memory shape and superelastic properties to enable bending and torsion of flexible segments, facilitating the robot’s movement and operations [29,30]. SMA-driven continuum robots offer advantages such as simple driving devices, fast response times, and low power consumption. However, they are also susceptible to drawbacks like high material costs, low load capacity, and sensitivity to temperature and stress.
- Cable-driven continuum robots, sometimes referred to as tendon-driven or line-driven robots, rely on flexible supporting structures (backbones) and driving cables to achieve motion by adjusting cable lengths and tension [31,32,33]. These robots can change shapes and positions continuously, making them lightweight and intrinsically safe. They are particularly suited for more precise operations in confined spaces and exhibit smaller response lag compared to pneumatic robots [34,35,36]. They also offer a larger working space and higher load capacity compared to SMA-driven systems. However, CDCRs face challenges such as complex motion, modeling difficulty, low control accuracy, actuation redundancy, and relatively large drive mechanisms. Consequently, the design analysis, kinematics and dynamics modelling, motion planning, and control for CDCRs have become complex interdisciplinary fields that attract growing interest among researchers.
2. CDCR Configurations and Cable Arrangements
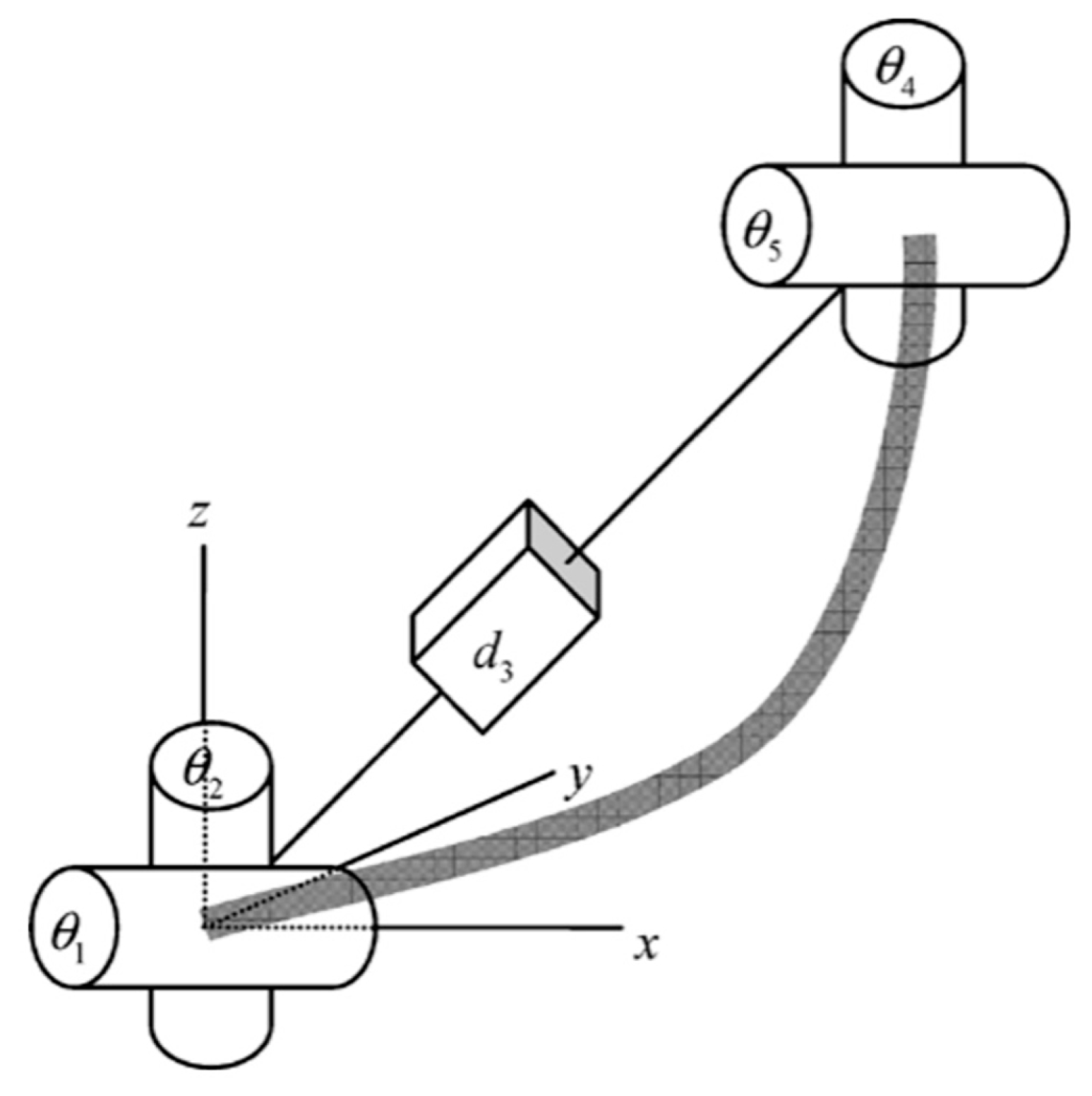
2.1. CDCR Configurations with Different Backbone Stuctures
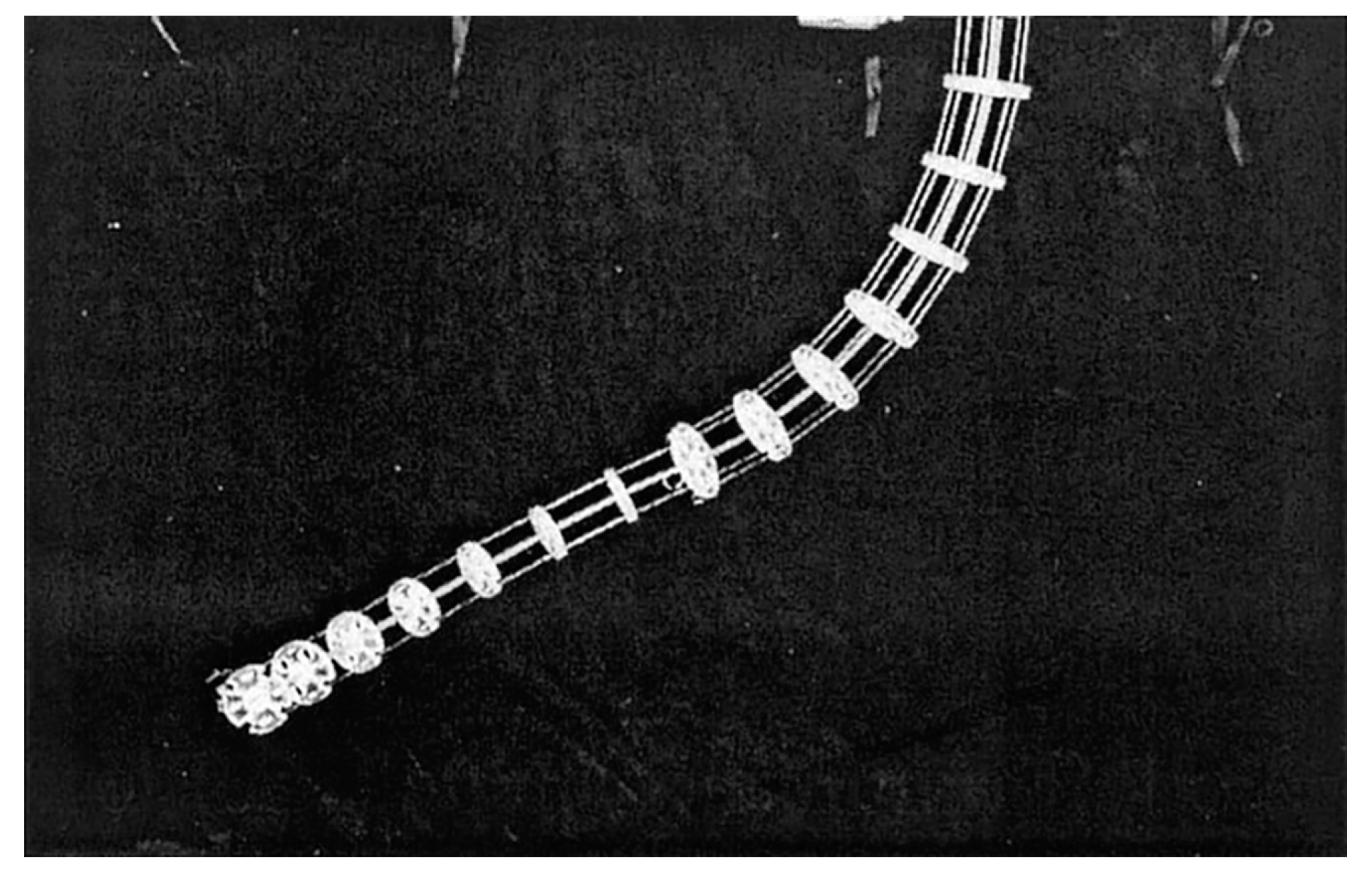
2.1.1. CDCR with Sheet Type Backbone
2.1.2. CDCR with Rod Type Backbone
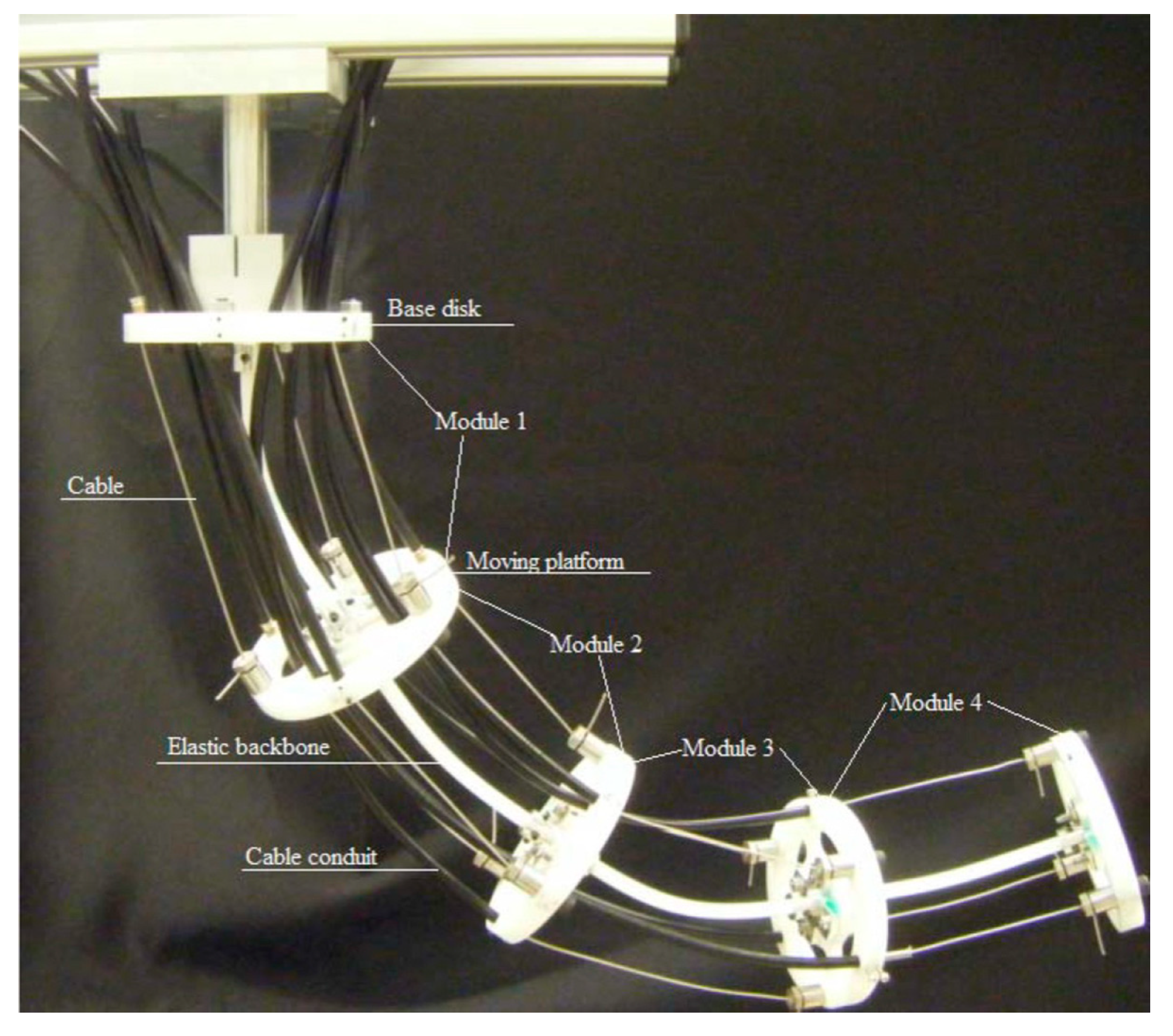
2.1.3. Modular CDCR with Rod Type Backbone
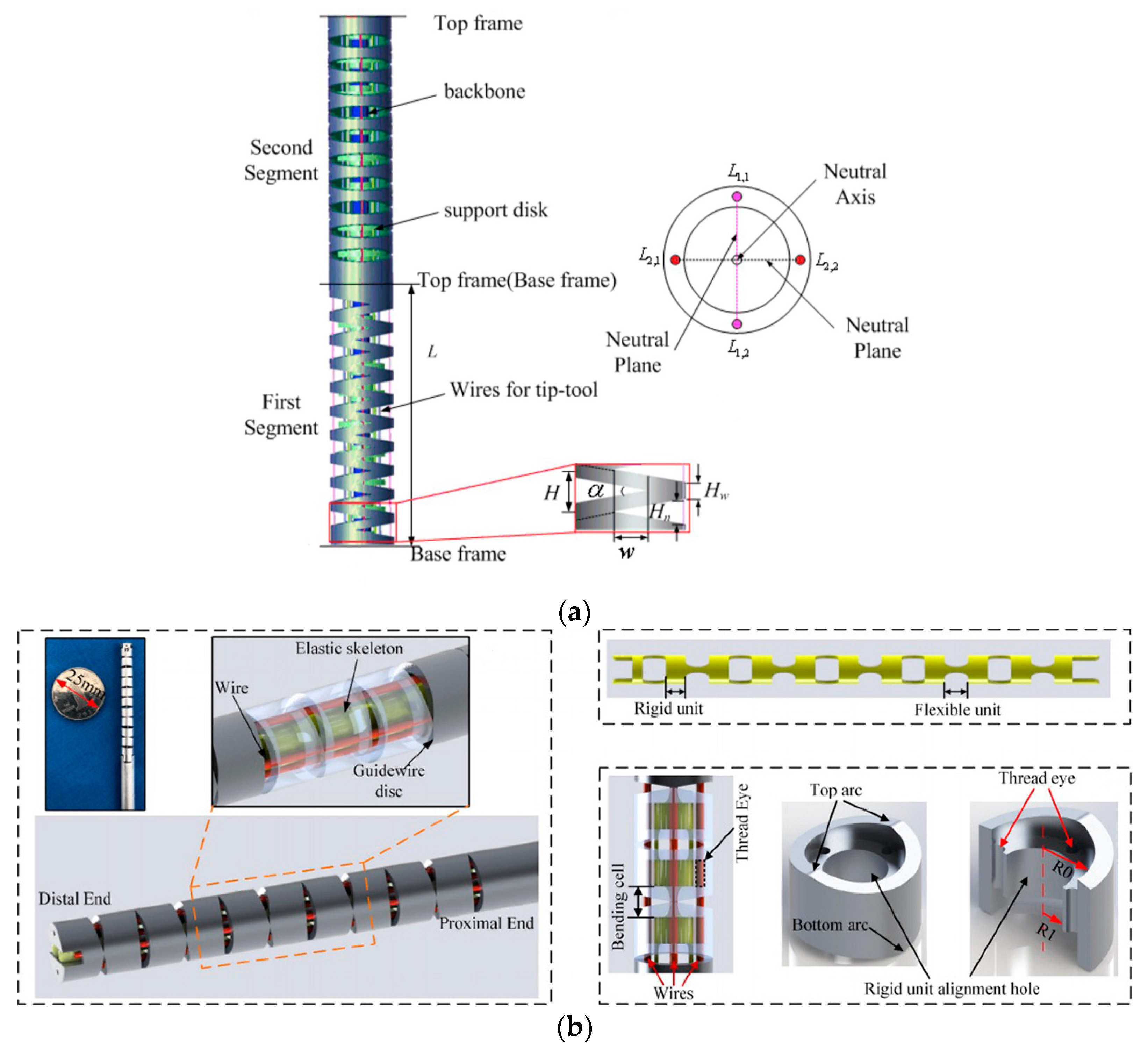
2.1.4. CDCR with Notch Elastic Backbone
2.1.5. CDCR with Extensible Backbone
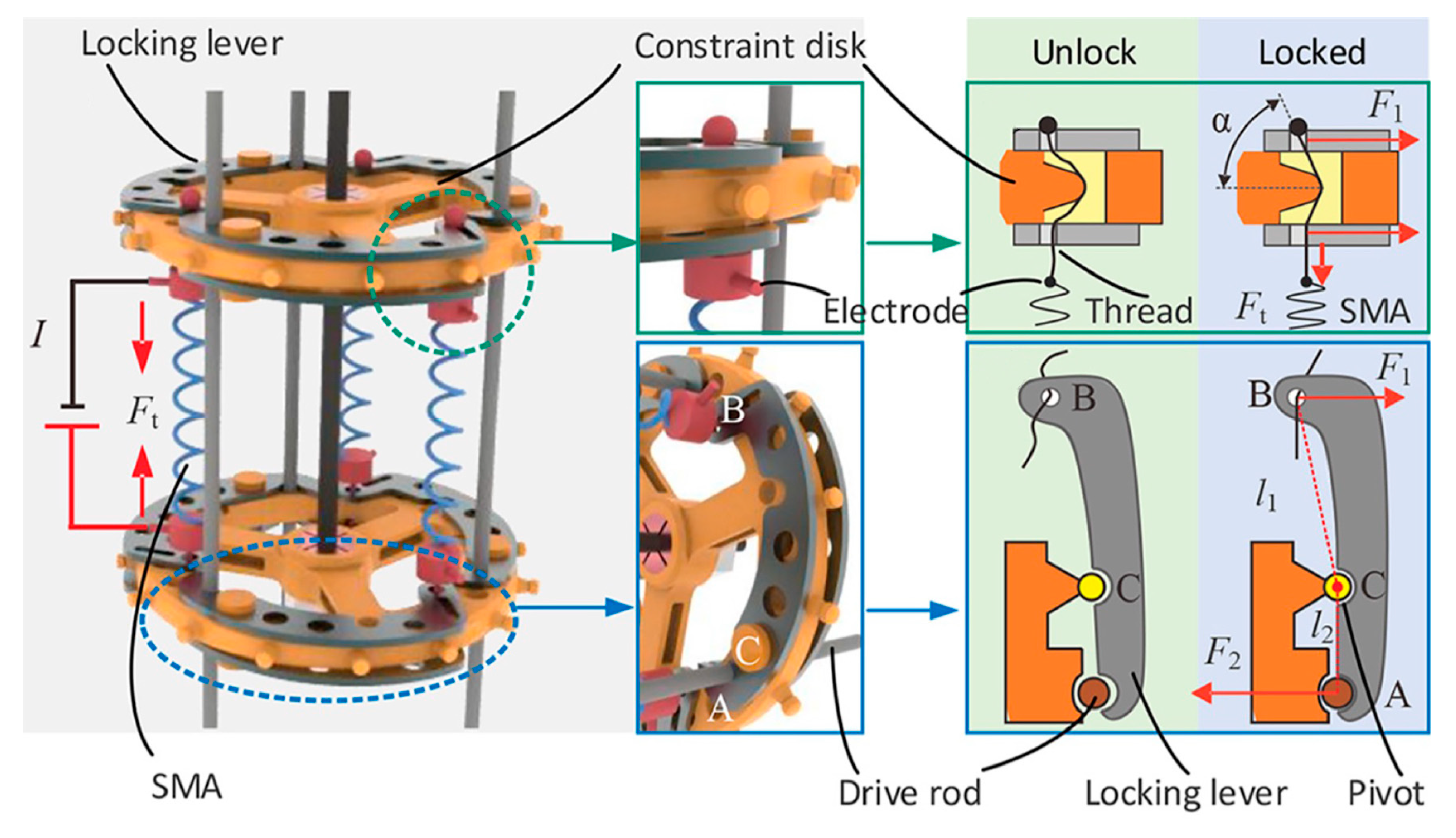
2.1.6. CDCR with Multi-Backbone
2.1.7. Discussions on Backbone Structures
2.2. CDCR Cable Arrangements
2.2.1. Cable Arrangement in Existing CDCRs
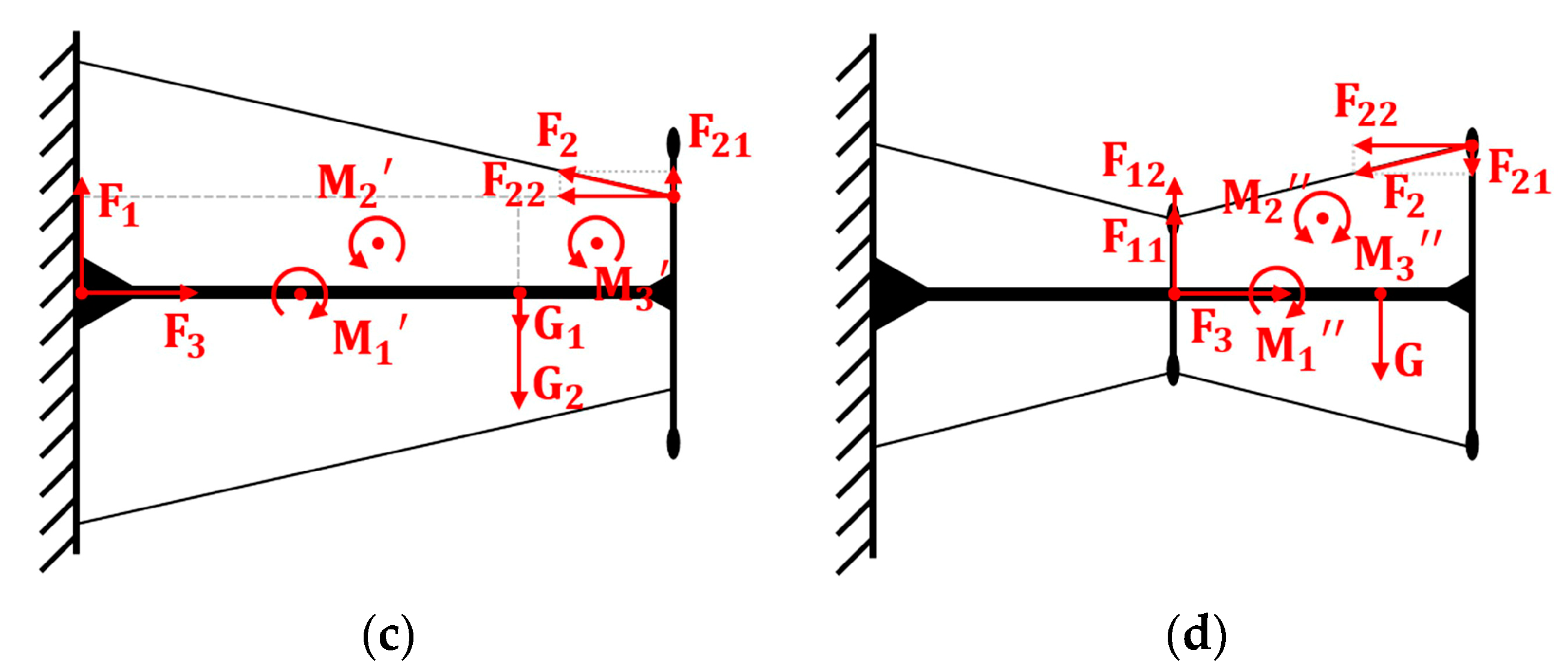
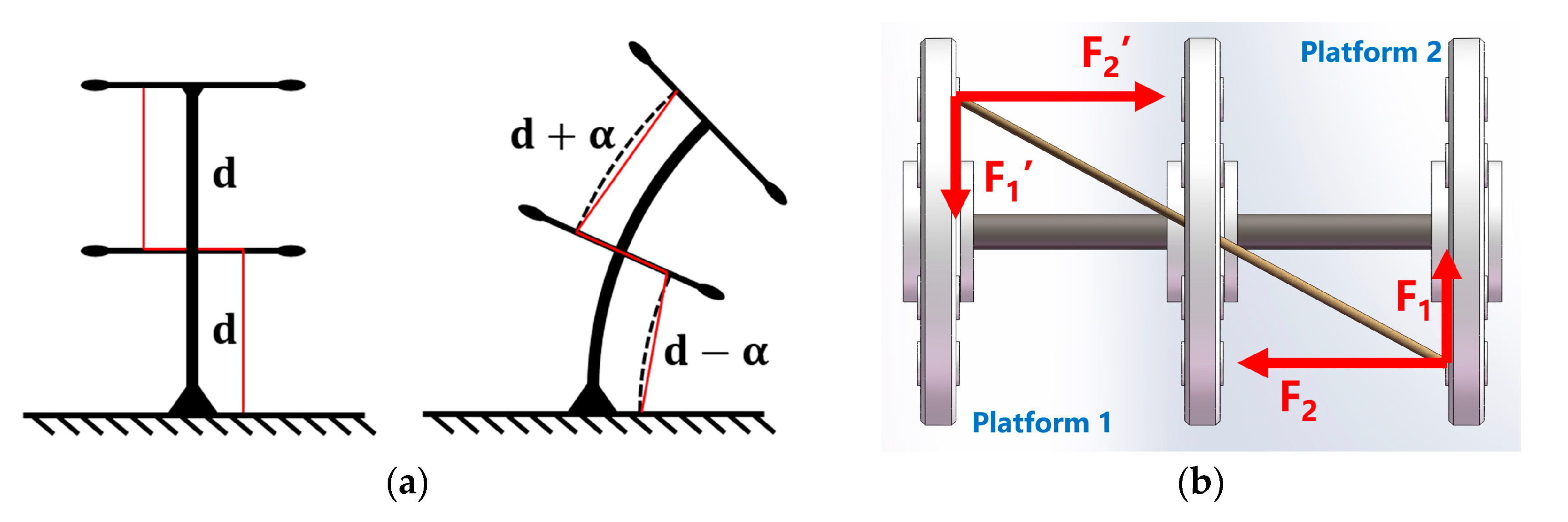
2.2.2. Force Analysis for Different Cable Arrangements
2.2.3. Discussions on Cable Arrangements
3. CDCR Kinematic and Dynamical Modelling
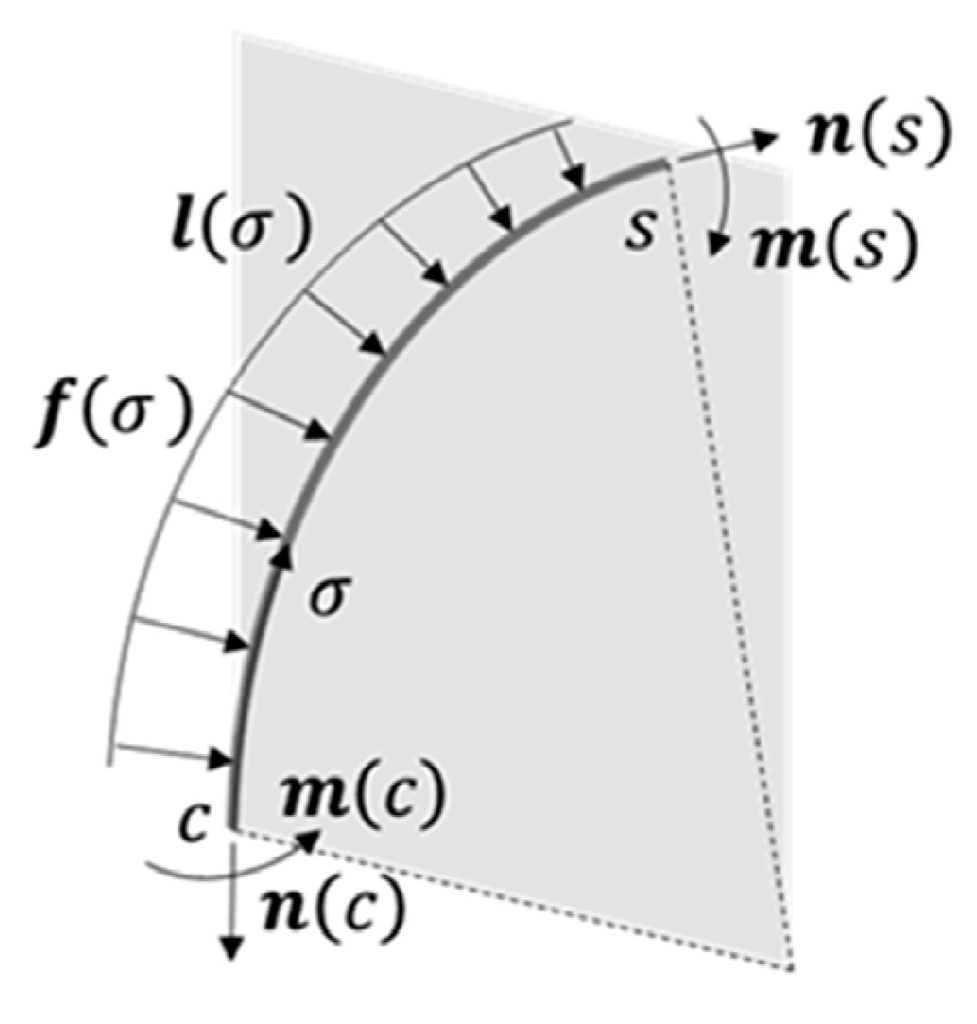
3.1. Backbone Curvature Model
3.2. Kinematics Modelling
3.2.1. Forward Kinematics
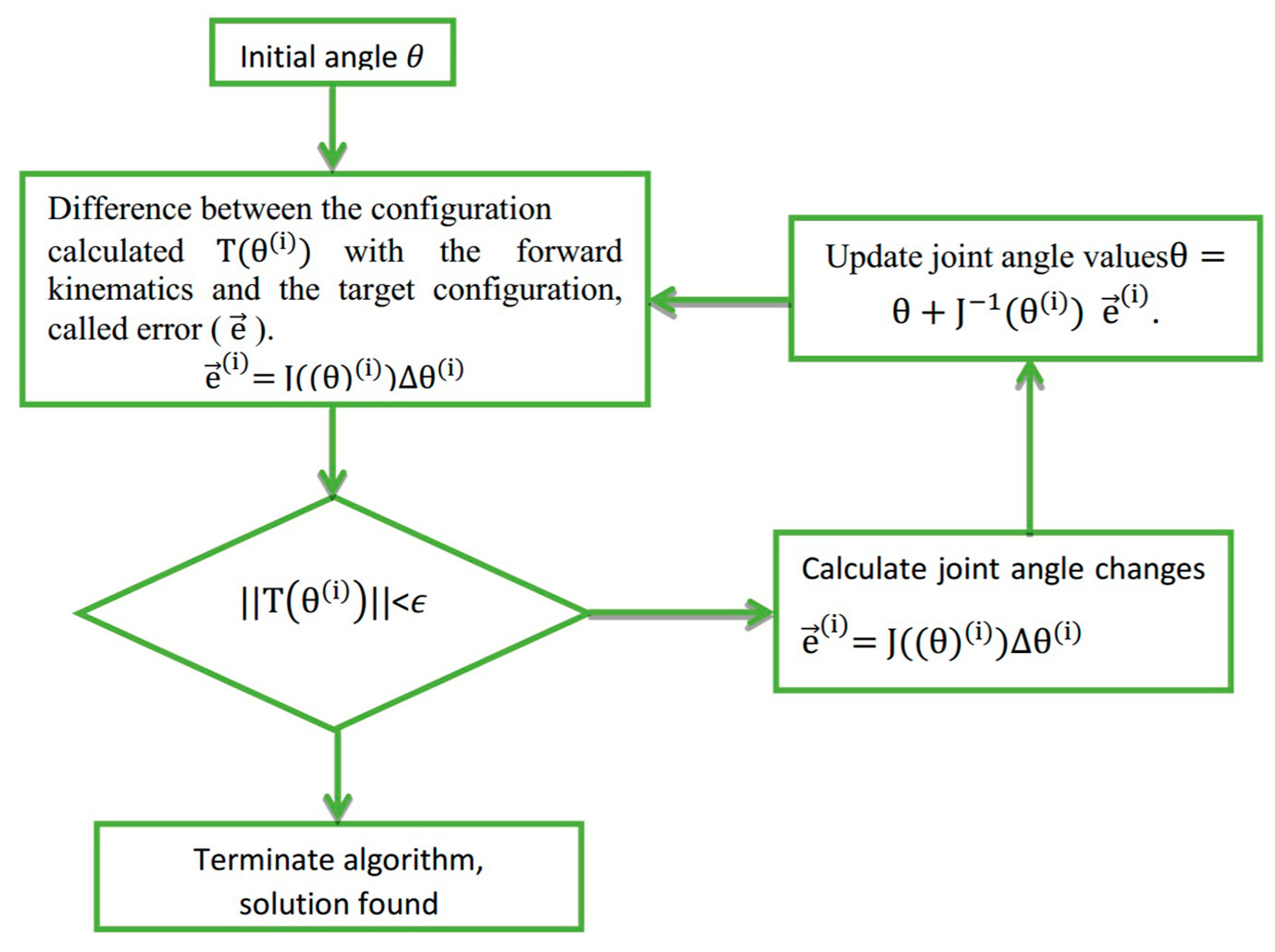
3.2.2. Inverse Kinematics
3.3. Dynamics Modelling
4. CDCR Motion Planning
- Tunnel type: In this scenario, obstacles are densely distributed, and the feasible workspace for the manipulator resembles a pipeline. This configuration is particularly suitable for applications in fields such as pipeline cleaning, endoscopic surgery in the human large intestine, and internal maintenance of aerospace engines, all of which require minimal invasion.
- Scattered obstacle type: Obstacles are dispersed throughout the workspace in the form of objects or surfaces. This situation is found in tasks involving narrow openings (e.g., firefighting through narrow doors and windows), automatic object retrieval from supermarket shelves (unmanned supermarkets), and similar contexts.
- Barrier-free: This scenario involves no obstacles in the workspace, allowing the manipulator to reach its target position freely. It is encountered in settings like underwater environments (cleaning underwater cages), routine tasks (object manipulation, desktop writing, posture teaching), and more.
4.1. Follow-the-Leader (FTL) Method
4.2. Coiling Method
4.3. Sensing-Based Navigation
5. CDCR Motion Control
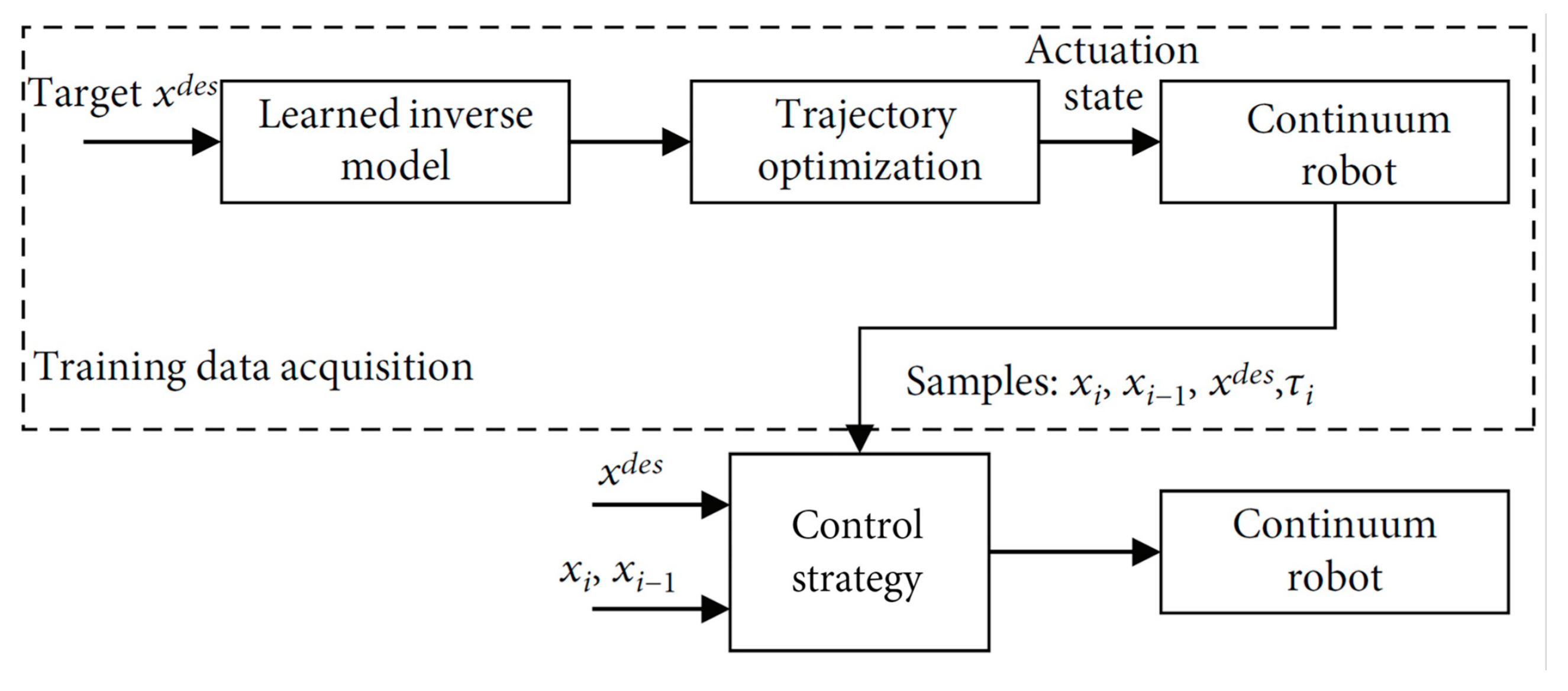
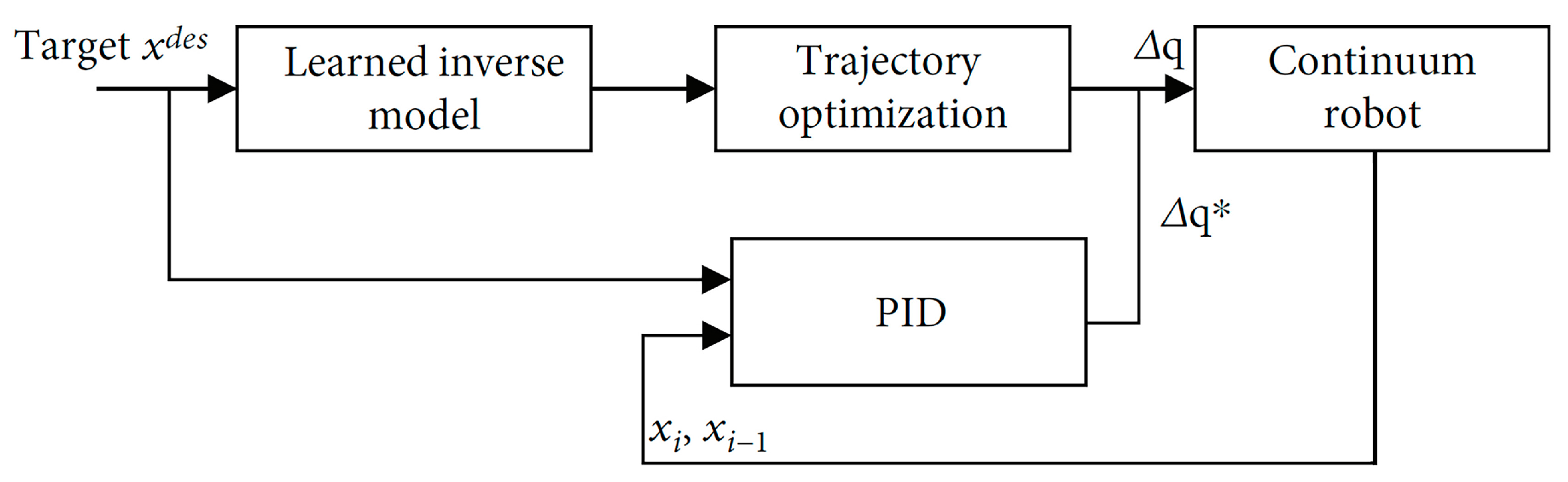
5.1. Model-Based Control
5.2. Model-Free Control
5.3. Hybrid Control
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Villani, V.; Pini, F.; Leali, F.; Secchi, C. Survey on human–robot collaboration in industrial settings: Safety, intuitive interfaces and applications. Mechatronics 2018, 55, 248–266. [Google Scholar] [CrossRef]
- IFR International Federation of Robotics. Executive Summary World Robotics 2016 Industrial Robots; IFR International Federation of Robotics: Frankfurt, Germany, 2016. [Google Scholar]
- Matheson, E.; Minto, R.; Zampieri, E.G.G.; Faccio, M.; Rosati, G. Human–Robot Collaboration in Manufacturing Applications: A Review. Robotics 2019, 8, 100. [Google Scholar] [CrossRef]
- Walker, I.D. Continuous Backbone “Continuum” Robot Manipulators. ISRN Robot. 2013, 2013, 726506. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Zuo, S. Actuation and design innovations in earthworm-inspired soft robots: A review. Front. Bioeng. Biotechnol. 2023, 11, 1088105. [Google Scholar] [CrossRef]
- Tavsan, F.; Sonmez, E. Biomimicry in Furniture Design. Procedia Soc. Behav. Sci. 2015, 197, 2285–2292. [Google Scholar] [CrossRef]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef]
- Anderson, V.C.; Horn, R.C. Tensor Arm Manipulator Design. Trans Asme. 1967, 67, 1–12. [Google Scholar]
- Robinson, G.; Davies, J.B.C. Continuum Robots: A State of the Art. In Proceedings of the IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999. [Google Scholar]
- Kumar Singh, P.; Krishna, C.M. Continuum Arm Robotic Manipulator: A Review. Univers. J. Mech. Eng. 2014, 2, 193–198. [Google Scholar] [CrossRef]
- Hannan, M.W.; Walker, I.D. Analysis and experiments with an elephant’s trunk robot. Adv Robot 2001, 15, 847–858. [Google Scholar] [CrossRef] [PubMed]
- Chirikjian, G.S. Theory and Applications of Hyper-Redundant Robotic Manipulators; California Institute of Technology: Pasadena, CA, USA, 1992. [Google Scholar]
- Hannan, M.W.; Walker, I.D. Kinematics and the Implementation of an Elephant’s Trunk Manipulator and Other Continuum Style Robots. J. Robot. Syst. 2003, 20, 45–63. [Google Scholar] [CrossRef] [PubMed]
- Laschi, C.; Cianchetti, M.; Mazzolai, B.; Margheri, L.; Follador, M.; Dario, P. Soft Robot Arm Inspired by the Octopus. Adv. Robot. 2012, 26, 709–727. [Google Scholar] [CrossRef]
- Kier, W.M.; Smith, K.K. Tongues, tentacles and trunks: The biomechanics of movement in muscular-hydrostats. Zool. J. Linn. Soc. 1985, 83, 307–324. [Google Scholar] [CrossRef]
- Wilson, J.F.; Mahajan, U.; Wainwright, S.A.; Croner, L.J. A continuum model of elephant trunks. J. Biomech. Eng. 1991, 113, 79–84. [Google Scholar] [CrossRef] [PubMed]
- Chopin, R. What is a Continuum Robot. Available online: https://www.zhihu.com/question/452689468/answer/2623665287 (accessed on 12 August 2022).
- Zhang, J.; Fang, Q.; Xiang, P.; Sun, D.; Xue, Y.; Jin, R.; Qiu, K.; Xiong, R.; Wang, Y.; Lu, H. A Survey on Design, Actuation, Modeling, and Control of Continuum Robot. Cyborg Bionic Syst. 2022, 2022, 9754697. [Google Scholar] [CrossRef]
- Hirayama, A.; Ito, K. Development of rescue manipulator to search narrow space for victims. Artif. Life Robot. 2008, 13, 331–335. [Google Scholar] [CrossRef]
- Bishop, C.; Russo, M.; Dong, X.; Axinte, D.A. A Novel Underactuated Continuum Robot With Shape Memory Alloy Clutches. IEEE/ASME Trans. Mechatron. 2022, 27, 5339–5350. [Google Scholar] [CrossRef]
- Mohammad, A.; Russo, M.; Fang, Y.; Dong, X.; Axinte, D.A.; Kell, J. An Efficient Follow-the-Leader Strategy for Continuum Robot Navigation and Coiling. IEEE Robot. Autom. Lett. 2021, 6, 7493–7500. [Google Scholar] [CrossRef]
- Simaan, N.; Xu, K.; Kapoor, A.; Wei, W.; Kazanzides, P.; Flint, P.; Taylor, R. Design and Integration of a Telerobotic System for Minimally Invasive Surgery of the Throat. Int. J. Rob. Res. 2009, 28, 1134–1153. [Google Scholar] [CrossRef]
- Li, Z.; Du, R. Design and Analysis of a Bio-Inspired Wire-Driven Multi-Section Flexible Robot. Int. J. Adv. Robot. Syst. 2013, 10, 209. [Google Scholar] [CrossRef]
- Ahmed, F.; Waqas, M.; Jawed, B.; Soomro, A.M.; Kumar, S.; Hina, A.; Khan, U.; Kim, K.H.; Choi, K.H. Decade of bio-inspired soft robots: A review. Smart Mater. Struct. 2022, 31, 073002. [Google Scholar] [CrossRef]
- Greer, J.D.; Morimoto, T.K.; Okamura, A.M.; Hawkes, E.W. Series pneumatic artificial muscles (sPAMs) and application to a soft continuum robot. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5503–5510. [Google Scholar]
- Farrow, N.; Correll, N. A soft pneumatic actuator that can sense grasp and touch. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 2317–2323. [Google Scholar]
- McMahan, W.; Chitrakaran, V.K.; Csencsits, M.A.; Dawson, D.M.; Walker, I.D.; Jones, B.A.; Pritts, M.B.; Dienno, D.; Grissom, M.D.; Rahn, C.D. Field trials and testing of the OctArm continuum manipulator. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, 2006, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 2336–2341. [Google Scholar]
- Mohd Jani, J.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Zheng, T.; Yang, Y.; Branson, D.T.; Kang, R.; Guglielmino, E.; Cianchetti, M.; Caldwell, D.G.; Yang, G. Control design of shape memory alloy based multi-arm continuum robot inspired by octopus. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 1108–1113. [Google Scholar]
- Mandolino, M.A.; Goergen, Y.; Motzki, P.; Rizzello, G. Design and Characterization of a Fully Integrated Continuum Robot Actuated by Shape Memory Alloy Wires. In Proceedings of the 2022 IEEE 17th International Conference on Advanced Motion Control (AMC), Padova, Italy, 18–20 February 2022; pp. 6–11. [Google Scholar]
- Hu, H. Kinematic Analysis and Simulation for Cable-driven Continuum Robot. J. Mech. Eng. 2010, 46, 1–8. [Google Scholar] [CrossRef]
- Shen, W.; Yang, G.; Zheng, T.; Wang, Y.; Yang, K.; Fang, Z.; Zhang, C. An Integrated Accuracy Enhancement Method for Cable-driven Flexible Continuum Robot. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 1121–1126. [Google Scholar]
- Shen, W.; Yang, G.; Zheng, T.; Wang, Y.; Yang, K.; Fang, Z. An Accuracy Enhancement Method for a Cable-Driven Continuum Robot with a Flexible Backbone. IEEE Access 2020, 8, 37474–37481. [Google Scholar] [CrossRef]
- Walker, I.D.; Hannan, M.W. A novel ‘elephant’s trunk’ robot. In Proceedings of the 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (Cat. No.99TH8399), Atlanta, GA, USA, 19–23 September 1999; pp. 410–415. [Google Scholar]
- Simaan, N. Snake-Like Units Using Flexible Backbones and Actuation Redundancy for Enhanced Miniaturization. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3012–3017. [Google Scholar]
- Zhang, Z.; Yang, G.; Yeo, S.H.; Lim, W.B.; Mustafa, S.K. Design optimization of a cable-driven two-DOF joint module with a flexible backbone. In Proceedings of the 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Montreal, QC, Canada, 6–9 July 2010; pp. 385–390. [Google Scholar]
- Fang, Y.; Lin, H. Structural design and kinematics analysis of the continuum parallel grasping manipulator. J. Beijing Jiaotong Univ. 2019, 43, 9. [Google Scholar]
- Gravagne, I.A.; Walker, I.D. On the kinematics of remotely-actuated continuum robots. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 3, pp. 2544–2550. [Google Scholar]
- Gravagne, I.A.; Walker, I.D. Kinematic transformations for remotely-actuated planar continuum robots. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 19–26. [Google Scholar]
- Gravagne, I.A.; Rahn, C.D.; Walker, I.D. Large Deflection Dynamics and Control for Planar Continuum Robots. IEEE/ASME Trans. Mechatron. 2003, 8, 299–307. [Google Scholar] [CrossRef]
- Rucker, D.C.; Webster Iii, R.J. Statics and Dynamics of Continuum Robots With General Tendon Routing and External Loading. IEEE Trans. Robot. 2011, 27, 1033–1044. [Google Scholar] [CrossRef]
- Rone, W.S.; Ben-Tzvi, P. Continuum Manipulator Statics Based on the Principle of Virtual Work. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; pp. 321–328. [Google Scholar]
- Rone, W.S.; Ben-Tzvi, P. Continuum Robot Dynamics Utilizing the Principle of Virtual Power. IEEE Trans. Robot. 2014, 30, 275–287. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, G.; Yeo, S.H. Inverse kinematics of modular Cable-driven Snake-like Robots with flexible backbones. In Proceedings of the 2011 IEEE 5th International Conference on Robotics, Automation and Mechatronics (RAM), Qingdao, China, 17–19 September 2011; pp. 41–46. [Google Scholar]
- Zhang, Z. Design and Analysis of Cable-driven Snake-like Robot Arm with Flexible Backbone. Doctoral Dissertation, Nanyang Technological University, Singapore, 2014. [Google Scholar]
- Wenlong, Y.; Wei, D.; Zhijiang, D. Mechanics-Based Kinematic Modeling of a Continuum Manipulator. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 5052–5058. [Google Scholar]
- Wang, H.; Wang, X.; Yang, W.; Du, Z. Design and Kinematic Modeling of a Notch Continuum Manipulator for Laryngeal Surgery. Int. J. Control Autom. Syst. 2020, 18, 2966–2973. [Google Scholar] [CrossRef]
- Ba, W.; Dong, X.; Mohammad, A.; Wang, M.; Axinte, D.; Norton, A. Design and Validation of a Novel Fuzzy-Logic-Based Static Feedback Controller for Tendon-Driven Continuum Robots. IEEE/ASME Trans. Mechatron. 2021, 26, 3010–3021. [Google Scholar] [CrossRef]
- Dong, X.; Raffles, M.; Cobos-Guzman, S.; Axinte, D.; Kell, J. A Novel Continuum Robot Using Twin-Pivot Compliant Joints: Design, Modeling, and Validation. J. Mech. Robot. 2016, 8, 021010. [Google Scholar] [CrossRef]
- Wang, M.; Palmer, D.; Dong, X.; Alatorre, D.; Axinte, D.A.; Norton, A. Design and Development of a Slender Dual-Structure Continuum Robot for In-Situ Aeroengine Repair. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 5648–5653. [Google Scholar]
- Mehling, J.S.; Diftler, M.A.; Chu, M.; Valvo, M.C. A Minimally Invasive Tendril Robot for In-Space Inspection. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, BioRob 2006, Pisa, Italy, 20–22 February 2006; pp. 690–695. [Google Scholar]
- Tonapi, M.M.; Godage, I.S.; Vijaykumar, A.M.; Walker, I.D. A novel continuum robotic cable aimed at applications in space. Adv. Robot. 2015, 29, 861–875. [Google Scholar] [CrossRef]
- Tonapi, M.M.; Godage, I.; Walker, I.D. Design, modeling and performance evaluation of a long and slim continuum robotic cable. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2852–2859. [Google Scholar]
- Nguyen, T.-D.; Burgner-Kahrs, J. A tendon-driven continuum robot with extensible sections. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 2130–2135. [Google Scholar]
- Neumann, M.; Burgner-Kahrs, J. Considerations for follow-the-leader motion of extensible tendon-driven continuum robots. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 917–923. [Google Scholar]
- Simaan, N.; Taylor, R. A Dexterous System for Laryngeal Surgery Multi-Backbone Bending Snakelike Slaves for Teleoperated Dexterous Surgical Tool Manipulation. In Proceedings of the IEEE International Conference on Robotics & Automation, New Orleans, LA, USA, 26 April–1 May 2004. [Google Scholar]
- Xu, K.; Simaan, N. An Investigation of the Intrinsic Force Sensing Capabilities of Continuum Robots. IEEE Trans. Robot. 2008, 24, 576–587. [Google Scholar] [CrossRef]
- Yang, C.; Geng, S.; Walker, I.; Branson, D.T.; Liu, J.; Dai, J.S.; Kang, R. Geometric constraint-based modeling and analysis of a novel continuum robot with Shape Memory Alloy initiated variable stiffness. Int. J. Robot. Res. 2020, 39, 1620–1634. [Google Scholar] [CrossRef]
- Li, M.; Kang, R.; Geng, S.; Guglielmino, E. Design and control of a tendon-driven continuum robot. Trans. Inst. Meas. Control 2017, 40, 3263–3272. [Google Scholar] [CrossRef]
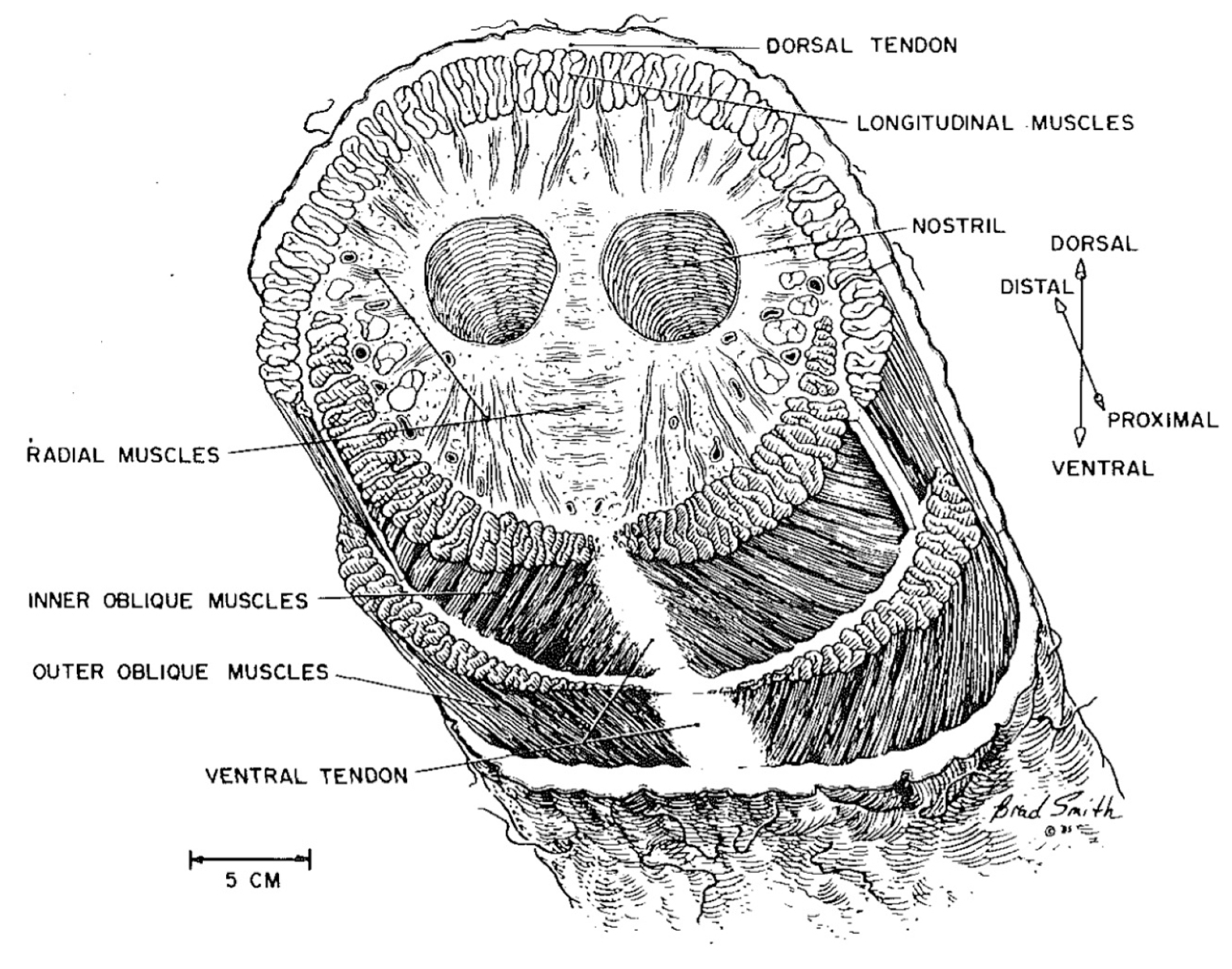
- Boas, J.E.V.; Paulli, S. The Elephant’s Head: Studies in the Comparative Anatomy of the Organs of the Head of the Indian Elephant and Other Mammals; Carlsberg-Fund: Copenhagen, Denmark, 1908. [Google Scholar] [CrossRef]
- Webster, R.J.; Jones, B.A. Design and Kinematic Modeling of Constant Curvature Continuum Robots: A Review. Int. J. Robot. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]
- Kim, J.S.; Chirikjian, G.S. Conformational Analysis of Stiff Chiral Polymers with End-Constraints. Mol. Simul. 2006, 32, 1139–1154. [Google Scholar] [CrossRef] [PubMed]
- Janabi-Sharifi, F.; Jalali, A.; Walker, I.D. Cosserat Rod-Based Dynamic Modeling of Tendon-Driven Continuum Robots: A Tutorial. IEEE Access 2021, 9, 68703–68719. [Google Scholar] [CrossRef]
- Jones, B.A.; Walker, I.D. Kinematics for multisection continuum robots. IEEE Trans. Robot. 2006, 22, 43–55. [Google Scholar] [CrossRef]
- Murray, R.M.; Li, Z.; Sastry, S.S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Sears, P.; Dupont, P.E. A Steerable Needle Technology Using Curved Concentric Tubes. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 2850–2856. [Google Scholar]
- Webster, R.J.; Kim, J.S.; Cowan, N.J.; Chirikjian, G.S.; Okamura, A.M. Nonholonomic Modeling of Needle Steering. Int. J. Robot. Res. 2006, 25, 509–525. [Google Scholar] [CrossRef]
- Webster, R.J.; Romano, J.M.; Cowan, N.J. Mechanics of Precurved-Tube Continuum Robots. IEEE Trans. Robot. 2009, 25, 67–78. [Google Scholar] [CrossRef]
- Jing, W.; Tao, P.Y.; Yang, G.; Shimada, K. Calibration of industry robots with consideration of loading effects using Product-Of-Exponential (POE) and Gaussian Process (GP). In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4380–4385. [Google Scholar]
- Shen, W.; Yang, G.; Wang, Y.; Fang, Z.; Li, F.; Wang, H. Design and Performance Analysis of a Cable-Driven Continuum Robotic Joint Module. In Proceedings of the 2021 3rd International Symposium on Robotics & Intelligent Manufacturing Technology (ISRIMT), Changzhou, China, 24–26 September 2021; pp. 427–433. [Google Scholar]
- Dulęba, I.; Opałka, M. A comparison of Jacobian-based methods of inverse kinematics for serial robot manipulators. Int. J. Appl. Math. Comput. Sci. 2013, 23, 373–382. [Google Scholar] [CrossRef]
- Jones, B.A.; Walker, I.D. A New Approach to Jacobian Formulation for a Class of Multi-Section Continuum Robots. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 3268–3273. [Google Scholar]
- Sears, P.; Dupont, P.E. Inverse Kinematics of Concentric Tube Steerable Needles. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1887–1892. [Google Scholar]
- Webster, R.J.; Swensen, J.P.; Romano, J.M.; Cowan, N.J. Closed-Form Differential Kinematics for Concentric-Tube Continuum Robots with Application to Visual Servoing. In Proceedings of the International Symposium on Experimental Robotics, Athens, Greece, 13–16 July 2008. [Google Scholar]
- Nakamura, Y. Advanced Robotics: Redundancy and Optimization; Addison-Wesley Longman Publishing Co., Inc.: North York, ON, Canada, 1990. [Google Scholar]
- Zhao, J.; Xu, T.; Fang, Q.; Xie, Y.; Zhu, Y. A Synthetic Inverse Kinematic Algorithm for 7-DOF Redundant Manipulator. In Proceedings of the 2018 IEEE International Conference on Real-time Computing and Robotics (RCAR), Kandima, Maldives, 1–5 August 2018; pp. 112–117. [Google Scholar]
- Craig, J.J. Introduction to Robotics: Mechanics and Control. In Introduction to Robotics: Mechanics and Control; Pearson: Bloomington, MN, USA, 1986. [Google Scholar]
- Farzan, S.; DeSouza, G.N. From D-H to inverse kinematics: A fast numerical solution for general robotic manipulators using parallel processing. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2507–2513. [Google Scholar]
- Wu, H.; Yu, J.; Pan, J.; Pei, X. A New Approach for Solving the Inverse Kinematics of Continuum Robot Based on Piecewise Constant Curvature Model. Res. Sq. 2021. [Google Scholar] [CrossRef]
- Chiaverini, S.; Siciliano, B.; Egeland, O. Review of the damped least-squares inverse kinematics with experiments on an industrial robot manipulator. IEEE Trans. Control. Syst. Technol. 1994, 2, 123–134. [Google Scholar] [CrossRef]
- Neppalli, S.; Csencsits, M.A.; Jones, B.A.; Walker, I.D. Closed-Form Inverse Kinematics for Continuum Manipulators. Adv. Robot. 2009, 23, 2077–2091. [Google Scholar] [CrossRef]
- Bieze, T.M.; Largilliere, F.; Kruszewski, A.; Zhang, Z.; Merzouki, R.; Duriez, C. Finite Element Method-Based Kinematics and Closed-Loop Control of Soft, Continuum Manipulators. Soft Robot. 2018, 5, 348–364. [Google Scholar] [CrossRef] [PubMed]
- Puglisi, L.J.; Saltaren, R.; Garcia, C.; Cardenas, P.; Moreno, H. Implementation of a generic constraint function to solve the direct kinematics of parallel manipulators using Newton-Raphson approach. J. Control Eng. Appl. Inform. 2017, 19, 71–79. [Google Scholar]
- Zhang, Z.Y. The Research on the Quick Method for 6-DOF Parallel Robot Forward Kinematics. Adv. Mater. Res. 2012, 466–467, 849–853. [Google Scholar] [CrossRef]
- Jain, T.; Jain, J.; Roy, D. Joint space redundancy resolution of serial link manipulator: An inverse kinematics and continuum structure numerical approach. Mater. Today Proc. 2020, 38, 423–431. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, Z.; Liu, X.; Chen, X.; Jin, Y.; You, X.; Chen, X. A two-level approach for solving the inverse kinematics of an extensible soft arm considering viscoelastic behavior. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 6127–6133. [Google Scholar]
- Melingui, A.; Merzouki, R.; Mbede, J.B.; Escande, C.; Benoudjit, N. Neural Networks based approach for inverse kinematic modeling of a Compact Bionic Handling Assistant trunk. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 1239–1244. [Google Scholar]
- Thuruthel, T.G.; Shih, B.; Laschi, C.; Tolley, M.T. Soft robot perception using embedded soft sensors and recurrent neural networks. Sci. Robot. 2019, 4, eaav1488. [Google Scholar] [CrossRef]
- Chirikjian, G.S. Hyper-redundant manipulator dynamics: A continuum approximation. Adv. Robot. 2012, 9, 217–243. [Google Scholar] [CrossRef]
- Antman, S.S. Nonlinear Problems of Elasticity; Springer Science Business Media, LLC: Berlin/Heidelberg, Germany, 1994; Volume 107, p. 698. [Google Scholar]
- Renda, F.; Giorelli, M.; Calisti, M.; Cianchetti, M.; Laschi, C. Dynamic Model of a Multibending Soft Robot Arm Driven by Cables. IEEE Trans. Robot. 2014, 30, 1109–1122. [Google Scholar] [CrossRef]
- Till, J.; Aloi, V.; Rucker, C. Real-time dynamics of soft and continuum robots based on Cosserat rod models. Int. J. Robot. Res. 2019, 38, 723–746. [Google Scholar] [CrossRef]
- Doroudchi, A.; Berman, S. Configuration Tracking for Soft Continuum Robotic Arms Using Inverse Dynamic Control of a Cosserat Rod Model. In Proceedings of the 2021 IEEE 4th International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 12–16 April 2021; pp. 207–214. [Google Scholar]
- Rucker, D.C.; Jones, B.A.; Webster, R.J. A model for concentric tube continuum robots under applied wrenches. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 1047–1052. [Google Scholar]
- Russo, M.; Sadati, S.M.H.; Dong, X.; Mohammad, A.; Walker, I.D.; Bergeles, C.; Xu, K.; Axinte, D.A. Continuum Robots: An Overview. Adv. Intell. Syst. 2023, 5, 2200367. [Google Scholar] [CrossRef]
- Falkenhahn, V.; Mahl, T.; Hildebrandt, A.; Neumann, R.; Sawodny, O. Dynamic Modeling of Bellows-Actuated Continuum Robots Using the Euler–Lagrange Formalism. IEEE Trans. Robot. 2015, 31, 1483–1496. [Google Scholar] [CrossRef]
- Till, J.; Aloi, V.A.; Riojas, K.E.; Anderson, P.L.; Webster III, R.J.; Rucker, C. A Dynamic Model for Concentric Tube Robots. IEEE Trans. Robot. 2020, 36, 1704–1718. [Google Scholar] [CrossRef] [PubMed]
- Mochiyama, H.; Suzuki, T. Dynamical modelling of a hyper-flexible manipulator. In Proceedings of the 41st SICE Annual Conference, SICE 2002, Osaka, Japan, 5–7 August 2002; Volume 3, pp. 1505–1510. [Google Scholar]
- Tatlicioglu, E.; Walker, I.D.; Dawson, D.M. Dynamic Modelling for Planar Extensible Continuum Robot Manipulators. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1357–1362. [Google Scholar]
- Tatlicioglu, E.; Walker, I.D.; Dawson, D.M. New dynamic models for planar extensible continuum robot manipulators. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1485–1490. [Google Scholar]
- Godage, I.; Medrano-Cerda, G.A.; Branson, D.T.; Guglielmino, E.; Caldwell, D.G. Dynamics for variable length multisection continuum arms. Int. J. Robot. Res. 2016, 35, 695–722. [Google Scholar] [CrossRef]
- Gallot, G.; Ibrahim, O.; Khalil, W. Dynamic Modeling and simulation of a 3-D Hybrid structure Eel-Like Robot. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 1486–1491. [Google Scholar]
- Boyer, F.; Lebastard, V.; Candelier, F.; Renda, F. Dynamics of Continuum and Soft Robots: A Strain Parameterization Based Approach. IEEE Trans. Robot. 2021, 37, 847–863. [Google Scholar] [CrossRef]
- Caasenbrood, B.; Pogromsky, A.; Nijmeijer, H. Control-Oriented Models for Hyperelastic Soft Robots Through Differential Geometry of Curves. Soft Robot. 2023, 10, 129–148. [Google Scholar] [CrossRef]
- Della Santina, C.; Katzschmann, R.K.; Bicchi, A.; Rus, D. Model-based dynamic feedback control of a planar soft robot: Trajectory tracking and interaction with the environment. Int. J. Robot. Res. 2020, 39, 490–513. [Google Scholar] [CrossRef]
- Godage, I.; Branson, D.T.; Guglielmino, E.; Medrano-Cerda, G.A.; Caldwell, D.G. Dynamics for biomimetic continuum arms: A modal approach. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011; pp. 104–109. [Google Scholar]
- Mustaza, S.M.; Elsayed, Y.; Lekakou, C.; Saaj, C.; Fras, J. Dynamic Modeling of Fiber-Reinforced Soft Manipulator: A Visco-Hyperelastic Material-Based Continuum Mechanics Approach. Soft Robot. 2019, 6, 305–317. [Google Scholar] [CrossRef]
- Sadati, S.; Naghibi, S.E.; Shiva, A.; Michael, B.; Renson, L.; Howard, M.J.; Rucker, C.; Althoefer, K.; Nanayakkara, T.; Zschaler, S.; et al. TMTDyn: A Matlab package for modeling and control of hybrid rigid–continuum robots based on discretized lumped systems and reduced-order models. Int. J. Robot. Res. 2020, 40, 296–347. [Google Scholar] [CrossRef]
- Wisse, M.; Van der Linde, R.Q. Delft pneumatic bipeds; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 34. [Google Scholar]
- Sadati, S.M.H.; Naghibi, S.E.; Walker, I.D.; Althoefer, K.; Nanayakkara, T. Control Space Reduction and Real-Time Accurate Modeling of Continuum Manipulators Using Ritz and Ritz–Galerkin Methods. IEEE Robot. Autom. Lett. 2018, 3, 328–335. [Google Scholar] [CrossRef]
- Sadati, S.M.H.; Mitros, Z.; Henry, R.; Zeng, L.; Cruz, L.d.; Bergeles, C. Real-Time Dynamics of Concentric Tube Robots With Reduced-Order Kinematics Based on Shape Interpolation. IEEE Robot. Autom. Lett. 2022, 7, 5671–5678. [Google Scholar] [CrossRef]
- Lynch, K.M.; Park, F.C. Modern Robotics: Mechanics, Planning, and Control; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Li, F. Research on Motion Planning of Continuous Robot Operation. Master’s Thesis, North China University of Technology, Beijing, China, 2020. [Google Scholar]
- Choset, H.; Henning, W. A Follow-the-Leader Approach to Serpentine Robot Motion Planning. J. Aerosp. Eng. 1999, 12, 65–73. [Google Scholar] [CrossRef]
- Kang, B.; Kojcev, R.; Sinibaldi, E. The First Interlaced Continuum Robot, Devised to Intrinsically Follow the Leader. PLoS ONE 2016, 11, e0150278. [Google Scholar] [CrossRef] [PubMed]
- Amanov, E.; Nguyen, T.-D.; Burgner-Kahrs, J. Tendon-driven continuum robots with extensible sections—A model-based evaluation of path-following motions. Int. J. Robot. Res. 2019, 40, 7–23. [Google Scholar] [CrossRef]
- Gilbert, H.B.; Neimat, J.; Webster, R.J., 3rd. Concentric Tube Robots as Steerable Needles: Achieving Follow-the-Leader Deployment. IEEE Trans. Robot. 2015, 31, 246–258. [Google Scholar] [CrossRef]
- Isnard, S.; Silk, W.K. Moving with climbing plants from Charles Darwin’s time into the 21st century. Am. J. Bot. 2009, 96, 1205–1221. [Google Scholar] [CrossRef]
- Dottore, E.D.; Mondini, A.; Sadeghi, A.; Mattoli, V.; Mazzolai, B. Circumnutations as a penetration strategy in a plant-root-inspired robot. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4722–4728. [Google Scholar]
- Wooten, M.; Walker, I. Vine-Inspired Continuum Tendril Robots and Circumnutations. Robotics 2018, 7, 58. [Google Scholar] [CrossRef]
- Mazzolai, B.; Tramacere, F.; Fiorello, I.; Margheri, L. The Bio-Engineering Approach for Plant Investigations and Growing Robots. A Mini-Review. Front. Robot. AI 2020, 7, 573014. [Google Scholar] [CrossRef]
- Dottore, E.D.; Sadeghi, A.; Mondini, A.; Mazzolai, B. Continuous Growth in Plant-Inspired Robots Through 3D Additive Manufacturing. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1–7. [Google Scholar]
- Wooten, M.B.; Frazelle, C.G.; Walker, I.D.; Kapadia, A.D.; Lee, J.H. Exploration and Inspection with Vine-Inspired Continuum Robots. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1–5. [Google Scholar]
- Sadeghi, A.; Mondini, A.; Del Dottore, E.; Mattoli, V.; Beccai, L.; Taccola, S.; Lucarotti, C.; Totaro, M.; Mazzolai, B. A plant-inspired robot with soft differential bending capabilities. Bioinspir. Biomim. 2016, 12, 015001. [Google Scholar] [CrossRef]
- Gallentine, J.; Wooten, M.B.; Thielen, M.; Walker, I.D.; Speck, T.; Niklas, K. Searching and Intertwining: Climbing Plants and GrowBots. Front. Robot. AI 2020, 7, 118. [Google Scholar] [CrossRef]
- El-Hussieny, H.; Mehmood, U.; Mehdi, S.Z.; Jeong, S.-G.; Usman, M.; Hawkes, E.W.; Okarnura, A.M.; Ryu, J.-H. Development and Evaluation of an Intuitive Flexible Interface for Teleoperating Soft Growing Robots. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4995–5002. [Google Scholar]
- Vidoni, R.; Mimmo, T.; Pandolfi, C. Tendril-Based Climbing Plants to Model, Simulate and Create Bio-Inspired Robotic Systems. J. Bionic Eng. 2015, 12, 250–262. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, J.; Hunter, I.W. Modular continuum robotic endoscope design and path planning. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 5393–5400. [Google Scholar]
- Palmer, D.; Axinte, D. Active uncoiling and feeding of a continuum arm robot. Robot. Comput. -Integr. Manuf. 2019, 56, 107–116. [Google Scholar] [CrossRef]
- Moradi Dalvand, M.; Nahavandi, S.; Howe, R.D. Fast vision-based catheter 3D reconstruction. Phys. Med. Biol. 2016, 61, 5128–5148. [Google Scholar] [CrossRef]
- Mahl, T.; Hildebrandt, A.; Sawodny, O. A Variable Curvature Continuum Kinematics for Kinematic Control of the Bionic Handling Assistant. IEEE Trans. Robot. 2014, 30, 935–949. [Google Scholar] [CrossRef]
- Alatorre, D.; Axinte, D.; Rabani, A. Continuum Robot Proprioception: The Ionic Liquid Approach. IEEE Trans. Robot. 2022, 38, 526–535. [Google Scholar] [CrossRef]
- Ho, M.; Kim, Y.; Cheng, S.S.; Gullapalli, R.; Desai, J.P. Design, development, and evaluation of an MRI-guided SMA spring-actuated neurosurgical robot. Int. J. Rob. Res. 2015, 34, 1147–1163. [Google Scholar] [CrossRef]
- Guo, H.; Ju, F.; Cao, Y.; Qi, F.; Bai, D.; Wang, Y.; Chen, B. Continuum robot shape estimation using permanent magnets and magnetic sensors. Sens. Actuators A Phys. 2019, 285, 519–530. [Google Scholar] [CrossRef]
- Roesthuis, R.J.; Misra, S. Steering of Multisegment Continuum Manipulators Using Rigid-Link Modeling and FBG-Based Shape Sensing. IEEE Trans. Robot. 2016, 32, 372–382. [Google Scholar] [CrossRef]
- Rahman, N.; Deaton, N.; Sheng, J.; Cheng, S.S.; Desai, J.P. Modular FBG Bending Sensor for Continuum Neurosurgical Robot. IEEE Robot. Autom. Lett. 2019, 4, 1424–1430. [Google Scholar] [CrossRef] [PubMed]
- Alambeigi, F.; Pedram, S.A.; Speyer, J.L.; Rosen, J.; Iordachita, I.; Taylor, R.H.; Armand, M. SCADE: Simultaneous Sensor Calibration and Deformation Estimation of FBG-Equipped Unmodeled Continuum Manipulators. IEEE Trans. Robot. 2020, 36, 222–239. [Google Scholar] [CrossRef] [PubMed]
- Khan, F.; Denasi, A.; Barrera, D.; Madrigal, J.; Sales, S.; Misra, S. Multi-Core Optical Fibers with Bragg Gratings as Shape Sensor for Flexible Medical Instruments. IEEE Sens. J. 2019, 19, 5878–5884. [Google Scholar] [CrossRef]
- Bai, H.; Li, S.; Barreiros, J.A.; Tu, Y.; Pollock, C.R.; Shepherd, R.F. Stretchable distributed fiber-optic sensors. Science 2020, 370, 848–852. [Google Scholar] [CrossRef] [PubMed]
- Hofer, M.; Sferrazza, C.; D’Andrea, R. A Vision-Based Sensing Approach for a Spherical Soft Robotic Arm. Front. Robot. AI 2020, 8, 630935. [Google Scholar] [CrossRef] [PubMed]
- Poignonec, T.; Zanne, P.; Rosa, B.; Nageotte, F. Towards In Situ Backlash Estimation of Continuum Robots Using an Endoscopic Camera. IEEE Robot. Autom. Lett. 2020, 5, 4788–4795. [Google Scholar] [CrossRef]
- Yao, S.; Zhu, Y. Wearable multifunctional sensors using printed stretchable conductors made of silver nanowires. Nanoscale 2014, 6, 2345–2352. [Google Scholar] [CrossRef] [PubMed]
- Shintake, J.; Piskarev, Y.; Jeong, S.H.; Floreano, D. Ultrastretchable Strain Sensors Using Carbon Black-Filled Elastomer Composites and Comparison of Capacitive Versus Resistive Sensors. Adv. Mater. Technol. 2017, 3, 1700284. [Google Scholar] [CrossRef]
- Cheng, S.; Narang, Y.S.; Yang, C.; Suo, Z.; Howe, R.D. Stick-On Large-Strain Sensors for Soft Robots. Adv. Mater. Interfaces 2019, 6, 1900985. [Google Scholar] [CrossRef]
- Truby, R.L.; Santina, C.D.; Rus, D. Distributed Proprioception of 3D Configuration in Soft, Sensorized Robots via Deep Learning. IEEE Robot. Autom. Lett. 2020, 5, 3299–3306. [Google Scholar] [CrossRef]
- Scimeca, L.; Hughes, J.; Maiolino, P.; Iida, F. Model-Free Soft-Structure Reconstruction for Proprioception Using Tactile Arrays. IEEE Robot. Autom. Lett. 2019, 4, 2479–2484. [Google Scholar] [CrossRef]
- Rucker, D.C.; Webster, R.J. Deflection-based force sensing for continuum robots: A probabilistic approach. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 3764–3769. [Google Scholar]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. Int. J. Robot. Res. 1985, 5, 90–98. [Google Scholar] [CrossRef]
- Ha, J.; Dupont, P.E. Designing Stable Concentric Tube Robots Using Piecewise Straight Tubes. IEEE Robot. Autom. Lett. 2017, 2, 298–304. [Google Scholar] [CrossRef]
- Riojas, K.E.; Hendrick, R.J.; Webster, R.J., 3rd. Can Elastic Instability be Beneficial in Concentric Tube Robots? IEEE Robot. Autom. Lett. 2018, 3, 1624–1630. [Google Scholar] [CrossRef]
- Della Santina, C.; Duriez, C.; Rus, D. Model-Based Control of Soft Robots: A Survey of the State of the Art and Open Challenges. IEEE Control Syst. 2021, 43, 30–65. [Google Scholar] [CrossRef]
- Chikhaoui, M.T.; Burgner-Kahrs, J. Control of continuum robots for medical applications: State of the art. In Proceedings of the ACTUATOR 2018, 16th International Conference on New Actuators, Bremen, Germany, 25–27 June 2018; pp. 1–11. [Google Scholar]
- Penning, R.S.; Jung, J.; Borgstadt, J.A.; Ferrier, N.J.; Zinn, M.R. Towards closed loop control of a continuum robotic manipulator for medical applications. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4822–4827. [Google Scholar]
- Chen, G.; Pham, M.T.; Redarce, T. Sensor-based guidance control of a continuum robot for a semi-autonomous colonoscopy. Robot. Auton. Syst. 2009, 57, 712–722. [Google Scholar] [CrossRef]
- Zhao, Q.; Lai, J.; Huang, K.; Hu, X.; Chu, H.K. Shape Estimation and Control of a Soft Continuum Robot Under External Payloads. IEEE/ASME Trans. Mechatron. 2022, 27, 2511–2522. [Google Scholar] [CrossRef]
- Croom, J.M.; Rucker, D.C.; Romano, J.M.; Webster, R.J. Visual sensing of continuum robot shape using self-organizing maps. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4591–4596. [Google Scholar]
- Norouzi-Ghazbi, S.; Janabi-Sharifi, F. A Switching Image-Based Visual Servoing Method for Cooperative Continuum Robots. J. Intell. Robot. Syst. 2021, 103, 42. [Google Scholar] [CrossRef]
- George Thuruthel, T.; Ansari, Y.; Falotico, E.; Laschi, C. Control Strategies for Soft Robotic Manipulators: A Survey. Soft Robot. 2018, 5, 149–163. [Google Scholar] [CrossRef]
- Campisano, F.; Caló, S.; Remirez, A.A.; Chandler, J.H.; Obstein, K.L.; Webster, R.J.; Valdastri, P. Closed-loop control of soft continuum manipulators under tip follower actuation. Int. J. Robot. Res. 2021, 40, 923–938. [Google Scholar] [CrossRef]
- Goldman, R.E.; Bajo, A.; Simaan, N. Compliant motion control for continuum robots with intrinsic actuation sensing. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1126–1132. [Google Scholar]
- Xu, K.; Simaan, N. Actuation compensation for flexible surgical snake-like robots with redundant remote actuation. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, 2006, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 4148–4154. [Google Scholar]
- Dong, Z.; Wang, X.; Fang, G.; He, Z.; Ho, J.D.-L.; Cheung, C.-L.; Tang, W.L.; Xie, X.; Liang, L.; Chang, H.-C.; et al. Shape Tracking and Feedback Control of Cardiac Catheter Using MRI-Guided Robotic Platform—Validation with Pulmonary Vein Isolation Simulator in MRI. IEEE Trans. Robot. 2022, 38, 2781–2798. [Google Scholar] [CrossRef]
- Edelmann, J.; Petruska, A.J.; Nelson, B.J. Magnetic control of continuum devices. Int. J. Robot. Res. 2017, 36, 68–85. [Google Scholar] [CrossRef]
- Mbakop, S.; Tagne, G.; Frouin, M.-H.; Achille, M.; Merzouki, R. Inverse Dynamics Model-Based Shape Control of Soft Continuum Finger Robot Using Parametric Curve. IEEE Robot. Autom. Lett. 2021, 6, 8053–8060. [Google Scholar] [CrossRef]
- Xu, R.; Asadian, A.; Naidu, A.S.; Patel, R.V. Position control of concentric-tube continuum robots using a modified Jacobian-based approach. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 5813–5818. [Google Scholar]
- Yip, M.C.; Camarillo, D.B. Model-Less Feedback Control of Continuum Manipulators in Constrained Environments. IEEE Trans. Robot. 2014, 30, 880–889. [Google Scholar] [CrossRef]
- da Veiga, T.; Chandler, J.H.; Lloyd, P.; Pittiglio, G.; Wilkinson, N.J.; Hoshiar, A.K.; Harris, R.A.; Valdastri, P. Challenges of continuum robots in clinical context: A review. Prog. Biomed. Eng. 2020, 2, 032003. [Google Scholar] [CrossRef]
- Shi, C.; Luo, X.; Qi, P.; Li, T.; Song, S.; Najdovski, Z.; Fukuda, T.; Ren, H. Shape Sensing Techniques for Continuum Robots in Minimally Invasive Surgery: A Survey. IEEE Trans. Biomed. Eng. 2017, 64, 1665–1678. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Li, Y.; Kwok, K.W. A Survey for Machine Learning-Based Control of Continuum Robots. Front. Robot. AI 2021, 8, 730330. [Google Scholar] [CrossRef]
- Thuruthel, T.G.; Falotico, E.; Renda, F.; Laschi, C. Model-Based Reinforcement Learning for Closed-Loop Dynamic Control of Soft Robotic Manipulators. IEEE Trans. Robot. 2019, 35, 124–134. [Google Scholar] [CrossRef]
- Peters, J.; Schaal, S. Reinforcement learning of motor skills with policy gradients. Neural. Netw. 2008, 21, 682–697. [Google Scholar] [CrossRef] [PubMed]
- Mordatch, I.; Todorov, E. Combining the benefits of function approximation and trajectory optimization. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014. [Google Scholar]
- Levine, S.; Koltun, V. Guided Policy Search. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Levine, S.; Abbeel, P. Learning Neural Network Policies with Guided Policy Search under Unknown Dynamics. In Proceedings of the Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Fang, G.; Wang, X.; Wang, K.; Lee, K.-H.; Ho, J.D.L.; Fu, H.-C.; Fu, D.K.C.; Kwok, K.-W. Vision-Based Online Learning Kinematic Control for Soft Robots Using Local Gaussian Process Regression. IEEE Robot. Autom. Lett. 2019, 4, 1194–1201. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, T.; Zhao, B.; He, Y.; Hu, Y.; Li, B.; Zhang, P.; Meng, M.Q.H. Hybrid Adaptive Control Strategy for Continuum Surgical Robot Under External Load. IEEE Robot. Autom. Lett. 2021, 6, 1407–1414. [Google Scholar] [CrossRef]
- Bruder, D.; Fu, X.; Gillespie, R.B.; Remy, C.D.; Vasudevan, R. Data-Driven Control of Soft Robots Using Koopman Operator Theory. IEEE Trans. Robot. 2021, 37, 948–961. [Google Scholar] [CrossRef]
- Abraham, I.; Murphey, T.D. Active Learning of Dynamics for Data-Driven Control Using Koopman Operators. IEEE Trans. Robot. 2019, 35, 1071–1083. [Google Scholar] [CrossRef]











| Year | References | DOF | Number of Drives | Drive Types | Backbone |
|---|---|---|---|---|---|
| 2000 | [38,39] | 1 | 2 | Cable | Sheet-type spring steel |
| 2001 | [40] | 4 | 4 | Cable | Thin elastic rod |
| 2004 | [56] | 2 | 3 | Ni-Ti tube | 4 Ni-Ti tubes |
| 2006 | [51] | 4 | 2 | Cable | Extensible spring steel |
| 2008 | [57] | 2 | 3 | Ni-Ti tube | 4 Ni-Ti tubes |
| 2010 | [36,44,45] | 8 | 3 | Cable | Elastic rod |
| 2011 | [41] | 2 | 3 | Fiberglass | Rod-type spring steel |
| 2012 | [42,43] | 2 | 3 | Fiberglass | Rod-type spring steel |
| 2013 | [46] | 1 | 2 | Cable | Notch elastic Ni-Ti backbone |
| 2015 | [52,53] | 9 | 3 | Cable | Extensible concentric tubes and springs |
| 2015 | [54,55] | 9 | 3 | Cable | Extensible Ni-Ti concentric tubes |
| 2020 | [47] | 2 | 4 | Cable | Notch elastic Ni-Ti backbone |
| 2020 | [58,59] | 4 | 3 | Ni-Ti rod | 4 Ni-Ti rods |
| 2021 | [48,49,50] | 16 | 2 and 3 | Cable | Notch elastic metal backbone |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, H.; Lee, B.G.; Yang, G.; Shen, W.; Qian, S.; Zhang, H.; Zhou, J.; Fang, Z.; Zheng, T.; Yang, S.; et al. Unlocking the Potential of Cable-Driven Continuum Robots: A Comprehensive Review and Future Directions. Actuators 2024, 13, 52. https://doi.org/10.3390/act13020052
Bai H, Lee BG, Yang G, Shen W, Qian S, Zhang H, Zhou J, Fang Z, Zheng T, Yang S, et al. Unlocking the Potential of Cable-Driven Continuum Robots: A Comprehensive Review and Future Directions. Actuators. 2024; 13(2):52. https://doi.org/10.3390/act13020052
Chicago/Turabian StyleBai, Haotian, Boon Giin Lee, Guilin Yang, Wenjun Shen, Shuwen Qian, Haohao Zhang, Jianwei Zhou, Zaojun Fang, Tianjiang Zheng, Sen Yang, and et al. 2024. "Unlocking the Potential of Cable-Driven Continuum Robots: A Comprehensive Review and Future Directions" Actuators 13, no. 2: 52. https://doi.org/10.3390/act13020052
APA StyleBai, H., Lee, B. G., Yang, G., Shen, W., Qian, S., Zhang, H., Zhou, J., Fang, Z., Zheng, T., Yang, S., Huang, L., & Yu, B. (2024). Unlocking the Potential of Cable-Driven Continuum Robots: A Comprehensive Review and Future Directions. Actuators, 13(2), 52. https://doi.org/10.3390/act13020052








