Two-Stage Predefined-Time Exact Sliding Mode Control Based on Predefined-Time Exact Disturbance Observer
Abstract
1. Introduction
Notation
2. Problem Formulation and Preliminaries
2.1. Preliminaries
2.2. Problem Formulation of the Paper
3. Main Results
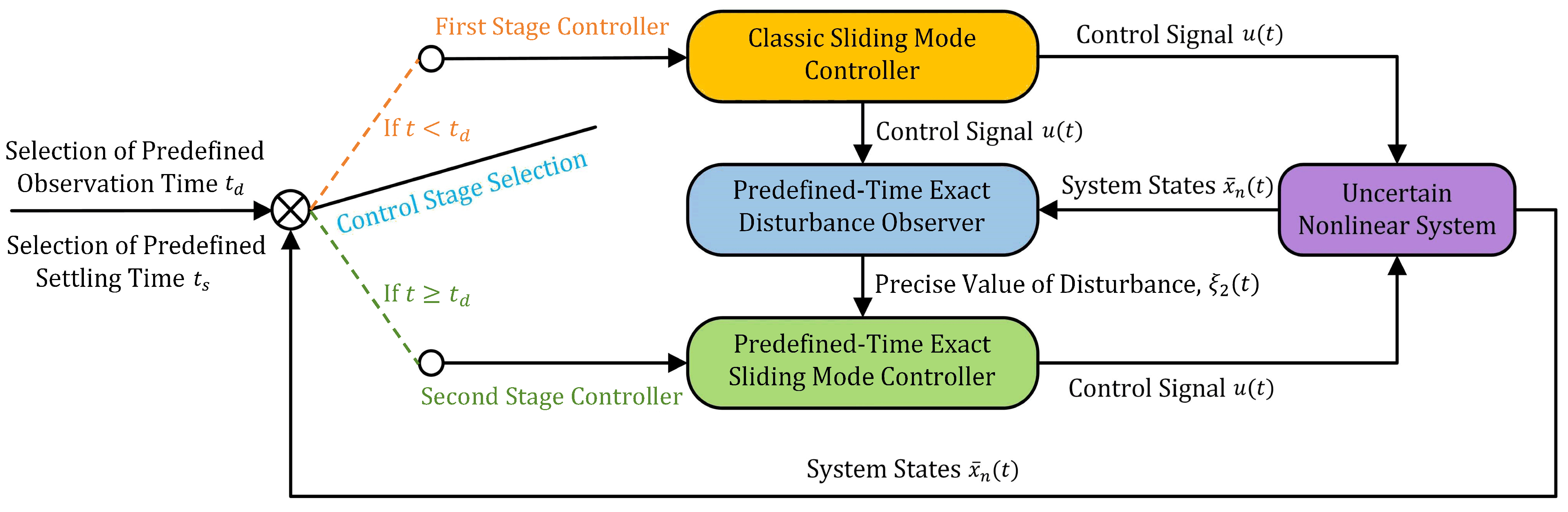
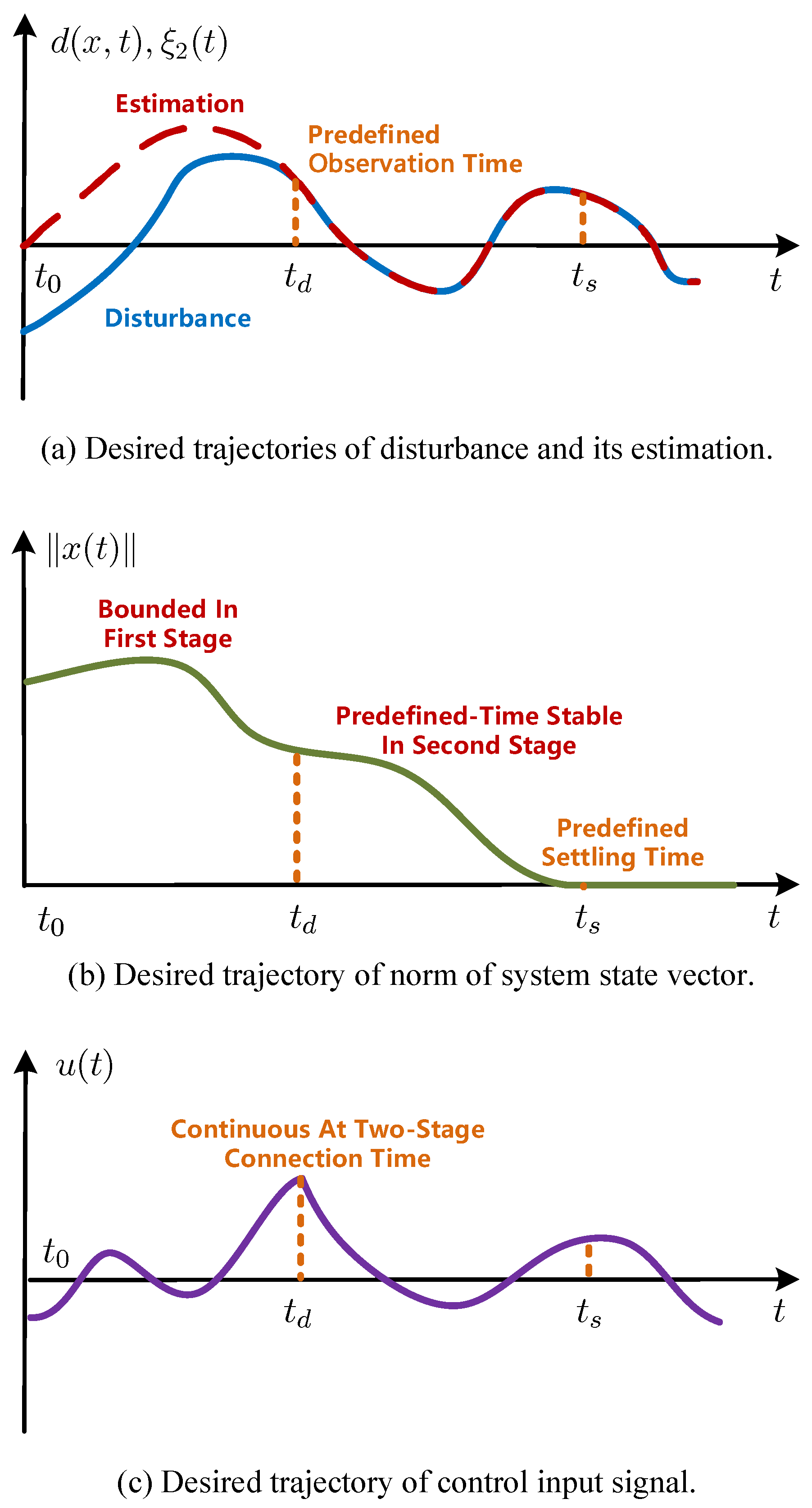
3.1. Two-Stage Control Scheme
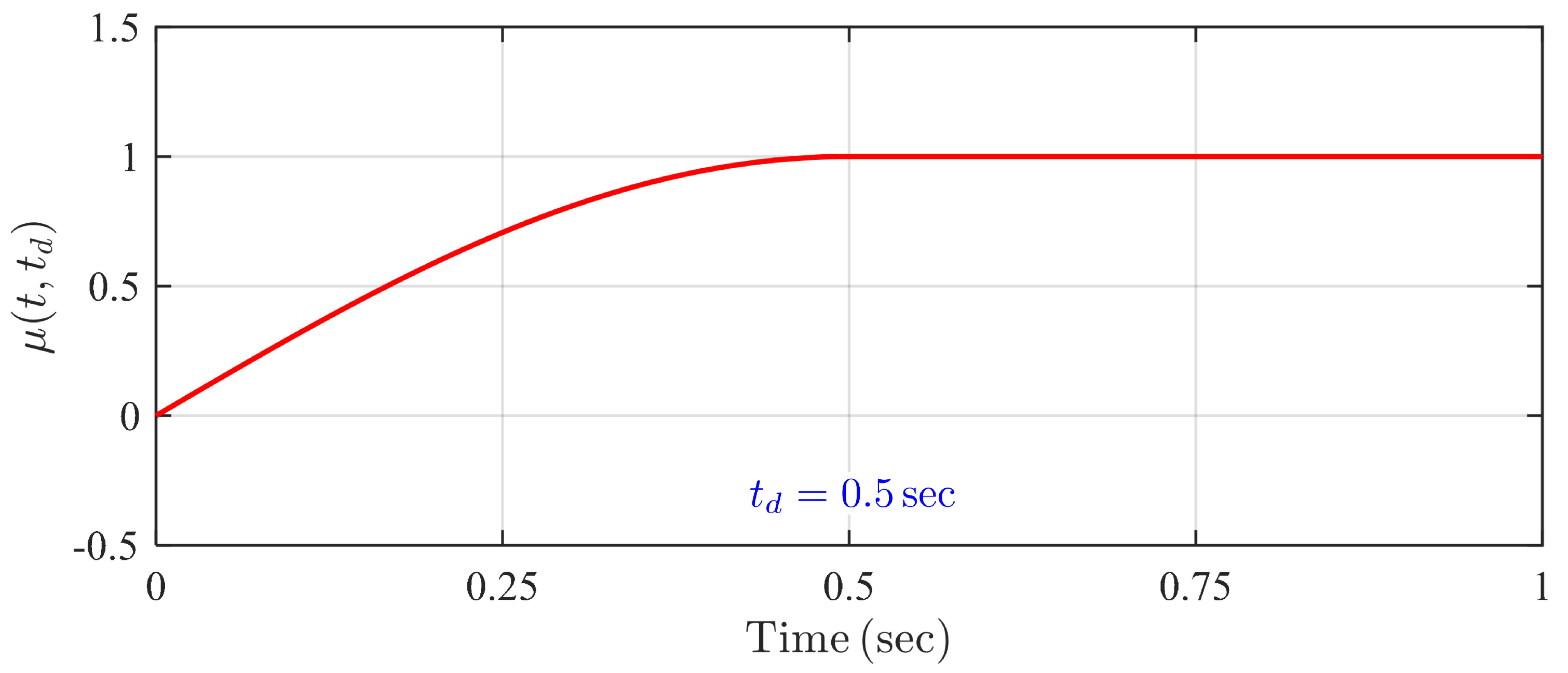
3.2. Predefined-Time Exact Disturbance Observer
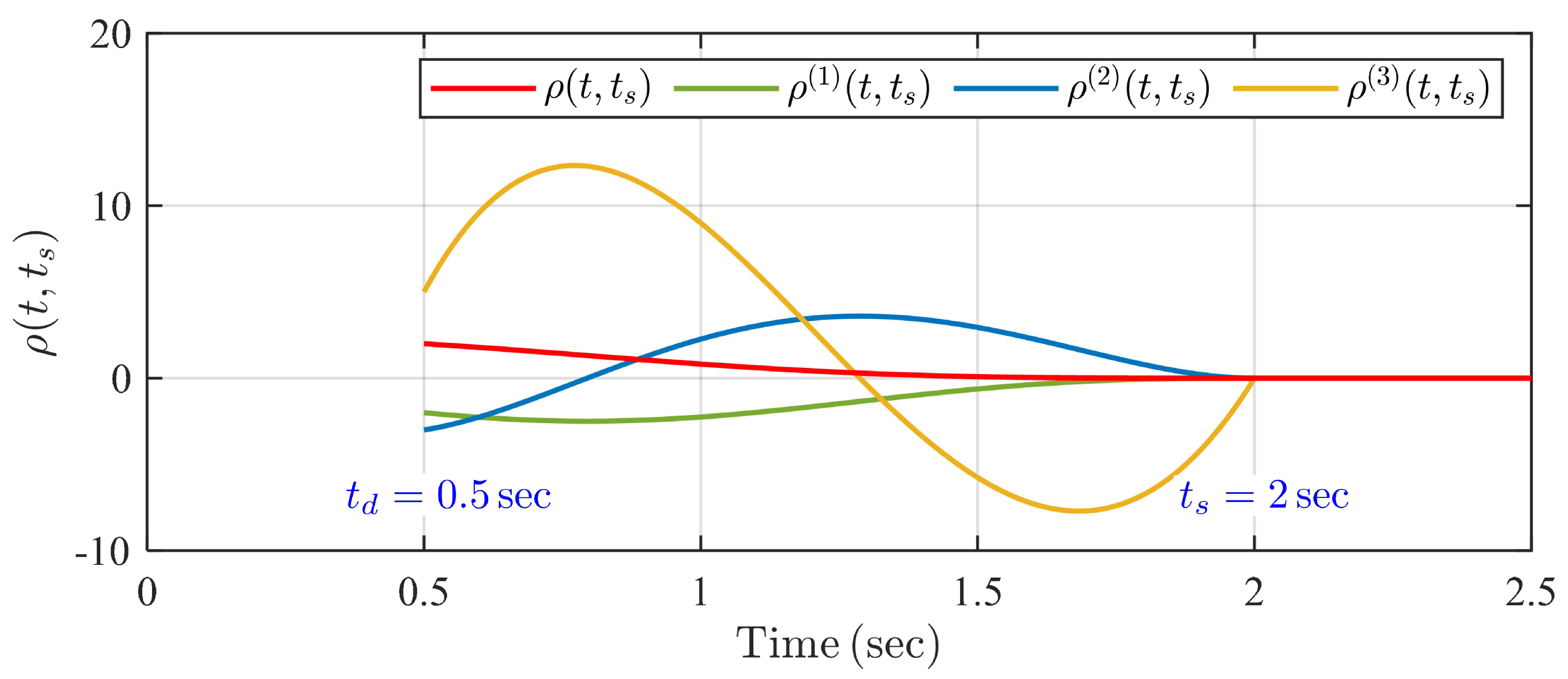
3.3. First-Stage Control Design
3.4. Second-Stage Control Design
3.5. System Analysis
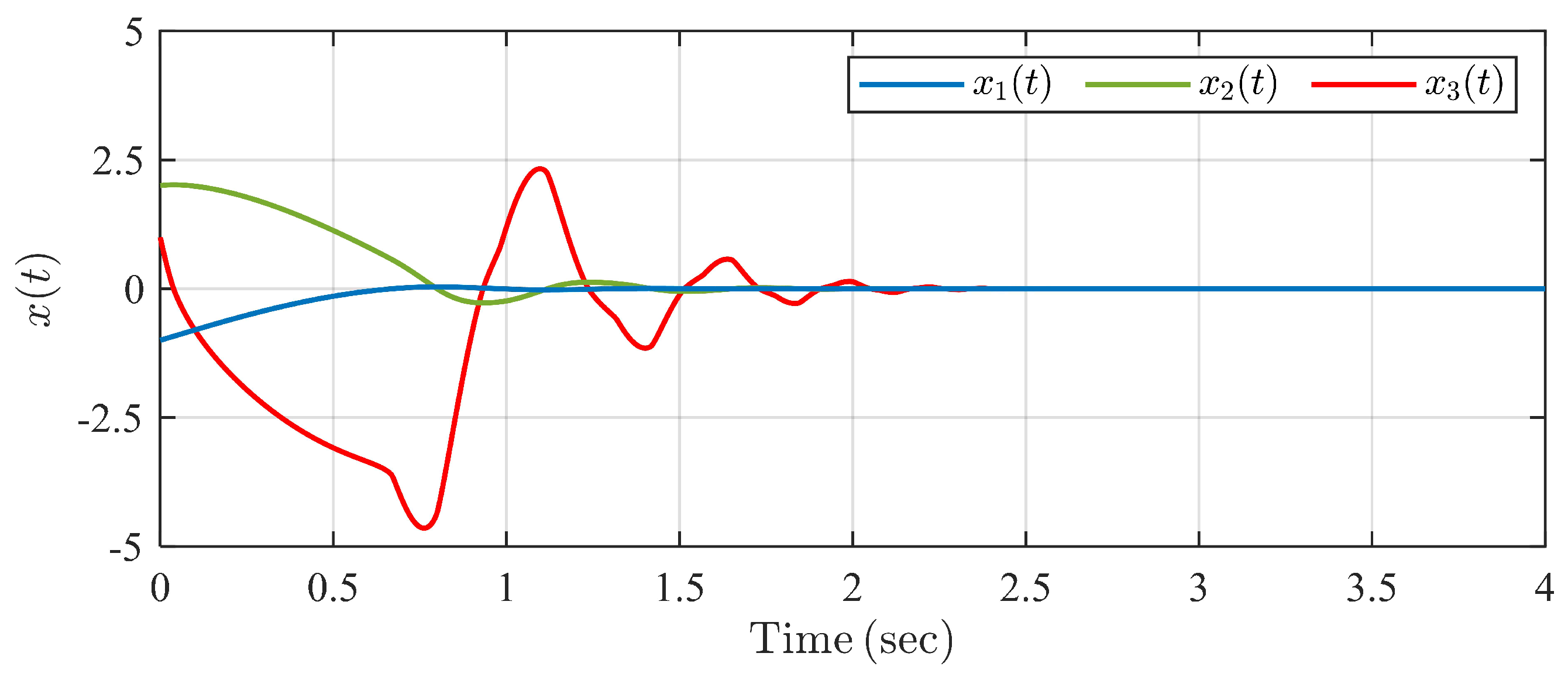
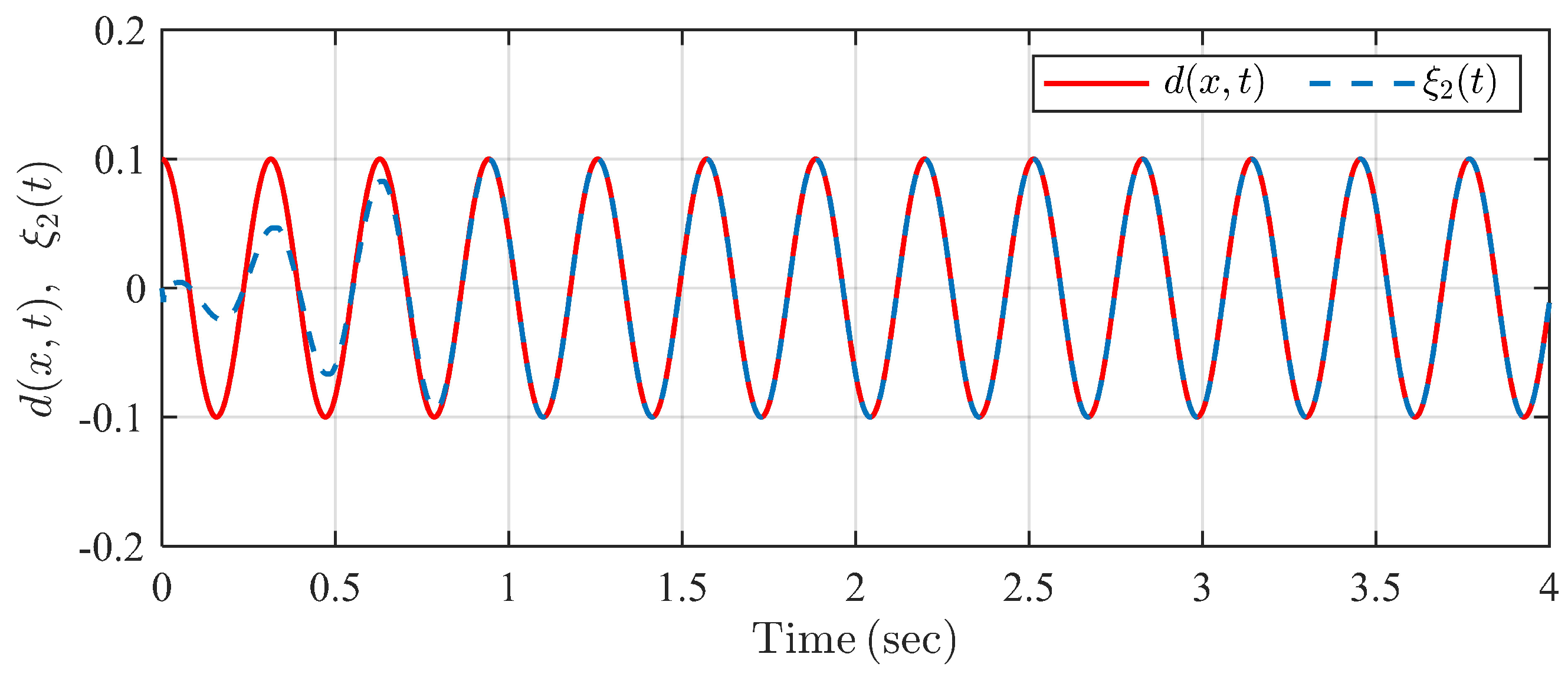
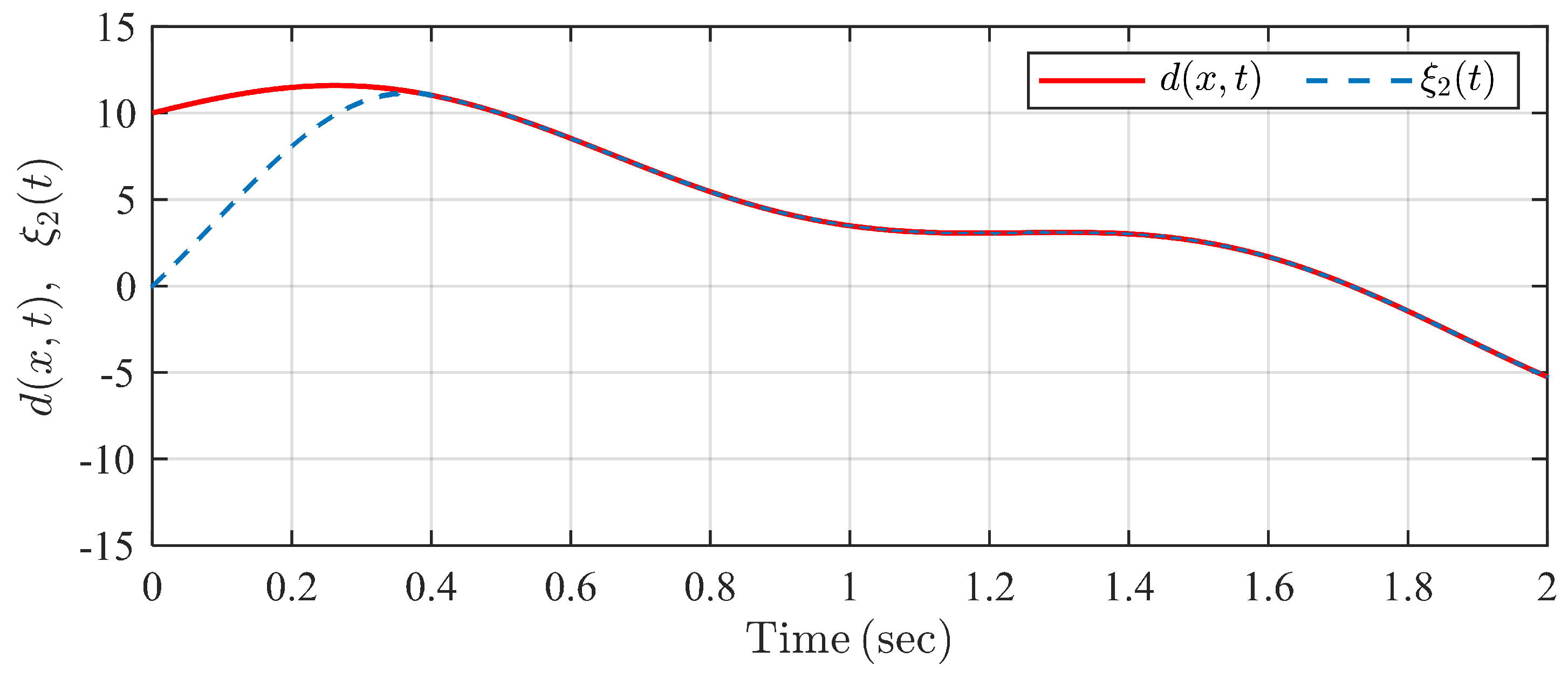
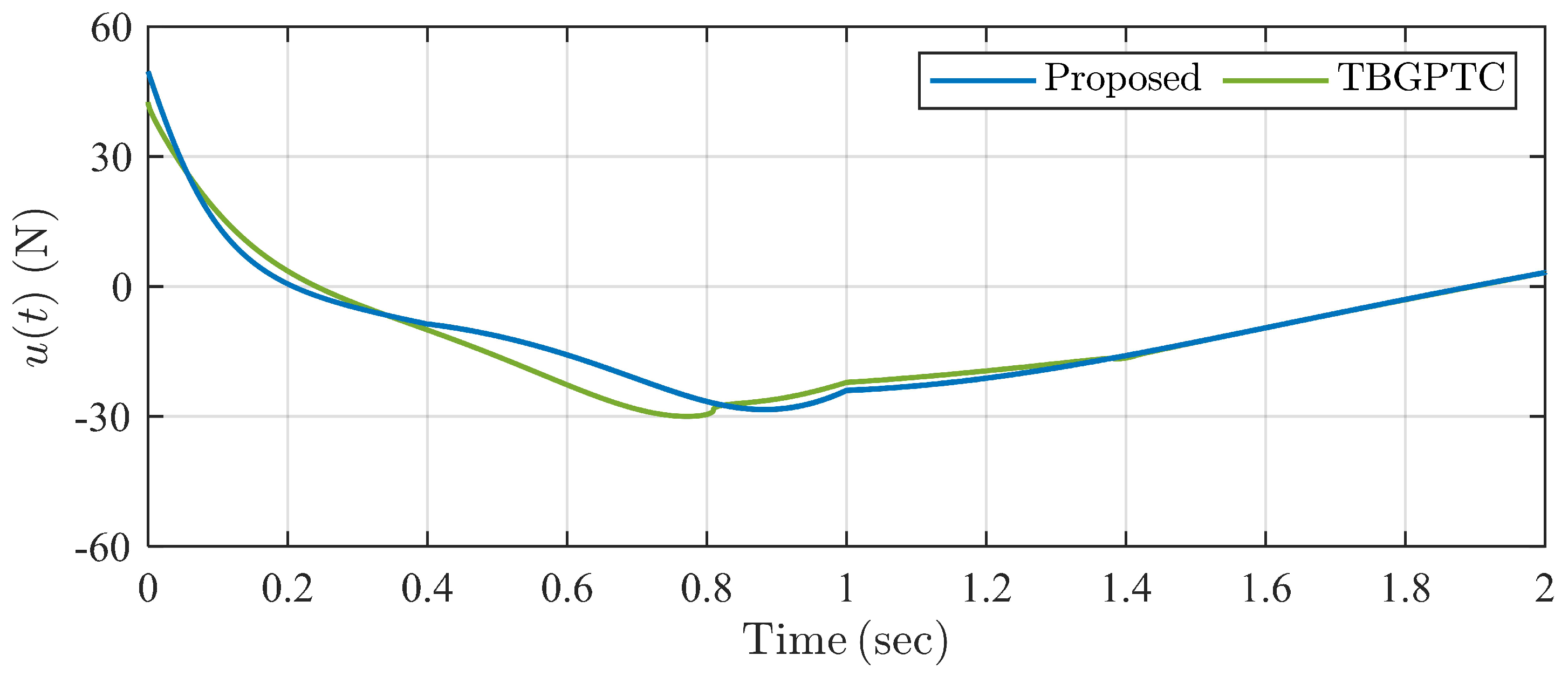
4. Simulation Examples
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Initial control time | |
| Predefined observation time of disturbance observer | |
| Predefined settling time of controlled system | |
| First control stage | |
| Second control stage | |
| System state vector | |
| u | System input |
| f | System drift dynamics |
| b | System input dynamics |
| d | System disturbance |
| Disturbance observer states | |
| g | Disturbance observer dynamics |
| Upper bound of | |
| Upper bound of | |
| Time-varying tuning function in disturbance observer | |
| Time-varying tuning function in controller | |
| Upper bound of | |
| Upper bound of | |
| Composite estimation errors of disturbance observer | |
| Perturbation of composite estimation error dynamics | |
| L | Upper bound of |
| Positive design parameters in disturbance observer | |
| Sliding mode variables in first and second control stages | |
| Positive design parameters in first stage controller | |
| Positive design parameters in second-stage controller | |
| Negative constant or Hurwitz matrix composed of | |
| Negative constant or Hurwitz matrix composed of | |
| B | Positive constant parameter or constant vector |
| Partial state vector in first control stage | |
| Partial state vector in second control stage | |
| Composite state variables in second control stage |
References
- Bhat, S.P.; Bernstein, D.S. Continuous finite-time stabilization of the translational and rotational double integrators. IEEE Trans. Autom. Control 1998, 43, 678–682. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Sánchez-Torres, J.D.; Gómez-Gutiérrez, D.; López, E.; Loukianov, A.G. A class of predefined-time stable dynamical systems. IMA J. Math. Control Inf. 2018, 35, I1–I29. [Google Scholar] [CrossRef]
- Jiménez-Rodríguez, E.; Muñoz-Vázquez, A.J.; Sánchez-Torres, J.D.; Defoort, M.; Loukianov, A.G. A lyapunov-like characterization of predefined-time stability. IEEE Trans. Autom. Control 2020, 65, 4922–4927. [Google Scholar] [CrossRef]
- Ferrara, A.; Incremona, G.P. Predefined-time output stabilization with second order sliding mode generation. IEEE Trans. Autom. Control 2021, 66, 1445–1451. [Google Scholar] [CrossRef]
- Song, Y.; Ye, H.; Lewis, F.L. Prescribed-time control and its latest developments. IEEE Trans. Syst. Man, Cybern. Syst. 2023, 53, 4102–4116. [Google Scholar] [CrossRef]
- Pal, A.K.; Kamal, S.; Nagar, S.K.; Bandyopadhyay, B.; Fridman, L. Design of controllers with arbitrary convergence time. Automatica 2020, 112, 108710. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Holloway, J.; Krstic, M. Time-varying feedback for regulation of normal-form nonlinear systems in prescribed finite time. Automatica 2017, 83, 243–251. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Krstic, M. Time-varying feedback for stabilization in prescribed finite time. Int. J. Robust Nonlinear Control 2019, 29, 618–633. [Google Scholar] [CrossRef]
- Ye, H.; Song, Y. Prescribed-time control of uncertain strict-feedback-like systems. Int. J. Robust Nonlinear Control 2021, 31, 5281–5297. [Google Scholar] [CrossRef]
- Singh, B.; Pal, A.K.; Kamal, S.; Dinh, T.N.; Mazenc, F. Vector control lyapunov function based stabilization of nonlinear systems in predefined time. IEEE Trans. Autom. Control 2023, 68, 4984–4989. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, D. On the design of nonautonomous fixed-time controllers with a predefined upper bound of the settling time. Int. J. Robust Nonlinear Control 2020, 30, 3871–3885. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, D.; Aldana-López, R.; Seeber, R.; Angulo, M.T.; Fridman, L. An arbitrary-order exact differentiator with predefined convergence time bound for signals with exponential growth bound. Automatica 2023, 153, 110995. [Google Scholar] [CrossRef]
- Orlov, Y. Time space deformation approach to prescribed-time stabilization: Synergy of time-varying and non-lipschitz feedback designs. Automatica 2022, 144, 110485. [Google Scholar] [CrossRef]
- Fu, L.; Ma, R.; Pang, H.; Fu, J. Predefined-time tracking of nonlinear strict-feedback systems with time-varying output constraints. J. Frankl. Inst. 2022, 359, 3492–3516. [Google Scholar] [CrossRef]
- Ma, R.; Fu, L.; Fu, J. Prescribed-time tracking control for nonlinear systems with guaranteed performance. Automatica 2022, 146, 110573. [Google Scholar] [CrossRef]
- Ye, H.; Song, Y. Prescribed-time tracking control of mimo nonlinear systems with nonvanishing uncertainties. IEEE Trans. Autom. Control 2023, 68, 3664–3671. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Sánchez-Torres, J.D.; Jiménez-Rodríguez, E.; Loukianov, A.G. Predefined-time robust stabilization of robotic manipulators. IEEE/ASME Trans. Mechatronics 2019, 24, 1033–1040. [Google Scholar] [CrossRef]
- Sánchez-Torres, J.D.; Muñoz-Vázquez, A.J.; Defoort, M.; Jiménez-Rodríguez, E.; Loukianov, A.G. A class of predefined-time controllers for uncertain second-order systems. Eur. J. Control 2020, 53, 52–58. [Google Scholar] [CrossRef]
- Liang, C.D.; Ge, M.F.; Liu, Z.W.; Ling, G.; Zhao, X.W. A novel sliding surface design for predefined-time stabilization of euler-lagrange systems. Nonlinear Dyn. 2021, 106, 445–458. [Google Scholar] [CrossRef]
- Xie, S.; Chen, Q. Adaptive nonsingular predefined-time control for attitude stabilization of rigid spacecrafts. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 189–193. [Google Scholar] [CrossRef]
- Ding, M.; Wu, H.; Zheng, X.; Guo, Y. Adaptive predefined-time attitude stabilization control of space continuum robot. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 647–651. [Google Scholar] [CrossRef]
- Xu, H.; Yu, D.; Sui, S.; Chen, C.L.P. An event-triggered predefined time decentralized output feedback fuzzy adaptive control method for interconnected systems. IEEE Trans. Fuzzy Syst. 2023, 31, 631–644. [Google Scholar] [CrossRef]
- Zhang, T.; Su, S.; Wei, W.; Yeh, R.H. Practically predefined-time adaptive fuzzy tracking control for nonlinear stochastic systems. IEEE Trans. Cybern. 2023, 53, 8000–8012. [Google Scholar] [CrossRef] [PubMed]
- Becerra, H.M.; Vazquez, C.R.; Arechavaleta, G.; Delfin, J. Predefined-time convergence control for high-order integrator systems using time base generators. IEEE Trans. Control Syst. Technol. 2018, 26, 1866–1873. [Google Scholar] [CrossRef]
- Chalanga, A.; Plestan, F. High-order sliding-mode control with predefined convergence time for electropneumatic actuator. IEEE Trans. Control Syst. Technol. 2021, 29, 910–917. [Google Scholar] [CrossRef]
- Sun, L.; Liu, Y. Fixed-time adaptive sliding mode trajectory tracking control of uncertain mechanical systems. Asian J. Control 2020, 22, 2080–2089. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Zuo, Z. Bipartite consensus tracking for second-order multiagent systems: A time-varying function-based preset-time approach. IEEE Trans. Autom. Control 2021, 66, 2739–2745. [Google Scholar] [CrossRef]
- Liu, B.; Hou, M.; Wu, C.; Wang, W.; Wu, Z.; Huang, B. Predefined-time backstepping control for a nonlinear strict-feedback system. Int. J. Robust Nonlinear Control 2021, 31, 3354–3372. [Google Scholar] [CrossRef]
- Lv, J.; Ju, X.; Wang, C. Neural network-based nonconservative predefined-time backstepping control for uncertain strict-feedback nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 1–12. [Google Scholar] [CrossRef]
- Cao, Y.; Cao, J.; Song, Y. Practical prescribed time tracking control over infinite time interval involving mismatched uncertainties and non-vanishing disturbances. Automatica 2022, 136, 110050. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J. Predefined-time sliding mode control with prescribed convergent region. IEEE/CAA J. Autom. Sin. 2022, 9, 934–936. [Google Scholar] [CrossRef]
- Ye, D.; Zou, A.M.; Sun, Z. Predefined-time predefined-bounded attitude tracking control for rigid spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 464–472. [Google Scholar] [CrossRef]
- Seeber, R.; Horn, M. Stability proof for a well-established super-twisting parameter setting. Automatica 2017, 84, 241–243. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Patience Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Feng, Y.; Han, F.; Yu, X. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Filippov, A.F. Differential Equations with Discontinuous Right-Hand Side; Kluwer Academic Publishing: Dordrecht, The Netherlands, 1988. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Ma, W.; Zhang, Z.; Yi, Y. Two-Stage Predefined-Time Exact Sliding Mode Control Based on Predefined-Time Exact Disturbance Observer. Actuators 2024, 13, 133. https://doi.org/10.3390/act13040133
Liu B, Ma W, Zhang Z, Yi Y. Two-Stage Predefined-Time Exact Sliding Mode Control Based on Predefined-Time Exact Disturbance Observer. Actuators. 2024; 13(4):133. https://doi.org/10.3390/act13040133
Chicago/Turabian StyleLiu, Bojun, Wenle Ma, Zhanpeng Zhang, and Yingmin Yi. 2024. "Two-Stage Predefined-Time Exact Sliding Mode Control Based on Predefined-Time Exact Disturbance Observer" Actuators 13, no. 4: 133. https://doi.org/10.3390/act13040133
APA StyleLiu, B., Ma, W., Zhang, Z., & Yi, Y. (2024). Two-Stage Predefined-Time Exact Sliding Mode Control Based on Predefined-Time Exact Disturbance Observer. Actuators, 13(4), 133. https://doi.org/10.3390/act13040133





