Analysis of Parameter Matching on the Steady-State Characteristics of Permanent Magnet-Assisted Synchronous Reluctance Motors under Vector Control
Abstract
1. Introduction
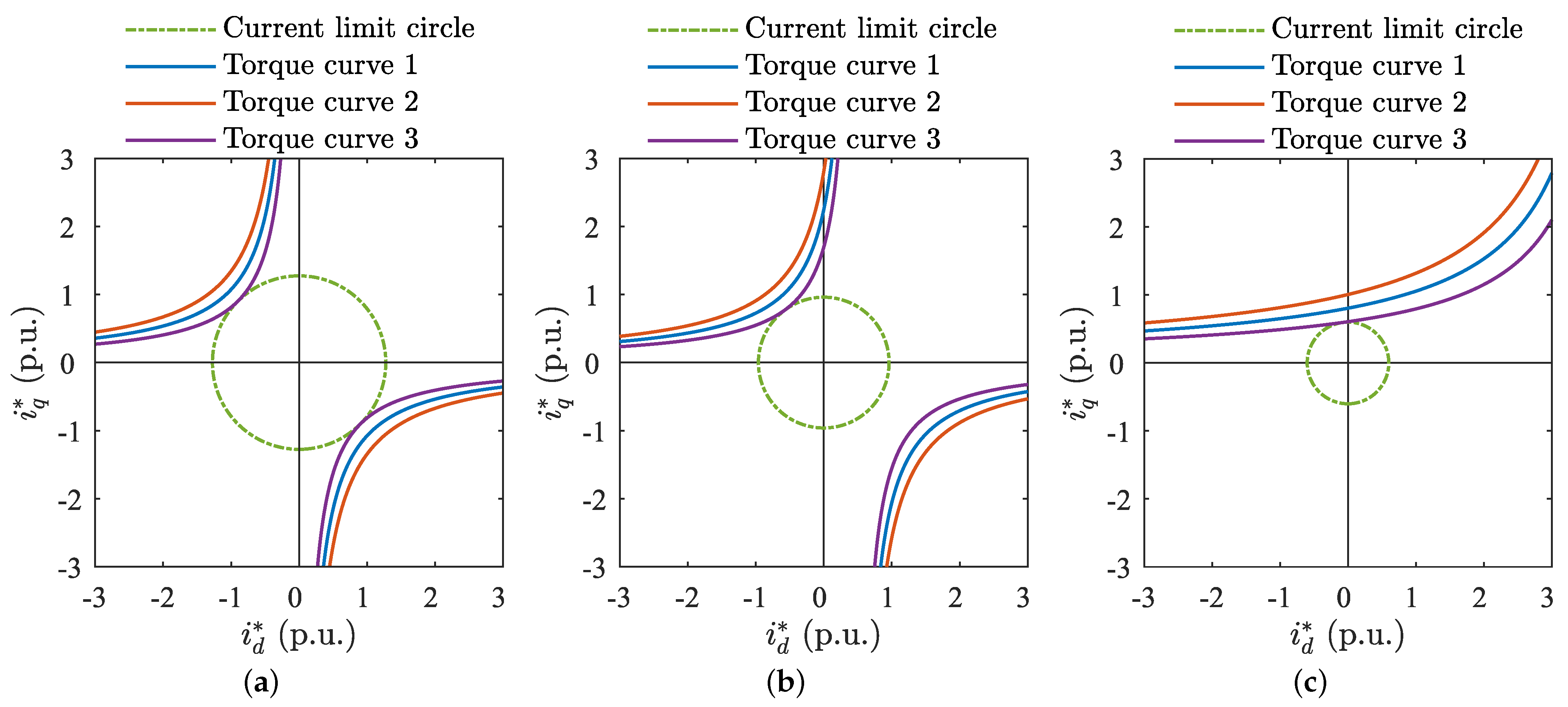
2. Typical Operational State of PMaSynRMs under MTPA Control Strategy
3. Analysis of Operational State of PMaSynRM under MTPA Control Strategy
3.1. Mathematical Model of Motors under MTPA Control
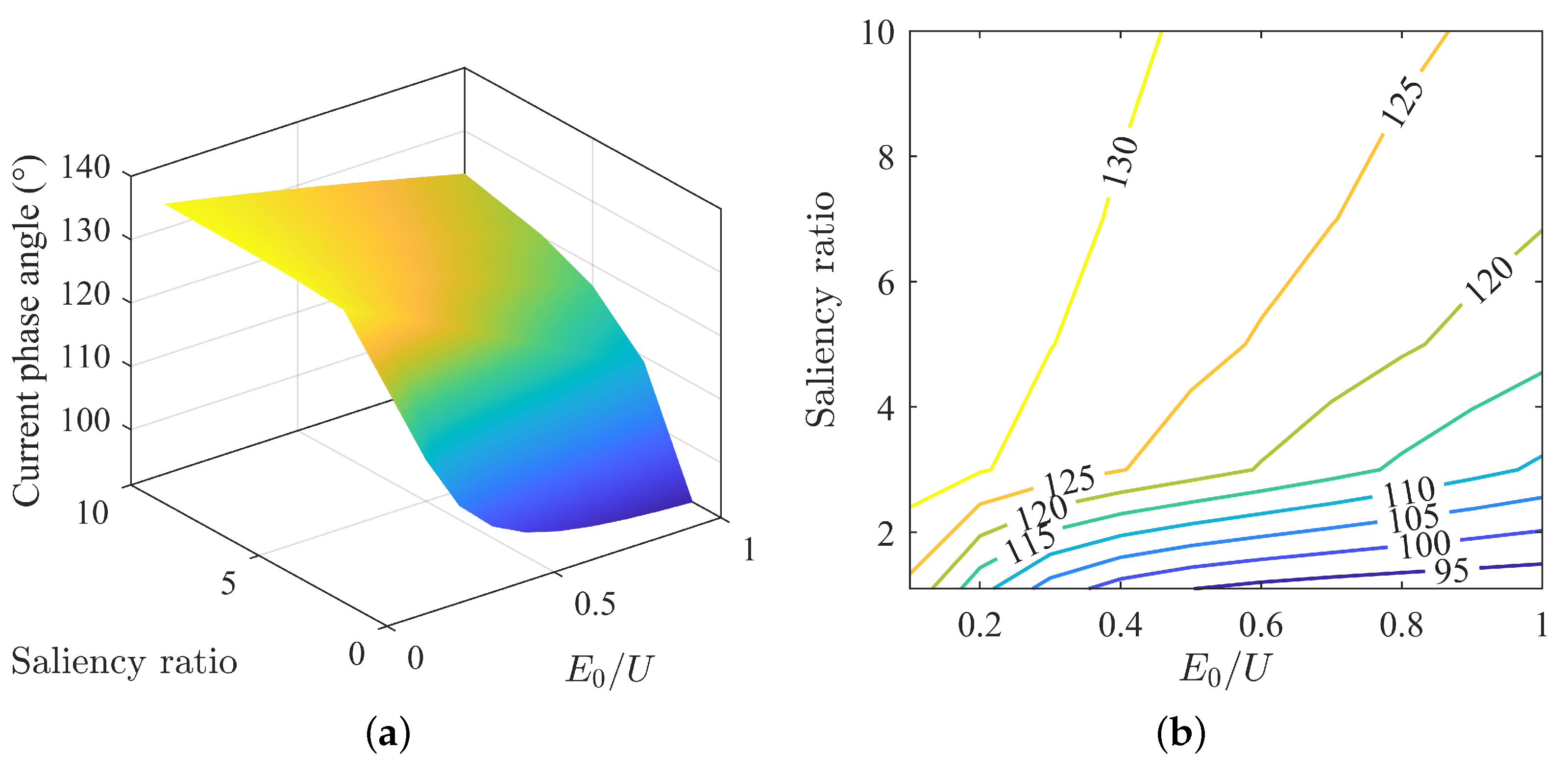
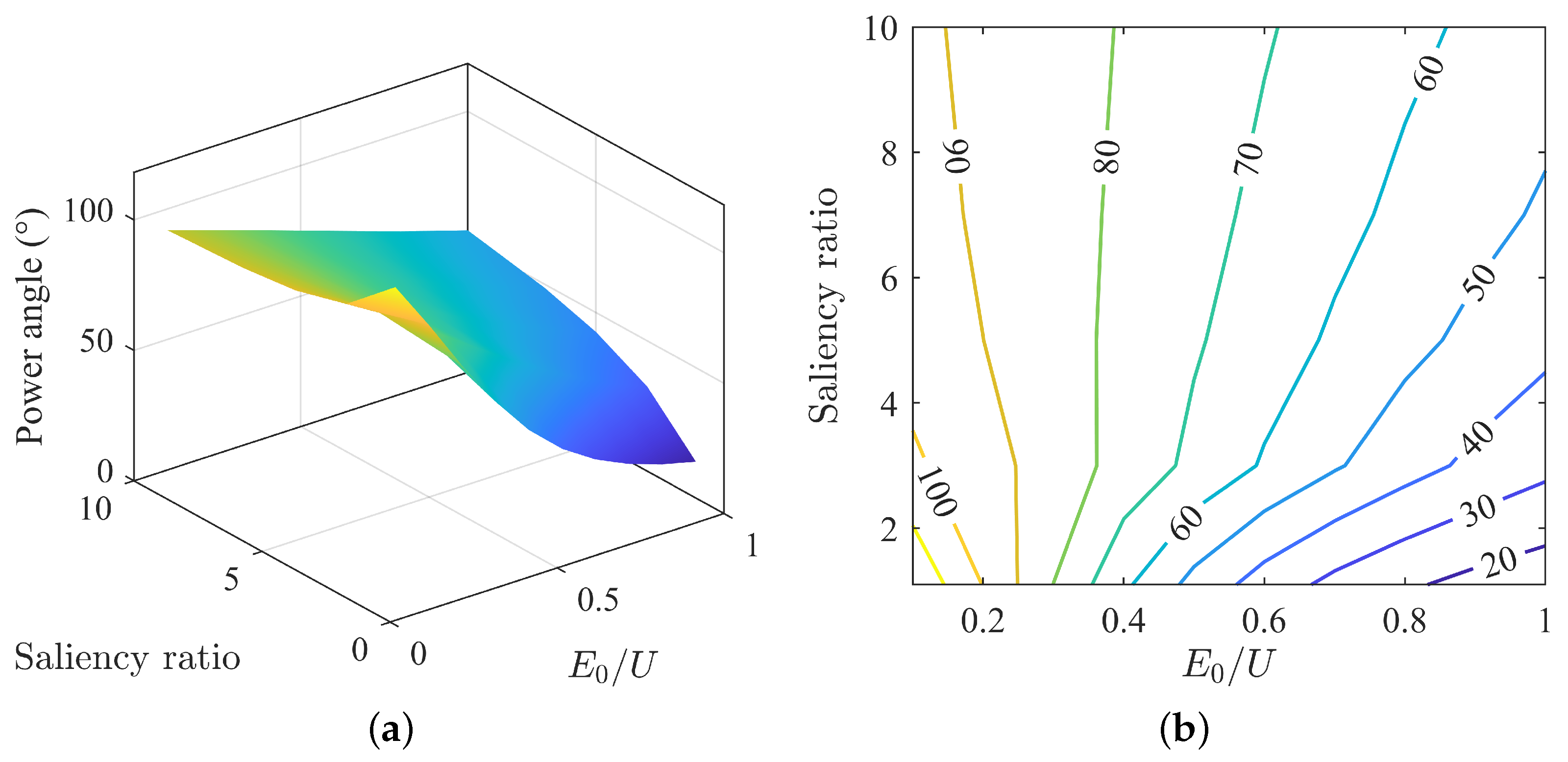
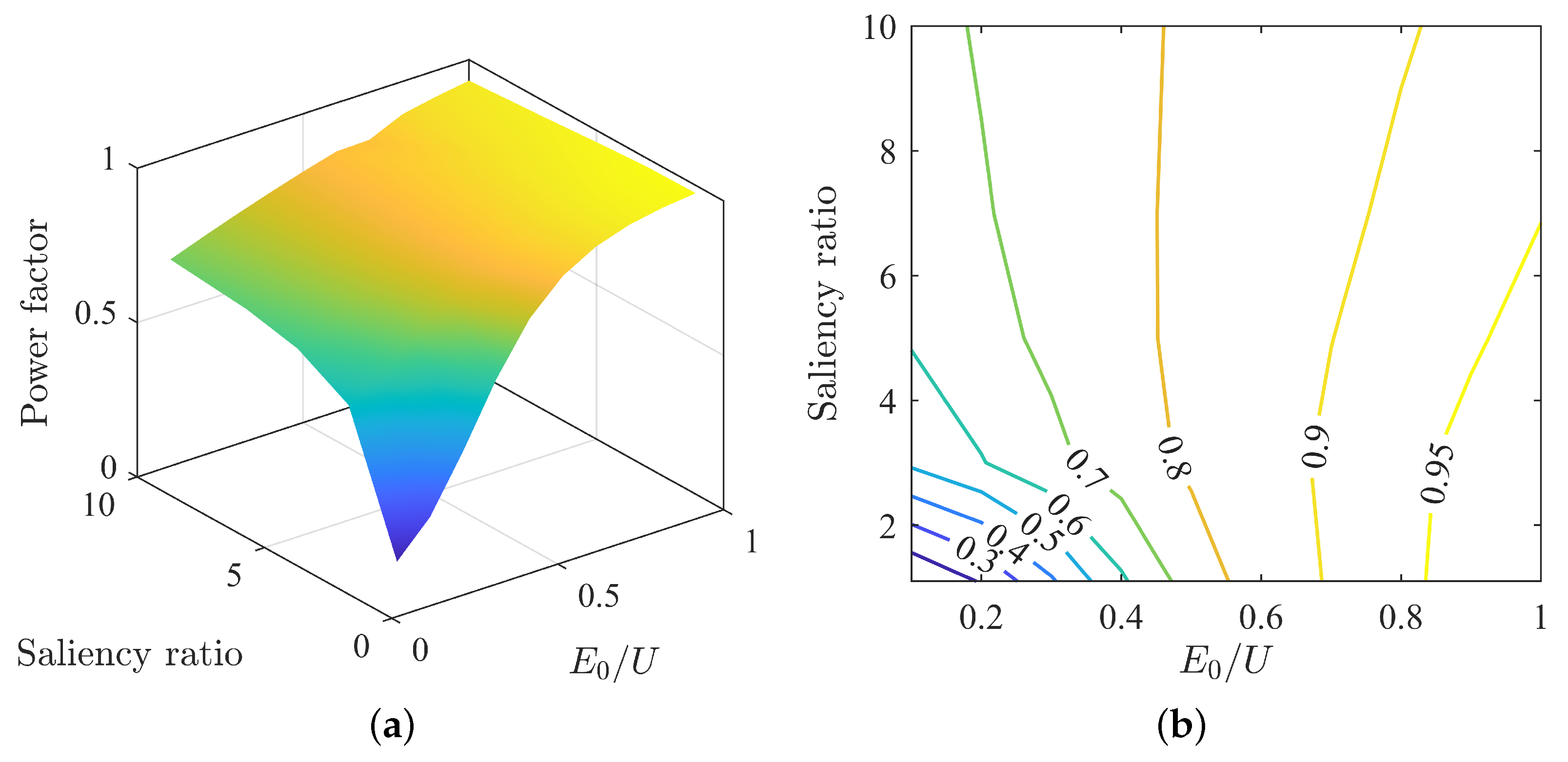
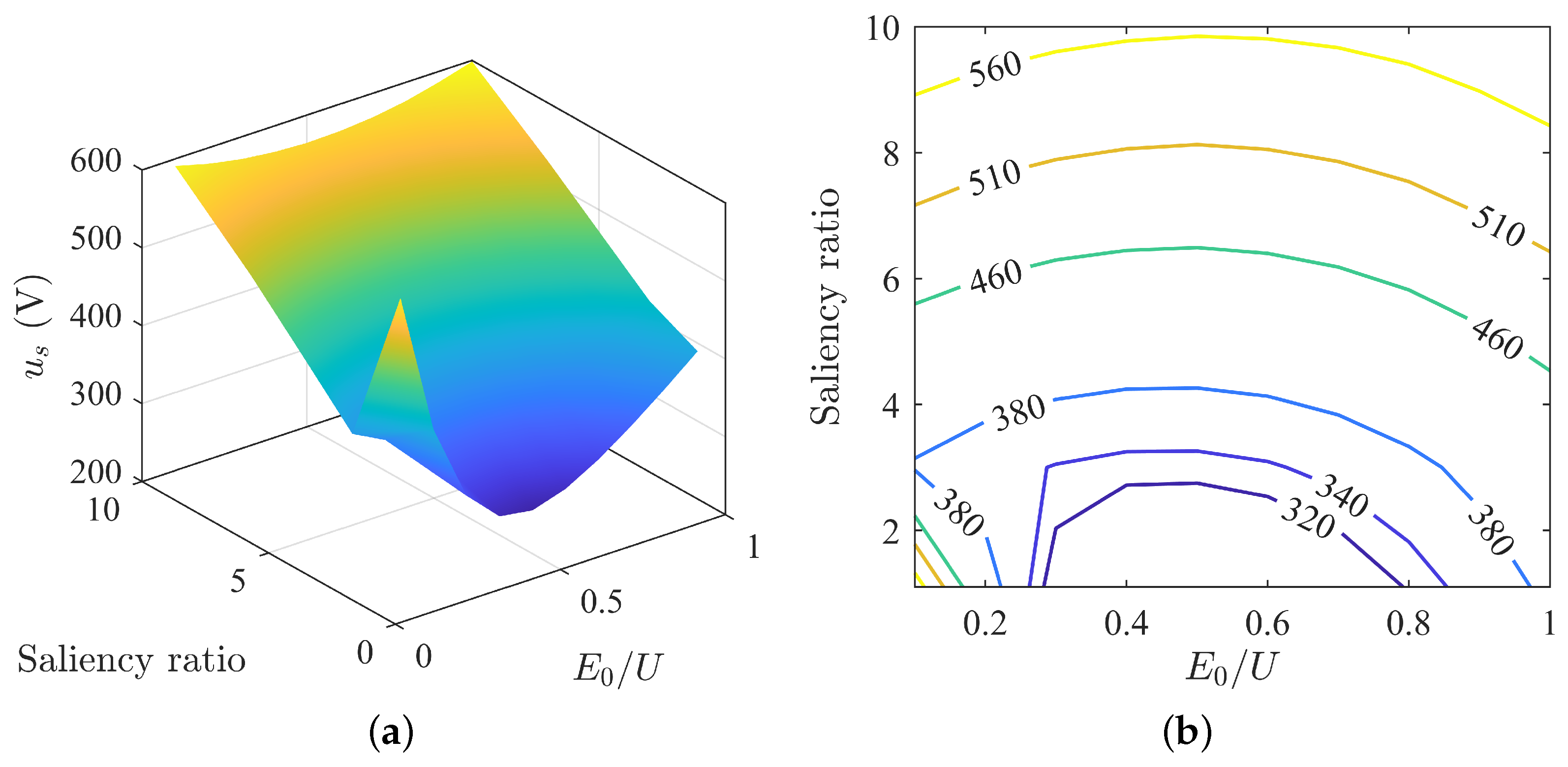
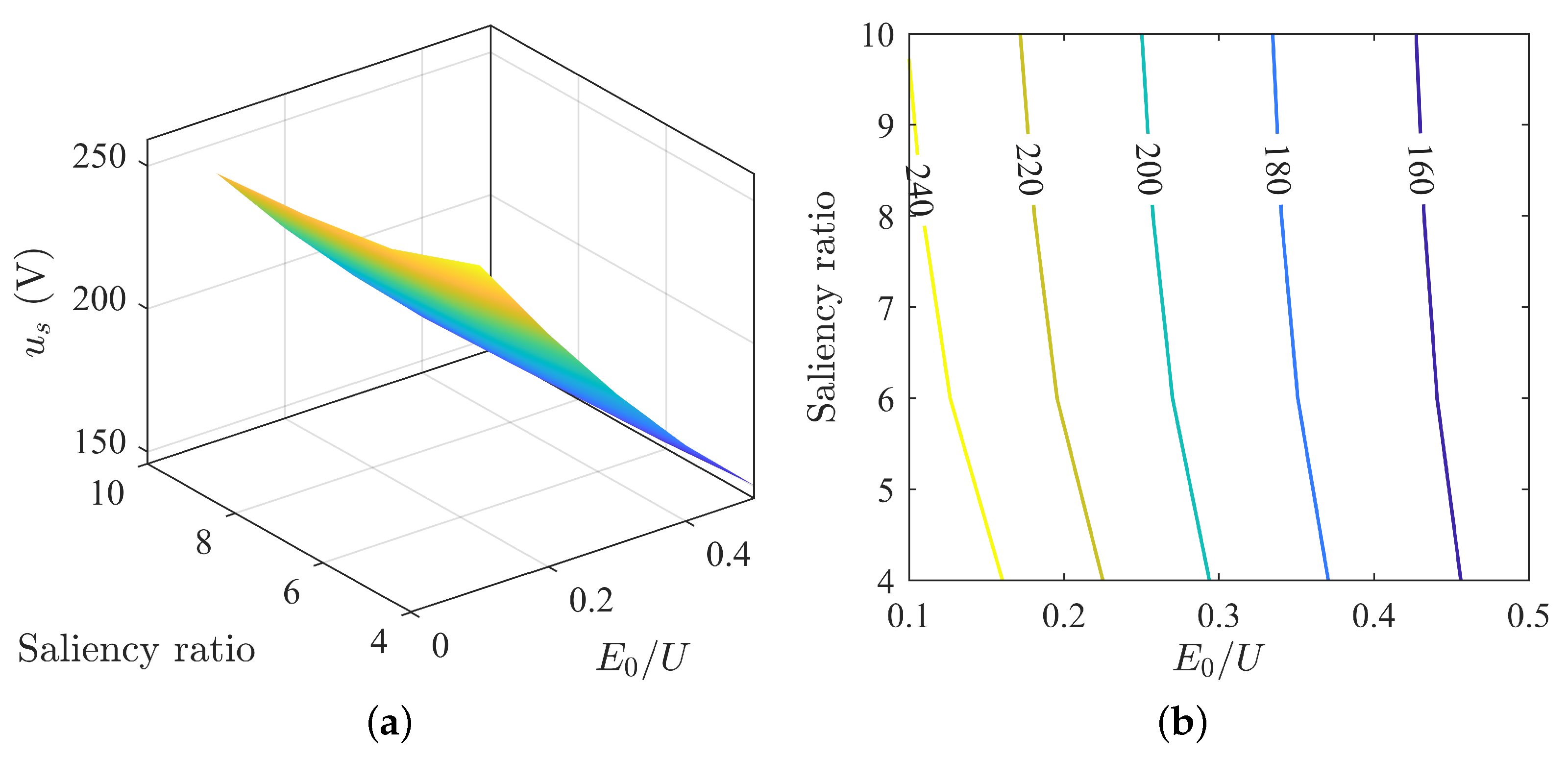
3.2. Impact of Back-EMF and Saliency Ratio on Motor Operating Characteristics under MTPA Control Strategy
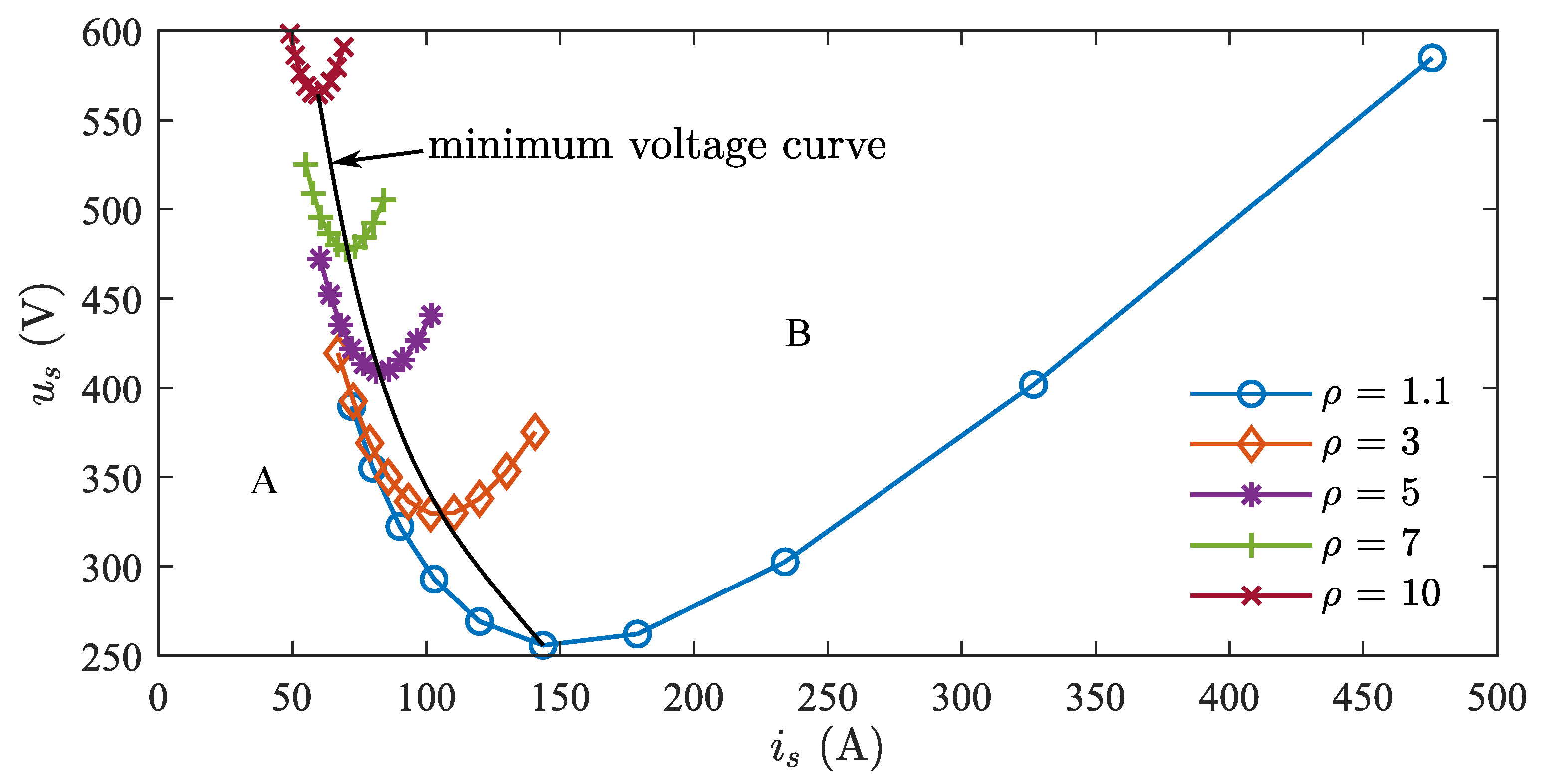
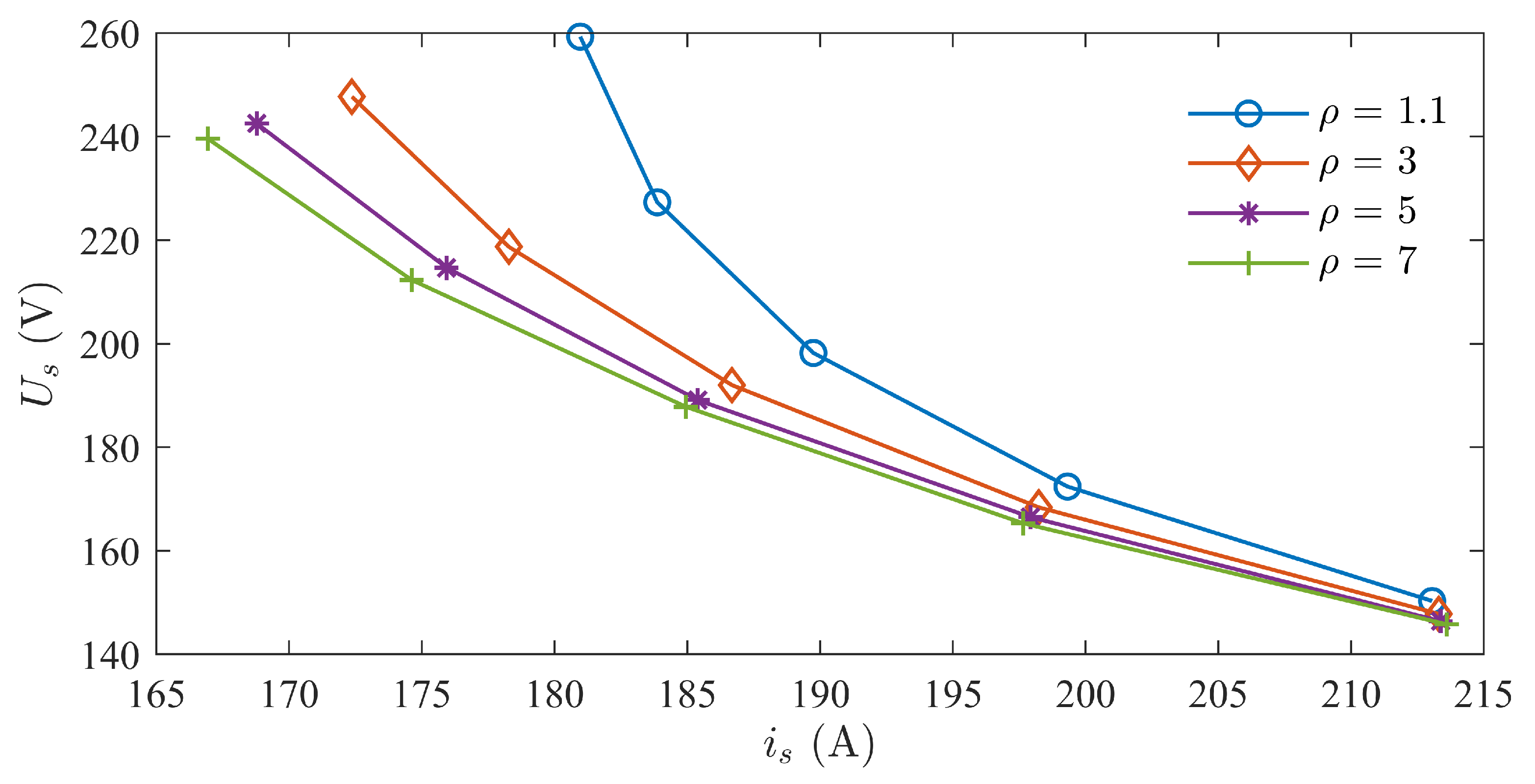
3.3. Analysis of Parameter Matching under MTPA Control Strategy
4. Optimal Parameter Matching of PMaSynRM under Vector Control Strategy
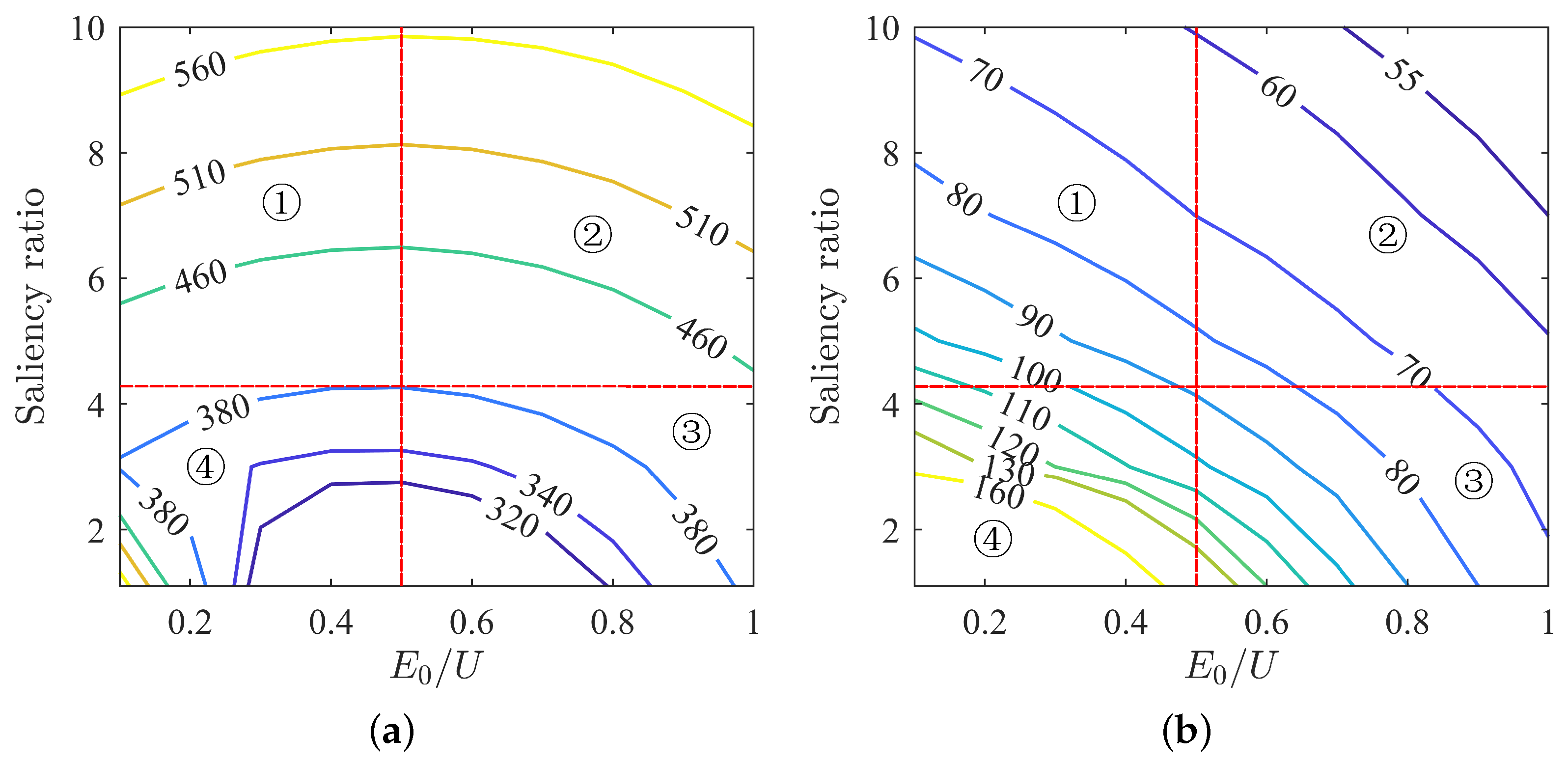
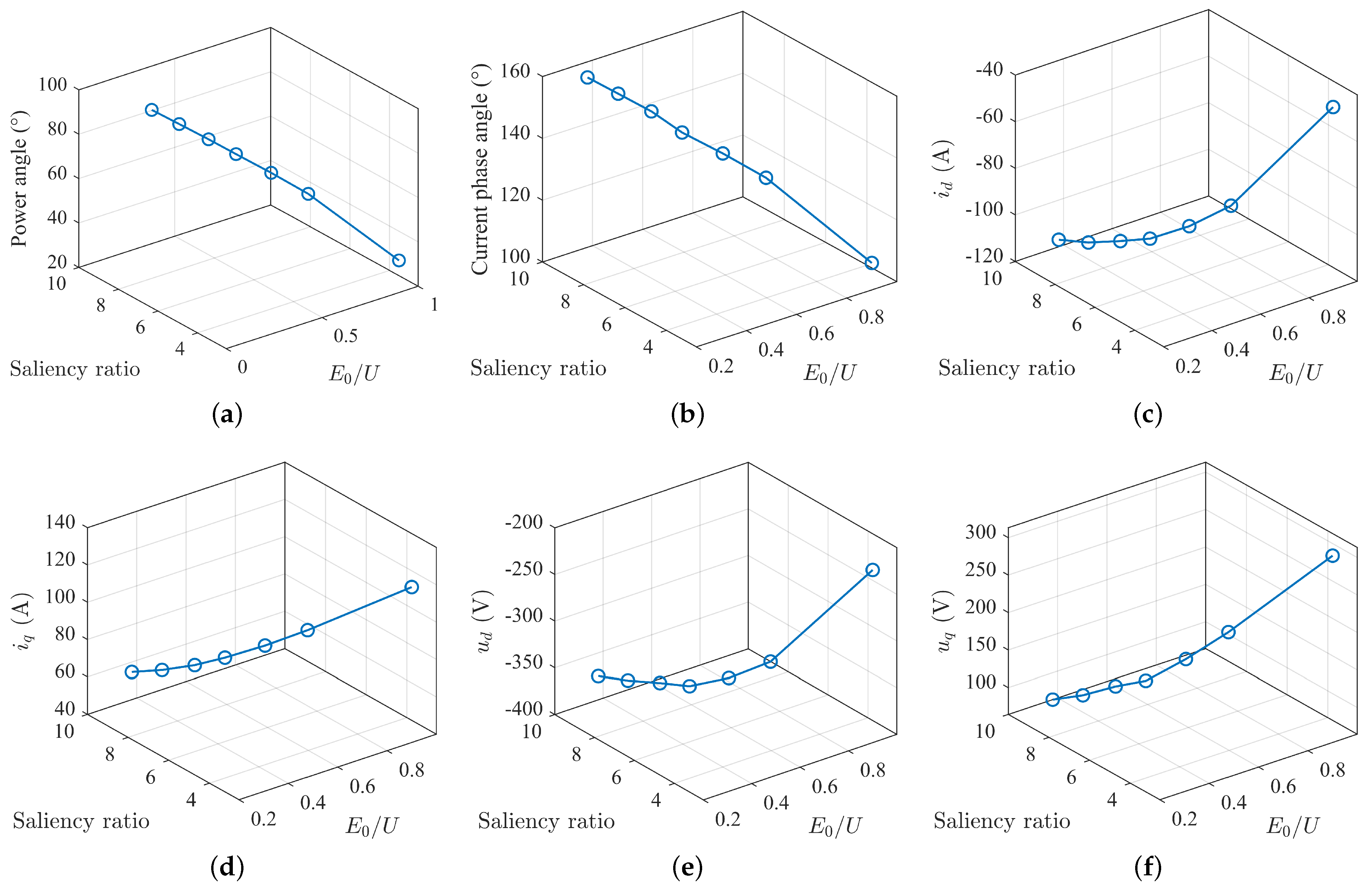
4.1. Analysis of Operating States under MTPV Control Strategy
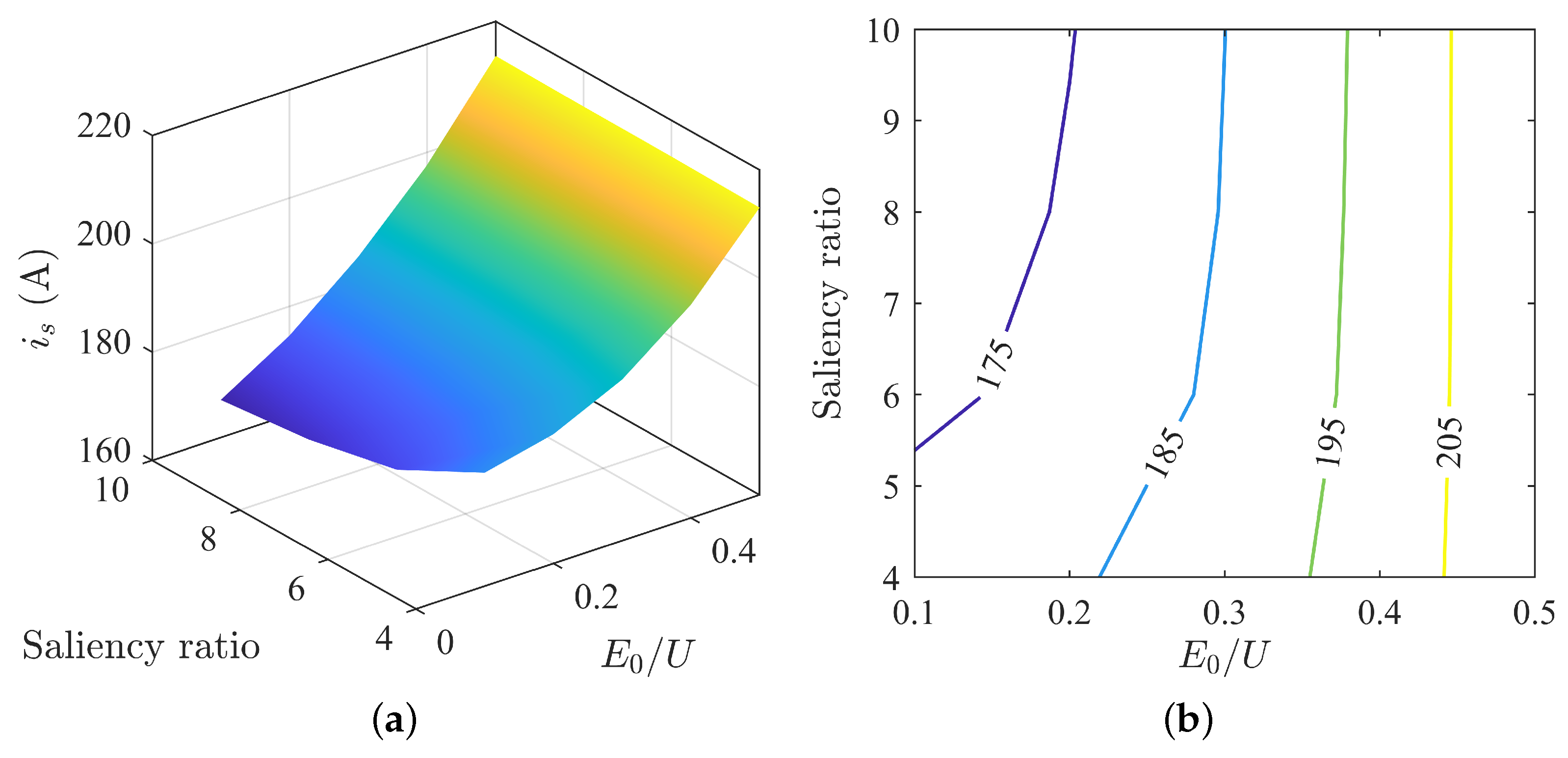
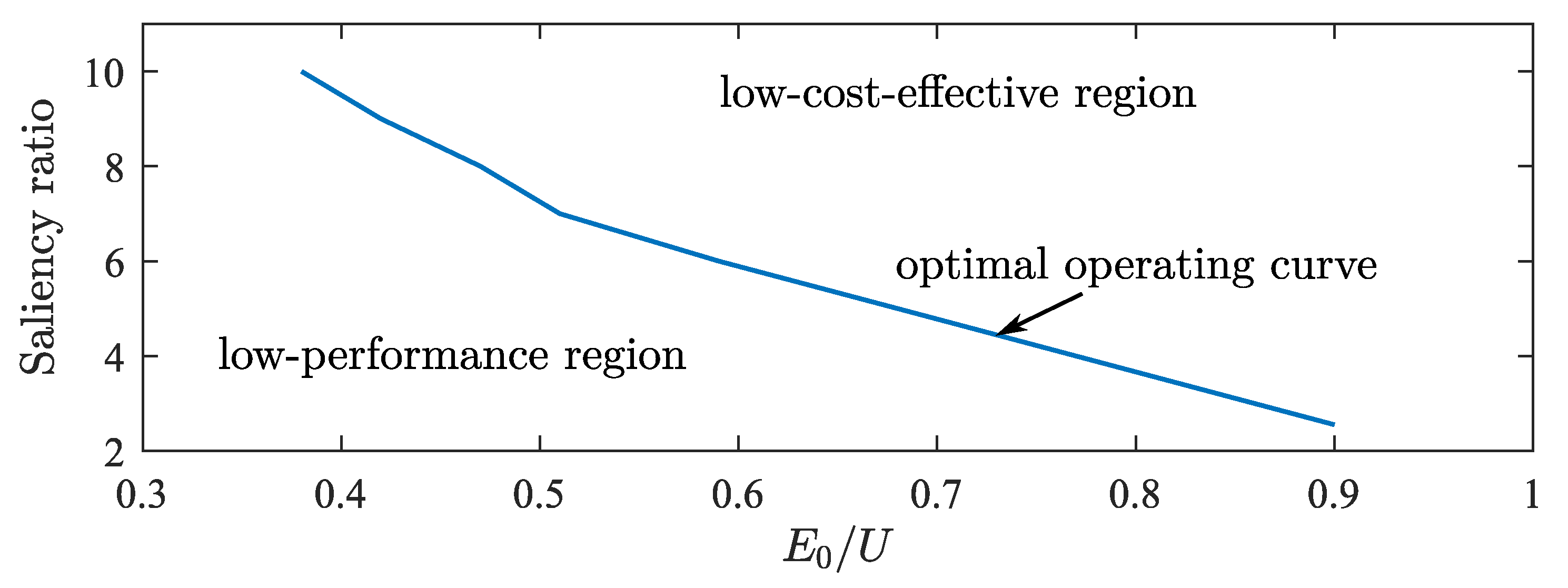
4.2. Optimal Parameter-Matching Curve under Vector Control
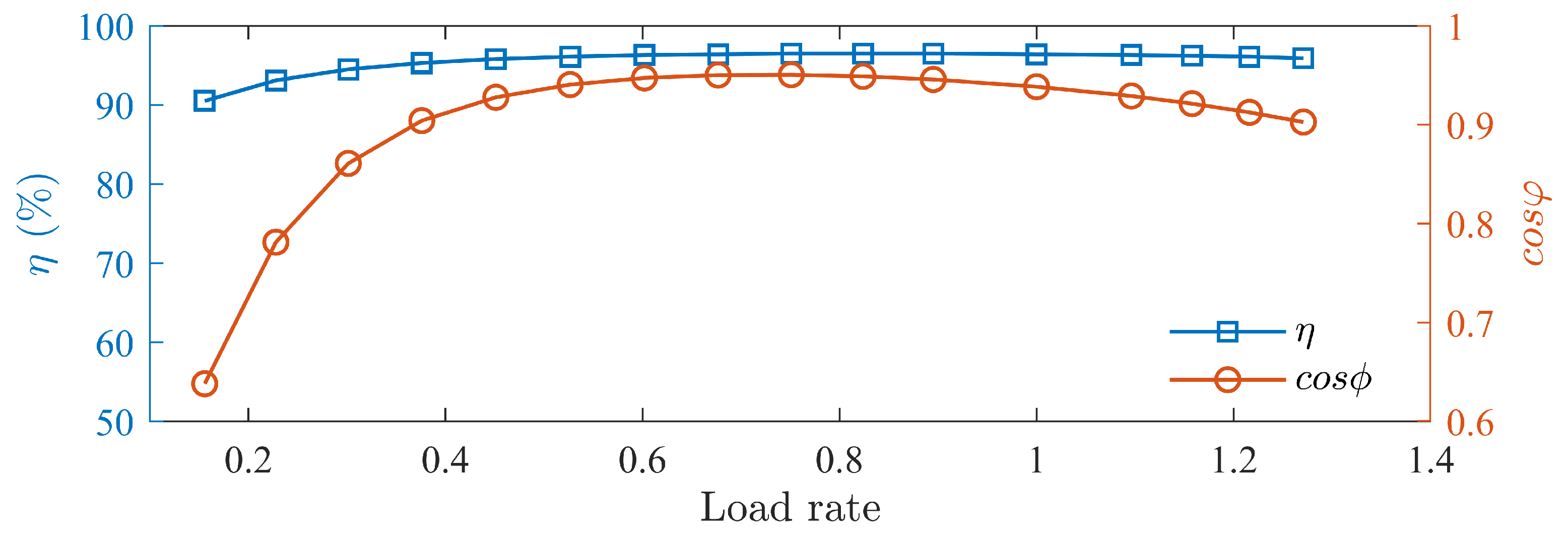
5. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Zhu, D.; Jian, W.; Hu, W.; Peng, G.; Chen, Y.; Wang, Z. Fractional Order Complementary Non-Singular Terminal Sliding Mode Control of PMSM Based on Neural Network. Int. J. Automot. Technol. 2024, 25, 213–224. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Y.; Gao, Y.; Wang, Z.; Peng, G. Cascade ADRC Speed Control Base on FCS-MPC for Permanent Magnet Synchronous Motor. J. Circuits Syst. Comput. 2021, 30, 2150202. [Google Scholar] [CrossRef]
- Sun, Q.; Lyu, G.; Liu, X.; Niu, F.; Gan, C. Virtual Current Compensation-Based Quasi-Sinusoidal-Wave Excitation Scheme for Switched Reluctance Motor Drives. IEEE Trans. Ind. Electron. 2023, 1–11. [Google Scholar] [CrossRef]
- Lu, Y.; Li, J.; Xu, H.; Yang, K.; Xiong, F.; Qu, R.; Sun, J. Comparative study on vibration behaviors of permanent magnet assisted synchronous reluctance machines with different rotor topologies. IEEE Trans. Ind. Appl. 2021, 57, 1420–1428. [Google Scholar] [CrossRef]
- Xu, M.; Liu, G.; Chen, Q.; Ji, J.; Zhao, W. Design and optimization of a fault tolerant modular permanent magnet assisted synchronous reluctance motor with torque ripple minimization. IEEE Trans. Ind. Electron. 2020, 68, 8519–8530. [Google Scholar] [CrossRef]
- Guo, H.; He, X.; Xu, J.; Tian, W.; Sun, G.; Ju, L.; Li, D. Design of an aviation dual-three-phase high-power high-speed permanent magnet assisted synchronous reluctance starter-generator with antishort-circuit ability. IEEE Trans. Power Electron. 2022, 37, 12619–12635. [Google Scholar] [CrossRef]
- Gallicchio, G.; Di Nardo, M.; Palmieri, M.; Marfoli, A.; Degano, M.; Gerada, C.; Cupertino, F. High speed permanent magnet assisted synchronous reluctance machines—Part I: A general design approach. IEEE Trans. Energy Convers. 2022, 37, 2556–2566. [Google Scholar] [CrossRef]
- Di Nardo, M.; Gallicchio, G.; Palmieri, M.; Marfoli, A.; Degano, M.; Gerada, C.; Cupertino, F. High Speed Permanent Magnet Assisted Synchronous Reluctance Machines—Part II: Performance Boundaries. IEEE Trans. Energy Convers. 2022, 37, 2567–2577. [Google Scholar] [CrossRef]
- Michalski, T.D.; Romeral, J.L.; Mino-Aguilar, G. Open-Phase Faulty Five-Phase Permanent Magnet Assisted Synchronous Reluctance Motor Model With Stepped Skew. IEEE Trans. Magn. 2021, 57, 1–7. [Google Scholar] [CrossRef]
- Chai, W.; Yang, H.M.; Xing, F.; Kwon, B.I. Analysis and Design of a PM-Assisted Wound Rotor Synchronous Machine With Reluctance Torque Enhancement. IEEE Trans. Ind. Electron. 2021, 68, 2887–2897. [Google Scholar] [CrossRef]
- Maroufian, S.S.; Pillay, P. Design and Analysis of a Novel PM-Assisted Synchronous Reluctance Machine Topology With AlNiCo Magnets. IEEE Trans. Ind. Appl. 2019, 55, 4733–4742. [Google Scholar] [CrossRef]
- Huynh, T.A.; Hsieh, M.F.; Shih, K.J.; Kuo, H.F. An Investigation Into the Effect of PM Arrangements on PMa-SynRM Performance. IEEE Trans. Ind. Appl. 2018, 54, 5856–5868. [Google Scholar] [CrossRef]
- Baka, S.; Sashidhar, S.; Fernandes, B.G. Design of an Energy Efficient Line-Start Two-Pole Ferrite Assisted Synchronous Reluctance Motor for Water Pumps. IEEE Trans. Energy Convers. 2021, 36, 961–970. [Google Scholar] [CrossRef]
- Shen, J.X.; Cai, S.; Shao, H.; Hao, H. Evaluation of low-cost high-performance synchronous motors for ventilation application. In Proceedings of the 2015 International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Kuwait City, Kuwait, 23–25 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, X.; Quan, L.; Du, Y.; Xiang, Z.; Zhu, X. Design and Analysis of a Hybrid Permanent Magnet Assisted Synchronous Reluctance Motor Considering Magnetic Saliency and PM Usage. IEEE Trans. Appl. Supercond. 2018, 28, 5200306. [Google Scholar] [CrossRef]
- Dong-liang, L.; Aqiang, L.; Wei, L.; Jian, W. Rotor optimization of permanent magnet-assisted synchronous reluctance motor for electric vehicles. Electr. Mach. Control 2022, 26, 119–129. [Google Scholar] [CrossRef]
- Yingqian, L.; Yi, S.; Yunchong, W.; Jianxin, S. A Hybrid PM-Assisted SynRM with Ferrite and Rare-Earth Magnets. Trans. China Electrotech. Soc. 2022, 37, 1145–1157. [Google Scholar] [CrossRef]
- Yi, S.; Shun, C.; Yingqian, L.; Yunchong, W.; Jianxin, S. Top-Level Design Pattern of PM-Assisted Synchronous Reluctance Machines. Trans. China Electrotech. Soc. 2022, 37, 2306–2318. [Google Scholar] [CrossRef]
- Korman, O.; Nardo, M.D.; Degano, M.; Gerada, C. A Novel Flux Barrier Parametrization for Synchronous Reluctance Machines. IEEE Trans. Energy Convers. 2022, 37, 675–684. [Google Scholar] [CrossRef]
- Credo, A.; Fabri, G.; Villani, M.; Popescu, M. Adopting the Topology Optimization in the Design of High-Speed Synchronous Reluctance Motors for Electric Vehicles. IEEE Trans. Ind. Appl. 2020, 56, 5429–5438. [Google Scholar] [CrossRef]
- Mohammadi, A.; Mirimani, S.M. Design of a Novel PM-Assisted Synchronous Reluctance Motor Topology Using V-Shape Permanent Magnets for Improvement of Torque Characteristic. IEEE Trans. Energy Convers. 2022, 37, 424–432. [Google Scholar] [CrossRef]
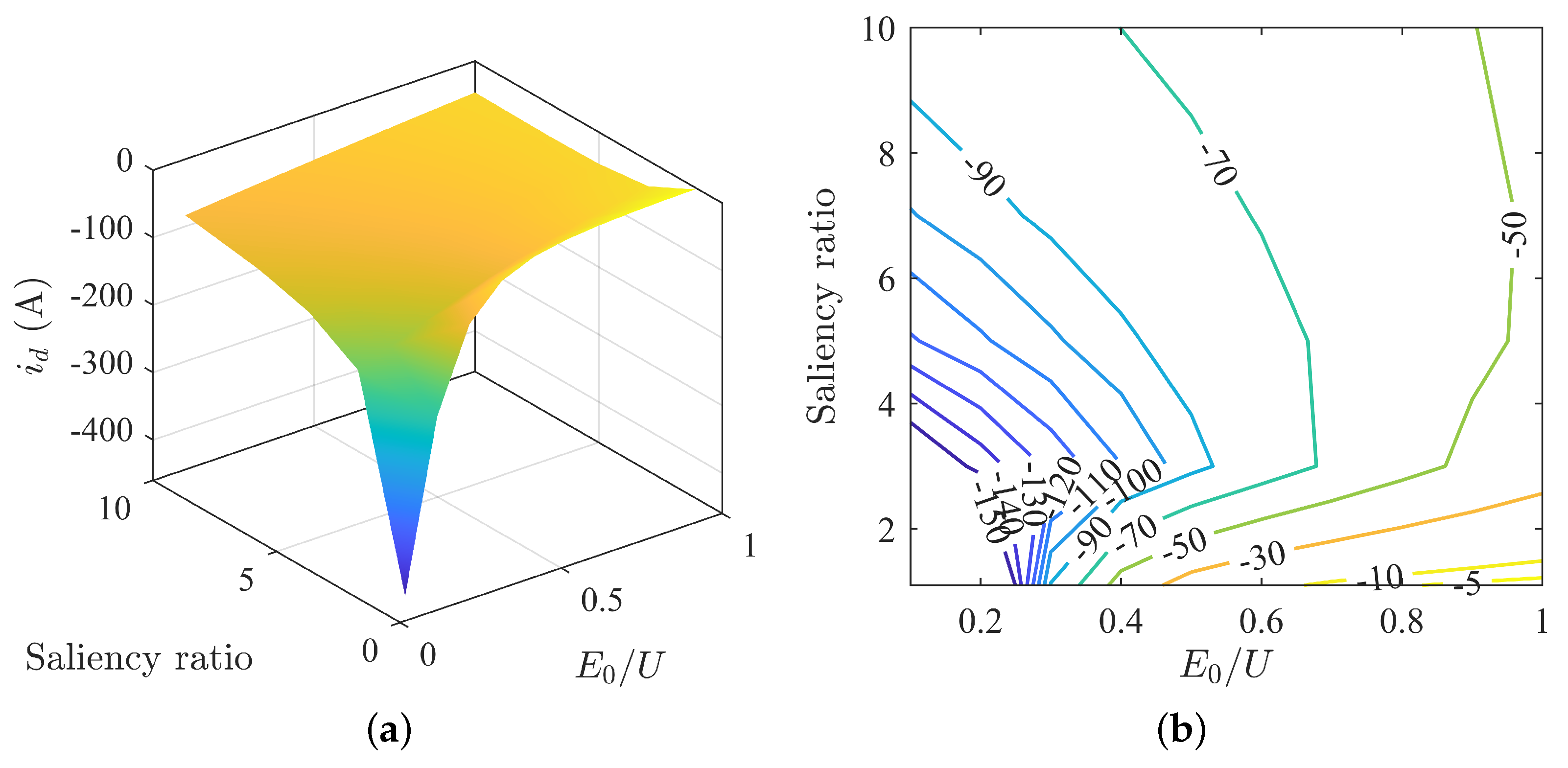
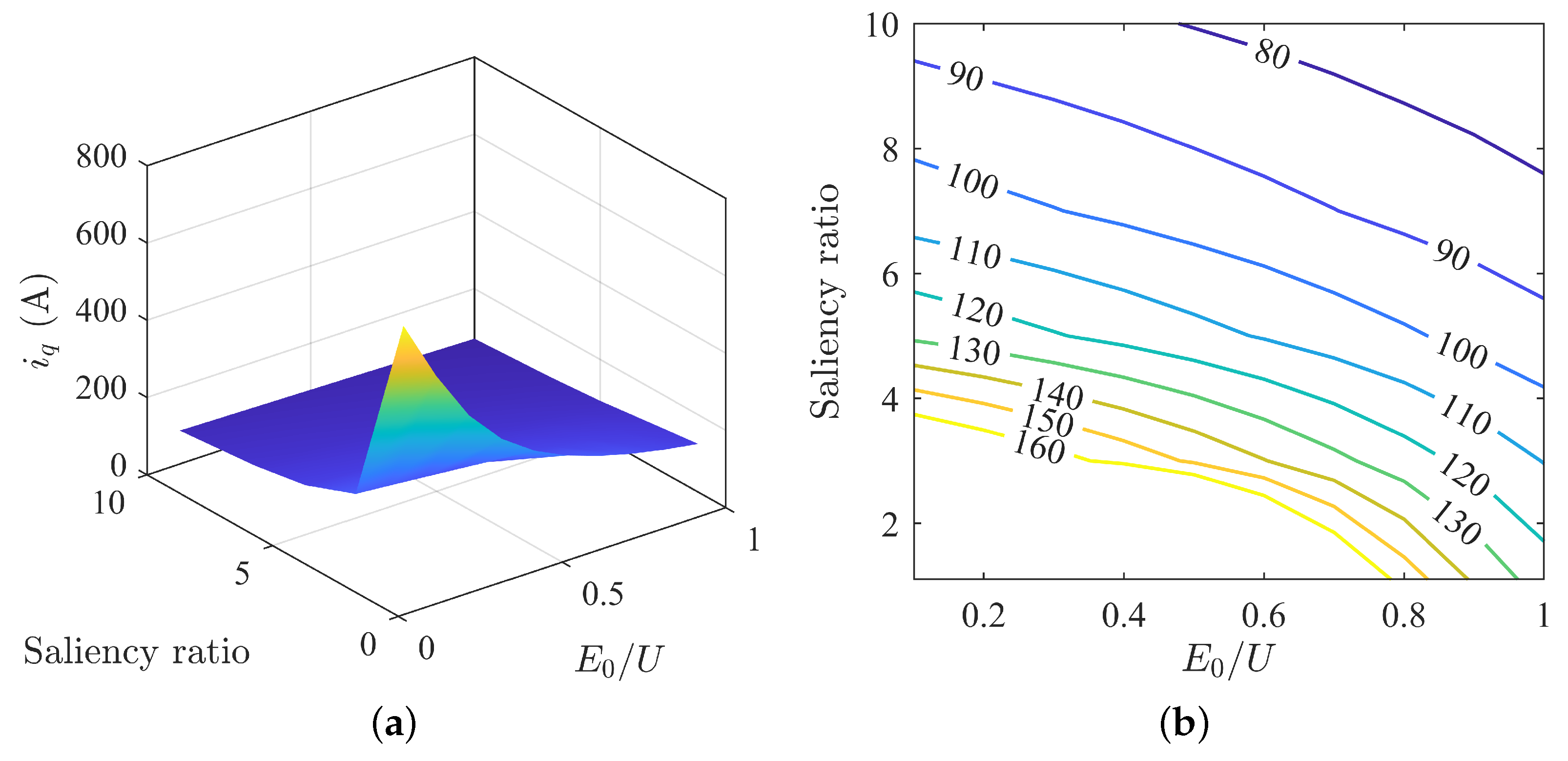
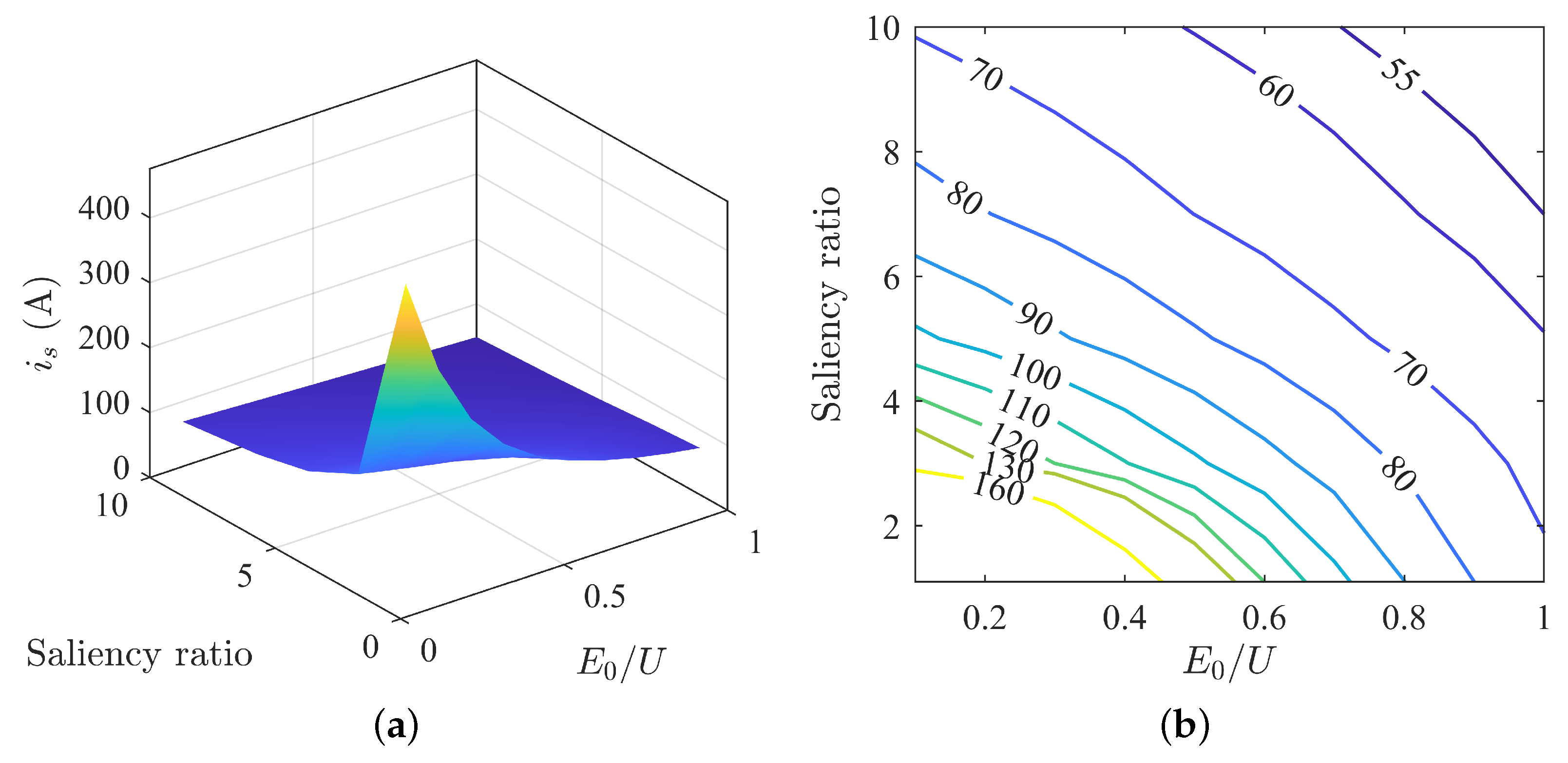
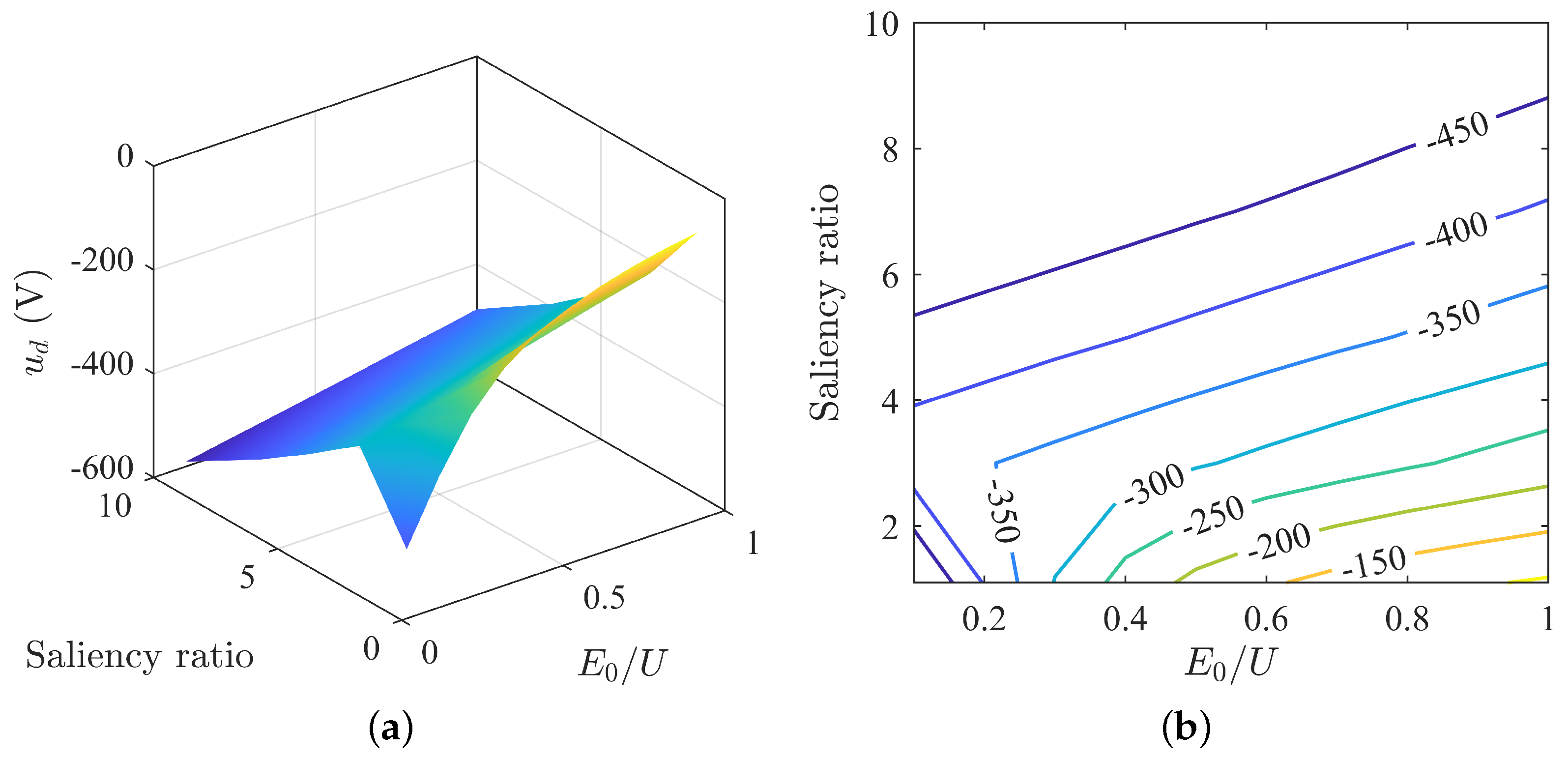



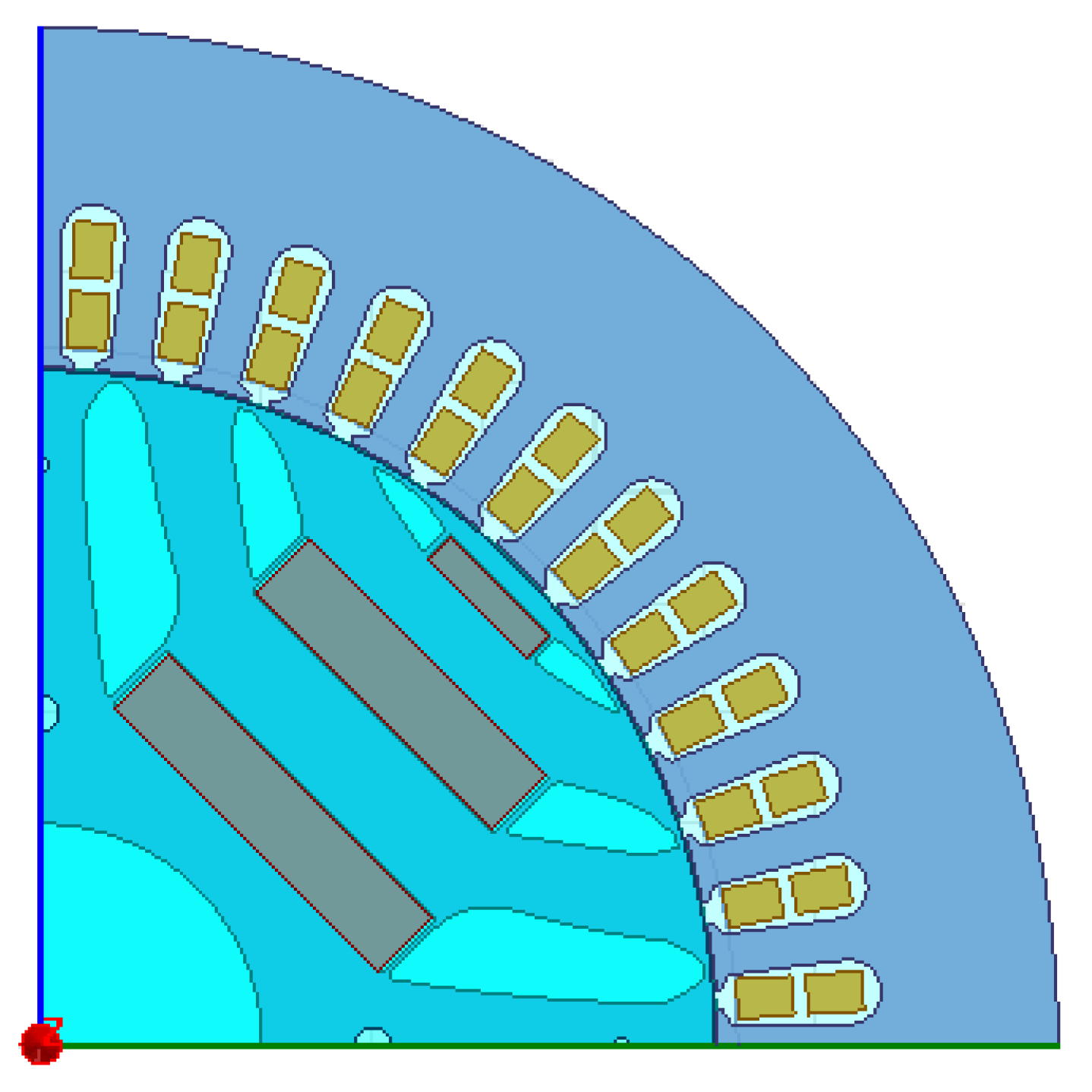
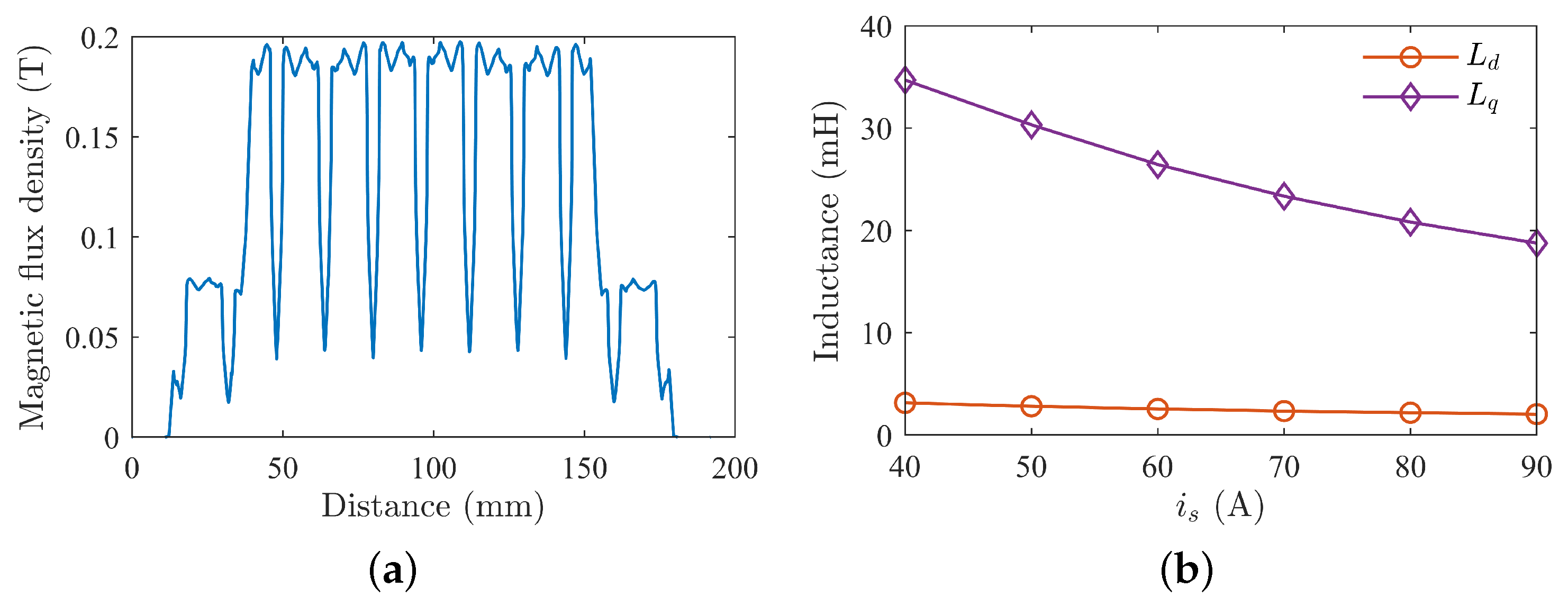


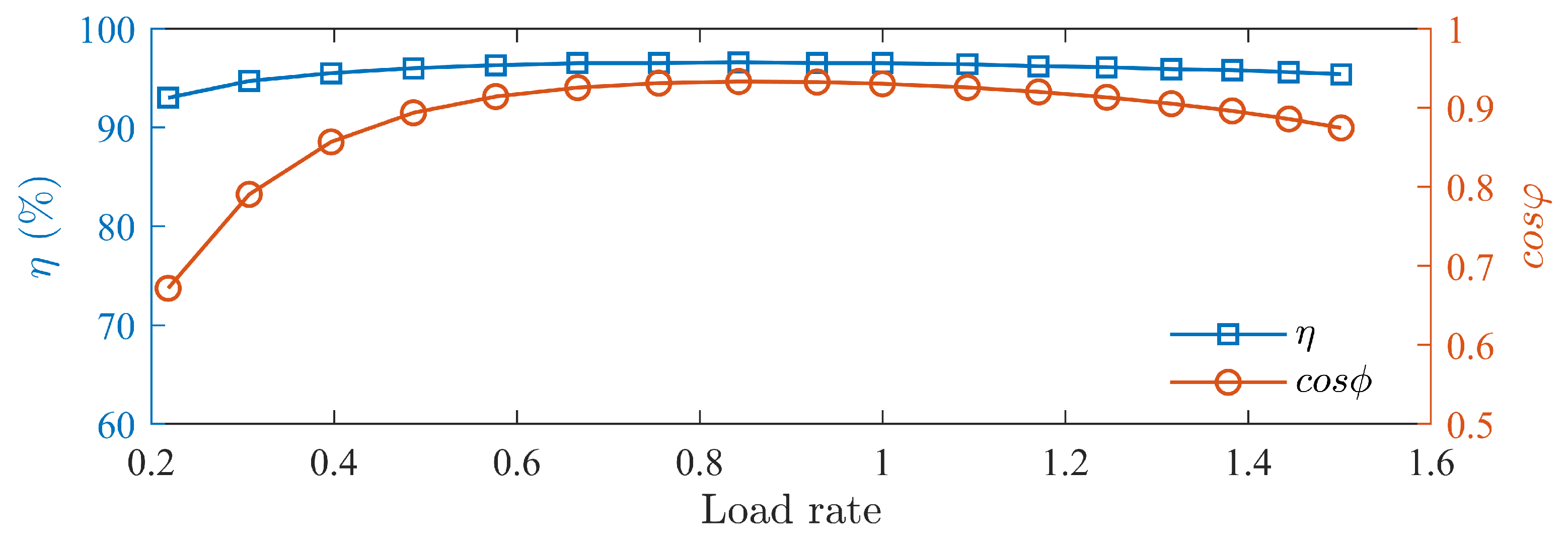
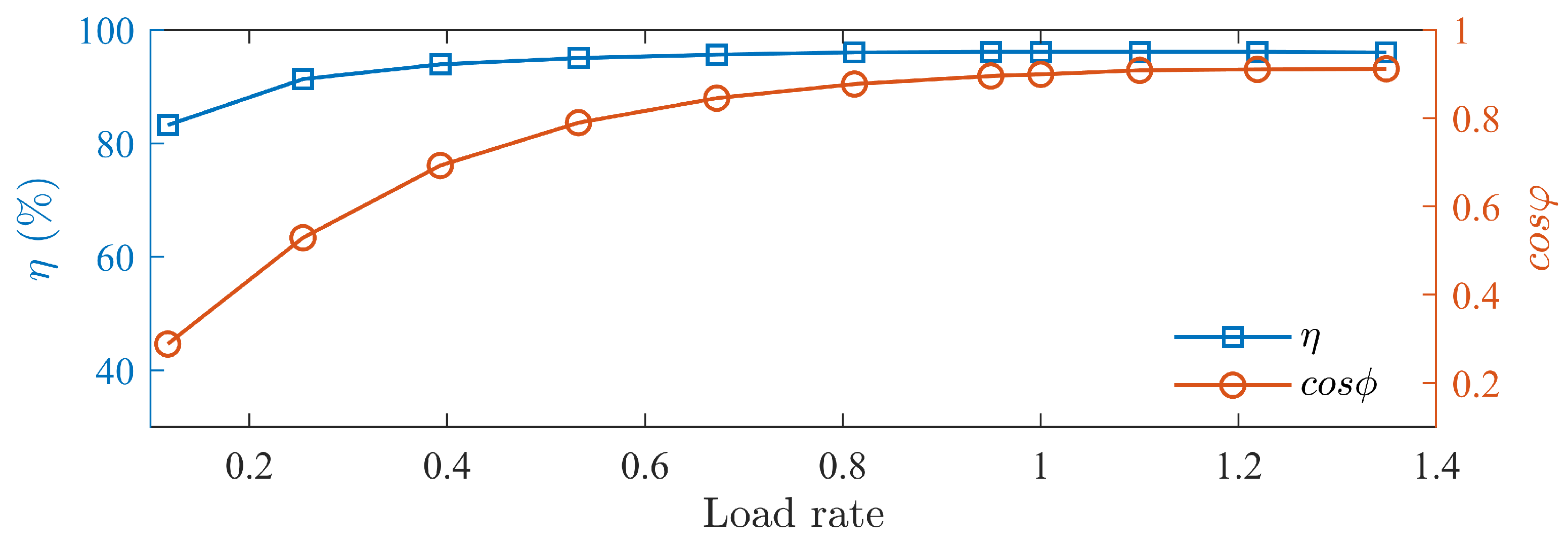
| Parameter | Stator Current/A |
|---|---|
| = 0.9, = 2.55 | 75.07 |
| = 0.68, = 5 | 74.75 |
| = 0.59, = 6 | 74.98 |
| = 0.51, = 7 | 75.16 |
| = 0.47, = 8 | 74.72 |
| = 0.42, = 9 | 74.76 |
| = 0.38, = 10 | 74.57 |
| Parameter | Value |
|---|---|
| Power | 45 kW |
| Speed | 1500 rpm |
| Number of poles | 4 |
| Stator inner/outer diameter | 368 mm/245 mm |
| Number of stator slots | 48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, Y.-H.; Wan, W.-J.; Wang, J. Analysis of Parameter Matching on the Steady-State Characteristics of Permanent Magnet-Assisted Synchronous Reluctance Motors under Vector Control. Actuators 2024, 13, 198. https://doi.org/10.3390/act13060198
Lan Y-H, Wan W-J, Wang J. Analysis of Parameter Matching on the Steady-State Characteristics of Permanent Magnet-Assisted Synchronous Reluctance Motors under Vector Control. Actuators. 2024; 13(6):198. https://doi.org/10.3390/act13060198
Chicago/Turabian StyleLan, Yu-Hua, Wen-Jie Wan, and Jin Wang. 2024. "Analysis of Parameter Matching on the Steady-State Characteristics of Permanent Magnet-Assisted Synchronous Reluctance Motors under Vector Control" Actuators 13, no. 6: 198. https://doi.org/10.3390/act13060198
APA StyleLan, Y.-H., Wan, W.-J., & Wang, J. (2024). Analysis of Parameter Matching on the Steady-State Characteristics of Permanent Magnet-Assisted Synchronous Reluctance Motors under Vector Control. Actuators, 13(6), 198. https://doi.org/10.3390/act13060198






