The Design and Analysis of a Tunnel Retro-Reflective Ring Climbing and Cleaning Robot
Abstract
1. Introduction
2. Problem Description and System Design
2.1. The Tunnel Retro-Reflective Ring Exhibits Inherent Issues That Merit Attention
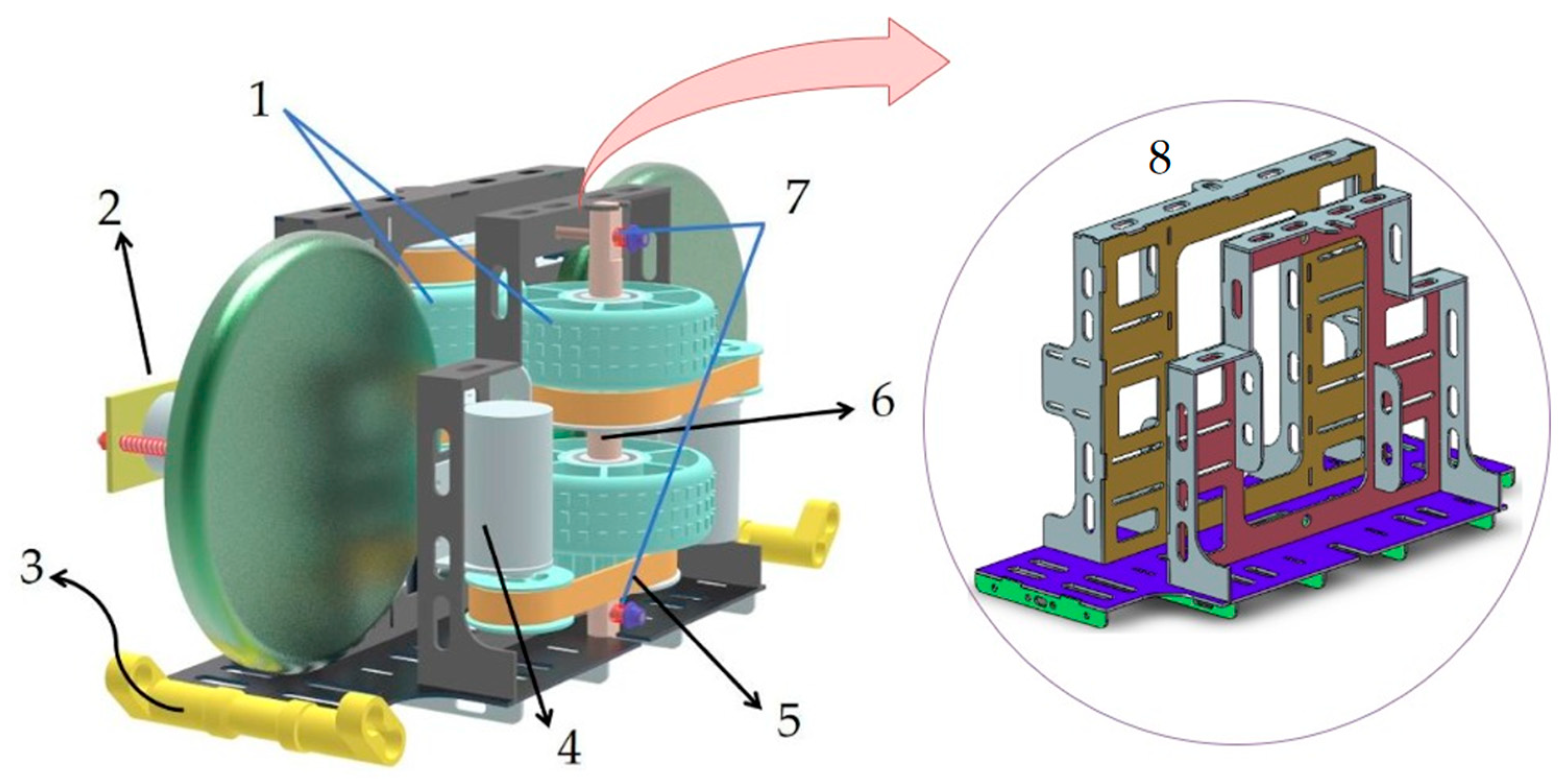
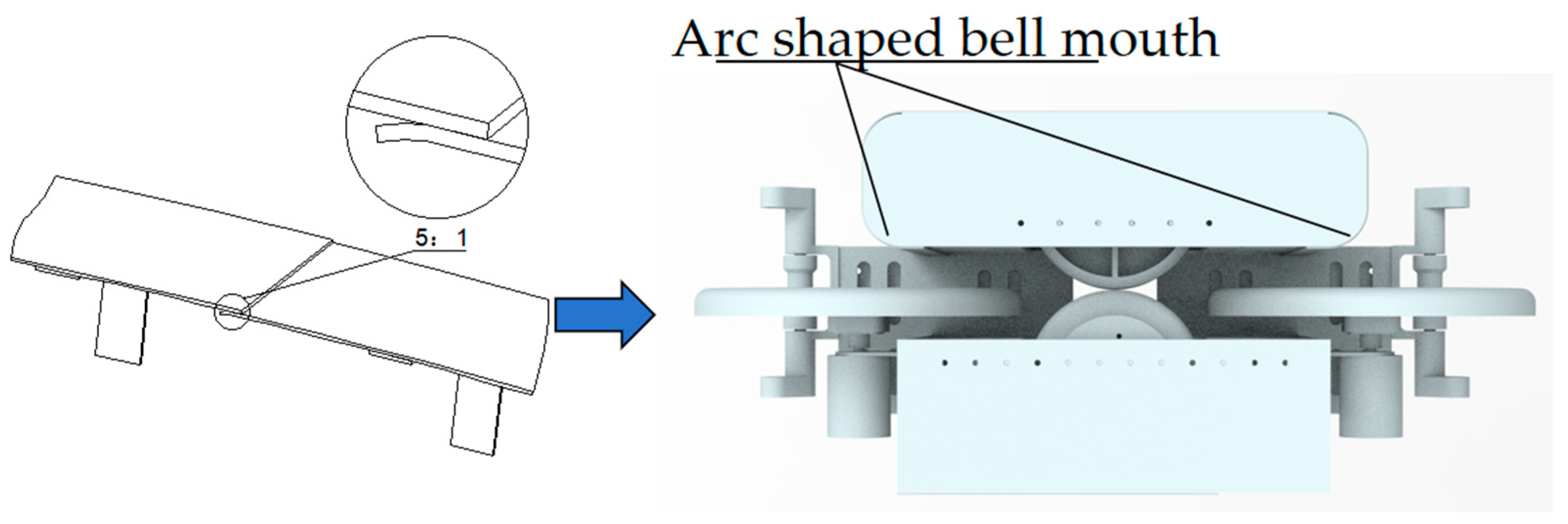
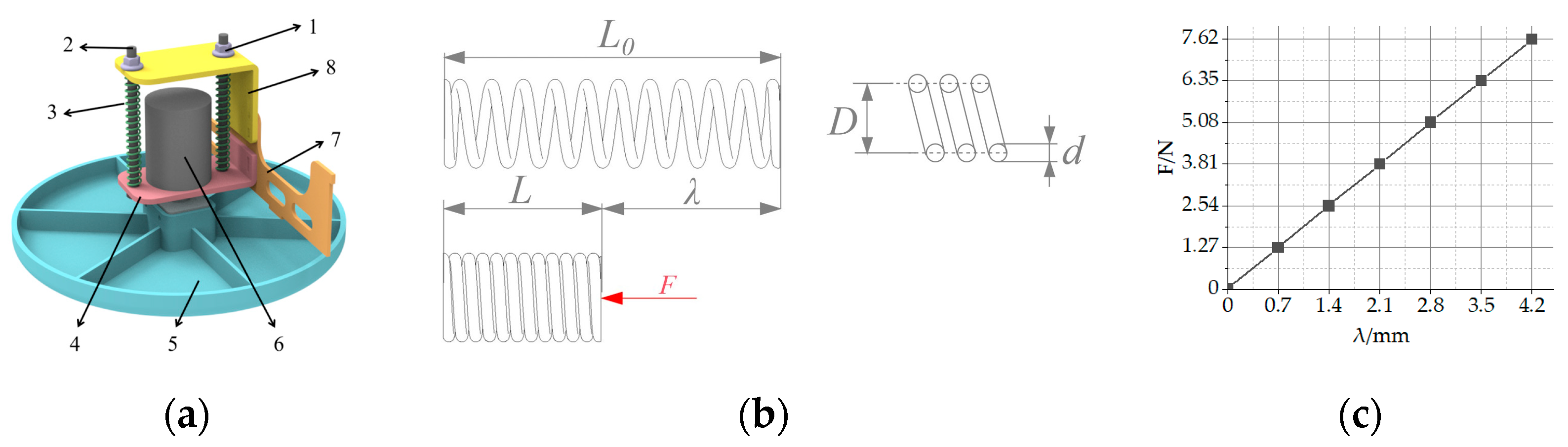
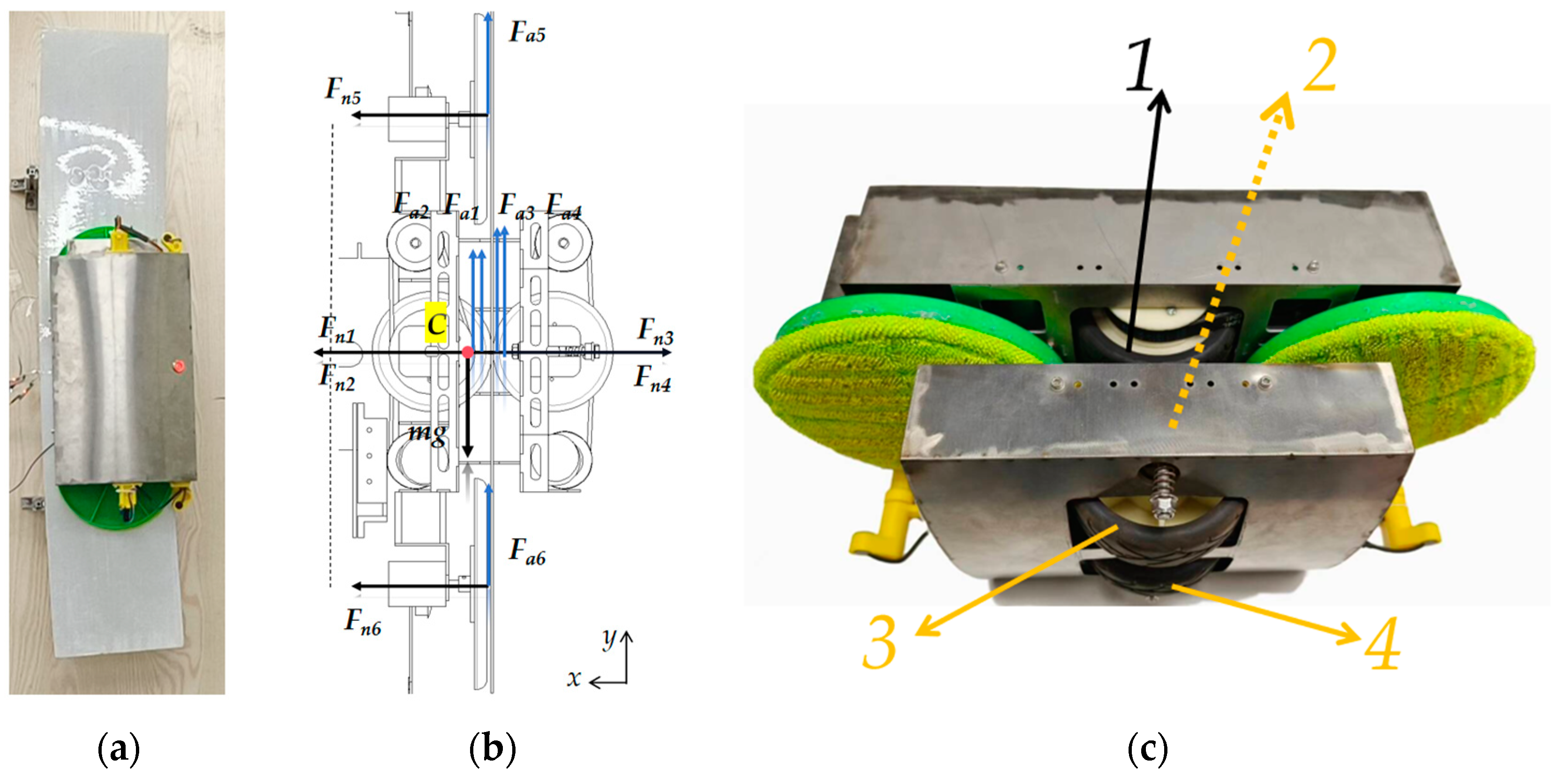
2.2. Mechanical Structure Design
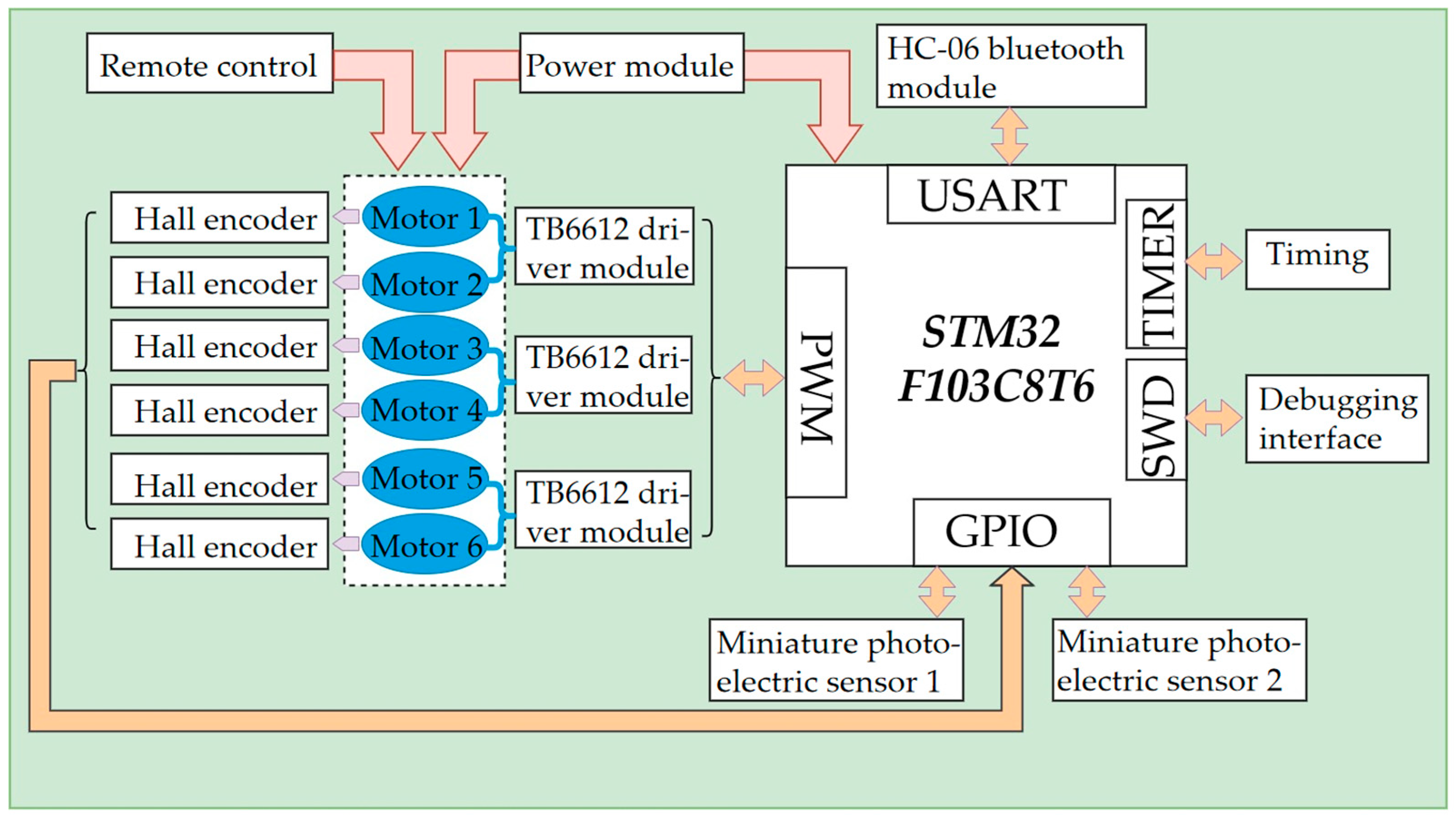
2.3. Hardware Design
2.4. Microcontroller Programming
2.5. Control of Miniature Photoelectric Sensor
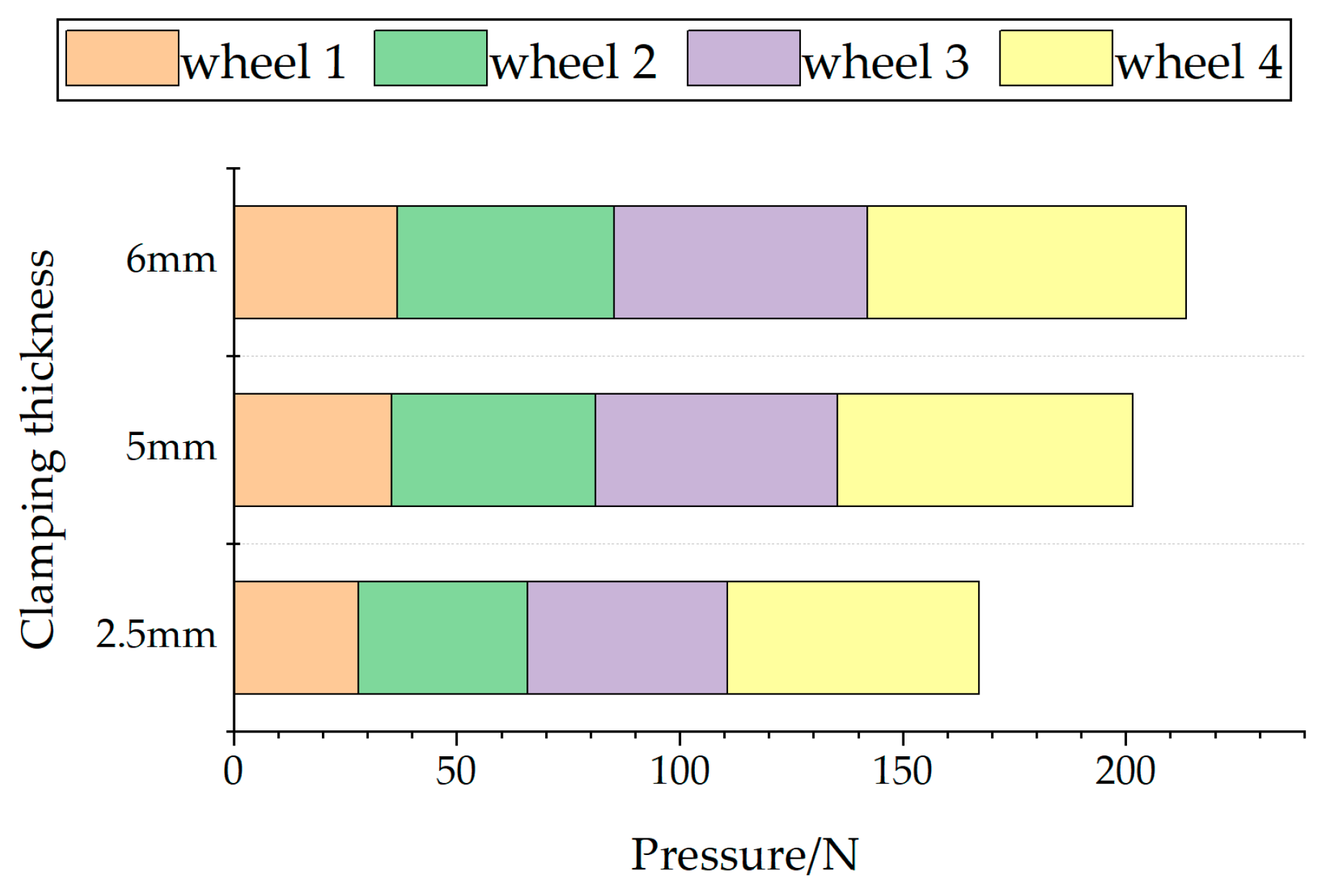
3. Stability Analysis
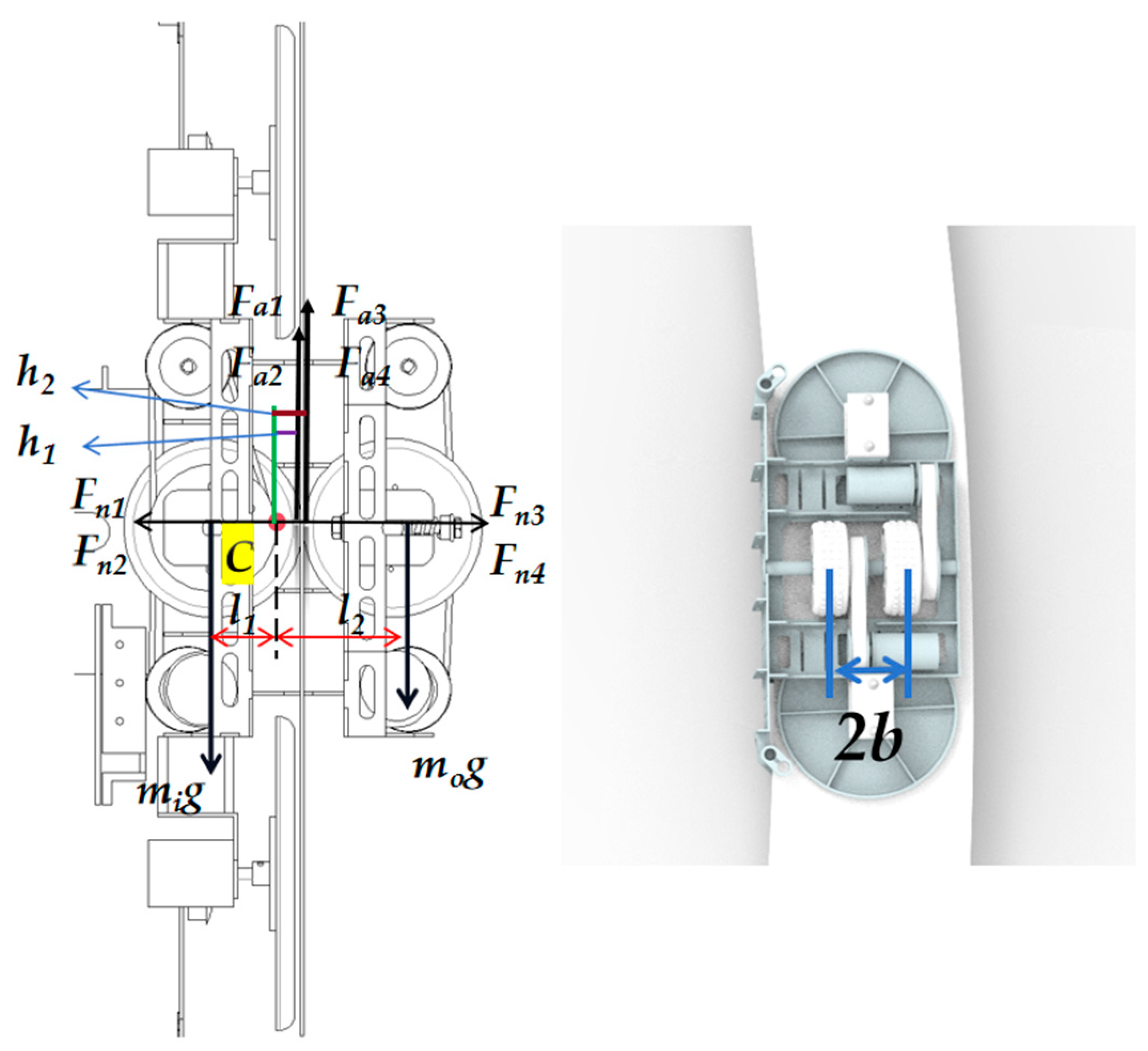
3.1. Static Force Analysis
3.2. Static Moment Analysis
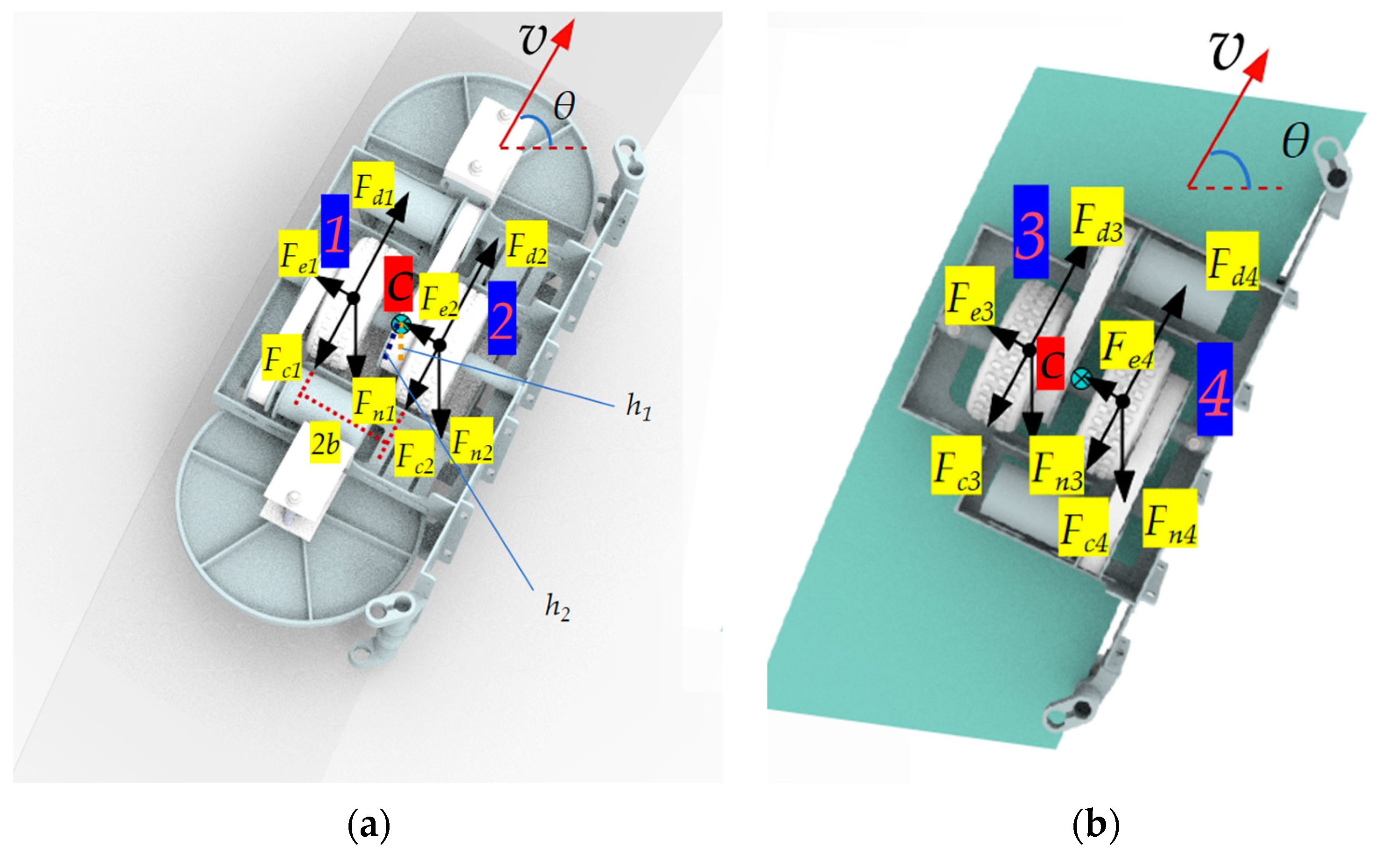
3.3. Dynamics Analysis
- (1)
- The external forces on the robot are evenly distributed;
- (2)
- The robot does not exhibit wheel slippage, overturning, or lateral sliding;
- (3)
- When the robot moves on the retro-reflective ring, its acceleration and rotational acceleration about the center of mass are zero, that is, = 0, = 0.
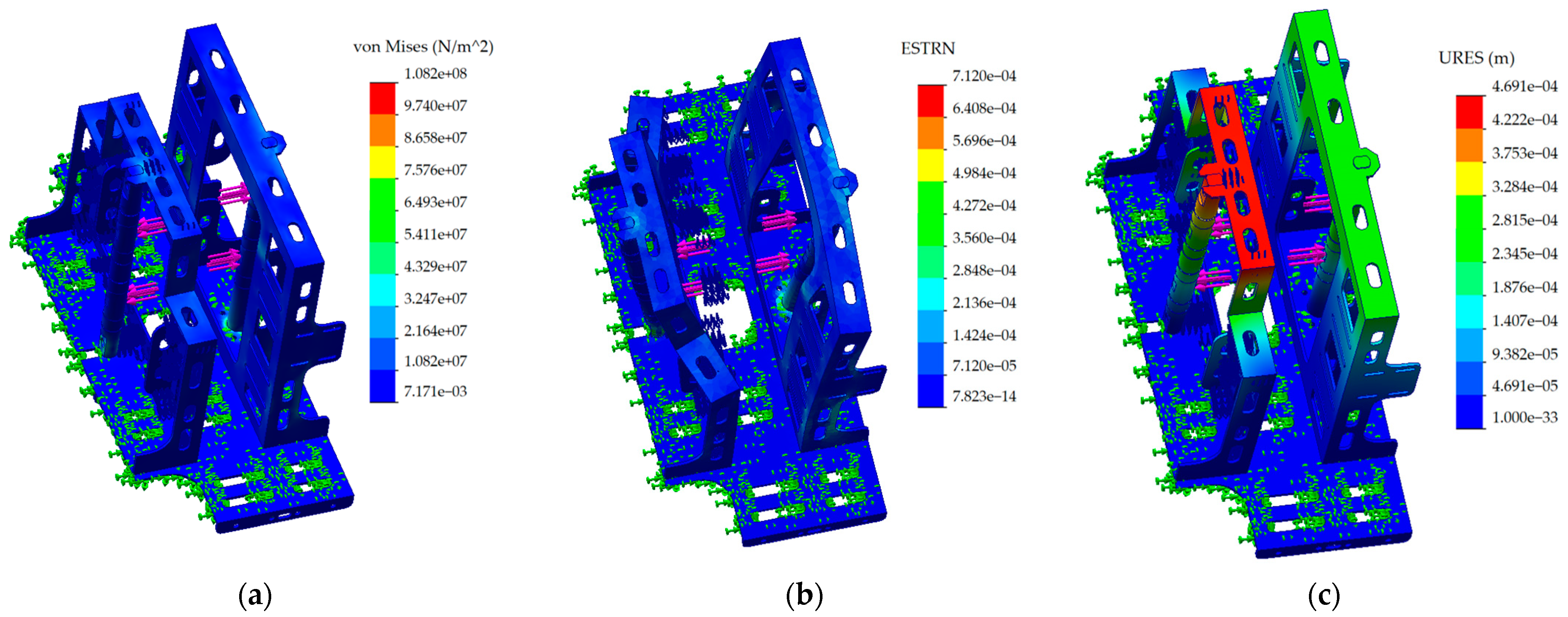
4. Optimization Design
- (1)
- The influence of different materials on the deformation of the frame.
- (2)
- The influence of sheet thickness on the deformation of the frame.
5. Experiments and Analysis
5.1. Analysis of Stable Climbing Experiments
5.2. Response Surface Methodology (RSM) Optimization Experiment
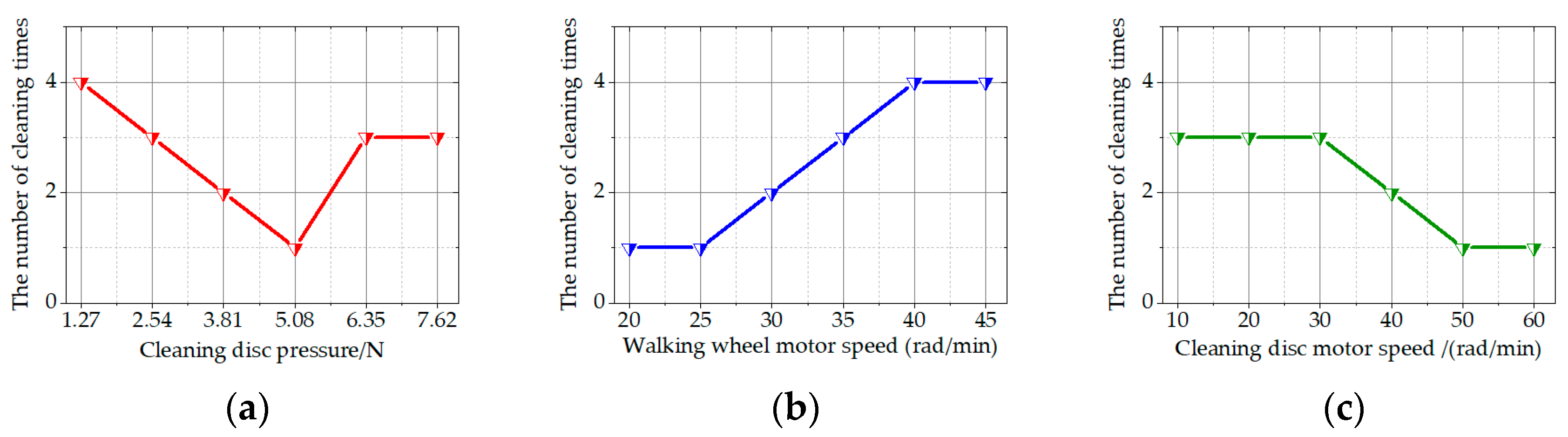
5.2.1. Single-Factor Test
5.2.2. Response Surface Experimental Design
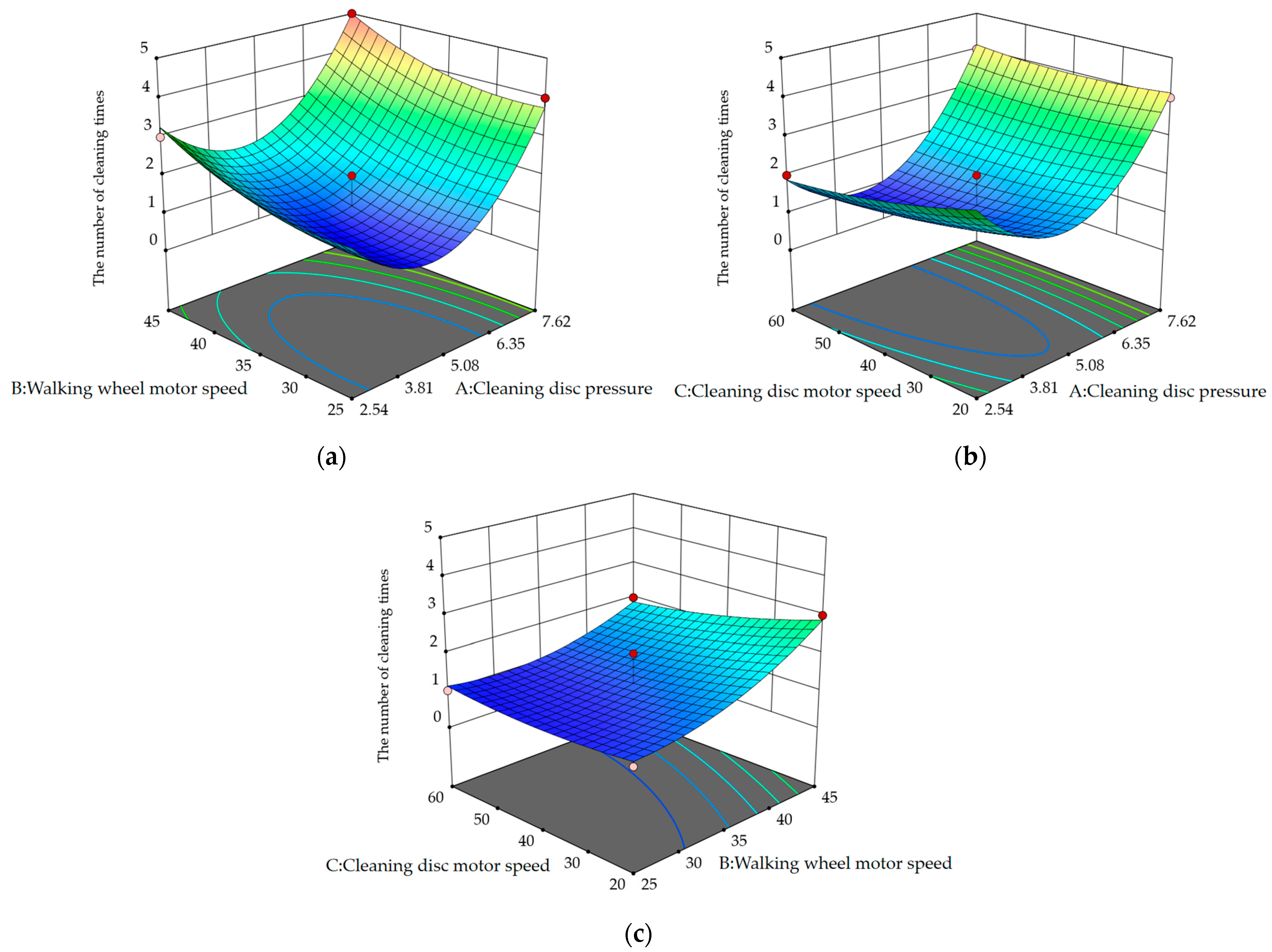
5.2.3. Response Surface Experimental Analysis
5.3. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Zhang, C.; Ju, Y.; Li, J.; Bian, Y.; Ma, J. Evaluation of tunnel retro-reflective arch in an extra-long tunnel based on the matter-element extension method. Accid. Anal. Prev. 2021, 150, 105913. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z. A Tunnel Retro-Reflective Ring Cleaning Device. CN213086674U, 30 April 2021. [Google Scholar]
- Yang, Y.; Cao, J. A Highway Tunnel Retro-Reflective Ring Self-Cleaning Device and Its Cleaning Method. CN110882957B, 14 July 2023. [Google Scholar]
- Liu, J.H.; Padrigalan, K.E. The Kinematic Analysis of a Wind Turbine Climbing Robot Mechanism. Appl. Sci. 2022, 12, 1210. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, S.; Liu, X.; Wang, Y. Design and analysis of a climbing robot for pylon maintenance. Ind. Rob. 2018, 45, 206–219. [Google Scholar] [CrossRef]
- Bogue, R. Climbing robots: Recent research and emerging applications. Ind. Rob. 2019, 46, 721–727. [Google Scholar] [CrossRef]
- Chu, B.; Jung, K.; Han, C.S.; Hong, D. A survey of climbing robots: Locomotion and adhesion. Int. J. Precis. Eng. Manuf. 2010, 11, 633–647. [Google Scholar] [CrossRef]
- Murphy, M.P.; Kute, C.; Mengüç, Y.; Sitti, M. Waalbot II: Adhesion recovery and improved performance of a climbing robot using fibrillar adhesives. Int. J. Robot. Res. 2011, 30, 118–133. [Google Scholar] [CrossRef]
- Schultz, J.T.; Beck, H.K.; Haagensen, T.; Proost, T.; Clemente, C.J. Using a biologically mimicking climbing robot to explore the performance landscape of climbing in lizards. Proc. R. Soc. B 2021, 288, 20202576. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Feng, S.; Yan, S.; Liu, X.; Yang, P.A.; Yang, X.; Shou, M.; Yu, Z. Wind Resistance Mechanism of an Anole Lizard-Inspired Climbing Robot. Sensors 2022, 22, 7826. [Google Scholar] [CrossRef]
- Zhu, H.; Guan, Y.; Wu, W.; Zhang, L.; Zhou, X.; Zhang, H. Autonomous pose detection and alignment of suction modules of a biped wall-climbing robot. IEEE/ASME Trans. Mechatron. 2014, 20, 653–662. [Google Scholar] [CrossRef]
- Guan, Y.; Zhu, H.; Wu, W.; Zhou, X.; Jiang, L.; Cai, C.; Zhang, L.; Zhang, H. A modular biped wall-climbing robot with high mobility and manipulating function. IEEE/ASME Trans. Mechatron. 2012, 18, 1787–1798. [Google Scholar] [CrossRef]
- Hu, Q.; Dong, E.; Sun, D. Soft modular climbing robots. IEEE Trans. Robot. 2022, 39, 399–416. [Google Scholar] [CrossRef]
- Enjikalayil Abdulkader, R.; Veerajagadheswar, P.; Htet Lin, N.; Kumaran, S.; Vishaal, S.R.; Mohan, R.E. Sparrow: A magnetic climbing robot for autonomous thickness measurement in ship hull maintenance. J. Mar. Sci. Eng. 2020, 8, 469. [Google Scholar] [CrossRef]
- Zhao, Z.; Tao, Y.; Wang, J.; Hu, J. The multi-objective optimization design for the magnetic adsorption unit of wall-climbing robot. J. Mech. Sci. Technol. 2022, 36, 305–316. [Google Scholar] [CrossRef]
- Spenko, M.J.; Haynes, G.C.; Saunders, J.A.; Cutkosky, M.R.; Rizzi, A.A.; Full, R.J.; Koditschek, D.E. Biologically inspired climbing with a hexapedal robot. J. Field Robot. 2008, 25, 223–242. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, S.; Wu, X.; Mei, T. A wheeled wall-climbing robot with bio-inspired spine mechanisms. J. Bionic Eng. 2015, 12, 17–28. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Yang, H.; Lee, K.; Seo, K.; Chang, D.; Kim, J. Development of a wall-climbing robot using a tracked wheel mechanism. J. Mech. Sci. Technol. 2008, 22, 1490–1498. [Google Scholar] [CrossRef]
- Seo, K.; Cho, S.; Kim, T.; Kim, H.S.; Kim, J. Design and stability analysis of a novel wall-climbing robotic platform (ROPE RIDE). Mech. Mach. Theory 2013, 70, 189–208. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Y.; Huang, Y. Failure analysis of a helical compression spring for a heavy vehicle’s suspension system. Case Stud. Eng. Fail. Anal. 2014, 2, 169–173. [Google Scholar] [CrossRef]
- Akinfiev, T.; Armada, M.; Prieto, M.; Uquillas, M. Concerning a Technique for Increasing Stability of Climbing Robots. J. Intell. Robot. Syst. 2000, 27, 195–209. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y.; Liu, H.; Zhong, D. Design and Analysis of wheel-foot Magnetic Adsorption Barrier Climbing Robot. J. Mech. Eng. 2024, 60, 248–261. [Google Scholar]
- Wang, D.; Xu, S.; Li, Z.; Cao, W. Analysis of the influence of parameters of a spraying system designed for UAV application on the spraying quality based on Box–Behnken response surface method. Agriculture 2022, 12, 131. [Google Scholar] [CrossRef]
- Benyounis, K.Y.; Olabi, A.G.; Hashmi, M.S.J. Multi-response optimization of CO2 laser-welding process of austenitic stainless steel. Opt. Laser Technol. 2008, 40, 76–87. [Google Scholar] [CrossRef]








| 201 Stainless Steel | QT600 Cast Iron | 7075 Aluminum Alloy | |
|---|---|---|---|
| Density | 7859 kg/m3 | 7200 kg/m3 | 2830 kg/m3 |
| Elastic modulus | 2.07 × 1011 Pa | 6.62 × 1010 Pa | 7.20 × 1010 Pa |
| Factors | Level | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| Cleaning disc pressure (A/N) | 2.54 | 5.08 | 7.62 |
| Walking wheel motor speed(B/(rad/min)) | 25 | 35 | 45 |
| Cleaning disc motor speed(C/(rad/min)) | 20 | 40 | 60 |
| NO. | A | B | C | S |
|---|---|---|---|---|
| 1 | 5.08 | 25 | 60 | 1 |
| 2 | 5.08 | 35 | 40 | 1 |
| 3 | 5.08 | 35 | 40 | 1 |
| 4 | 2.54 | 35 | 20 | 3 |
| 5 | 5.08 | 35 | 40 | 2 |
| 6 | 7.62 | 45 | 40 | 5 |
| 7 | 5.08 | 45 | 60 | 2 |
| 8 | 5.08 | 35 | 40 | 1 |
| 9 | 2.54 | 45 | 40 | 3 |
| 10 | 7.62 | 35 | 20 | 4 |
| 11 | 5.08 | 35 | 40 | 1 |
| 12 | 5.08 | 25 | 20 | 1 |
| 13 | 7.62 | 35 | 60 | 4 |
| 14 | 7.62 | 25 | 40 | 4 |
| 15 | 2.54 | 25 | 40 | 2 |
| 16 | 5.08 | 45 | 20 | 3 |
| 17 | 2.54 | 35 | 60 | 2 |
| Sum of Squares | Freedom of Degree | Mean Square | F-Value | p-Value | Significance | |
|---|---|---|---|---|---|---|
| Model | 26.83 | 9 | 2.98 | 19.88 | 0.0003 | significant |
| A | 6.13 | 1 | 6.13 | 40.83 | 0.0004 | ** |
| B | 3.13 | 1 | 3.13 | 20.83 | 0.0026 | ** |
| C | 0.5 | 1 | 0.5 | 3.33 | 0.1106 | |
| AB | 3.55 × 10–15 | 1 | 3.55 × 10–15 | 2.37 × 10–14 | 1 | |
| AC | 0.25 | 1 | 0.25 | 1.67 | 0.2377 | |
| BC | 0.25 | 1 | 0.25 | 1.67 | 0.2377 | |
| A2 | 15.2 | 1 | 15.2 | 101.33 | <0.0001 | ** |
| B2 | 0.6737 | 1 | 0.6737 | 4.49 | 0.0718 | |
| C2 | 0.0947 | 1 | 0.0947 | 0.6316 | 0.4529 | |
| Residual | 1.05 | 7 | 0.15 | |||
| Lack of Fit | 0.25 | 3 | 0.0833 | 0.4167 | 0.751 | not significant |
| Pure Error | 0.8 | 4 | 0.2 | |||
| Cor Total | 27.88 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Ye, S.; Cui, R.; Shou, Z. The Design and Analysis of a Tunnel Retro-Reflective Ring Climbing and Cleaning Robot. Actuators 2024, 13, 197. https://doi.org/10.3390/act13060197
Li Y, Ye S, Cui R, Shou Z. The Design and Analysis of a Tunnel Retro-Reflective Ring Climbing and Cleaning Robot. Actuators. 2024; 13(6):197. https://doi.org/10.3390/act13060197
Chicago/Turabian StyleLi, Yuhan, Shiqing Ye, Rongxu Cui, and Zhaoyu Shou. 2024. "The Design and Analysis of a Tunnel Retro-Reflective Ring Climbing and Cleaning Robot" Actuators 13, no. 6: 197. https://doi.org/10.3390/act13060197
APA StyleLi, Y., Ye, S., Cui, R., & Shou, Z. (2024). The Design and Analysis of a Tunnel Retro-Reflective Ring Climbing and Cleaning Robot. Actuators, 13(6), 197. https://doi.org/10.3390/act13060197







