A Reliable and Efficient I-f Startup Method of Sensorless Ultra-High-Speed SPMSM for Fuel Cell Air Compressors

Abstract

Extended back electromotive force (EEMF)-based position sensorless field-oriented control (FOC) is widely utilized for ultra-high-speed surface-mounted permanent magnet synchronous motors (UHS-SPMSMs) driven fuel cell air compressors in medium-high speed applications. Unfortunately, the estimated position is imprecise due to too small EEMF under low speed operation. Hence, current-to-frequency (I-f) control is more suitable for startup. Conventional I-f methods rarely achieve the tradeoff between startup acceleration and load capacity, and the transition to sensorless FOC is mostly realized in the constant-speed stage, which is unacceptable for UHS-SPMSM considering the critical requirement of startup time. In this article, a new closed-loop I-f control approach is proposed to achieve fast and efficient startup. The frequency of reference current vector is corrected automatically based on the active power and the real-time motor torque, which contributes to damping effect for startup reliability. Moreover, an amplitude compensator of reference current vector is designed based on the reactive power, ensuring the maximum torque per ampere operation and higher efficiency. Furthermore, the speed PI controller is enhanced by variable bandwidth design for smoother sensorless transition. These theoretical advantages are validated through experiments with a 550 V, 35 kW UHS-SPMSM. The experimental results demonstrated the enhanced startup performance compared with conventional I-f control.

1. Introduction

Due to high efficiency, high power density, and stable rotor structural strength [1,2], ultra-high-speed surface-mounted permanent magnet synchronous motors (UHS-SPMSMs) are being widely used to drive fuel cell air compressors [3,4,5], which in turn provide pressurized air to fuel cell stacks to ensure the power output demand and energy conversion efficiency of hydrogen fuel cell vehicles. UHS-SPMSMs and centrifugal compressors are integrated as the overall compressor system, whose rational speed is typically capable of 100 kr/min and above. Therefore, the mechanical rotor position sensor is replaced by position sensorless control technology in consideration of installation space and reliability, which also reduces maintenance cost.

For medium–high speed applications of UHS-SPMSM, the most commonly used position sensorless methods are based on back electromotive force (EMF) estimation, including the use of sliding mode observer [6,7], extended Kalman filter [8], extended state observer [9], etc. Unfortunately, the EMF is too small to be estimated accurately during low speed operation. For zero–low speed applications of UHS-SPMSM, the typical high frequency signal injection (HFSI) methods [10,11] will no longer be applicable considering the lack of motor saliency due to the equal dq-axes inductances, and the high-frequency noise and torque fluctuations of HFSI are undesirable. The rotor of UHS-SPMSM is carried by a self-acting gas bearing, in which the fluid film is formed by viscous shear forces resulting from the relative motion of journal and bushing under rotation [12]. Therefore, UHS-SPMSM needs to be started rapidly from standstill to a certain speed to ensure the normal performance of gas bearing, and UHS-SPMSM is generally designed with a minimum operating speed (i.e., idle speed) ranging from 20,000 r/min to 30,000 r/min. Under these requirements, the UHS-SPMSM do not operate at ultra-low speed except during startup. Preferably, an uncomplicated yet effective startup strategy, characterized by high dynamic performance, is more advantageous than HFSI methods for expediting the UHS-SPMSM to a speed conducive to accurate EMF estimation.

Voltage-to-frequency (V/f) control has been employed for the startup and speed regulation of UHS-SPMSM owing to its straightforward configuration and reduced number of control loops, including the open-loop optimal V/f control with design consideration to the stator resistance [13], and the closed-loop V/f control with correction of the voltage amplitude and phase [14]. Owing to uncontrollable current and torque ripple, open-loop V/f control is gradually replaced by closed-loop V/f control. In [15], correction loops are designed based on d-axis current error with integrated maximum torque per ampere (MTPA) block, which guarantees good dynamic performance especially at a very low speed. Additionally, a closed-loop V/f control is realized in the voltage vector plane [16]. However, the algorithm complexity increases similar to sensorless field-oriented control (FOC) due to load angle calculation in [15] and rotor position and speed estimation in [16], respectively. In summary, the V/f control has insufficient with-load startup ability, and the control accuracy and efficiency are limited in the medium–high speed range compared with FOC. Therefore, the V/f control is not recommended for the UHS-SPMSM used in hydrogen fuel cell vehicles.

In contrast, another simple and effective startup strategy known as the current-to-frequency (I-f) control is more widely used for the startup of UHS-SPMSM because of its advantages of strong robustness with controllable current loop. The UHS-SPMSM does not always start successfully under open-loop I-f control [17] due to large speed oscillation during the startup stage [18]. The inherent speed oscillation can be suppressed by correcting the frequency of the reference current vector based on active power fluctuation [19]. Meanwhile, with a summary of the change law of the fluctuation amplitude and frequency of torque angle with the motor parameters and the reference current vector [20], the method proposed in [19] can be adaptively designed. Additionally, any signal reflecting speed or torque perturbation can be used to obtain the frequency correction value [21], such as the power factor angle, the calculated torque current, the estimated electromagnetic torque [22], etc. In combination with adaptive back-stepping control [23], fully unknown parameters of SPMSM are able to be estimated accurately, ensuring the effectiveness of I-f control on variation of load and motor parameters.

The reference torque of UHS-SPMSM with conventional I-f startup method far exceeds actual load torque, leading to low motor efficiency. Although adjusting the amplitude of the reference current vector based on reactive power [24,25] and based on power factor [26] can actualize i_d = 0 control to enhance efficiency; this is only realized after the motor speed remains constant. The implementation mode is not applicable for UHS-SPMSM, which needs to complete the transition of the I-f control to EMF-based sensorless control during acceleration process to ensure the dynamic performance and high efficiency of the startup. In [27], variable reference current vector position is designed in the current compensation loop to avoid large transients. However, additional estimated rotor position is needed from EMF-based method. Moreover, the frequency ramp slope of the reference current vector can be dynamically adjusted during motor acceleration using an angle controller [24] or a torque controller [28].The load torque of UHS-SPMSM increases approximately quadratically in terms of the motor speed. In order to prevent the demand torque from exceeding the maximum output torque, the frequency ramp slope needs to be gradually reduced as a result of the dynamic adjustments, which significantly deteriorates the dynamic performance of UHS-SPMSM startup.

The overall requirement of the UHS-SPMSM startup process is high dynamic response with high efficiency. Considering that the frequency ramp slope cannot be set too high for avoiding startup failure, the transition speed from I-f control to sensorless FOC should be set as small as possible. Meanwhile, a smooth transition with a reduced convergence time and speed fluctuations needs to be addressed. The method proposed in [29] of adjusting the initial value of the integrator of the PI controller of the speed loop and current loop can reduce the speed fluctuations. The design of variable decreasing step size of reference current can contribute positively to reducing the transition time [17]. To improve the stability of the transition process, a feedback regulator is designed [30] to automatically adjust the reference current based on the position difference. However, merely with consideration of the constant speed operation, the above I-f control strategies have neglected the transition process during the motor acceleration, where the load torque increases apace in UHS-SPMSM application. The prevailing transition strategies, including the reduction of reference current [31], an adaptive transition algorithm [32], weighted processing method [33], and a first-order lag compensator of position [34], have hitherto placed insufficient emphasis on evaluating the performance of the I-f control preceding the transition.

The novelty in this article, as an extension of the conventional I-f control, is to propose a closed-loop I-f startup strategy with transition enhancement applicable to UHS-SPMSM to achieve a fast, efficient, and stable startup process, which is summarized as:

(1)

The speed convergence performance can be effectively improved by correcting the frequency of reference current vector adaptively based on not only the instantaneous active power but also the real-time motor torque, which reduces speed fluctuations distinctly.

(2)

The amplitude of reference current vector is compensated dynamically during speedup stage instead of during a constant speed stage, which is the basic requirement and distinctiveness for the UHS-SPMSM. Therefore, the reference startup torque can be reduced with improved efficiency under the premise of guaranteeing the startup rapidity.

(3)

The transition process to EMF-based sensorless FOC can be enhanced by designing a bandwidth-variable regulating scheme of speed loop PI controller, which achieves low transitional speed fluctuation. Moreover, the designed scheme can ensure high control stability over rated motor speed, compared with fixed-gain speed loop PI controller.

(4)

To the best of our knowledge, this is the first time that an innovative closed-loop I-f startup strategy is used for UHS-SPMSM startup, especially for driving fuel cell air compressors.

The rest of this article is organized as follows. Section 2 describes the mathematical model of UHS-SPMSM under I-f control. The stability performance of the conventional I-f startup strategy is analyzed in Section 3. Section 4 elaborates on the proposed closed-loop I-f startup strategy with transition enhancement. In Section 5, the effectiveness of the proposed method is verified by bench experiments with a 35 kW (at 95 kr/min) UHS-SPMSM. Finally, the paper is concluded in Section 6.

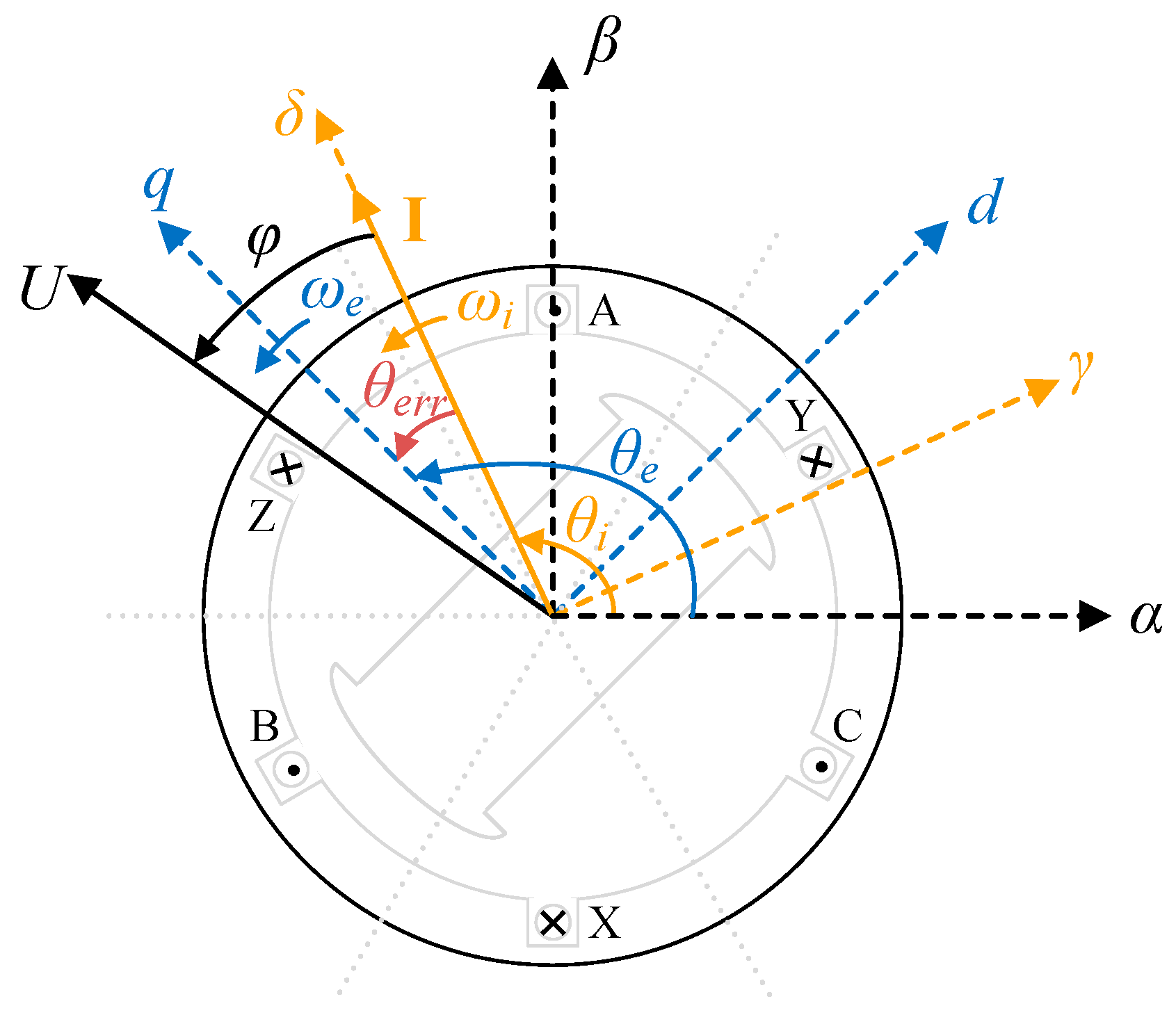
2. Mathematical UHS-SPMSM Model with I-f Control

Due to unknown actual rotor position information during I-f control, the actual d-q reference coordinate frame is also undetermined. Therefore, in order to analyze the characteristics of the controllable current vector, a γ-δ reference coordinate frame is introduced, in which the δ-axis is aligned with the current vector I, as shown in Figure 1. The angles from α-axis to δ-axis and to q-axis are referred to as θ_i and θ_e, respectively. The angle error between θ_i and θ_e is denoted as θ_err = θ_e−θ_i. The frequencies ω_i and ω_e denote angular velocities of current vector and rotor, respectively. φ is the angle between the voltage vector U and the current vector. Without loss of generality, the UHS-SPMSM voltage mathematical model [24] in the γ-δ reference coordinate frame can be expressed as:

$$\left\{\begin{array}{l}{u}_{\gamma }=R_s{i}_{\gamma }+L_d\frac{d}{dt}{i}_{\gamma }-{\omega }_i{L}_q{i}_{\delta }-{\omega }_e{\phi }_f\sin {\theta }_{err}\\ u_{\delta }=R_s{i}_{\delta }+L_q\frac{d}{dt}{i}_{\delta }+{\omega }_i{L}_d{i}_{\gamma }+{\omega }_e{\phi }_f\cos {\theta }_{err}\end{array}\right.$$

(1)

where u_γ, u_δ, i_γ, and i_δ denote the voltages and currents in the γ-δ reference coordinate frame, respectively. R_s, φ_f, L_d, and L_q denote stator resistance, rotor permanent magnet flux linkage, and d- and q-axis inductances, respectively. The condition L_d = L_q holds throughout this article for the studied UHS-SPMSM. ω_e denotes the motor electrical frequency.

Considering that i_γ = 0, (1) can be rewritten as:

$$\left\{\begin{array}{l}{u}_{\gamma }=-{\omega }_i{L}_q{i}_{\delta }-{\omega }_e{\phi }_f\sin {\theta }_{err}\\ u_{\delta }=R_s{i}_{\delta }+L_q\frac{d}{dt}{i}_{\delta }+{\omega }_e{\phi }_f\cos {\theta }_{err}\end{array}\right.$$

(2)

The frequency error between ω_i and ω_e can be obtained from the derivative of angle error.

$$\Delta \omega ={\omega }_e-{\omega }_i=\frac{d}{dt}{\theta }_{err}=\frac{d}{dt}({\theta }_e-{\theta }_i)$$

(3)

In addition, the UHS-SPMSM electromagnetic torque [24] can be expressed by the current vector amplitude I_m and angle θ_err as follows with L_d = L_q.

$$\begin{array}{ll}{T}_e& =1.5n_p{i}_q[{\phi }_f+(L_d-L_q)i_d]\hfill \\ & =1.5n_p{\phi }_f{I}_m\cos {\theta }_{err}\hfill \end{array}$$

(4)

where n_p denotes the number of pole pairs.

Therefore, the motion equation [24] of UHS-SPMSM is expressed as:

$$J\frac{d{\omega }_m}{dt}=T_e-T_L-B{\omega }_m$$

(5)

where ω_m = ω_e/n_p is the rotor mechanical frequency. J is the motor inertia, B is the damping coefficient, and T_L denotes the load torque.

3. Conventional I-f Startup Method

I-f control establishes the relationship between reference current and reference frequency under the current closed-loop control so that the output torque is load-capable. Conventionally, the current vector amplitude is set at a large constant value, while the current vector frequency ramps up with time at a fixed ramp slope, as shown in Figure 2. The integration of the frequency yields the rotor position information needed by park and anti-park transformation, i.e.,

$${\theta }_i={\displaystyle \int {\omega }_i}dt.$$

(6)

Since the electrical response is much faster than the mechanical effect, the actual current vector can be considered to be the same as the reference current vector, where the δ-axis reference current is equal to the reference current vector amplitude (e.g., the rated value I_n), while the γ-axis reference current is set to 0, i.e.,

$$i_{\gamma }=0,i_{\delta }=I_n.$$

(7)

When the UHS-SPMSM exceeds the transition speed during the ramp up stage, according to the self-stabilization mechanism [31], the θ_err decreases with the reduction of the reference current amplitude. Therefore, the transition from I-f control to sensorless FOC can be successfully accomplished when the θ_err is smaller than a certain threshold value (e.g., 0.05 rad). It is worth noting that the estimated rotor position ${\widehat{\theta }}_e$ by extended EMF (EEMF)-based method proposed in [35] can be used to replace the actual one during the transition process:

$${\theta }_{err}={\theta }_e-{\theta }_i\approx {\widehat{\theta }}_e-{\theta }_i.$$

(8)

Generally, after successful transition, the UHS-SPMSM operates in double closed-loop control of speed and current. However, the inherent properties of speed oscillation and prone asynchronous operation of conventional I-f control cause incidental startup failures.

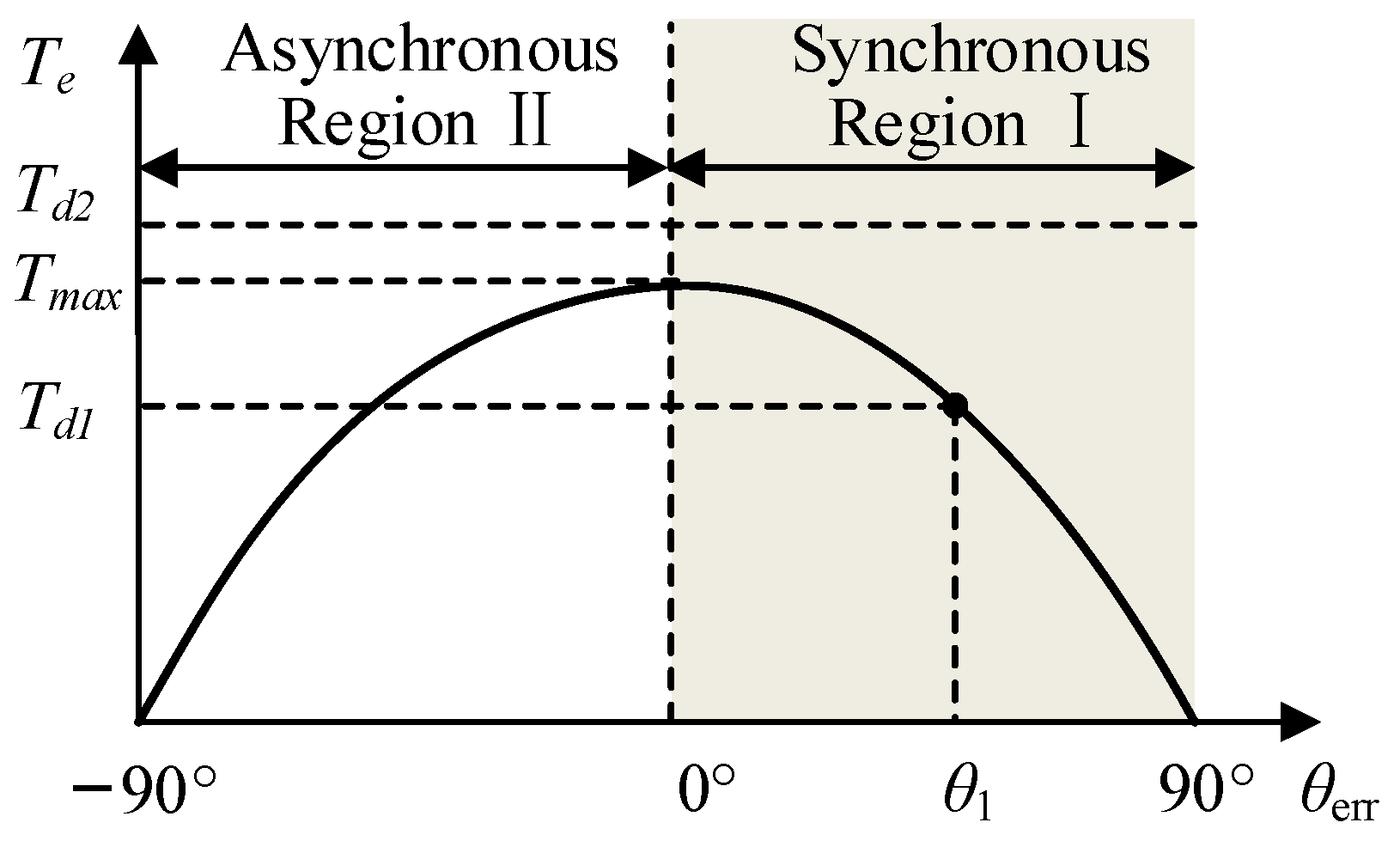
3.1. Inherent Speed Oscillation

Small signal model is aptly utilized to analyze the performance of UHS-SPMSM under I-f control. Therefore, the torque Equation (4) is linearized to represent the dynamic characteristics at a certain static operating point, i.e.,

$$\Delta T_e=K_I\Delta I-K_{\theta }\Delta {\theta }_{err}$$

(9)

with:

$$\left\{\begin{array}{l}{K}_I=\frac{\partial T_e}{\partial I_m}=1.5n_p{\phi }_f\cos {\theta }_{err}\\ K_{\theta }=-\frac{\partial T_e}{\partial {\theta }_{err}}=1.5n_p{\phi }_f{I}_m\sin {\theta }_{err}.\end{array}\right.$$

(10)

Further based on (3) and (5), small-signal models for angular error and motion equation can be obtained:

$$\Delta {\theta }_{err}=\frac{1}{s}(\Delta {\omega }_e-\Delta {\omega }_i),$$

(11)

$$\Delta {\omega }_e=\frac{n_p}{Js+B}(\Delta T_e-\Delta T_L).$$

(12)

The small signal model is schematically shown in Figure 3 with combination of (9)–(12).

With Δω_i = 0 and ΔI = 0, the closed-loop transfer function from ΔT_L to Δω_e is obtained as follows:

$$G(s)=\frac{\Delta {\omega }_e}{\Delta T_L}=\frac{-n_{p}s}{J{s}^2+Bs+n_p{K}_{\theta }}.$$

(13)

The characteristic equation of the system under I-f control is obtained as:

$$J{s}^2+Bs+n_p{K}_{\theta }=s^2+2\zeta {\omega }_{n}s+{\omega }_n^2=0$$

(14)

with:

$$\zeta =\frac{B}{2\sqrt{J{n}_p{K}_{\theta }}},{\omega }_n=\sqrt{\frac{n_p{K}_{\theta }}{J}}$$

(15)

where ζ and ω_n denote the damping ratio and natural frequency.

ζ is very small with consideration to the relatively small B of UHS-SPMSM, which causes slow system response and large speed oscillation. At a certain static operating point, the load torque variation can be approximated considered as a step change, so the unit step response of the UHS-SPMSM according to (13) is derived as:

$$\begin{array}{ll}c(t)& ={\mathcal{L}}^{-1}(G(s)\cdot \frac{1}{s})={\mathcal{L}}^{-1}(\frac{-n_{p}s}{J{s}^2+Bs+n_p{K}_{\theta }}\cdot \frac{1}{s})\hfill \\ & =-\frac{J{\omega }_n{e}^{-\zeta {\omega }_{n}t}}{K_{\theta }\sqrt{1-{\zeta }^2}}\sin {\omega }_{d}t=-A\sin {\omega }_{d}t\hfill \end{array}$$

(16)

with ${\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}$.

It is evident that Δω_e and ΔT_L exhibit opposite changing trends, and the increase of ΔT_L leads to the inherent speed oscillation with oscillation frequency ω_d and oscillation amplitude A. Excessive speed oscillation during initial startup interval and transition process tends to cause startup failure and transition failure, respectively.

3.2. Prone Asynchronous Operation

The UHS-SPMSM is typically characterized by a steep ramp slope (e.g., 1000 π rad/s²) to facilitate rapid startup, and by considerable load torque considering the approximate quadratic correlation between motor load torque and speed. According (5), the demand torque T_d comprises the load torque T_L, the acceleration torque T_a, and the friction torque T_f.

$$\begin{array}{ll}{T}_d& =J\frac{d{\omega }_m}{dt}+T_L+B{\omega }_m\\ & =T_a+T_L+T_f\hfill \end{array}$$

(17)

Once T_d exceeds the maximum electromagnetic torque T_max under high-ramp-slope and heavy-load conditions, the I-f control may be prone to failure, leading to losing synchronization issues. Referring to (4), the variation between T_e and θ_err can be roughly illustrated in Figure 4. Depending on whether θ_err exceeds 0, the operating region can be categorized into synchronous region I and asynchronous region II.

According to (4), when the electromagnetic torque T_e is balanced with the T_d, θ_err maintains constant, and the rotor synchronously follows the current vector. Upon a sudden increase in T_L, the rotor undergoes deceleration, leading to a reduction in θ_err. This prompts T_e and T_L to establish a new balance. Maintaining a constant current vector amplitude, as T_L gradually rises, θ_err continues to decrease, reaching a minimum value at θ_err = 0, signifying synchronization with the δ-axis for the reference current vector. The above characteristics manifest in synchronous region I. Conversely, in asynchronous region II, θ_err and T_e have the same trend. Once T_e loses its capacity to match T_d, the motor loses synchronization. In summary, the permissible range of θ_err is defined as:

$$0°<{\theta }_{err}<90°.$$

(18)

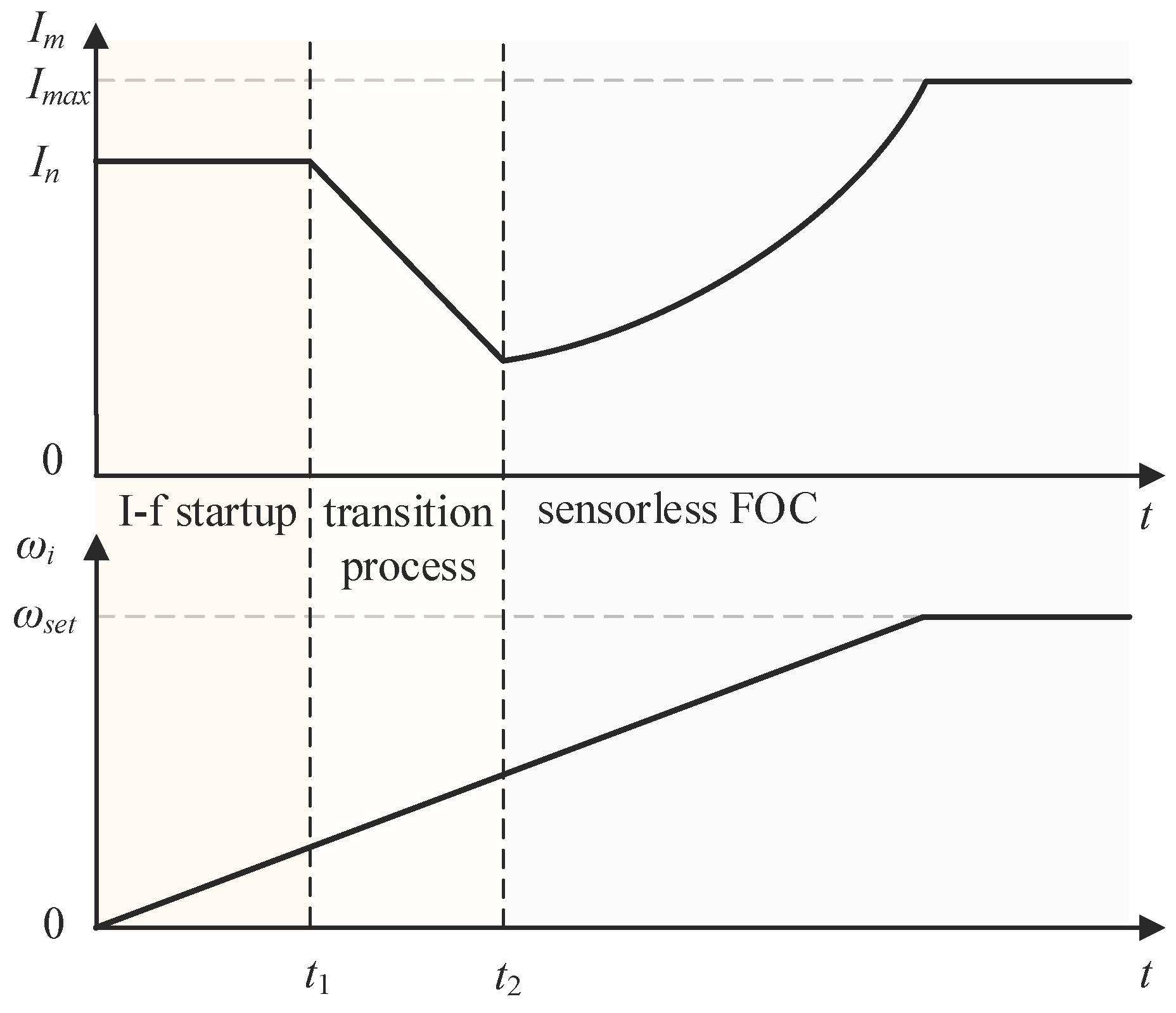
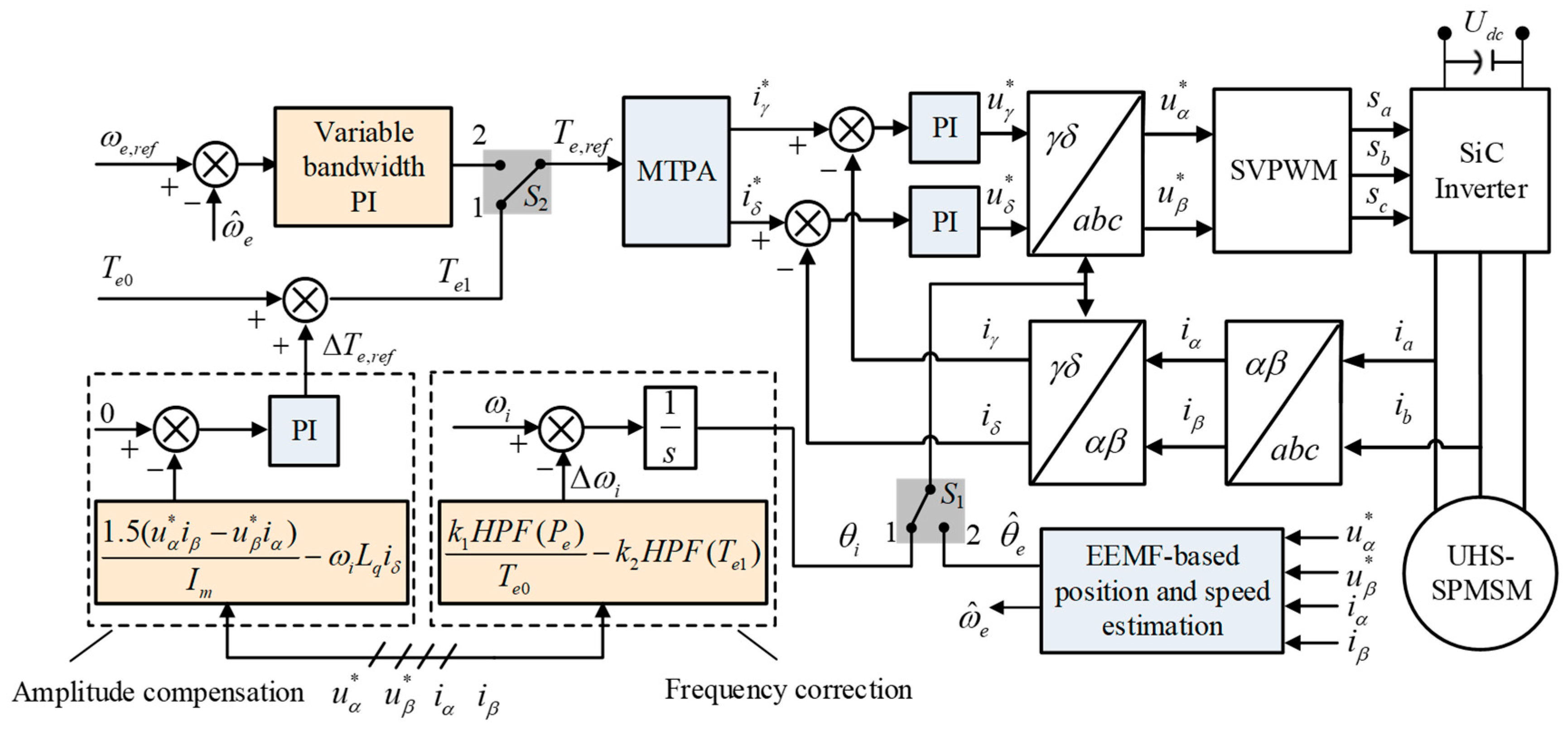
4. Proposed Closed-Loop I–f Startup Method with Transition Enhancement

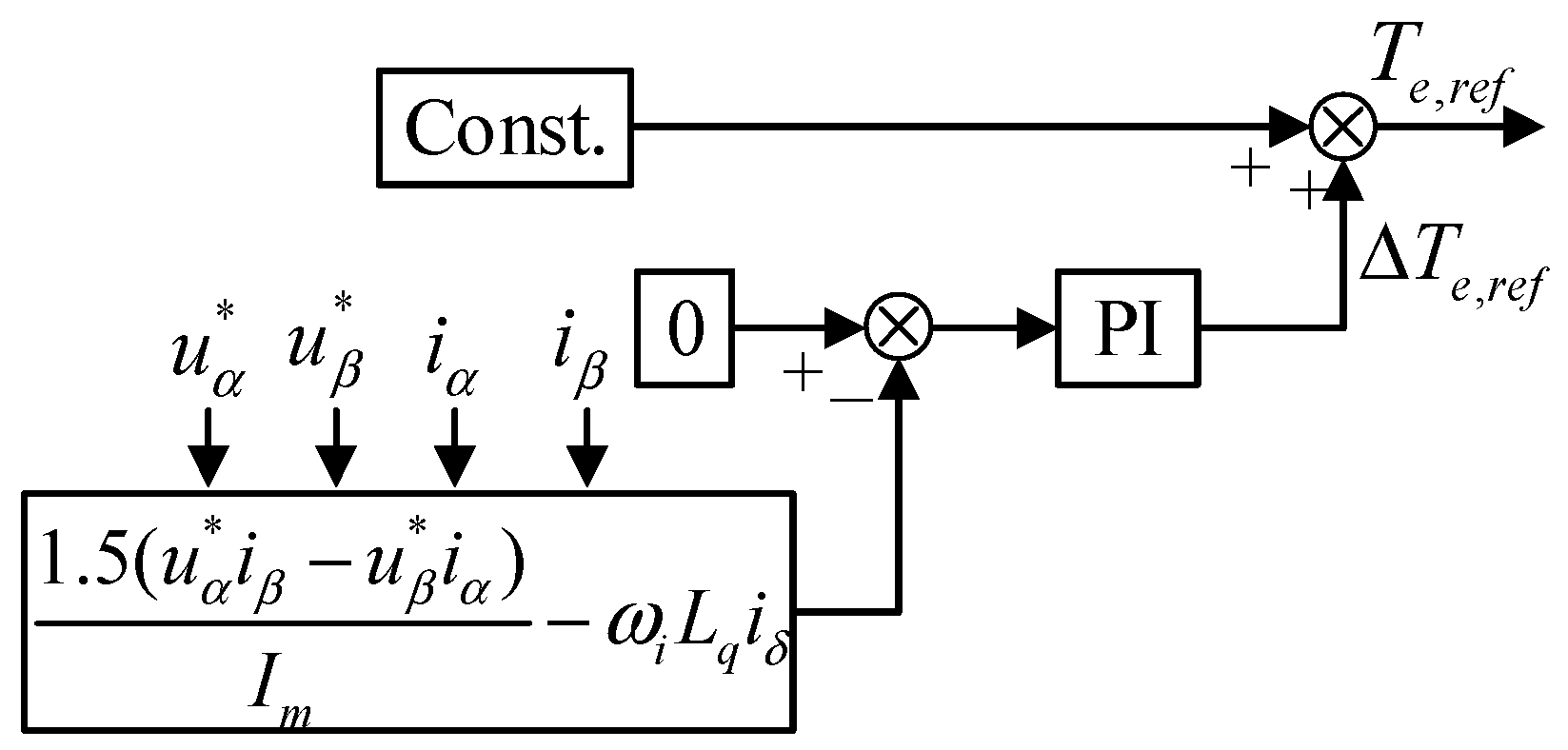
4.1. Frequency Correction Design

According to active power equation, the motor frequency satisfies ω_e = P_e/T_e, where P_e represents the active power. Thus, the derivative of motor frequency is obtained as:

$$\frac{d}{dt}{\omega }_e=\frac{d}{dt}(\frac{P_e}{T_e})\approx \frac{HPF(P_e)}{T_e}$$

(19)

with $P_e=1.5(u_{\alpha }^{*}{i}_{\alpha }+u_{\beta }^{*}{i}_{\beta })$, where $u_{\alpha }^{*},u_{\beta }^{*},i_{\alpha },i_{\beta }$ are the voltage commands and currents in the α-β reference coordinate frame.

The prerequisite for the establishment of (19) is that T_e keeps constant under θ_err = 0 during ramp up stage. The high pass filter (HPF) is utilized as a differentiator approximately under low frequency. Therefore, the following correction frequency ∆ω_i1 is designed proportional to the derivative of motor frequency in [24]:

$$\Delta {\omega }_{i1}=-k_1\frac{d}{dt}{\omega }_e=-k_1\frac{HPF(P_e)}{T_{e0}}$$

(20)

where k₁ > 0 denotes the active power based correction gain, and T_e0 denotes the initial reference motor torque at startup, which is set as the constant rated value.

However, the reference motor torque changes significantly in the whole startup process due to amplitude compensation (see Section 4.2 for details) and sensorless transition. Therefore, the above frequency correction method is underperforming. The additional correction frequency ∆ω_i2 proportional to the electromagnetic torque variation is designed in this paper to enhance the startup performance:

$$\Delta {\omega }_{i2}=k_2\frac{d}{dt}{T}_{e2}=k_{2}HPF(T_{e1})$$

(21)

where k₂ > 0 denotes the electromagnetic torque based correction gain, and T_e1 is the real-time reference motor torque.

Therefore, the whole correction frequency can be expressed as:

$${\omega }_i-{\omega }_{i0}=\Delta {\omega }_{i1}+\Delta {\omega }_{i2}.$$

(22)

where ω_i0 is current vector frequency without frequency correction. The whole correction frequency is activated at zero motor speed. The corresponding small-signal equation of (22) can be obtained:

$$\Delta {\omega }_i=\Delta {\omega }_{i0}-k_1\frac{d}{dt}\Delta {\omega }_e+k_2\frac{d}{dt}\Delta T_e.$$

(23)

Substituting (23) into (11), the angle error θ_err with frequency correction can be obtained as:

$${\theta }_{err}=\frac{1}{s}[(1+k_{1}s)\Delta {\omega }_e-\Delta {\omega }_{i0}-k_{2}s\Delta T_e].$$

(24)

With combination of (9), (10), (12), and (24), the closed-loop transfer function from ΔT_L to Δω_e is renewed with frequency correction as follows:

$$G^{\prime }(s)=\frac{\Delta {\omega }_e}{\Delta T_L}=\frac{(k_2{K}_{\theta }-1)n_{p}s}{(1-k_2{K}_{\theta })J{s}^2+B_{e}s+n_p{K}_{\theta }}$$

(25)

with $B_e=(1-k_2{K}_{\theta })B+n_p{k}_1{K}_{\theta }\approx n_p{k}_1{K}_{\theta }(B\ll n_p{k}_1{K}_{\theta })$.

Therefore, the new system damping ratio ζ_e can be obtained as follows:

$${\zeta }_e=\frac{n_p{k}_1{K}_{\theta }}{2\sqrt{(1-k_2{K}_{\theta })J{n}_p{K}_{\theta }}}.$$

(26)

Compared with system damping ratio ζ_e0 with only correction frequency Δω_i1 as follows [24]:

$${\zeta }_{e0}=\frac{n_p{k}_1{K}_{\theta }}{2\sqrt{J{n}_p{K}_{\theta }}},$$

(27)

ζ_e is larger with the increase of k₂ in a certain range. Thus, faster convergence with less oscillation can be guaranteed with the increase of system damping ratio.

4.2. Amplitude Compensation Design

Conventional I-f control necessitates setting the reference current amplitude I_m (proportional to reference motor torque) to a relatively large value to ensure that θ_err remains well within the stability domain boundaries. This is performed to provide the motor with an ample stabilization margin when encountering disturbances. However, such an approach significantly increases motor losses.

According to (4), T_e generated under the same I_m increases with the rise of cosθ_err. By maintaining cosθ_err at its maximum value throughout the motor startup process, i.e., cosθ_err = 1 with θ_err = 0, the UHS-SPMSM under I-f control can be effectively operated in the MTPA state. This approach reduces I_m, enhancing the motor’s overall operating efficiency.

The information containing θ_err can be obtained from (2):

$${\omega }_e{\phi }_f\sin {\theta }_{err}=-u_{\gamma }-{\omega }_i{L}_q{i}_{\delta }$$

(28)

where u_γ can be derived from reactive power as follows [36]:

$$u_{\gamma }=-U\sin \phi =\frac{1.5(u_{\beta }^{*}{i}_{\alpha }-u_{\alpha }^{*}{i}_{\beta })}{I_m}.$$

(29)

It is worth stating that the used reactive power is calculated from voltages and currents in the α-β reference coordinate frame instead of γ-δ ones, which reduces the influence of inaccurate position information on the calculation result. Hence, a PI controller can be devised to regulate I_m with compensation of ΔI_m. For the ease of transition to sensorless FOC, in this paper, the regulation of reference motor torque is utilized with compensation of ΔT_e,_ref, as illustrated in Figure 5, where ω_eφ_fsinθ_err serves as the feedback value with a reference set at 0.

Notably, $u_{\alpha }^{*}$ and $u_{\beta }^{*}$ can be obtained from the α-β axes voltage commands for SVPWM. i_α and i_β can be obtained from the sampled three-phase currents through Clarke coordinate transformation, and thus I_m is also obtained. Additionally, i_δ can be obtained through Park coordinate transformation based on corrected rotor position information (integral of corrected frequency). L_q is known from the motor manufacturer. In view of the above known signals, ω_eφ_fsinθ_err can be calculated directly avoiding additional observation. Therefore, the amplitude-compensated PI controller is activated at zero speed. Utilizing the amplitude-compensated PI controller, ω_eφ_fsinθ_err can converge to 0, signifying the convergence of θ_err to 0. Referencing (10), it becomes apparent that K_θ = 0 when θ_err = 0. By substituting K_θ = 0 to (25), the proposed I-f control with frequency correction can be likened to a first-order delay system. Therefore, adjustments in the control variables (current and frequency) influence the motor’s electromagnetic torque and speed response over time, leading to a dampened response and diminishing speed oscillations effectively.

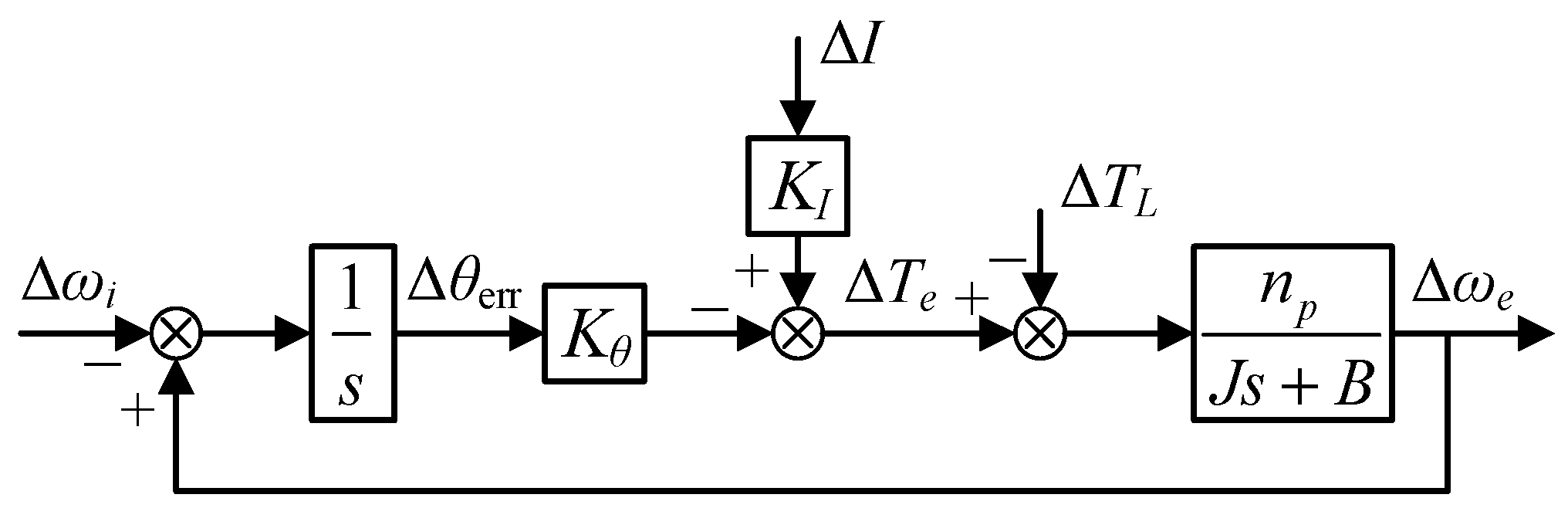
4.3. Sensorless Transition Enhancement

After transition from I-f startup strategy to EEMF-based sensorless FOC, the estimated rotor position and speed will be utilized to coordinate transformation and as feedback value of speed PI controller, respectively. Taking the first-order low-pass filtering effect for high-frequency noise suppression in digital sampling system into consideration, the closed-loop transfer function of the speed loop can be expressed as follows [37,38]:

$$\begin{array}{ll}{G}_s^c(s)& =\frac{{\omega }_m(s)}{{\omega }_m^{*}(s)}=\frac{K_T{K}_i}{J{s}^2+(K_T{K}_p+B)s+K_T{K}_i}\hfill \\ & =\frac{{\omega }_{ns}^2}{s^2+2{\zeta }_s{\omega }_{ns}s+{\omega }_{ns}^2}\hfill \end{array}$$

(30)

with:

$${\zeta }_s=\frac{K_T{K}_p+B}{2\sqrt{J{K}_T{K}_i}},{\omega }_{ns}=\sqrt{\frac{K_T{K}_i}{J}}$$

(31)

where K_p and K_i are the proportional and integral gains of speed PI controller; K_T = 1.5n_pφ_f denotes the torque constant; ζ_s and ω_ns denote the damping ratio and natural frequency of the speed loop control system.

The amplitude-frequency characteristic of (30) at the closed-loop bandwidth is:

$$M({\omega }_b)=\frac{{\omega }_{ns}^2}{\sqrt{{({\omega }_{ns}^2-{\omega }_b^2)}^2+(2{\zeta }_s{\omega }_{ns}{\omega }_b)}}=\frac{\sqrt{2}}{2}.$$

(32)

Therefore, speed loop bandwidth ω_b is derived with ζ_s and ω_ns:

$${\omega }_b={\omega }_{ns}\sqrt{1-2{\zeta }_s^2+\sqrt{2-4{\zeta }_s^2+4{\zeta }_s^4}}.$$

(33)

Without variation of motor parameters, ω_b is only dependent on the control gains of speed PI controller. Generally, UHS-SPMSM operates over a wide frequency range with fast response requirement, a large ω_b is often designed more reasonably with matched constant K_p and K_i. When the UHS-SPMSM operates at low speed, particularly during the sensorless transition stage, lager speed overshoot and increased sensitivity to high-frequency noise result from an excessive ω_b, heightening the risk of transition failure. Therefore, in this paper, a variable bandwidth speed PI controller is designed based on variable PI control gains, which are designed as:

$$\left\{\begin{array}{l}{K}_p=-2.1176\times {10}^{-9}{\omega }_m+2.4776\times {10}^{-4}\\ K_i=2.2353\times {10}^{-8}{\omega }_m+0.0016.\end{array}\right.$$

(34)

Considering the variation trend of K_p and K_i with ω_m ramping up, it is evident that ζ_s decreases and ω_ns varies oppositely. From (33), with ω_ns remaining constant, ω_b monotonically increases with the decrease in ζ_s. In summary, the design of (34) prompts the increasing trend of ω_b during motor speedup in the whole speed range. This mitigates the risk of transition failure from large speed oscillation after enabling speed PI controller. Hereto, the overall schematic diagram of the proposed I-f startup method with transition to FOC is illustrated as Figure 6.

5. Experimental Results

In order to validate the proposed startup method, the experiments are conducted on the test platform as shown in Figure 7, mainly including a test UHS-SPMSM, a homemade inverter, and some other ancillary equipment for control of cooling system, measuring system, and power supply system. The parameters of this UHS-SPMSM drive system are given in

Table 1. Parameters of the UHS-SPMSM drive system.

Symbol	Parameter	Value
PN	Rated power	35 kW
ωe,rated	Rated speed	9245 rad/s (90 kr/min)
ωe,max	Maximum speed	9948 rad/s (95 kr/min)
ωe,min	Minimum speed	3142 rad/s (30 kr/min)
ωN	Fundamental frequency	1.583 kHz
np	Pole pairs	1
Rs	Stator resistance	0.0085 Ω
Ld	d-axis inductance	66.46 μH
Lq	q-axis inductance	66.46 μH
φf	Flux linkage	0.02387 Wb
J	Motor inertia	0.0005672 kg·m2
UDC	DC bus voltage	550 V
fsw	Switching frequency	40 kHz
fc	Control frequency	20 kHz
Ts	Sampling period	0.00005 s

. For the homemade inverter, Wolfspeed CAB011M12FM3 Half-Bridge SiC power modules are designed as power switches and microprocessor TMS320F28335 DSP (provided by Texas Instruments) is designed as the control board. The switching frequency is 40 kHz and the sampling frequency is 20 kHz.

The main control parameters used are: the PI controllers for regulating γδ-axes currents are K_p,cur = 0.7 and K_i,cur = 0.002, and for regulating motor speed (without variable bandwidth design) are K_p,spd = 0.0000095 and K_i,spd = 0.0095; for frequency correction design, the correction gains are designed as k₁ = 3 and k₂ = 35; for amplitude compensation design, the PI control parameters are K_p,amp = 0.000006 and K_i,amp = 0.005. All the results presented in this section are analyzed via CAN communication. That is, γδ-axes currents and motor speed are logged, parsed, and plotted via Busmaster, CANoe, and Origin, respectively. After transition to FOC, EEMF-based sensorless control method proposed in our previous research [35] works. While the estimated position may be distorted at low speeds, the estimated speed remains precise, effectively representing the actual motor speed without reliance on mechanical speed measurement.

In fact, without a position sensor installation for the UHS-SPMSM, the actual dq-axes currents cannot be obtained in the experiments due to lack of real rotor position information. Therefore, the γδ-axes currents are used in this section for effectiveness validation of the proposed method. On one hand, before the sensorless transition, the γδ-axes currents are derived from the position θ_i in the γ-δ reference coordinate frame. On the other hand, after the sensorless transition, the γδ-axes currents are derived from the position ${\widehat{\theta }}_e$ in the d-q reference coordinate frame (assuming that θ_err ≈ 0, γ-δ reference coordinate frame is aligned with d-q one).

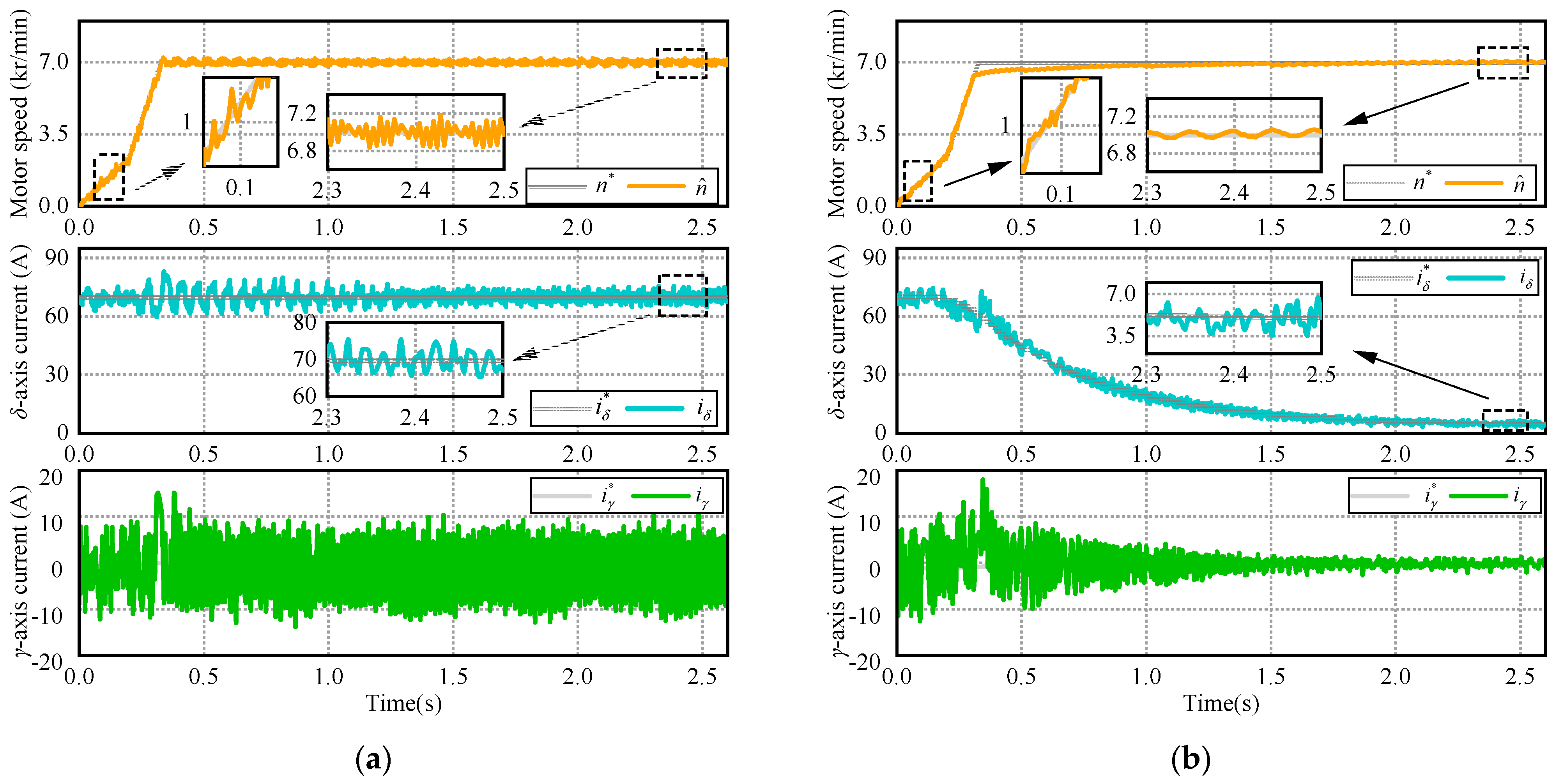
5.1. Startup Performance Comparison with Conventional I–f Startup Strategy

To verify the superior startup performance of the proposed method compared with the conventional open-loop I-f control, the UHS-SPMSM is started to 7000 r/min from a standstill.

Figure 8 shows the startup performance of the conventional I-f control. The δ-axis reference current $i_{\delta }^{*}$ for the I-f control is generally chosen to be a large value for a reliable startup with large output torque, and $i_{\delta }^{*}=70\mathrm{A}$ (80% rated current) is used here. In Figure 8a, the actual δ-axis current i_δ converges to the initial set value of reference current under the whole startup process, and oscillates with a maximum amplitude of 9.8 A in steady state. In addition, even the actual γ-axis current converges to 0 A under current loop PI control, the fluctuations are noticeable with an average amplitude over 10 A. This implies that an obvious position error exists between the γ-δ and d-q reference coordinate frame without amplitude compensation of reference current vector, which is not desired. Furthermore, under conventional I-f control, motor speed fluctuations occur both in dynamic process and steady-state operation, and the root mean square errors (RMSEs) are 296 r/min and 348 r/min, respectively.

Figure 8b shows the startup performance of the proposed I-f control. The initial δ-axis reference current $i_{\delta }^{*}$ is set the same as the conventional I-f control; however, $i_{\delta }^{*}$ decreases gradually with motor speedup. Only 5.1 A δ-axis current can maintain motor’s steady-state operation; compared with a conventional I-f control, it decreased 92.7%. This is due to the designed amplitude compensation of reference current. Although the effect of amplitude compensation is not so obvious at zero speed, the preliminary calculation of reactive power after motor startup is also helpful for the subsequent adjustment of amplitude compensator with motor speedup. Notably, the steady-state current oscillation of i_δ is significantly decreased with maximum amplitude of only 3.2 A, which decreased 67.3% compared with the conventional I-f control. Under proposed I-f control, stable i_γ = 0 operation is achieved easily, which leads to higher motor efficiency avoiding too large current amplitude fluctuations. Except slightly poorer dynamic speed tracking performance, the proposed method also has smaller dynamic and steady-state speed fluctuation of just 130 r/min and 78 r/min, respectively.

It is worth noting that to ensure fast startup, in practical engineering applications, the I-f control is only used to drive the UHS-SPMSM from standstill to a certain speed, and then transitions to the closed-loop FOC during the acceleration process. In other words, the I-f control does not enable under steady-state operating conditions. The transition process will be demonstrated in the Section 5.2. Therefore, the proposed I-f control is unaffected from the slightly poor dynamic convergence performance in practical applications.

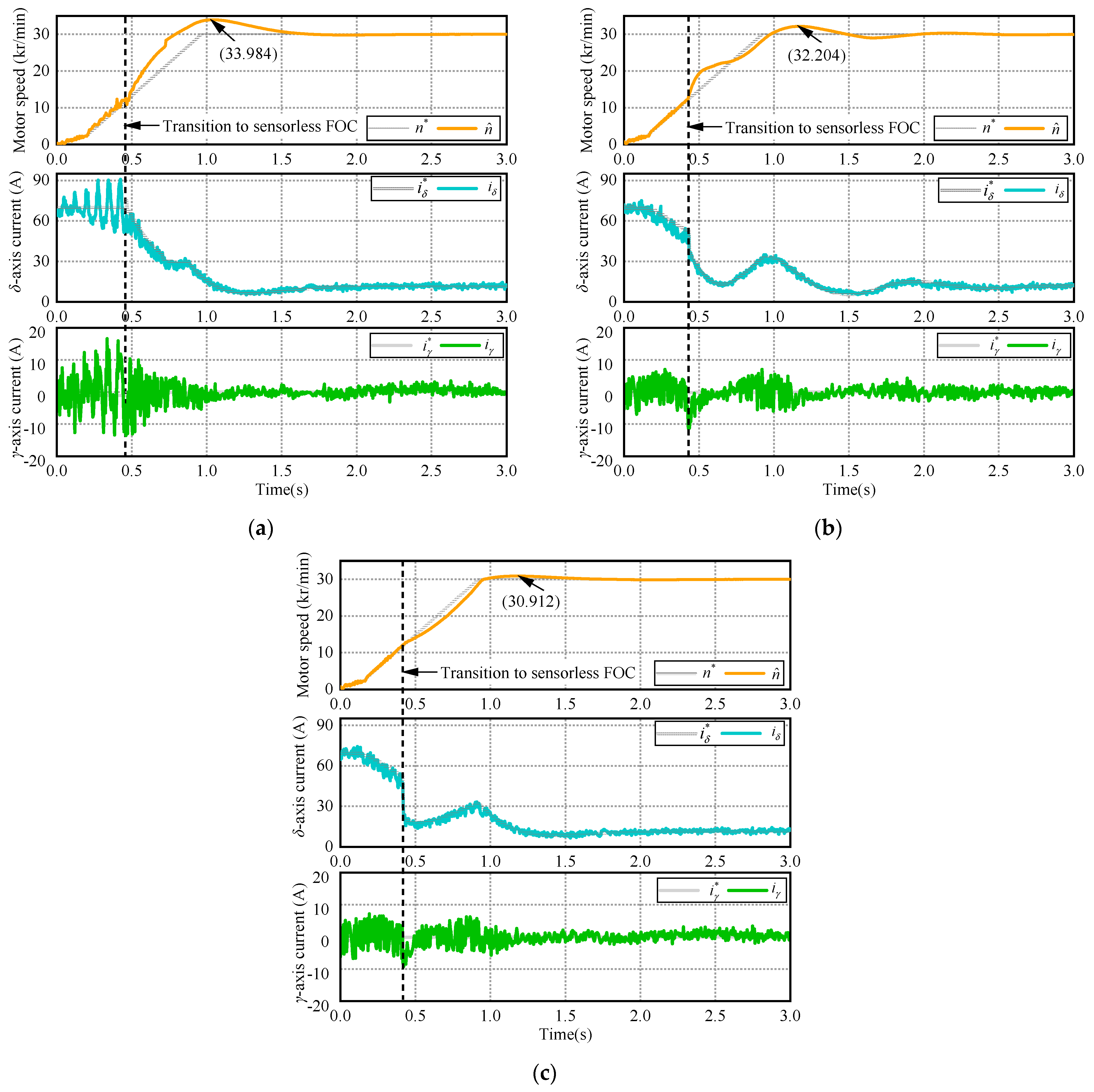
5.2. Transition Performance Comparison from I–f Startup to Sensorless FOC

To ensure the fast startup ability of the UHS-SPMSM, the transition from I-f control to sensorless FOC is usually accomplished during the acceleration process, rather than in the steady-state condition. The transition speed should be set as low as possible under the premise of position estimation accuracy of the sensorless control. Generally, the UHS-SPMSM is only operated above the idle speed (30,000 r/min for the test motor) in the actual working condition for extending the life of air bearing. Therefore, Figure 9 shows the transition performance comparison, where the UHS-SPMSM is started from a standstill to the idle speed, and the transition speed is set to 12,000 r/min.

Figure 9a shows the transition performance of conventional I-f control, where the speed PI controller is set fixed-gain. During the conventional I-f control stage, the actual δ-axis current converges poorly to the constant reference δ-axis current. The γδ-axes current tracking error increases with the gradual rise of motor speed, which indicates that the used rotor position gained from I-f control exists, growing the position error as the motor speed increases. This leads to considerable current amplitude and the increasing possibility of motor shutdown due to the overcurrent protection trigger. In addition, significant speed oscillation is evident. This is due to the poor damping as analyzed in Section 3. At the transition instant of t = 0.46 s, the reference δ-axis current has an obvious pulse due to position mismatch between the I-f control and sensorless control, which may lead to transition failure. After successful transition to the sensorless FOC, the actual motor speed has a large overshoot in the process of tracking the reference speed. The dynamic overshoot gradually increases, and the steady-state overshoot value reaches 3984 r/min.

Figure 9b shows the transition performance of the proposed closed-loop I-f control, where the speed PI controller is also set fixed-gain. During the proposed I-f control stage, the δ-axis current gradually decreases with motor speedup. This is attributed to the amplitude compensation design. In other words, the UHS-SPMSM can achieve the same motor speed under the proposed I-f control at a smaller current, which is conductive to improve the motor efficiency. Meanwhile the γδ-axes current fluctuation and speed oscillation are significantly reduced compared to the conventional I-f control, which confirms the damping effect of the frequency correction. The UHS-SPMSM can instantly switch to the sensorless FOC without any reference δ-axis current pulses, which indicates more precision in used rotor position and contributes to smoother transition.

During initial sensorless FOC stage, the δ-axis current showed a certain extent of fluctuation, which brought the simultaneous speed fluctuation. Compared with the conventional I-f control, the average δ-axis current from the transition instant to the steady state is significantly reduced, which also reflects the improvement of the motor efficiency, and its steady-state speed overshoot value is very small, only 2204 r/min. It is worth noting that the fixed-gain speed PI controller, after transition, featuring in a large bandwidth of effectiveness in the whole speed range, holds redundant bandwidth at the transition speed of 12,000 r/min. This causes the speed and current fluctuation.

Figure 9c shows the transition performance of the proposed closed-loop I-f control with variable bandwidth speed PI controller. Clearly, the δ-axis current and speed fluctuation are significantly reduced after transition, and the steady-state speed overshoot is reduced to 912 r/min. Sensorless transition enhancement obtains a smooth transition compared with fixed-bandwidth speed PI controller. Therefore, transition failure can be avoided for high startup reliability.

6. Conclusions

In this article, a reliable and efficient I-f control method with transition enhancement is introduced for UHS-SPMSMs driving fuel cell air compressors. The startup reliability and transition smoothness are visibly enhanced. The main conclusions are summarized as follows:

(1)

During the speed up stage, the proposed frequency correction of reference current vector considering the active power and motor torque simultaneously, which reduces the speed oscillation significantly, while decreasing the possibility of startup failure.

(2)

The proposed amplitude compensator of reference current vector obviously reduces the current amplitude under the same startup condition, which ensures MTPA operation. This characteristic improves the motor efficiency significantly and prerequisites smoother transition from I-f startup to sensorless FOC due to minimizing the current vector angle.

(3)

After the transition to sensorless FOC with an enabling speed PI controller, the proposed variable bandwidth scheme ensures reduction of current amplitude and speed fluctuation, avoiding transition failure.

Generally, the contributions investigated in this paper can be extendedly applied to UHS-SPMSM driving gas turbines, electric turbochargers, flywheels for energy storage, and turbo-electric distributed propulsion system for aircraft, rather than merely driving fuel cell air compressors.