Active Composite Control of Disturbance Compensation for Vibration Isolation System with Uncertainty
Abstract
:1. Introduction
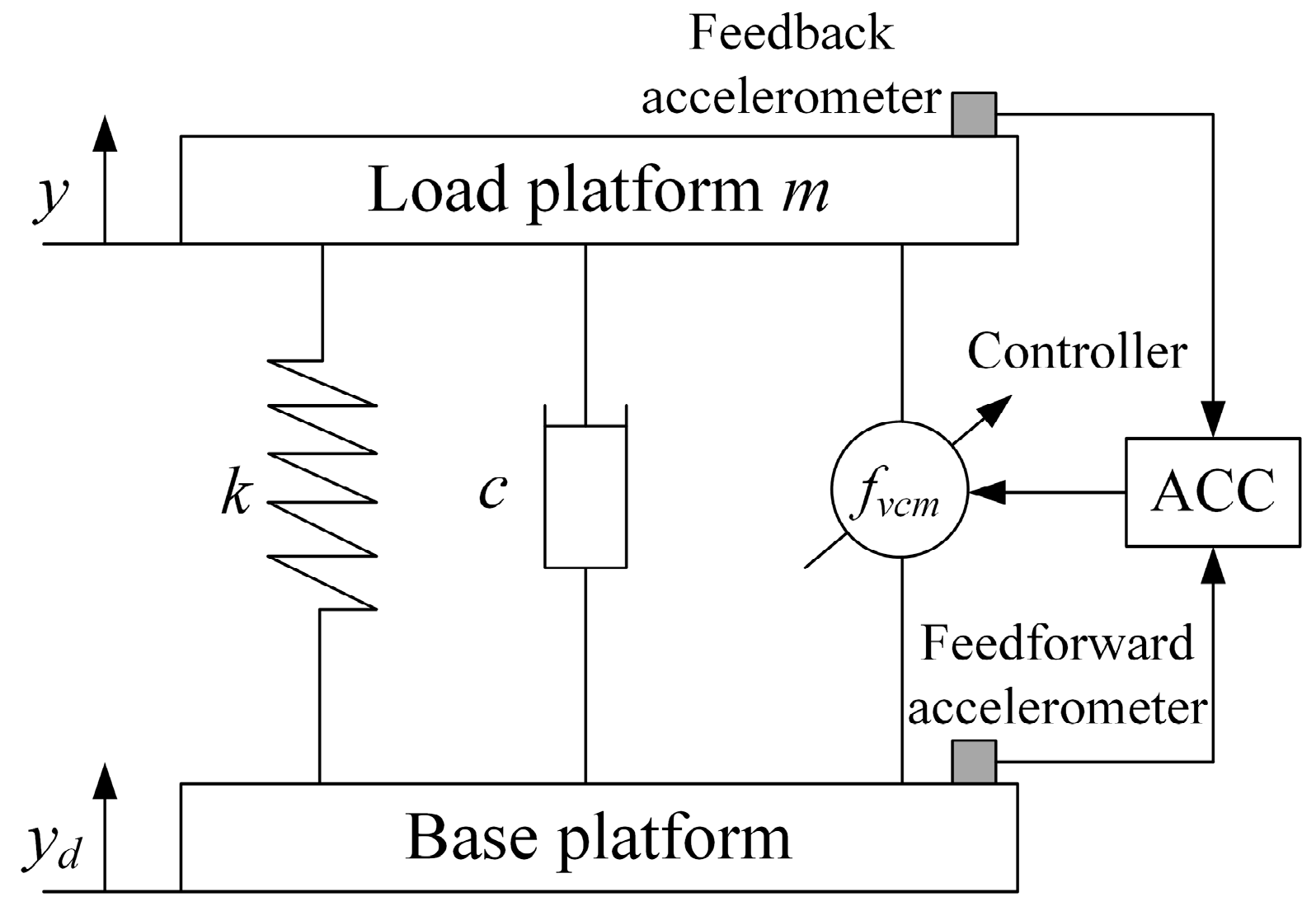
2. System Description and Control Strategy
2.1. Problem Formulation
2.2. System Dynamics Modeling with Uncertainty
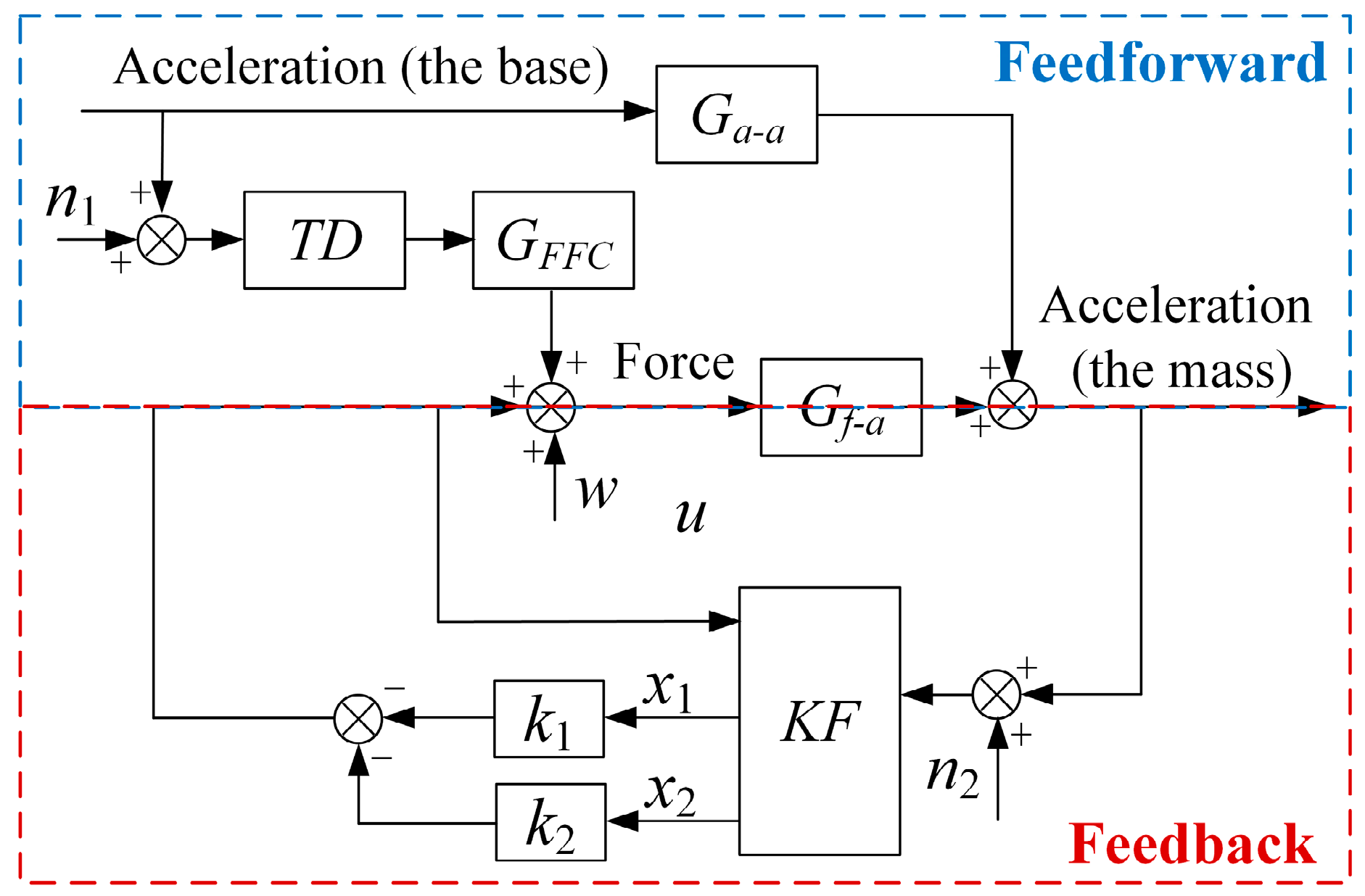
2.3. Composite Control Strategy
3. Composite Controller Design
3.1. Feedforward Control Loop
3.2. Feedback Control Loop
3.2.1. Kalman Filter Design
3.2.2. LQR Controller Design
3.3. Stability Analysis
3.3.1. Kalman Filter
3.3.2. LQR Controller
4. Vibration Isolation of System with Uncertainty
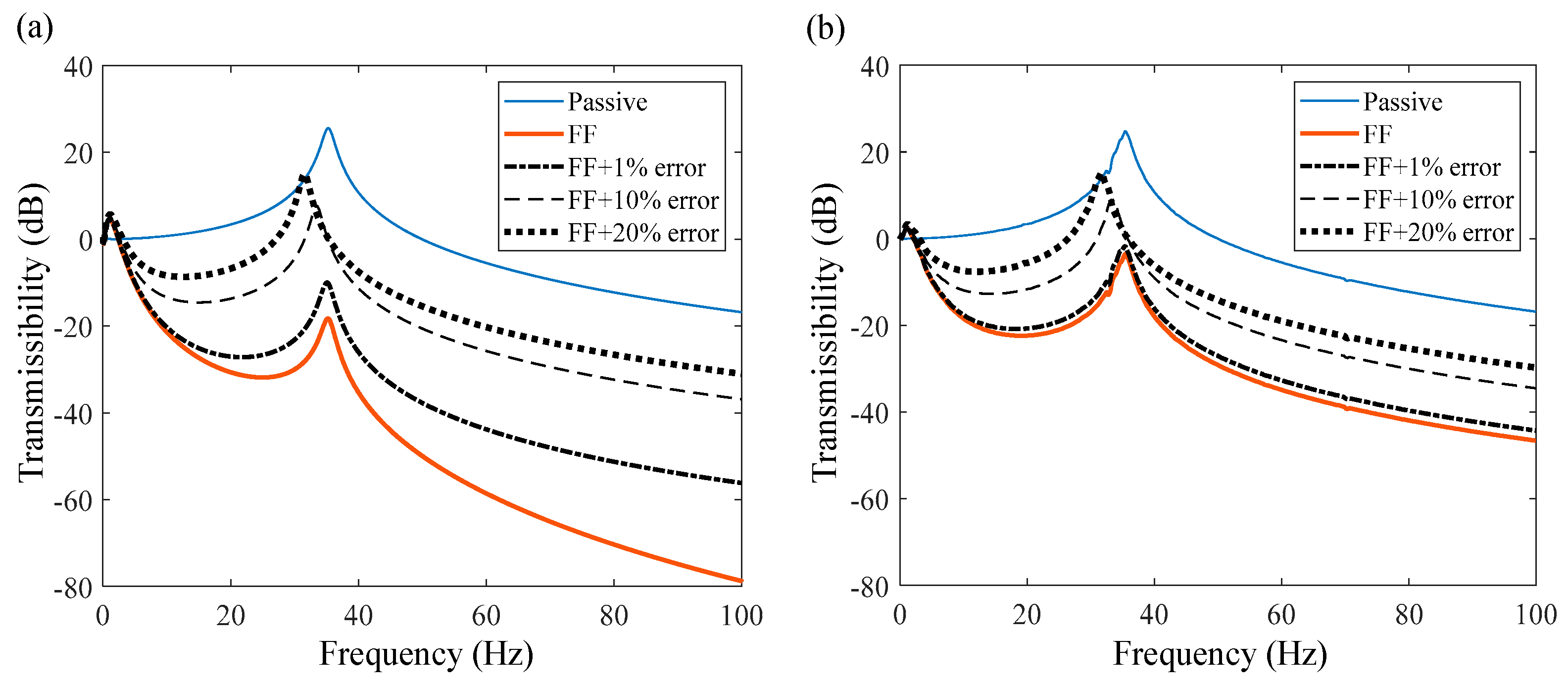
4.1. Influence of System Uncertainty on Feedforward
4.2. Tolerance Analysis of Kalman Filter
4.3. Performance Analysis of Proposed Composite Controller
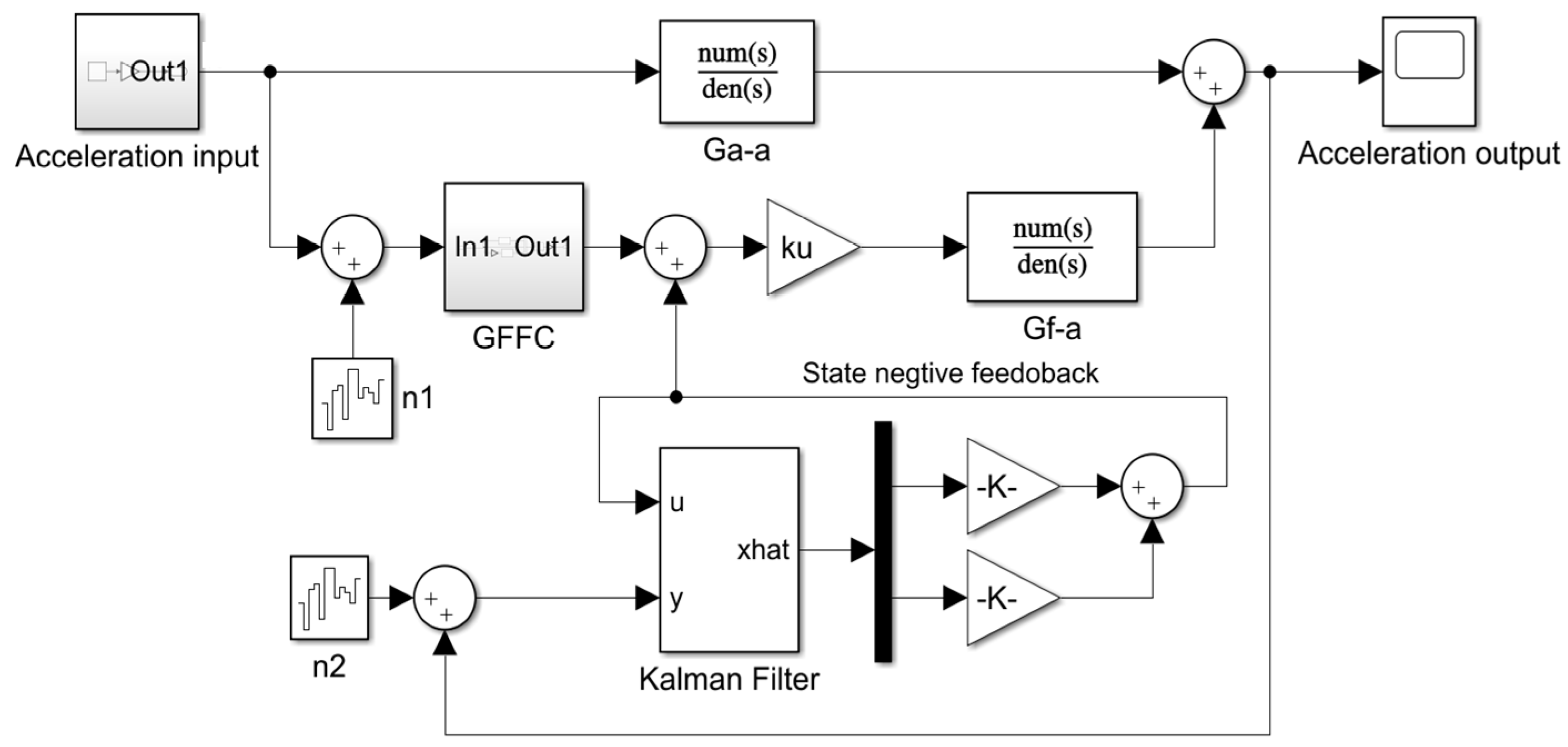
5. Experiments
5.1. Experiments Setup
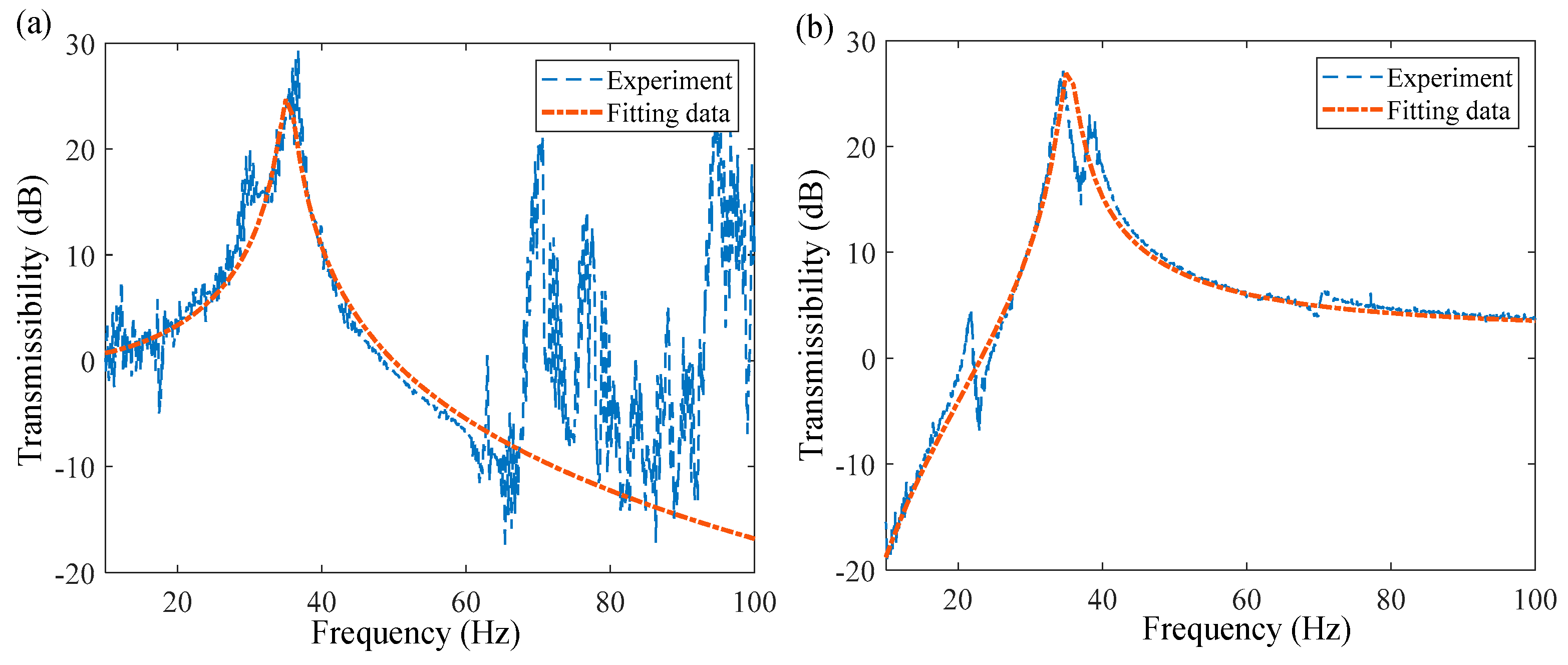
5.2. System Identification
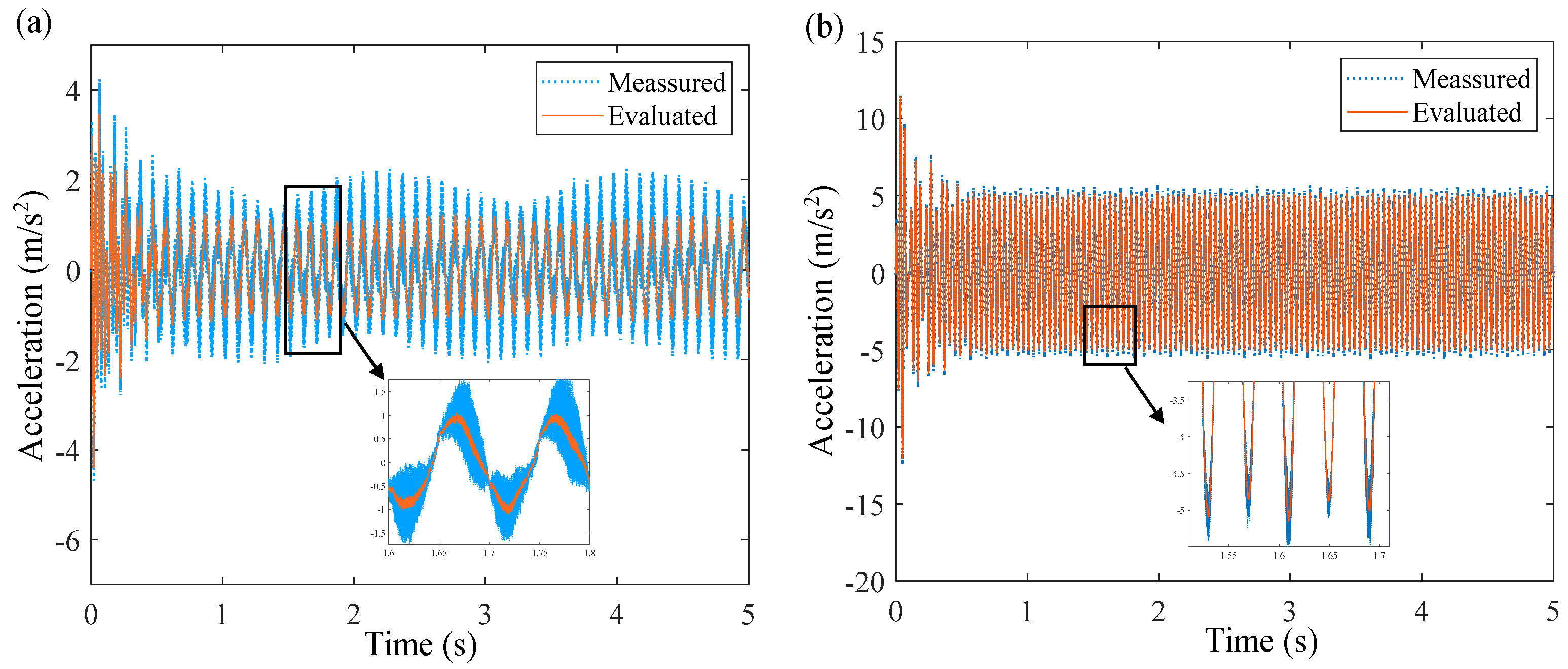
5.3. Kalman Filtering Effect
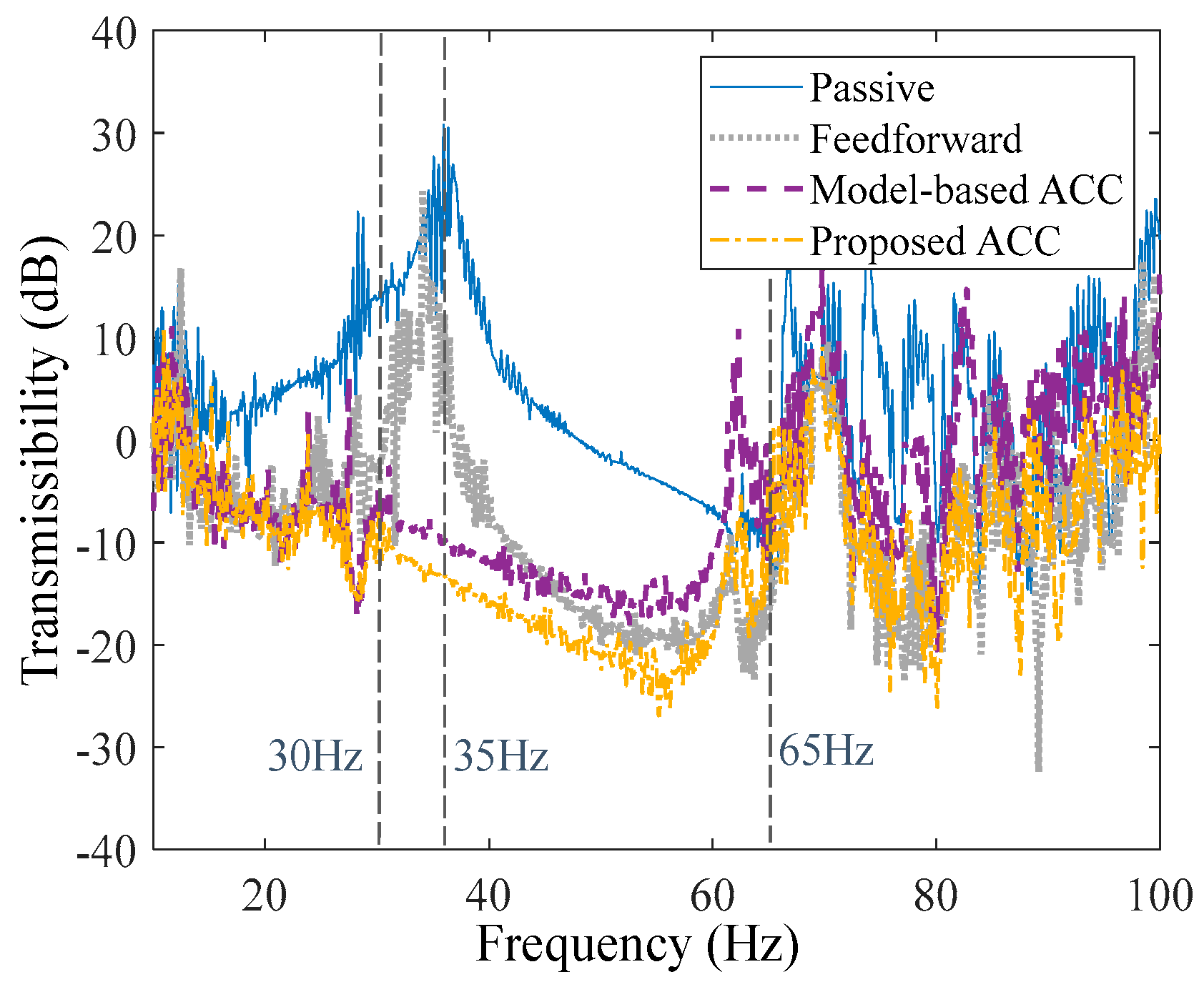
5.4. Vibration Isolation Performance
6. Conclusions
- The feedforward controller designed with the known model can effectively obtain a lower and wider vibration isolation band.
- The Kalman filter can effectively filter the output signal, and can accurately and effectively estimate the state (velocity) of the uncertain system.
- Using more accurate estimated state feedback can achieve a better vibration isolation effect, and does not affect the performance of the feedforward controller.
- The proposed ACC can not only reduce the influence of system uncertainty on the control effect, but also effectively suppress the influence of noise on the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cetinkaya, M.B.; Isci, M. Analysis of the Vibration Characteristics of a Leaf Spring System Using Artificial Neural Networks. Sensors 2022, 22, 4507. [Google Scholar] [CrossRef] [PubMed]
- Sjöberg, M.M.; Kari, L. Non-linear behavior of a rubber isolator system using fractional derivatives. Veh. Syst. Dyn. 2002, 37, 217–236. [Google Scholar] [CrossRef]
- Salvatore, A.; Carboni, B.; Chen, L.; Lacarbonara, W. Nonlinear dynamic response of a wire rope isolator: Experiment, identification and validation. Eng. Struct. 2021, 238, 112121. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J.; Waters, T.P. A study of a nonlinear vibration isolator with a quasi-zero stiffness characteristic. J. Sound Vib. 2008, 315, 700–711. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C.; Brown, T. Design of a quasi-zero stiffness isolation system for supporting different loads. J. Sound Vib. 2020, 471, 115198. [Google Scholar] [CrossRef]
- Wang, M.; Hu, Y.; Sun, Y.; Ding, J.; Pu, H.; Yuan, S.; Zhao, J.; Peng, Y.; Xie, S.; Luo, J. An adjustable low-frequency vibration isolation Stewart platform based on electromagnetic negative stiffness. Int. J. Mech. Sci. 2020, 181, 105714. [Google Scholar] [CrossRef]
- He, K.; Li, Q.; Liu, L.; Yang, H. Active vibration isolation of ultra-stable optical reference cavity of space optical clock. Aerosp. Sci. Technol. 2021, 112, 106633. [Google Scholar] [CrossRef]
- Song, H.; Shan, X.; Hou, W.; Wang, C.; Sun, K.; Xie, T. A novel piezoelectric-based active-passive vibration isolator for low-frequency vibration system and experimental analysis of vibration isolation performance. Energy. 2023, 278, 127870. [Google Scholar] [CrossRef]
- Beijen, M.A.; Heertjes, M.F.; Butler, H.; Steinbuch, M. Disturbance feedforward control for active vibration isolation systems with internal isolator dynamics. J. Sound Vib. 2018, 436, 220–235. [Google Scholar] [CrossRef]
- Beijen, M.A.; Heertjes, M.F.; Van Dijk, J.; Hakvoort, W.B.J. Self-tuning MIMO disturbance feedforward control for active hard-mounted vibration isolators. Control Eng. Pract. 2018, 72, 90–103. [Google Scholar] [CrossRef]
- Paknejad, A.; Zhao, G.; Chesné, S.; Deraemaeker, A.; Collette, C. Design and optimization of a novel resonant control law using force feedback for vibration mitigation. Struct. Control Health Monit. 2022, 29, e2933. [Google Scholar] [CrossRef]
- Huang, C.; Yang, Y.; Dai, C.; Long, Z. Tracking-Differentiator-Based Position and Acceleration Feedback Control in Active Vibration Isolation with Electromagnetic Actuator. Actuators 2023, 12, 271. [Google Scholar] [CrossRef]
- Yan, T.H.; Pu, H.Y.; Chen, X.D.; Li, Q.; Xu, C. Integrated hybrid vibration isolator with feedforward compensation for fast high-precision positioning X/Y tables. Meas. Sci. Technol. 2010, 21, 065901. [Google Scholar] [CrossRef]
- Xu, A.; Xu, Z.; Zhang, H.; Wang, L.; He, S. An adaptive feed-forward active vibration isolation algorithm for input disturbance unbalanced MIMO systems. Signal Process. 2024, 217, 109346. [Google Scholar] [CrossRef]
- Zhao, G.; Paknejad, A.; Deraemaeker, A.; Collette, C. ∞ optimization of an integral force feedback controller. J. Vib. Control 2019, 25, 2330–2339. [Google Scholar] [CrossRef]
- Zhao, G.; Paknejad, A.; Raze, G.; Deraemaeker, A.; Kerschen, G.; Collette, C. Nonlinear positive position feedback control for mitigation of nonlinear vibrations. Mech. Syst. Signal Process. 2019, 132, 457–470. [Google Scholar] [CrossRef]
- Beijen, M.A.; Heertjes, M.F.; Butler, H.; Steinbuch, M. Mixed feedback and feedforward control design for multi-axis vibration isolation systems. Mechatronics 2019, 61, 106–116. [Google Scholar] [CrossRef]
- Wang, M.; Fu, S.; Ding, J.; Sun, Y.; Peng, Y.; Luo, J.; Pu, H. Analytical and experimental validation of vibration isolation system with complementary stiffness and composite control. Aerosp. Sci. Technol. 2023, 133, 108117. [Google Scholar] [CrossRef]
- Pu, H.; Fu, S.; Wang, M.; Fang, X.; Cai, Y.; Ding, J.; Sun, Y.; Peng, Y.; Xie, S.; Luo, J. Active vibration hybrid control strategy based on multi-DOFs piezoelectric platform. J. Intell. Mater. Syst. Struct. 2024, 35, 352–366. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Huang, R.; Qiu, Z. Active vibration and noise control of vibro-acoustic system by using PID controller. J. Sound Vib. 2015, 348, 57–70. [Google Scholar] [CrossRef]
- Zhang, S.; Schmidt, R.U.D.; Qin, X. Active vibration control of piezoelectric bonded smart structures using PID algorithm. Chin. J. Aeronaut. 2015, 28, 305–313. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.; Yang, C.; Wu, D. A novel interval dynamic reliability computation approach for the risk evaluation of vibration active control systems based on PID controllers. Appl. Math. Model. 2021, 92, 422–446. [Google Scholar] [CrossRef]
- Zhao, G.; Raze, G.; Paknejad, A.; Deraemaeker, A.; Kerschen, G.; Collette, C. Active tuned inerter-damper for smart structures and its ∞ optimisation. Mech. Syst. Signal Process. 2019, 129, 470–478. [Google Scholar] [CrossRef]
- Beijen, M.A.; Heertjes, M.F.; Butler, H.; Steinbuch, M. H ∞ feedback and feedforward controller design for active vibration isolators. IFAC-Pap. 2017, 50, 13384–13389. [Google Scholar] [CrossRef]
- Zhao, B.; Shi, W.; Tan, J. Design and Control of a Dual-Stage Actuation Active Vibration Isolation System. IEEE Access 2019, 7, 134556–134563. [Google Scholar] [CrossRef]
- Shen, Y.; Yao, W.; Wen, J.; He, H.; Chen, W. Adaptive Supplementary Damping Control of VSC-HVDC for Interarea Oscillation Using GrHDP. IEEE Trans. Power Syst. 2018, 33, 1777–1789. [Google Scholar] [CrossRef]
- Hakvoort, W.B.J.; Beijen, M.A. Filtered-error RLS for self-tuning disturbance feedforward control with application to a multi-axis vibration isolator. Mechatronics 2023, 89, 102934. [Google Scholar] [CrossRef]
- Batista, E.L.O.; Barghouthi, M.R.; Lopes, E.M.D.O. A Novel Adaptive Scheme to Improve the Performance of Feedforward Active Vibration Control Systems. IEEE/ASME Trans. Mechatron. 2022, 27, 2322–2332. [Google Scholar] [CrossRef]
- Xie, L.; Qiu, Z.; Zhang, X. Analysis and experiments of adaptive feedforward and combined vibration control system with variable step size and reference filter. Aerosp. Sci. Technol. 2017, 61, 109–120. [Google Scholar] [CrossRef]
- Wang, M.; Fang, X.; Wang, Y.; Ding, J.; Sun, Y.; Luo, J.; Pu, H. A dual-loop active vibration control technology with an RBF-RLS adaptive algorithm. Mech. Syst. Signal Process. 2023, 191, 110079. [Google Scholar] [CrossRef]
- Landau, I.D.; Airimitoaie, T.; Alma, M. IIR Youla-Kucera Parameterized Adaptive Feedforward Compensators for Active Vibration Control with Mechanical Coupling. IEEE Trans. Control Syst. Technol. 2013, 21, 765–779. [Google Scholar] [CrossRef]
- Airimitoaie, T.; Landau, I.D. Robust and Adaptive Active Vibration Control Using an Inertial Actuator. IEEE Trans. Ind. Electron. 2016, 63, 6482–6489. [Google Scholar] [CrossRef]
- Landau, I.D.E.; Melendez, R.; Airimitoaie, T.; Dugard, L. Beyond the delay barrier in adaptive feedforward active noise control using Youla–Kučera parametrization. J. Sound Vib. 2019, 455, 339–358. [Google Scholar] [CrossRef]
- Landau, I.D.E.; Constantinescu, A.; Rey, D. Adaptive narrow band disturbance rejection applied to an active suspension—an internal model principle approach. Automatica 2005, 41, 563–574. [Google Scholar] [CrossRef]
- Airimitoaie, T.; Landau, I.D. Combined adaptive feedback and feedforward compensation for active vibration control using Youla–Kučera parametrization. J. Sound Vib. 2018, 434, 422–441. [Google Scholar] [CrossRef]
- Wang, Y.P.; Sinha, A. Adaptive sliding mode control algorithm for a microgravity isolation system. Acta Astronaut. 1998, 43, 377–384. [Google Scholar] [CrossRef]
- Davis, L.; Hyland, D.; Yen, G.; Das, A. Adaptive neural control for space structure vibration suppression. Smart Mater. Struct. 1999, 8, 753. [Google Scholar]
- Deshpande, V.S.; Mohan, B.; Shendge, P.D.; Phadke, S.B. Disturbance observer based sliding mode control of active suspension systems. J. Sound Vib. 2014, 333, 2281–2296. [Google Scholar] [CrossRef]
- Kempf, C.J.; Kobayashi, S. Disturbance observer and feedforward design for a high-speed direct-drive positioning table. IEEE Trans. Control Syst. Technol. 1999, 7, 513–526. [Google Scholar] [CrossRef]
- Su, J.; Wang, L.; Yun, J.N. A design of disturbance observer in standard H ∞ control framework. Int. J. Robust Nonlinear Control 2015, 25, 2894–2910. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.; Li, S.; Su, J. A Time Delay Estimation Interpretation of Extended State Observer-Based Controller with Application to Structural Vibration Suppression. IEEE Trans. Autom. Sci. Eng. 2024, 21, 1965–1973. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.; Zhang, M.; Li, S.; Su, J.; Luo, L. Multi-modal vibration control for all-clamped plate subjected to periodic disturbances by ESO-based frequency-shaped LQR. Mech. Syst. Signal Process. 2023, 201, 110658. [Google Scholar] [CrossRef]
- Zhang, M.; Jing, X. Switching logic-based saturated tracking control for active suspension systems based on disturbance observer and bioinspired X-dynamics. Mech. Syst. Signal Process. 2021, 155, 107611. [Google Scholar] [CrossRef]
- Ai, C.; Guo, J.; Gao, W.; Chen, L.; Zhou, G.; Han, Z.; Kong, X. Active Disturbance Rejection Control With Linear Quadratic Regulator for Power Output of Hydraulic Wind Turbines. IEEE Access 2020, 8, 159581–159594. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R. New results in linear filtering and prediction theory. J. Basic Eng. Trans. ASME Ser. D 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Bandopadhya, D.; Njuguna, J. A Study on the Effects of Kalman Filter on Performance of IPMC-Based Active Vibration Control Scheme. IEEE Trans. Control Syst. Technol. 2010, 18, 1315–1324. [Google Scholar] [CrossRef]
- Papadimitriou, C.; Fritzen, C.; Kraemer, P.; Ntotsios, E. Fatigue predictions in entire body of metallic structures from a limited number of vibration sensors using Kalman filtering. Struct. Control Health Monit. 2011, 18, 554–573. [Google Scholar] [CrossRef]
- Erazo, K.; Sen, D.; Nagarajaiah, S.; Sun, L. Vibration-based structural health monitoring under changing environmental conditions using Kalman filtering. Mech. Syst. Signal Process. 2019, 117, 1–15. [Google Scholar] [CrossRef]
- Hamel, T.; Samson, C. Position estimation from direction or range measurements. Automatica 2017, 82, 137–144. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Xiao, Y.; Zhou, M.; Li, Y.; Yu, D. Active Composite Control of Disturbance Compensation for Vibration Isolation System with Uncertainty. Actuators 2024, 13, 334. https://doi.org/10.3390/act13090334
Zhu Z, Xiao Y, Zhou M, Li Y, Yu D. Active Composite Control of Disturbance Compensation for Vibration Isolation System with Uncertainty. Actuators. 2024; 13(9):334. https://doi.org/10.3390/act13090334
Chicago/Turabian StyleZhu, Zhijun, Yong Xiao, Minrui Zhou, Yongqiang Li, and Dianlong Yu. 2024. "Active Composite Control of Disturbance Compensation for Vibration Isolation System with Uncertainty" Actuators 13, no. 9: 334. https://doi.org/10.3390/act13090334




