Nonlinear Robust Control for Missile Unsupported Random Launch Based on Dynamic Surface and Time Delay Estimation
Abstract
1. Introduction
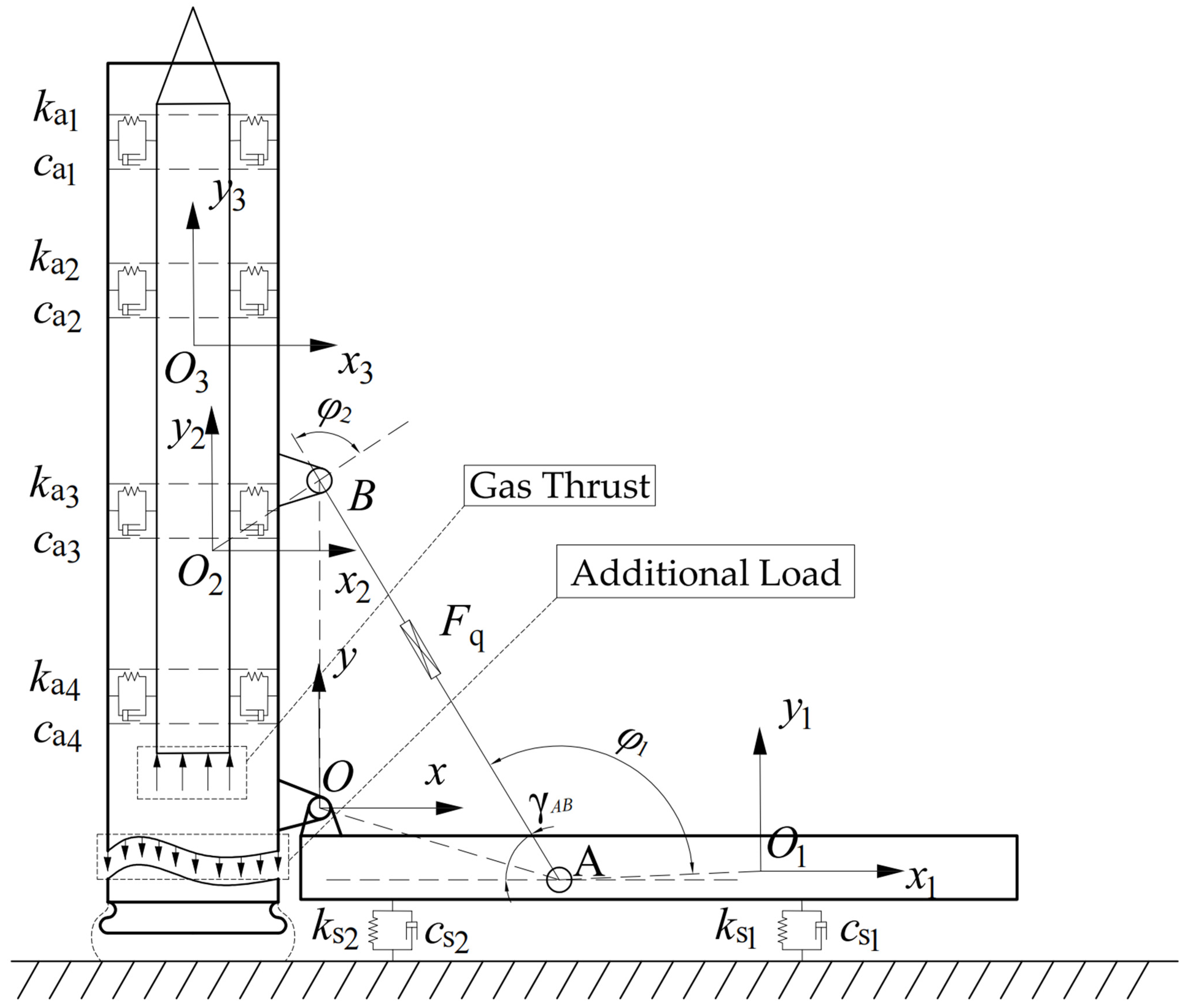
2. Problem Description and System Modeling
2.1. Unsupported Random Vertical Launch Dynamics Modeling
2.2. Hydraulic System Modeling
2.3. State-Space Equation Derivation
- The interference-fit joint between the adapters and the launch canister makes it difficult to express the state-space equation and prove the stability of the subsequent controller design. Therefore, the interference amount is ignored, making .
- The trigonometric relations regarding and are simplified so that , , and when , the errors are all within 0.4%.
- Considering the superelastic compressible properties of the adapter rubber foam material, the damping effect is very small, and therefore, the damping terms () are neglected.
- The effect of measurement noise on the system is neglected for all measured state variables ().
3. Control Design
3.1. Time Delay Estimation Controller Design
3.2. DSC Design with Nonlinear Robust Control
3.3. Stability Analysis
4. Numerical Simulation
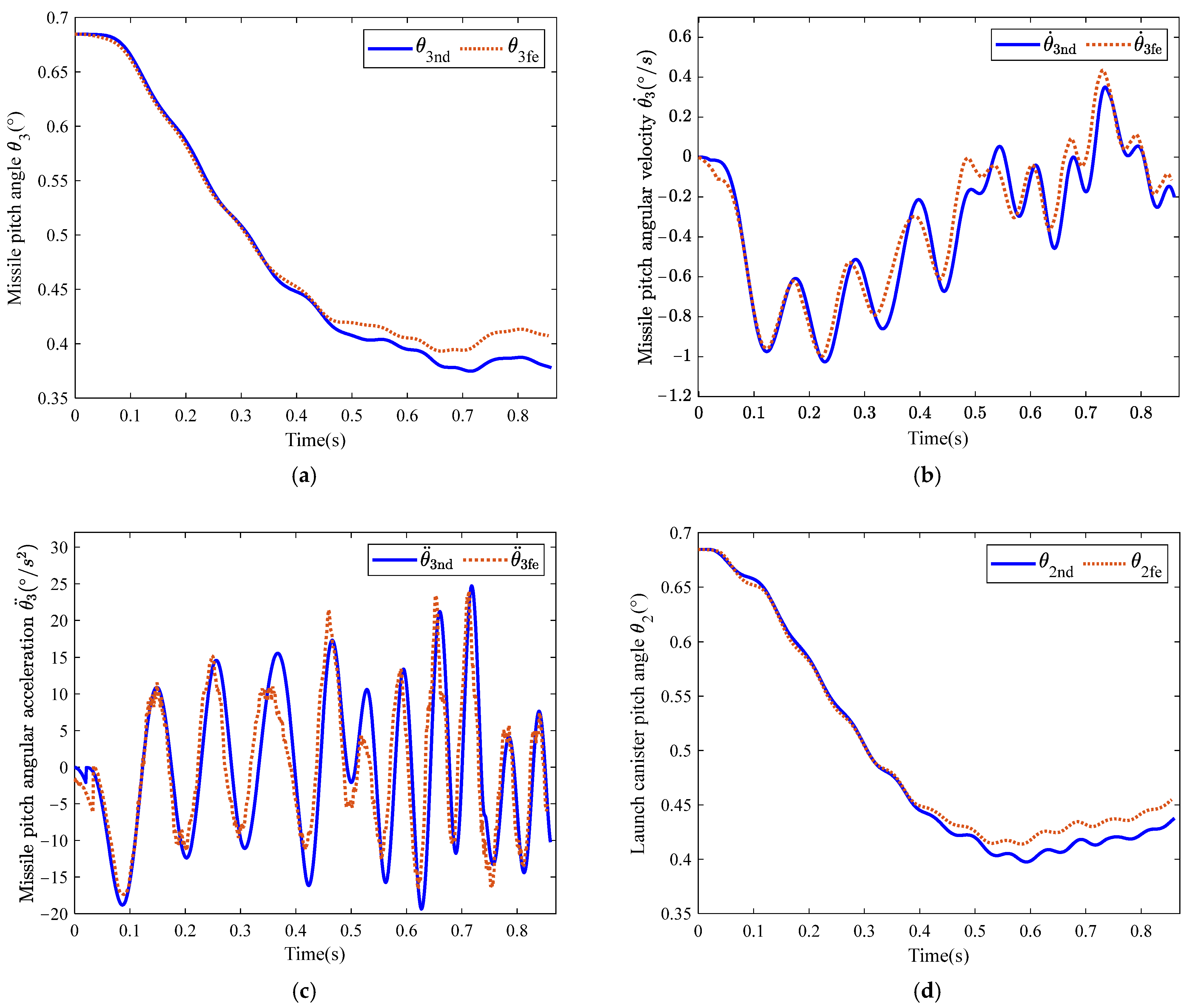
4.1. Verification of the 6-DOF Multi-Rigid-Body Launch Dynamic Model
4.2. Launch Dynamics in Uncontrolled State with Lumped Disturbances
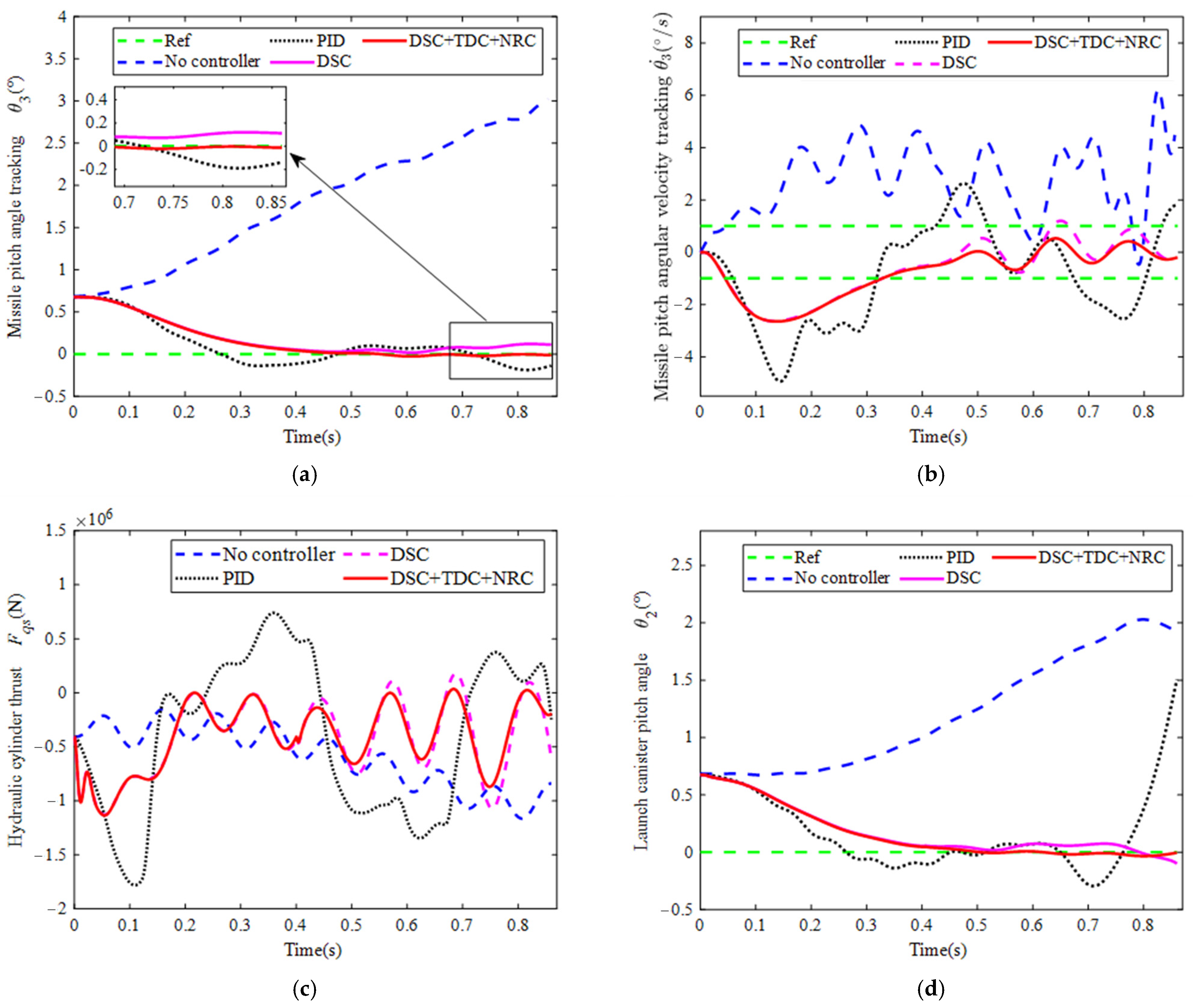
4.3. Launch Dynamics in Controlled State with Lumped Disturbances
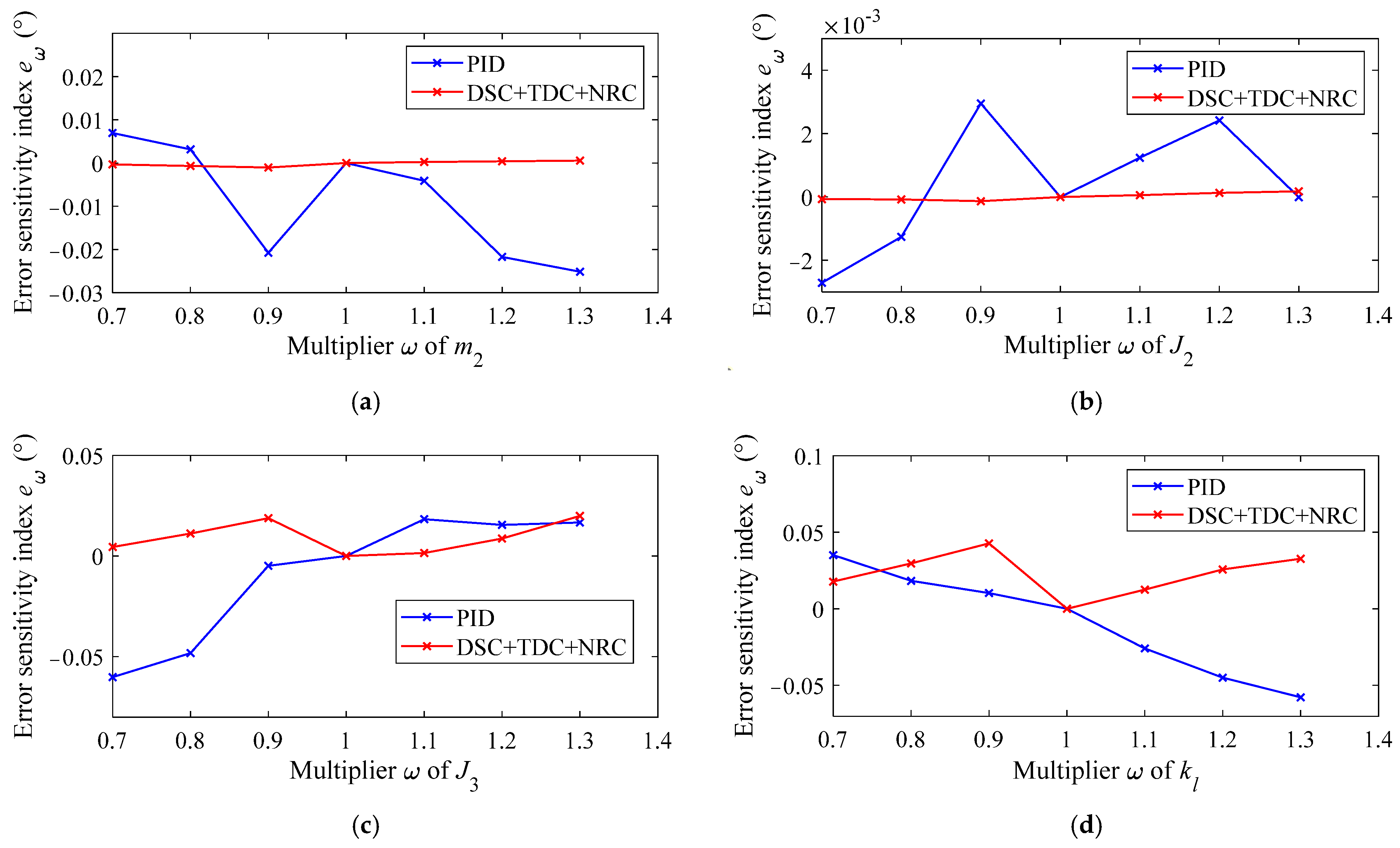
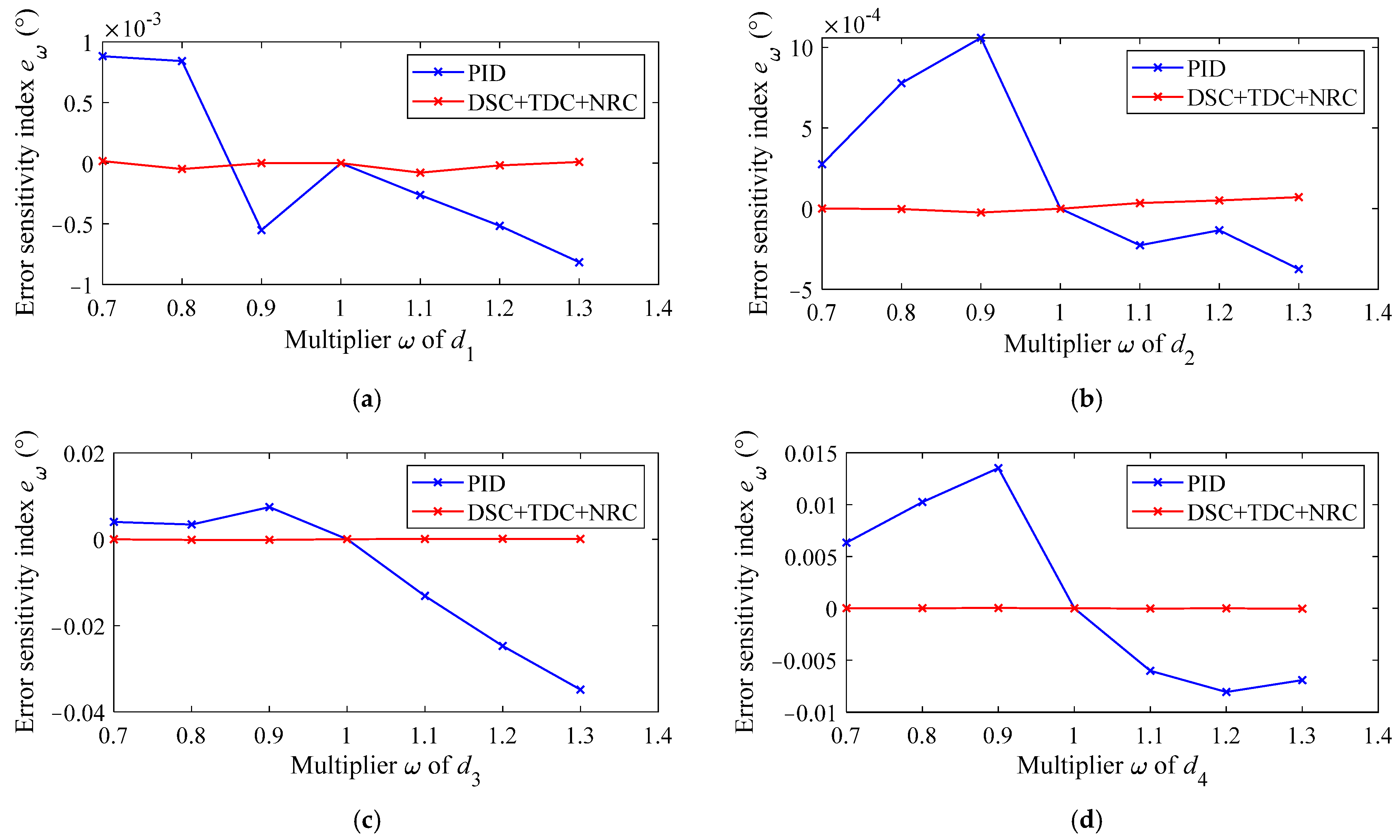
4.4. Error Sensitivity Analysis of System Parameters and Lumped Disturbance Terms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, H.; Qian, Z.; Zhao, Y.; Li, B. Study on the load to ground on missile erection process. Ordn. Ind. Autom. 2011, 30, 1–3. [Google Scholar]
- Zhou, X.; Ma, D.; Hu, J.; Zhong, J. Research on dynamic response of launching site for missile unsupported random launch. Acta Armamentarii 2014, 35, 1595–1603. [Google Scholar]
- Zhang, Z.; Ma, D.; Zhong, J.; Gao, Y.; Wang, X. Research on adaptability of a cold launching system of missile to launching site. Acta Armamentarii 2020, 41, 280–290. [Google Scholar]
- Zhang, T.; Liu, X.; Zheng, B. Rigid-flexible coupling dynamic analysis during launching based on component model synthesis. Missiles Space Veh. 2009, 1, 51–54. [Google Scholar]
- Gao, X.; Bi, S.; Chen, Z. The Simulation study on multi-body launching dynamics for a vehicular missile launcher. J. Project. Rock. Miss. Guid. 2010, 30, 60–62. [Google Scholar]
- Rui, X. Launch dynamics of multibody systems and its applications. Str. St. CAE 2011, 13, 76–82. [Google Scholar]
- Işık, C.; Ider, S.; Acar, B. Modeling and verification of a missile launcher system. Proc. Inst. Mech. Eng. 2013, 228, 100–107. [Google Scholar] [CrossRef]
- Yang, C.; Ma, D.; Wang, X. Sensitivity analysis of factors affecting launching-site dynamic response of missile with unsupported random launch. J. Ball. 2016, 28, 87–92. [Google Scholar]
- Cheng, H.; Zhang, Y.; Li, B.; Zhan, J. Research on the bearing capacity of unsupported random launching site. In Proceedings of the 2011 International Conference on Advanced Materials and Engineering Materials (ICAMEM), Shenyang, China, 22–24 January 2012. [Google Scholar]
- Zhang, Z.; Ma, D.; Ren, J.; He, Q.; Zhu, Z. Dynamic response of cold launching equipment to prepared launching site subjected to loading. Ordn. Ind. Autom. 2015, 36, 279–286. [Google Scholar]
- Zhou, X.; Wang, H.; Ma, D.; Gao, Y.; Ren, J. Study on unsupported launching site quasi-static response during missile standby phase. J. Ball. 2015, 27, 91–96. [Google Scholar]
- Sun, C.; Ma, D.; Ren, J. Study on vertical launching response characteristics of cold launch platform. J. Nanjing Univ. Sci. Techn. 2015, 39, 516–522+555. [Google Scholar]
- Pan, Q.; Liang, G.; Lyu, Y.; Qi, Z.; Liu, H. Fast simulation on rigid multibody dynamics for vehicular cold launch systems. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 71–78. [Google Scholar]
- Wang, X.; Rui, X.; Yang, F.; Zhou, Q. Launch dynamics modeling and simulation of vehicular missile system. J. Guid. Control Dyn. 2018, 41, 1370–1379. [Google Scholar] [CrossRef]
- Zhou, F.; Li, D.; Zhou, S.; Jiang, R. Semianalytical model for dynamic analysis of missile vertical cold launch. J. Spacecr. Rockets 2022, 59, 1966–1986. [Google Scholar] [CrossRef]
- Pan, Q.; Liang, G.; Lyu, Y.; Qi, Z.; Wang, X. Modeling and simulation of rigid-flexible coupling dynamics of vehicular cold launch system. Ordn. Ind. Autom. 2017, 38, 2386–2394. [Google Scholar]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Automat. Contr. 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Jing, C.; Xu, H.; Jiang, J. Dynamic surface disturbance rejection control for electro-hydraulic load simulator. Mech. Syst. Signal Process. 2019, 134, 106293. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, J.; Ding, H.; Zhang, H. Dynamic surface control based on high-gain disturbance observer for electro-hydraulic systems with position/velocity constraints. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2021, 235, 3485–3494. [Google Scholar] [CrossRef]
- Sa, Y.; Zhu, Z.; Tang, Y.; Li, X.; Shen, G. Adaptive dynamic surface control using nonlinear disturbance observers for position tracking of electro-hydraulic servo systems. Proc. Inst. Mech. Eng. I J. Syst. Control Eng. 2022, 236, 634–653. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, G. Dual extended state observer-based adaptive dynamic surface control for a hydraulic manipulator with actuator dynamics. Mech. Mach. Theory 2022, 169, 104647. [Google Scholar] [CrossRef]
- Gao, Q.; Wei, X.; Li, D.; Ji, Y.; Chao, J. Tracking control for a quadrotor via dynamic surface control and adaptive dynamic programming. Int. J. Control Autom. Syst. 2022, 20, 349–363. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Deng, W.; Yao, J. Precision motion control for electro-hydraulic axis systems under unknown time-variant parameters and disturbances. Chin. J. Aeronaut. 2024, 37, 463–471. [Google Scholar] [CrossRef]
- Chen, W.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Sun, C.; Fang, J.; Wei, J.; Li, M. Nonlinear motion control of a hydraulic press based on an extended disturbance observer. IEEE Access 2018, 6, 18502–18510. [Google Scholar] [CrossRef]
- Liu, J.; Gai, W.; Zhang, J.; Li, Y. Nonlinear adaptive backstepping with ESO for the quadrotor trajectory tracking control in the multiple disturbances. Int. J. Control Autom. Syst. 2019, 17, 2754–2768. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J.; Wang, Y.; Yang, X.; Chen, J. Output feedback backstepping control of hydraulic actuators with valve dynamics compensation. Mech. Syst. Signal Process. 2021, 158, 107769. [Google Scholar] [CrossRef]
- Shao, X.; Xu, L.; Zhang, W. Quantized control capable of appointed-time performances for quadrotor attitude tracking: Experimental validation. IEEE Trans. Ind. Electron. 2021, 69, 5100–5110. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J.; Ullah, N. Neuroadaptive control of saturated nonlinear systems with disturbance compensation. ISA Trans. 2022, 122, 49–62. [Google Scholar] [CrossRef]
- Hsia, T.S. A new technique for robust control of servo systems. IEEE Trans. Ind. Electron. 1989, 36, 1–7. [Google Scholar] [CrossRef]
- Youcef-Toumi, K.; Ito, O. A time delay controller for systems with unknown dynamics. J. Dyn. Syst. Meas. Control 1990, 112, 133–142. [Google Scholar] [CrossRef]
- Lee, S.U.; Chang, P.H. Control of a heavy-duty robotic excavator using time delay control with integral sliding surface. Control Eng. Pract. 2002, 10, 697–711. [Google Scholar] [CrossRef]
- Jin, M.; Lee, J.; Ahn, K.K. Continuous nonsingular terminal sliding-mode control of shape memory alloy actuators using time delay estimation. IEEE/ASME Trans. Mech. 2014, 20, 899–909. [Google Scholar] [CrossRef]
- Kim, J.; Joe, H.; Yu, S.; Lee, J.; Kim, M. Time-delay controller design for position control of autonomous underwater vehicle under disturbances. IEEE Trans. Ind. Electron. 2015, 63, 1052–1061. [Google Scholar] [CrossRef]
- Lee, J.; Chang, P.H.; Jin, M. Adaptive integral sliding mode control with time-delay estimation for robot manipulators. IEEE Trans. Ind. Electron. 2017, 64, 6796–6804. [Google Scholar] [CrossRef]
- Vo, C.P.; Dao, H.V.; Ahn, K.K. Actuator fault-tolerant control for an electro-hydraulic actuator using time delay estimation and feedback linearization. IEEE Access 2021, 9, 107111–107123. [Google Scholar]
- Wang, C. Research on Launching Attitude of Ballistic Missile Unsupported Random Cold Launching. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 30 June 2019. [Google Scholar]


| Model Parameter | Value | Model Parameter | Value |
|---|---|---|---|
| m1/kg | 38,000 | /m | −6.065 |
| m2/kg | 14,950 | D/m | 2 |
| m3/kg | 42,470 | z1/m | 5.324 |
| J1/kg·m2 | 1.42 × 106 | z2/m | 1.634 |
| J2/kg·m2 | 2.98 × 105 | z3/m | −2.826 |
| J3/kg·m2 | 1.11 × 106 | z4/m | −7.226 |
| kl/N·m−3 | 1.6 × 107 | μ | 0.16 |
| ca/N·m−1·s−1 | 10 | βe/Pa | 7 × 108 |
| ks1/N·m−1 | 6 × 107 | Ps/Pa | 3.5 × 107 |
| cs1/N·m−1·s−1 | 6 × 105 | Pr/Pa | 0 |
| ks2/N·m−1 | 6 × 107 | A1/m2 | 0.0283 |
| cs2/N·m−1·s−1 | 6 × 105 | A2/m2 | 0.017 |
| /m | −10.580 | V01/m2 | 0.051 |
| /m | 0.591 | V02/m2 | 0.0119 |
| /m | 1.198 | kq | 0.7 |
| Index ) | No Control | PID | DSC | DSC + TDC + NRC |
|---|---|---|---|---|
| 3.1175 | 0.1121 | 0.0839 | 0.0145 | |
| 3.0233 | 0.1887 | 0.12 | 0.0271 | |
| 3.3015 | 1.5397 | 0.6092 | 0.3346 | |
| 6.2344 | 2.5472 | 1.2024 | 0.3030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Sun, H.; Liu, H.; Liang, X.; Yang, X.; Yao, J. Nonlinear Robust Control for Missile Unsupported Random Launch Based on Dynamic Surface and Time Delay Estimation. Actuators 2025, 14, 142. https://doi.org/10.3390/act14030142
Yu X, Sun H, Liu H, Liang X, Yang X, Yao J. Nonlinear Robust Control for Missile Unsupported Random Launch Based on Dynamic Surface and Time Delay Estimation. Actuators. 2025; 14(3):142. https://doi.org/10.3390/act14030142
Chicago/Turabian StyleYu, Xiaochuan, Hui Sun, Haoyang Liu, Xianglong Liang, Xiaowei Yang, and Jianyong Yao. 2025. "Nonlinear Robust Control for Missile Unsupported Random Launch Based on Dynamic Surface and Time Delay Estimation" Actuators 14, no. 3: 142. https://doi.org/10.3390/act14030142
APA StyleYu, X., Sun, H., Liu, H., Liang, X., Yang, X., & Yao, J. (2025). Nonlinear Robust Control for Missile Unsupported Random Launch Based on Dynamic Surface and Time Delay Estimation. Actuators, 14(3), 142. https://doi.org/10.3390/act14030142






