Structural Optimization and Fluid–Structure Interaction Analysis of a Novel High-Speed Switching Control Valve
Abstract
1. Introduction
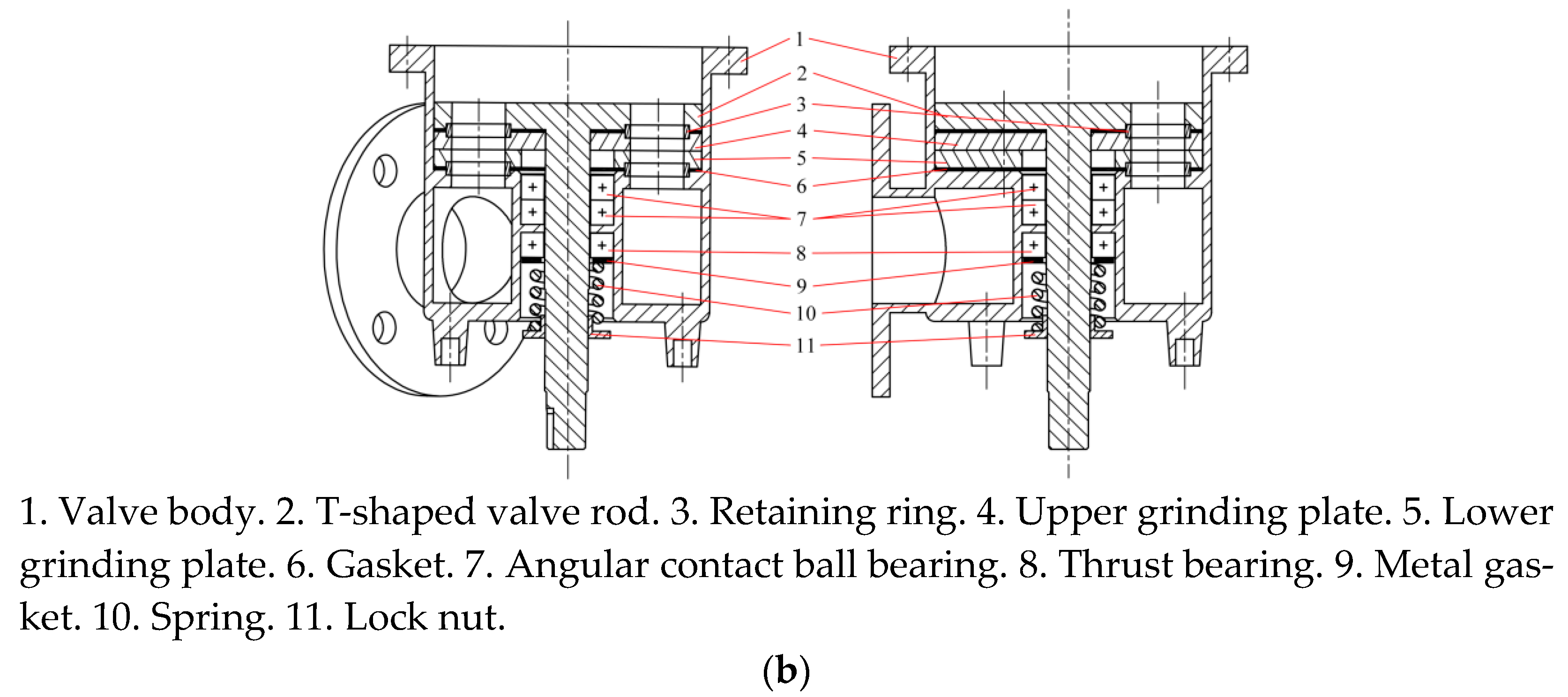
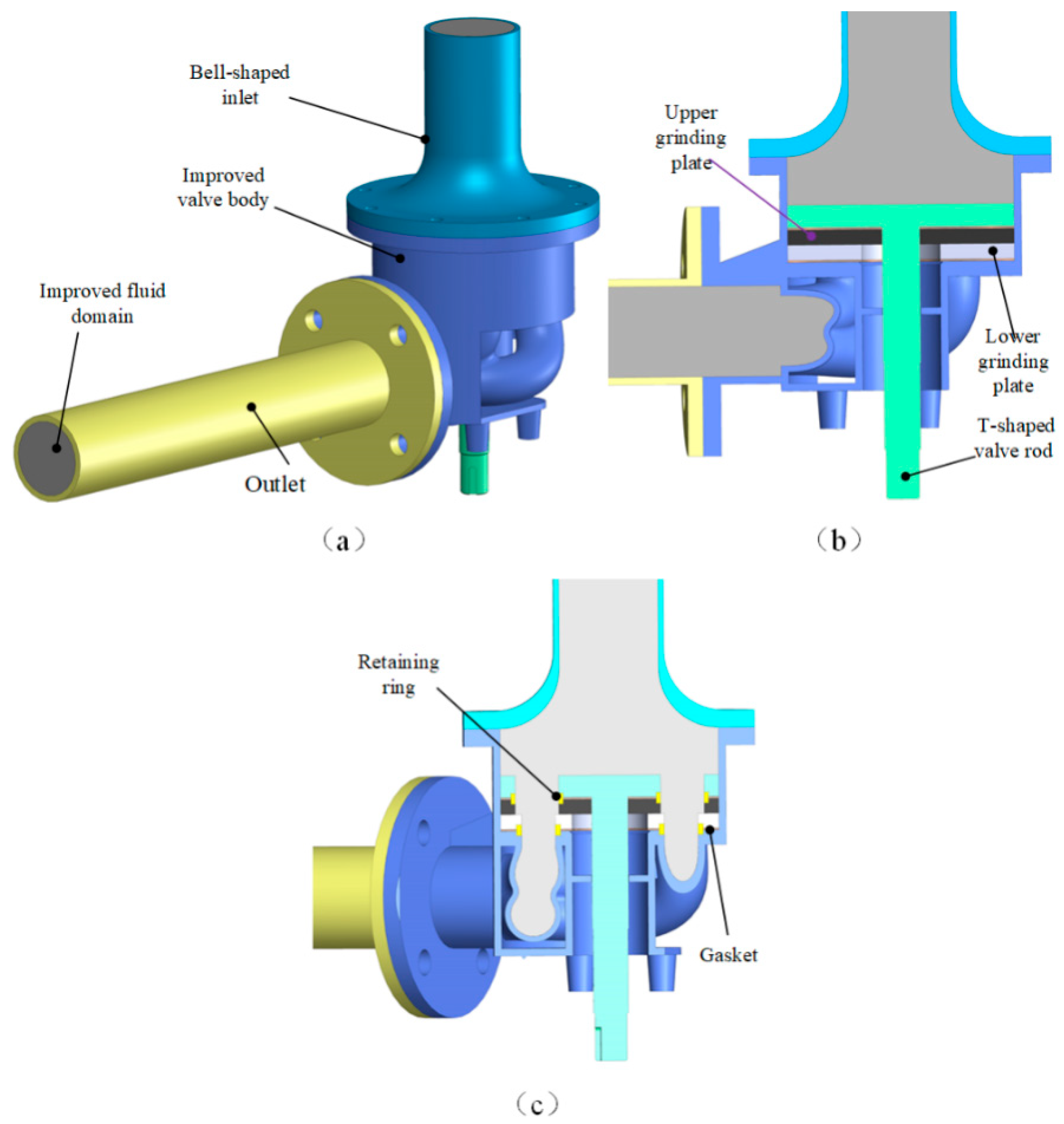
2. Structure and Principle of Laver Fluffy Control Valve
3. Methodology
3.1. Flow Field Simulation Method of Laver Fluffiness Control Valve
3.1.1. Model Construction
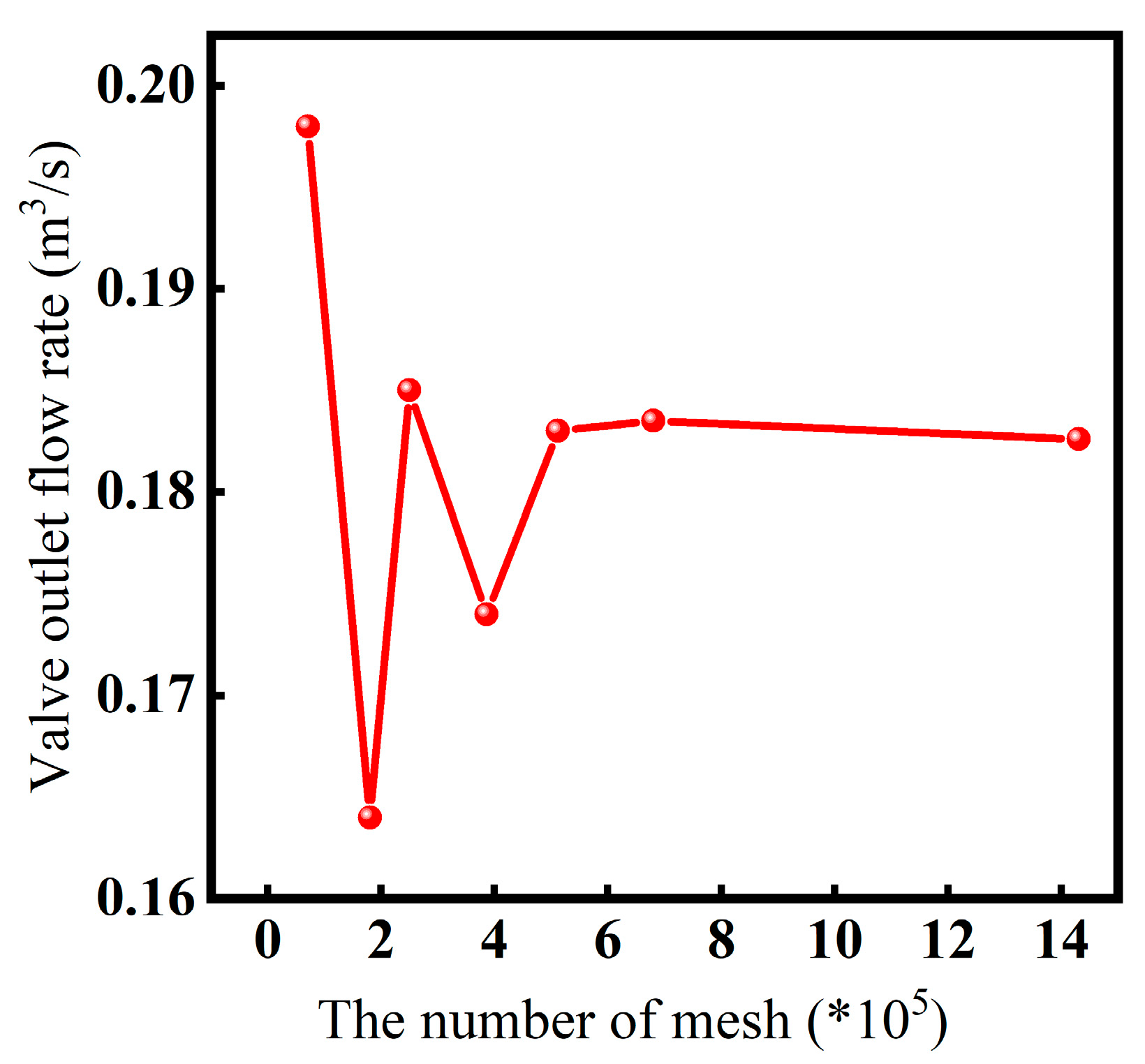
3.1.2. Grid Division and Boundary Condition Setting
3.2. Fluid–Structure Interaction Method for Laver Fluffiness Control Valve
3.2.1. Fluid–Structure Interaction Finite Element Model
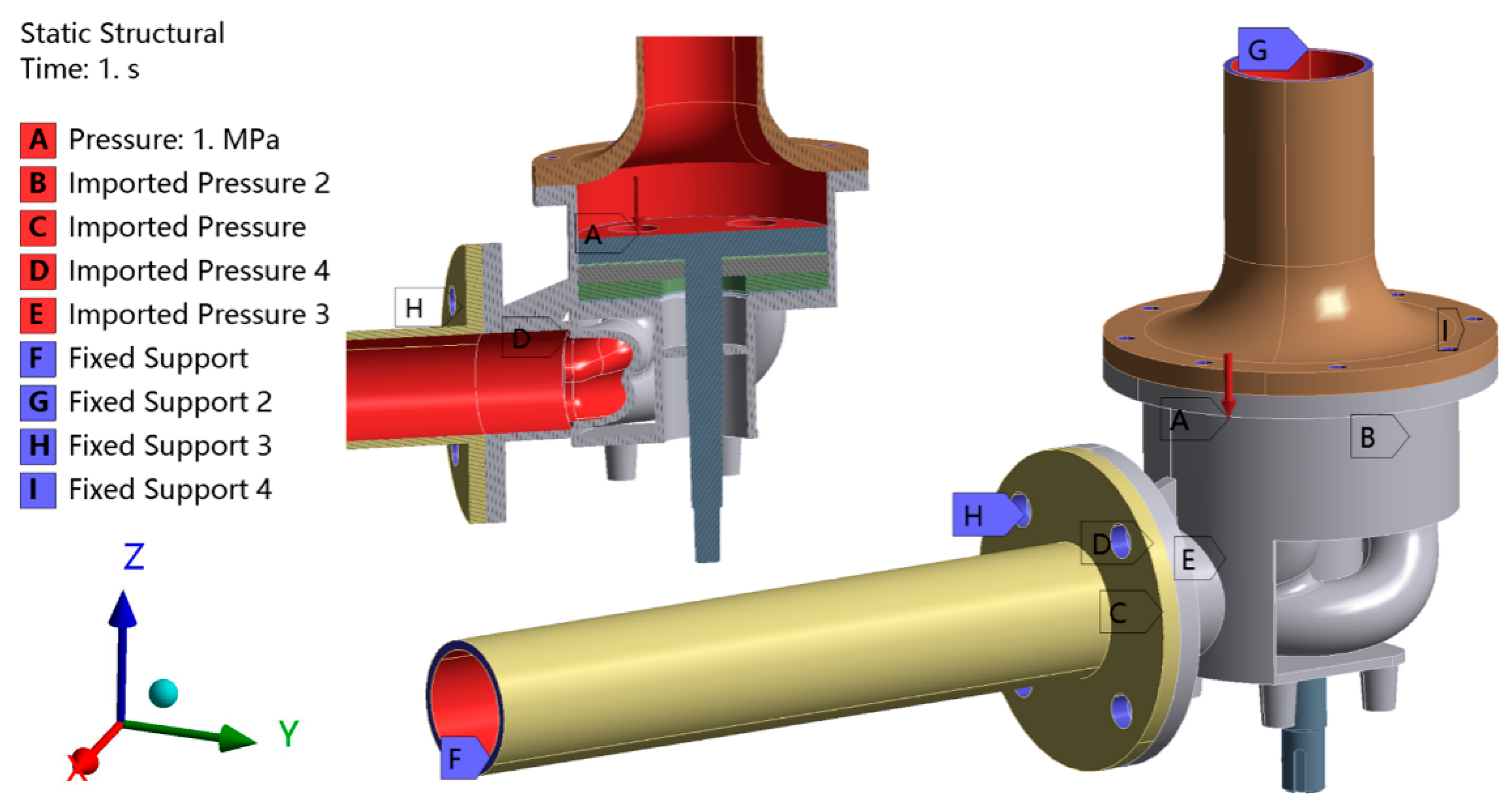
3.2.2. Boundary Conditions and Related Parameters
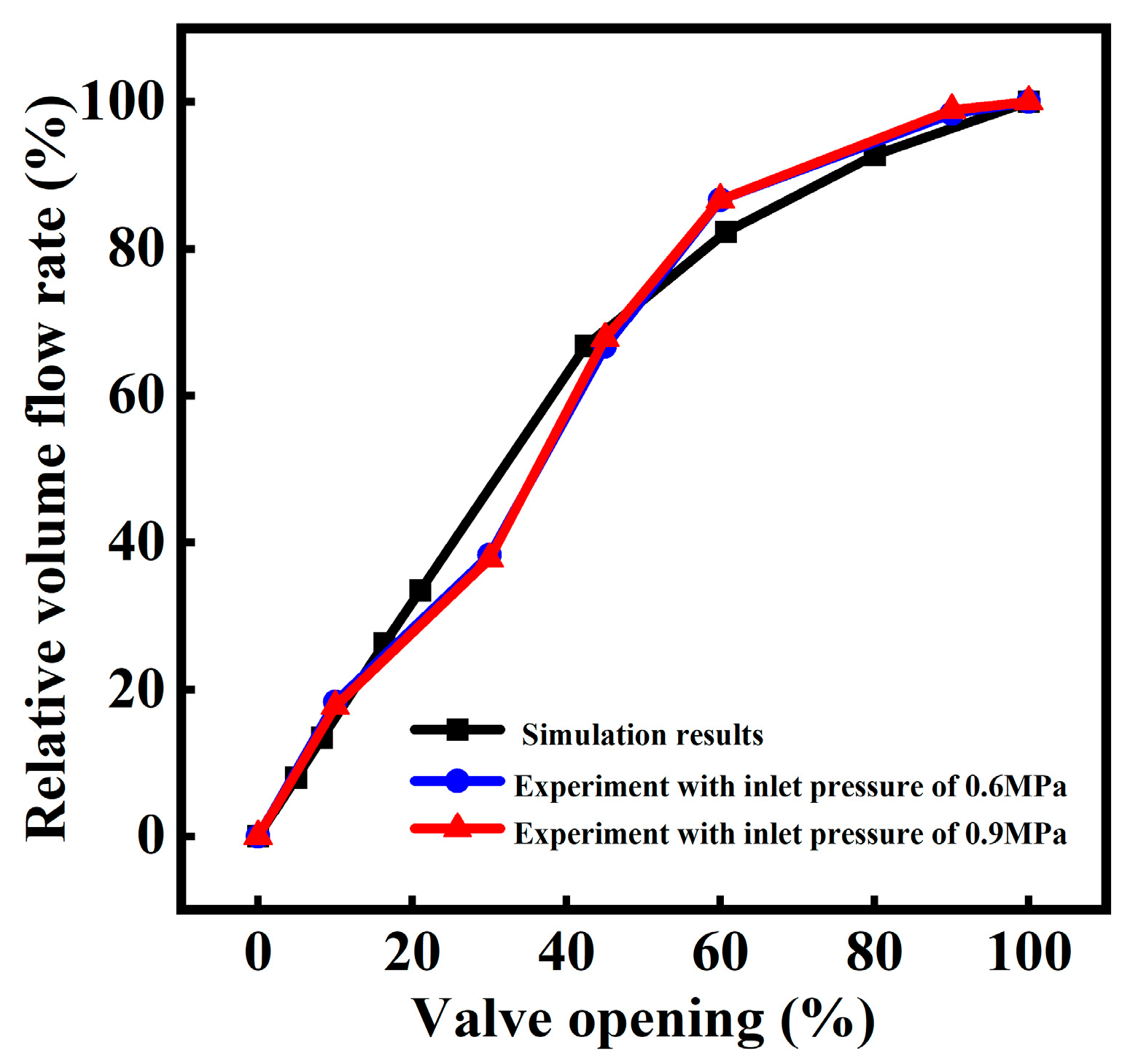
3.3. Simulation Validation
4. Results and Discussion
4.1. Flow Field Analysis of Laver Fluffiness Control Valve Under Different Valve Structures
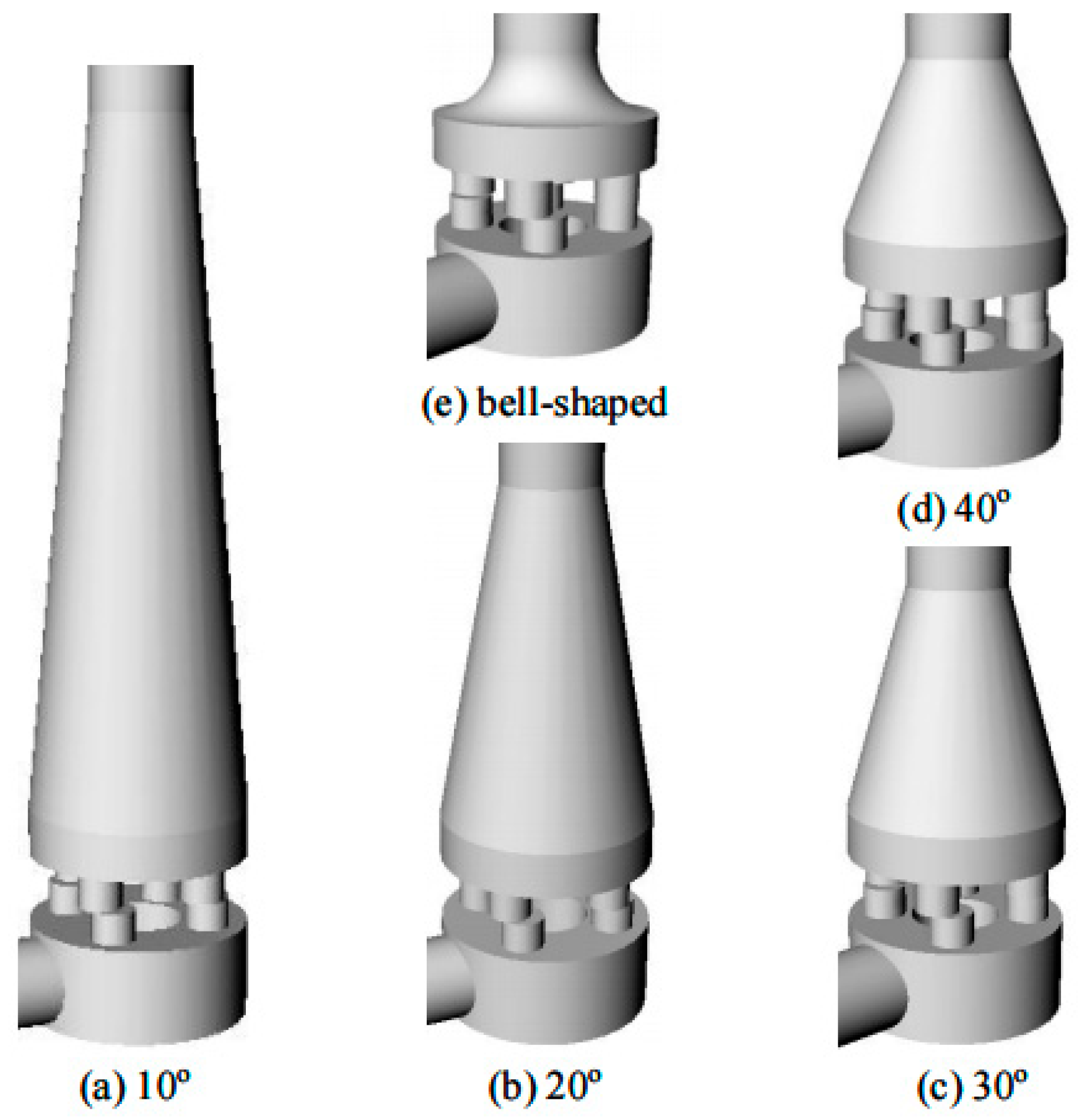
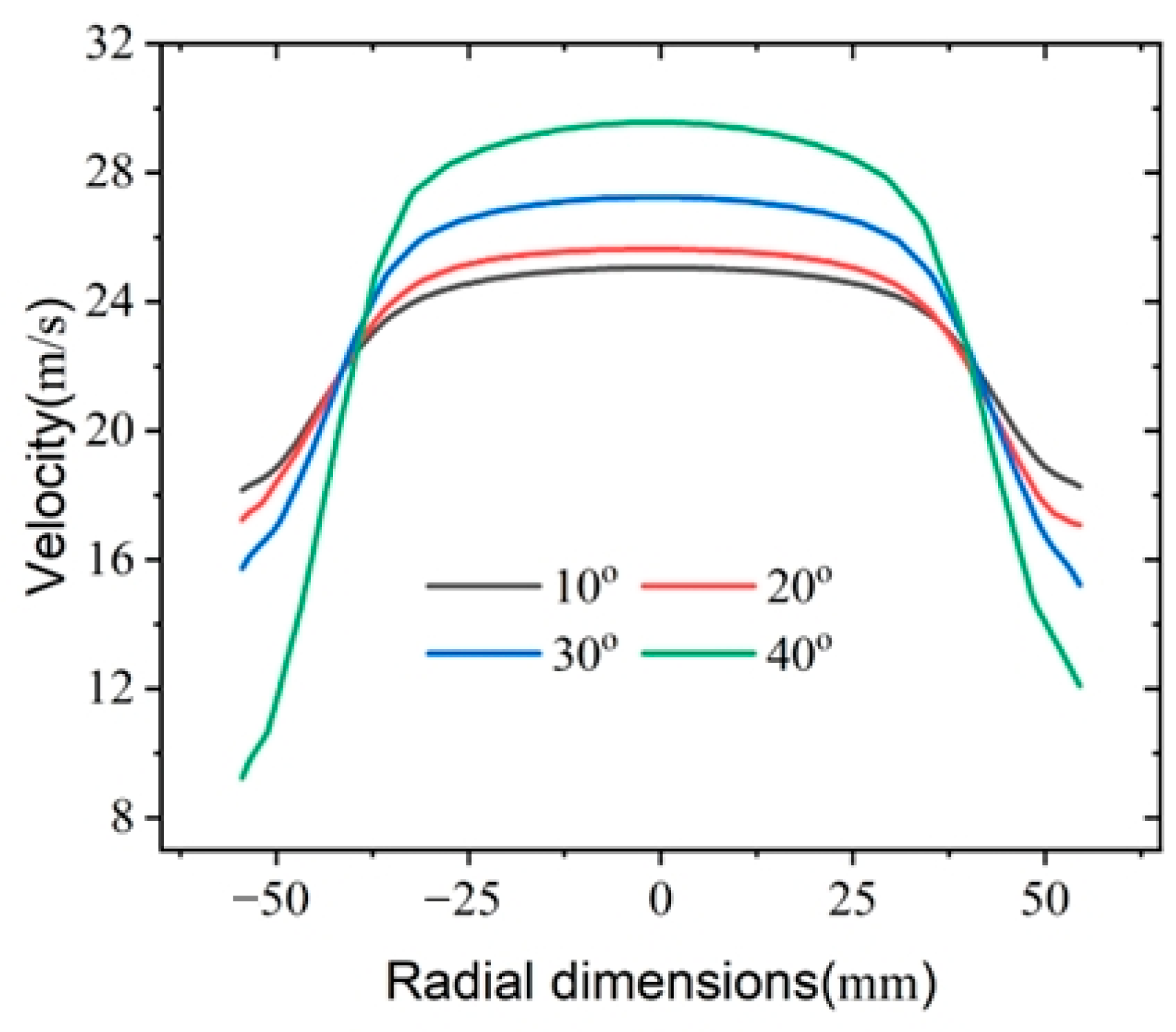
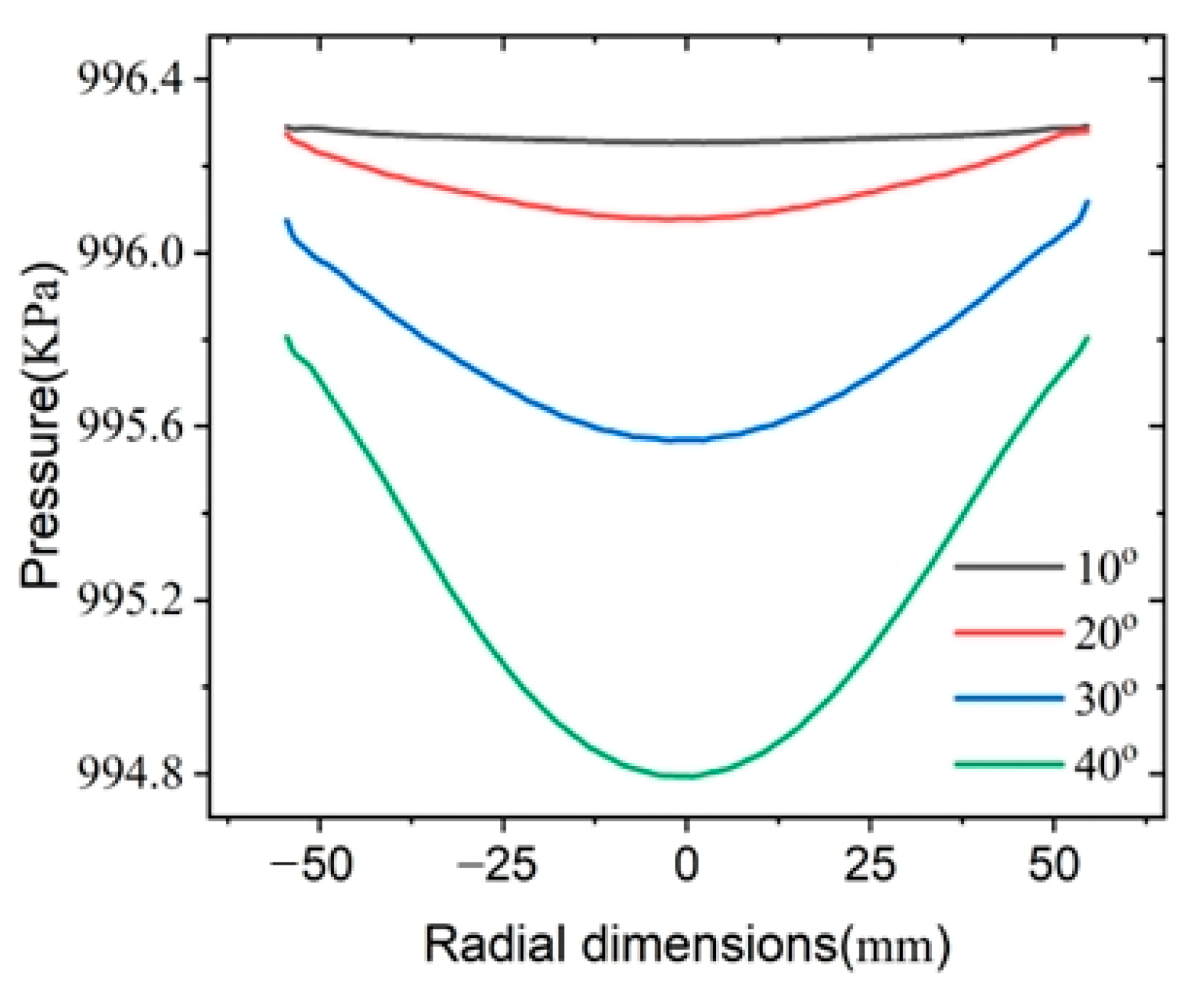
4.1.1. Influence of Inlet Shape
- (1)
- Choice of Entrance Shape
- (2)
- Volume Flow of Outlet
- (3)
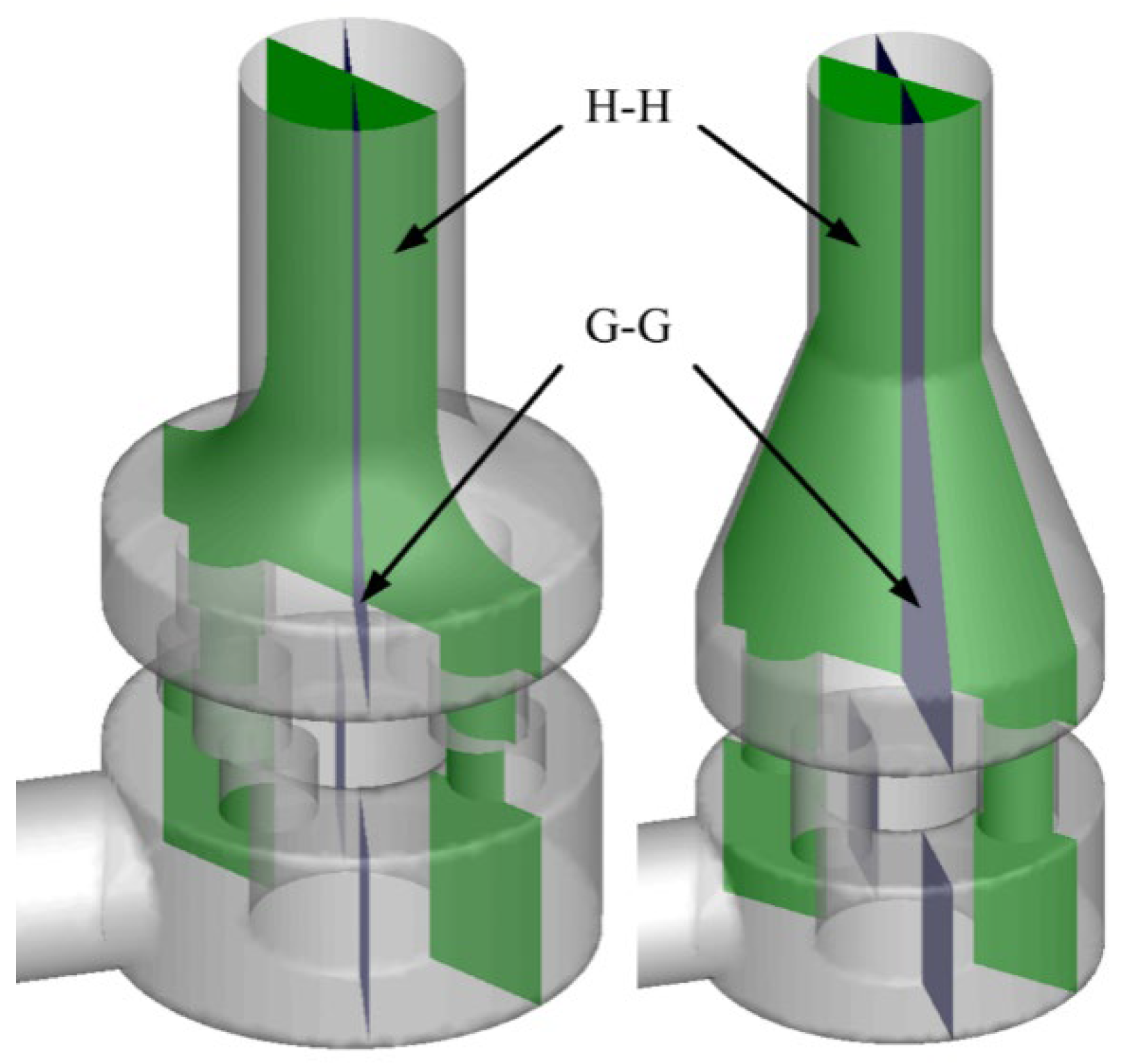
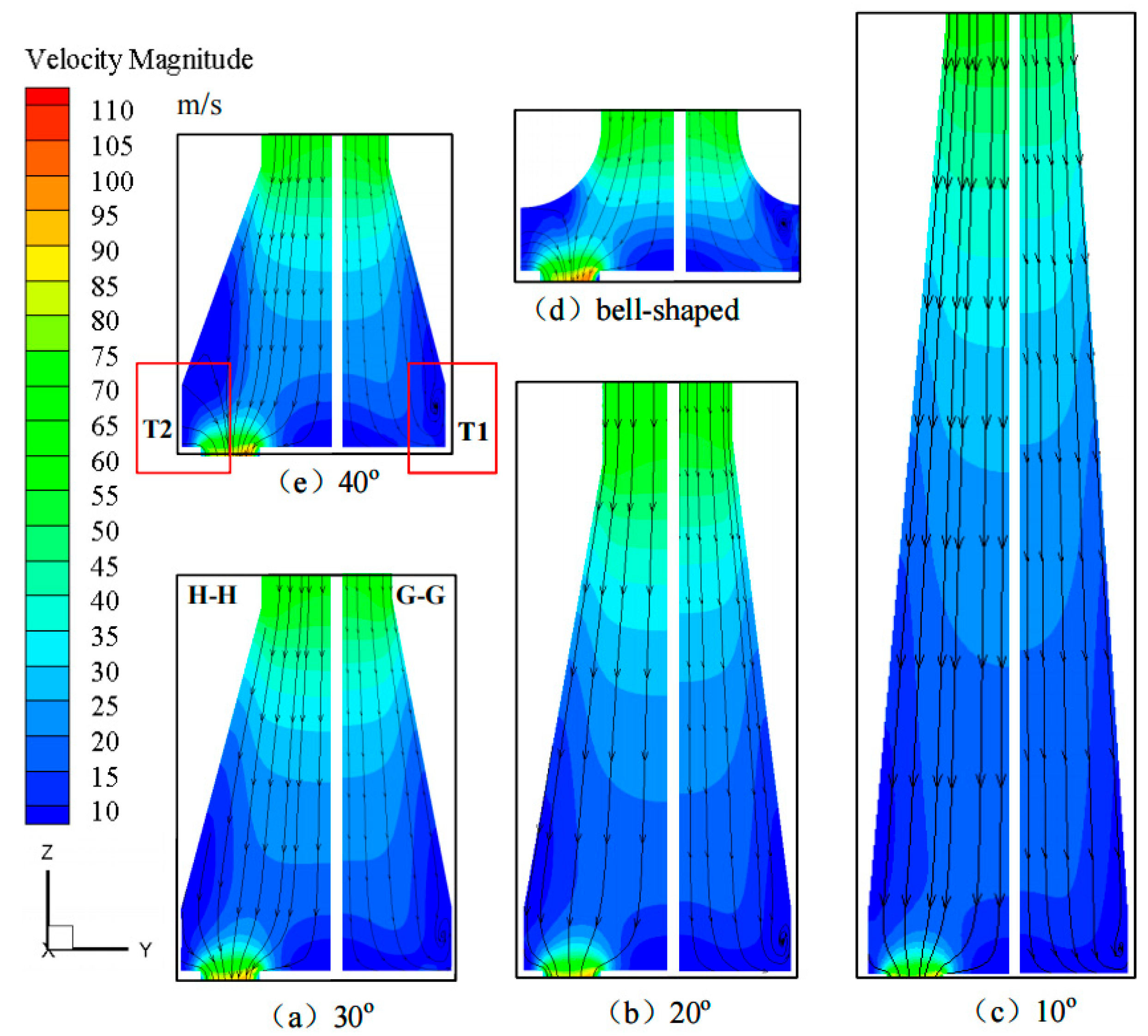
- Comparison of Flow Field Results
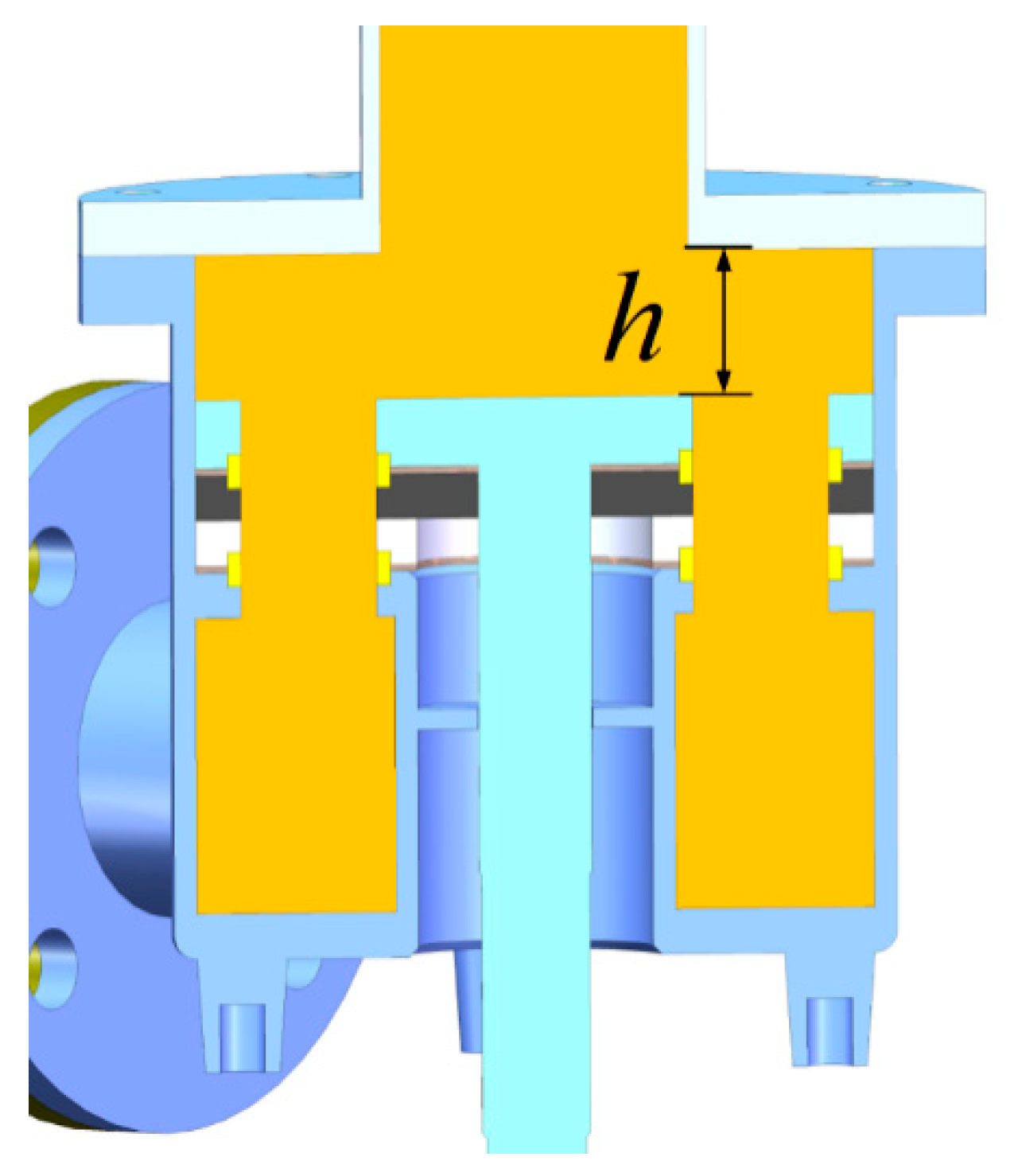
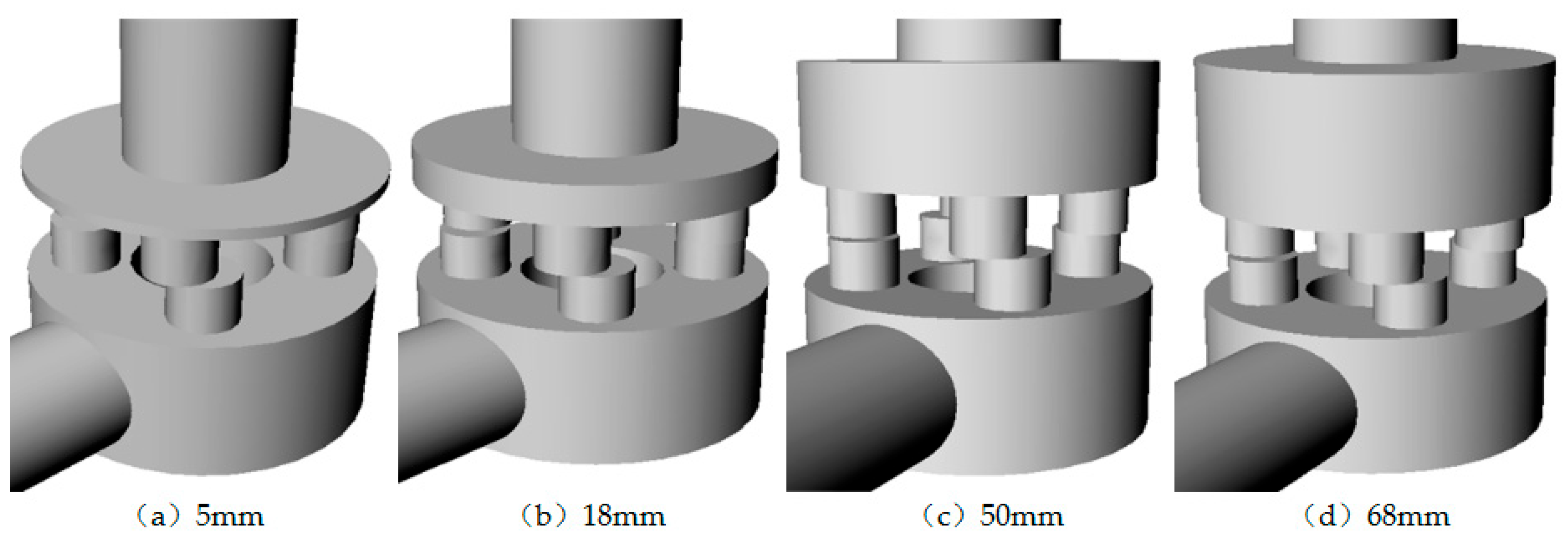
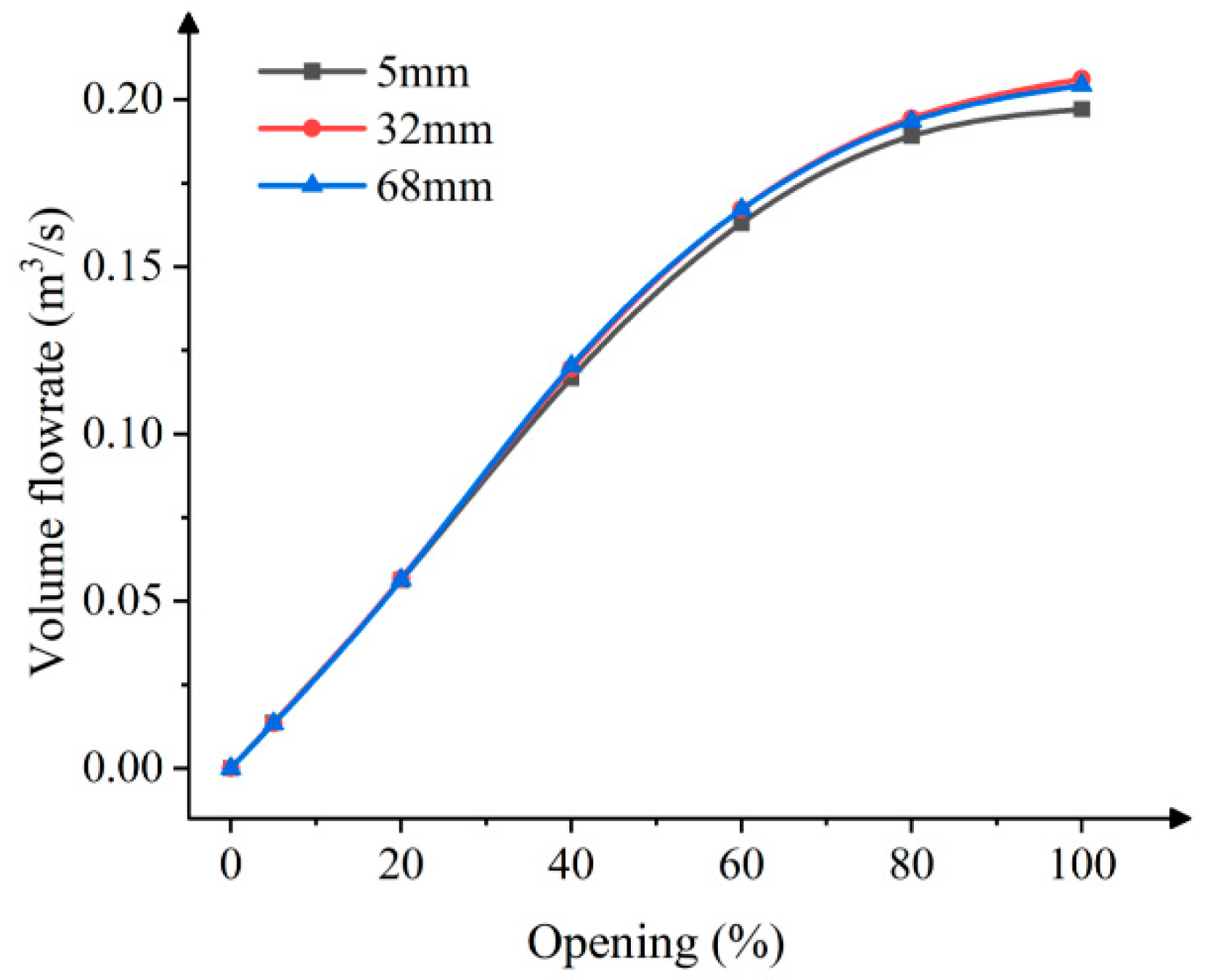
4.1.2. Influence of Upper Chamber Height
- (1)
- Selection of the Height of the Upper Chamber
- (2)
- Volume Flow of Outlet
- (3)
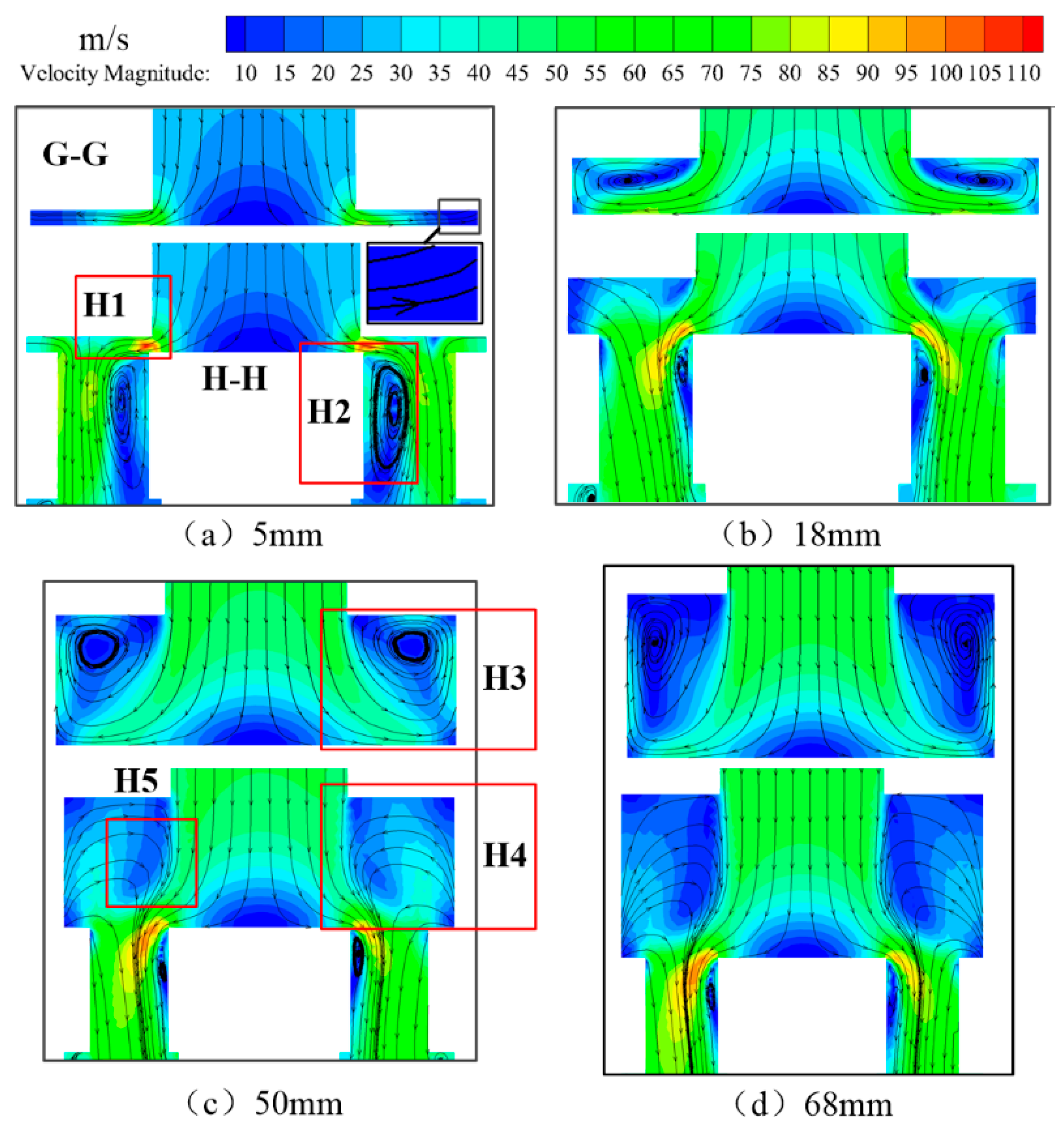
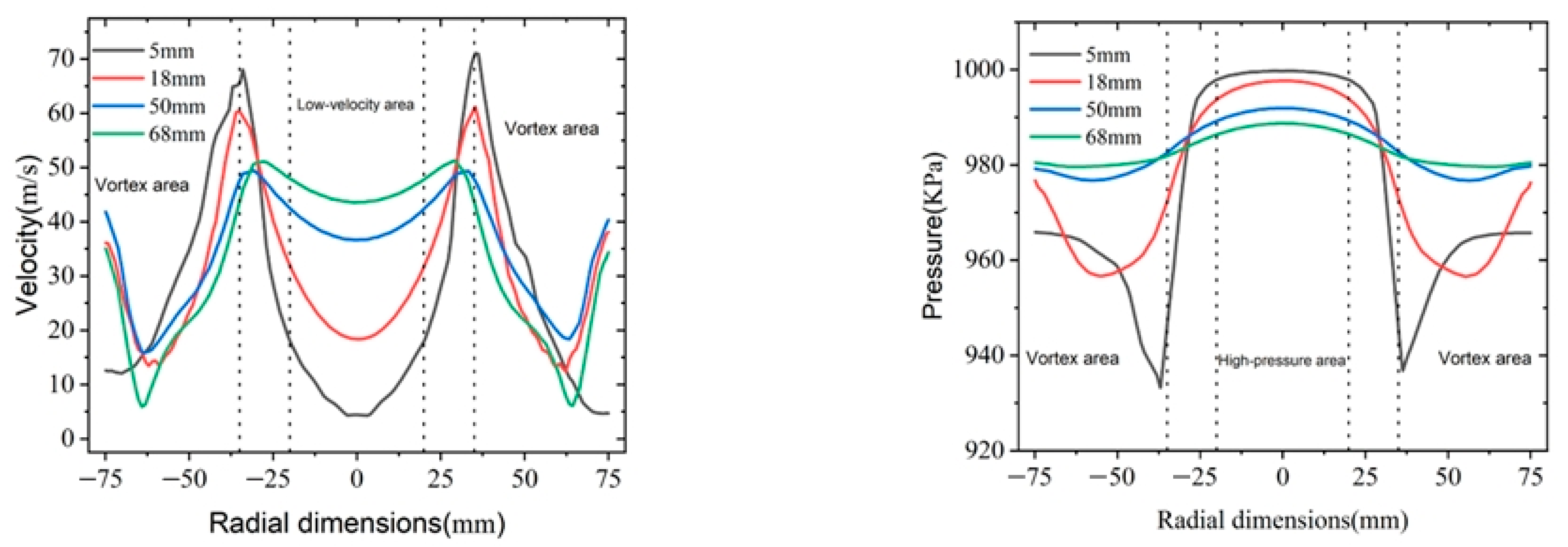
- Comparison of Flow Field Results
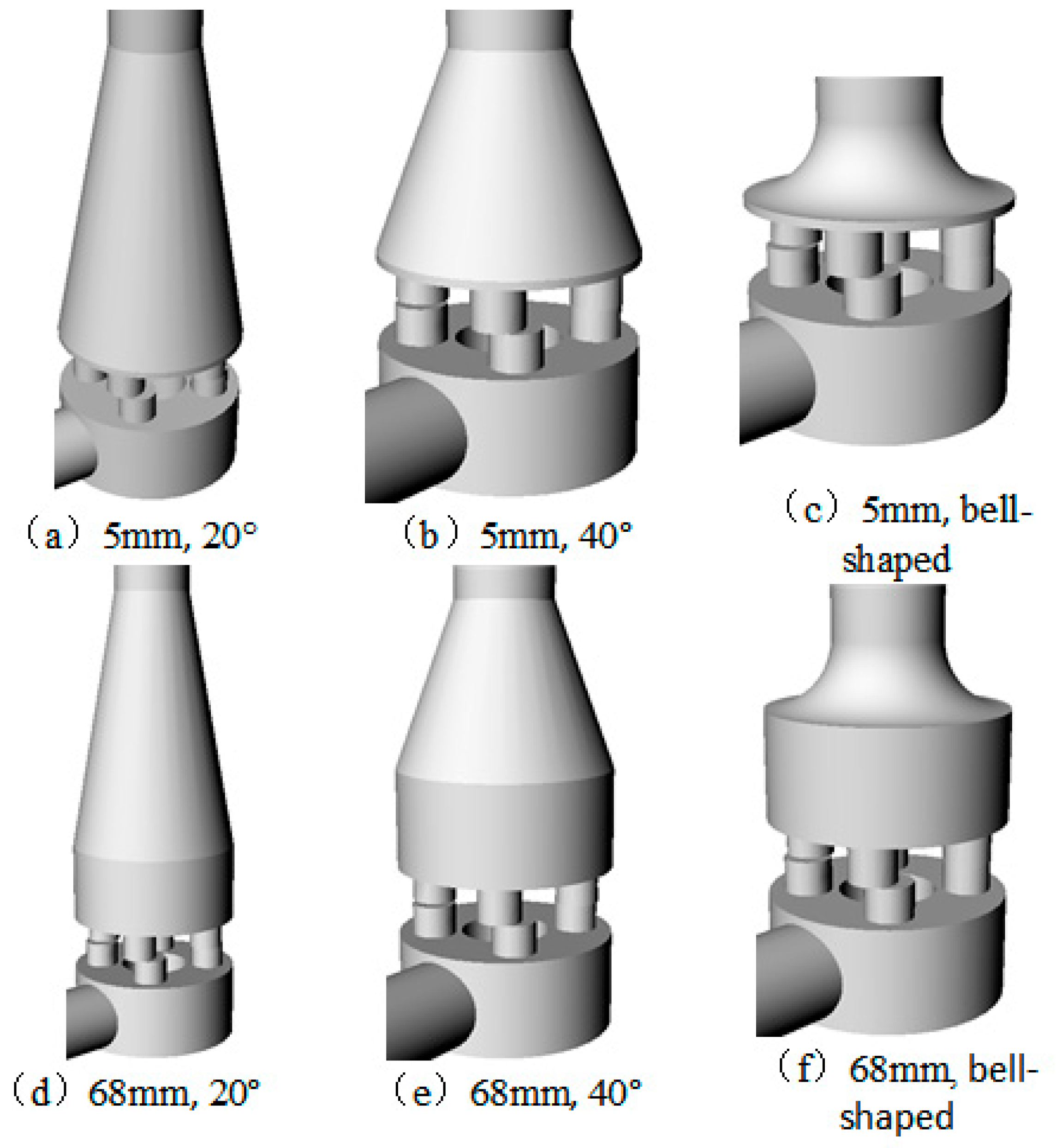
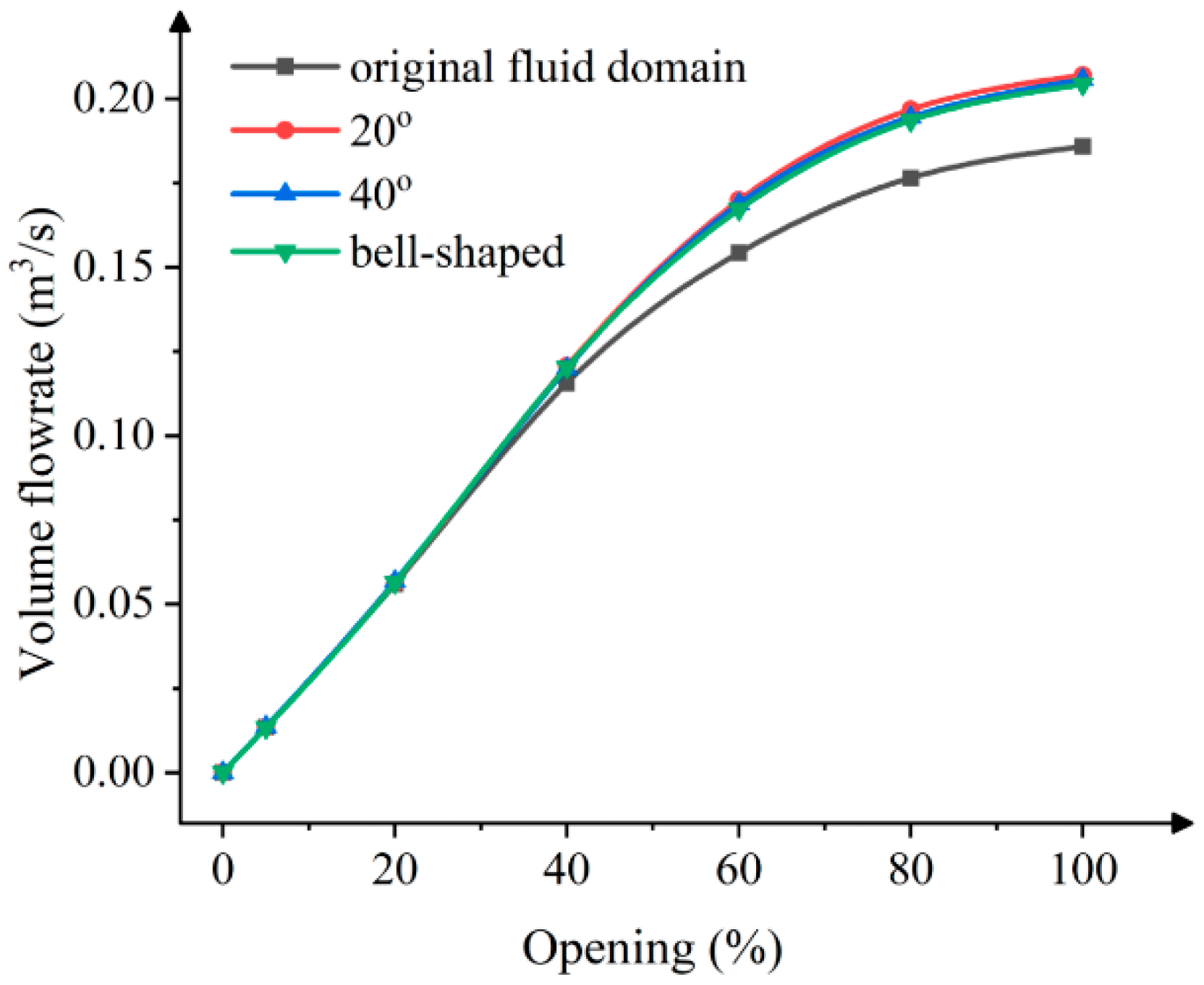
4.1.3. The Combined Influence of the Shape and Height of the Upper Chamber Inlet
- (1)
- Selection of Models
- (2)
- Changes in Volume Flow
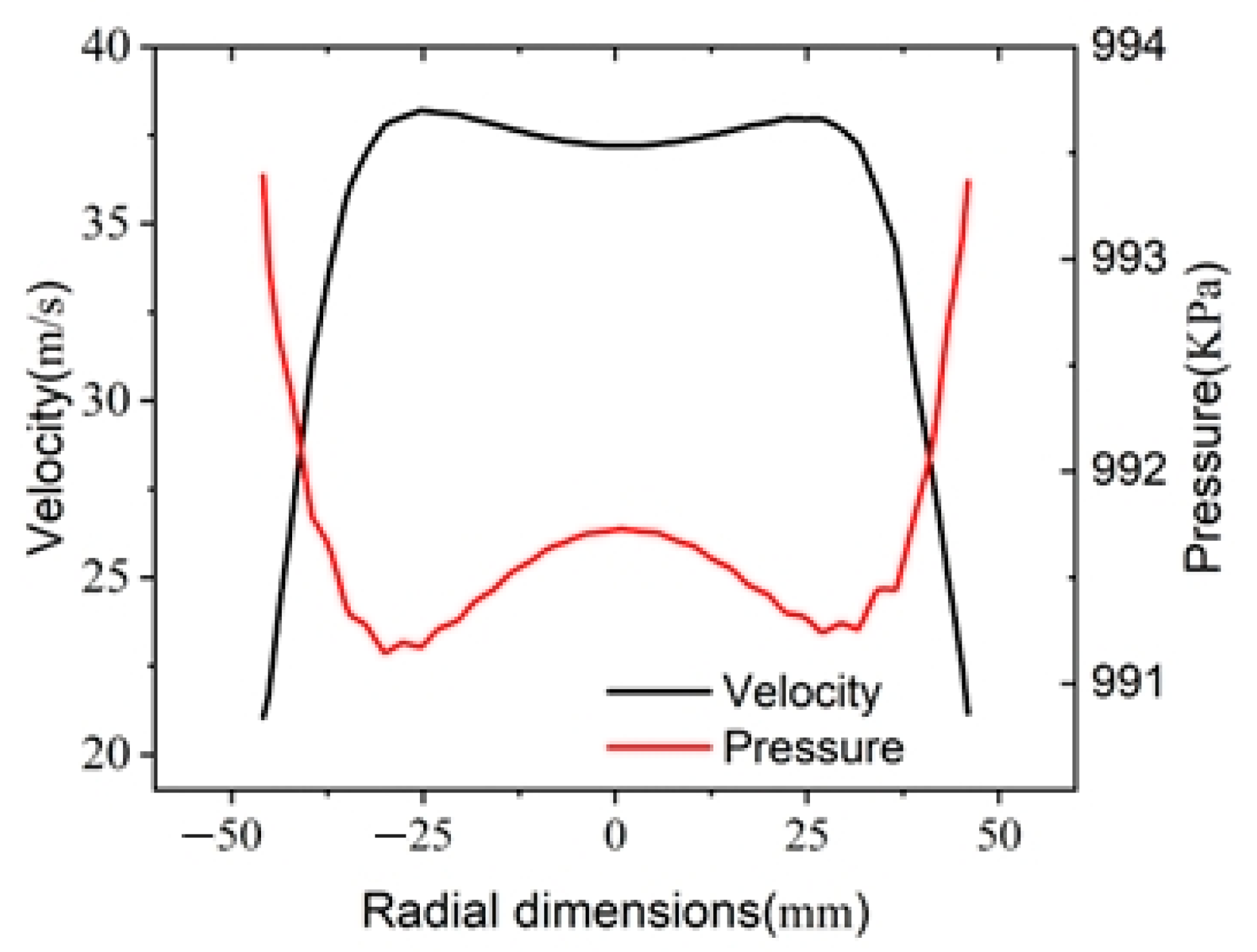
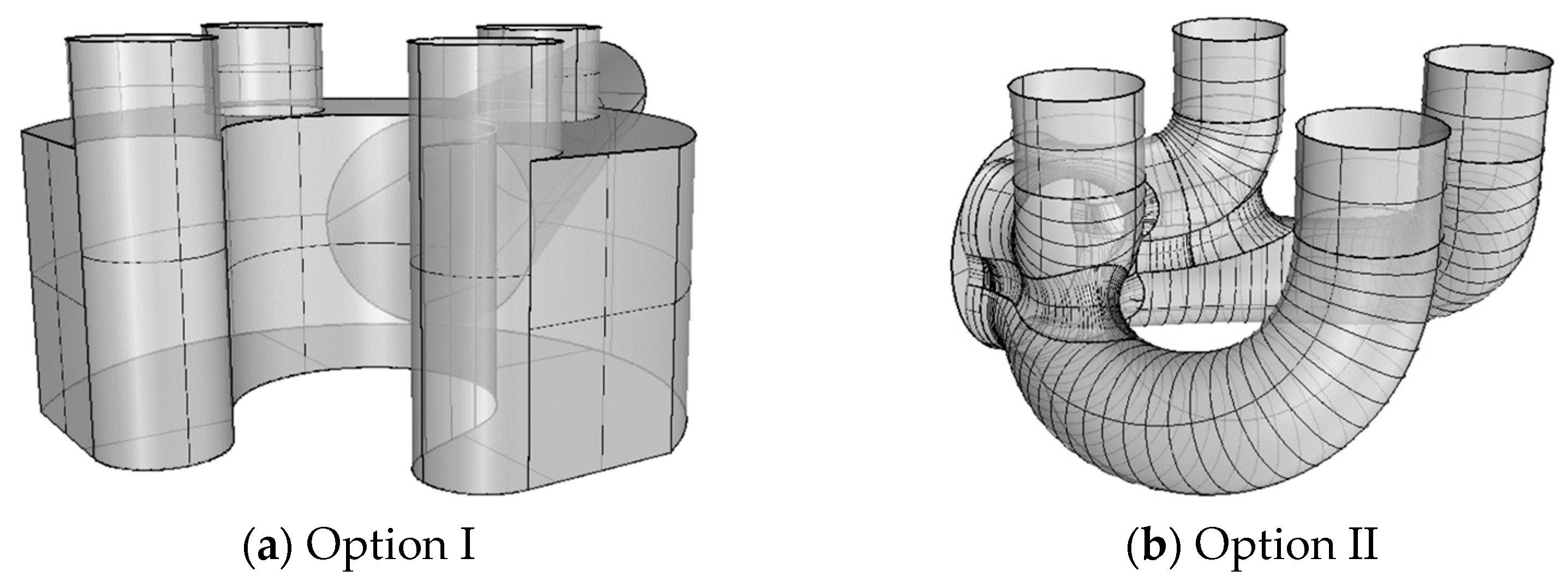
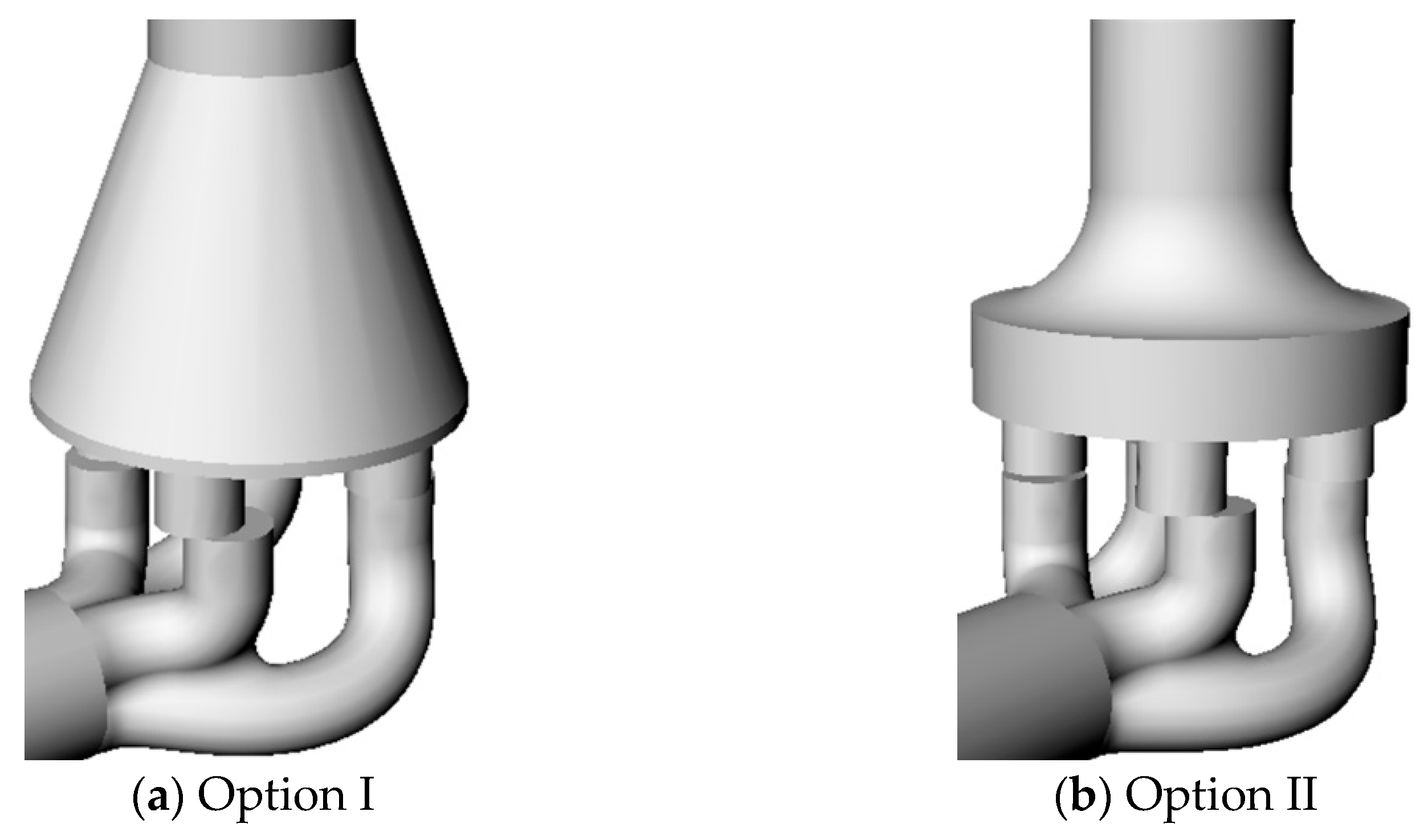
4.1.4. Effects of the Lower Chamber
- (1)
- Selection of the Lower Chamber Shape
- (2)
- Volume Flow of Outlet
- (3)
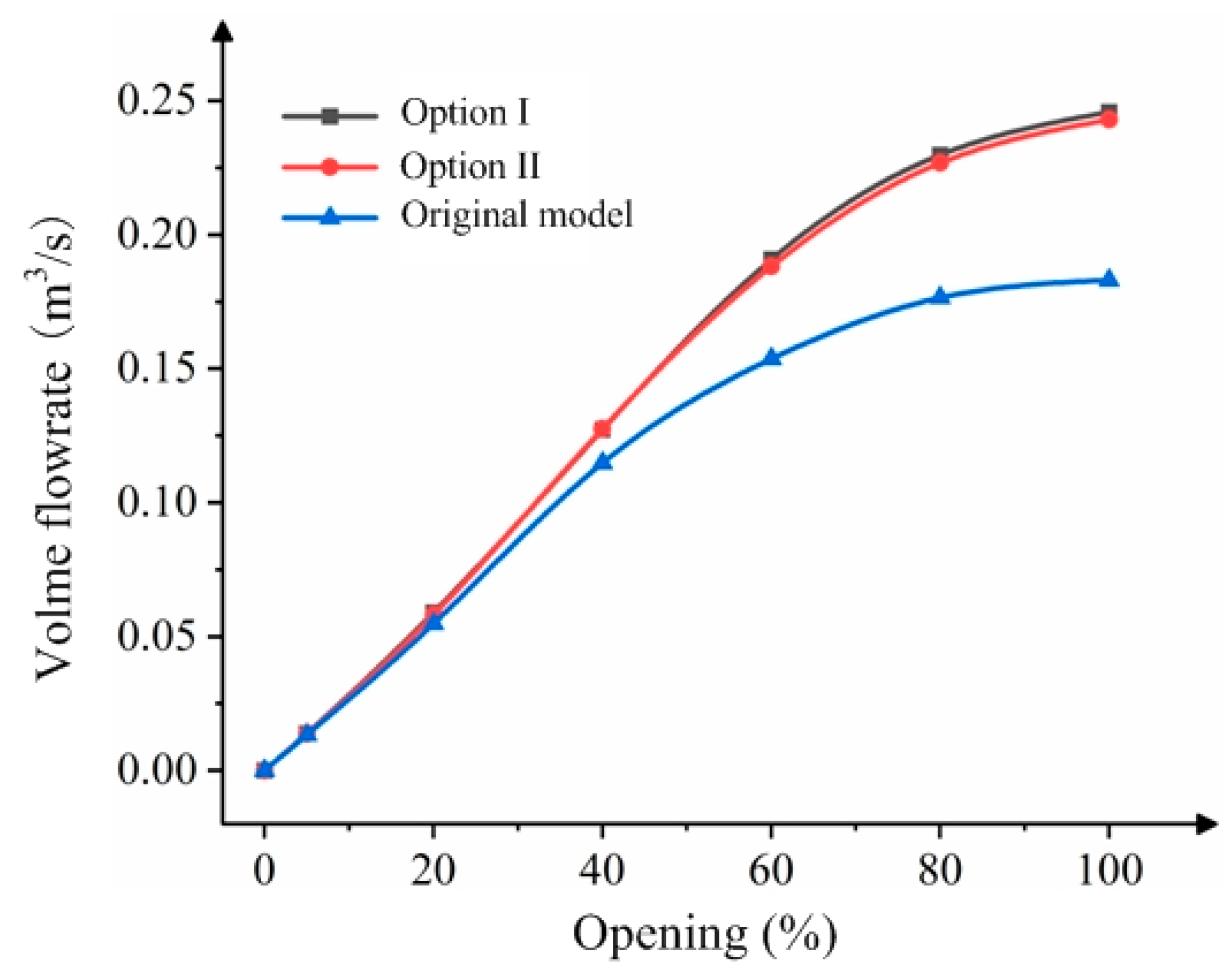
- Comparison of Flow Field Results
- (1)
- Pressure flow field
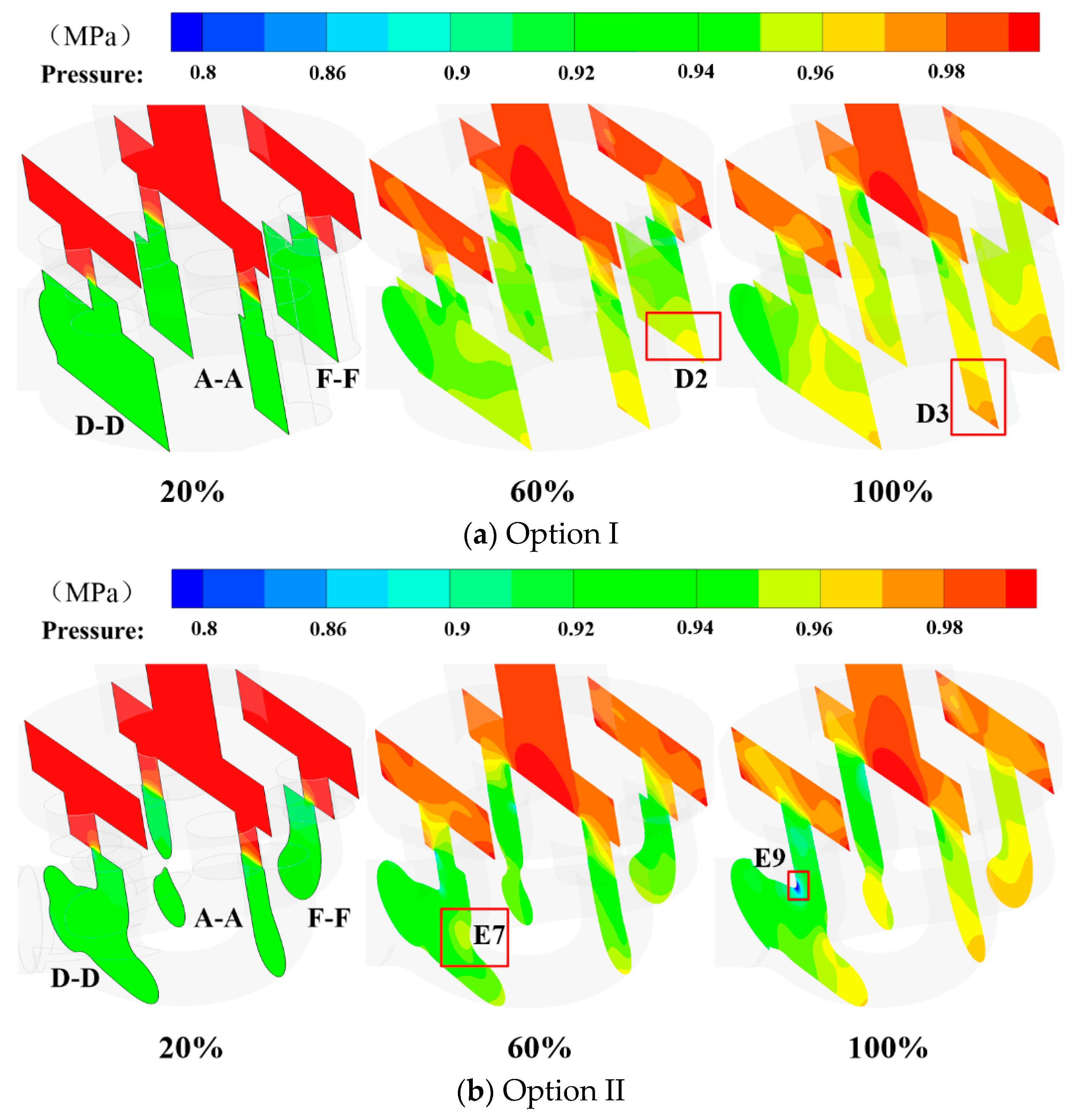
- (2)
- The velocity flow field for Option I
- (3)
- The velocity flow field for Option II

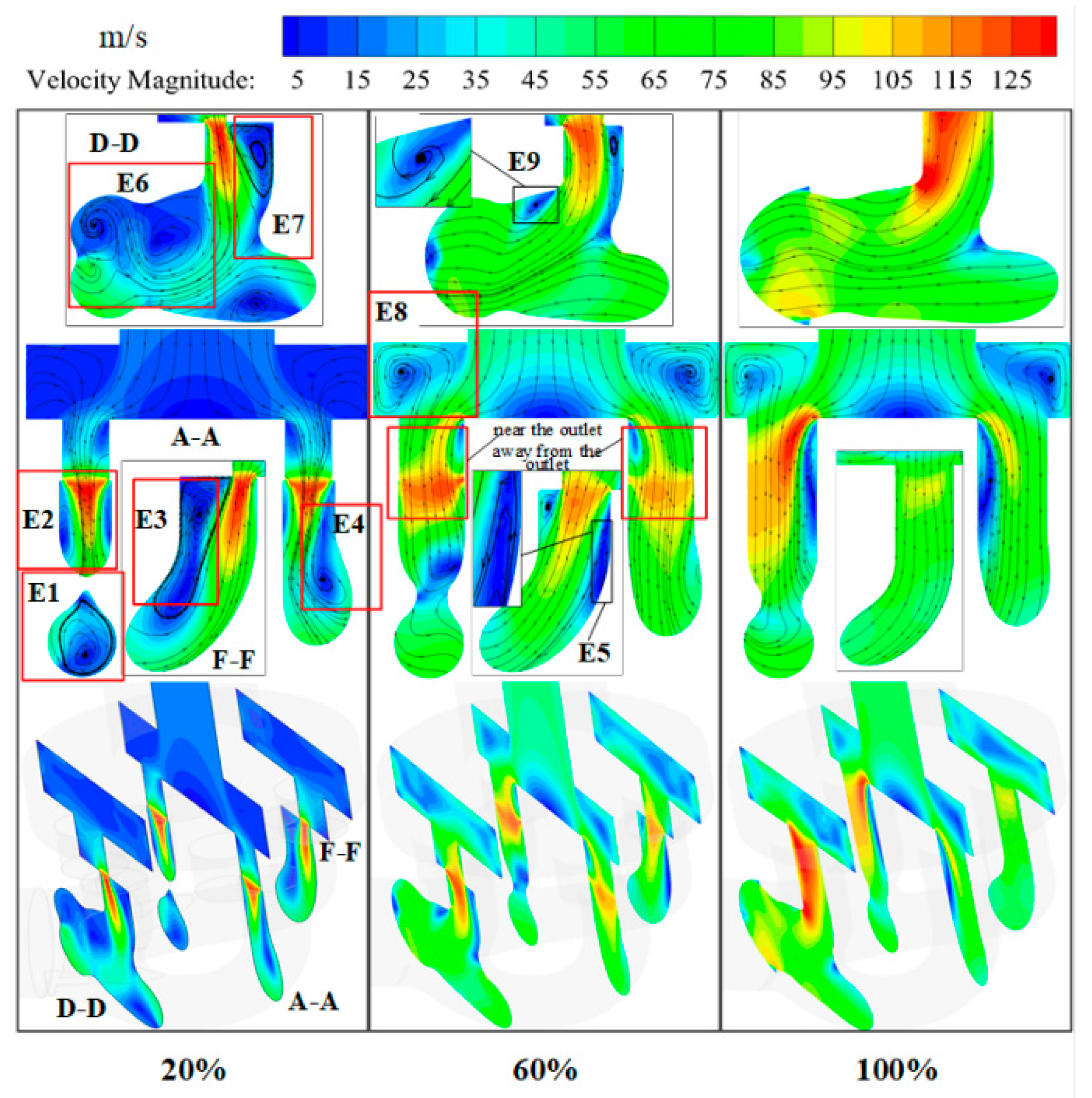
4.1.5. Determination of the Optimized Fluid Domain Model
4.2. Fluid–Structure Interaction Analysis of Laver Fluffiness Control Valve
4.2.1. The Force of Each Opening Under the Action of 1 MPa Preload Pressure
4.2.2. The Force of Each Opening Under Different Preload Pressures
5. Conclusions
- (1)
- A gradual expansion of the inlet flow in the upper chamber can effectively decrease the number and intensity of vortices in the upper chamber. Compared to the original fluid domain, when the valve opening is 100%, the outlet flow rates of the conical tube and bell-shaped inlet increase by 12.77% and 12.59%, respectively.
- (2)
- If the shape of the inlet of the upper cavity and its inlet height are modified simultaneously, it is possible to effectively avoid the formation of a throttle port due to the height of the upper cavity. The outlet flow rate is increased while reducing the increase in the height of the upper cavity. The lower cavity adopts the elbow transition, which can effectively reduce the energy loss of the fluid in the lower cavity. Specifically, when the valve opening reaches 100%, the outlet flow of the configuration with the bend transition demonstrates a 15.35% increase compared to that of the original fluid domain.
- (3)
- Based on the influence of the valve cavity structure on the flow field, after comprehensive consideration, the control valve fluid domain adopts a bell-shaped inlet, a 32 mm upper cavity height and an elbow transition. When the opening is 100%, the outlet flow of the control valve increases by 32.70%, the valve is switched on and off once, and the gas release is increased by 22.11%.
- (4)
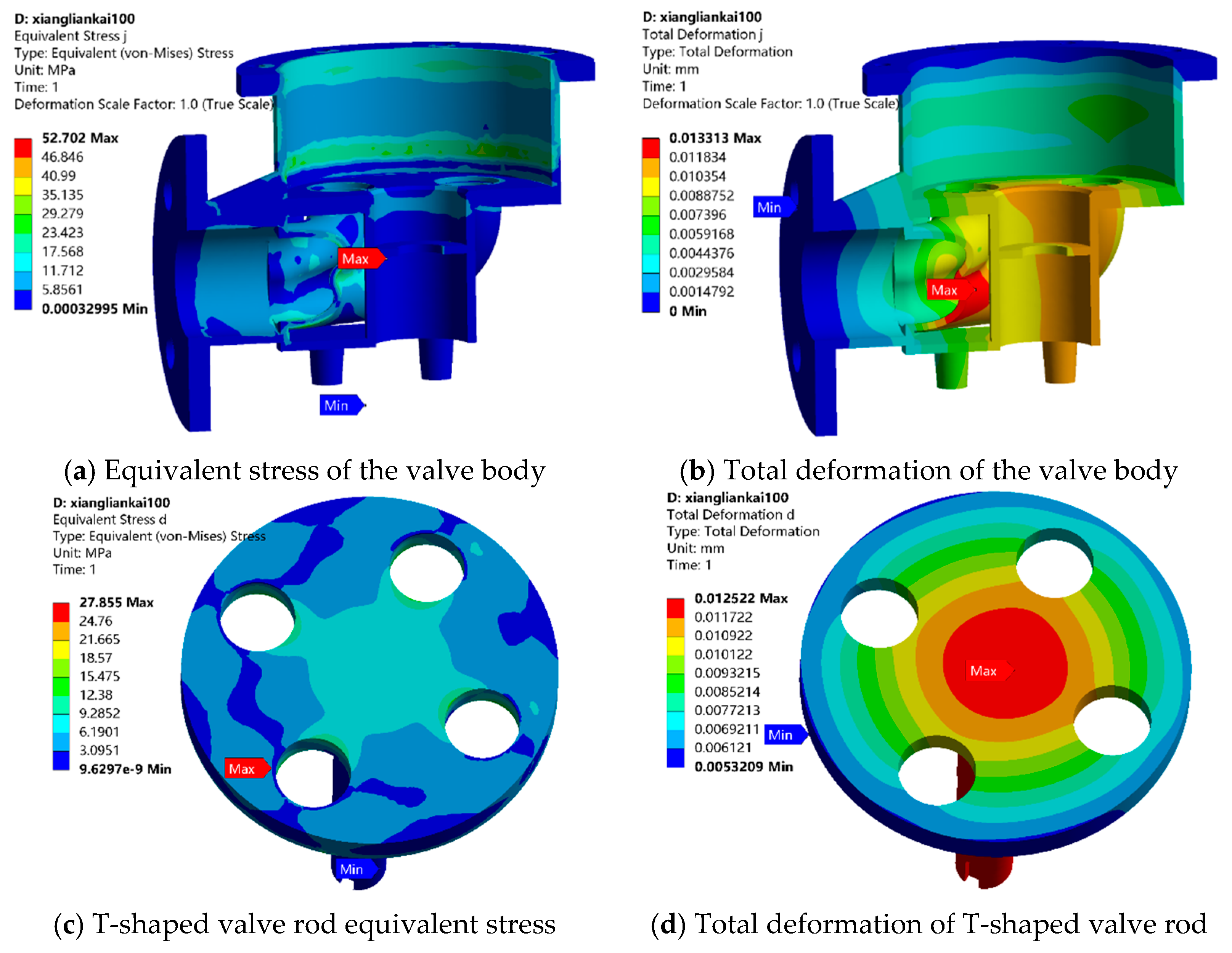
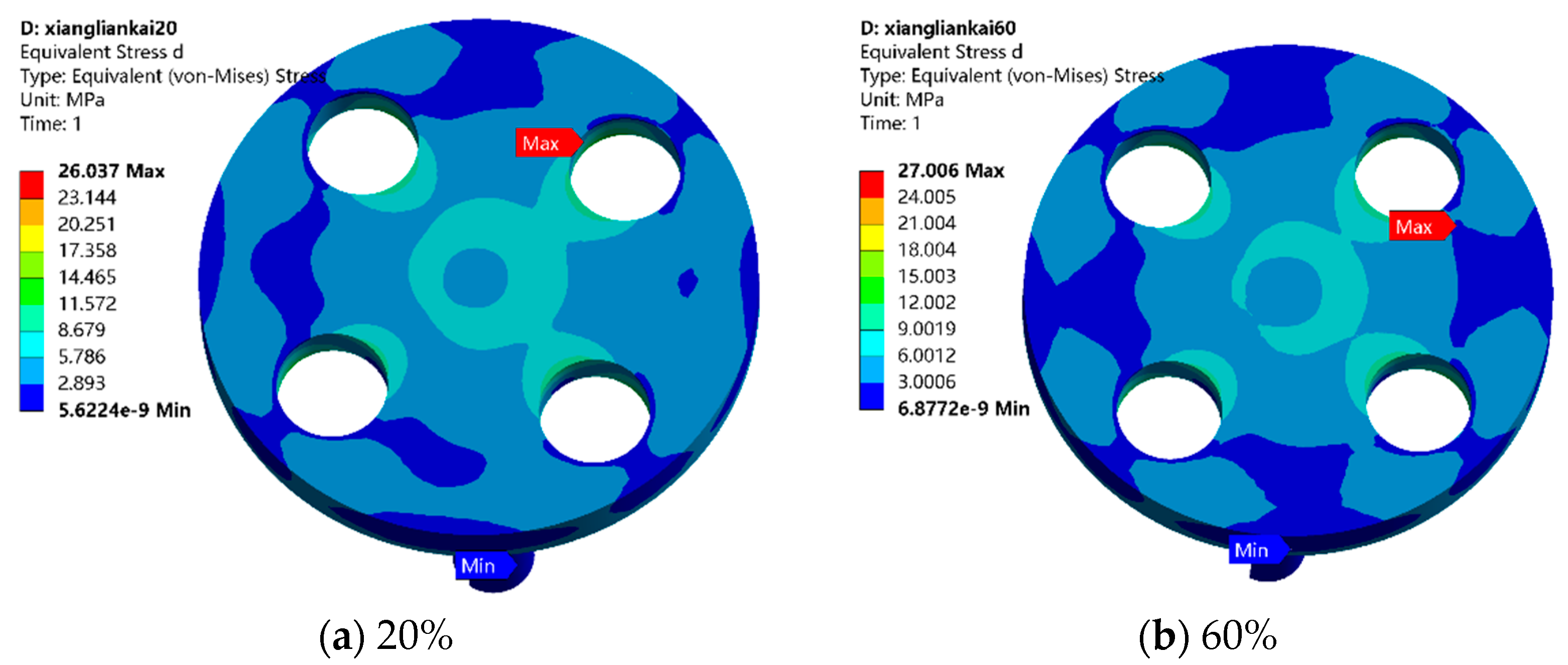
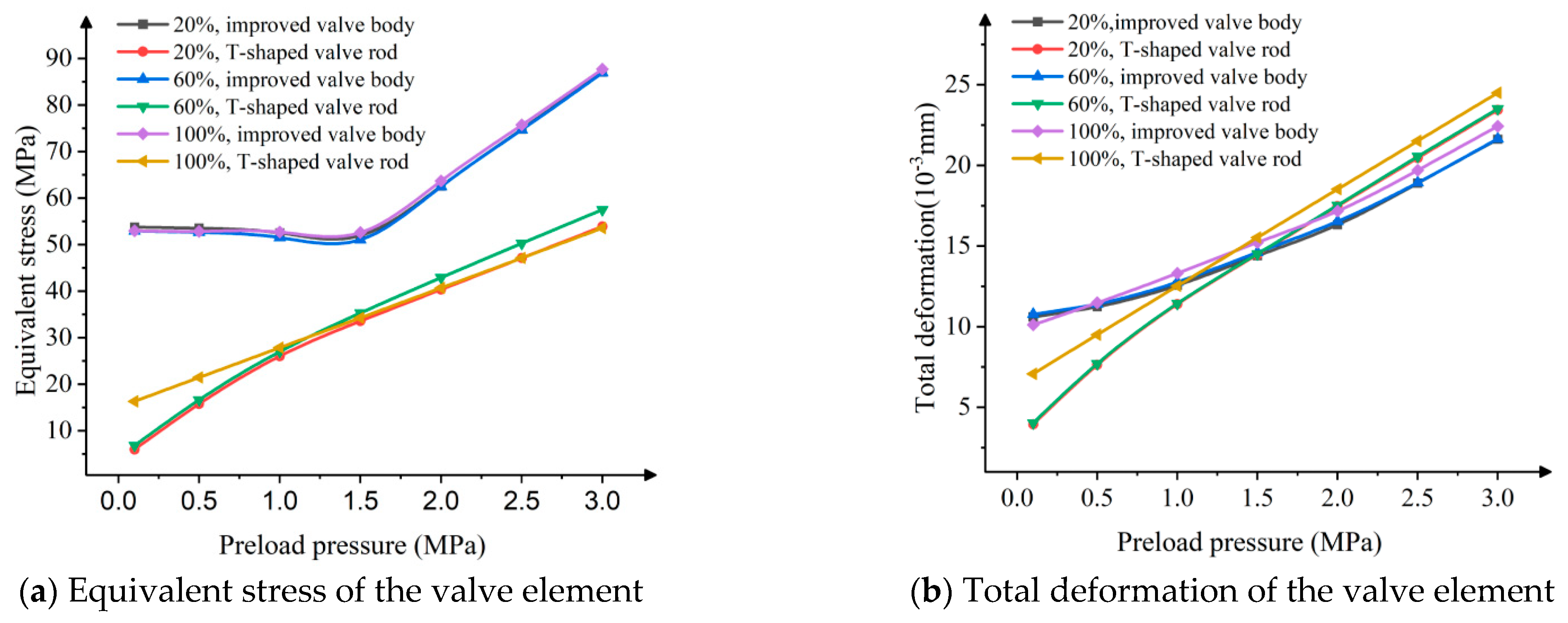
- Under the small opening, medium opening and large opening, the equivalence force and total deformation distribution of the control valve body are similar. The maximum equivalent force and total deformation occur at the intersection of the elbow. The maximum equivalent stress of the T-shaped valve rod is mainly concentrated at the center of the rod, while the maximum deformation is offset from the outlet. When the pre-load pressure exceeds 1.5 MPa, as the pre-load pressure increases, the equivalent stress and total deformation of the control-valve body and T-shaped valve rod also increase.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ou, Y.J.; Guo, Y.H.; Xu, L.; Lu, X.D.; Guo, Z.B.; Zheng, B.D. Structural characterization and hypoglycemic activity of glycoproteins extracted from porphyra haitanensis by ammonium sulfate and ethanol extraction methods. Food Biosci. 2023, 54, 102868. [Google Scholar] [CrossRef]
- Zheng, M.; Ma, M.; Yang, Y.; Liu, Z.; Liu, S.; Hong, T.; Ni, H.; Jiang, Z. Structural characterization and antioxidant activity of polysaccharides extracted from Porphyra haitanensis by different methods. Int. J. Biol. Macromol. 2023, 242, 125003. [Google Scholar] [CrossRef]
- Moujaes, S.F.; Jagan, R. 3D CFD predictions and experimental comparisons of pressure drop in a ball valve at different partial openings in turbulent flow. J. Energy Eng. 2008, 134, 24–28. [Google Scholar] [CrossRef]
- Palau-Salvador, G.; Gonzalez-Altozano, P.; Arviza-Valverde, J. Three-dimensional modeling and geometrical influence on the hydraulic performance of a control valve. J. Fluids Eng. Trans. ASME 2008, 130, 011102. [Google Scholar] [CrossRef]
- Large, J.; Fouque, J.; Reungoat, D. Study of the hydrodynamic phenomena and fluid–structure interactions of a bypass butterfly valve with double disc. Adv. Hydroinformatics 2014, 337–347. [Google Scholar] [CrossRef]
- Zaryankin, A.E.; Zroichikov, N.A.; Paramonov, A.N.; Noskov, V.V.; Ev, E.Y.G. Pressure pulsations in the turbine steam-admission path and their influence on the vibration state of the turbine control valves. Therm. Eng. 2012, 59, 106–112. [Google Scholar] [CrossRef]
- Shin, C.H.; Ha, J.M.; Lee, C.G. Transient pressure characteristics in a pressure regulating system by using 1-D analytic valve modeling. J. Mech. Sci. Technol. 2008, 22, 374–381. [Google Scholar] [CrossRef]
- Shin, C.H. A numerical study on the characteristics of transient flow in a pressure regulator resulting from closure of the pressure control valve. J. Mech. Sci. Technol. 2013, 27, 443–449. [Google Scholar] [CrossRef]
- Chern, M.J.; Hsu, P.H.; Cheng, Y.J.; Tseng, P.Y.; Hu, C.M. Numerical study on cavitation occurrence in globe valve. J. Energy Eng. 2013, 139, 25–34. [Google Scholar] [CrossRef]
- Mazur, Z.; Urquiza, G.; Campos, R. Improvement of the turbine main stop valves with flow simulation in erosion by solid particle impact CFD. Int. J. Rotating Mach. 2004, 10, 1–12. [Google Scholar] [CrossRef]
- Chernus, P.; Sharovatov, V. Consideration of influence of peculiarities of compressed gas on mathematical model parameters of spool valve. Procedia Eng. 2015, 100, 1046–1054. [Google Scholar] [CrossRef][Green Version]
- Merati, P.; Macelt, M.J.; Erickson, R.B. Flow investigation around a V-sector ball valve. J. Fluids Eng. 2001, 123, 662–671. [Google Scholar] [CrossRef]
- Choi, Y.S.; Lee, J.H.; Jeong, W.B.; Kim, I.G. Dynamic behavior of valve system in linear compressor based on fluid-structure interaction. J. Mech. Sci. Technol. 2010, 24, 1371–1377. [Google Scholar] [CrossRef]
- Gamboa, A.R.; Morris, C.J.; Forster, F.K. Improvements in fixed-valve micropump performance through shape optimization of valves. J. Fluids Eng. 2005, 127, 339–346. [Google Scholar] [CrossRef]
- Simic, M.; Herakovic, N. Reduction of the flow forces in a small hydraulic seat valve as alternative approach to improve the valve characteristics. Energy Convers. Manag. 2015, 89, 708–718. [Google Scholar] [CrossRef]
- Zhou, Q.Y.; Liu, L.; Zheng, C.; Xu, Z.P.; Wang, X.H. Design of Valve Seating Buffer for Electromagnetic Variable Valve System. Actuators 2023, 12, 19. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G.; Rajda, J. Analysis of flow forces in the initial phase of throttle gap opening in a proportional control valve. Flow Meas. Instrum. 2018, 59, 157–167. [Google Scholar] [CrossRef]
- Amirante, R.; Catalano, L.A.; Tamburrano, P. The importance of a full 3D fluid dynamic analysis to evaluate the flow forces in a hydraulic directional proportional valve. Eng. Comput. 2014, 31, 898–922. [Google Scholar] [CrossRef]
- Amirante, R.; Moscatelli, P.G.; Catalano, L.A. Evaluation of the flow forces on a direct (single stage) proportional valve by means of a computational fluid dynamic analysis. Energy Convers. Manag. 2007, 48, 942–953. [Google Scholar] [CrossRef]
- Ji, H.X.; Han, J.Z.; Wang, Y.; Wang, Q.X.; Yang, S.; Xie, Y.D.; Song, Y.L.; Wang, H.B. Numerical study on the internal flow field characteristics of a novel high-speed switching control valve. Actuators 2024, 13, 213. [Google Scholar] [CrossRef]
- Han, J.Z.; Xie, Y.D.; Wang, Y.; Wang, Q.X. Dynamic simulation of a warship control valve based on a mechanical-electric-fluid cosimulation model. Sci. Technol. Nucl. Install. 2021, 2021, 6683871. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, Y.D.; Han, J.Z.; Wang, Y. Design of control valve with low energy consumption based on Isight platform. Energy 2022, 239, 122328. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Peng, J.H.; Li, S.J. Flow characteristic investigation on Laval-type flow rate regulating valves by fluid-thermal-structure interaction. Int. Commun. Heat Mass Transf. 2023, 144, 106771. [Google Scholar] [CrossRef]
- Chen, C.; Shi, W.K.; Shen, Y.M.; Chen, J.Q.; Zhang, A.M. A multi-resolution SPH-FEM method for fluid-structure interactions. Comput. Methods Appl. Mech. Eng. 2022, 401, 115659. [Google Scholar] [CrossRef]
- Chattopadhyay, H.; Kundu, A.; Saha, B.K.; Gangopadhyay, T. Analysis of flow structure inside a spool type pressure regulating valve. Energy Convers. Manag. 2012, 53, 196–204. [Google Scholar] [CrossRef]
- Beune, A.; Kuerten, J.G.M.; Heumen, M.P.C.V. CFD analysis with fluid-structure interaction of opening high-pressure safety valves. Comput. Fluids 2012, 64, 108–116. [Google Scholar] [CrossRef]
- Zheng, X.L.; Wei, J.F. On the prediction of P–S–N curves of 45 steel notched elements and probability distribution of fatigue life under variable amplitude loading from tensile properties. Int. J. Fatigue 2005, 27, 601–609. [Google Scholar] [CrossRef]







| Material | Density (kg/m3) | Modulus of Elasticity (GPa) | Poisson’s Ratio |
|---|---|---|---|
| Gray iron | 7250 | 150 | 0.25 |
| 45# steel | 7850 | 209 | 0.269 |
| Polytetrafluoroethylene | 2300 | 500 | 0.4 |
| Silica gel | 1230 | 2.9 | 0.47 |
| Rotation Angle (Degrees) | Valve Opening (%) | Volume Flow (m3/s) | Relative Volume Flow Rate (%) |
|---|---|---|---|
| 34.92 | 0 | 0 | 0 |
| 30.6 | 4.92 | 0.0204 | 8.08 |
| 28.8 | 8.27 | 0.0340 | 13.47 |
| 25.2 | 16.39 | 0.0664 | 26.30 |
| 23.4 | 21.03 | 0.0846 | 33.50 |
| 16.2 | 42.48 | 0.1685 | 66.73 |
| 10.8 | 60.72 | 0.2078 | 82.30 |
| 5.4 | 80.01 | 0.2342 | 92.75 |
| 0 | 100 | 0.2525 | 100 |
| Valve Opening (%) | Valve Inlet Pressure (Bar) | Valve Outlet Pressure (Bar) | Volume Flow Rate (m3/s) | Relative Volume Flow Rate (%) |
|---|---|---|---|---|
| 0 | 6.00 | 0 | 0 | 0 |
| 10 | 6.00 | 0.90 | 0.011 | 18.33 |
| 30 | 6.00 | 2.48 | 0.023 | 38.33 |
| 45 | 6.00 | 3.90 | 0.040 | 66.67 |
| 60 | 6.00 | 5.00 | 0.052 | 86.67 |
| 90 | 6.00 | 5.90 | 0.059 | 98.33 |
| 100 | 6.00 | 6.00 | 0.060 | 100 |
| Valve Opening (%) | Valve Inlet Pressure (Bar) | Valve Outlet Pressure (Bar) | Volume Flow Rate (m3/s) | Relative Volume Flow Rate (%) |
|---|---|---|---|---|
| 0 | 9.00 | 0 | 0 | 0 |
| 10 | 9.00 | 1.37 | 0.016 | 17.78 |
| 30 | 9.00 | 3.70 | 0.034 | 37.78 |
| 45 | 9.00 | 5.90 | 0.061 | 67.78 |
| 60 | 9.00 | 7.50 | 0.078 | 86.67 |
| 90 | 9.00 | 8.86 | 0.089 | 98.89 |
| 100 | 9.00 | 9.00 | 0.090 | 100 |
| Flow Rate (m3/s) | Opening (%) | ||||||
|---|---|---|---|---|---|---|---|
| 5 | 20 | 40 | 60 | 80 | 100 | ||
| Inlet shape (degrees or type) | 10° | 0.0135 | 0.0567 | 0.1193 | 0.1699 | 0.1970 | 0.2065 |
| 20° | 0.0133 | 0.0565 | 0.1207 | 0.1696 | 0.1971 | 0.2067 | |
| 30° | 0.0134 | 0.0564 | 0.1193 | 0.1694 | 0.1963 | 0.2064 | |
| 40° | 0.0134 | 0.0566 | 0.1201 | 0.1671 | 0.1952 | 0.2059 | |
| Bell-shaped | 0.0134 | 0.0567 | 0.1196 | 0.1672 | 0.1944 | 0.2062 | |
| Flow Rate (m3/s) | Opening (%) | ||||||
|---|---|---|---|---|---|---|---|
| 5% | 20% | 40% | 60% | 80% | 100% | ||
| Upper cavity height (mm) | 5 | 0.0136 | 0.0494 | 0.0782 | 0.0895 | 0.0924 | 0.0929 |
| 18 | 0.0134 | 0.0548 | 0.1092 | 0.1428 | 0.1601 | 0.1684 | |
| 32 | 0.0133 | 0.0548 | 0.1148 | 0.1537 | 0.1765 | 0.1831 | |
| 50 | 0.0135 | 0.0558 | 0.1135 | 0.1508 | 0.1721 | 0.1818 | |
| 68 | 0.0135 | 0.0560 | 0.1156 | 0.1543 | 0.1765 | 0.1859 | |
| Entrance Type | Upper Cavity Height (mm) | Opening (%) | |||||
|---|---|---|---|---|---|---|---|
| 5% | 20% | 40% | 60% | 80% | 100% | ||
| 20° cone | 5 | 0.0137 | 0.0564 | 0.1192 | 0.1694 | 0.1977 | 0.2080 |
| 68 | 0.0134 | 0.0564 | 0.1206 | 0.1699 | 0.1969 | 0.2070 | |
| 40° cone | 5 | 0.0137 | 0.0566 | 0.1183 | 0.1680 | 0.1956 | 0.2081 |
| 68 | 0.0136 | 0.0568 | 0.1200 | 0.1688 | 0.1946 | 0.2058 | |
| Bell-shaped | 5 | 0.0137 | 0.0563 | 0.1167 | 0.1631 | 0.1891 | 0.1971 |
| 68 | 0.0133 | 0.0564 | 0.1204 | 0.1672 | 0.1936 | 0.2043 | |
| Volume Flow Rate (m3/s) | Opening (%) | ||||||
|---|---|---|---|---|---|---|---|
| 5% | 20% | 40% | 60% | 80% | 100% | ||
| Lower chamber scheme | Original fluid domain | 0.0133 | 0.0548 | 0.1148 | 0.1537 | 0.1765 | 0.1831 |
| Option I | 0.0131 | 0.0555 | 0.1114 | 0.1535 | 0.1753 | 0.1841 | |
| Option II | 0.0165 | 0.0574 | 0.1195 | 0.1780 | 0.2011 | 0.2112 | |
| Flow Rate (m3/s) | Opening (%) | ||||||
|---|---|---|---|---|---|---|---|
| 5% | 20% | 40% | 60% | 80% | 100% | ||
| Lower chamber scheme | Original model | 0.0133 | 0.0548 | 0.1148 | 0.1537 | 0.1765 | 0.1831 |
| Option I | 0.0138 | 0.0589 | 0.1272 | 0.1909 | 0.2298 | 0.2458 | |
| Option II | 0.0137 | 0.0582 | 0.1276 | 0.1883 | 0.2268 | 0.2430 | |
| Flow Rate (m3/s) | Opening (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 5% | 20% | 40% | 60% | 80% | 100% | |||
| Lower chamber scheme | Option I | Increase the amount | 0.0005 | 0.0041 | 0.0124 | 0.0372 | 0.0533 | 0.0627 |
| growth rate | 3.76% | 7.48% | 10.80% | 24.20% | 30.20% | 34.24% | ||
| Option II | Increase the amount | 0.0004 | 0.0034 | 0.0128 | 0.0346 | 0.0503 | 0.0599 | |
| growth rate | 3.00% | 6.20% | 11.15% | 22.51% | 28.50% | 32.71% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, H.; Han, J.; Wang, Y.; Liu, Y.; Xie, Y.; Yang, S.; Shi, D.; Song, Y. Structural Optimization and Fluid–Structure Interaction Analysis of a Novel High-Speed Switching Control Valve. Actuators 2025, 14, 163. https://doi.org/10.3390/act14040163
Ji H, Han J, Wang Y, Liu Y, Xie Y, Yang S, Shi D, Song Y. Structural Optimization and Fluid–Structure Interaction Analysis of a Novel High-Speed Switching Control Valve. Actuators. 2025; 14(4):163. https://doi.org/10.3390/act14040163
Chicago/Turabian StyleJi, Hexi, Jiazhen Han, Yong Wang, Yongkang Liu, Yudong Xie, Sen Yang, Derui Shi, and Yilong Song. 2025. "Structural Optimization and Fluid–Structure Interaction Analysis of a Novel High-Speed Switching Control Valve" Actuators 14, no. 4: 163. https://doi.org/10.3390/act14040163
APA StyleJi, H., Han, J., Wang, Y., Liu, Y., Xie, Y., Yang, S., Shi, D., & Song, Y. (2025). Structural Optimization and Fluid–Structure Interaction Analysis of a Novel High-Speed Switching Control Valve. Actuators, 14(4), 163. https://doi.org/10.3390/act14040163






