Stability Analysis of a Fractional-Order African Swine Fever Model with Saturation Incidence
Abstract
:Simple Summary
Abstract
1. Introduction
2. Model Formulation
| Variables | Description | ||
|---|---|---|---|
| S | The density of susceptible pigs | ||
| E | The density of exposed pigs | ||
| I | The density of infected pigs | ||
| M | The density of virus in contaminated items | ||
| R | The density of recovered pigs | ||
| Parameters | Description | Value | Refs |
| The recruitment rate of pigs | [12,27] | ||
| ASFV transmission rate with direct contact of infectious pigs | [0.0017, 0.017] | [27] | |
| Virus transmission rate in contaminated items | [0.0003, 0.0017] | Assumed | |
| The saturation constant | [0.003, 0.5] | Assumed | |
| The natural death rate of pigs | [0.0025, 0.0045] | [11,12,14] | |
| The rate of the recovered pigs who become susceptible | [0.02, 0.4243] | [12,27] | |
| The average rate at which an individual passes through the incubation period | [0.12, 0.667] | [12,27] | |
| The rate of the infected pigs who recover | [0.018, 0.418] | Assumed | |
| d | The death rate due to the disease | 0.27 | [11,12] |
| h | The release rate of virus from symptomatic infectious pigs | [0.18, 0.38] | Assumed |
| The clearance rate of virus | [0.026, 0.126] | [14] |
3. Qualitatively Analysis of System (2)
3.1. The Existence and Uniqueness of Positive Solution for System (2)
3.2. Basic Reproduction Number and the Existence of Equilibriums
- (i)
- If then ; if then ;
- (ii)
- If then ; if then .
3.3. Stability of the Disease-Free Equilibrium
3.4. Stability of the Endemic Equilibrium
- (i)
- If then the endemic equilibrium is locally asymptotically stable.
- (ii)
- When , according to Lemma 3 in [33], if all roots of Equation (7) satisfy then is still locally stable.
4. Examples and Numerical Simulations
Examples and Numerical Simulations for System (2)
- (i)
- Figure 1 shows the variation between threshold and parameter α, with different values of φ and h (φ = 0.026, 0.057, 0.126, 0.226; h = 0.08, 0.18, 0.28, 0.38).
- (ii)
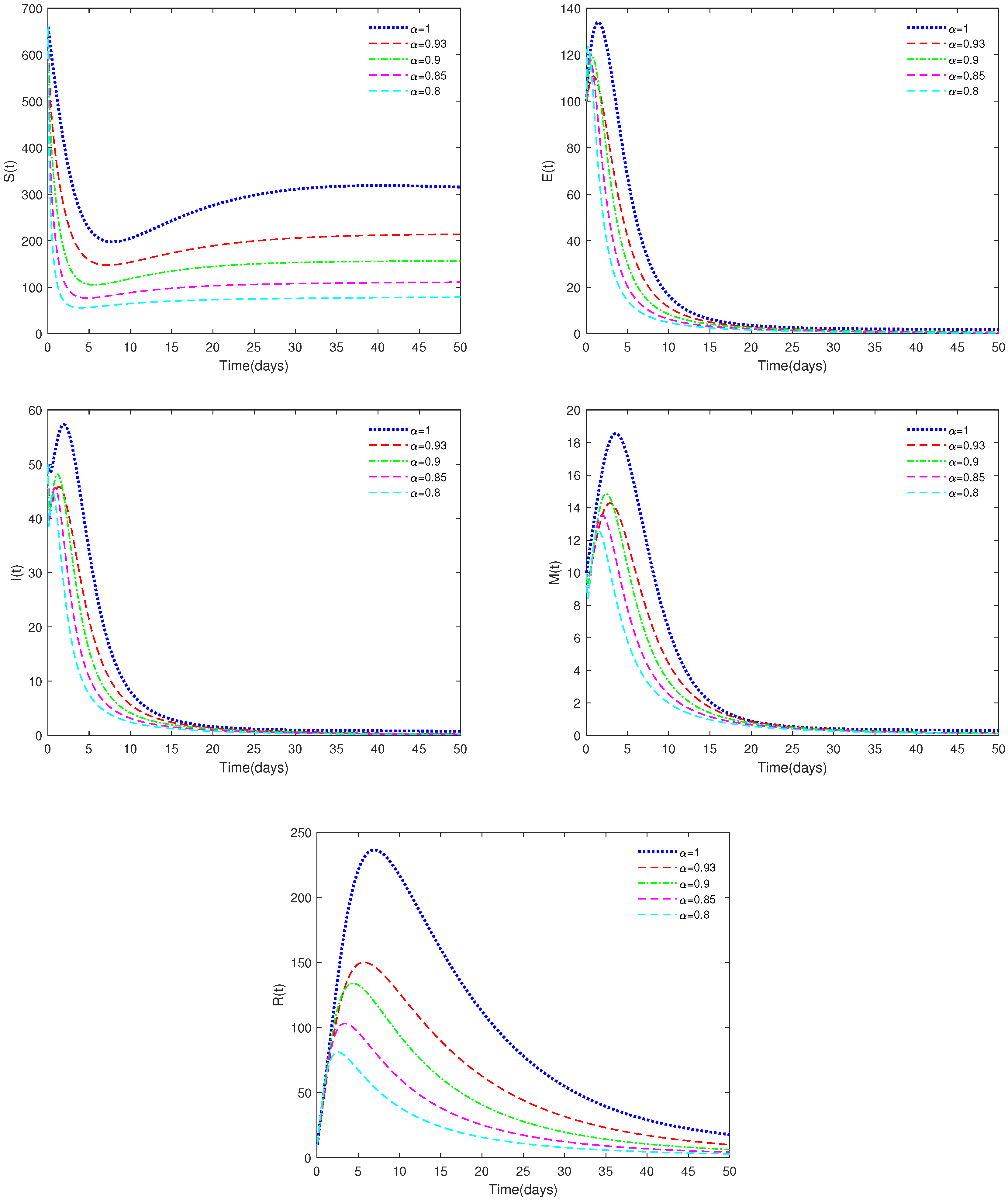
- In Figure 2, the initial value is = [660, 100, 50, 10, 10], and , , α have different values (α = 0.8, 0.85, 0.90, 0.93, 1). In this case, we get .
- (iii)
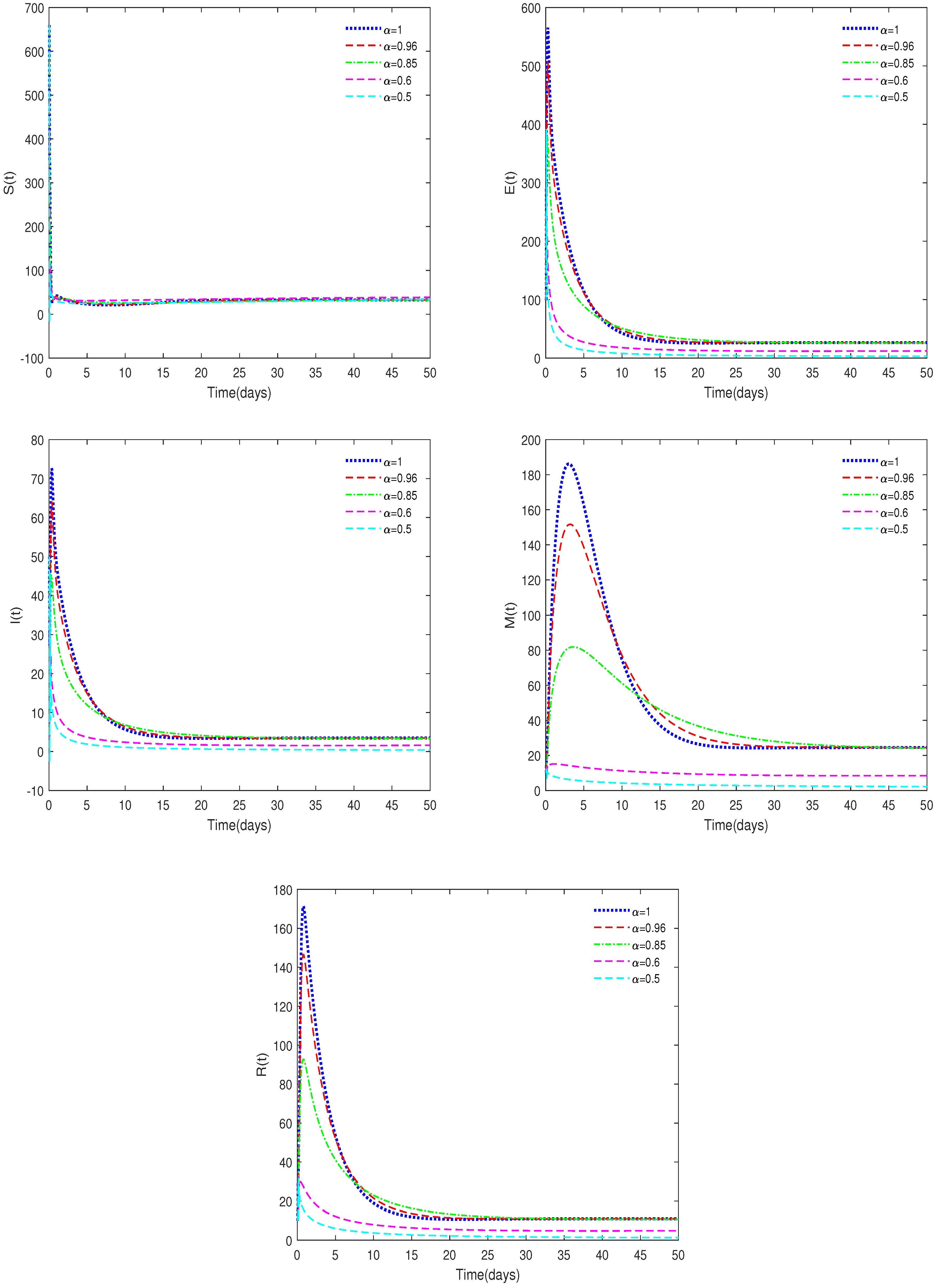
- In Figure 3, the value of α is fixed to 0.93, , , and different initial values are taken with = [450, 80, 30, 10, 10], [660, 100, 50, 10, 10], [800, 150, 70, 20, 10]. In this case, we get .
- (i)
- In Figure 5, , , , and have different values ( = 0.003, 0.01, 0.08, 0.2, 0.5).
- (ii)
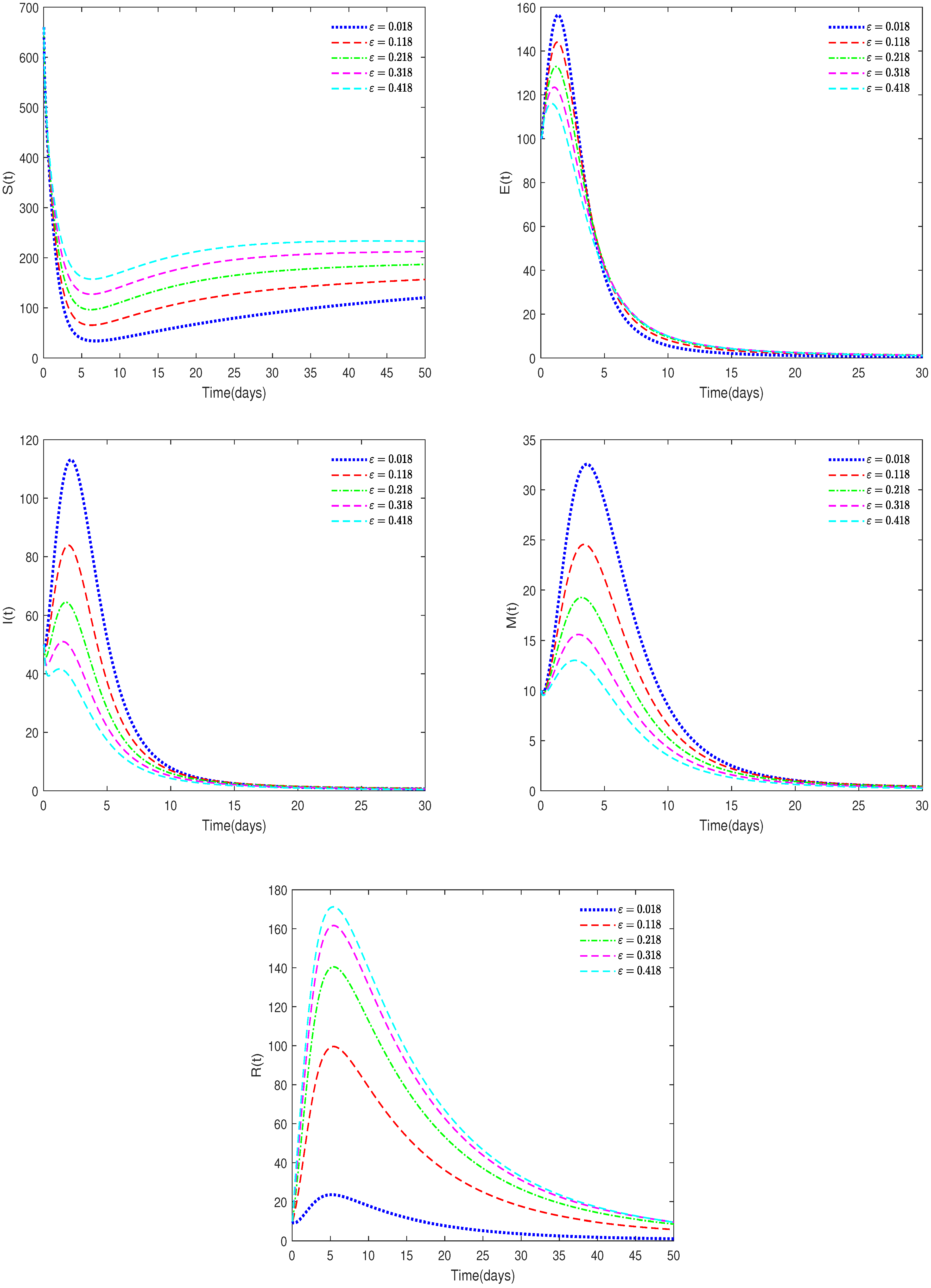
- In Figure 6, , , , and ε have different values (ε = 0.018, 0.118, 0.218, 0.318, 0.418).
- (iii)
- In Figure 7, , , , and ω have different values (ω = 0.267, 0.367, 0.467, 0.567, 0.667).
- (iv)
- In Figure 8, , , , , and δ have different values (δ = 0.0243, 0.1243, 0.2243, 0.3243, 0.4243).
- (i)
- Figure 1 shows the relationship between and the parameter α under different values of φ and h. Through observation, it can be seen that when the value of φ is relatively large, always holds, which means that the disease-free equilibrium, , is stable. When the value of φ is relatively small, both or exist, indicating that the stability of System (2) depends on the value of α.
- (ii)
- From Figure 1, we can also conclude that when the value of h is relatively small, always holds, which means that the disease-free equilibrium, , is stable. When the value of h is relatively large, both or exist, indicating that the stability of System (2) depends on the value of α.
- (iii)
- From a biological perspective, Figure 1 indicates that the virus release rate on diseased pigs and the virus cleaning rate in the pig breeding environment will affect the final development trend of the disease. As the cleaning rate increases, the disease will gradually move from persistence to extinction.
- (i)
- Figure 2 indicates that different values of α will affect the speed at which the equilibrium, , approaches stability and the coordinates of . When , the disease-free equilibrium, , is always stable, which is in accordance with Theorems 3 and 4.
- (ii)
- Figure 3 indicates that the initial values will not affect the stability, which is in accordance with Theorem 1.
- (i)
- Figure 5 shows that the saturation constant affects the rate at which the equilibriums tend to stabilization, but does not affect the final stable state.
- (ii)
- Figure 6 shows that the value of parameter ε will affect the peak value of each state variable and the coordinates of the final stable state. Therefore, taking corresponding treatment measures for sick pigs is very effective for disease control.
- (iii)
5. Discussion
- ♢
- The existence and uniqueness of the positive solutions are proven and the basic reproduction numbers is obtained.
- ♢
- The sufficient conditions for the existence and stability of disease-free equilibrium, , and endemic equilibrium, , are obtained.
- ♢
- When , the disease-free equilibrium, , is globally asymptotically stable.
- ♢
- From Figure 1, we can see that the value of has a significant impact on the threshold , which in turn affects the stability of the equilibriums.
- ♢
- Figure 1 also shows that the system is very sensitive to the values of and h. It can be seen that implementing strict cleaning measures for pig houses to reduce the virus content in the environment is an effective means of controlling the spread of the disease.
- ♢
- Figure 2 and Figure 4 indicate that the value of can affect the stable state of the system. For example, when and , the equilibrium, , is unstable, while it is stable for the corresponding integer-order system. This shows the differences between fractional-order systems and the classical integer-order systems. This also indicates that fractional-order systems have better non-locality and memory effects compared to integer-order systems.
- ♢
- Figure 6 shows that the recovery rate parameter has a significant impact on the peak values of various state variables of the system. Therefore, timely treatment of sick pigs can effectively prevent healthy pigs from being infected.
- ♢
- Compared to existing conclusions, this article focuses on discussing the difference between fractional-order systems and integer-order systems, indicating that fractional-order systems with memory characteristics are more sensitive to the dynamic of the system, and through sensitivity analysis of important parameters, effective cleaning measures have been found to have a significant impact on disease control.
6. Conclusions
- (i)
- Regular disinfection and cleaning of pigstys is essential for preventing further spread of ASF.
- (ii)
- The staff and external vehicles entering the pig farm should also be thoroughly disinfected to prevent the virus from being carried into the farm.
- (iii)
- Pigs suspected of being infected should be immediately isolated to prevent cross infection of the virus.
- (iv)
- The veterinarian states that pig farms should actively cooperate with local animal disease prevention and control agencies to carry out disease monitoring and investigation. The symptoms of ASF are initially very similar to those of ordinary swine fever. Therefore, when there is a failure in vaccination against swine fever or unexplained death, it is necessary to assess whether or not it is ASFV infection. The local veterinary department should be reported to in a timely manner. This is an effective means to block the further spread of ASF and reduce economic losses.
- (i)
- In this article, a deterministic model is considered. However, in the real world, the environment may be affected by some stochastic factors, so the results obtained from deterministic models may have some deviation between the model and reality. In future research, we will consider using stochastic differential equations to address current shortcomings.
- (ii)
- This article discusses the impact of biosecurity measures on the spread of ASF. In fact, geographical factors may have a significant impact on the spread of the disease, and professional geographic information system software is available to monitor the spread of the disease [34]. This method should be applied in subsequent research.
- (i)
- It is well known that time delay is common in epidemic models. Thus, in the future, we can explore the cyclical impact of the incubation period of diseases on the process of disease transmission.
- (ii)
- This article mainly discussed the stability of the system. In fact, the exact solution to the equilibrium of the system can be obtained through the Lie algebra method [35]. In future, this method will be combined to conduct more detailed research regarding the model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dixon, L.K.; Chapman, D.A.G.; Netherton, C.L.; Upton, C. African swine fever virus replication and genomics. Virus Res. 2013, 173, 3–14. [Google Scholar] [CrossRef] [PubMed]
- European Food Safety Authority, African Swine Fever. Available online: https://www.efsa.europa.eu/en/topics/topic/african-swine-fever (accessed on 1 January 2024).
- Portugal, R.; Coelho, J.; Hoper, D.; Little, N.S.; Smithson, C.; Upton, C.; Martins, C.; Leitao, A.; Keil, G.M. Related strains of African swine fever virus with different virulence: Genome comparison and analysis. J. Gen. Virol. 2015, 96, 408–419. [Google Scholar] [CrossRef]
- Galindo, I.; Alonso, C. African swine fever virus: A review. Viruses 2017, 9, 103. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Zhang, B. Diagnosis of African swine fever and its prevention and control measures. Swine Ind. Sci. 2020, 37, 96–98. (In Chinese) [Google Scholar]
- Halasa, T.; Btner, A.; Mortensen, S.; Christensen, H.; Toft, N.; Boklund, A. Simulating the epidemiological and economic effects of an African swine fever epidemic in industrialized swine populations. Vet. Microbiol. 2016, 193, 7–16. [Google Scholar] [CrossRef] [PubMed]
- World Organization for Animal Health, African Swine Fever. Available online: https://www.woah.org/en/disease/african-swine-fever/ (accessed on 1 January 2024).
- Jori, F.; Vial, L.; Penrith, M.L.; Pérez-Sánchez, R.; Etter, E.; Albina, E.; Michaud, V.; Roger, F. Review of the sylvatic cycle of African swine fever in sub-Saharan Africa and the Indian ocean. Virus Res. 2013, 173, 212–227. [Google Scholar] [CrossRef] [PubMed]
- Barongo, M.B.; Bishop, R.P.; Fèvre, E.M.; Knobe, D.L.; Ssematimba, A. A Mathematical Model that Simulates Control Options for African Swine Fever Virus (ASFV). PLoS ONE 2016, 11, e0158658. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, I.; Montes, F.; Martinez, M.; Perez, A.; Gogin, A.; Kolbasovd, D.; Torre, A. Spatio-temporal kriging analysis to identify the role of wild boar in the spread of African swine fever in the Russian Federation. Spat. Stat. 2018, 28, 226–235. [Google Scholar] [CrossRef]
- Zhang, X.; Rong, X.; Li, J.; Fan, M.; Wang, Y.; Sun, X.; Huang, B.; Zhu, H. Modeling the outbreak and control of African swine fever virus in large-scale pig farms. J. Theor. Biol. 2021, 526, 110798. [Google Scholar] [CrossRef]
- Shi, R.; Li, Y.; Wang, C. Stability analysis and optimal control of a fractional-order model for African swine fever. Virus Res. 2020, 288, 198111. [Google Scholar] [CrossRef]
- Kouidere, A.; Balatif, O.; Rachik, M. Analysis and optimal control of a mathematical modeling of the spread of African swine fever virus with a case study of South Korea and cost-effectiveness. Chaos Soliton Fract. 2021, 146, 110867. [Google Scholar] [CrossRef]
- Song, H.; Li, J.; Jin, Z. Nonlinear dynamic modelling and analysis of African swine fever with culling in China. Commun. Nonlinear. Sci. 2023, 117, 106915. [Google Scholar] [CrossRef]
- Huang, C.; Cai, L.; Cao, J. Linear control for synchronization of a fractional-order time-delayed chaotic financial system. Chaos Soliton Fract. 2018, 113, 326–332. [Google Scholar] [CrossRef]
- Rihan, F.A.; Abdel Rahman, D.H.; Lakshmanan, S.; Alkhajeh, A.S. A time delay model of tumour-immune system interactions: Global dynamics, parameter estimation, sensitivity analysis. Appl. Math. Comput. 2014, 232, 606–623. [Google Scholar] [CrossRef]
- Joshi, H. Mechanistic insights of COVID-19 dynamics by considering the influence of neurodegeneration and memory trace. Phys. Scr. 2024, 99, 035254. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Vatsala, A.S. Theory of fractional differential equations. Nonlinear Anal. 2008, 69, 2677–2682. [Google Scholar] [CrossRef]
- Joshi, H.; Yavuz, M.; Townley, S.; Jha, B.K. Stability analysis of a non-singular fractional-order covid-19 model with nonlinear incidence and treatment rate. Phys. Scr. 2023, 98, 045216. [Google Scholar] [CrossRef]
- Joshi, H.; Yavuz, M. Transition dynamics between a novel coinfection model of fractional-order for COVID-19 and tuberculosis via a treatment mechanism. Eur. Phys. J. Plus 2023, 138, 468. [Google Scholar] [CrossRef] [PubMed]
- Muresan, C.; Ionescu, C.; Folea, S.; Keyser, R.D. fractional-order control of unstable processes: The magnetic levitation study case. Nonlinear Dyn. 2015, 80, 1761–1772. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Velmurugan, G.; Cao, J. Stability analysis of fractional-order complex-valued neural networks with time delays. Chaos Soliton Fract. 2015, 78, 297–316. [Google Scholar] [CrossRef]
- Alidousti, J.; Ghaziani, R.K. Spiking and bursting of a fractional order of the modified FitzHugh-Nagumo neuron model. Math. Models Comput. Simul. 2017, 9, 390–403. [Google Scholar] [CrossRef]
- Omame, A.; Isah, M.E.; Abbas, M.; Abdel-Aty, A.H. A fractional order model for Dual Variants of COVID-19 and HIV co-infection via Atangana-Baleanu derivative. Alexandria Eng. J. 2022, 61, 9715–9731. [Google Scholar] [CrossRef]
- Pinto, C.; Carvalho, A. The role of synaptic transmission in a HIV model with memory. Appl. Math. Comput. 2017, 292, 76–95. [Google Scholar] [CrossRef]
- Sardar, T.; Rana, S.; Bhattacharya, S.; Al-Khaled, K.; Chattopadhyay, J. A generic model for a single strain mosquitotransmitted disease with memory on the host and the vector. Math. Biosci. 2015, 263, 18–36. [Google Scholar] [CrossRef] [PubMed]
- Shi, R.; Li, Y.; Wang, C. Analysis of a fractional-order model for African swine fever with effect of limited medical resources. Fractal Fract. 2023, 7, 430. [Google Scholar] [CrossRef]
- Diethelm, K. Monotonicity of functions and sign changes of their Caputo derivatives. Fract. Calc. Appl. Anal. 2016, 19, 561–566. [Google Scholar] [CrossRef]
- van Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental systems of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef]
- Ahmed, E.; Ama, E.S.; Haa, E.S. On some Routh–Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rssler, Chua and Chen systems. Phys. Lett. A 2006, 358, 1–4. [Google Scholar] [CrossRef]
- LaSalle, J.P. Stability theory for ordinary differential equations. J. Differ. Equ. 1968, 4, 57–65. [Google Scholar] [CrossRef]
- Kou, C.; Yan, Y.; Liu, J. Stability analysis for fractional differential equations and their applications in the models of HIV-1 infection. Comput. Model. Eng. Sci. 2009, 39, 301–317. [Google Scholar]
- Catalano, S.; La Morgia, V.; Molinar Min, A.R.; Fanelli, A.; Meneguz, P.G.; Tizzani, P. Gastrointestinal Parasite Community and Phenotypic Plasticity in Native and Introduced Alien Lagomorpha. Animals 2022, 12, 1287. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y. A Lie algebra approach to susceptible-infected-susceptible epidemics. Electron. J. Differ. 2012, 233, 1–7. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, R.; Zhang, Y. Stability Analysis of a Fractional-Order African Swine Fever Model with Saturation Incidence. Animals 2024, 14, 1929. https://doi.org/10.3390/ani14131929
Shi R, Zhang Y. Stability Analysis of a Fractional-Order African Swine Fever Model with Saturation Incidence. Animals. 2024; 14(13):1929. https://doi.org/10.3390/ani14131929
Chicago/Turabian StyleShi, Ruiqing, and Yihong Zhang. 2024. "Stability Analysis of a Fractional-Order African Swine Fever Model with Saturation Incidence" Animals 14, no. 13: 1929. https://doi.org/10.3390/ani14131929
APA StyleShi, R., & Zhang, Y. (2024). Stability Analysis of a Fractional-Order African Swine Fever Model with Saturation Incidence. Animals, 14(13), 1929. https://doi.org/10.3390/ani14131929






