Evidence of High-Shear-Velocity Anomalies Inside the Pacific LLSVP
Abstract
1. Introduction
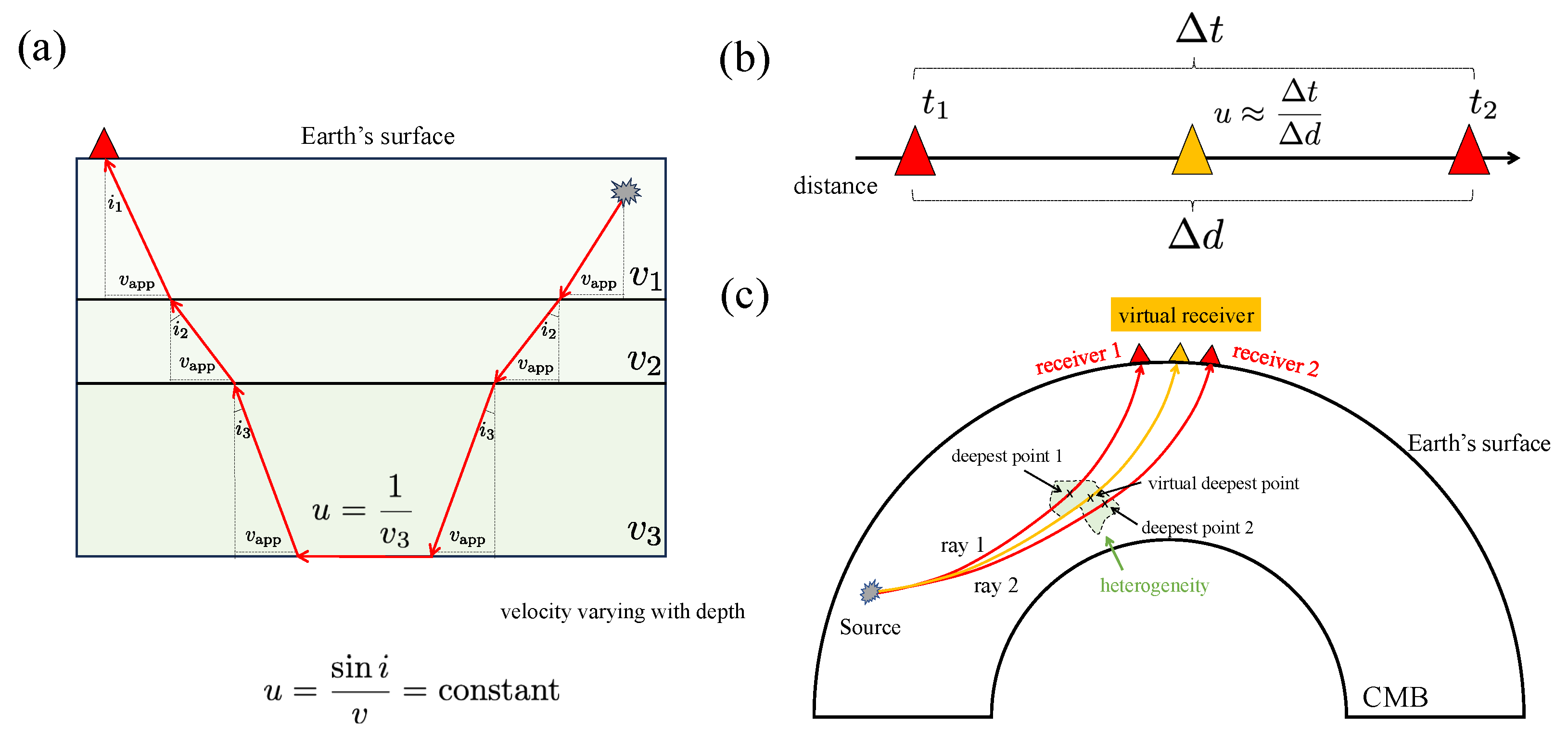
2. Methodology: The Virtual Receiver Approach (VRA)
3. Validation
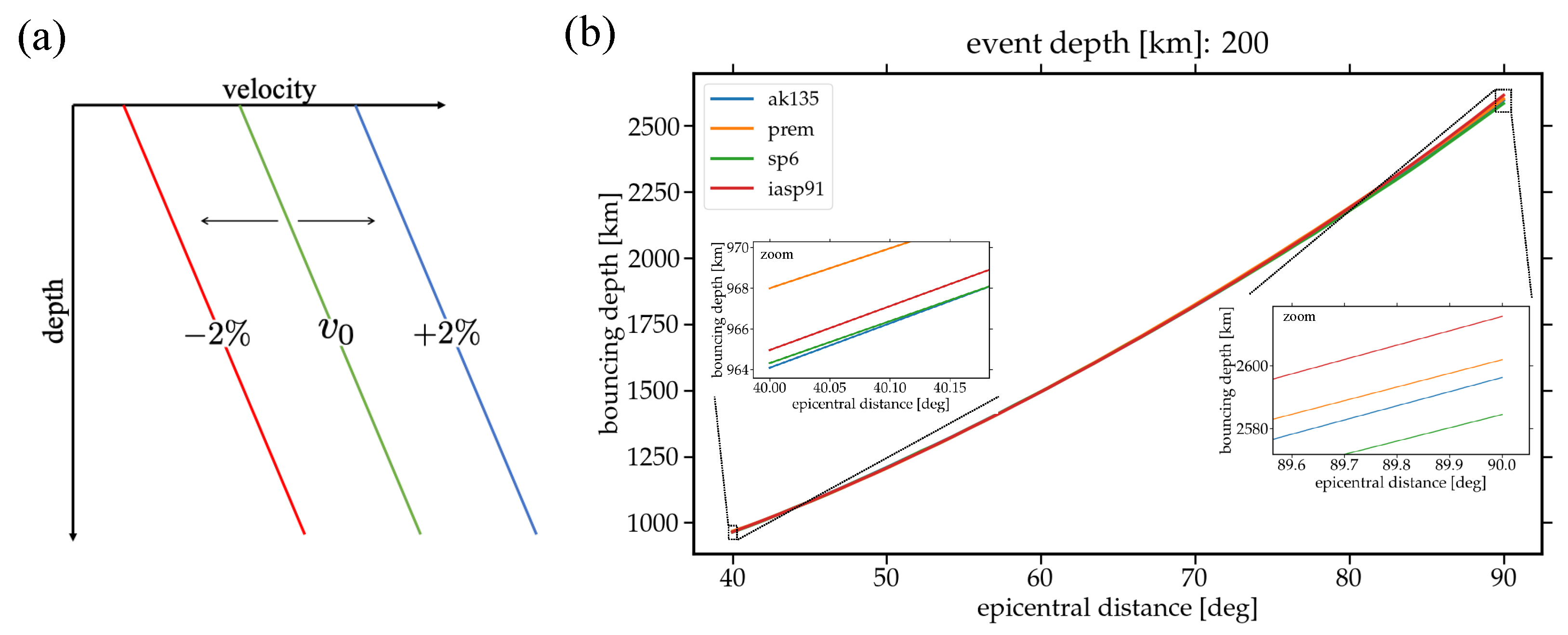
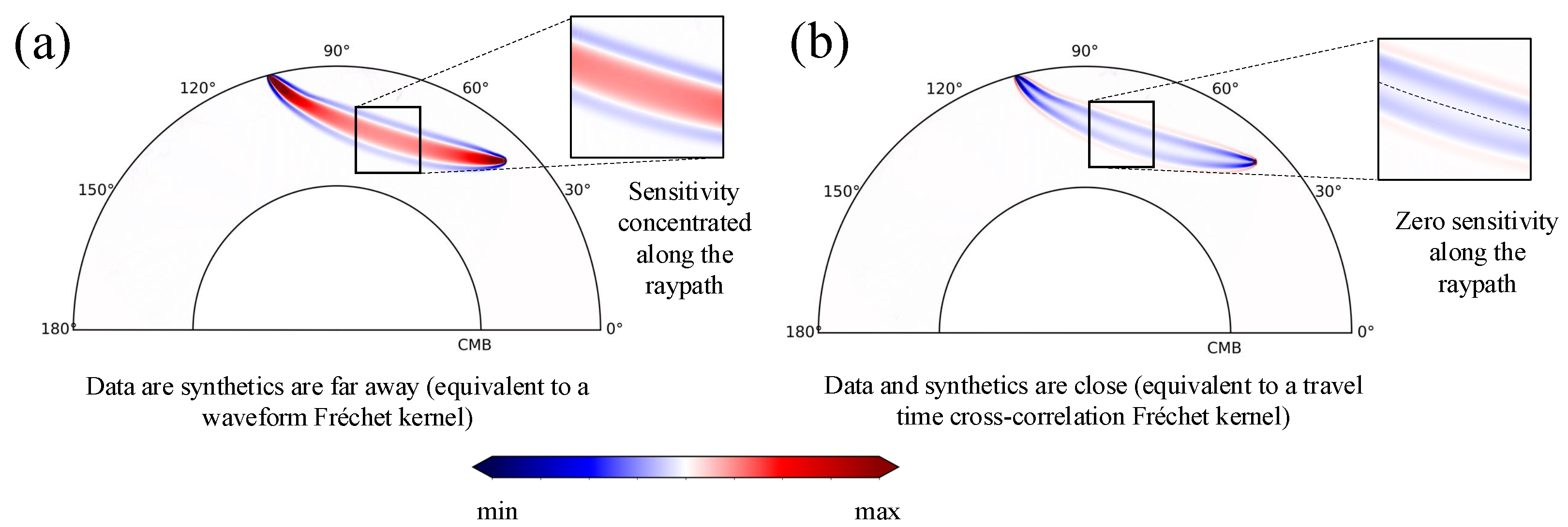
3.1. Theory
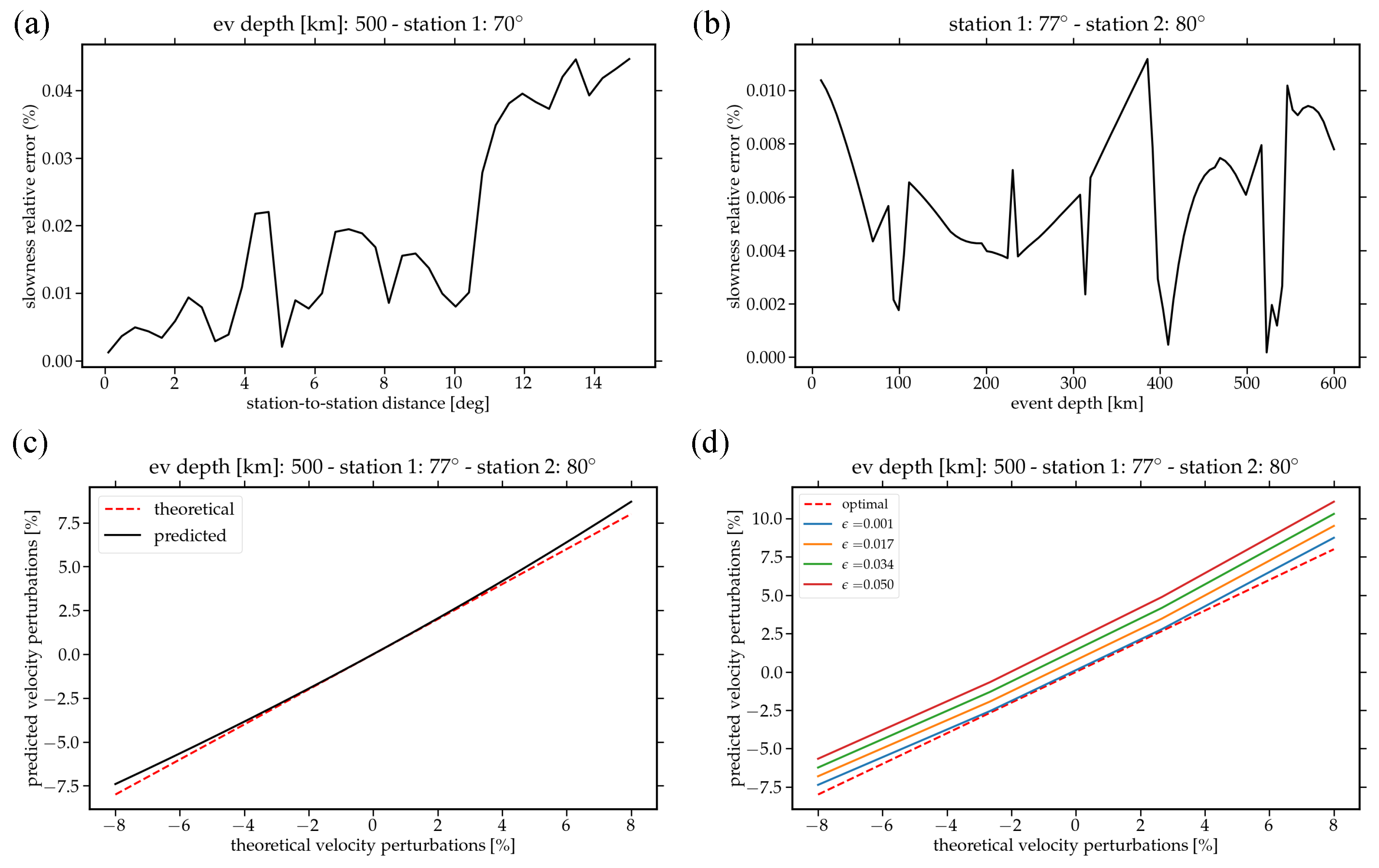
3.2. Numerical Results
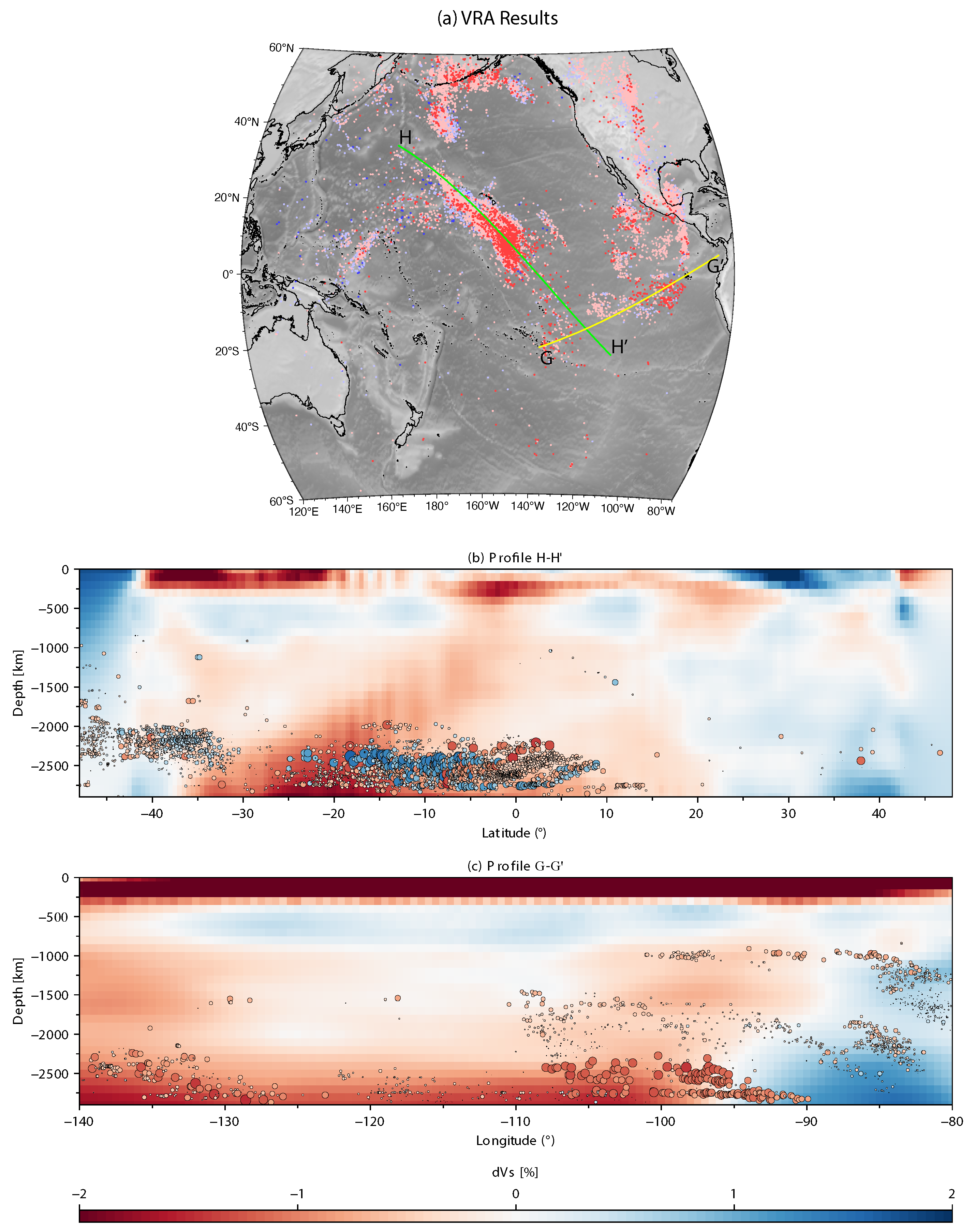
4. Application to Seismological Observations
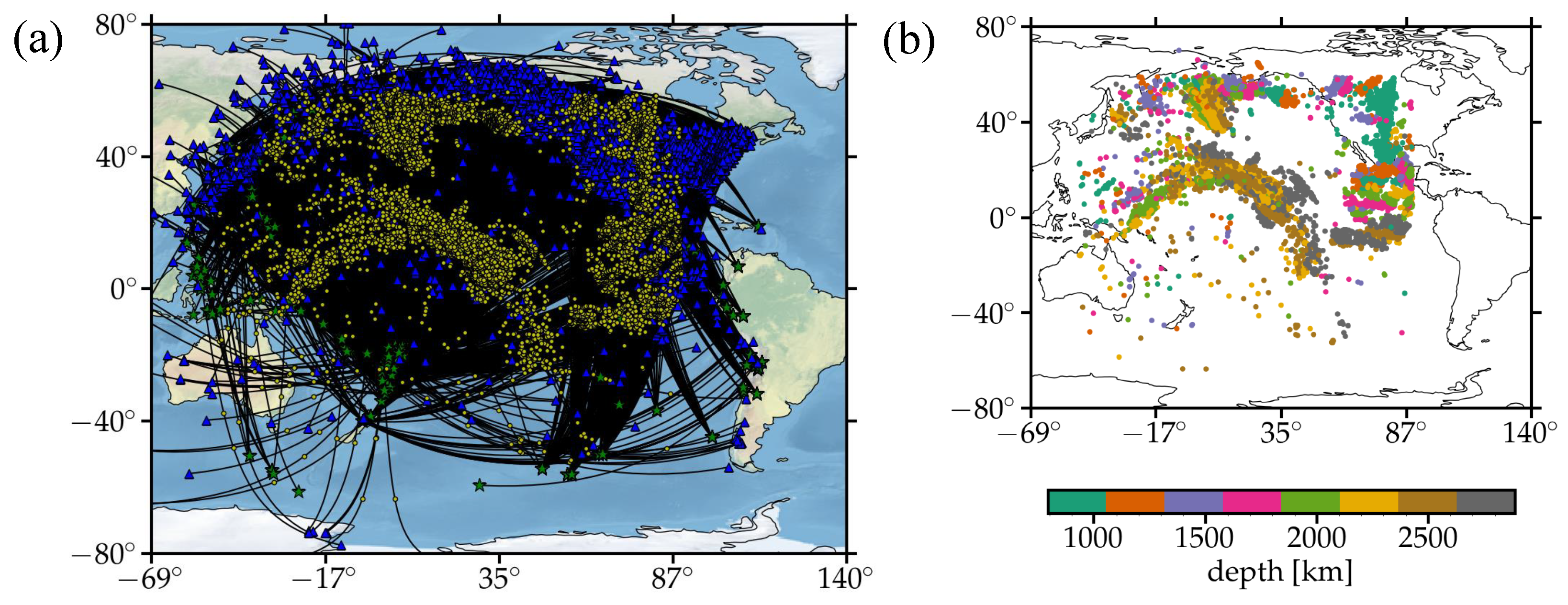
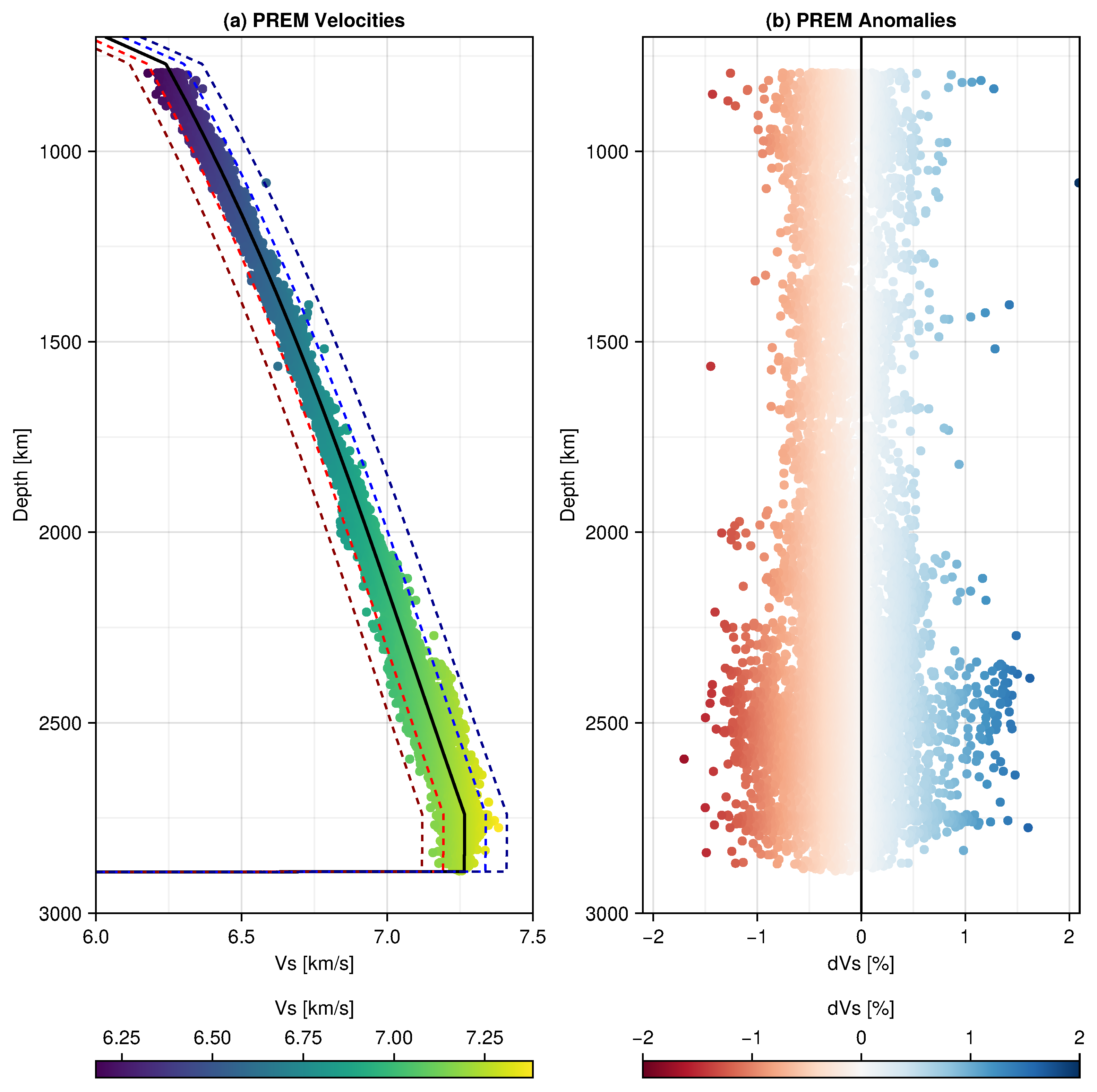
4.1. Data Set
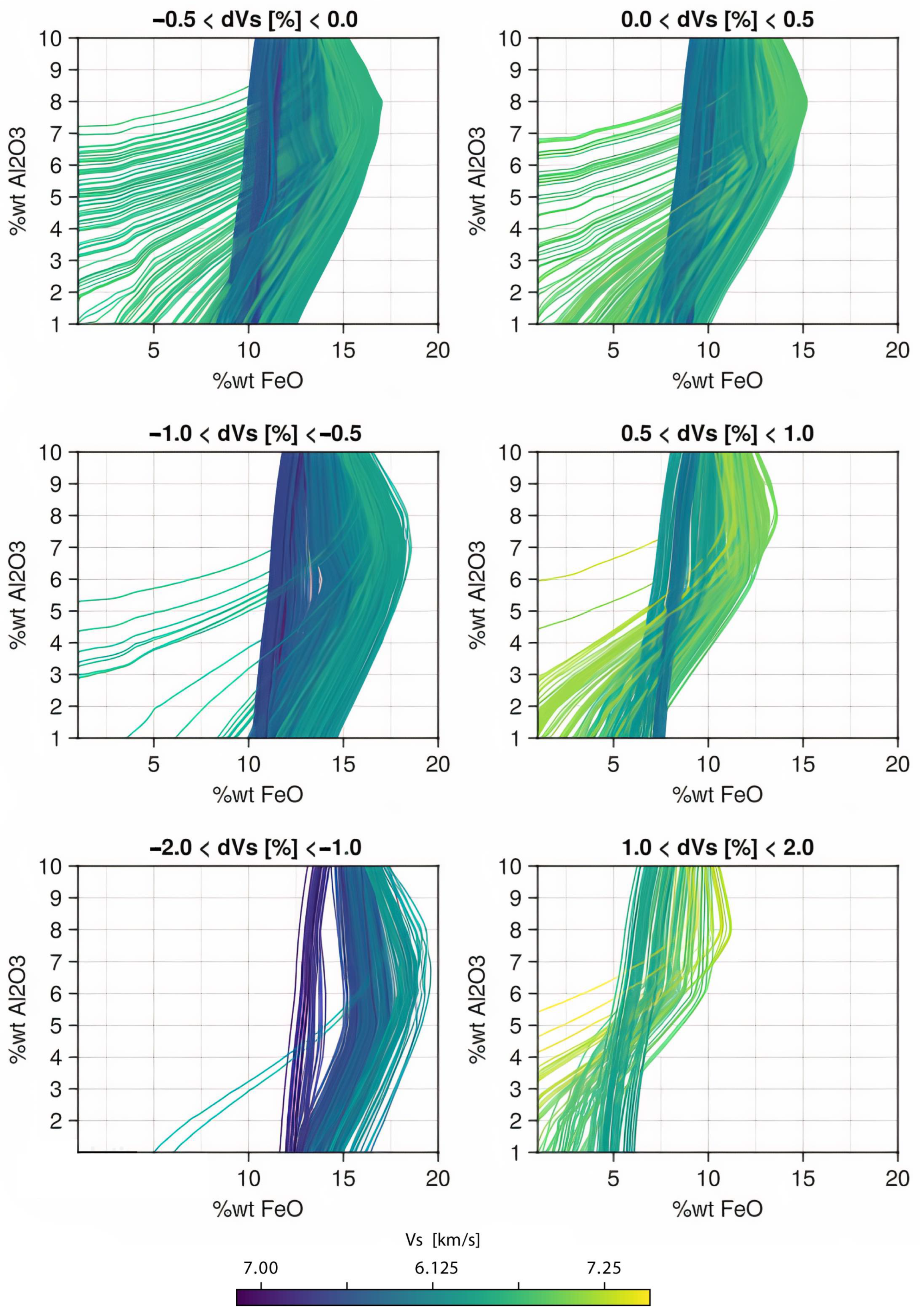
4.2. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parsons, B.; McKenzie, D. Mantle convection and the thermal structure of the plates. J. Geophys. Res. Solid Earth 1978, 83, 4485–4496. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Schubert, G. Geodynamics; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Lay, T.; Hernlund, J.; Buffett, B.A. Core–mantle boundary heat flow. Nat. Geosci. 2008, 1, 25–32. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Hager, B.H.; O’Connell, R.J. Large-scale heterogeneities in the lower mantle. J. Geophys. Res. 1977, 82, 239–255. [Google Scholar] [CrossRef]
- Frost, D.J.; Liebske, C.; Langenhorst, F.; McCammon, C.A.; Trønnes, R.G.; Rubie, D.C. Experimental evidence for the existence of iron-rich metal in the Earth’s lower mantle. Nature 2004, 428, 409–412. [Google Scholar] [CrossRef]
- Kesson, S.; Fitz Gerald, J.; Shelley, J. Mineralogy and dynamics of a pyrolite lower mantle. Nature 1998, 393, 252–255. [Google Scholar] [CrossRef]
- Helffrich, G.R.; Wood, B.J. The Earth’s mantle. Nature 2001, 412, 501–507. [Google Scholar] [CrossRef]
- Garnero, E.J.; McNamara, A.K. Structure and Dynamics of Earth’s Lower Mantle. Science 2008, 320, 626–628. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Tsuchiya, J.; Umemoto, K.; Wentzcovitch, R.M. Phase transition in MgSiO3 perovskite in the Earth’s lower mantle. Earth Planet. Sci. Lett. 2004, 224, 241–248. [Google Scholar] [CrossRef]
- Hirose, K.; Fei, Y.; Ma, Y.; Mao, H.K. The fate of subducted basaltic crust in the Earth’s lower mantle. Nature 1999, 397, 53–56. [Google Scholar] [CrossRef]
- Davies, G.; Dziewonski, A. Homogeneity and constitution of the Earth’s lower mantle and outer core. Phys. Earth Planet. Inter. 1975, 10, 336–343. [Google Scholar] [CrossRef]
- Kaminsky, F. Mineralogy of the lower mantle: A review of ‘super-deep’ mineral inclusions in diamond. Earth-Sci. Rev. 2012, 110, 127–147. [Google Scholar] [CrossRef]
- Murakami, M.; Ohishi, Y.; Hirao, N.; Hirose, K. A perovskitic lower mantle inferred from high-pressure, high-temperature sound velocity data. Nature 2012, 485, 90–94. [Google Scholar] [CrossRef] [PubMed]
- Oganov, A.R.; Ono, S. Theoretical and experimental evidence for a post-perovskite phase of MgSiO3 in Earth’s D" layer. Nature 2004, 430, 445–448. [Google Scholar] [CrossRef]
- Iitaka, T.; Hirose, K.; Kawamura, K.; Murakami, M. The elasticity of the MgSiO3 post-perovskite phase in the Earth’s lowermost mantle. Nature 2004, 430, 442–445. [Google Scholar] [CrossRef]
- Murakami, M.; Hirose, K.; Kawamura, K.; Sata, N.; Ohishi, Y. Post-perovskite phase transition in MgSiO3. Science 2004, 304, 855–858. [Google Scholar] [CrossRef] [PubMed]
- Garnero, E.J.; Helmberger, D.V. A very slow basal layer underlying large-scale low-velocity anomalies in the lower mantle beneath the Pacific: Evidence from core phases. Phys. Earth Planet. Inter. 1995, 91, 161–176. [Google Scholar] [CrossRef]
- Ritsema, J.; van Heijst, H.J.; Woodhouse, J.H. Complex shear wave velocity structure imaged beneath Africa and Iceland. Science 1999, 286, 1925–1928. [Google Scholar] [CrossRef]
- Lay, T.; Hernlund, J.; Garnero, E.J.; Thorne, M.S. A post-perovskite lens and D" heat flux beneath the central Pacific. Science 2006, 314, 1272–1276. [Google Scholar] [CrossRef]
- Sun, D.; Miller, M.S. Study of the western edge of the African large low shear velocity province. Geochem. Geophys. Geosyst. 2013, 14, 3109–3125. [Google Scholar] [CrossRef]
- He, Y.; Wen, L. Structural features and shear-velocity structure of the “Pacific Anomaly”. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- McNamara, A.K.; Garnero, E.J.; Rost, S. Tracking deep mantle reservoirs with ultra-low velocity zones. Earth Planet. Sci. Lett. 2010, 299, 1–9. [Google Scholar] [CrossRef]
- Avants, M.; Lay, T.; Russell, S.A.; Garnero, E.J. Shear velocity variation within the D″ region beneath the central Pacific. J. Geophys. Res. Solid Earth 2006, 111, B05305. [Google Scholar] [CrossRef]
- Thorne, M.S.; Zhang, Y.; Ritsema, J. Evaluation of 1-D and 3-D seismic models of the Pacific lower mantle with S, SKS, and SKKS traveltimes and amplitudes. J. Geophys. Res. Solid Earth 2013, 118, 985–995. [Google Scholar] [CrossRef]
- Ni, S.; Tan, E.; Gurnis, M.; Helmberger, D. Sharp sides to the African superplume. Science 2002, 296, 1850–1852. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wen, L. Mapping the geometry and geographic distribution of a very low velocity province at the base of the Earth’s mantle. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- King, S.D.; Anderson, D.L. Edge-driven convection. Earth Planet. Sci. Lett. 1998, 160, 289–296. [Google Scholar] [CrossRef]
- Frost, D.A.; Rost, S. The P-wave boundary of the large-low shear velocity province beneath the Pacific. Earth Planet. Sci. Lett. 2014, 403, 380–392. [Google Scholar] [CrossRef]
- Burke, K.; Steinberger, B.; Torsvik, T.H.; Smethurst, M.A. Plume generation zones at the margins of large low shear velocity provinces on the core–mantle boundary. Earth Planet. Sci. Lett. 2008, 265, 49–60. [Google Scholar] [CrossRef]
- Ford, S.R.; Garnero, E.J.; McNamara, A.K. A strong lateral shear velocity gradient and anisotropy heterogeneity in the lowermost mantle beneath the southern Pacific. J. Geophys. Res. Solid Earth 2006, 111, B0330. [Google Scholar] [CrossRef]
- He, Y.; Wen, L.; Zheng, T. Geographic boundary and shear wave velocity structure of the “Pacific anomaly” near the core–mantle boundary beneath western Pacific. Earth Planet. Sci. Lett. 2006, 244, 302–314. [Google Scholar] [CrossRef]
- Brown, S.P.; Thorne, M.S.; Miyagi, L.; Rost, S. A compositional origin to ultralow-velocity zones. Geophys. Res. Lett. 2015, 42, 1039–1045. [Google Scholar] [CrossRef]
- Jensen, K.J.; Thorne, M.S.; Rost, S. SPdKS analysis of ultralow-velocity zones beneath the western Pacific. Geophys. Res. Lett. 2013, 40, 4574–4578. [Google Scholar] [CrossRef]
- Rost, S.; Garnero, E.J.; Stefan, W. Thin and intermittent ultralow-velocity zones. J. Geophys. Res. Solid Earth 2010, 115, B06312. [Google Scholar] [CrossRef]
- Rost, S.; Garnero, E.J.; Williams, Q. Fine-scale ultralow-velocity zone structure from high-frequency seismic array data. J. Geophys. Res. Solid Earth 2006, 111, B09310. [Google Scholar] [CrossRef]
- Rost, S.; Garnero, E.J. Detection of an ultralow velocity zone at the core–mantle boundary using diffracted PKKPab waves. J. Geophys. Res. Solid Earth 2006, 111, B07309. [Google Scholar] [CrossRef]
- Rost, S.; Revenaugh, J. Small-scale ultralow-velocity zone structure imaged by ScP. J. Geophys. Res. Solid Earth 2003, 108, 2056. [Google Scholar] [CrossRef]
- Wen, L.; Helmberger, D.V. Ultra-low velocity zones near the core–mantle boundary from broadband PKP precursors. Science 1998, 279, 1701–1703. [Google Scholar] [CrossRef]
- Zhang, Y.; Ritsema, J.; Thorne, M.S. Modeling the ratios of SKKS and SKS amplitudes with ultra-low velocity zones at the core–mantle boundary. Geophys. Res. Lett. 2009, 36, L19303. [Google Scholar] [CrossRef]
- Vanacore, E.; Rost, S.; Thorne, M. Ultralow-velocity zone geometries resolved by multidimensional waveform modelling. Geophys. J. Int. 2016, 206, 659–674. [Google Scholar] [CrossRef]
- Mao, W.L.; Mao, H.k.; Sturhahn, W.; Zhao, J.; Prakapenka, V.B.; Meng, Y.; Shu, J.; Fei, Y.; Hemley, R.J. Iron-rich post-perovskite and the origin of ultralow-velocity zones. Science 2006, 312, 564–565. [Google Scholar] [CrossRef]
- Garnero, E.J.; Revenaugh, J.; Williams, Q.; Lay, T.; Kellogg, L.H. Ultralow velocity zone at the core–mantle boundary. In The Core–Mantle Boundary Region; Wiley Online Library: Hoboken, NJ, USA, 1998; Volume 28, pp. 319–334. [Google Scholar]
- Ritsema, J.; Deuss, A.; van Heijst, H.J.; Woodhouse, J.H. S40RTS: A degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophys. J. Int. 2011, 184, 1223–1236. [Google Scholar] [CrossRef]
- Bozdağ, E.; Peter, D.; Lefebvre, M.; Komatitsch, D.; Tromp, J.; Hill, J.; Podhorszki, N.; Pugmire, D. Global adjoint tomography: First-generation model. Geophys. J. Int. 2016, 207, 1739–1766. [Google Scholar] [CrossRef]
- French, S.; Romanowicz, B. Whole-mantle radially anisotropic shear velocity structure from spectral-element waveform tomography. Geophys. J. Int. 2014, 199, 1303–1327. [Google Scholar] [CrossRef]
- Ishii, M.; Tromp, J. Constraining large-scale mantle heterogeneity using mantle and inner-core sensitive normal modes. Phys. Earth Planet. Inter. 2004, 146, 113–124. [Google Scholar] [CrossRef]
- Davaille, A.; Le Bars, M.; Carbonne, C. Thermal convection in a heterogeneous mantle. Comptes Rendus Geosci. 2003, 335, 141–156. [Google Scholar] [CrossRef]
- Hansen, U.; Yuen, D. Extended-Boussinesq thermal–chemical convection with moving heat sources and variable viscosity. Earth Planet. Sci. Lett. 2000, 176, 401–411. [Google Scholar] [CrossRef]
- Maruyama, S.; Santosh, M.; Zhao, D. Superplume, supercontinent, and post-perovskite: Mantle dynamics and anti-plate tectonics on the Core–Mantle Boundary. Gondwana Res. 2007, 11, 7–37. [Google Scholar] [CrossRef]
- Tanaka, S.; Suetsugu, D.; Shiobara, H.; Sugioka, H.; Kanazawa, T.; Fukao, Y.; Barruol, G.; Reymond, D. On the vertical extent of the large low shear velocity province beneath the South Pacific Superswell. Geophys. Res. Lett. 2009, 36, L07305. [Google Scholar] [CrossRef]
- McNamara, A.K.; Zhong, S. Thermochemical structures within a spherical mantle: Superplumes or piles? J. Geophys. Res. Solid Earth 2004, 109, B07402. [Google Scholar] [CrossRef]
- McNamara, A.K.; Zhong, S. Thermochemical structures beneath Africa and the Pacific Ocean. Nature 2005, 437, 1136–1139. [Google Scholar] [CrossRef]
- Ballmer, M.D.; Schumacher, L.; Lekic, V.; Thomas, C.; Ito, G. Compositional layering within the large low shear-wave velocity provinces in the lower mantle. Geochem. Geophys. Geosyst. 2016, 17, 5056–5077. [Google Scholar] [CrossRef]
- Thorne, M.S.; Garnero, E.J.; Jahnke, G.; Igel, H.; McNamara, A.K. Mega ultra low velocity zone and mantle flow. Earth Planet. Sci. Lett. 2013, 364, 59–67. [Google Scholar] [CrossRef]
- Aki, K.; Christoffersson, A.; Husebye, E.S. Determination of the three-dimensional seismic structure of the lithosphere. J. Geophys. Res. 1977, 82, 277–296. [Google Scholar] [CrossRef]
- Dziewonski, A.M. Mapping the lower mantle: Determination of lateral heterogeneity in P velocity up to degree and order 6. J. Geophys. Res. Solid Earth 1984, 89, 5929–5952. [Google Scholar] [CrossRef]
- Rost, S.; Thomas, C. Array seismology: Methods and applications. Rev. Geophys. 2002, 40, 2-1–2-27. [Google Scholar] [CrossRef]
- Stein, S.; Wysession, M. An Introduction to Seismology, Earthquakes, and Earth Structure; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mula, A.H.; Müller, G. Ray parameters of diffracted long period P and S waves and the velocities at the base of the mantle. Pure Appl. Geophys. 1980, 118, 1272–1292. [Google Scholar] [CrossRef]
- Souriau, A.; Poupinet, G. Lateral variations in P velocity and attenuation in the D″ layer, from diffracted P waves. Phys. Earth Planet. Inter. 1994, 84, 227–234. [Google Scholar] [CrossRef]
- Crotwell, H.P.; Owens, T.J.; Ritsema, J. The TauP Toolkit: Flexible seismic travel time and ray path utilities. Seismol. Res. Lett. 1999, 70, 154–160. [Google Scholar] [CrossRef]
- Krischer, L.; Megies, T.; Barsch, R.; Beyreuther, M.; Lecocq, T.; Caudron, C.; Wassermann, J. ObsPy: A bridge for seismology into the scientific Python ecosystem. Comput. Sci. Discov. 2015, 8, 014003. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Kennett, B.L.; Engdahl, E.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
- Morelli, A.; Dziewonski, A.M. Body wave traveltimes and a spherically symmetric P-and S-wave velocity model. Geophys. J. Int. 1993, 112, 178–194. [Google Scholar] [CrossRef]
- Kennett, B.; Engdahl, E. Traveltimes for global Earthquake location and phase identification. Geophys. J. Int. 1991, 105, 429–465. [Google Scholar] [CrossRef]
- Lai, H.; Garnero, E.J.; Grand, S.P.; Porritt, R.W.; Becker, T.W. Global travel time dataset from adaptive empirical wavelet construction. Geochem. Geophys. Geosyst. 2019, 20, 2175–2198. [Google Scholar] [CrossRef]
- Schubert, G.; Masters, G.; Olson, P.; Tackley, P. Superplumes or plume clusters? Phys. Earth Planet. Inter. 2004, 146, 147–162. [Google Scholar] [CrossRef]
- McNamara, A.K. A review of large low shear velocity provinces and ultra low velocity zones. Tectonophysics 2019, 760, 199–220. [Google Scholar] [CrossRef]
- Durand, S.; Debayle, E.; Ricard, Y.; Zaroli, C.; Lambotte, S. Confirmation of a change in the global shear velocity pattern at around 1000 km depth. Geophys. J. Int. 2017, 211, 1628–1639. [Google Scholar] [CrossRef]
- Hosseini, K.; Matthews, K.J.; Sigloch, K.; Shephard, G.E.; Domeier, M.; Tsekhmistrenko, M. SubMachine: Web-based tools for exploring seismic tomography and other models of Earth’s deep interior. Geochem. Geophys. Geosyst. 2018, 19, 1464–1483. [Google Scholar] [CrossRef]
- Moulik, P.; Ekström, G. An anisotropic shear velocity model of the Earth’s mantle using normal modes, body waves, surface waves and long-period waveforms. Geophys. J. Int. 2014, 199, 1713–1738. [Google Scholar] [CrossRef]
- Lu, C.; Grand, S.P. The effect of subducting slabs in global shear wave tomography. Geophys. J. Int. 2016, 205, 1074–1085. [Google Scholar]
- Koelemeijer, P.; Ritsema, J.; Deuss, A.; Van Heijst, H.J. SP12RTS: A degree-12 model of shear-and compressional-wave velocity for Earth’s mantle. Geophys. J. Int. 2016, 204, 1024–1039. [Google Scholar] [CrossRef]
- Lu, C.; Grand, S.P.; Lai, H.; Garnero, E.J. TX2019slab: A new P and S tomography model incorporating subducting slabs. J. Geophys. Res. Solid Earth 2019, 124, 11549–11567. [Google Scholar] [CrossRef]
- Tesoniero, A.; Auer, L.; Boschi, L.; Cammarano, F. Hydration of marginal basins and compositional variations within the continental lithospheric mantle inferred from a new global model of shear and compressional velocity. J. Geophys. Res. Solid Earth 2015, 120, 7789–7813. [Google Scholar] [CrossRef]
- Marquering, H.; Dahlen, F.; Nolet, G. Three-dimensional sensitivity kernels for finite-frequency traveltimes: The banana-doughnut paradox. Geophys. J. Int. 1999, 137, 805–815. [Google Scholar] [CrossRef]
- De Hoop, M.V.; van Der Hilst, R.D. On sensitivity kernels for “wave-equation” transmission tomography. Geophys. J. Int. 2005, 160, 621–633. [Google Scholar] [CrossRef]
- Van Der Hilst, R.D.; De Hoop, M.V. Banana-doughnut kernels and mantle tomography. Geophys. J. Int. 2005, 163, 956–961. [Google Scholar] [CrossRef]
- De Hoop, M.V.; Van Der Hilst, R.D. Reply to comment by FA Dahlen and G. Nolet on “On sensitivity kernels for “wave-equation” transmission tomography”. Geophys. J. Int. 2005, 163, 952–955. [Google Scholar] [CrossRef]
- Montelli, R.; Nolet, G.; Dahlen, F. Comment on “Banana–Doughnut kernels and mantle tomography" by van der Hilst and de Hoop. Geophys. J. Int. 2006, 167, 1204–1210. [Google Scholar] [CrossRef]
- van Der Hilst, R.D.; De Hoop, M.V. Reply to comment by R. Montelli, G. Nolet and FA Dahlen on “banana—doughnut kernels and mantle tomography”. Geophys. J. Int. 2006, 167, 1211–1214. [Google Scholar] [CrossRef]
- Abreu, R. Understanding the Adjoint Method in Seismology: Theory and Implementation in the Time Domain. Surv. Geophys. 2024, 45, 1363–1434. [Google Scholar] [CrossRef]
- Cottaar, S.; Martin, C.; Li, Z.; Parai, R. The root to the Galápagos mantle plume on the core–mantle boundary. Seismica 2022, 1. [Google Scholar] [CrossRef]
- Villagómez, D.R.; Toomey, D.R.; Geist, D.J.; Hooft, E.E.; Solomon, S.C. Mantle flow and multistage melting beneath the Galápagos hotspot revealed by seismic imaging. Nat. Geosci. 2014, 7, 151–156. [Google Scholar] [CrossRef]
- Nolet, G.; Hello, Y.; Lee, S.v.d.; Bonnieux, S.; Ruiz, M.C.; Pazmino, N.A.; Deschamps, A.; Regnier, M.M.; Font, Y.; Chen, Y.J.; et al. Imaging the Galápagos mantle plume with an unconventional application of floating seismometers. Sci. Rep. 2019, 9, 1326. [Google Scholar] [CrossRef]
- Harpp, K.S.; Weis, D. Insights into the origins and compositions of mantle plumes: A comparison of Galápagos and Hawai’i. Geochem. Geophys. Geosyst. 2020, 21, e2019GC008887. [Google Scholar] [CrossRef]
- Vanacore, E.; Niu, F. Characterization of the D″ beneath the Galapagos Islands using SKKS and SKS waveforms. Earthq. Sci. 2011, 24, 87–99. [Google Scholar]
- Hirose, K.; Brodholt, J.; Lay, T.; Yuen, D. Post-Perovskite: The Last Mantle Phase Transition; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 174. [Google Scholar]
- Shim, S.H.; Kubo, A.; Duffy, T.S. Raman spectroscopy of perovskite and post-perovskite phases of MgGeO3 to 123 GPa. Earth Planet. Sci. Lett. 2007, 260, 166–178. [Google Scholar] [CrossRef]
- Williams, Q.; Jeanloz, R.; McMillan, P. Vibrational spectrum of MgSiO3 perovskite: Zero-pressure Raman and mid-infrared spectra to 27 GPa. J. Geophys. Res. Solid Earth 1987, 92, 8116–8128. [Google Scholar] [CrossRef]
- Shim, S.H. The postperovskite transition. Annu. Rev. Earth Planet. Sci. 2008, 36, 569–599. [Google Scholar] [CrossRef]
- Tateno, S.; Hirose, K.; Sata, N.; Ohishi, Y. Determination of post-perovskite phase transition boundary up to 4400 K and implications for thermal structure in D″ layer. Earth Planet. Sci. Lett. 2009, 277, 130–136. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Tsuchiya, J. Effect of impurity on the elasticity of perovskite and postperovskite: Velocity contrast across the postperovskite transition in (Mg, Fe, Al)(Si, Al) O3. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Wookey, J.; Stackhouse, S.; Kendall, J.M.; Brodholt, J.; Price, G.D. Efficacy of the post-perovskite phase as an explanation for lowermost-mantle seismic properties. Nature 2005, 438, 1004–1007. [Google Scholar] [CrossRef] [PubMed]
- Stackhouse, S.; Brodholt, J.P.; Dobson, D.P.; Price, G.D. Electronic spin transitions and the seismic properties of ferrous iron-bearing MgSiO3 post-perovskite. Geophys. Res. Lett. 2006, 33, L12S03. [Google Scholar] [CrossRef]
- Wentzcovitch, R.M.; Tsuchiya, T.; Tsuchiya, J. MgSiO3 postperovskite at D″conditions. Proc. Natl. Acad. Sci. USA 2006, 103, 543–546. [Google Scholar] [CrossRef] [PubMed]
- Deschamps, F.; Cobden, L.; Tackley, P.J. The primitive nature of large low shear-wave velocity provinces. Earth Planet. Sci. Lett. 2012, 349, 198–208. [Google Scholar] [CrossRef]
- Vilella, K.; Bodin, T.; Boukaré, C.E.; Deschamps, F.; Badro, J.; Ballmer, M.D.; Li, Y. Constraints on the composition and temperature of LLSVPs from seismic properties of lower mantle minerals. Earth Planet. Sci. Lett. 2021, 554, 116685. [Google Scholar] [CrossRef]
- Jordan, T.H.; Lynn, W.S. A velocity anomaly in the lower mantle. J. Geophys. Res. 1974, 79, 2679–2685. [Google Scholar] [CrossRef]
- Suzuki, Y.; Kawai, K.; Geller, R.J.; Tanaka, S.; Siripunvaraporn, W.; Boonchaisuk, S.; Noisagool, S.; Ishihara, Y.; Kim, T. High-resolution 3-D S-velocity structure in the D″ region at the western margin of the Pacific LLSVP: Evidence for small-scale plumes and paleoslabs. Phys. Earth Planet. Inter. 2020, 307, 106544. [Google Scholar] [CrossRef]
- Tackley, P.J. Three-Dimensional Simulations of Mantle Convection with a Thermo-Chemical Basal Boundary Layer: D″? In The Core-Mantle Boundary Region; American Geophysical Union (AGU): Washington, DC, USA, 1998; pp. 231–253. [Google Scholar]
- Christensen, U.R.; Hofmann, A.W. Segregation of subducted oceanic crust in the convecting mantle. J. Geophys. Res. Solid Earth 1994, 99, 19867–19884. [Google Scholar] [CrossRef]
- Khan, A.; Boschi, L.; Connolly, J. On mantle chemical and thermal heterogeneities and anisotropy as mapped by inversion of global surface wave data. J. Geophys. Res. Solid Earth 2009, 114, B09305. [Google Scholar] [CrossRef]
- Müntener, O.; Ulmer, P. Arc crust formation and differentiation constrained by experimental petrology. Am. J. Sci. 2018, 318, 64–89. [Google Scholar] [CrossRef]
- Fullea, J.; Lebedev, S.; Martinec, Z.; Celli, N.L. WINTERC-G: Mapping the upper mantle thermochemical heterogeneity from coupled geophysical–petrological inversion of seismic waveforms, heat flow, surface elevation and gravity satellite data. Geophys. J. Int. 2021, 226, 146–191. [Google Scholar] [CrossRef]
- Connolly, J.A. Computation of phase equilibria by linear programming: A tool for geodynamic modeling and its application to subduction zone decarbonation. Earth Planet. Sci. Lett. 2005, 236, 524–541. [Google Scholar] [CrossRef]
- Harley, S.L. An experimental study of the partitioning of Fe and Mg between garnet and orthopyroxene. Contrib. Mineral. Petrol. 1984, 86, 359–373. [Google Scholar] [CrossRef]
- Nakagawa, T.; Tackley, P.J.; Deschamps, F.; Connolly, J.A. The influence of MORB and harzburgite composition on thermo-chemical mantle convection in a 3-D spherical shell with self-consistently calculated mineral physics. Earth Planet. Sci. Lett. 2010, 296, 403–412. [Google Scholar] [CrossRef]
- Nakagawa, T.; Tackley, P.J.; Deschamps, F.; Connolly, J.A. Incorporating self-consistently calculated mineral physics into thermochemical mantle convection simulations in a 3-D spherical shell and its influence on seismic anomalies in Earth’s mantle. Geochem. Geophys. Geosyst. 2009, 10, Q03004. [Google Scholar] [CrossRef]
- Afonso, J.C.; Fullea, J.; Yang, Y.; Connolly, J.; Jones, A. 3-D multi-observable probabilistic inversion for the compositional and thermal structure of the lithosphere and upper mantle. II: General methodology and resolution analysis. J. Geophys. Res. Solid Earth 2013, 118, 1650–1676. [Google Scholar] [CrossRef]
- McDonough, W.F.; Sun, S.S. The composition of the Earth. Chem. Geol. 1995, 120, 223–253. [Google Scholar] [CrossRef]
- Workman, R.K.; Hart, S.R. Major and trace element composition of the depleted MORB mantle (DMM). Earth Planet. Sci. Lett. 2005, 231, 53–72. [Google Scholar] [CrossRef]
- Palme, H.; O’Neill, H. 2.01 - Cosmochemical Estimates of Mantle Composition. In Treatise on Geochemistry; Holland, H.D., Turekian, K.K., Eds.; Pergamon: Oxford, UK, 2007; pp. 1–38. [Google Scholar]
- Fei, Y.; Wang, Y.; Finger, L.W. Maximum solubility of FeO in (Mg, Fe) SiO3-perovskite as a function of temperature at 26 GPa: Implication for FeO content in the lower mantle. J. Geophys. Res. Solid Earth 1996, 101, 11525–11530. [Google Scholar] [CrossRef]
- Sinmyo, R.; Ozawa, H.; Hirose, K.; Yasuhara, A.; Endo, N.; Sata, N.; Ohishi, Y. Ferric iron content in (Mg, Fe) SiO3 perovskite and post-perovskite at deep lower mantle conditions. Am. Mineral. 2008, 93, 1899–1902. [Google Scholar] [CrossRef]
- Dorfman, S.M.; Duffy, T.S. Effect of Fe-enrichment on seismic properties of perovskite and post-perovskite in the deep lower mantle. Geophys. J. Int. 2014, 197, 910–919. [Google Scholar] [CrossRef]
- Tateno, S.; Hirose, K.; Sata, N.; Ohishi, Y. Solubility of FeO in (Mg, Fe) SiO3 perovskite and the post-perovskite phase transition. Phys. Earth Planet. Inter. 2007, 160, 319–325. [Google Scholar] [CrossRef]
- Catalli, K.; Shim, S.H.; Prakapenka, V. Thickness and Clapeyron slope of the post-perovskite boundary. Nature 2009, 462, 782–785. [Google Scholar] [CrossRef]
- Hernlund, J.; Thomas, C.; Tackley, P. A doubling of the post-perovskite phase boundary and structure of the Earth’s lowermost mantle. Nature 2005, 434, 882–886. [Google Scholar] [CrossRef] [PubMed]
- Sun, N.; Wei, W.; Han, S.; Song, J.; Li, X.; Duan, Y.; Prakapenka, V.B.; Mao, Z. Phase transition and thermal equations of state of (Fe, Al)-bridgmanite and post-perovskite: Implication for the chemical heterogeneity at the lowermost mantle. Earth Planet. Sci. Lett. 2018, 490, 161–169. [Google Scholar] [CrossRef]
- Nowacki, A.; Wookey, J.; Kendall, J.M. New advances in using seismic anisotropy, mineral physics and geodynamics to understand deformation in the lowermost mantle. J. Geodyn. 2011, 52, 205–228. [Google Scholar] [CrossRef]
- Fouch, M.J.; Fischer, K.M.; Wysession, M.E. Lowermost mantle anisotropy beneath the Pacific: Imaging the source of the Hawaiian plume. Earth Planet. Sci. Lett. 2001, 190, 167–180. [Google Scholar] [CrossRef]
- Russell, S.A.; Lay, T.; Garnero, E.J. Seismic evidence for small-scale dynamics in the lowermost mantle at the root of the Hawaiian hotspot. Nature 1998, 396, 255–258. [Google Scholar] [CrossRef]
- Russell, S.A.; Lay, T.; Garnero, E.J. Small-scale lateral shear velocity and anisotropy heterogeneity near the core–mantle boundary beneath the central Pacific imaged using broadband ScS waves. J. Geophys. Res. Solid Earth 1999, 104, 13183–13199. [Google Scholar] [CrossRef]
- Vinnik, L.; Romanowicz, B.; Le Stunff, Y.; Makeyeva, L. Seismic anisotropy in the D″ layer. Geophys. Res. Lett. 1995, 22, 1657–1660. [Google Scholar] [CrossRef]
- Vinnik, L.; Breger, L.; Romanowicz, B. Anisotropic structures at the base of the Earth’s mantle. Nature 1998, 393, 564–567. [Google Scholar] [CrossRef]
- Pulliam, J.; Sen, M.K. Seismic anisotropy in the core—Mantle transition zone. Geophys. J. Int. 1998, 135, 113–128. [Google Scholar] [CrossRef]
- Ritsema, J.; Lay, T.; Garnero, E.J.; Benz, H. Seismic anisotropy in the lowermost mantle beneath the Pacific. Geophys. Res. Lett. 1998, 25, 1229–1232. [Google Scholar] [CrossRef]
- Kendall, J.M.; Silver, P.G. Investigating Causes of D″ Anistropy. In The Core-Mantle Boundary Region; American Geophysical Union (AGU): Washington, DC, USA, 1998; pp. 97–118. [Google Scholar]
- Kawai, K.; Geller, R.J. The vertical flow in the lowermost mantle beneath the Pacific from inversion of seismic waveforms for anisotropic structure. Earth Planet. Sci. Lett. 2010, 297, 190–198. [Google Scholar] [CrossRef]
- Yamazaki, D.; Karato, S.I. Lattice-Preferred Orientation of Lower Mantle Materials and Seismic Anisotropy in the D″ Layer. In Post-Perovskite: The Last Mantle Phase Transition; American Geophysical Union (AGU): Washington, DC, USA, 2007; pp. 69–78. [Google Scholar]
- Wolf, J.; Long, M.D. Slab-driven flow at the base of the mantle beneath the northeastern Pacific Ocean. Earth Planet. Sci. Lett. 2022, 594, 117758. [Google Scholar] [CrossRef]
- Wang, J.; Lekić, V.; Schmerr, N.C.; Gu, Y.J.; Guo, Y.; Lin, R. Mesozoic intraoceanic subduction shaped the lower mantle beneath the East Pacific Rise. Sci. Adv. 2024, 10, eado1219. [Google Scholar] [CrossRef] [PubMed]
- Métaxian, J.P.; Lesage, P.; Valette, B. Locating sources of volcanic tremor and emergent events by seismic triangulation: Application to Arenal volcano, Costa Rica. J. Geophys. Res. Solid Earth 2002, 107, ECV–10. [Google Scholar] [CrossRef]
- Igel, H.; Schreiber, K.U.; Gebauer, A.; Bernauer, F.; Egdorf, S.; Simonelli, A.; Liny, C.J.; Wassermann, J.; Donner, S.; Hadziioannou, C.; et al. Romy: A multi-component ring laser for geodesy and geophysics. Geophys. J. Int. 2021, 225, 684–698. [Google Scholar] [CrossRef]
- Fichtner, A.; Igel, H. Sensitivity densities for rotational ground-motion measurements. Bull. Seismol. Soc. Am. 2009, 99, 1302–1314. [Google Scholar] [CrossRef]
- Bernauer, F.; Wassermann, J.; Igel, H. Dynamic tilt correction using direct rotational motion measurements. Seismol. Soc. Am. 2020, 91, 2872–2880. [Google Scholar] [CrossRef]
- Bernauer, M.; Fichtner, A.; Igel, H. Measurements of translation, rotation and strain: New approaches to seismic processing and inversion. J. Seismol. 2012, 16, 669–681. [Google Scholar] [CrossRef]
- Trifunac, M.D. Effects of torsional and rocking excitations on the response of structures. In Earthquake Source Asymmetry, Structural Media and Rotation Effects; Springer: Berlin/Heidelberg, Germany, 2006; pp. 569–582. [Google Scholar]
- Bernauer, M.; Fichtner, A.; Igel, H. Inferring Earth structure from combined measurements of rotational and translational ground motions. Geophysics 2009, 74, WCD41–WCD47. [Google Scholar] [CrossRef]
- Bernauer, M.; Fichtner, A.; Igel, H. Reducing nonuniqueness in finite source inversion using rotational ground motions. J. Geophys. Res. Solid Earth 2014, 119, 4860–4875. [Google Scholar] [CrossRef]
- Reinwald, M.; Bernauer, M.; Igel, H.; Donner, S. Improved finite-source inversion through joint measurements of rotational and translational ground motions: A numerical study. Solid Earth 2016, 7, 1467–1477. [Google Scholar] [CrossRef]
- Abreu, R.; Durand, S.; Rost, S.; Thomas, C. Deep Earth rotational seismology. Geophys. J. Int. 2023, 234, 2365–2374. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abreu, R.; Arnaiz-Rodríguez, M.S.; Nagesh, C. Evidence of High-Shear-Velocity Anomalies Inside the Pacific LLSVP. Geosciences 2025, 15, 102. https://doi.org/10.3390/geosciences15030102
Abreu R, Arnaiz-Rodríguez MS, Nagesh C. Evidence of High-Shear-Velocity Anomalies Inside the Pacific LLSVP. Geosciences. 2025; 15(3):102. https://doi.org/10.3390/geosciences15030102
Chicago/Turabian StyleAbreu, Rafael, Mariano S. Arnaiz-Rodríguez, and Chahana Nagesh. 2025. "Evidence of High-Shear-Velocity Anomalies Inside the Pacific LLSVP" Geosciences 15, no. 3: 102. https://doi.org/10.3390/geosciences15030102
APA StyleAbreu, R., Arnaiz-Rodríguez, M. S., & Nagesh, C. (2025). Evidence of High-Shear-Velocity Anomalies Inside the Pacific LLSVP. Geosciences, 15(3), 102. https://doi.org/10.3390/geosciences15030102





