Effect of Hot Water Setting Temperature on Performance of Solar Absorption-Subcooled Compression Hybrid Cooling Systems
Abstract
1. Introduction
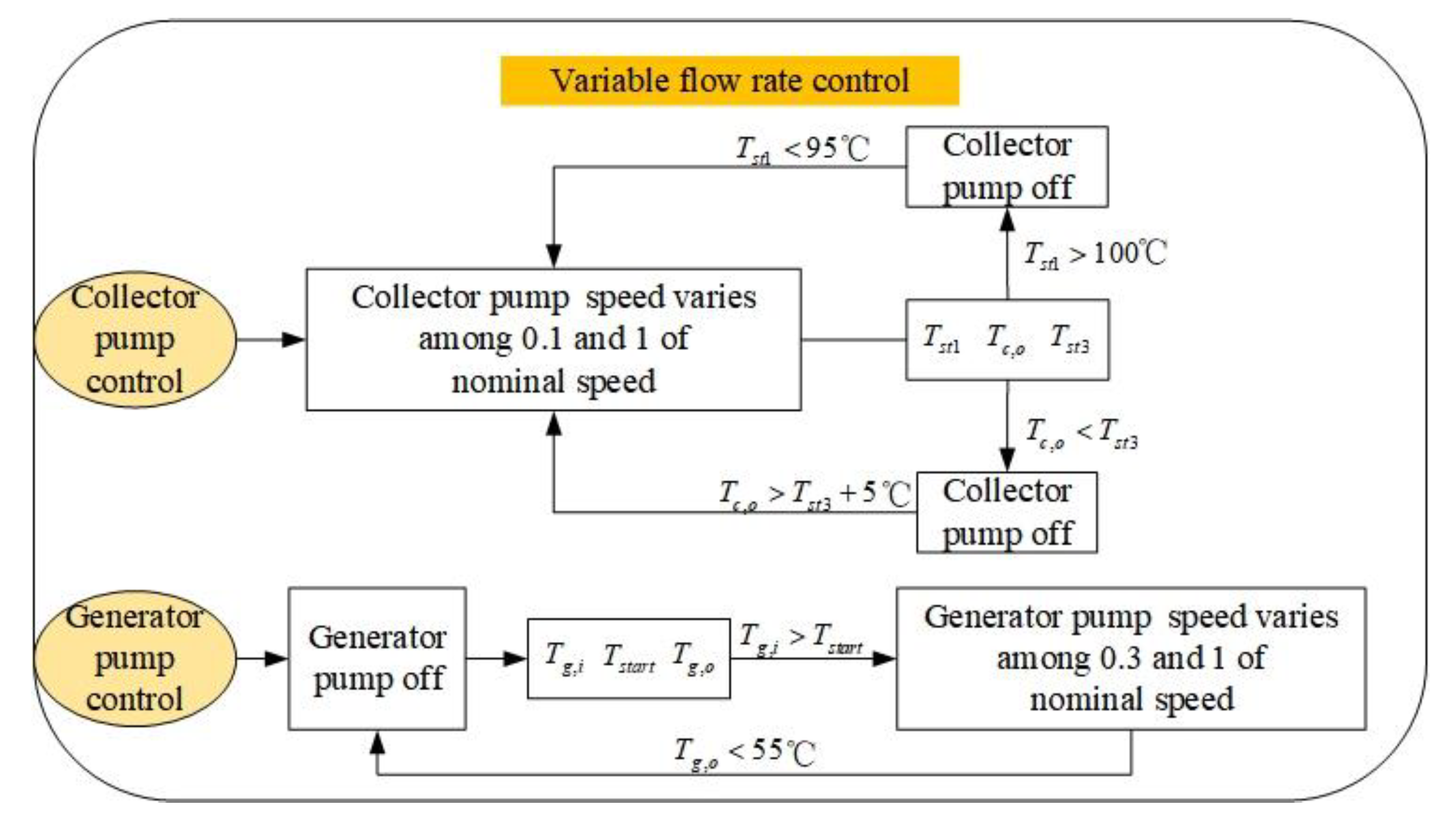
2. System Description: Operation Modes and Control Strategies
3. Model
3.1. Modeling of SASCHCS
- The system operates under quasi-steady state;
- The cooling facility (absorption and compression subsystem) is adiabatic;
- The evaporator and the condenser exit of compression subsystems are saturated;
- The pressure loss of pipelines and heat exchangers is ignored;
- The inlet hot water temperature of generator is equal to the top layer temperature of the storage tanks;
- The inlet hot water of collectors is equal to the bottom layer temperature of storage tanks.
3.1.1. ETC and Storage Tank
3.1.2. Absorption Subsystem and Compression Subsystem
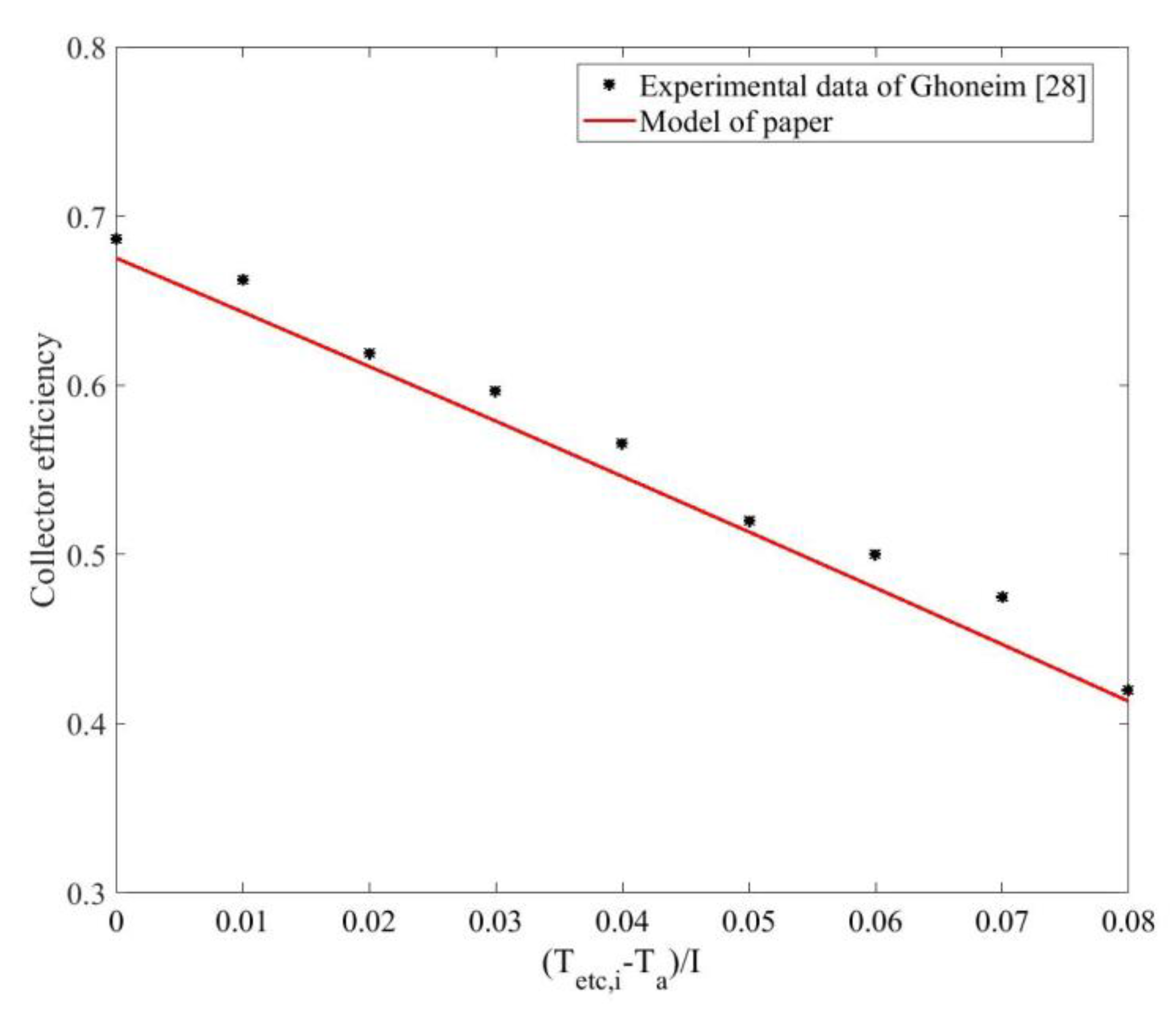
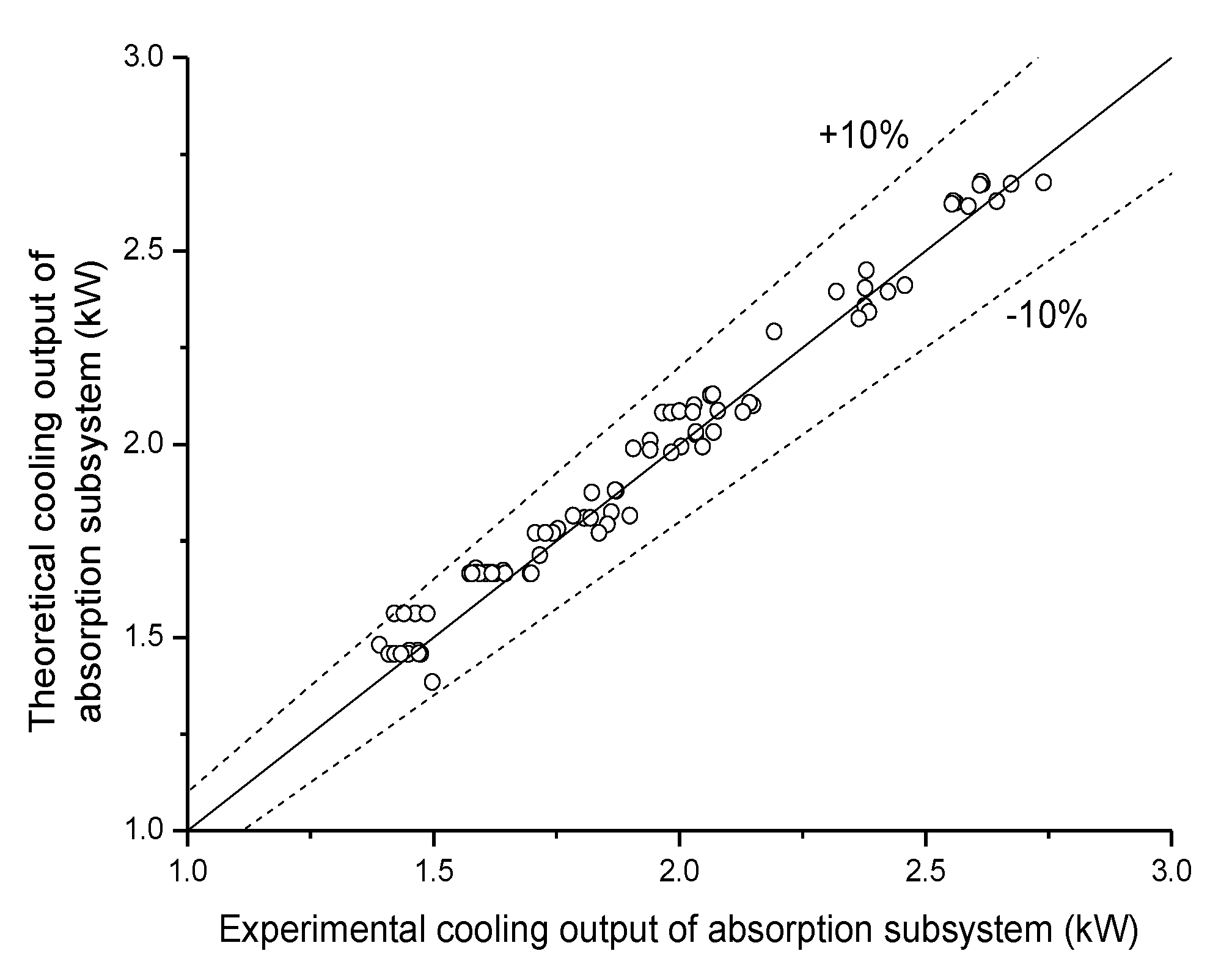
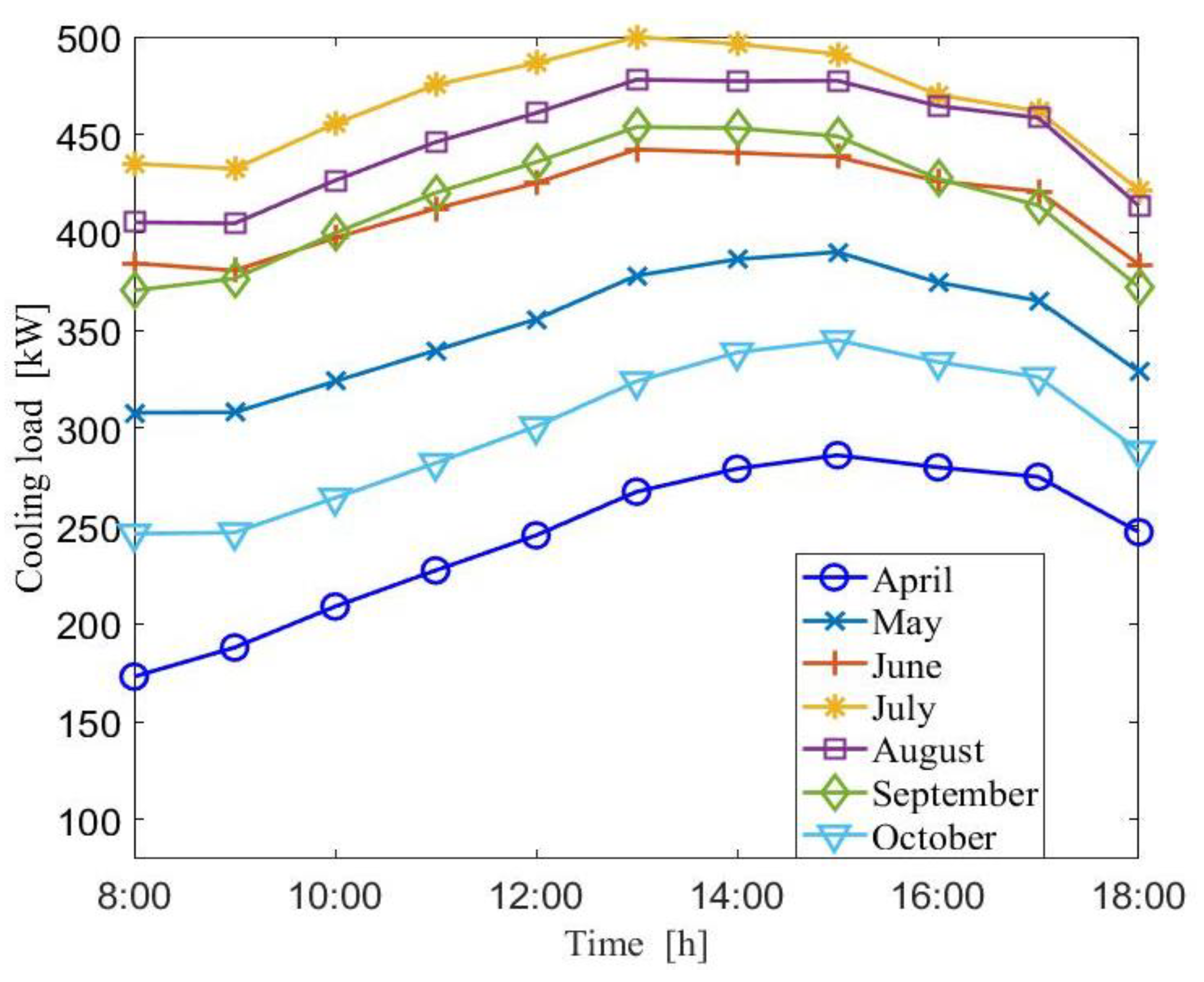
3.2. Model Validation and Case Study
4. Results and Discussion
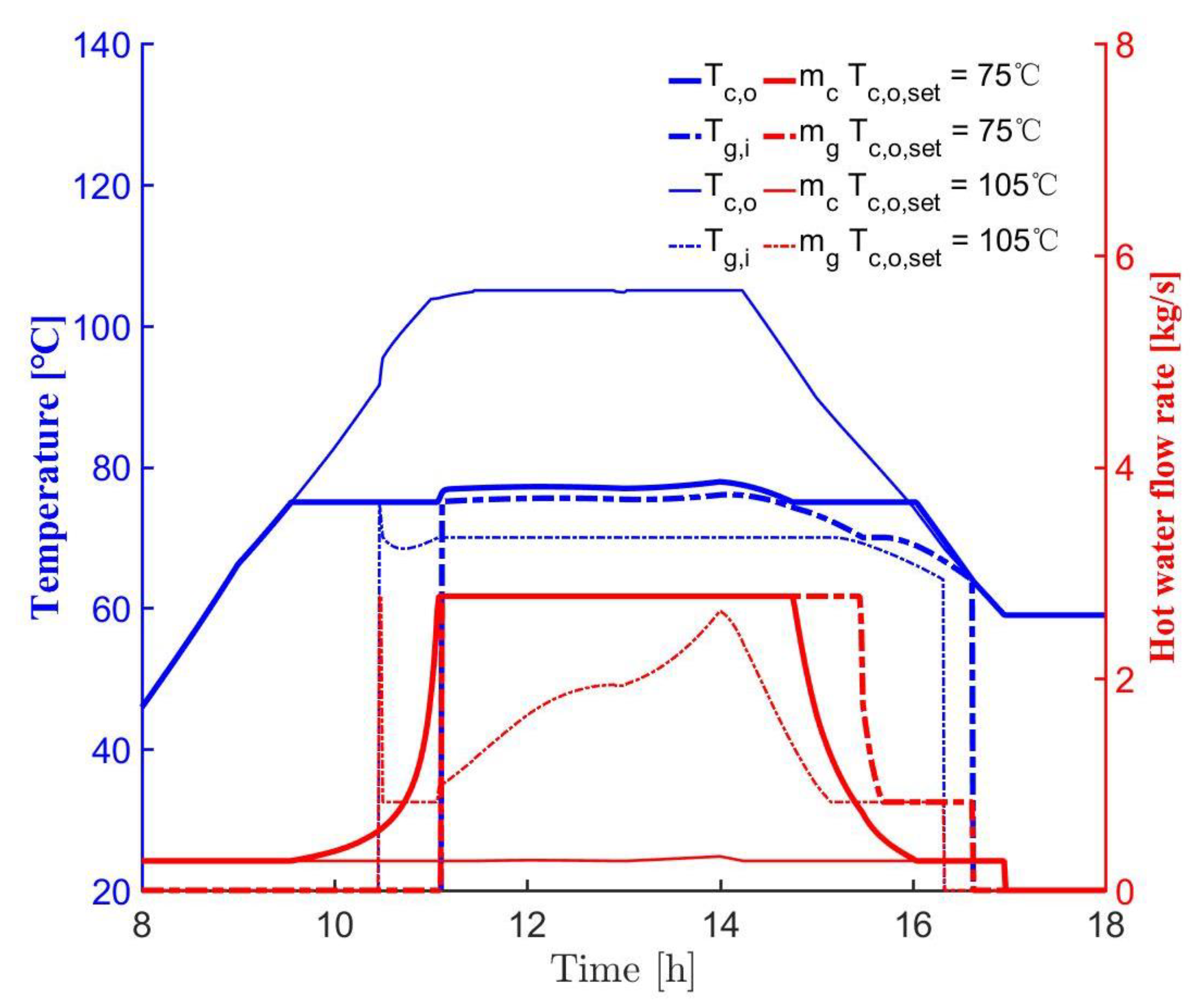
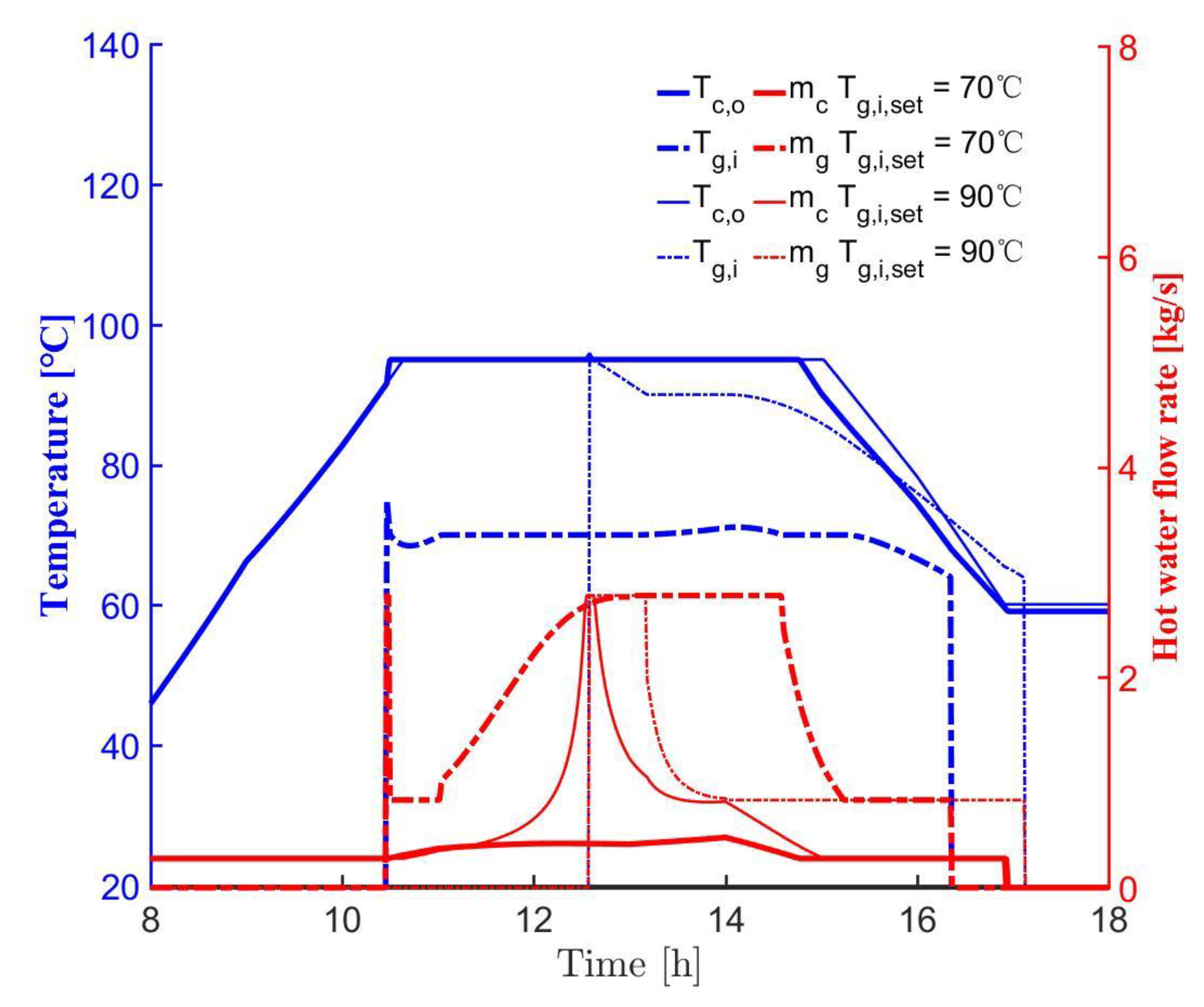
4.1. Effect of Hot Water Setting Temperature
4.2. Global Optimization of Setting Temperature in Two Hot Water Cycles
5. Conclusions
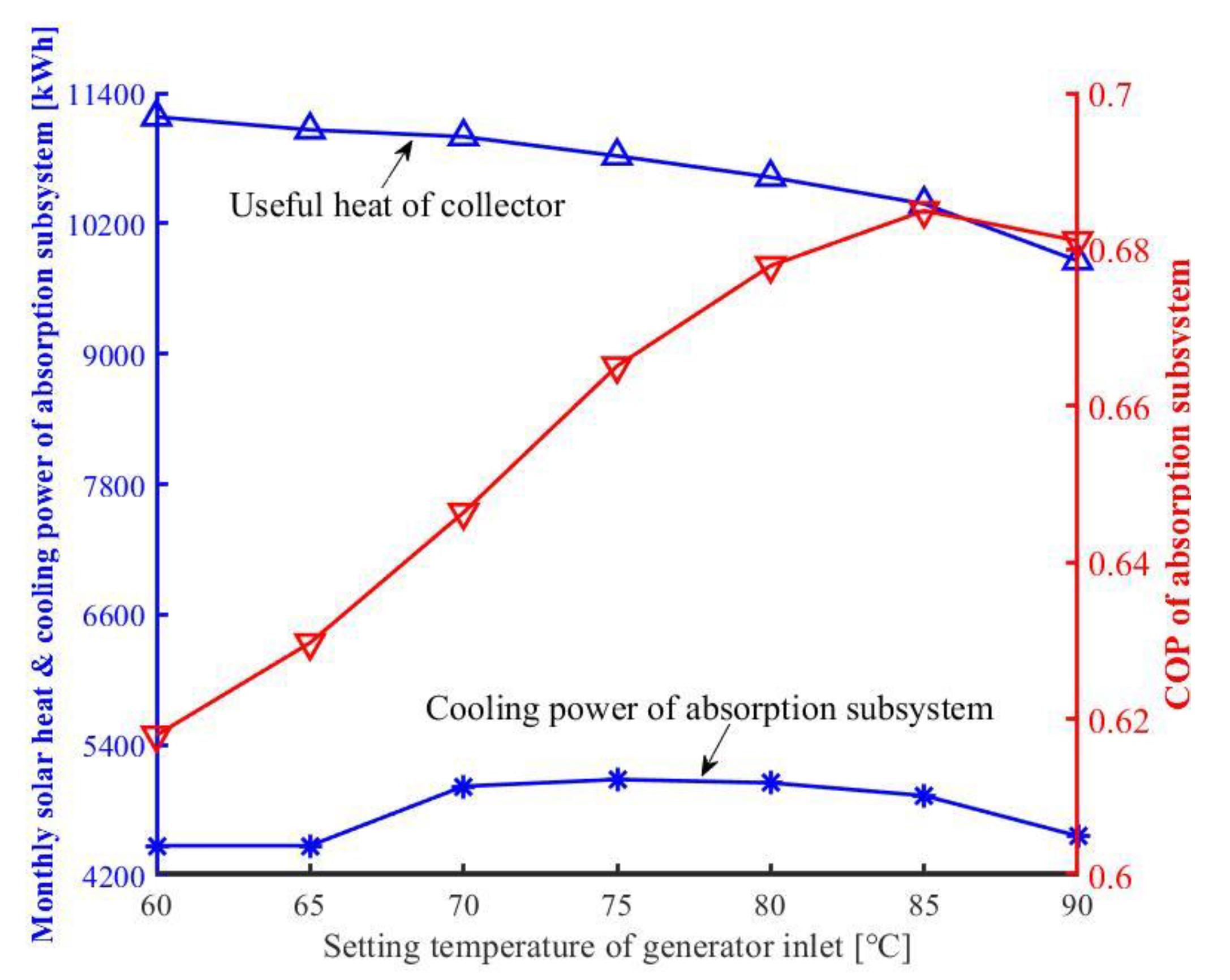
- Despite the fact that the COP of the absorption subsystem went up slightly with the increased hot water temperature, the excessive improvement of the collector setting temperature was harmful for the energy saving, since the serious reduction of heat transfer caused by the low flow rate notably decreased the amount of collector useful heat. It was derived that the daily cooling output of the absorption subsystem based on August data dropped by 11.6% as the collector set point temperature went up from 80 °C to 105 °C.
- Although the enhanced temperature of generator hot water lowered the amount of solar heat, the appropriate rise of generator set point temperature was favorable for the solar cooling owing to the remarkable growth of COP in absorption subsystems, i.e., the daily cooling capacity of the absorption subsystem based on August data enhanced by 13.6% if the setting temperature of the generator grew from 60 °C to 75 °C.
- The collector set point temperature should be 8–10 °C above the generator one in terms of the tradeoff of collector useful heat and absorption subsystem COP. In particular, the above-mentioned relationship is independent from the meteorological data.
- It was demonstrated that a 71.6 °C collector setting temperature with a 64.5 °C generator one was optimal for the annual operation by the global optimization. The corresponding peak annual specific energy saving of SASCHCS was 32.75 kWh/m2. In addition, the annual collector efficiencies, the COP of absorption and compression subsystems, were 0.39, 0.63, and 4.86, respectively, in the optimal case.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| area (m2) | volume (m3) | ||
| the outer surface area of absorber tube (m2) | compressor work (kW) | ||
| coefficient of performance | temperature difference (°C) | ||
| synthetic conductance W/(mK) | double difference of temperatures (°C) | ||
| bond conductance W/(mK) | Greek symbols | ||
| specific heat (kJ/kgK) | absorptivity, distribution UA parameter | ||
| diameter of the U-tube (m) | efficiency | ||
| external diameter of insulation (m) | header pipe insulation thermal conductivity (W/mK) | ||
| internal diameter of insulation (m) | pi | ||
| energy saving (kWh) | density (kg/m3) | ||
| fin efficiency of straight fin collector efficient factor | transmissivity | ||
| heat removal factor | Subscripts | ||
| heat transfer coefficient (W/m2K) | a | ambient | |
| specific enthalpy (kJ/kg) | absorption subsystem | ||
| convection heat transfer coefficient between the fluid and the U-tube W/(m2K) | average | ||
| convection heat transfer coefficient W/(m2K) | compression subsystem | ||
| radiation heat transfer coefficient, W/(m2K) | discharge | ||
| heat transfer coefficient due to the conduction W/(m2K) | evaporator | ||
| solar irradiance (W/m2) | evacuated tube collector | ||
| the circumferential distance between the U-tubes (m) | generator | ||
| logarithmic mean temperature difference (°C) | inlet, current time | ||
| length of the header pipe per one U-tube (m) | loss | ||
| mass flow rate (kg/s) | min | minimum | |
| heat load (kW) | outlet | ||
| time | rated | ||
| temperature (°C) | ref | reference | |
| multiplication of heat transfer coefficient and area (W/K) | isentropic | ||
| the heat loss coefficient from absorber tube to ambient W/(m2K) | suction | ||
| overall loss coefficient W/(m2K) | storage tank | ||
| the edge loss coefficient of the header tube W/(m2K) |
References
- Mohammed, O.W.; Yanling, G. Comprehensive Parametric Study of a Solar Absorption Refrigeration System to Lower Its Cut In/Off Temperature. Energies 2017, 10, 1746. [Google Scholar] [CrossRef]
- Perez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, R. Comparison of CPC driven solar absorption cooling systems with single, double and variable effect absorption chillers. Sol. Energy 2017, 158, 511–519. [Google Scholar] [CrossRef]
- Noro, M.; Lazzarin, R. Solar cooling between thermal and photovoltaic: An energy and economic comparative study in the Mediterranean conditions. Energy 2014, 73, 453–464. [Google Scholar] [CrossRef]
- Colmenar-Santos, A.; Vale-Vale, J.; Borge-Diez, D.; Requena-Pérez, R. Solar thermal systems for high rise buildings with high consumption demand: Case study for a 5 star hotel in Sao Paulo, Brazil. Energy Build. 2014, 69, 481–489. [Google Scholar] [CrossRef]
- Li, Z.; Jing, Y.; Liu, J. Thermodynamic study of a novel solar LiBr/H2O absorption chiller. Energy Build. 2016, 133, 565–576. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, N.; Pan, F.; Wang, Q.; Gao, Z.; Chen, G. Comparative study on two low-grade heat driven absorption-compression refrigeration cycles based on energy, exergy, economic and environmental (4E) analyses. Energy Convers. Manag. 2017, 133, 535–547. [Google Scholar] [CrossRef]
- Yu, J.; Li, Z.; Chen, E.; Xu, Y.; Chen, H.; Wang, L. Experimental assessment of solar absorption-subcooled compression hybrid cooling system. Sol. Energy 2019, 185, 245–254. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L. Economic and environmental study of solar absorption-subcooled compression hybrid cooling system. Int. J. Sustain. Energy 2019, 38, 123–140. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Jing, Y. Exergoeconomic analysis of solar absorption-subcooled compression hybrid cooling system. Energy Convers. Manag. 2017, 144, 205–216. [Google Scholar] [CrossRef]
- Jing, Y.; Li, Z.; Chen, H.; Lu, S.; Lv, S. Exergoeconomic design criterion of solar absorption-subcooled compression hybrid cooling system based on the variable working conditions. Energy Convers. Manag. 2019, 180, 889–903. [Google Scholar] [CrossRef]
- Zamfir, E.; Bǎdescu, V.; Badescu, V. Different strategies for operation of flat-plate solar collectors. Energy 1994, 19, 1245–1254. [Google Scholar] [CrossRef]
- Csordas, G.; Brunger, A.; Hollands, K.; Lightstone, M. Plume entrainment effects in solar domestic hot water systems employing variable-flow-rate control strategies. Sol. Energy 1992, 49, 497–505. [Google Scholar] [CrossRef]
- Rehman, H.U.; Hirvonen, J.; Sirén, K. Design of a Simple Control Strategy for a Community-size Solar Heating System with a Seasonal Storage. Energy Procedia 2016, 91, 486–495. [Google Scholar] [CrossRef]
- Araújo, A.; Silva, R.; Pereira, V. Solar thermal modeling for rapid estimation of auxiliary energy requirements in domestic hot water production: On-off versus proportional flow rate control. Sol. Energy 2019, 177, 68–79. [Google Scholar] [CrossRef]
- Bava, F.; Furbo, S. Impact of different improvement measures on the thermal performance of a solar collector field for district heating. Energy 2018, 144, 816–825. [Google Scholar] [CrossRef]
- Tehrani, S.S.M.; Taylor, R.A. Off-design simulation and performance of molten salt cavity receivers in solar tower plants under realistic operational modes and control strategies. Appl. Energy 2016, 179, 698–715. [Google Scholar] [CrossRef]
- Yilmazoglu, M.Z. Effects of the selection of heat transfer fluid and condenser type on the performance of a solar thermal power plant with technoeconomic approach. Energy Convers. Manag. 2016, 111, 271–278. [Google Scholar] [CrossRef]
- Camacho, E.; Gallego, A. Optimal operation in solar trough plants: A case study. Sol. Energy 2013, 95, 106–117. [Google Scholar] [CrossRef]
- Brodrick, P.G.; Brandt, A.R.; Durlofsky, L.J. Operational optimization of an integrated solar combined cycle under practical time-dependent constraints. Energy 2017, 141, 1569–1584. [Google Scholar] [CrossRef]
- Qu, M.; Yin, H.; Archer, D.H. A solar thermal cooling and heating system for a building: Experimental and model based performance analysis and design. Sol. Energy 2010, 84, 166–182. [Google Scholar] [CrossRef]
- Calise, F.; D’Accadia, M.D.; Vanoli, R. Dynamic simulation and parametric optimisation of a solar-assisted heating and cooling system. Int. J. Ambient. Energy 2010, 31, 173–194. [Google Scholar] [CrossRef]
- Petela, K.; Manfrida, G.; Szlek, A. Advantages of variable driving temperature in solar absorption chiller. Renew. Energy 2017, 114, 716–724. [Google Scholar] [CrossRef]
- Weber, C.; Berger, M.; Mehling, F.; Heinrich, A.; Núñez, T. Solar cooling with water–ammonia absorption chillers and concentrating solar collector—Operational experience. Int. J. Refrig. 2014, 39, 57–76. [Google Scholar] [CrossRef]
- Shirazi, A.; Pintaldi, S.; White, S.D.; Morrison, G.L.; Rosengarten, G.; Taylor, R.A. Solar-assisted absorption air-conditioning systems in buildings: Control strategies and operational modes. Appl. Therm. Eng. 2016, 92, 246–260. [Google Scholar] [CrossRef]
- Li, Z.; Chen, E.; Jing, Y.; Lv, S. Thermodynamic relationship of subcooling power and increase of cooling output in vapour compression chiller. Energy Convers. Manag. 2017, 149, 254–262. [Google Scholar] [CrossRef]
- Chen, E.; Li, Z.; Yu, J.; Xu, Y.; Yu, Y. Experimental research of increased cooling output by dedicated subcooling. Appl. Therm. Eng. 2019, 154, 9–17. [Google Scholar] [CrossRef]
- Ghoneim, A.A. Performance optimization of9 evacuated tube collector for solar cooling of a house in hot climate. Int. J. Sustain. Energy 2018, 37, 193–208. [Google Scholar] [CrossRef]
- Ma, L.; Lu, Z.; Zhang, J.; Liang, R. Thermal performance analysis of the glass evacuated tube solar collector with U-tube. Build. Environ. 2010, 45, 1959–1967. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Chen, E.; Jing, Y. Off-Design Modeling and Simulation of Solar Absorption-Subcooled Compression Hybrid Cooling System. Appl. Sci. 2018, 8, 2612. [Google Scholar] [CrossRef]
- Miao, D. Simulation Model of a Single-Stage Lithium Bromide-Water Absorption Unit; NASA Technical Paper 1296; NASA: Washington, DC, USA, 1978.
- Arnavat, M.P.; López-Villada, J.; Bruno, J.C.; Coronas, A. Analysis and parameter identification for characteristic equations of single- and double-effect absorption chillers by means of multivariable regression. Int. J. Refrig. 2010, 33, 70–78. [Google Scholar] [CrossRef]
- Chen, H.; Li, Z.; Xu, Y. Evaluation and comparison of solar trigeneration systems based on photovoltaic thermal collectors for subtropical climates. Energy Convers. Manag. 2019, 199, 111959. [Google Scholar] [CrossRef]
- Li, Z.; Ye, X.; Liu, J. Performance analysis of solar air cooled double effect LiBr/H2O absorption cooling system in subtropical city. Energy Convers. Manag. 2014, 85, 302–312. [Google Scholar] [CrossRef]
- De ST. Available online: http://update.dest.com.cn/ (accessed on 12 October 2019).
- MATLAB. Available online: https://ww2.mathworks.cn/ (accessed on 12 October 2019).
- Refprop9. Available online: http://www.nist.gov/srd/nist23.cfm (accessed on 12 October 2019).







| Parameter | Value | ||
|---|---|---|---|
| Model | Experiment | Relative Error | |
| (°C) | 31.53 | 32.7 | 3.58% |
| (°C) | 10 | 9.9 | 1.01% |
| (°C) | 59.68 | 59.4 | 0.47% |
| (°C) | 14.28 | 14.1 | 1.28% |
| Parameter | Value |
|---|---|
| Floor area | 384 m2 |
| Floor height | 3.3 m |
| Floor number | 10 |
| Total area | 3840 m2 |
| Cooling season | From April to October |
| Air conditioning operation period | 8:00–18:00 |
| Window-to-wall ratio | 0.5 |
| Space temperature control | 22–26 °C |
| Space humidity control | 40–60% |
| Occupant density in office/meeting room/rest room/corridor and lobby | 0.1/0.3/0.3/0.2 person/m2 |
| Sensible heat load regarding people in office/meeting room/rest room/corridor and lobby | 66/61/62/58 W/person |
| Humidity load regarding people in office/meeting room/rest room/corridor and lobby | 0.102/0.109/0.068/0.184 kg/(Hr·person) |
| Lighting power density | 9 W/m2 |
| Electrical equipment power density in office/meeting room/rest room/corridor and lobby | 18/11/5/11 W/m2 |
| Ventilation rate | 1 vol/h |
| Heat transfer coefficients of walls/windows/roof | 1.081/2.7/0.812 W/(m2K) |
| Parameters | Unit | Value |
|---|---|---|
| ETC→ | ||
| Aperture area | m2 | 270 |
| Outer diameter of absorber tube | m | 0.037 |
| Thickness of absorber tube | m | 0.0012 |
| Outer diameter of glass tube | m | 0.047 |
| Thickness of glass tube | m | 0.0012 |
| Outer diameter of U-tube | m | 0.008 |
| Thickness of air layer | m | 0.001 |
| Thickness of copper fin | m | 0.0006 |
| Length of the header pipe per one U-tube | m | 1.2 |
| Nominal hot water flow of collector | kg/s | 2.78 |
| Tilted angle | 20 | |
| Storage tank | ||
| Aspect ratio | 3.5 | |
| Heat loss coefficient | W/(m2 K) | 0.83 |
| Nominal hot water flow of generator | kg/s | 2.78 |
| Volume of storage tank | m3 | 2.7 |
| Absorption subsystem | ||
| Flow rate of cooling water in condenser 1/absorber/subcooler | kg/s | 2.5/2.2/2.9 |
| Inlet temperature of cooling water | °C | 32 |
| Nominal coefficient of performance (COP) | 0.73 | |
| Compression subsystem | ||
| Flow rate of cooling water in condenser 2 | kg/s | 27.3 |
| Inlet temperature of cooling water | °C | 32 |
| Inlet/outlet temperature of chilled water | °C | 12/7 |
| Isentropic efficiency of compressor | 0.7 | |
| Nominal COP | 4.26 |
| (°C) | Optimal Collector Outlet Set Temperature (°C) | ||||||
|---|---|---|---|---|---|---|---|
| Apr | May | Jun | Jul | Aug | Sept | Oct | |
| 65 | 75 | 75 | 75 | 75 | 75 | 75 | 75 |
| 75 | - | 83 | 83 | 83 | 83 | 84 | 83 |
| 85 | - | 94 | 94 | 94 | 94 | 95 | 94 |
| (kWh) | (kWh) | (kWh) | |||
|---|---|---|---|---|---|
| 73310.7 | 30854.7 | 8841.3 | 0.39 | 0.63 | 4.86 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, Z.; Chen, H.; Xu, Y. Effect of Hot Water Setting Temperature on Performance of Solar Absorption-Subcooled Compression Hybrid Cooling Systems. Appl. Sci. 2020, 10, 258. https://doi.org/10.3390/app10010258
Zhang J, Li Z, Chen H, Xu Y. Effect of Hot Water Setting Temperature on Performance of Solar Absorption-Subcooled Compression Hybrid Cooling Systems. Applied Sciences. 2020; 10(1):258. https://doi.org/10.3390/app10010258
Chicago/Turabian StyleZhang, Jinfang, Zeyu Li, Hongkai Chen, and Yongrui Xu. 2020. "Effect of Hot Water Setting Temperature on Performance of Solar Absorption-Subcooled Compression Hybrid Cooling Systems" Applied Sciences 10, no. 1: 258. https://doi.org/10.3390/app10010258
APA StyleZhang, J., Li, Z., Chen, H., & Xu, Y. (2020). Effect of Hot Water Setting Temperature on Performance of Solar Absorption-Subcooled Compression Hybrid Cooling Systems. Applied Sciences, 10(1), 258. https://doi.org/10.3390/app10010258





