Displacement-Dependent Damping Inerter System for Seismic Response Control

Abstract

Various inerter systems utilizing velocity-dependent damping for vibration control have been developed. However, a velocity-dependent damping element may exhibit relatively poor performance compared to a displacement-dependent damping element (DDE) of equivalent damping ratio, when the structural deformation is small in the early stage of the seismic response. To address this issue, the advantage of DDE in generating a larger control force in the early stage of excitation is promoted here and enhanced by a supplemental inerter-spring-system, thus realizing a proposed novel displacement-dependent damping inerter system (DDIS). First, the influence of various DDIS-parameters is carried out by resorting to the stochastic linearization method to handle non-linear terms. Then, seismic responses of the DDIS-controlled system are evaluated in the time domain taking the non-linearity into account, thus validating the accuracy of the stochastic dynamic analysis. Several design cases are considered, all of which demonstrated damping enhancement and timely control achieved by the DDIS. The results show that the energy dissipation as well as reduction of structural displacement and acceleration accomplished by the proposed system are significant. DDIS suppresses structural responses in a timely manner, as soon as the peak excitation occurs. In addition, it is demonstrated that interactions among the inerter, spring, and DDE, which constitute the damping-enhancement mechanism, lead to a higher energy-dissipation efficiency compared to the DDE alone.

1. Introduction

Structural control technology is proven to be effective in suppressing structural responses with the aid of various control devices and methods. Among these devices, inerter systems have been found to be very effective owing to their tuning frequency, mass enhancement, and damping enhancement mechanisms [1,2,3]. The performance evaluation and benefits of inerter-based systems for the protection of building structures [4,5,6,7,8], storage tanks [9,10,11], wind turbine towers [12,13,14], semi-submersible platform [15], and for vibration suppression of cables [16,17], machine [18] and suspension systems [19,20] have been studied in recent literature. An inerter is a mechanical element with two terminals [21,22,23,24,25] and ideally produces a resistive force proportional to its inner relative acceleration and large apparent mass designated as inertance. An essential property of the inerter is that a large inertance can be produced by devices with negligible physical masses. In the past, Kawamata [26] developed a vibration control device that used fluid inertance, which is designated as a mass pump, to suppress the seismic responses of a structure; this device has an inertial mass enhancement mechanism. Arakaki et al. [27,28] utilized the rotation mechanism to amplify the effective damping force of a viscous damper, which is a type of velocity-dependent damping element (VDE). However, these devices did not explicitly use the mass enhancement effect until Ikago et al. [1] proposed the tuned viscous mass damper, which belongs to a type of velocity-dependent damping inerter system (VDIS). The performance of the tuned viscous mass damper control system was subsequently investigated via shaking table tests conducted on single-story systems equipped with scaled-down versions of the damper [29]. Garrido et al. [30] proposed a rotational inertia double-tuned mass damper by replacing the viscous damping of the tuned mass damper with a tuned viscous mass damper, which achieved significantly greater control than the tuned mass damper with similar additional mass ratio. Through the incorporation of an electromagnetic damper, which is a type of VDE, Nakamura et al. [31] developed an electromagnetic inerter mass damper with variable damping force. Asai et al. [32,33] achieved enhanced energy-harvesting performance using a tuned inerter. Zhang et al. [10,34] proposed an isolation inerter system that used an inerter and a VDE to mitigate the vibration of a storage tank. The effect of the mechanical layout of the system was also investigated and considered in the development of a demand-based optimal design method for the system. Ikago et al. [1] presented the closed-form optimal design formulae for a VDIS based on the fixed-point method (an optimal design method to minimize the $H_{\infty }$ norm of the transfer function). On the basis of consideration of both the response mitigation effect and control cost, Pan et al. [35] proposed a demand-performance-based optimal design methodology for a structure equipped with a VDIS to achieve the desired seismic performance level from the primary structure. Pan and Zhang [36] subsequently derived a closed-form expression of the root-mean-square (RMS) response of a single-degree-of-freedom (SDOF) structure with three representative VDISs, namely, the series layout inerter system, series–parallel layout I inerter system (SPIS-I), and series–parallel layout II inerter system. Chen et al. [37] analyzed the effect of the soil-structure interaction on the vibration mitigation effect of a VDIS. Based on the determined effect, they proposed an optimal design method that utilized a simulated annealing algorithm.

As mentioned above, recent studies in the field have mainly focused on the development and optimal design of inerter systems that utilize VDEs for energy dissipation. As a classic example, the ball-screw inerter system utilizes fluid viscous damping, with the fluid fully filled into a small gap between the fixed inner cylinder and rotating outer cylinder connected to a ball screw [38]. However, the inertance of such a device cannot be adjusted or replaced once it is manufactured even if the mass enhancement ratio is found to be insufficient for vibration control afterwards. In addition, there is also a concern about the leakage risk of the damping fluid, with high pressure within the rotating cylindrical tube requiring thorough sealing of the device [39]. From the perspective of the constitutive relationship of the mechanical behavior, viscous damping and electromagnetic damping (mentioned earlier) are both VDE mechanisms, which means that the damping force is in-phase with the relative velocity of the VDE. Because the maximum displacement and maximum velocity never occur at the same time, there is an inevitable time difference between the maximum damping force and displacement [40,41]. Owing to this difference, the VDE would be incapable of mitigating the structural response greatly in the time domain if a peak response occurs in the early stage of excitation, which is generally true in most earthquake events. This sometimes unfavorable velocity dependence of a VDE can be replaced by a displacement-dependent damper that uses a displacement-dependent damping element (DDE) for energy dissipation, with the damping force directly depending on the relative deformation of the device [42]. Such systems are widely used because of their stable hysteretic behavior and relatively low production and maintenance costs. Kelly et al. [43] were the first to propose a displacement-dependent damper for vibration energy dissipation. Since then, considerable efforts [44,45,46,47] have been devoted to analyzing the dynamic behavior of structures controlled by displacement-dependent dampers and the design of these systems. There is no doubt that a displacement-dependent damper is effective for a vibration mitigation, theoretically as well as experimentally. In particular, this damper is preferentially chosen at the beginning of the excitation, based on the fact that displacement-dependent dampers reduce substantial displacements more effectively compared to viscous dampers with equivalent damping ratios (meaning that the energy dissipated per cycle for DDE and VDE [42] is the same). However, the energy dissipation effect of the damper is limited when the deformation in a DDE is small, especially in the early stage of shaking, in a seismic event. The main contribution of the tuned inerter in a displacement-dependent damping inerter system (DDIS) is to amplify the deformation in a DDE to ensure efficient energy dissipation during the early stage of excitation.

Based on these motivations, a novel DDIS is developed that overcomes the aforementioned drawbacks of the VDIS. The proposed DDIS consists of an inerter, a DDE, and a spring. Stochastic dynamic analysis of a structure equipped with the DDIS system is performed, considering a base acceleration modeled with a Kanai–Tajimi power spectral density function. The stochastic linearization technique is used to handle the non-linear terms. It is demonstrated that DDIS combines the advantageous properties of DDE and inerter in a single layout. The structural displacement, acceleration, and energy dissipation mitigation indices are determined from the stochastic analysis results and used to establish an evaluation method for the dynamic performance of the DDIS-equipped structure. A broad parametric analysis is performed within the evaluation framework, taking into consideration the effects of non-linearity of the DDIS and variability of its parameters. Finally, several design cases in the time domain are presented to illustrate the damping enhancement and quick-control provided by the proposed DDIS.

2. Theoretical Analysis of Displacement-Dependent Damping Inerter System (DDIS)

2.1. Mechanical Model

The inerter (in Figure 1) is a mechanical element that ideally provides a force proportional to its inertance $m_{in}$ (having dimensions of mass) and relative acceleration between its two terminals. Experimental research works show that the inertance can be amplified thousands of times that of the physical mass of the inerter [48], proving that the inerter is a very effective vibration mitigation device owing to this mass enhancement effect. A series of physical realizations have been proposed for the construction of the inerter, such as the rack-pinion [21], the ball screw [1], the fluid [49], and the electromagnetic mechanisms [50]. In the ideal model of the inerter, the output force of the inerter $F_{in}$ is given by [51,52,53,54,55,56]:

$$F_{in}=m_{in}\left({\ddot{u}}_1-{\ddot{u}}_2\right)$$

(1)

where ${\ddot{u}}_1$ and ${\ddot{u}}_2$ are the respective accelerations of the two terminals.

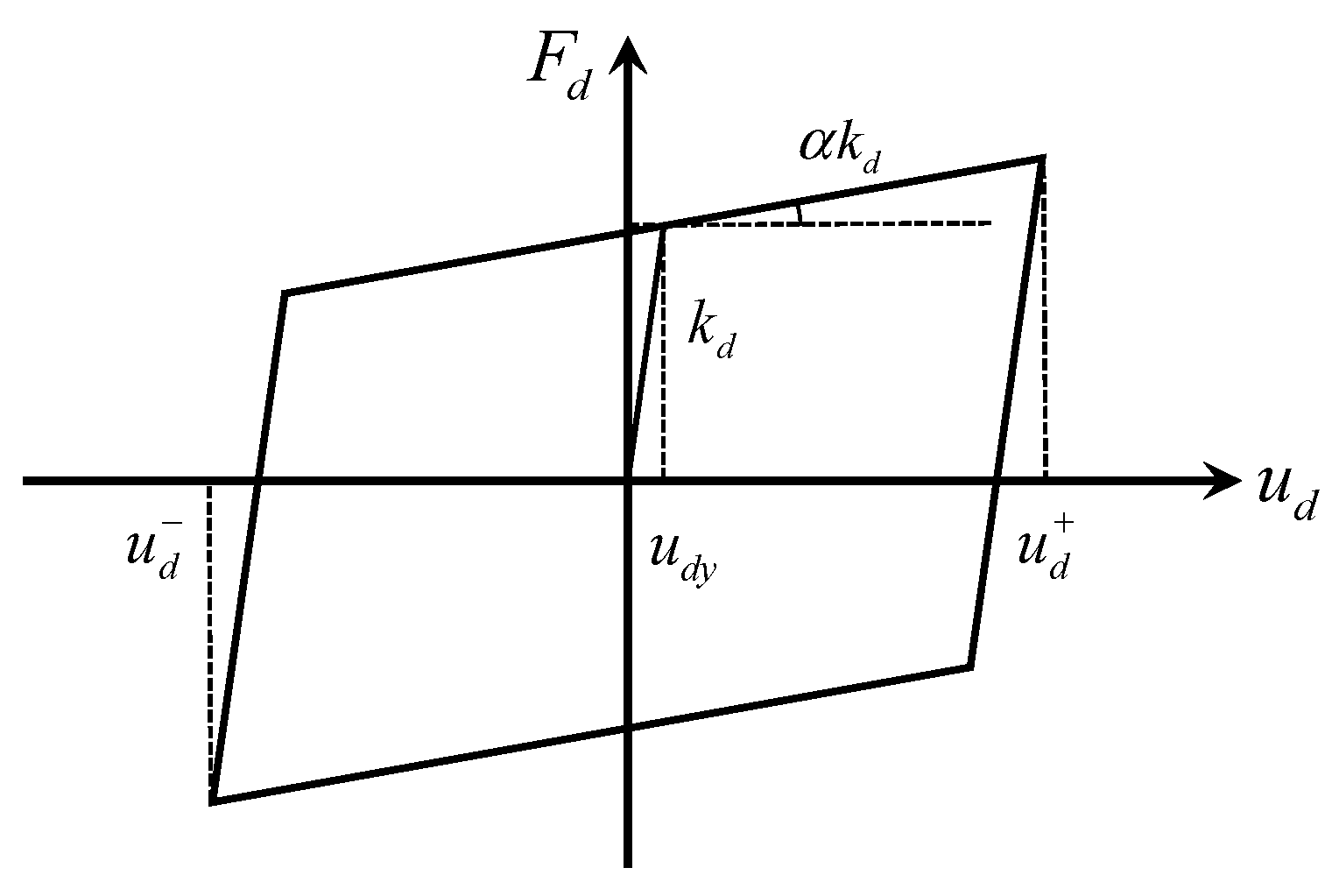
2.1.1. Model of Displacement-Dependent Damping Element (DDE)

The damping force of the DDE is dependent on the displacement rather than on the velocity response, and it is characterized by a stable and non-degrading mechanical behavior. The DDE is of significant engineering interest; several control devices have been proposed, which exploit the DDE characteristics (such as shape-memory alloys, wire-cable isolators, metallic dampers, and friction-based dampers) [45,46]. The bilinear model in Figure 2 is widely used to describe the DDE and give it a clear and simple physical meaning. When this model is used to represent the force-deformation relationship of the DDE, the restoring force $F_d$ is given by:

$$F_d\left(u_d,z_d\right)=\alpha k_d{u}_d+\left(1-\alpha \right)k_d{z}_h$$

(2)

where $k_d$ is the initial stiffness of the DDE, $\alpha$ is the ratio of the post-yielding stiffness to pre-yielding stiffness, $u_{dy}$ is the elastic limit displacement or yielding displacement of the corresponding bilinear model, and $u_d$ and $z_h$ are the deformation of the DDE and the hysteretic variable, respectively, which are related as follows:

$${\dot{z}}_h={\dot{u}}_d\left[\left(1-\mathrm{sgn}\left({\dot{u}}_d\right)\mathrm{sgn}\left(z_h-u_{dy}\right)-\mathrm{sgn}\left(-{\dot{u}}_d\right)\mathrm{sgn}\left(-z_h-u_{dy}\right)\right)\right]$$

(3)

where $\mathrm{sgn}(\cdot )$ is the signum function.

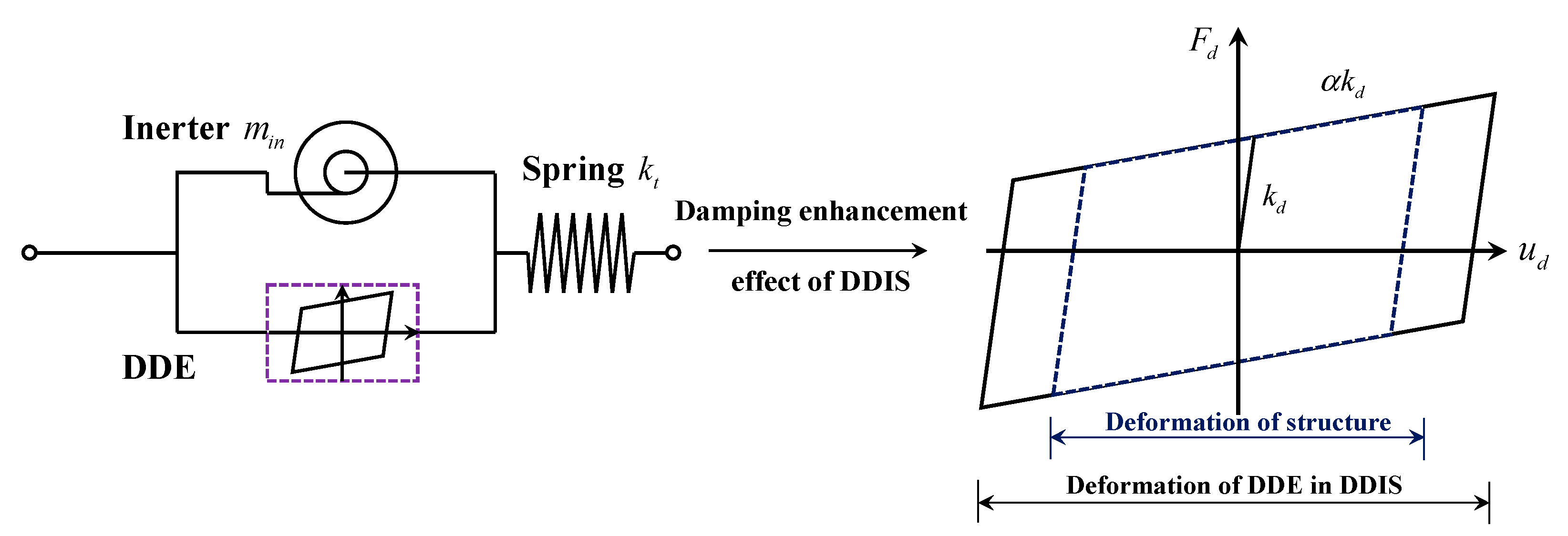
2.1.2. Model of DDIS

As depicted in Figure 3, the proposed DDIS consists of an inerter, a DDE, and a spring, where $k_t$ denotes the stiffness coefficient of the spring. In the DDIS, the inerter and DDE are mounted in parallel and are deployed in series with the spring. The supplemental vibratory system consisting of the spring and inerter is tuned to the primary structural frequency, resulting in enhanced energy absorption. Unlike the conventional VDIS in which the viscous damping element is used only for energy dissipation, the DDE of the DDIS provides both energy dissipation and additional stiffness, which further reduces the structural response. The mass enhancement effect [1] of the inerter ensures efficient energy absorption in the DDE without implying an additional weight. And the implements of the spring and inerter constitute the damping enhancement mechanism to dissipate more energy since the DDE deformation of DDIS is amplified and larger than the displacement of controlled structure (Figure 3). The detailed explanation of the intrinsic benefit of the DDIS is given in Section 3.2 and Section 4.1.

2.2. Equations of Motion

As shown in Figure 4, a DDIS is incorporated into an SDOF frame structure having mass $m$, stiffness $k$, and damping coefficient $c$. The governing equation for the present system can be expressed as follows:

$$\{\begin{array}{l}m\ddot{u}\left(t\right)+c\dot{u}\left(t\right)+ku\left(t\right)+k_t\left[u\left(t\right)-u_d^{}\left(t\right)\right]=-m{\ddot{u}}_g\left(t\right)\\ m_{in}^{}{\ddot{u}}_d^{}\left(t\right)+F_d\left(t\right)=k_t\left[u\left(t\right)-u_d^{}\left(t\right)\right]\end{array}$$

(4)

where ${\ddot{u}}_g(t)$ represents the acceleration of the ground motion, and $u\left(t\right)$ and $u_d\left(t\right)$ are respectively the displacement of the primary structure relative to the ground and deformation of the DDE. The force $F_d$ is given by Equation (2).

2.3. Stochastic Dynamic Analysis and Stochastic Linearization Method

Considering the uncertain nature of the seismic excitation, the acceleration of the applied ground motion ${\ddot{u}}_g$ in Equation (4) is modeled as a random process. The Kanai–Tajimi filtered white-noise process is adopted as excitation, as it has been widely employed in previous studies [35,57]. Denoting the bedrock white noise process as $W\left(t\right)$, the differential equation of the Kanai–Tajimi model can be established in time domain as follows:

$${\ddot{u}}_g\left(t\right)=-{\omega }_g^2{u}_g\left(t\right)-2{\xi }_g^{}{\omega }_g^{}{\dot{u}}_g\left(t\right)+W\left(t\right)$$

(5)

where ${\omega }_g\left(t\right)$ and ${\xi }_g\left(t\right)$ are, respectively, the fundamental circular frequency and damping ratio related to the soil characteristics. The power spectral density function corresponding to the Kanai–Tajimi model is as follows:

$$S_{{\ddot{u}}_g}\left(\omega \right)=\frac{{\omega }_g^4+4{\xi }_g^2{\omega }_g^2{\omega }_{}^2}{{\left({\omega }_g^2-{\omega }_{}^2\right)}^2+4{\xi }_g^2{\omega }_g^2{\omega }_{}^2}{S}_w$$

(6)

where $S_w$ is the power spectral density of the white noise excitation [58]. A relationship between $S_w$ and the peak ground acceleration was introduced in [59].

The solution of the governing equations of motion in Equation (4) is a non-linear problem owing to the non-linear restoring force of the bilinear model. Linear random vibration theory is thus not applicable. In this section, the stochastic linearization method (SLM) [60] is applied to solve Equation (4) using an equivalent linear–viscous damping $c_{eq}$ and a linear stiffness coefficient $k_{eq}$ to represent the bilinear model. Equation (4) can thus be rewritten in terms of SLM as follows:

$$\{\begin{array}{l}M\ddot{u}+C\dot{u}+Ku+r=EM{\ddot{u}}_g\left(t\right)\\ {\dot{z}}_h\left(t\right)+c_{eq}{\dot{u}}_d\left(t\right)+k_{eq}{z}_h\left(t\right)=0\end{array}$$

(7)

where,

$$\begin{array}{l}M=\left[\begin{array}{cc}m& 0\\ 0& m_{in}\end{array}\right],C=\left[\begin{array}{cc}c& 0\\ 0& 0\end{array}\right],K=\left[\begin{array}{cc}k+k_t& -k_t\\ -k_t& \alpha k_d+k_t\end{array}\right],\\ r=\left[\begin{array}{c}0\\ \left(1-\alpha \right)k_d{z}_h\end{array}\right],E=\left[\begin{array}{c}1\\ 0\end{array}\right]\end{array}$$

(8)

and $u={\left\{u,u_d\right\}}^T$ is the displacement vector. Here, $c_{eq}$ and $k_{eq}$ are determined by an equivalence principle [61,62], minimizing the squared error between the linearized Equation (7) and non-linear Equation (4), which leads to:

$$c_{eq}=\mathrm{E}\left[\frac{\partial F_d\left(u_d,z_h\right)}{\partial {\dot{u}}_d}\right],k_{eq}=\mathrm{E}\left[\frac{\partial F_d\left(u_d,z_h\right)}{\partial z_h}\right]$$

(9)

where $\mathrm{E}\left[\right]$ denotes the expectation operator to obtain the mean value. The coefficients $c_{eq}$ and $k_{eq}$ of the bilinear model resulting from Equation (9) are given by [61,62]

$$\begin{array}{l}{c}_{eq}=\left\{\begin{array}{l}-\frac{1}{2}\left[1+erf\left(\frac{u_{dy}}{\sqrt{2}{\sigma }_{z_h}}\right)\right]\\ +\frac{1}{{\sigma }_{z_h}\sqrt{2\pi }}{\displaystyle {\int }_{u_{dy}/\left(\sqrt{2}{\sigma }_{z_h}\right)}^{\infty }erf\left(\frac{{\rho }_{{\dot{u}}_d{z}_h}{z}_h/\left(\sqrt{2}{\sigma }_{z_h}\right)}{\sqrt{1-{\rho }_{{\dot{u}}_d{z}_h}}}\right)}\cdot \exp \left[-\frac{z_h^2}{2{\sigma }_{z_h}^2}\right]d{z}_h\end{array}\right\}\\ k_{eq}=\left\{\begin{array}{l}\frac{{\rho }_{{\dot{u}}_d{z}_h}{\sigma }_{{\dot{u}}_d}{u}_{dy}}{\sqrt{2\pi }{\sigma }_{z_h}^2}{\sigma }_{z_h}\exp \left[-\frac{u_{dy}^2}{2{\sigma }_{z_h}^2}\right]\left\{1+erf\left(\frac{{\rho }_{{\dot{u}}_d{z}_h}{u}_{dy}}{{\sigma }_{z_h}^{}\sqrt{2\left(1-{\rho }_{{\dot{u}}_d{z}_h}^2\right)}}\right)\right\}\\ +\frac{\sqrt{2\left(1-{\rho }_{{\dot{u}}_d{z}_h}^2\right)}}{\pi }\frac{{\sigma }_{{\dot{u}}_d}}{{\sigma }_{z_h}^{}}\exp \left[-\frac{u_{dy}^2}{2{\sigma }_{z_h}^2}\right]\exp \left[\frac{{\rho }_{{\dot{u}}_d{z}_h}^2{u}_{dy}^2}{{\sigma }_{z_h}^{2}2\left(1-{\rho }_{{\dot{u}}_d{z}_h}^2\right)}\right]\end{array}\right\}\end{array}$$

(10)

where ${\sigma }_{z_h}^{}$ and ${\sigma }_{{\dot{u}}_d}$ are respectively the RMS of hysteretic deformation $z_h$ and the RMS of the DDE velocity ${\dot{u}}_d$; ${\rho }_{{\dot{u}}_d{z}_h}$ is the correlation ratio of ${\dot{u}}_d$ and $z_h$, and $erf$ is the error function given by

$$erf\left(y\right)=\frac{2}{\sqrt{\pi }}{\displaystyle {\int }_0^y{e}^{-s^2}}ds$$

(11)

Using the SLM, the expected stochastic response can be approximated as a zero-mean Gaussian process under Gaussian excitation. Based on the Laplace transformation, the governing equation in Equation (7) can be rewritten as:

$$\{\begin{array}{l}\left(-{\omega }^{2}M+\mathrm{i}\omega C+K\right)U+R=EM{A}_g\left(\mathrm{i}\omega \right)\\ Z_h\left(\mathrm{i}\omega \right)\mathrm{i}\omega +c_{eq}{U}_d\left(\mathrm{i}\omega \right)\mathrm{i}\omega +k_{eq}{Z}_h\left(\mathrm{i}\omega \right)=0\end{array}$$

(12)

where $U={\left\{U,U_d\right\}}^T$ and $R={\left\{0,\left(1-\alpha \right)k_d{Z}_h\right\}}^T$ are the Laplace transformations of $u$ and $r$, respectively; $U_d$, $A_g$, and $Z_h$ are the Laplace transformations of $u_d$, ${\ddot{u}}_g$, and $z_h$, respectively. An inspection of Equations (10) and (12) reveals that the determination of $c_{eq}$ and $k_{eq}$ is not straightforward, since they implicitly depend upon the unknowns ${\sigma }_{z_h}^{}$, ${\sigma }_{{\dot{u}}_d}$, and ${\rho }_{{\dot{u}}_d{z}_h}$. Therefore, the values of $c_{eq}$ and $k_{eq}$ are determined by an interactive process, wherein Equation (12) is solved in an iterative manner given an initial guess.

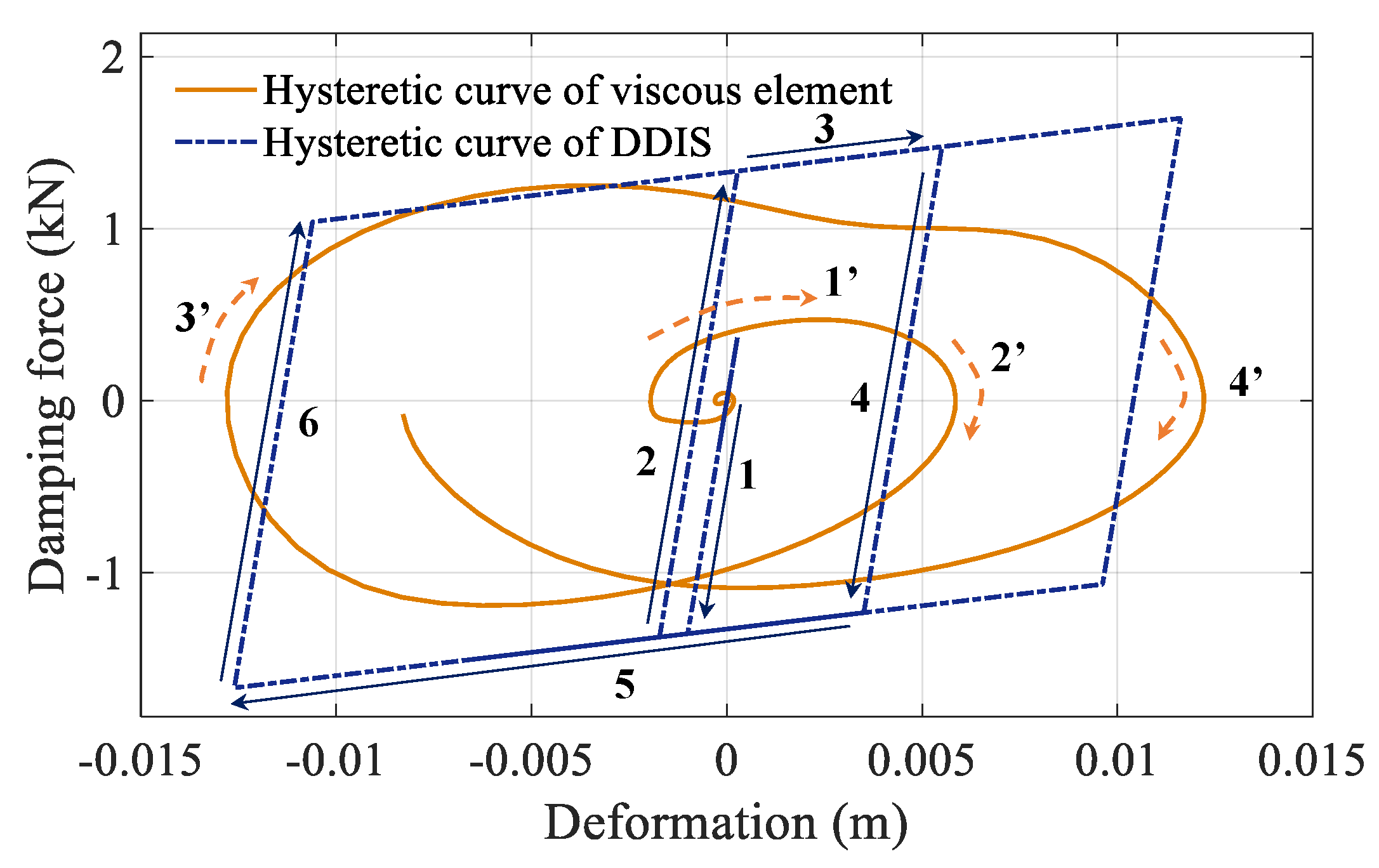
2.4. Energy Balance Analysis

From the perspective of energy balance evaluation, a part of the excitation-induced input vibrational energy is dissipated by the primary structure, and the rest is dissipated by the DDIS via the DDE. Equation (7) can be used to calculate the energy balance in the SDOF structure equipped with the DDIS by premultiplying with $u^T$ and integrating over the time domain. The energy balance equation in the time domain is given by:

$$e_{total}\left(t\right)=e_k\left(t\right)+e_{e,s}\left(t\right)+e_d\left(t\right)+e_{DDIS}\left(t\right)$$

(13)

where the total input energy $e_{total}\left(t\right)$ is composed of structural kinetic energy $e_k\left(t\right)$, structural elastic strain energy $e_{e,s}\left(t\right)$, structural inherent damping dissipated energy $e_d\left(t\right)$, and DDIS-dissipated energy $e_{HDIS}\left(t\right)$. With particular regard to the three elements of the DDIS, $e_{DDIS}\left(t\right)$ is the result of kinetic energy $e_{k,DDIS}\left(t\right)$, elastic strain energy $e_{e,DDIS}\left(t\right)$, and DDE-dissipated energy $e_{d,DDIS}\left(t\right)$. Because the input excitation is assumed to be a stochastic process, the energy response should be evaluated stochastically by applying the expectation operator to Equation (13). On the basis of the stationarity hypothesis, the expected values of $e_{e,DDIS}\left(t\right)$, $e_{k,DDIS}\left(t\right)$, $e_k\left(t\right)$, and $e_{e,s}\left(t\right)$ are all zero. Hence, the stochastically expected value of Equation (13) is given by:

$$\mathrm{E}\left[e_{total}\left(t\right)\right]=\mathrm{E}\left[e_d\left(t\right)\right]+\mathrm{E}\left[e_{d,DDIS}\left(t\right)\right]=c{\sigma }_{\dot{u}}^2+\left(1-\alpha \right)k_d{\sigma }_{z_h{\dot{u}}_d}$$

(14)

where ${\sigma }_{\dot{u}}^2$ and ${\sigma }_{z_h{\dot{u}}_d}$ are respectively the variance of the structural velocity and the cross-variance of $z_h$ and ${\dot{u}}_d$.

3. Characteristics of DDIS

3.1. Stochastic Performance Indices

To characterize the dynamic performance of the SDOF structure equipped with DDIS and further evaluate the vibration mitigation effect of the DDIS, different stochastic performance indices are introduced. First, the dimensionless parameters of the DDIS are defined, including the inertance–mass ratio $\mu$, DDE stiffness ratio $\kappa$, and stiffness ratio $\lambda$:

$$\mu =\frac{m_{in}}{m},\kappa =\frac{k_t}{k},\lambda =\frac{k_d}{k}$$

(15)

The commonly used index is the displacement mitigation ratio ${\gamma }_{Dis}$, which is the ratio of the RMS displacement of the structure–DDIS system ${\sigma }_{Dis,SDOF-DDIS}^{}$ to that of the original structure ${\sigma }_{Dis,SDOF}^{}$. Another index is the acceleration mitigation ratio ${\gamma }_{Acc}$, which is the ratio of the RMS acceleration of the structure–DDIS system ${\sigma }_{Acc,SDOF-DDIS}^{}$ to that of the original structure ${\sigma }_{Acc,SDOF}^{}$. The parameters ${\gamma }_{Dis}$ and ${\gamma }_{Acc}$ are, therefore, defined as follows:

$$\begin{array}{l}{\gamma }_{Dis}\left(\mu ,\kappa ,\lambda ,\alpha ,u_{dy}\right)=\frac{{\sigma }_{Dis,SDOF-DDIS}^{}}{{\sigma }_{Dis,SDOF}^{}},\\ {\gamma }_{Acc}\left(\mu ,\kappa ,\lambda ,\alpha ,u_{dy}\right)=\frac{{\sigma }_{Acc,SDOF-DDIS}^{}}{{\sigma }_{Acc,SDOF}^{}}\end{array}$$

(16)

However, an energy-based performance index is more robust against various types of input ground motion than displacement- and acceleration-based performance indices. Referring to the energy balance in Equation (14), the excitation-induced input energy is eventually dissipated by the structural inherent damping and DDE of the DDIS. The portion of the energy dissipated by the DDE is maximized, whereas the portion filtered into the primary structure and dissipated by the structural inherent damping should be minimized. A filtered energy ratio γ_E is thus defined here to quantify the portion of energy dissipated by DDIS out of the total input energy:

$$\begin{array}{ll}{\gamma }_E\left(\mu ,\kappa ,\lambda ,\alpha ,u_{dy}\right)& =\frac{\mathrm{E}\left[e_{total}\left(t\right)\right]-\mathrm{E}\left[e_{d,DDIS}\left(t\right)\right]}{\mathrm{E}\left[e_{total}\left(t\right)\right]}\\ & =1-\frac{\left(1-\alpha \right)k_d{\sigma }_{z_h{\dot{u}}_d}}{c{\sigma }_{\dot{u}}^2+\left(1-\alpha \right)k_d{\sigma }_{z_h{\dot{u}}_d}}\end{array}$$

(17)

A low value of ${\gamma }_E$ indicates that only a small portion of the vibrational energy is filtered into the primary structure, indicating the energy dissipation efficiency of the DDIS.

3.2. Parametric Analysis of DDIS

A thorough parametric analysis is conducted using ${\gamma }_{Dis}$, ${\gamma }_{Acc}$, and ${\gamma }_E$ as performance evaluation indices. The three indices are directly related to the design parameters of the DDIS, which contain $\mu$, $\kappa$, $\lambda$, $\alpha$, and $u_{dy}$.

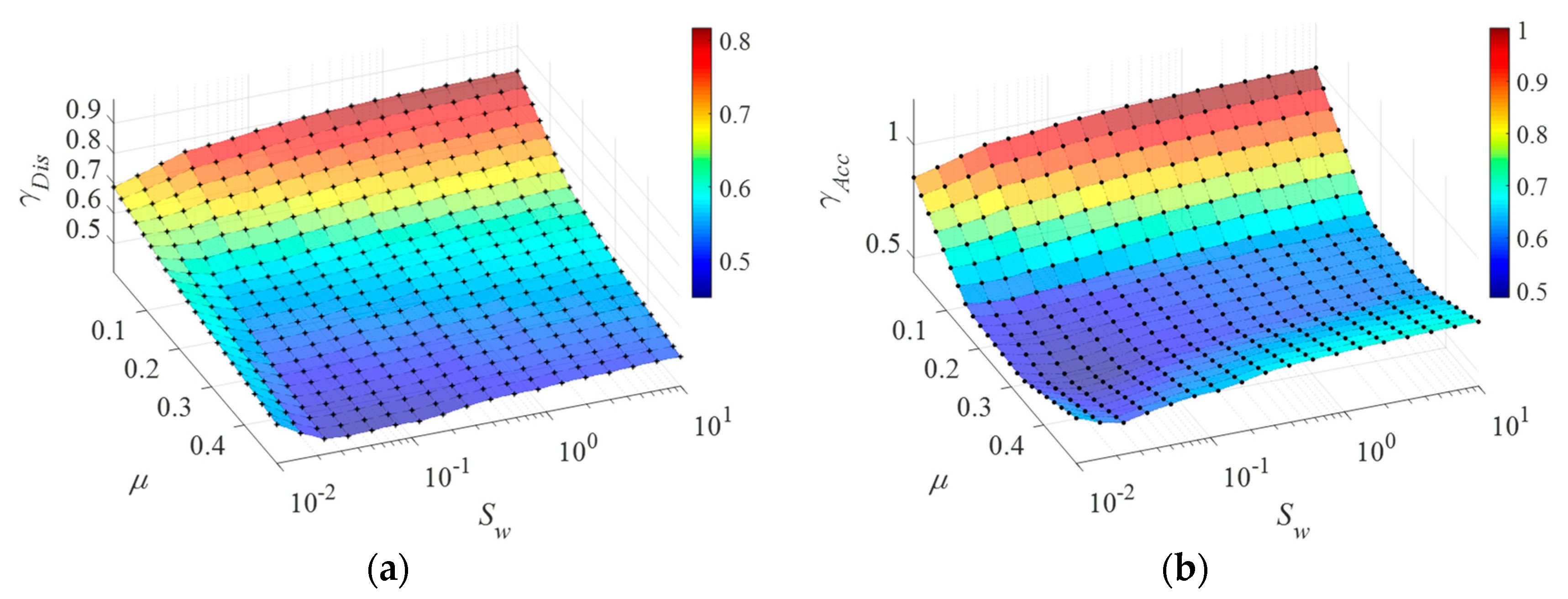
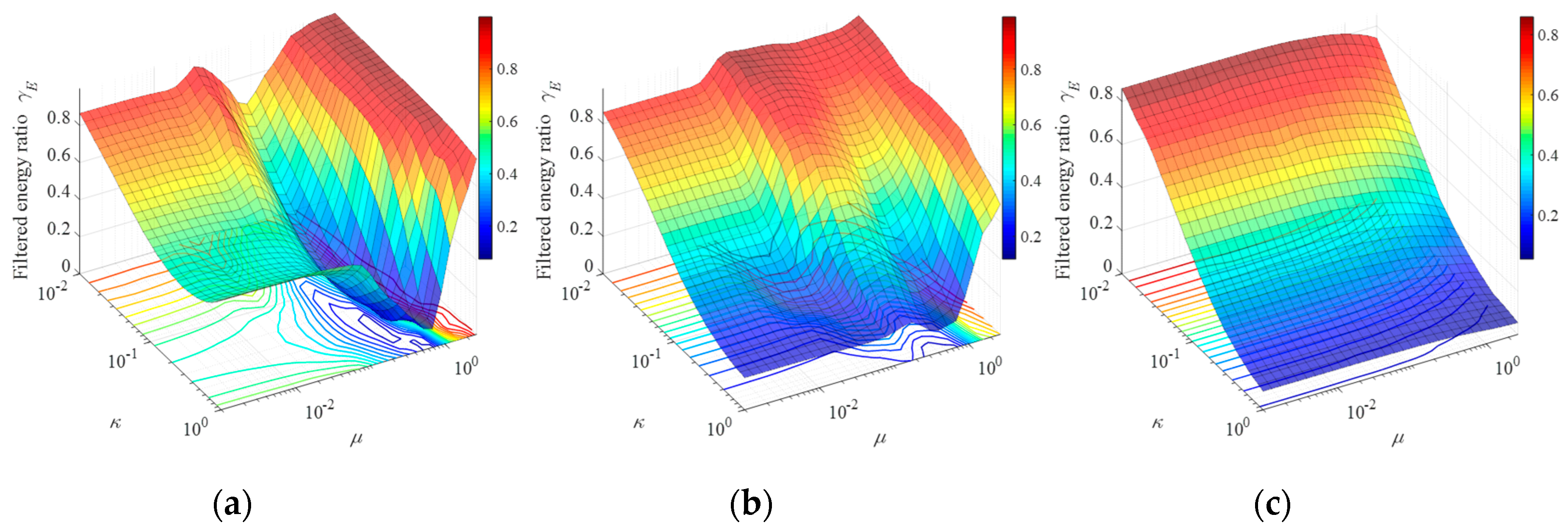
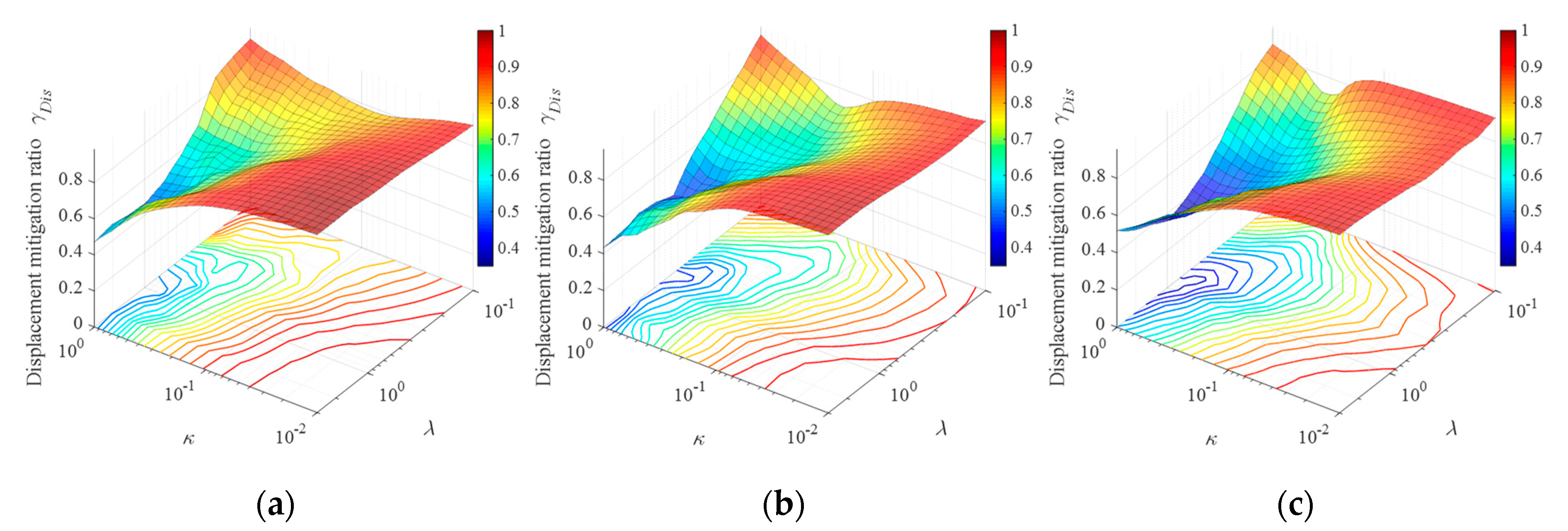
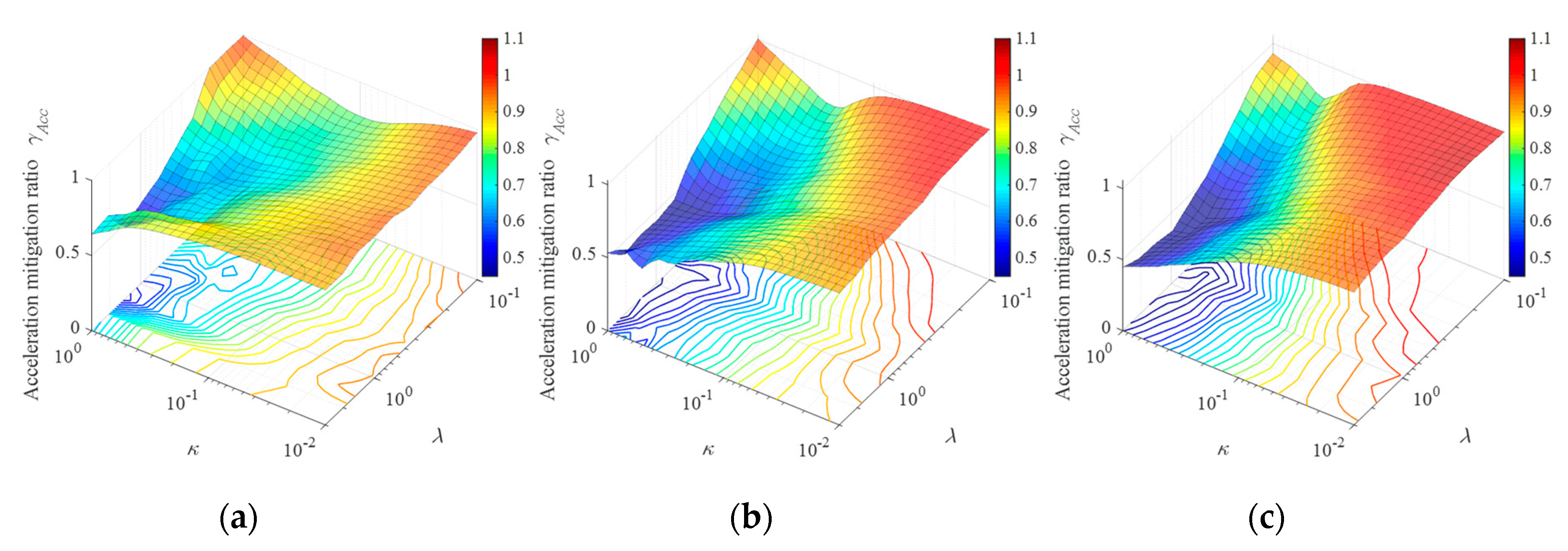
3.2.1. Influence of Excitation Severity

The performance evaluation of the structure equipped with the DDIS is a non-linear problem because of the signum function, and it is definitely influenced by the severity of the external excitation. In this section, the power spectrum density is considered as the Kanai–Tajimi model; whereas, the magnitude of $S_w$ varies in a wide range. A single-span, single-floor, SDOF frame structure is used for the parametric analysis, which is characterized by mass $m=20\mathrm{ton}$, fundamental natural period $T=0.54\mathrm{s}$, and inherent damping ratio $\zeta =0.02$. Regarding the bilinear model of the DDIS, $\alpha$ and $u_{dy}$ were assumed to be 0.02 and 0.001 m [44], respectively.

Figure 5 illustrates the variation pattern of the effect of ${\gamma }_{Dis}$ and ${\gamma }_{Acc}$ against the change of $S_w$, where $\mu$ of DDIS increases from 0 to 0.50. The increase of $S_w$ affects the structural response and the extent to which the non-linear effects of DDIS are triggered, which leads to the increase of ${\gamma }_{Dis}$ and ${\gamma }_{Acc}$. In terms of the special case, i.e., a stiff-supported DDE ($\mu =0$), the correspondingly minimum ${\gamma }_{Dis}$ and ${\gamma }_{Acc}$ are quantified as 0.68 and 0.85, respectively. For any specific value of $S_w$, the proposed DDIS exhibits an improved vibration mitigation effect compared with the displacement-dependent damper (which is represented by the limit case of DDIS having $\mu =0$). Although ${\gamma }_{Dis}$ and ${\gamma }_{Acc}$ of DDIS vary with the excitation severity, the advantage of DDIS over the displacement-dependent damper is definitely true for different levels of excitation severity. Furthermore, once the DDIS meets the target demand of vibration control under the excitation for the upper limit of concerned severity, it will be more effective for vibration mitigation when subjected to the excitation with lower severity ($S_w>0.02$).

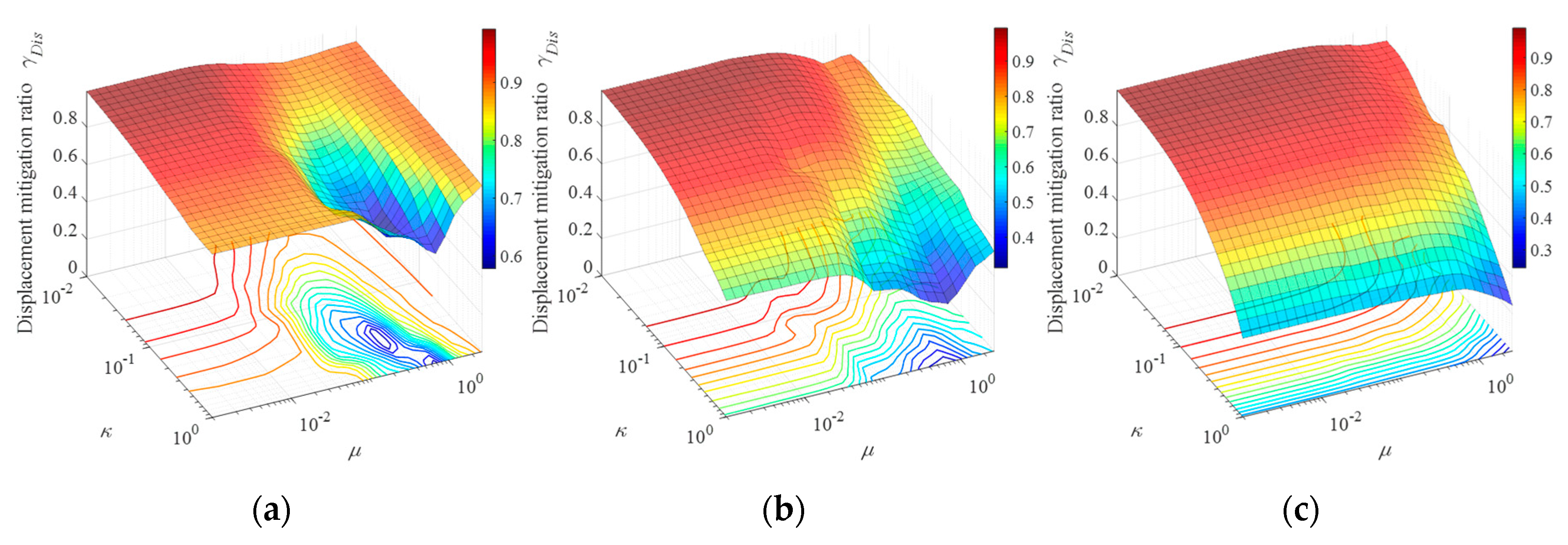
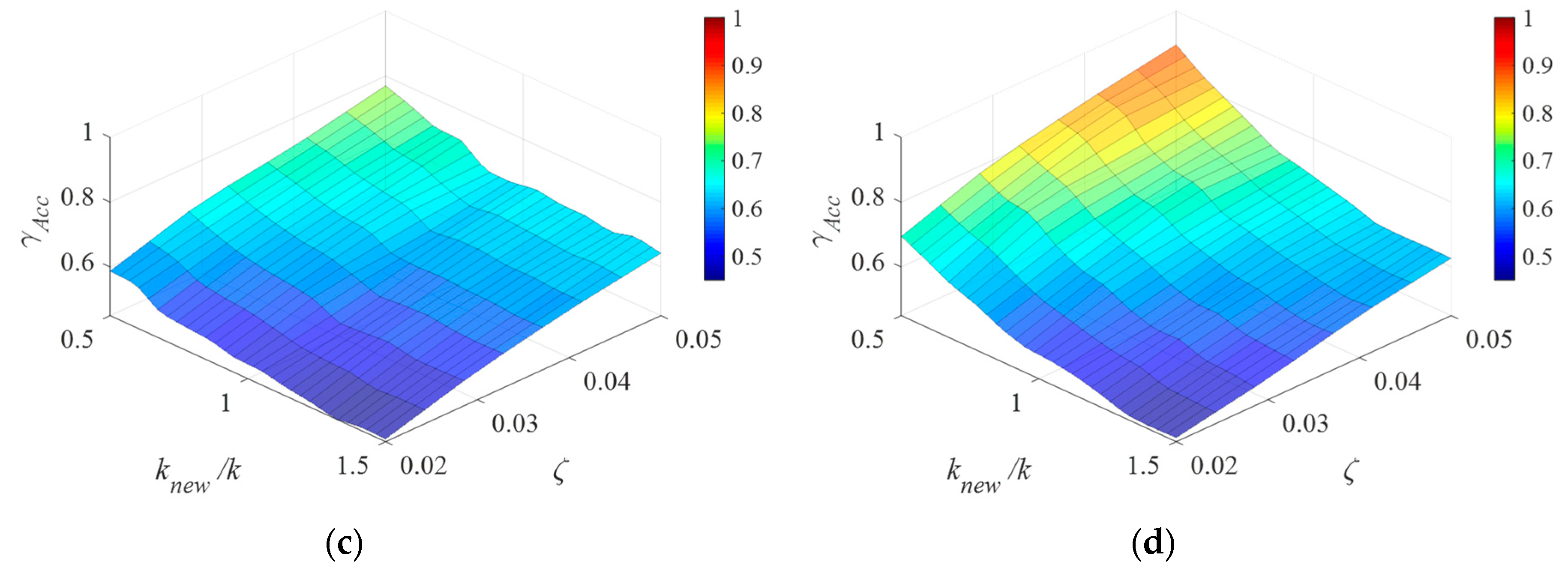
3.2.2. Influence of DDIS Parameters

In this section, several cases are considered to demonstrate the vibration mitigation effect of the DDIS, with $\kappa$ varying in the range of 10⁻²–1.00, and $\mu$ varying in the range of 10⁻³–3.00. $\lambda$ is set to 0.20, 1.00, and 1000.00 to simulate low, medium, and high stiffness of the support (i.e., the spring), respectively. A broad-band stochastic excitation is adopted, with ${\omega }_g$ = 15, and ${\xi }_g$ = 0.60 [57,63] to simulate the commonly used firm soil condition. The analysis results of ${\gamma }_{Dis}$,${\gamma }_{Acc}$, and ${\gamma }_E$ are summarized in Figure 6, Figure 7 and Figure 8, respectively.

As expected, the displacement performance of the structure-DDIS system, ${\gamma }_{Dis}$, gradually decreases with the increase in hysteretic stiffness ratio $\kappa$, especially for medium and rigid stiffness of the support. Similar to a conventional displacement-dependent damper, an increase in $\kappa$ implies greater stiffness of the primary structure to resist vibration, and hence, decreased structural displacement through increased non-linear damping. As can be observed from the surf plots in Figure 6, a decrease in $\mu$ is accompanied by an increase in ${\gamma }_{Dis}$. Considering the specific case in which $\mu$ decreases to zero, the DDIS degenerates into a conventional displacement-dependent damper with a stiff support. The proposed DDIS thus provides much greater displacement mitigation through the tuning effect of the spring and the energy storage effect of the inerter.

Regarding the acceleration mitigation ratio ${\gamma }_{Acc}$, Figure 7 shows that, for the DDIS with a tunable spring (Figure 7a,b), a medium inertance ($\mu \approx 0.50$) is beneficial to the mitigation of the acceleration response, while a small $\kappa$ ($<0.05$) and large inertance ($\mu >1.0$) have a detrimental effect. This can be attributed to a weak DDE being incapable of timely dissipation of the large amount of energy stored by a large inerter, with the energy filtering into the primary structure. Figure 7a shows that when the DDE and inerter are set in parallel with a low-stiffness spring, the supplemental inerter substantially decreases the structural acceleration effectively. For the DDIS without a tunable spring (Figure 7c), the significant reduction of structural acceleration (small ${\gamma }_{Acc}$) is reached at a high price of large inertance ($\mu >1.0$).

With regard to ${\gamma }_E$, Figure 8 shows that an increase in $\kappa$ ($\kappa \in [0.01,1.0]$) causes a decrease in ${\gamma }_E$, implying greater dissipation of vibrational energy by a large DDE ($\kappa >0.50$), with less energy filtering into the primary structure. Regarding the effect of the added inerter, an increase in inertance decreases ${\gamma }_E$, especially when the DDIS springs are tunable stiffness ($\lambda <1.0$). From the perspective of energy dissipation, the application of the inerter enhances the energy dissipation and vibration mitigation effect of the DDIS compared with only a stiff-supported DDE identical to that used in the system. For the DDIS without a tunable spring (Figure 8c), this benefit of the inerter is not evident. The damping enhancement effect of the proposed DDIS may be attributed to its combination mechanism in which the spring is used to tune the frequency of the inerter to improve energy absorption. This fundamental mechanism of the DDIS provides an alternative explanation of its advantage over a DDE identical to that utilized in the system.

An additional parametric analysis is conducted to investigate the effect of the variation of the mechanical parameters of the DDIS on its performance (evaluated with respect to $\kappa$ and $\lambda$). The corresponding surfs plots are shown in Figure 9 and Figure 10, which consider wide ranges of $\kappa$ and $\lambda$ values. The other mechanical parameters are the same as in the earlier parametric analysis. Non-zero values of $\mu$: 0.10, 0.20, and 0.30, are assumed for the DDIS. As the inertance-mass ratio increases from 0.10 to 0.30, the displacement and acceleration mitigation effects of the DDIS substantially increase. The minimum displacement and acceleration responses coincide with the areas that have the upper boundary of $\kappa$ and $\lambda \approx 1.0$. This is ascribed to the almost negligible deformation of the high-stiffness support (i.e., large $\lambda$), resulting in the vibration energy being rapidly and directly transferred to and dissipated by the DDE. It can be deduced from the surf plots that the DDIS is not sensitive to change in $\kappa$ and $\lambda$, because the surf plots in a blue zone that indicates the low value of the displacement and acceleration responses change slowly when the parameters ($\kappa$ and $\lambda$) vary rapidly. This indicates that a decrease in $\kappa$ and $\lambda$ does not considerably reduce the structural performance, including the acceleration and displacement responses. Furthermore, increasing the inertance makes the DDIS more effective for vibration control, in positive association with the increased energy storage provided by a larger inertance. Referring to the results of parametric analysis, it is suggested to design the DDIS with a medium inertance-mass ratio ($\mu \approx 0.5$), a large DDE $\kappa \ge 0.5$, and a tunable spring ($\lambda \le 1.0$).

3.2.3. Influence of Structural Parameters

Physical and model uncertainty of the primary structure may cause the practical behavior of the DDIS to deviate from theoretical expectations. The sensitivity of the vibration control effect of the DDIS to uncertainties of the primary structure is also worth analyzing. Therefore, the stiffness of the primary structure was considered to be variable owing to errors yielded by imprecise construction and deterioration during service.

Figure 11 illustrates the effect of the variation of $k_{new}/k$ and $\zeta$ on the vibration control effect (i.e., ${\gamma }_{Dis}$ and ${\gamma }_{Acc}$) of the DDIS, where $k_{new}$ is the changed stiffness of the SDOF frame structure mentioned in Section 3.2.1. The $k_{new}$ is set in the range of 50% variation of the stiffness $k$ of SDOF frame structure. The increase of $\mu$ from 0.00 to 0.40 causes the displacement-dependent damper to evolve into the proposed DDIS with a larger inertance. In accordance with the earlier analysis, the structural responses ${\gamma }_{Dis}$ and ${\gamma }_{Acc}$ of the SDOF structure equipped with the DDIS are all lower than those equipped with the displacement-dependent damper, implying that the addition of the inerter improves the structural performance. This improvement is observed in structures with different stiffness and is not significantly affected by a rapid change of $k_{new}$. For instance, in Figure 11 and Figure 12b–d ($\mu =0.10,0.25,0.40$, respectively), the degradation of $k_{new}$ and increase of $\zeta$ diminishes the acceleration mitigation effect of the DDIS to some extent; however, ${\gamma }_{Dis}$ and ${\gamma }_{Acc}$ still remain lower than those for the displacement-dependent damper depicted in Figure 11a and Figure 12a.

4. Non-Linear Time-History Analysis and Performance of DDIS

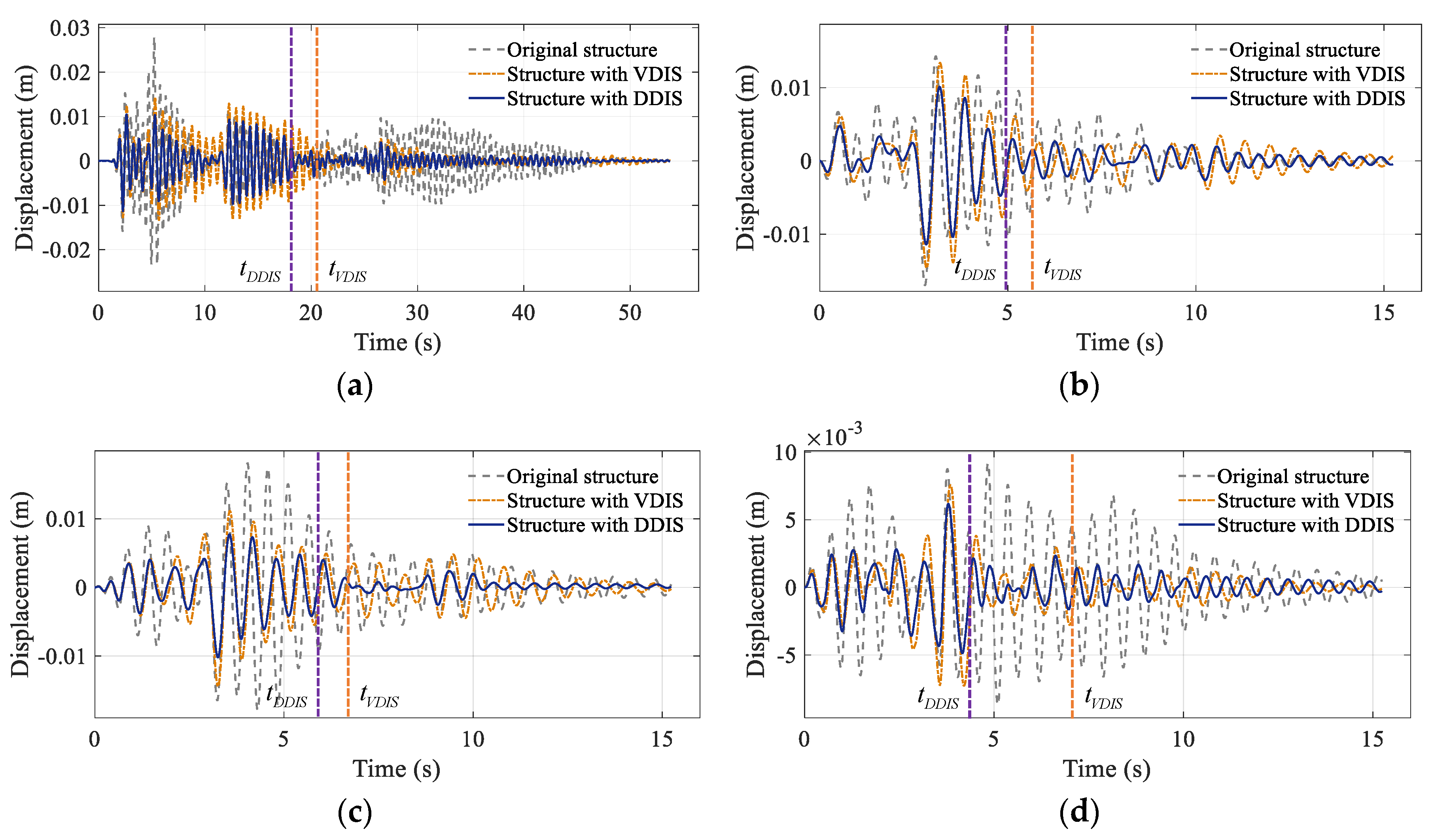
4.1. Displacement Mitigation Effect in Early Stage of Seismic Response

As mentioned above, the classic inerter system utilizes a VDE for energy dissipation. The damping reaction force of the system is proportional to the relative velocity of the damping element; furthermore, there is an inevitable time difference between the times when maximum damping force and maximum displacement are generated. The DDE of the proposed DDIS avoids this problem, as the maximum displacement and maximum damping force occur simultaneously. When an earthquake occurs, the deformation of the DDE induced by the structural vibration directly causes the DDIS to produce a timely reaction force for effective vibration control. This results in significant reduction of the dynamic responses of the structure during the early stage of the seismic response.

To characterize the displacement mitigation effect of the DDIS, its results are compared with those of a conventional VDIS when both were applied to the single-span, single-floor frame structure described in Section 3.2. The viscous damping ratio is considered to be equal to the equivalent damping ratio of the DDE [42,47] to achieve the maximum hysteresis loop area of VDE under the dynamic excitation being equal to that of DDE. The stiffness of the support ($\lambda$) is set to infinity to ignore its tuning effect and only compare the VDIS and DDIS in terms of the structural displacement mitigation difference induced by the difference in the damping element. The design parameters of the DDIS $\mu$ and $\kappa$ are both 0.50, a value that is chosen arbitrarily from the parametric analysis results. The characteristics of the DDIS and the benefits produced by the inerter also hold true for the DDIS with other parameter values. Regarding the hysteresis of the DDIS, $\alpha$ and $u_{dy}$ were assumed to be 0.02 and 0.001, respectively. The main conclusions drawn from the test results, as discussed below, are true for other parameter combinations ($\mu$, $\kappa$, and $\lambda$). The Kanai–Tajimi spectrum is adopted as the input power spectrum, with the predominant frequency of the dynamic excitation, ${\omega }_g$, set to $0.5{\omega }_{s0}$, ${\omega }_{s0}$, and $2.0{\omega }_{s0}$ (${\omega }_{s0}$ denoting the circular frequency of the primary structure) to simulate low-frequency seismic (LS) excitation, the severest seismic (SS) excitation (resonance condition), and high-frequency seismic (HS) excitation, respectively, and artificial records are generated accordingly. The well-studied ground motion record of the 1940 Imperial Valley Earthquake recorded at El Centro (N–S component) is also used as a representative natural excitation. Under the four excitations, the equivalent damping ratio ${\xi }_{VDIS}=c_d/2\sqrt{mk}$ ($c_d$ is the damping coefficient of the VDIS) is designed as 0.025, 0.032, 0.039, and 0.025. The displacement responses of the structures with the DDIS and VDIS under different excitations are shown in Figure 13. The figure shows that for all the excitations, the roof displacement is reduced more effectively by the DDIS compared with the VDIS despite the same equivalent damping ratio. The roof displacements of the structures with the DDIS and VDIS are substantially suppressed after $t_{DDIS}$ and $t_{VDIS}$, respectively, while negligible reduction is achieved before $t_{DDIS}$ and $t_{VDIS}$. Furthermore, $t_{DDIS}$ is definitely lower than $t_{VDIS}$, demonstrating the timely control advantage of the DDIS over the VDIS in the early stage of the seismic response. As shown in the hysteretic curves of the damping element in DDIS and VDIS (Figure 14), at the beginning of the excitation, the energy dissipated by DDIS (dotted line: 1-2-3-4-5-6) is definitely larger than that in the case of VDIS (solid line: 1′-2′-3′-4′). The larger damping force produced by DDIS in the early stage is beneficial for the roof displacement reduction in a timely and more effective manner.

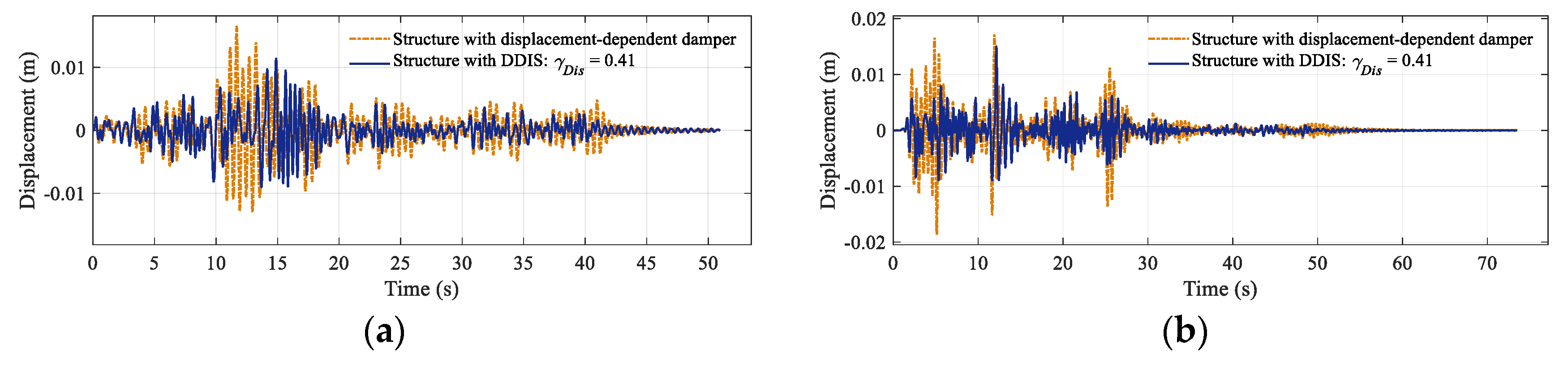
4.2. Seismic Performance of Structure Equipped with DDIS

The time-domain dynamic performance of structures equipped with the DDIS and displacement-dependent damper (as a special case of the DDIS without the inerter) are investigated by applying the DDIS and displacement-dependent damper to the SDOF structure described in Section 3.2.

The values of $\kappa$ and $\lambda$ of the damper and DDIS and the value of $\mu$ of the DDIS are all set to 0.50. A suite of ground motions, 10 LS waves, SS waves, and HS waves are generated using the Kanai–Tajimi spectrum mentioned in Section 4.1. In addition, El Centro 1940 N–S record is employed as a natural ground excitation. The peak ground acceleration of the input ground motion is scaled to a common value of 0.1 g. The average ${\gamma }_{Dis}$, ${\gamma }_{Acc}$, and ${\gamma }_E$ determined by the analyses for the artificial records and El Centro ground motion are presented in

Table 1. Analysis results of ${\gamma }_{Dis}$, ${\gamma }_{Acc}$, and ${\gamma }_E$ for case in Section 4.2.

Type of Excitation	${\mathit{\gamma }}_{\mathit{D}\mathit{i}\mathit{s}}*$	${\mathit{\gamma }}_{\mathit{A}\mathit{c}\mathit{c}}$	${\mathit{\gamma }}_{\mathit{E}}$
LS	0.47 (0.45)	0.49 (0.48)	0.11 (0.10)
SS	0.40 (0.37)	0.58 (0.54)	0.15 (0.15)
HS	0.39 (0.40)	0.70 (0.71)	0.12 (0.14)
El Centro	0.41	0.61	0.14

* Values reported in round brackets denote the corresponding standard deviation ratios computed from the stochastic analysis.

. The results show that for different types of excitations, 10% to 15% of the vibrational energy, as determined by ${\gamma }_E$, is filtered through the DDIS to the primary structure. This indicates that the DDIS considerably reduces the amount of energy that the primary structure needs to dissipate. Furthermore, the displacement and acceleration of the DDIS-fitted structure are suppressed to a low level (reduction ratios ranging from 30% to 60% compared to the uncontrolled case).

Considering the SS and El Centro waves as examples, the displacement response curves of the structures fitted with the displacement-dependent damper and DDIS are shown in Figure 15. The DDIS more effectively reduces the structural displacement compared with the displacement-dependent damper with a DDE identical to that used in the system. To explain the greater displacement reduction ability of the DDIS from the perspective of energy dissipation, Figure 16 shows the hysteresis curves of the DDEs of the displacement-dependent damper and DDIS. The values of the corresponding DDE deformation enhancement ratio, given by

$$\rho =\frac{\max \left(\mathrm{DDE}\mathrm{deformation}\right)}{\max \left(\mathrm{displacement}\mathrm{of}\mathrm{strucuture}\mathrm{with}\mathrm{DDIS}\right)},$$

are indicated in the figure. In agreement with the findings in Section 3.2.2, the DDE deformation of the DDIS is over 60% larger than the structural displacement. The amplified deformation is achieved by the damping enhancement mechanism of the DDIS, in the absence of which the deformation would be equal to the structural displacement, as for the structure with the conventional displacement-dependent damper. The mechanism of the damping enhancement achieved here is similar to that of a VDIS [1].

5. Conclusions

The response deformation of a structure is relatively small during the early stage of the seismic response, which leads to poor performance of velocity-dependent damping compared with the displacement-dependent damping with the same equivalent damper ratio [40,42]. In this study, the ability of the displacement-dependent damper to generate a larger control force during the early stage of the excitation is exploited and further enhanced by a supplemental inerter-spring system tuned to the primary structure, realizing an effective DDIS. A summary of the study and the main conclusions drawn from this investigation are reported below:

• The DDIS is observed to suppress the structural responses in a timely manner as soon as a peak response occurs during the early stage of the excitation. The proposed equivalent linearization method is effective to conduct the stochastic dynamic analysis of the DDIS-equipped structure. The dynamic response of the DDIS controlled systems are further evaluated in the time domain considering the non-linearity and validating the accuracy of the stochastic analysis.
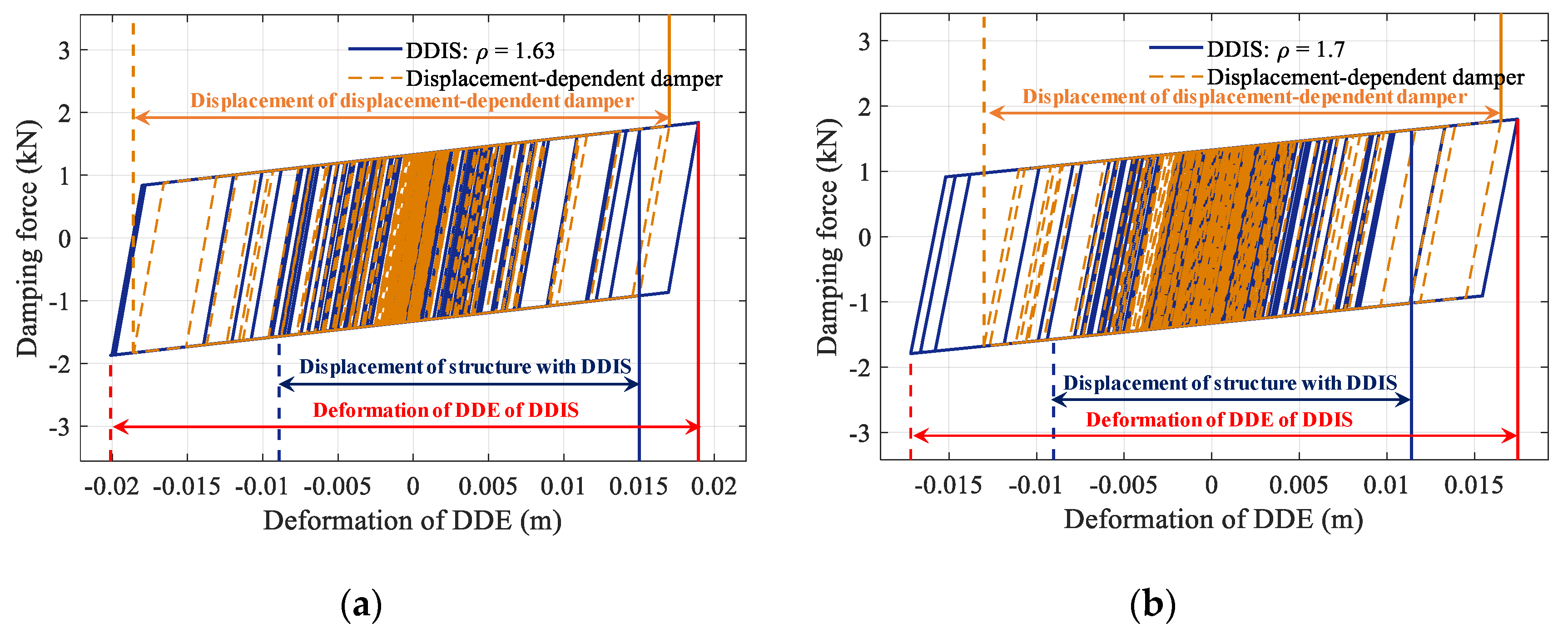
• The interaction between the inerter, spring and the DDE constitutes the damping enhancement mechanism of the DDIS. Compared with an identical DDE, the proposed mechanism amplifies the deformation of the DDE in the DDIS by over 60%; thus, the DDIS is characterized by a higher energy dissipation capability.
• The proposed DDIS considerably reduces the structural displacement and acceleration, which is a result of its damping and mass-enhancement mechanism. For the DDIS with medium value of stiffness ratio and inertance-mass ratio, the displacement and acceleration responses of original uncontrolled structure are reduced by 60% and 40%, respectively.
• The benefits and characteristics of the proposed DDIS are obtained from an extensive parametric analysis and not limited to any specific optimal design procedures. Further studies should be conducted on the parameter design methodology and practical design procedure of the DDIS. The equivalent linearization method proposed in this paper would help reduce the computational cost required to develop a design method.