A Three-Dimensional Cartesian Mesh Generation Algorithm Based on the GPU Parallel Ray Casting Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Baseline of Ray Casting Algorithm
2.2. Parallel Ray Generation
2.3. Parallel Lattice Grid Method
2.4. Parallel Intersection Calculation
2.5. Degenerate Detection
3. Results and Discussion
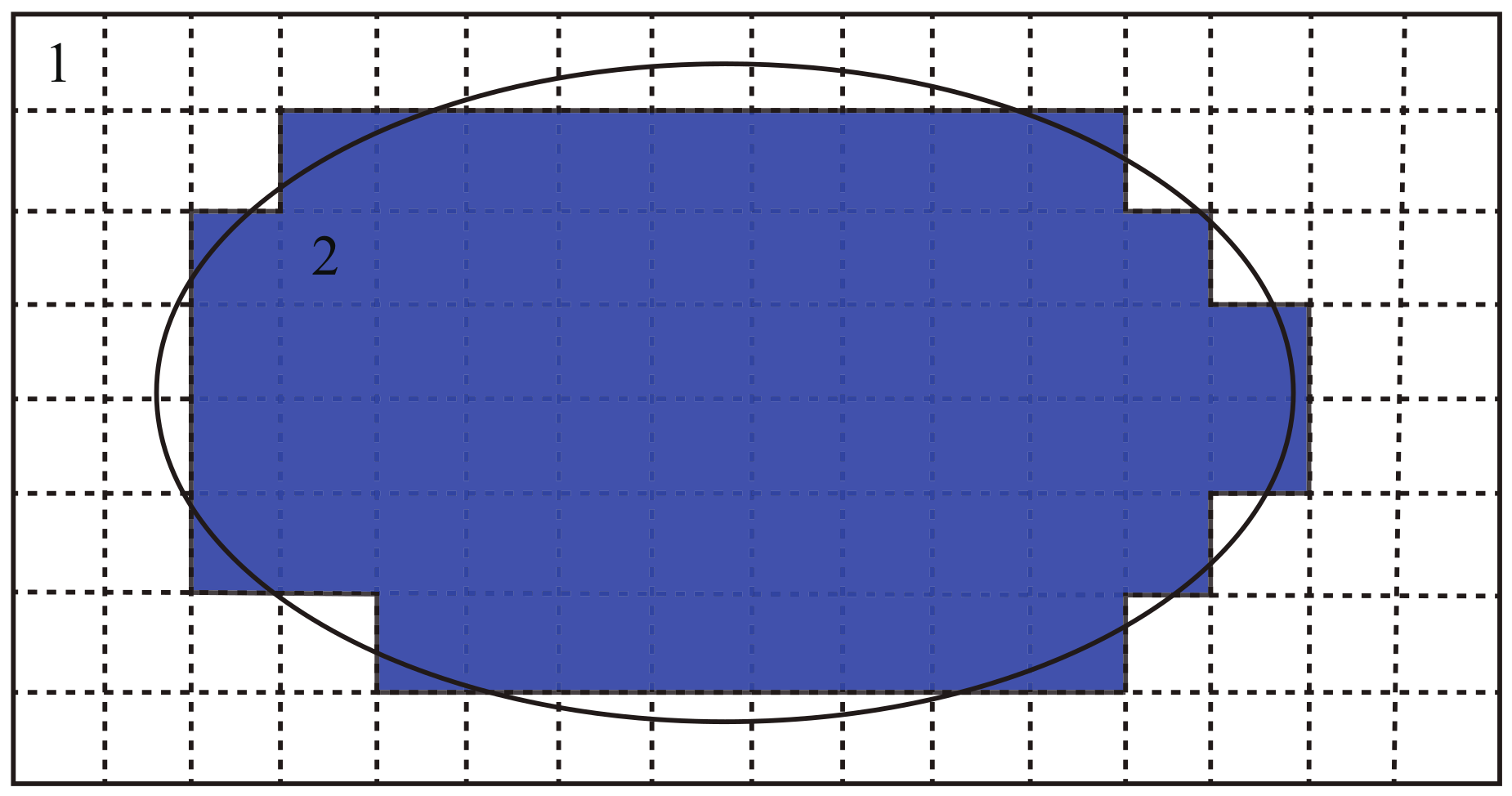
3.1. Result and Visualization of Cartesian Mesh Generation
3.2. Performance of Parallel Cartesian Mesh Generation Algorithm
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ning, J.; Chen, L. Fuzzy interface treatment in Eulerian method. Sci. China Ser. E 2004, 47, 550–568. [Google Scholar] [CrossRef]
- Dezeeuw, D.; Powell, K.G. An adaptively refined Cartesian mesh solver for the Euler equations. J. Comput. Phys. 1991, 104, 56–68. [Google Scholar] [CrossRef] [Green Version]
- Reguly, I.Z.; Giles, M.B. Finite element algorithms and data structures on graphical processing units. Int. J. Parallel Prog. 2015, 43, 203–239. [Google Scholar] [CrossRef] [Green Version]
- Sosnowski, M.; Gnatowska, R.; Grabowska, K.; Krzywański, J.; Jamrozik, A. Numerical analysis of flow in building arrangement: Computational domain discretization. Appl. Sci. 2019, 9, 941. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Ma, T.; Ning, J. A pseudo arc-length method for numerical simulation of shock waves. Chin. Phys. Lett. 2014, 31, 030201. [Google Scholar] [CrossRef]
- Jimenez, P.; Thomas, F.; Torras, C. 3D collision detection: A survey. Comput. Graph. UK 2001, 25, 269–285. [Google Scholar] [CrossRef] [Green Version]
- Mendoza, C.C.; Sullivan, O. Interruptible collision detection for deformable objects. Comput. Graph. UK 2006, 30, 432–438. [Google Scholar] [CrossRef]
- Ma, T.; Wang, J.; Ning, J. A hybrid VOF and PIC multi-material interface treatment method and its application in the penetration. Sci. China Phys. Mech. 2010, 53, 209–217. [Google Scholar] [CrossRef]
- Fang, S.; Chen, H. Hardware accelerated voxelization. Comput. Graph. UK 2000, 24, 433–442. [Google Scholar] [CrossRef]
- Haumont, D.; Warzée, N. Complete polygonal scene voxelization. J. Graph. Tools 2002, 7, 27–41. [Google Scholar] [CrossRef]
- Eisemann, E. Fast scene voxelization and applications. In Proceedings of the ACM SIGGRAPH 2006 Sketches, Boston, MA, USA, 30 July–3 August 2006. [Google Scholar]
- Ning, J.; Ma, T.; Fei, G. Multi-material Eulerian method and parallel computation for 3D explosion and impact problems. Int. J. Comp. Meth. 2014, 11, 1350079. [Google Scholar] [CrossRef]
- Srisukh, Y.; Nehrbass, J.; Teixeira, F.L.; Lee, J.F.; Lee, R. An approach for automatic mesh generation in three-dimensional FDTD simulations of complex geometries. IEEE Antenn. Propag. Mag. 2002, 44, 75–80. [Google Scholar] [CrossRef]
- Ning, J.; Ma, T.; Lin, G. A mesh generator for 3-D explosion simulations using the staircase boundary approach in Cartesian coordinates based on STL models. Adv. Eng. Softw. 2014, 67, 148–155. [Google Scholar] [CrossRef]
- Qin, Q.; Hu, C.; Ma, T. Study on complicated solid modeling and Cartesian mesh generation method. Sci. China Technol. Sci. 2014, 57, 630–636. [Google Scholar] [CrossRef]
- Pandey, P.M.; Reddy, N.V.; Dhande, S.G. Slicing procedures in layered manufacturing: A review. Rapid Prototyp. J. 2003, 9, 274–288. [Google Scholar] [CrossRef] [Green Version]
- Asiabanpour, B.; Khoshnevis, B. Machine path generation for the SIS process. Robot. Comput. Integr. Manuf. 2004, 20, 167–175. [Google Scholar] [CrossRef]
- Macgillivray, J.T. Trillion cell CAD-based Cartesian mesh generator for the finite-difference time-domain method on a single-processor 4-GB workstation. IEEE Trans. Antenn. Propag. 2008, 56, 2187–2190. [Google Scholar] [CrossRef]
- Park, S.; Shin, H. Efficient generation of adaptive Cartesian mesh for computational fluid dynamics using GPU. Int. J. Numer. Meth. Fluids 2012, 70, 1393–1404. [Google Scholar] [CrossRef]
- Schwarz, M.; Seidel, H.P. Fast parallel surface and solid voxelization on GPUs. ACM Trans. Graph. 2010, 29, 1–10. [Google Scholar] [CrossRef]
- Cohenor, D.; Kaufman, A. 3D line voxelization and connectivity control. IEEE Comput. Graph. 1997, 17, 80–87. [Google Scholar] [CrossRef] [Green Version]
- Pantaleoni, J. VoxelPipe: A programmable pipeline for 3D voxelization. In Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics, Vancouver, BC, Canada, 5–7 August 2011; pp. 99–106. [Google Scholar]
- Shevtsov, M.; Soupikov, A.; Kapustin, A. Highly parallel fast KD-tree construction for interactive ray tracing of dynamic scenes. Comput. Graph. Forum. 2010, 26, 395–404. [Google Scholar] [CrossRef] [Green Version]
- Wehr, D.; Radkowski, R. Parallel kd-tree construction on the GPU with an adaptive split and sort strategy. Int. J. Parallel Prog. 2018, 46, 1–18. [Google Scholar] [CrossRef]
- Lauterbach, C.; Garland, M.; Sengupta, S.; Luebke, D.; Manocha, D. Fast BVH construction on GPUs. Comput. Graph. Forum. 2010, 28, 375–384. [Google Scholar] [CrossRef]
- Ganestam, P.; Doggett, M. SAH guided spatial split partitioning for fast BVH construction. Comput. Graph. Forum. 2016, 35, 285–293. [Google Scholar] [CrossRef]
- Slater, M. Tracing a ray through uniformly subdivided n-dimensional space. Vis. Comput. 1992, 9, 39–46. [Google Scholar] [CrossRef]
- Szilvi-Nagy, M.; Matyasi, G.Y. Analysis of STL files. Math. Comput. Model. 2003, 38, 945–960. [Google Scholar] [CrossRef]
- Huang, X.; Yuan, Y.; Hu, Q. Research on the rapid slicing algorithm for NC milling based on STL Model. Commun. Comput. Inf. Sci. 2012, 325, 263–271. [Google Scholar]
- Berens, M.K.; Flintoft, I.D.; Dawson, J.F. Structured mesh generation: Open-source automatic nonuniform mesh generation for FDTD simulation. IEEE Antenn. Propag. Mag. 2016, 58, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Pineda, J. A parallel algorithm for polygon rasterization. Comput. Graph. 1988, 22, 17–20. [Google Scholar] [CrossRef] [Green Version]
- NVIDIA. CUDA C Programming Guide 4.2, CURAND Library, Profiler User’s Guide. 2012. Available online: http://docs.nvidia.com/cuda (accessed on 20 September 2017).













| Models | Model 1 | Model 2 | Model 3 | Model 4 | |
|---|---|---|---|---|---|
| Facet number | |||||
| Mesh cells number | |||||
| Traditional serial algorithm | Mesh line generation (s) | 0.36 | 7.90 | 0.21 | 0.26 |
| Property mapping (s) | |||||
| Total time (s) | |||||
| GPU parallel algorithm | Total time (s) | 35.37 | 8.45 | 61.23 | |
| Speed-up ratio | 14.3 | 15.3 | 14.4 | 14.6 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.; Li, P.; Ma, T. A Three-Dimensional Cartesian Mesh Generation Algorithm Based on the GPU Parallel Ray Casting Method. Appl. Sci. 2020, 10, 58. https://doi.org/10.3390/app10010058
Ma T, Li P, Ma T. A Three-Dimensional Cartesian Mesh Generation Algorithm Based on the GPU Parallel Ray Casting Method. Applied Sciences. 2020; 10(1):58. https://doi.org/10.3390/app10010058
Chicago/Turabian StyleMa, Tiechang, Ping Li, and Tianbao Ma. 2020. "A Three-Dimensional Cartesian Mesh Generation Algorithm Based on the GPU Parallel Ray Casting Method" Applied Sciences 10, no. 1: 58. https://doi.org/10.3390/app10010058





