Aerodynamic Analysis of a Flapping Wing Aircraft for Short Landing
Abstract
1. Introduction
2. Theoretical Analysis
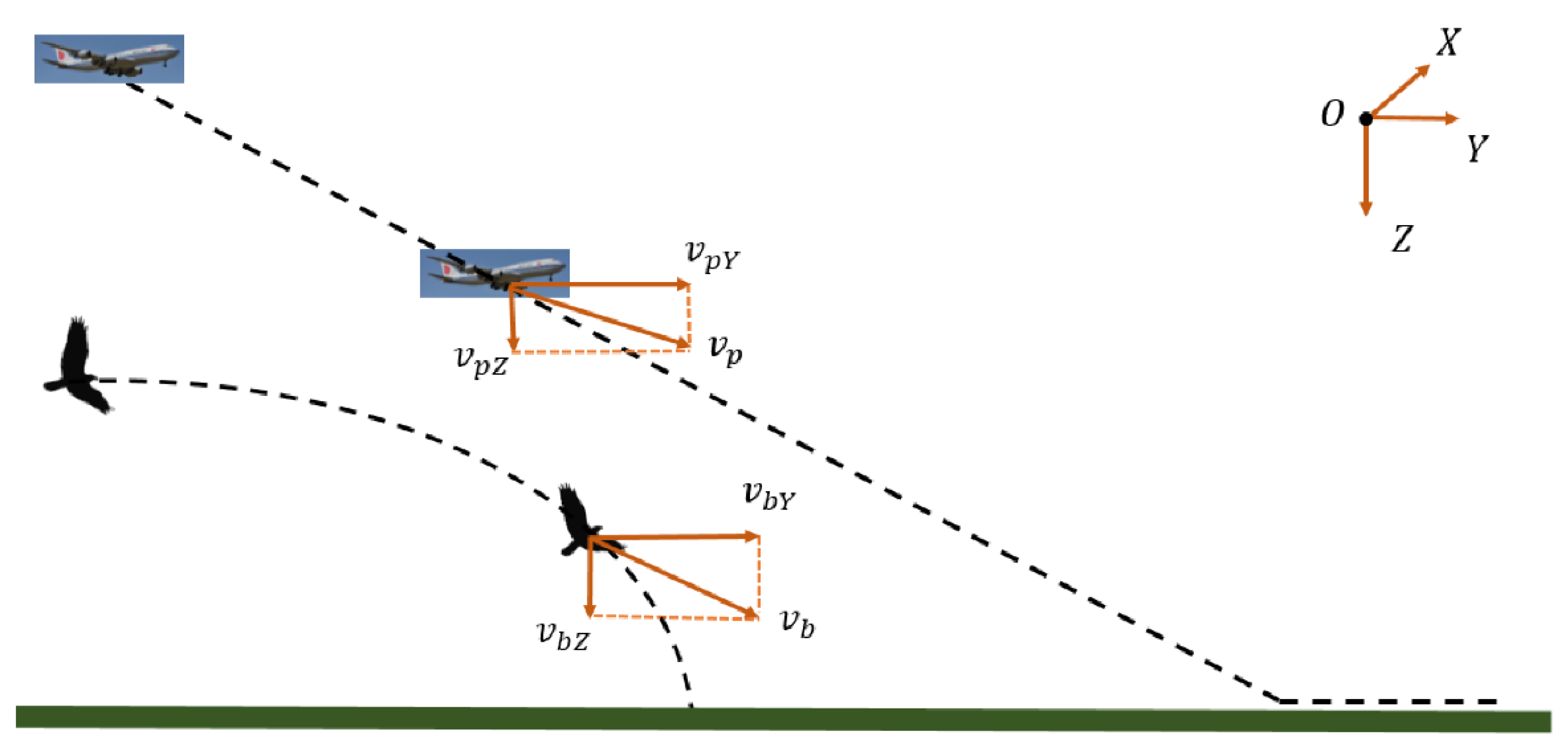
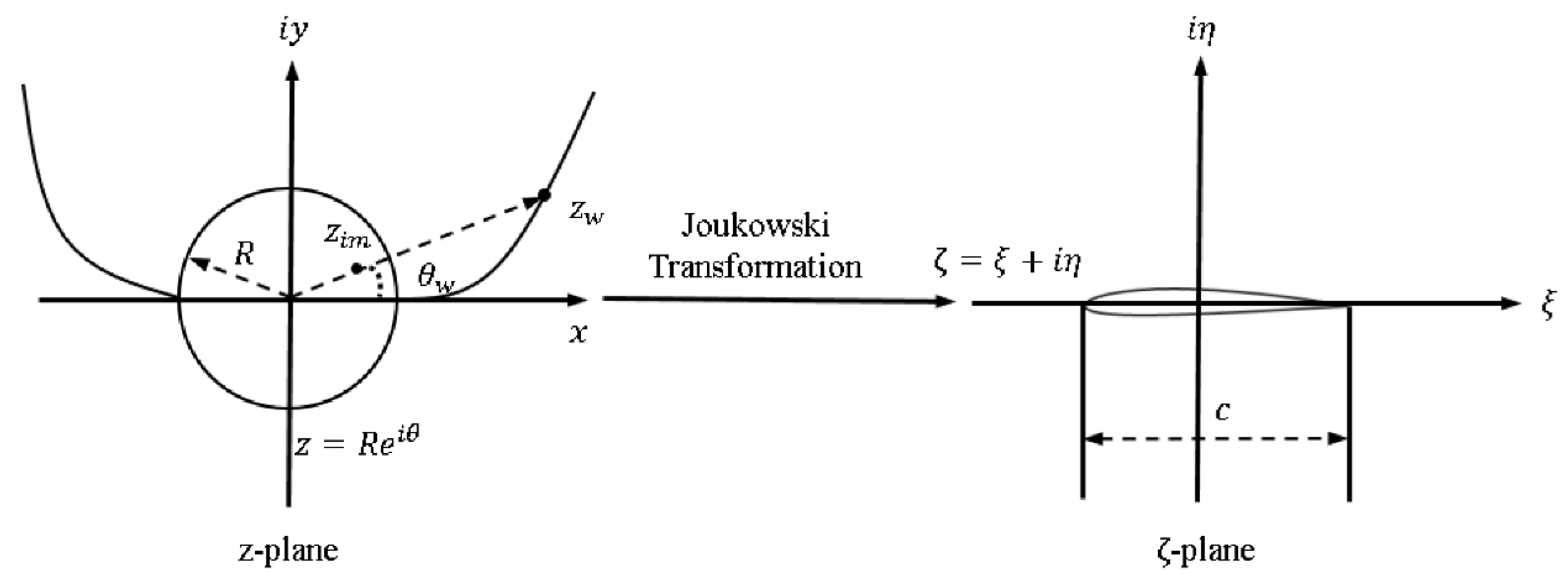
2.1. UAM Method
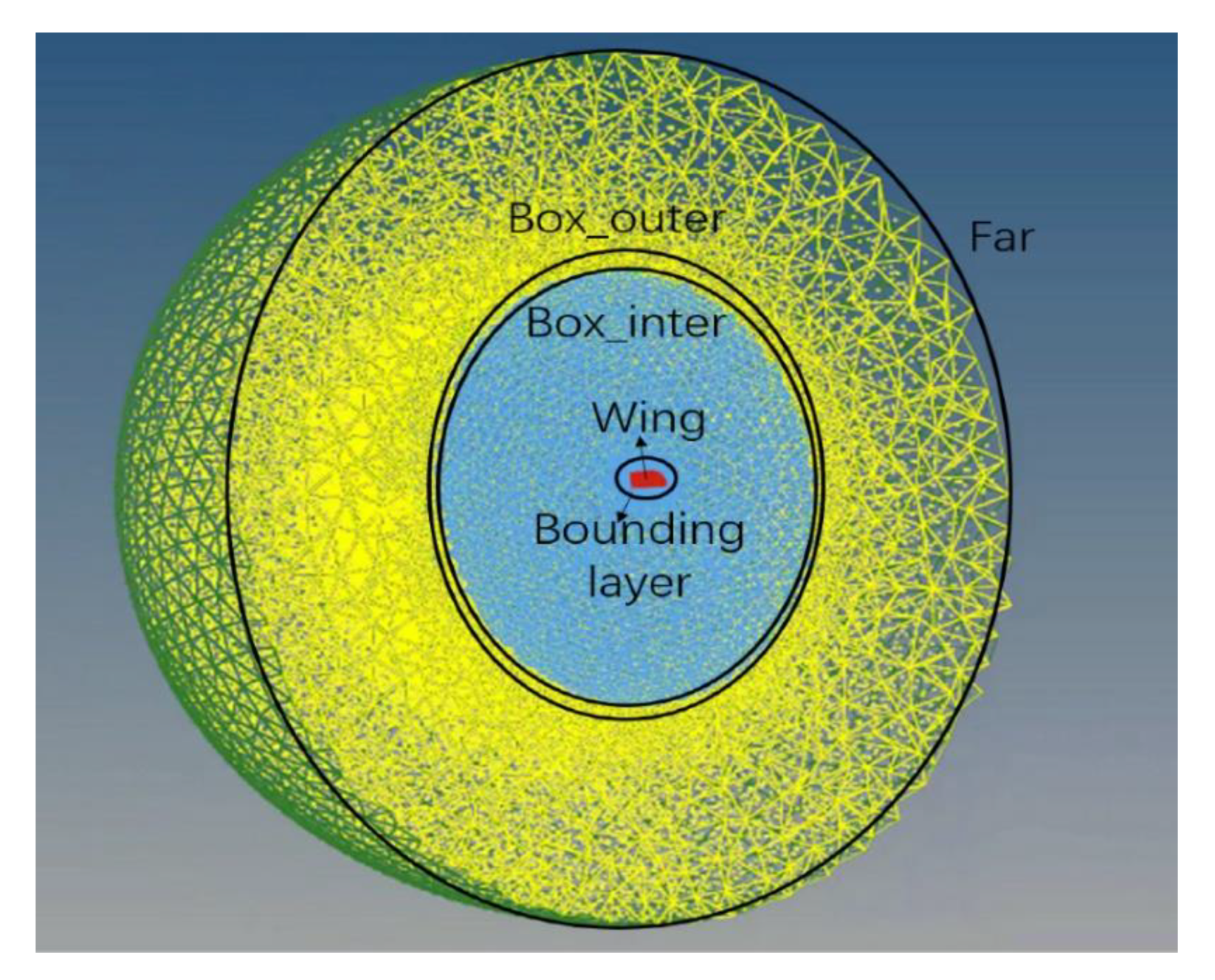
2.2. CFD Model of a Flapping Wing
3. Experimental Model Development
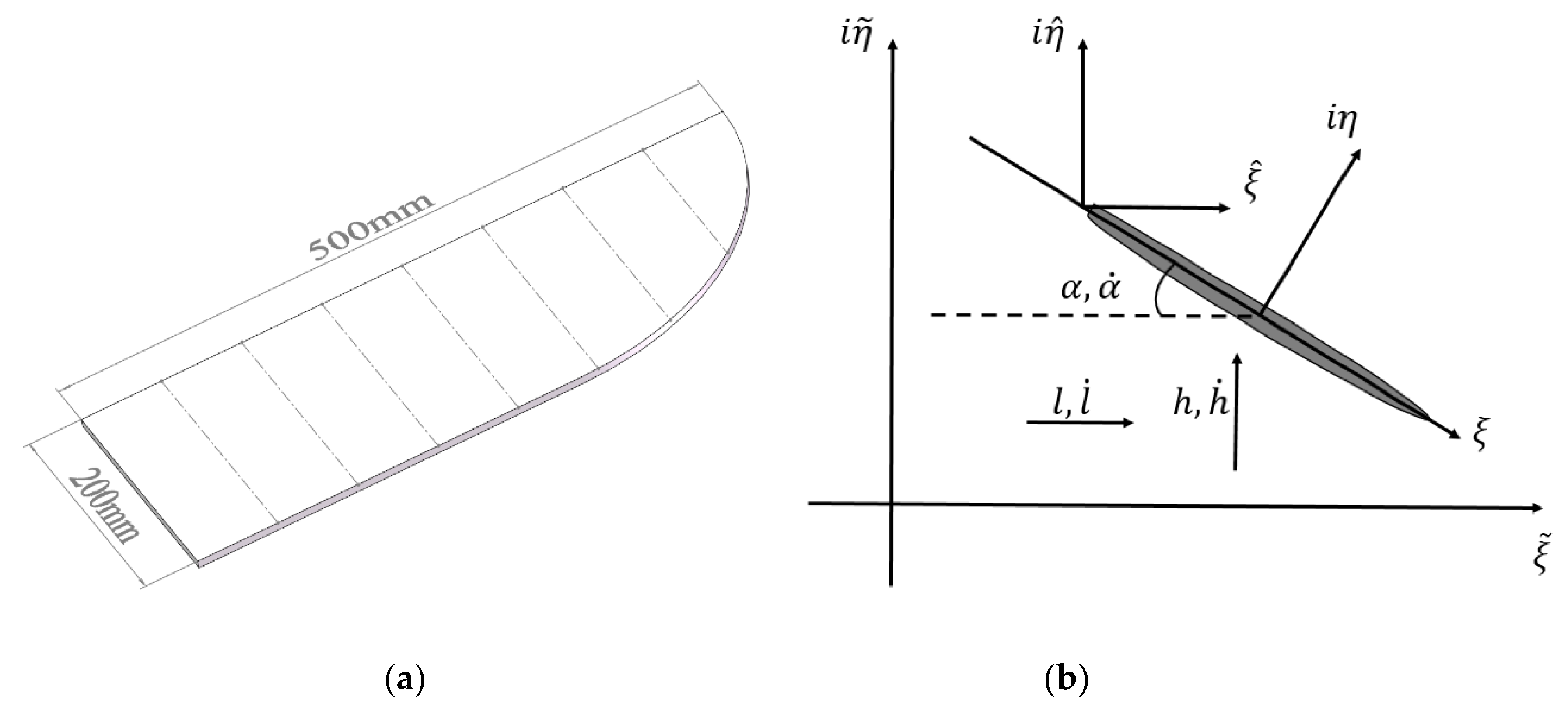
3.1. The Bird-Like Aircraft Model
3.2. Test Rig and Experiment Setting
3.3. Data Acquisition and Processing
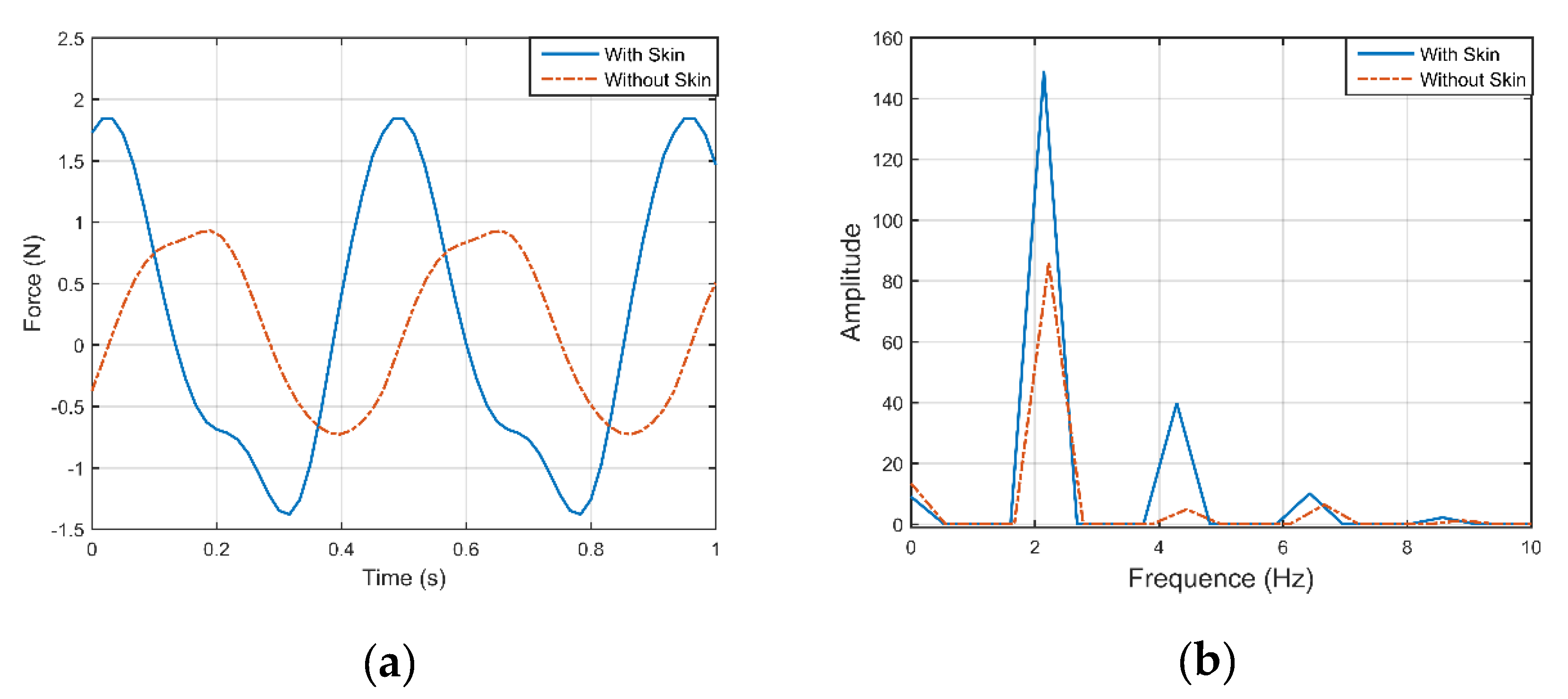
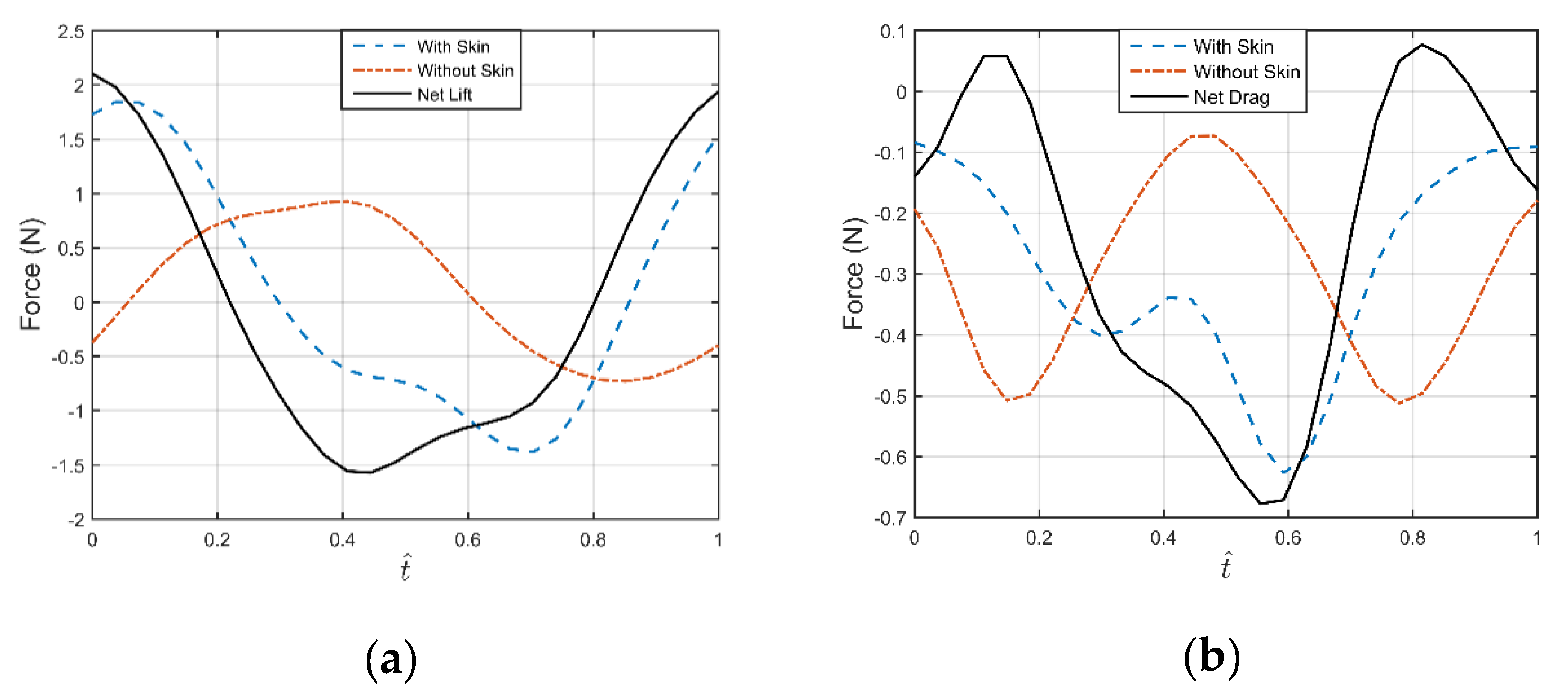
3.4. Aerodynamic Force Acquisition and Processing
4. Study Results and Discussion
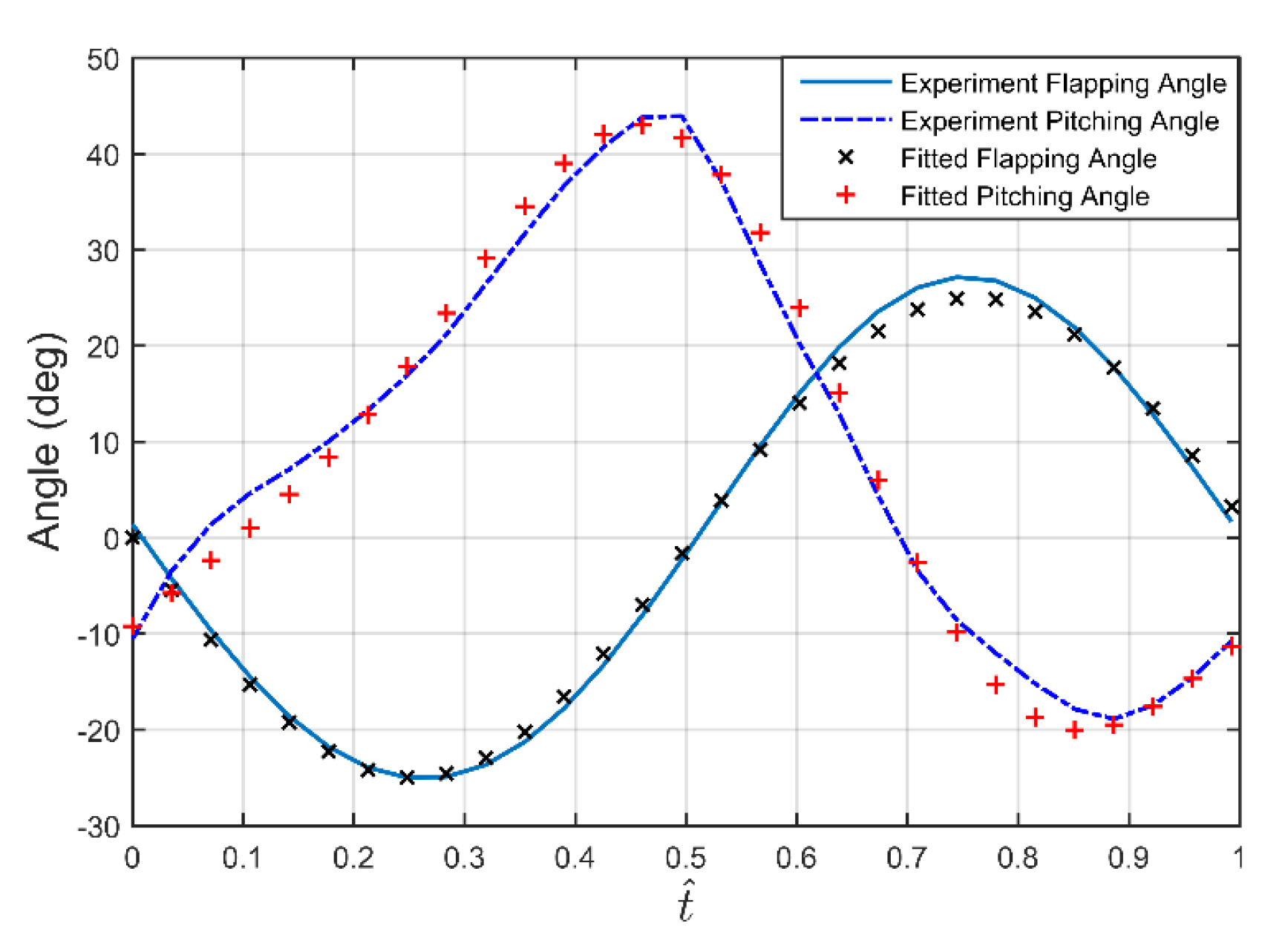
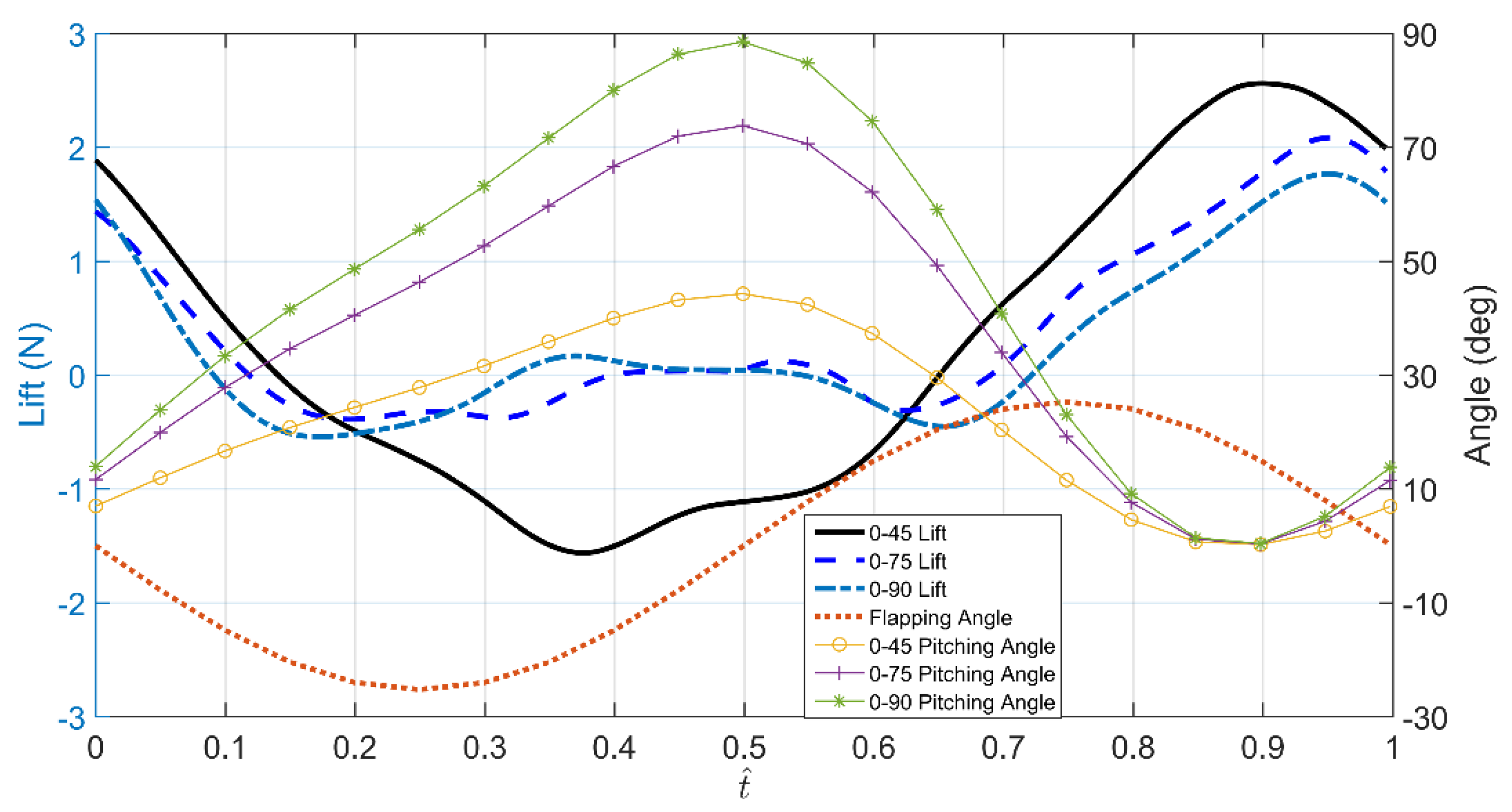
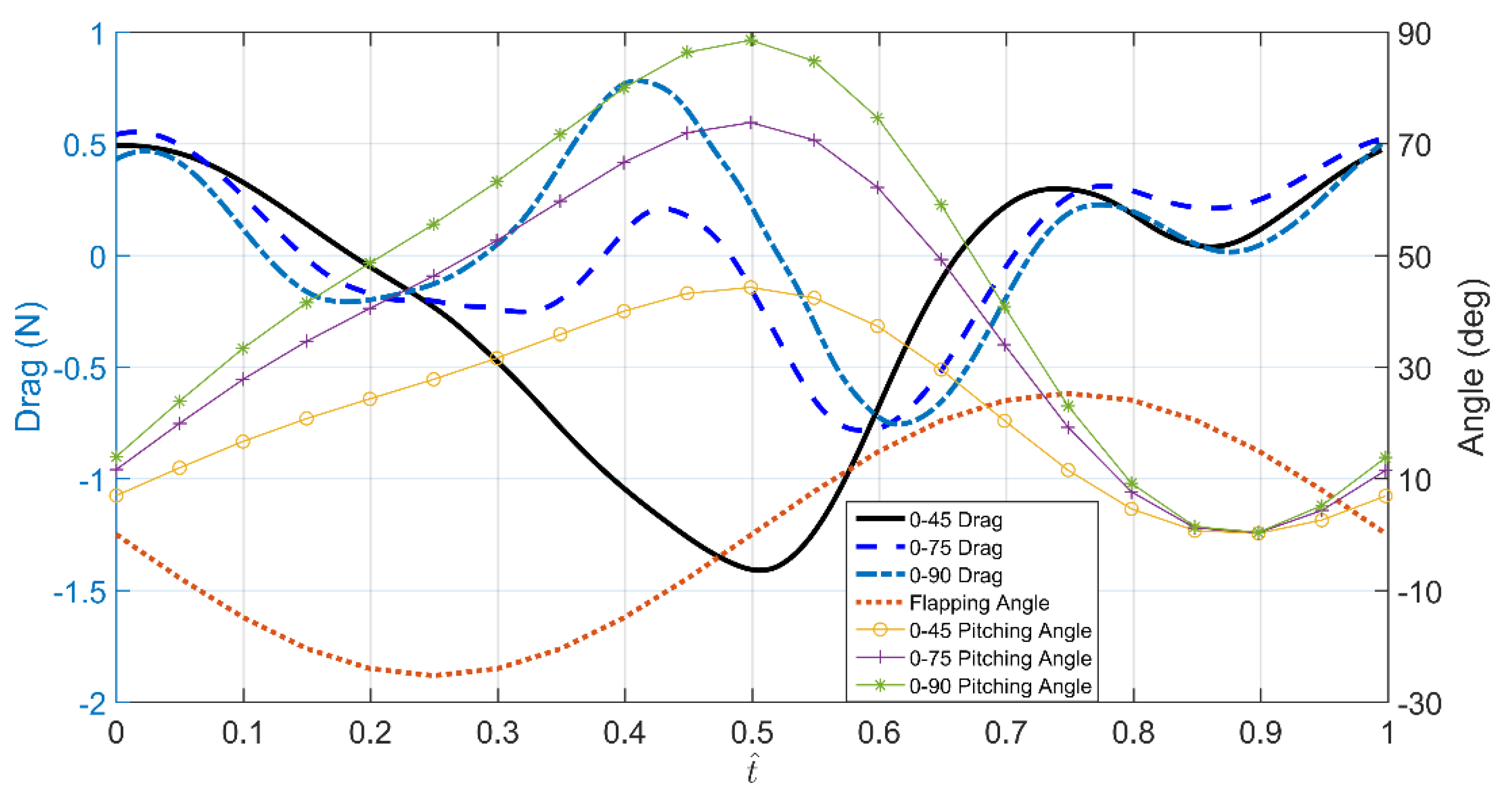
4.1. Experimental Results
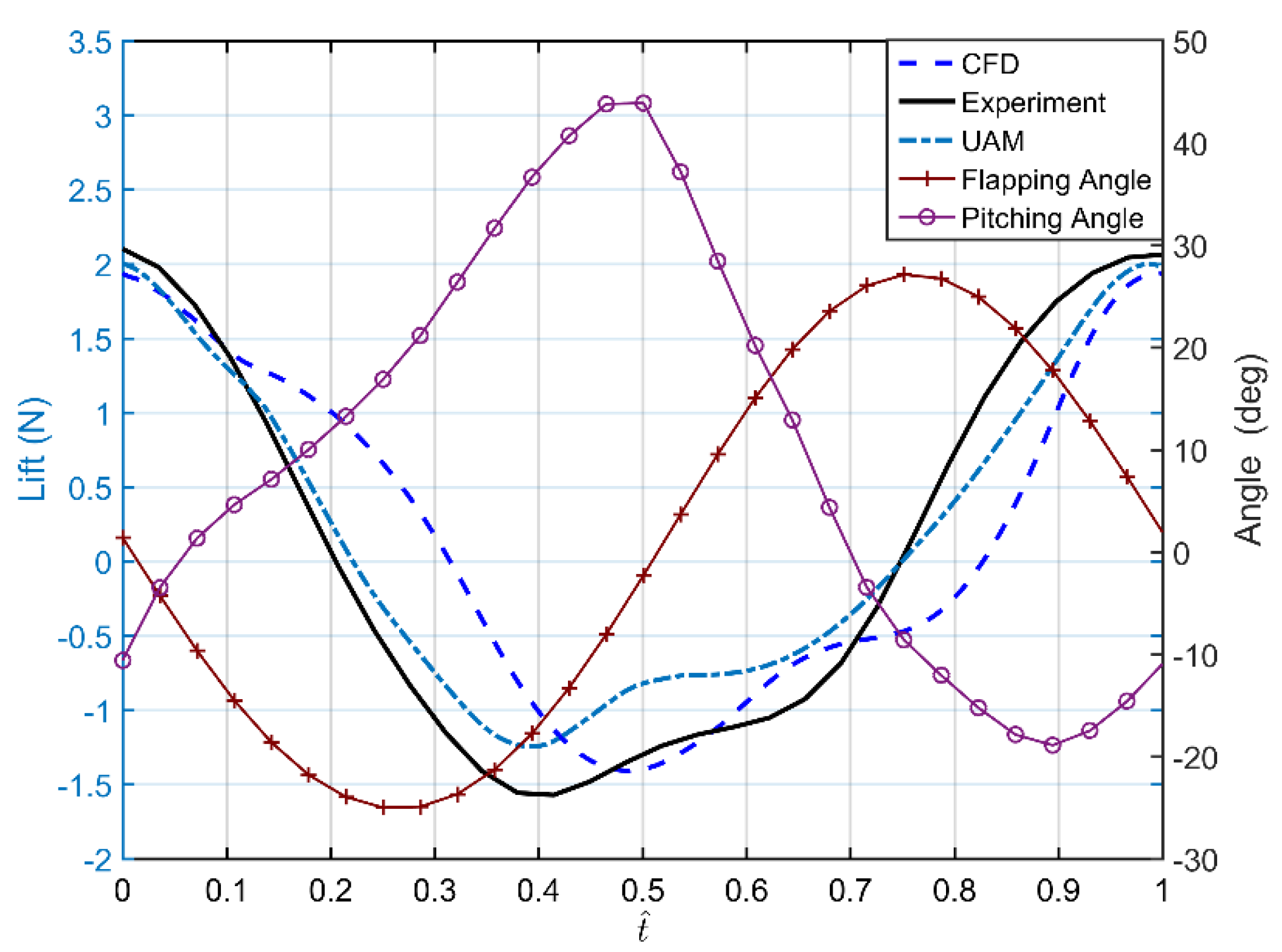
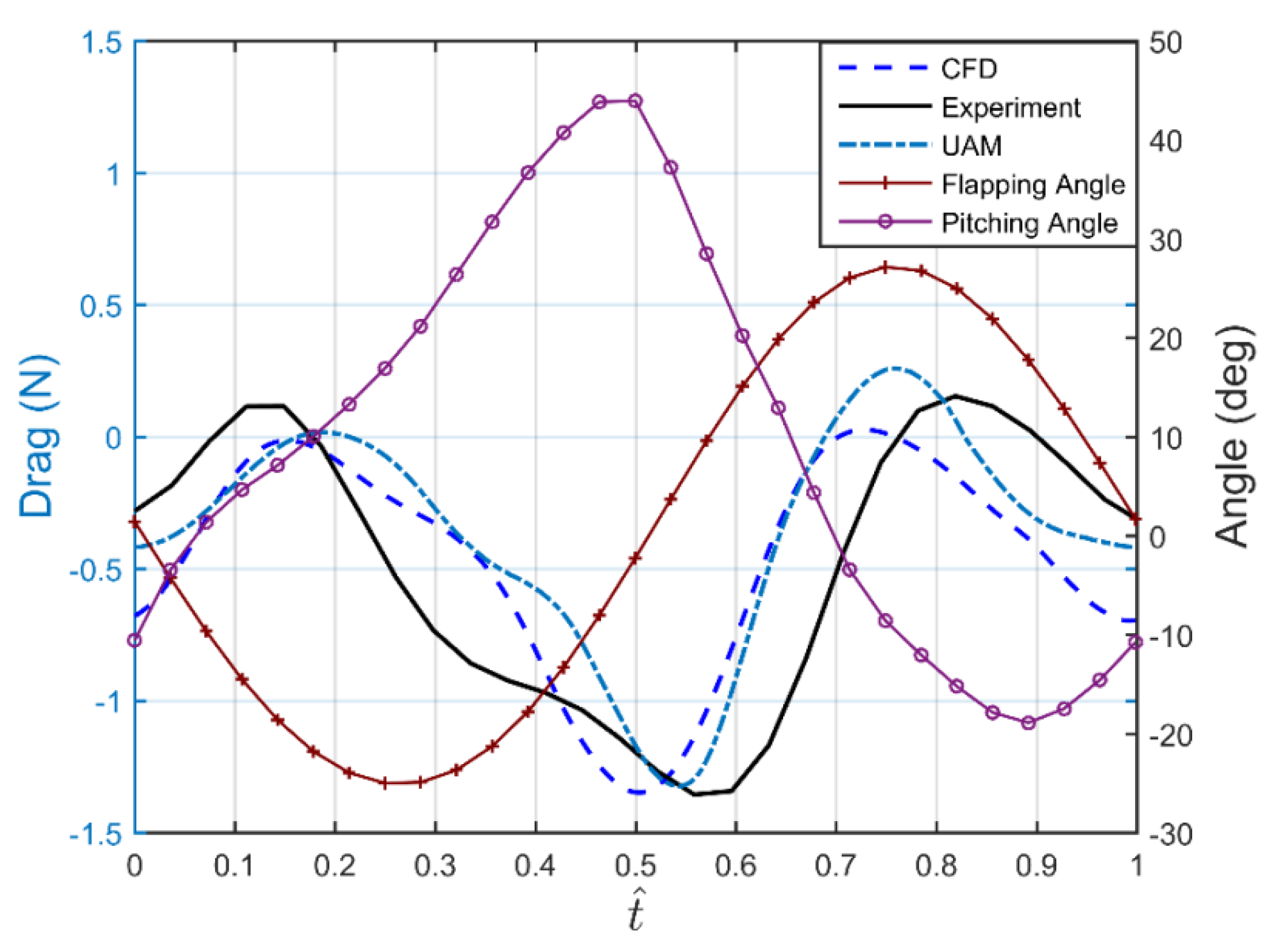
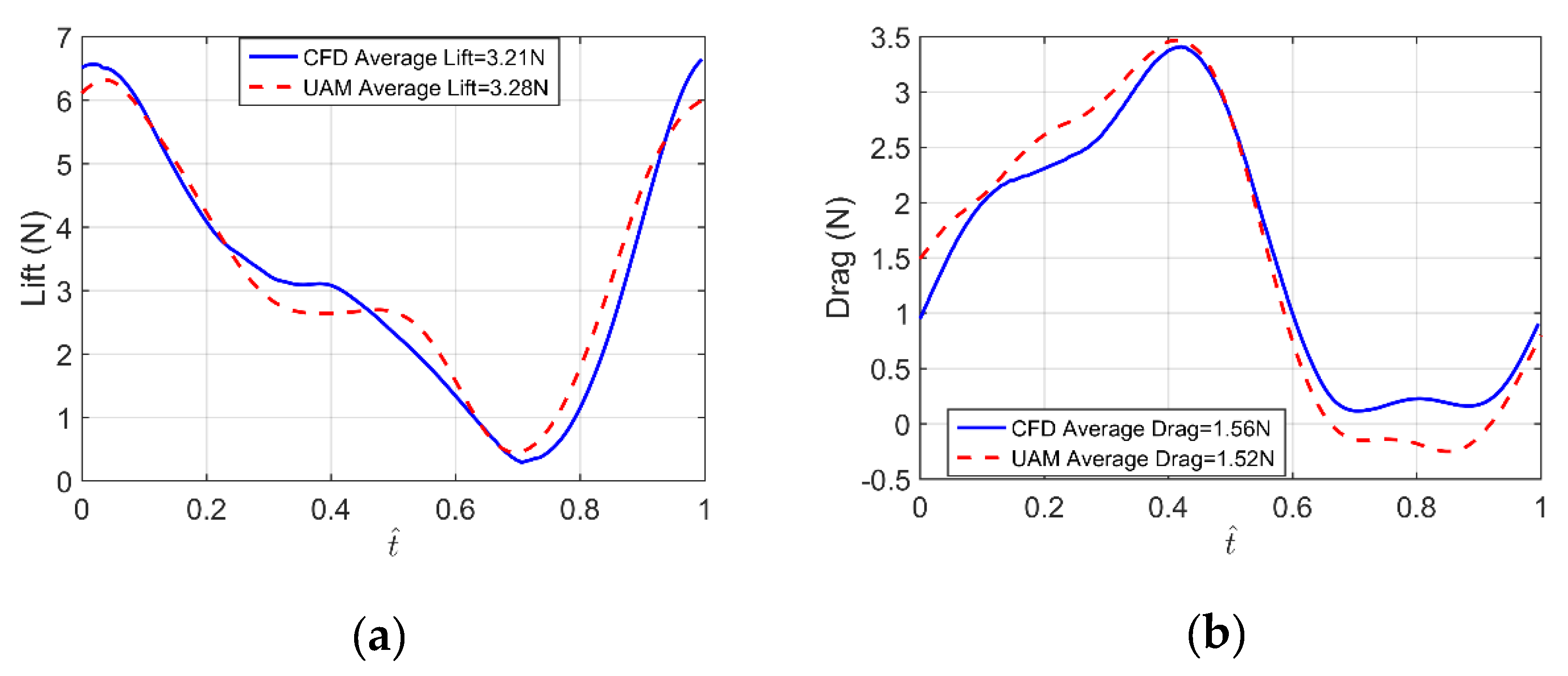
4.2. UAM Validation
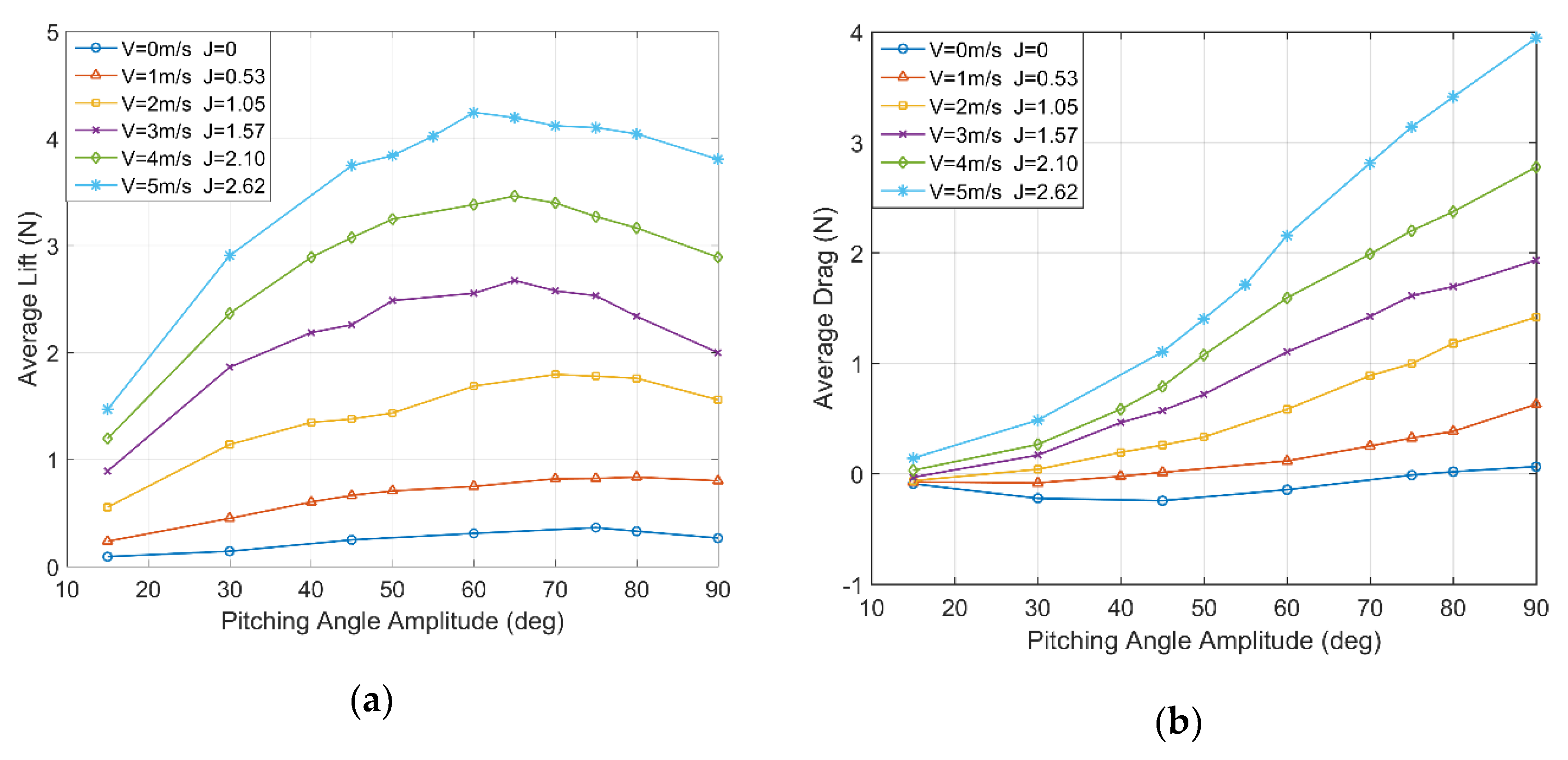
4.3. Parametric Study
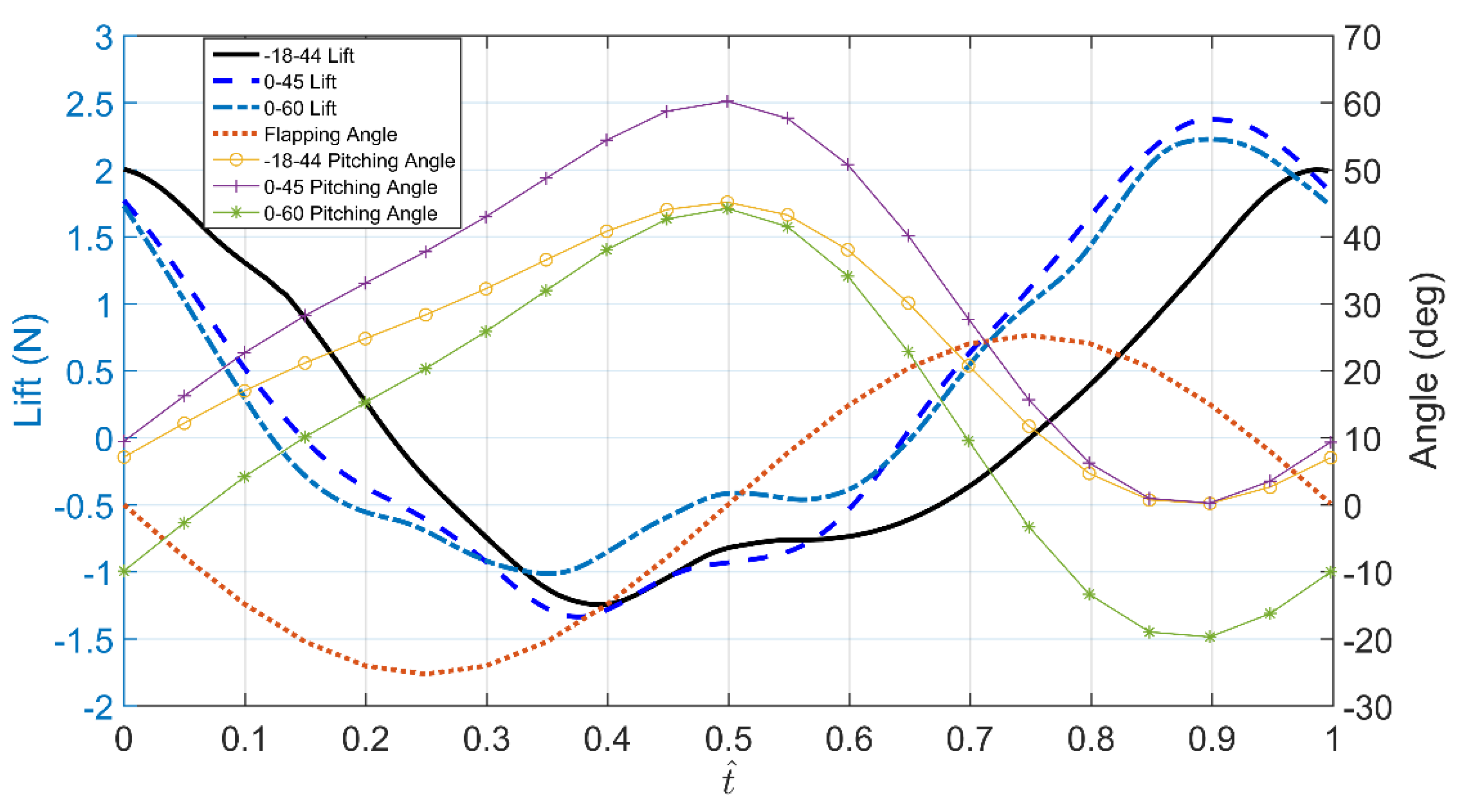
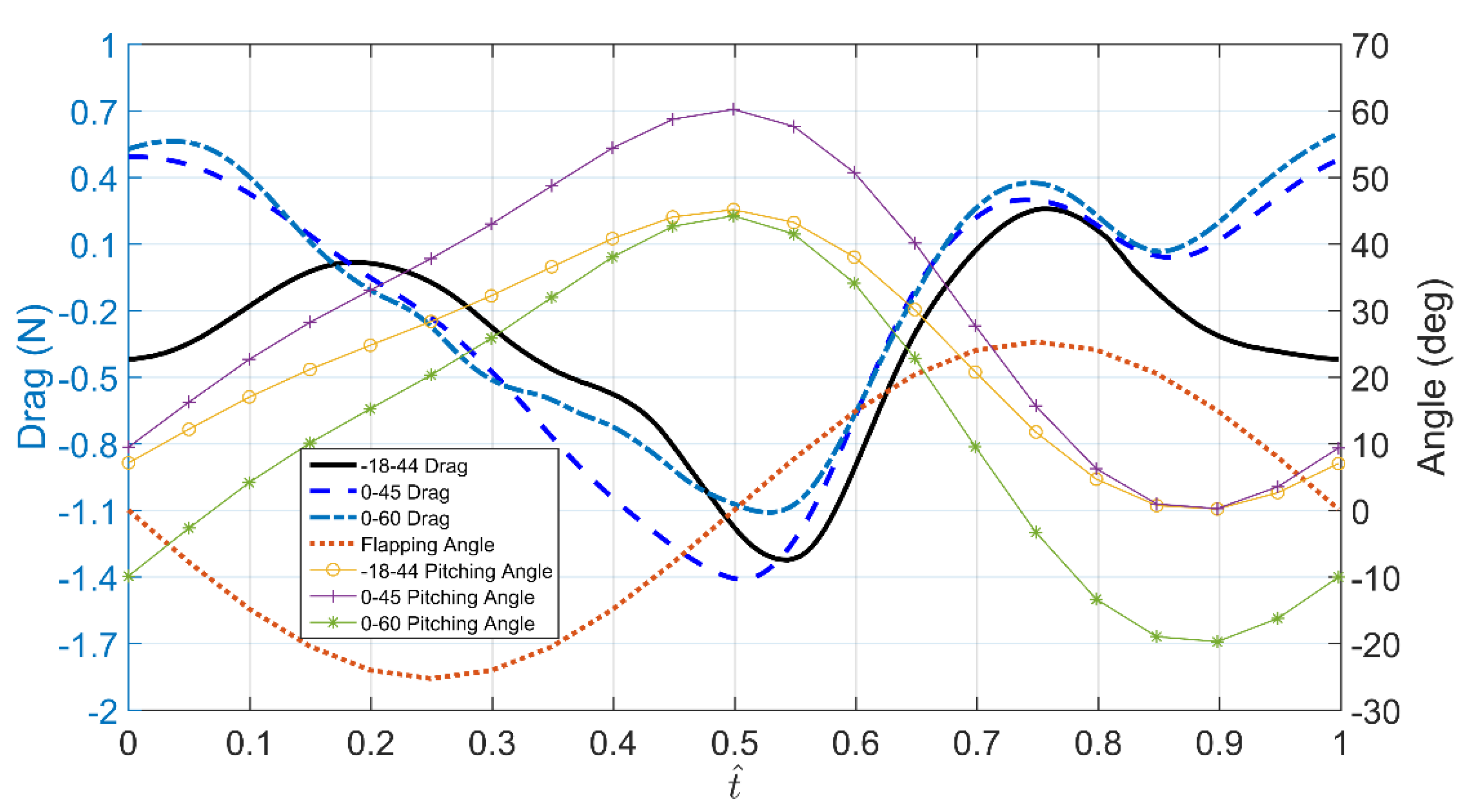
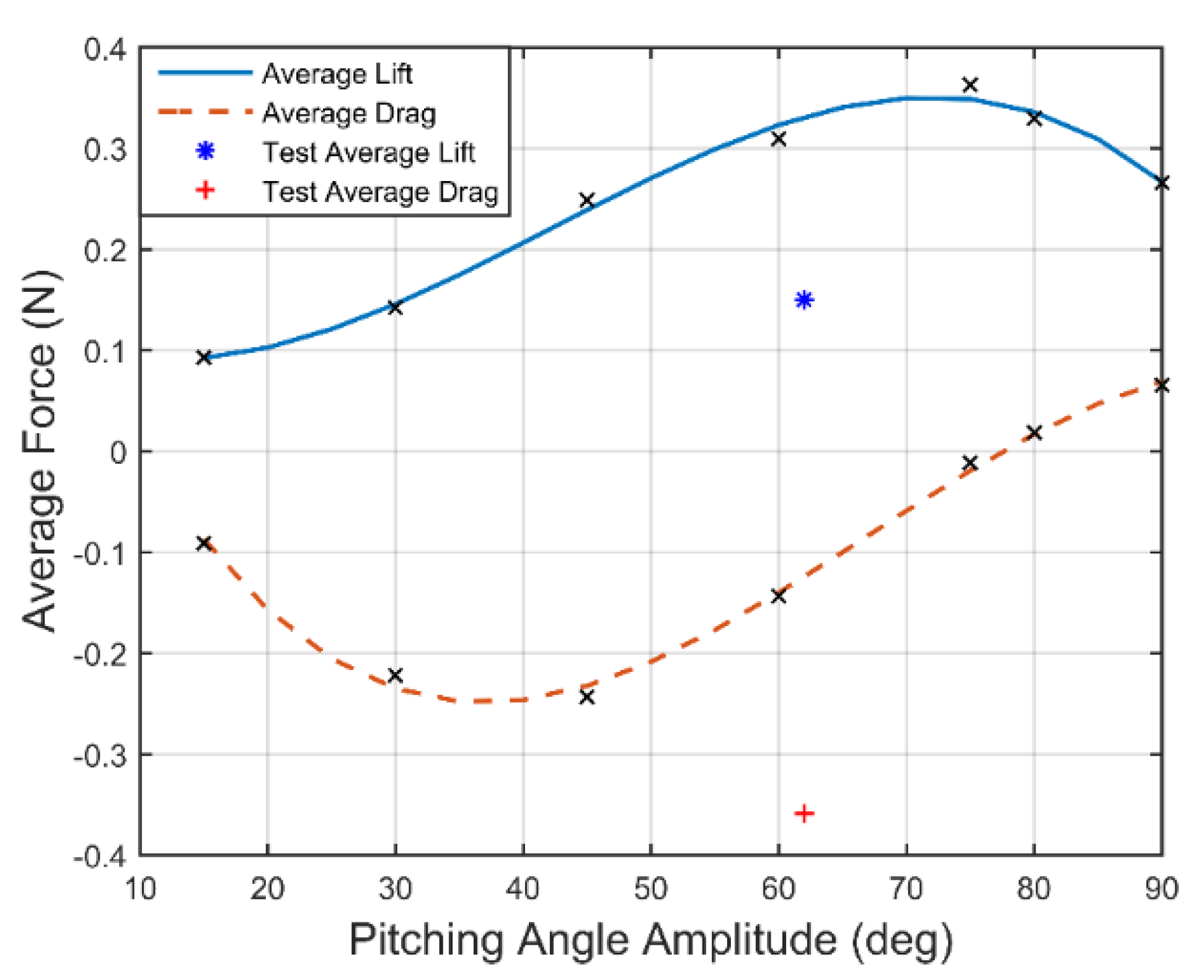
4.3.1. Effect of Pitching Angle of Aerodynamics
4.3.2. Effect of Flight Velocity
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Green, P.R.; Cheng, P. Variation in kinematics and dynamics of the landing flights of pigeons on a novel perch. J. Exp. Biol. 1998, 201, 3309–3316. [Google Scholar] [PubMed]
- Berg, A.M.; Biewener, A.A. Kinematics and power requirements of ascending and descending flight in the pigeon (Columba livia). J. Exp. Biol. 2008, 211, 1120–1130. [Google Scholar] [CrossRef] [PubMed]
- Berg, A.M.; Biewener, A.A. Wing and Body Kinematics of Takeoff and Landing Flight in the Pigeon (Columba livia). J. Exp. Biol. 2010, 213, 1651–1658. [Google Scholar] [CrossRef] [PubMed]
- Ellington, C.P.; Van Den Berg, C.; Willmott, A.P.; Thomas, A.L. Leading-edge vortices in insect flight. Nature 1996, 384, 626–630. [Google Scholar] [CrossRef]
- Pesavento, U.; Wang, Z.J. Flapping wing flight can save aerodynamic power compared to steady flight. Phys. Rev. Lett. 2009, 103, 118102. [Google Scholar] [CrossRef]
- Zhou, C.; Wu, J.; Guo, S.; Li, D. study on the lift generated by a flapping rotary wing applied in a micro air vehicle. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2013, 228, 2083–2093. [Google Scholar] [CrossRef]
- Li, H.; Guo, S.; Zhang, Y.L.; Zhou, C.; Wu, J.H. Unsteady aerodynamic and optimal kinematic analysis of a micro flapping wing rotor. Aerosp. Sci. Technol. 2017, 63, 167–178. [Google Scholar] [CrossRef]
- Wu, J.H.; Hu, J. Aerodynamic Analysis of the Rotor/Wing in Conversion Flight. AMM 2014, 670, 604–608. [Google Scholar] [CrossRef]
- Chadwick, E. A slender–wing theory in potential flow. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 415–432. [Google Scholar] [CrossRef]
- Singh, N.; Aikat, S.; Basu, B.C. Incompressible potential flow about complete aircraft configurations. Aeronaut J. 1989, 93, 335–343. [Google Scholar]
- Malonek, H.R.; De Almeida, R. A note on a generalized Joukowski transformation. Appl. Math. Lett. 2010, 23, 1174–1178. [Google Scholar] [CrossRef]
- Ysasi, A.; Kanso, E.; Newton, P.K. Wake structure of a deformable Joukowski airfoil. Phys. D 2011, 240, 1574–1582. [Google Scholar] [CrossRef]
- Ansari, S.A.; Żbikowski, R.; Knowles, K. Non-linear unsteady aerodynamic model for insect-like flapping wings in the hover. Part 1: Methodology and analysis. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2006, 220, 61–83. [Google Scholar] [CrossRef]
- Muijres, F.T.; Johansson, L.C.; Barfield, R.; Wolf, M.; Spedding, G.R.; Hedenström, A. Leading edge vortex improves lift in slow-flying bats. Science 2008, 319, 1250–1253. [Google Scholar] [CrossRef]
- Muijres, F.T.; Johansson, L.C.; Winter, Y.; Hedenström, A. Leading edge vortices in lesser long-nosed bats occurring at slow but not fast flight speeds. Bioinspir. Biomim. 2014, 9, 25006. [Google Scholar] [CrossRef]
- Pitt Ford, C.W.; Babinsky, H. Lift and the leading-edge vortex. J. Fluid Mech. 2013, 720, 280–313. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z. Unsteady lift for the Wagner problem in the presence of additional leading/trailing edge vortices. J. Fluid Mech. 2015, 769, 182–217. [Google Scholar] [CrossRef]
- ABID; MALEK. Nonlinear mode selection in a model of trailing line vortices. J. Fluid Mech. 2008, 605, 19–45. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, L.; Xu, J. Simulation of aerodynamic performance affected by vortex generators on blunt trailing-edge airfoils. Sci. China Ser. E Technol. Sci. 2010, 53, 1–7. [Google Scholar] [CrossRef]
- Chen, S.; Li, H.; Guo, S.; Tong, M.; Ji, B. Unsteady aerodynamic model of flexible flapping wing. Aerosp. Sci. Technol. 2018, 80, 354–367. [Google Scholar] [CrossRef]
- Vatandas, E.; Hacioglu, A.; Ozkol, I. Vibrational genetic algorithm (VGA) and dynamic mesh in the optimization of 3D wing geometries. Inverse Prob. Sci. Eng. 2007, 15, 643–657. [Google Scholar] [CrossRef]
- Xie, H.; Song, W.P.; Song, B.F. Airfoil design of a micro-flapping wing based on CFD. Acta Aerodyn. Sinica 2009, 27, 227–233. [Google Scholar]
- Zhang, F. Quaternions and matrices of quaternions. Linear Algebra Appl. 1997, 251, 21–57. [Google Scholar] [CrossRef]
- Zhu, Y.; Xiang, H.; Wei, F.; Li, S. Trajectory Planning Algorithm Based on Quaternion for 6-DOF Aircraft Wing Automatic Position and Pose Adjustment Method. Chin. J. Aeronaut. 2010, 23, 707–714. [Google Scholar]
- Norris, A.N. Euler-Rodrigues and Cayley Formulae for Rotation of Elasticity Tensors. Math. Mech. Solids. 2008, 13, 465–498. [Google Scholar] [CrossRef]
- Nguyen, Q.V.; Park, H.C.; Goo, N.S.; Byun, D. Aerodynamic force generation of an insect-inspired flapper actuated by a compressed unimorph actuator. Chin. Sci. Bull. 2009, 54, 2871–2879. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, Q.; Hu, M.L. The Inertia Force of Insect-Like Flapping Wing Micro Air Vehicle. Adv. Mater. Res. 2011, 327, 186–192. [Google Scholar] [CrossRef]
- Chen, M.W.; Zhang, Y.; Sun, M. Wing and body motion and aerodynamic and leg forces during take-off in droneflies. J. R. Soc. Interface 2013, 10, 20130808. [Google Scholar] [CrossRef]
- Guo, S.; Li, H.; Zhou, C.; Zhang, Y.L.; He, Y.; Wu, J.H. Analysis and Experiment of a Bio-inspired Flyable Micro Flapping Wing Rotor. Aerosp. Sci. Technol. 2018, 79, 506–517. [Google Scholar] [CrossRef]
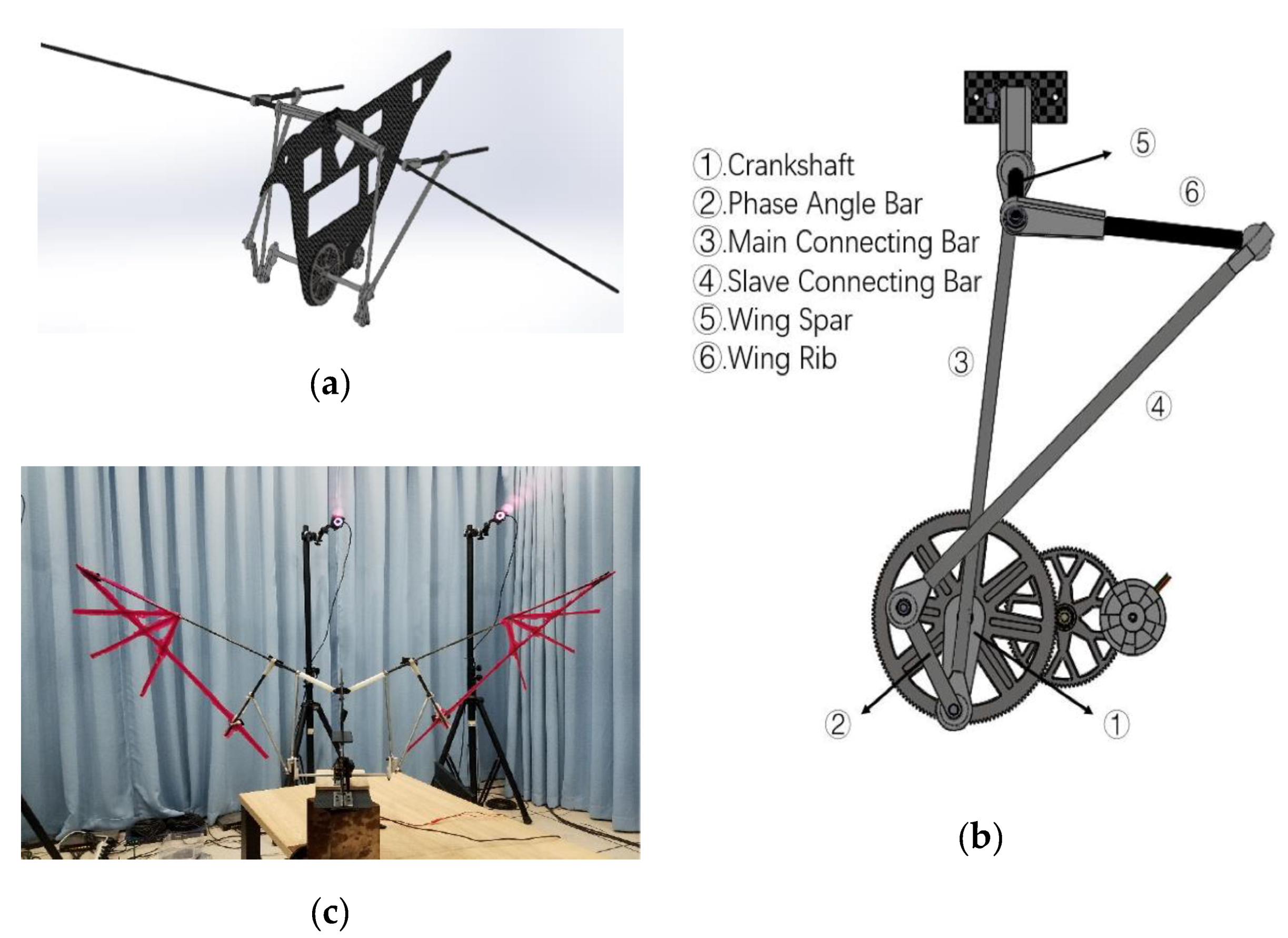
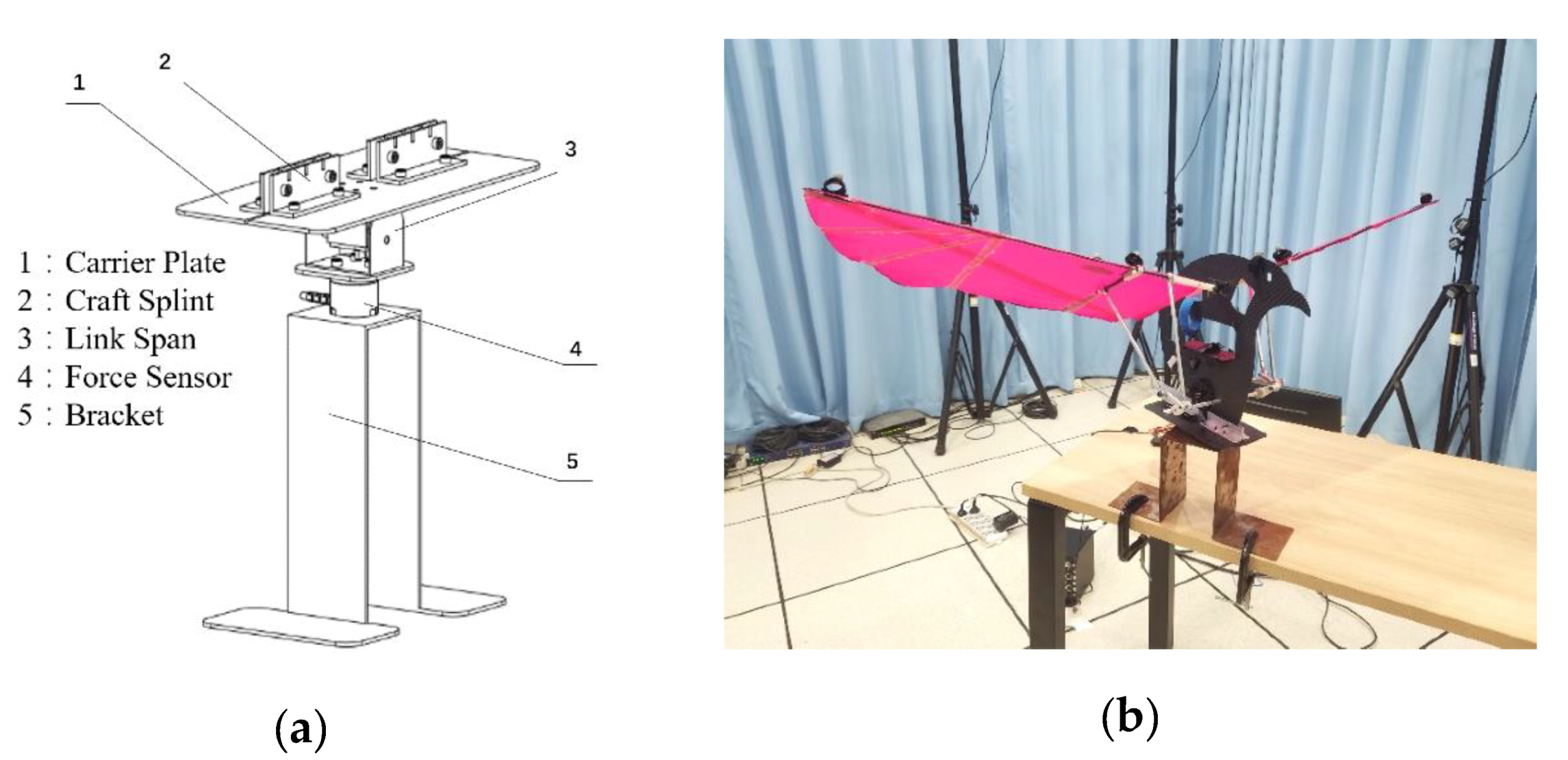
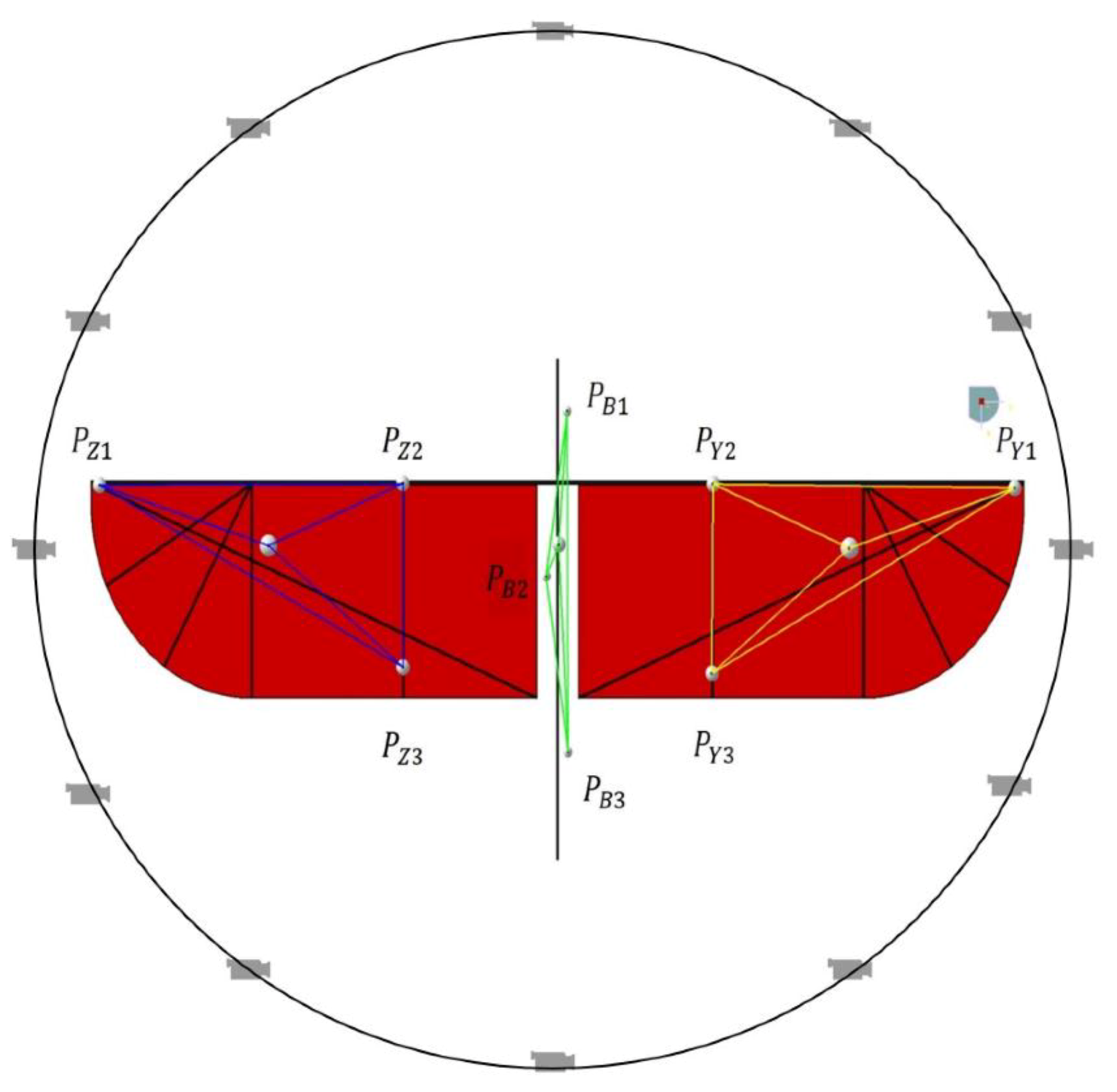
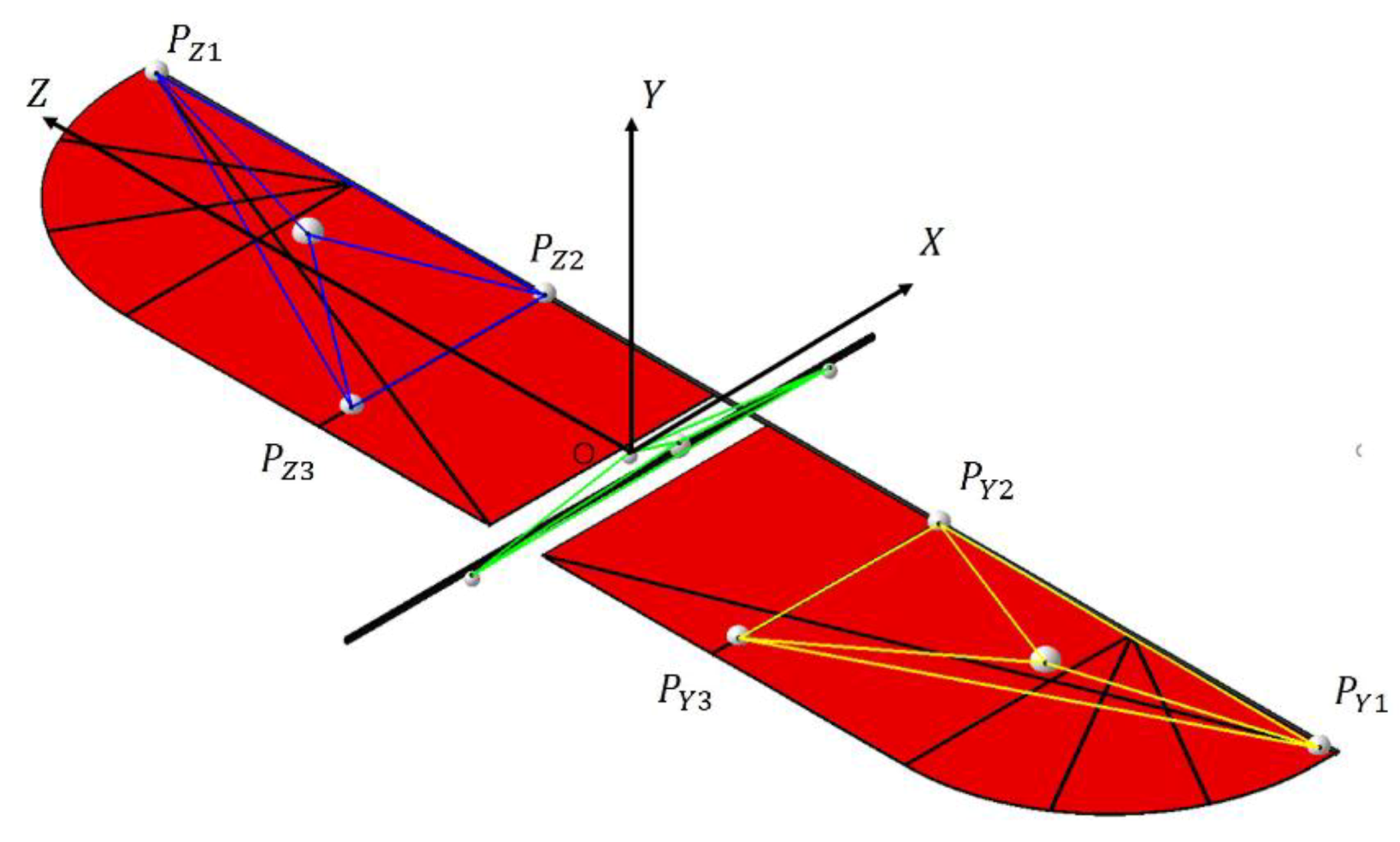

| Unit | Weight (g) | Unit | Weight (g) |
|---|---|---|---|
| Crankshaft | 4.33 | Slave Connecting Bar | 8.80 |
| Phase Angle Bar | 3.28 | Wing Spar | 12.35 |
| Main Connecting Bar | 9.53 | Wing Rib | 5.06 |
| Ball Bearing | 5.46 | Wing Spar Sleeve | 11.15 |
| Skin | 9.64 | Whole aircraft | 310.73 |
| Sensor | Sensing Ranges (N) | Deviation | ||
|---|---|---|---|---|
| Nano 17 | ||||
| SI-25-0.25 | 0.25–25 | 0.25–35 | 1/160 | 1/160 |
| Camera | Resolution | Frame Rate | 3D Accuracy | Latency |
|---|---|---|---|---|
| Prime13 | 1280 × 1024 | 120–240 Hz | 0.20 mm | 4.2 ms |
| Pitching Angle Range | 0°~15° | 0°~30° | 0°~45° | 0°~50° | 0°~60° | 0°~75° | 0°~80° | 0°~90° |
|---|---|---|---|---|---|---|---|---|
| Average Lift (N) | 0.0927 | 0.1420 | 0.2487 | 0.2623 | 0.3092 | 0.3627 | 0.3295 | 0.2661 |
| Average Drag (N) | −0.0932 | −0.2223 | −0.2435 | −0.1967 | −0.1435 | −0.0116 | 0.0184 | 0.0654 |
| Flapping Frequency (Hz) | 1 | 2.1 | 3 | 4 |
|---|---|---|---|---|
| Average Lift (N) | 0.085 | 0.248 | 0.486 | 1.097 |
| Average Drag (N) | −0.063 | −0.242 | −0.332 | −0.686 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, B.; Zhu, Z.; Guo, S.; Chen, S.; Zhu, Q.; Li, Y.; Yang, F.; Song, R.; Li, Y. Aerodynamic Analysis of a Flapping Wing Aircraft for Short Landing. Appl. Sci. 2020, 10, 3404. https://doi.org/10.3390/app10103404
Ji B, Zhu Z, Guo S, Chen S, Zhu Q, Li Y, Yang F, Song R, Li Y. Aerodynamic Analysis of a Flapping Wing Aircraft for Short Landing. Applied Sciences. 2020; 10(10):3404. https://doi.org/10.3390/app10103404
Chicago/Turabian StyleJi, Bing, Zenggang Zhu, Shijun Guo, Si Chen, Qiaolin Zhu, Yushuai Li, Fan Yang, Rui Song, and Yibin Li. 2020. "Aerodynamic Analysis of a Flapping Wing Aircraft for Short Landing" Applied Sciences 10, no. 10: 3404. https://doi.org/10.3390/app10103404
APA StyleJi, B., Zhu, Z., Guo, S., Chen, S., Zhu, Q., Li, Y., Yang, F., Song, R., & Li, Y. (2020). Aerodynamic Analysis of a Flapping Wing Aircraft for Short Landing. Applied Sciences, 10(10), 3404. https://doi.org/10.3390/app10103404






