Par3DNet: Using 3DCNNs for Object Recognition on Tridimensional Partial Views
Abstract
:1. Introduction
- A deep learning-based architecture that is able to take 3D data as input and perform classification.
- The architecture is able to classify partial 3D data like the one provided by a Kinect sensor.
- The architecture is trained on synthetic data and performs accurately when fed real 3D data.
2. Related Works
3. Proposal
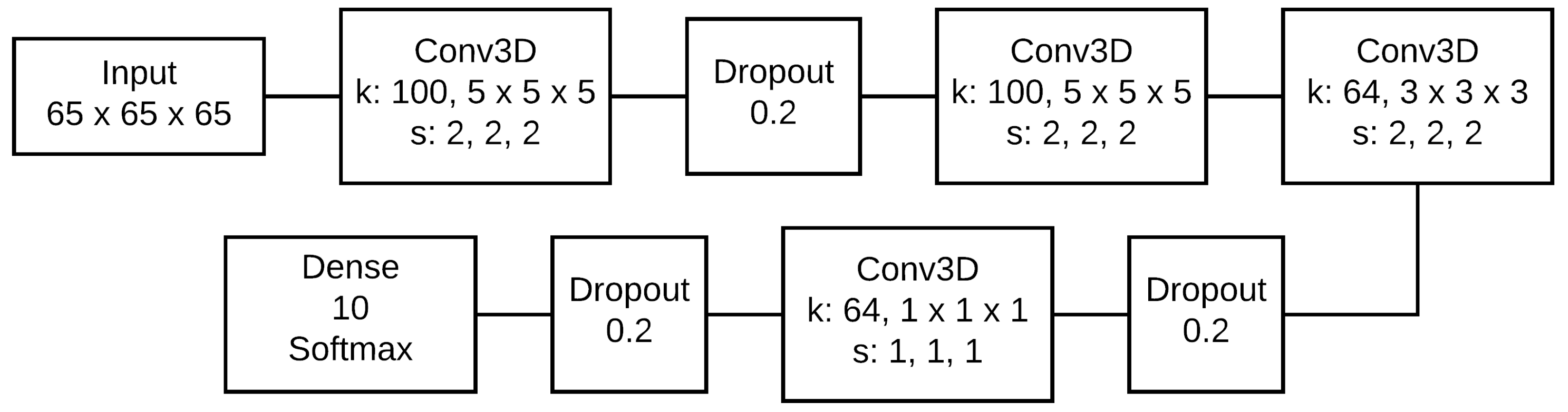
3.1. Par3DNet Architecture
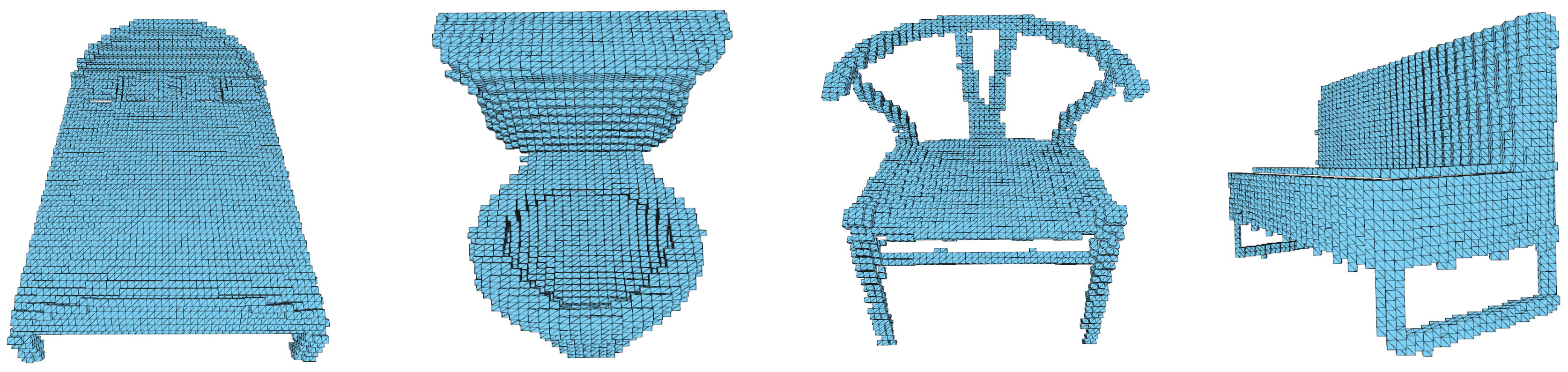
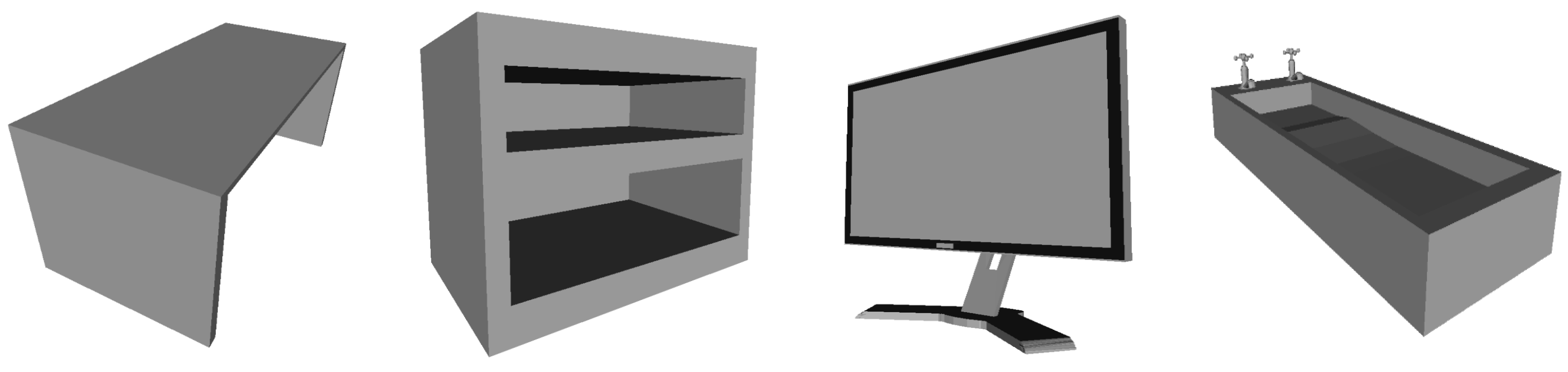
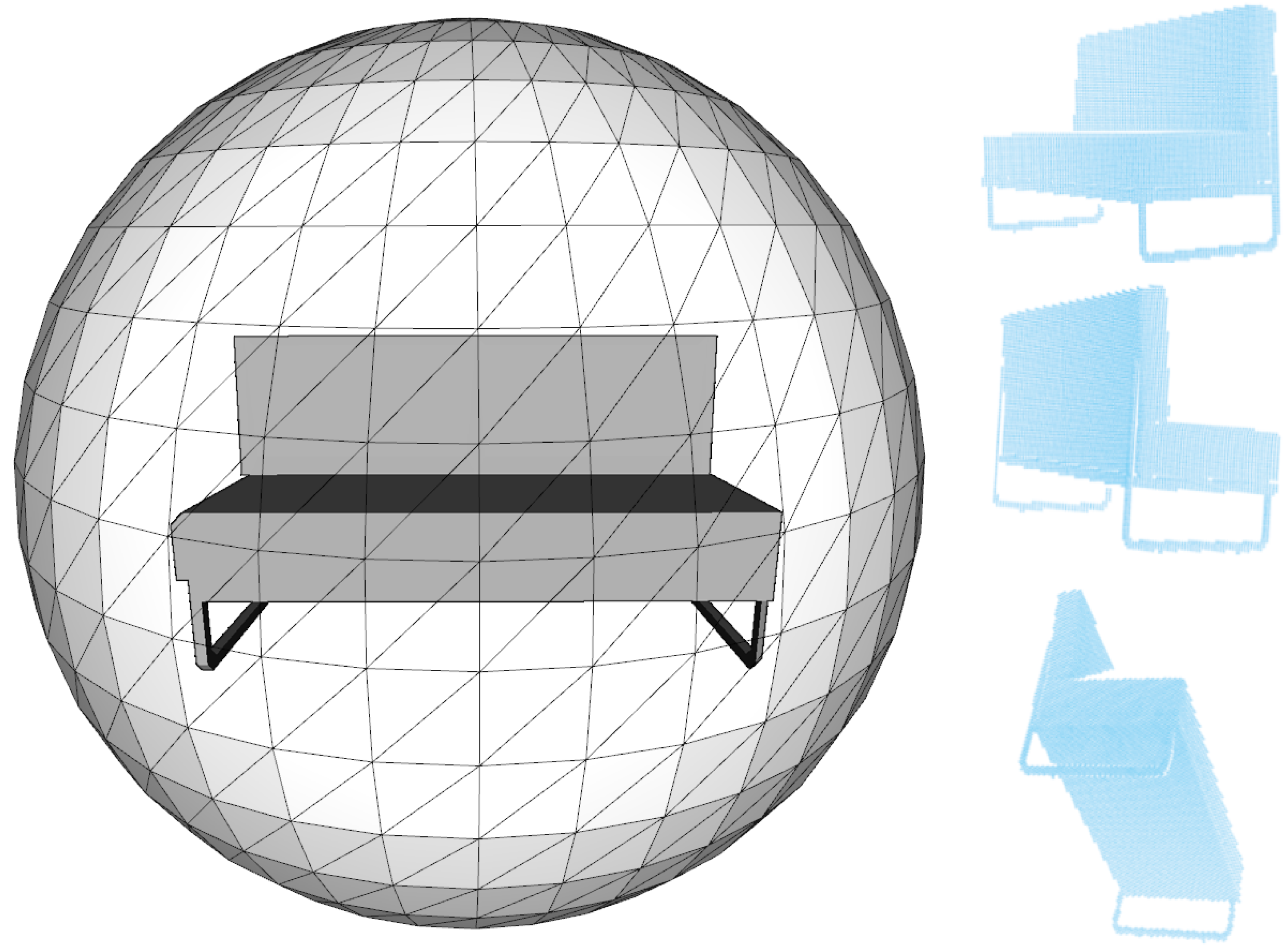
3.2. Training Data and Preprocessing
4. Experimentation
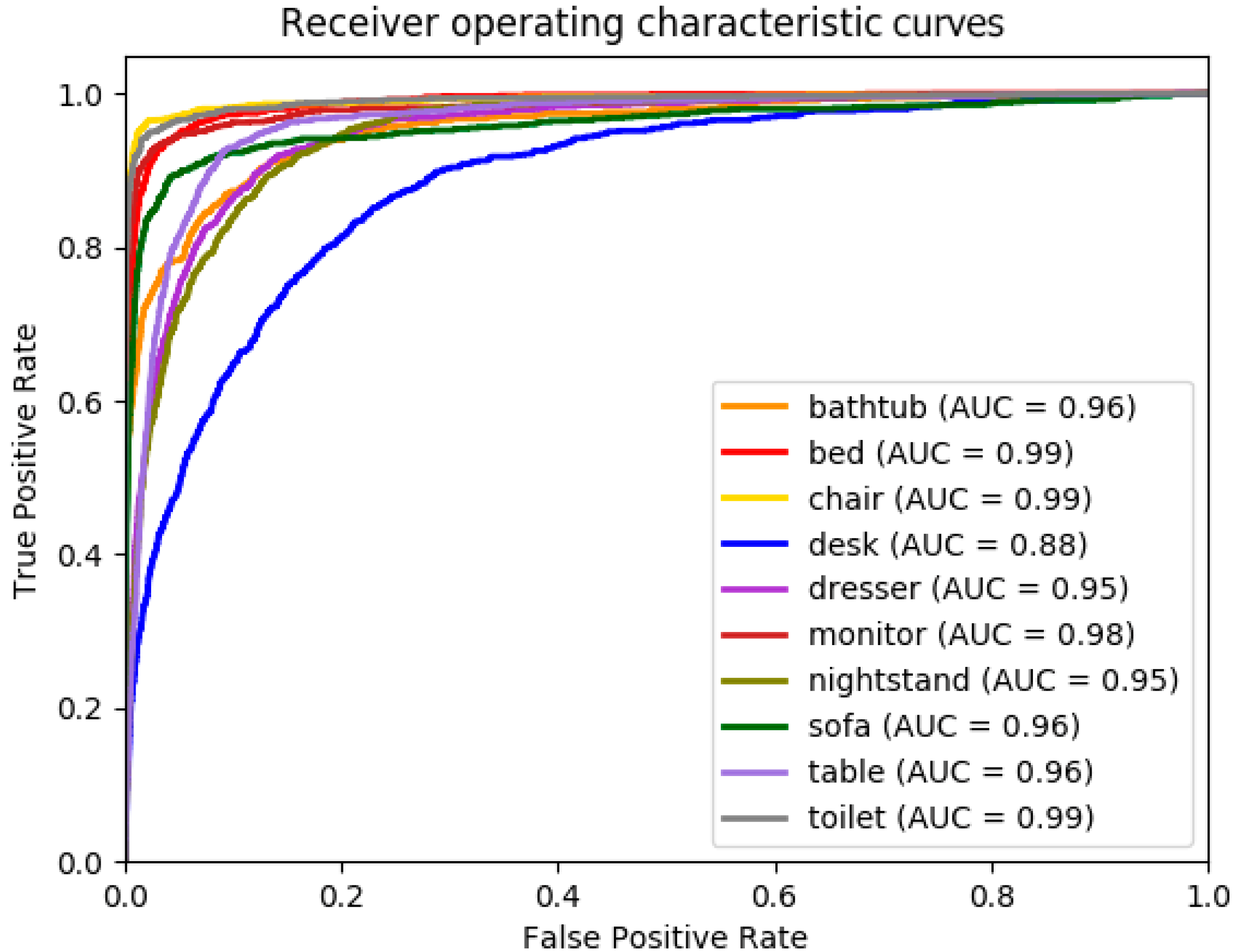
4.1. Results on the ModelNet10 Dataset
4.2. Results on Noisy ModelNet10 Dataset
4.3. Results on the ObjectNet Dataset
4.4. Results on the ShapeNetCoreV2 Dataset
4.5. Results on Real Data
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zrira, N.; Hannat, M.; Bouyakhf, E.H.; Khan, H.A. 2D/3D Object Recognition and Categorization Approaches for Robotic Grasping. In Advances in Soft Computing and Machine Learning in Image Processing; Springer: New York, NY, USA, 2018; pp. 567–593. [Google Scholar]
- Yang, K.; Tsai, T.; Yu, H.; Ho, T.Y.; Jin, Y. Beyond Digital Domain: Fooling Deep learning Based Recognition System in Physical World; American Association for Artificial Intelligence: Cambridge, CA, USA, 2020. [Google Scholar]
- Su, J.; Vargas, D.V.; Sakurai, K. One pixel attack for fooling deep neural networks. IEEE Trans. Evol. Comput. 2019, 23, 828–841. [Google Scholar] [CrossRef] [Green Version]
- Akhtar, N.; Mian, A. Threat of adversarial attacks on deep learning in computer vision: A survey. IEEE Access 2018, 6, 14410–14430. [Google Scholar] [CrossRef]
- Liu, Z.; Kersten, D. 2D observers for human 3D object recognition? Vision Res. 1998, 38, 2507–2519. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, E.; Saint, A.; Shabayek, A.E.R.; Cherenkova, K.; Das, R.; Gusev, G.; Aouada, D.; Ottersten, B. A survey on deep learning advances on different 3D data representations. arXiv 2018, arXiv:1808.01462. [Google Scholar]
- Naseer, M.; Khan, S.; Porikli, F. Indoor Scene Understanding in 2.5/3D for Autonomous Agents: A Survey. IEEE Access 2019, 7, 1859–1887. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, CA, USA, 2017; pp. 5099–5108. [Google Scholar]
- Klokov, R.; Lempitsky, V. Escape from Cells: Deep kd-Networks for the Recognition of 3d Point Cloud Models. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 863–872. [Google Scholar]
- Qi, C.R.; Litany, O.; He, K.; Guibas, L.J. Deep Hough Voting for 3d Object Detection in Point Clouds. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 9277–9286. [Google Scholar]
- Su, H.; Jampani, V.; Sun, D.; Maji, S.; Kalogerakis, E.; Yang, M.H.; Kautz, J. Splatnet: Sparse Lattice Networks for Point Cloud Processing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2530–2539. [Google Scholar]
- Li, J.; Chen, B.M.; Hee Lee, G. So-Net: Self-Organizing Network for Point Cloud Analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Lake City, UT, USA, 18–23 June 2018; pp. 9397–9406. [Google Scholar]
- Liu, Z.; Tang, H.; Lin, Y.; Han, S. Point-Voxel CNN for Efficient 3D Deep Learning. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2019; pp. 963–973. [Google Scholar]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-View Convolutional Neural Networks for 3d Shape Recognition. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar]
- Johns, E.; Leutenegger, S.; Davison, A.J. Pairwise Decomposition of Image Sequences for Active Multi-View Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3813–3822. [Google Scholar]
- Gomez-Donoso, F.; Garcia-Garcia, A.; Garcia-Rodriguez, J.; Orts-Escolano, S.; Cazorla, M. Lonchanet: A Sliced-Based cnn Architecture for Real-Time 3d Object Recognition. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, Alaska, 14–19 May 2017; pp. 412–418. [Google Scholar]
- Princeton ModelNet Challenge. Available online: https://modelnet.cs.princeton.edu (accessed on 13 May 2020).
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A Deep Representation for Volumetric Shapes. Available online: https://arxiv.org/abs/1406.5670 (accessed on 15 April 2015).
- Maturana, D.; Scherer, S. Voxnet: A 3d Convolutional Neural Network for Real-Time Object Recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 922–928. [Google Scholar]
- Le, T.; Duan, Y. Pointgrid: A Deep Network for 3d Shape Understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9204–9214. [Google Scholar]
- Sharma, A.; Grau, O.; Fritz, M. Vconv-dae: Deep Volumetric Shape Learning without Object Labels. In Proceedings of the IEEE European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 236–250. [Google Scholar]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. Generative and discriminative voxel modeling with convolutional neural networks. arXiv 2016, arXiv:1608.04236. [Google Scholar]
- Wu, J.; Zhang, C.; Xue, T.; Freeman, B.; Tenenbaum, J. Learning a Probabilistic Latent Space of Object Shapes via 3d Generative-Adversarial Modeling. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2016; pp. 82–90. [Google Scholar]
- Qi, C.R.; Su, H.; Nießner, M.; Dai, A.; Yan, M.; Guibas, L.J. Volumetric and Multi-View Cnns for Object Classification on 3d Data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5648–5656. [Google Scholar]
- Wang, P.S.; Liu, Y.; Guo, Y.X.; Sun, C.Y.; Tong, X. O-cnn: Octree-Based Convolutional Neural Networks for 3d Shape Analysis. ACM Trans. Graphics (TOG) 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Tatarchenko, M.; Dosovitskiy, A.; Brox, T. Octree Generating Networks: Efficient Convolutional Architectures for High-Resolution 3d Outputs. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2088–2096. [Google Scholar]
- Firman, M. RGBD Datasets: Past, Present and Future. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 19–31. [Google Scholar]
- Lai, K.; Bo, L.; Ren, X.; Fox, D. A Large-Scale Hierarchical Hulti-View rgb-d Object Dataset. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1817–1824. [Google Scholar]
- Liu, A.; Wang, Z.; Nie, W.; Su, Y. Graph-based characteristic view set extraction and matching for 3D model retrieval. Inf. Sci. 2015, 320, 429–442. [Google Scholar] [CrossRef]
- Singh, A.; Sha, J.; Narayan, K.S.; Achim, T.; Abbeel, P. Bigbird: A Large-Scale 3d Database of Object Instances. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 509–516. [Google Scholar]
- Calli, B.; Singh, A.; Walsman, A.; Srinivasa, S.; Abbeel, P.; Dollar, A.M. The ycb Object and Model set: Towards Common Benchmarks for Manipulation Research. In Proceedings of the 2015 International Conference on Advanced Robotics (ICAR), Istanbul, Turkey, 27–31 July 2015; pp. 510–517. [Google Scholar]
- Choi, S.; Zhou, Q.Y.; Miller, S.; Koltun, V. A large dataset of object scans. arXiv 2016, arXiv:1602.02481. [Google Scholar]
- Song, S.; Lichtenberg, S.P.; Xiao, J. SUN RGB-D: A RGB-D Scene Understanding Benchmark Suite; IEEE Computer Society: Washington DC, USA, 2015; pp. 567–576. [Google Scholar]
- Dai, A.; Chang, A.X.; Savva, M.; Halber, M.; Funkhouser, T.; Nießner, M. ScanNet: Richly-annotated 3D Reconstructions of Indoor Scenes. arXiv 2017, arXiv:1702.04405. [Google Scholar]
- Armeni, I.; Sax, A.; Zamir, A.R.; Savarese, S. Joint 2D-3D-Semantic Data for Indoor Scene Understanding. arXiv 2017, arXiv:1702.01105. [Google Scholar]
- Xiang, Y.; Kim, W.; Chen, W.; Ji, J.; Choy, C.; Su, H.; Mottaghi, R.; Guibas, L.; Savarese, S. ObjectNet3D: A Large Scale Database for 3D Object Recognition. In Proceedings of the European Conference Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Garcia-Garcia, A.; Gomez-Donoso, F.; Garcia-Rodriguez, J.; Orts-Escolano, S.; Cazorla, M.; Azorin-Lopez, J. PointNet: A 3D Convolutional Neural Network for Real-Time Object Class Recognition. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1578–1584. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. arXiv 2016, arXiv:1612.00593. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. ShapeNet: An Information-Rich 3D Model Repository. Available online: https://arxiv.org/abs/1512.03012 (accessed on 9 December 2015).




| Predicted | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bathtub | Bed | Chair | Desk | Dresser | Monitor | Nightstand | Sofa | Table | Toilet | ||
| Actual | bathtub | 59 | 5 | 3 | 2 | 3 | 4 | 1 | 15 | 2 | 4 |
| bed | 1 | 89 | 0 | 1 | 0 | 1 | 0 | 4 | 2 | 1 | |
| chair | 0 | 1 | 95 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | |
| desk | 1 | 5 | 2 | 41 | 7 | 3 | 6 | 10 | 23 | 2 | |
| dresser | 1 | 1 | 0 | 2 | 71 | 3 | 16 | 2 | 2 | 1 | |
| monitor | 0 | 1 | 1 | 1 | 2 | 91 | 1 | 1 | 2 | 1 | |
| nightstand | 1 | 1 | 0 | 5 | 20 | 2 | 64 | 1 | 6 | 1 | |
| sofa | 0 | 3 | 1 | 1 | 2 | 3 | 3 | 85 | 0 | 1 | |
| table | 0 | 2 | 1 | 14 | 2 | 0 | 2 | 2 | 77 | 0 | |
| toilet | 0 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 0 | 92 | |
| Bathtub | Bed | Chair | Desk | Dresser | Monitor | Night | Sofa | Table | Toilet | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| View ID | 1 | 75 | 75 | 95.7 | 48.6 | 64.3 | 97.5 | 68.8 | 62.7 | 78.9 | 91.1 |
| 2 | 66.7 | 76.5 | 84.2 | 48.1 | 63.5 | 95.9 | 79.4 | 74.5 | 67.4 | 96.1 | |
| 3 | 84.6 | 80 | 91.8 | 68 | 77.3 | 89.1 | 69.6 | 76.6 | 78.7 | 88.9 | |
| 4 | 100 | 90 | 89.1 | 56.5 | 77.8 | 87.7 | 69.6 | 74.5 | 71.7 | 86.4 | |
| 5 | 100 | 95.1 | 83.6 | 54.5 | 57.6 | 87.7 | 55.8 | 69.4 | 69.2 | 88 | |
| 6 | 80 | 92.9 | 83.9 | 50 | 58.5 | 83.3 | 57.5 | 75 | 71.7 | 83.6 | |
| 7 | 81.2 | 95.2 | 96.1 | 50 | 63.5 | 83.3 | 67.4 | 74.5 | 69.2 | 94.8 | |
| 8 | 81.2 | 80 | 92.5 | 54.2 | 75 | 90.7 | 72.5 | 75 | 70.2 | 100 | |
| 9 | 25 | 54.9 | 74.5 | 20 | 57.4 | 69 | 47.1 | 56.9 | 58.8 | 84.3 | |
| 10 | 100 | 87 | 92.5 | 62.5 | 72.2 | 96.2 | 82.9 | 84.4 | 77.3 | 86.4 | |
| 11 | 95 | 93.3 | 100 | 57.9 | 72.5 | 90.6 | 80 | 89.7 | 75.6 | 86.9 | |
| 12 | 90.5 | 86 | 94 | 65.2 | 72.3 | 96.2 | 67.4 | 81.8 | 64.3 | 98.1 | |
| 13 | 65 | 73.5 | 88 | 36.8 | 42.6 | 74.1 | 57.8 | 59.2 | 40 | 83.1 | |
| 14 | 100 | 86 | 98 | 69.6 | 72.3 | 90.9 | 77.1 | 81 | 64.3 | 96.4 | |
| 15 | 100 | 81.5 | 98 | 65.2 | 68.4 | 98 | 70.7 | 92.3 | 69.1 | 94.3 | |
| 16 | 90.9 | 93.8 | 100 | 74.1 | 76.6 | 96.2 | 71.7 | 86 | 75.9 | 98.1 | |
| 17 | 94.4 | 97.7 | 94.2 | 52.8 | 74.5 | 94.1 | 74 | 81 | 64.3 | 96.5 | |
| 18 | 100 | 95.3 | 98 | 57.5 | 69.1 | 91.1 | 73.3 | 83.7 | 76.3 | 100 | |
| 19 | 55.6 | 63.3 | 74.2 | 17.6 | 54.8 | 85.7 | 48.7 | 59.1 | 60 | 83.1 | |
| 20 | 92.9 | 91.3 | 88.7 | 73.9 | 75.5 | 92.6 | 73.9 | 75.6 | 78.4 | 86.7 | |
| 21 | 60 | 75 | 93.6 | 51.4 | 55.6 | 72.5 | 52.9 | 63.5 | 71.2 | 93.1 | |
| 22 | 100 | 91.5 | 98 | 73.1 | 76.5 | 89.5 | 86.4 | 81.4 | 81.2 | 98.2 | |
| 23 | 100 | 95.5 | 96 | 62.1 | 75.5 | 87.9 | 80 | 83.3 | 71.2 | 93.2 | |
| 24 | 50 | 81.8 | 89.6 | 44.1 | 52.5 | 74.5 | 48.8 | 53.5 | 53.1 | 94.5 | |
| 25 | 100 | 88 | 96.1 | 62.5 | 74.5 | 90.9 | 80.5 | 75 | 74 | 96.6 |
| Noise Level | 0.01 | 0.05 | 0.15 | 0.20 | 0.25 | 0.30 | 0.40 | 0.50 | 0.75 | 1.00 |
| Par3DNet Accuracy (%) | 78.41 | 78.14 | 76.27 | 73.76 | 70.9 | 56.79 | 54.81 | 52.35 | 45.63 | 43.61 |
| PointNet Accuracy (%) | 56.27 | 56.36 | 56.10 | 56.15 | 56.20 | 56.13 | 55.86 | 55.97 | 55.19 | 54.50 |
| Predicted | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bathtub | Bed | Chair | Sofa | Table | Toilet | Desk | Dresser | Monitor | Nightstand | ||
| Actual | bathtub | 32 | 22 | 2 | 16 | 4 | 5 | 2 | 4 | 9 | 4 |
| bed | 2 | 76 | 1 | 0 | 1 | 5 | 0 | 3 | 2 | 10 | |
| chair | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| sofa | 0 | 2 | 8 | 48 | 0 | 14 | 0 | 0 | 24 | 4 | |
| table | 0 | 0 | 0 | 0 | 96 | 0 | 2 | 0 | 0 | 2 | |
| toilet | 8 | 3 | 0 | 0 | 5 | 78 | 0 | 1 | 0 | 5 | |
| Predicted | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bathtub | Bed | Chair | Sofa | Table | Toilet | Desk | Dresser | Monitor | Nightstand | ||
| Actual | bathtub | 52 | 7 | 4 | 11 | 4 | 5 | 3 | 7 | 4 | 6 |
| bed | 1 | 46 | 8 | 6 | 11 | 4 | 9 | 3 | 4 | 9 | |
| chair | 1 | 4 | 78 | 2 | 2 | 6 | 1 | 1 | 3 | 3 | |
| sofa | 2 | 5 | 1 | 82 | 1 | 1 | 2 | 2 | 3 | 1 | |
| table | 1 | 4 | 2 | 3 | 67 | 1 | 12 | 3 | 2 | 6 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez-Donoso, F.; Escalona, F.; Cazorla, M. Par3DNet: Using 3DCNNs for Object Recognition on Tridimensional Partial Views. Appl. Sci. 2020, 10, 3409. https://doi.org/10.3390/app10103409
Gomez-Donoso F, Escalona F, Cazorla M. Par3DNet: Using 3DCNNs for Object Recognition on Tridimensional Partial Views. Applied Sciences. 2020; 10(10):3409. https://doi.org/10.3390/app10103409
Chicago/Turabian StyleGomez-Donoso, Francisco, Felix Escalona, and Miguel Cazorla. 2020. "Par3DNet: Using 3DCNNs for Object Recognition on Tridimensional Partial Views" Applied Sciences 10, no. 10: 3409. https://doi.org/10.3390/app10103409
APA StyleGomez-Donoso, F., Escalona, F., & Cazorla, M. (2020). Par3DNet: Using 3DCNNs for Object Recognition on Tridimensional Partial Views. Applied Sciences, 10(10), 3409. https://doi.org/10.3390/app10103409







