Seismic Performance of Various Piles Considering Soil–Pile Interaction under Lateral Cycle Loads for Integral Abutment Jointless Bridges (IAJBs)
Abstract
:1. Introduction
2. Description of Test
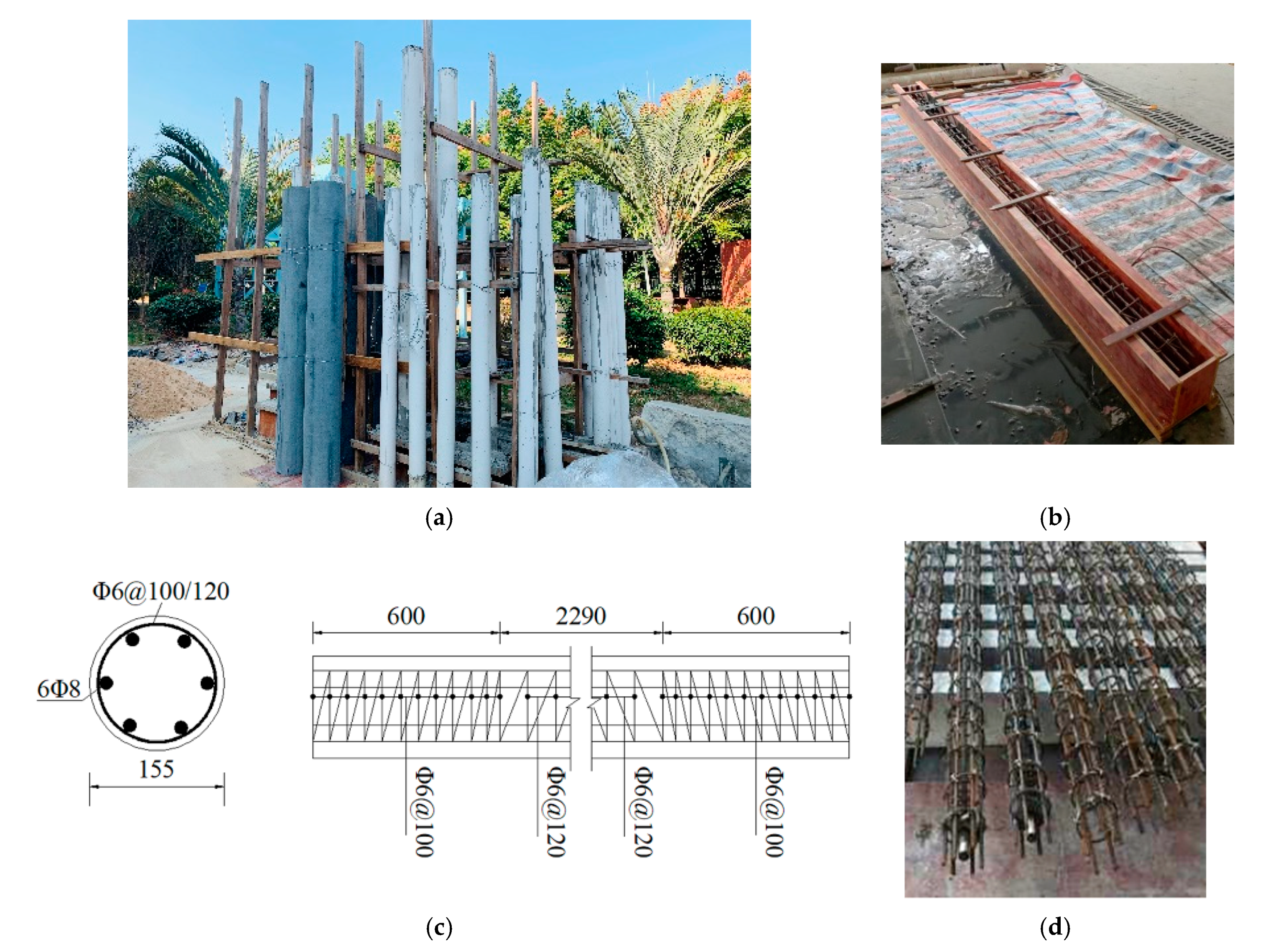
2.1. Specimen Design and Fabrication
2.1.1. Specimen Design
2.1.2. Specimen Materials and Soil Properties
Specimen Materials’ Characteristics
Soil Properties
2.1.3. Specimen Fabrication
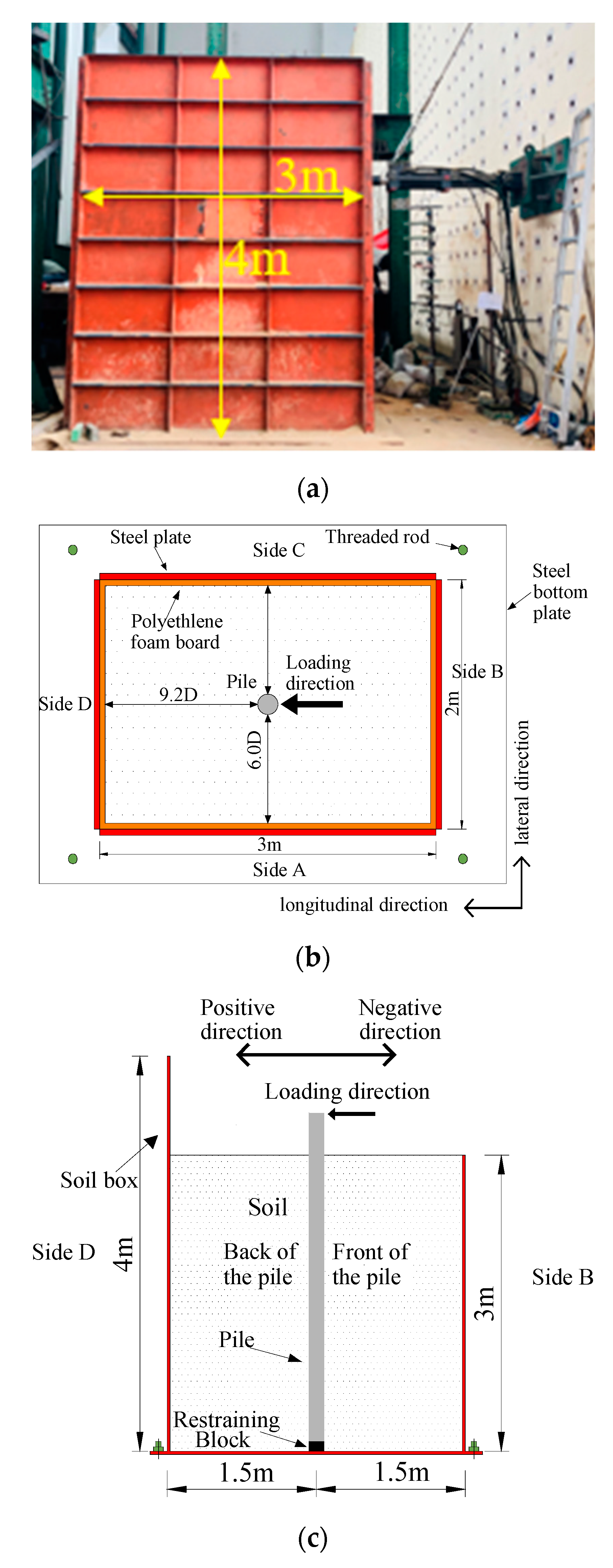
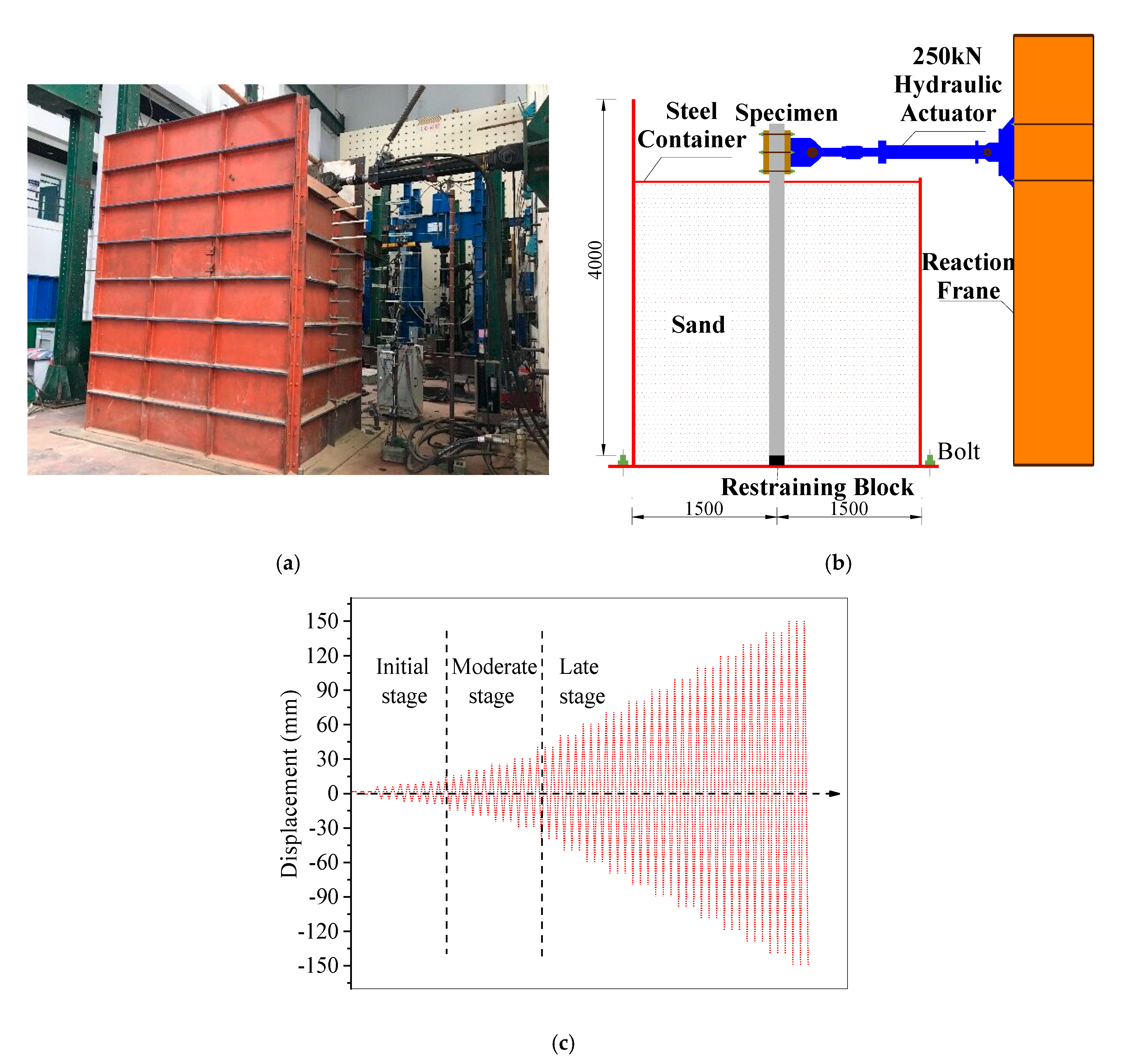
2.2. Soil Box Design and Specimen Installation
2.2.1. Soil Box Design
2.2.2. Specimen Installation
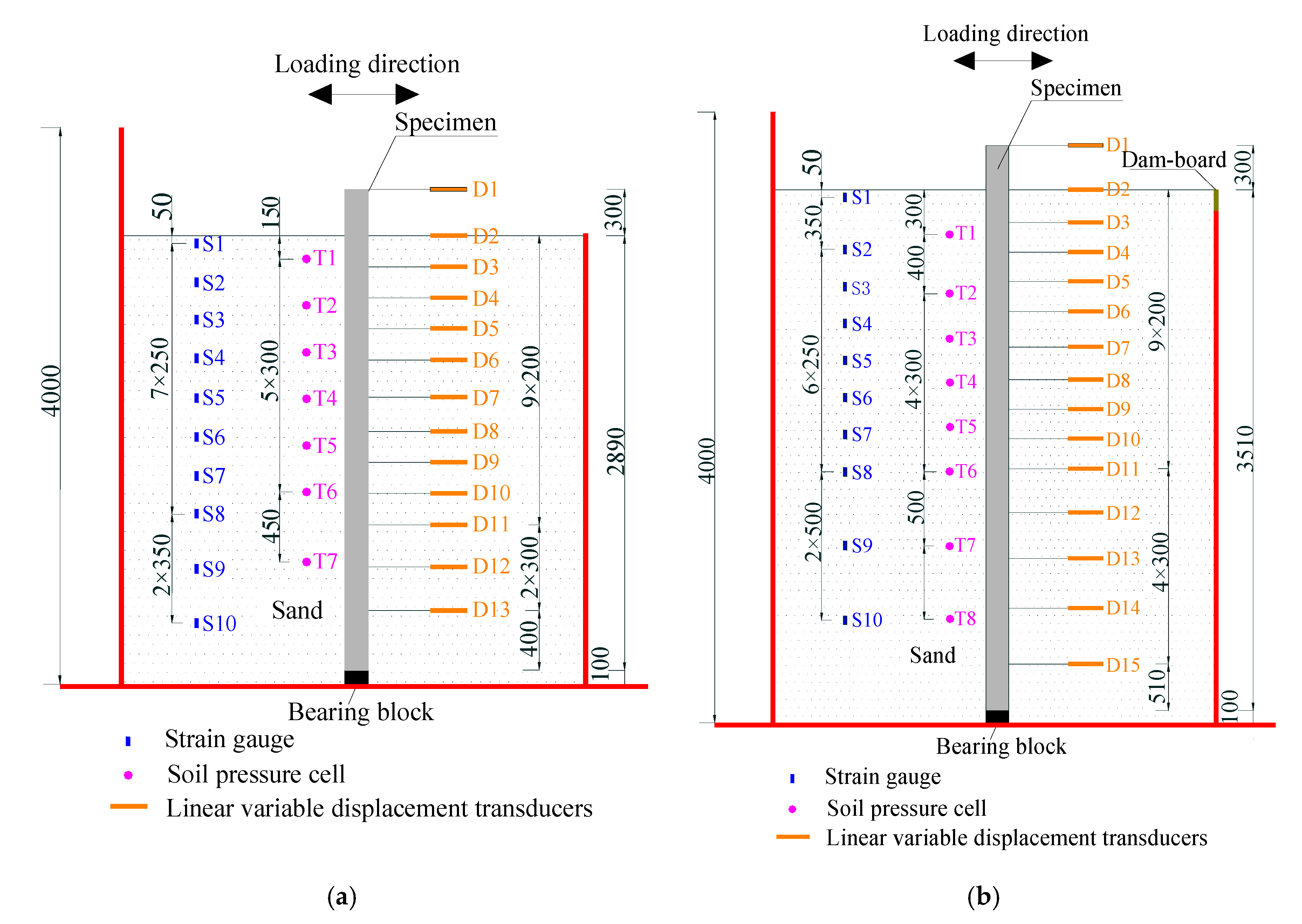
2.3. Layout of Measuring Sensors
2.4. Loading Protocol
3. Experimental Results
3.1. Damage Modes
3.2. Horizontal Deformations
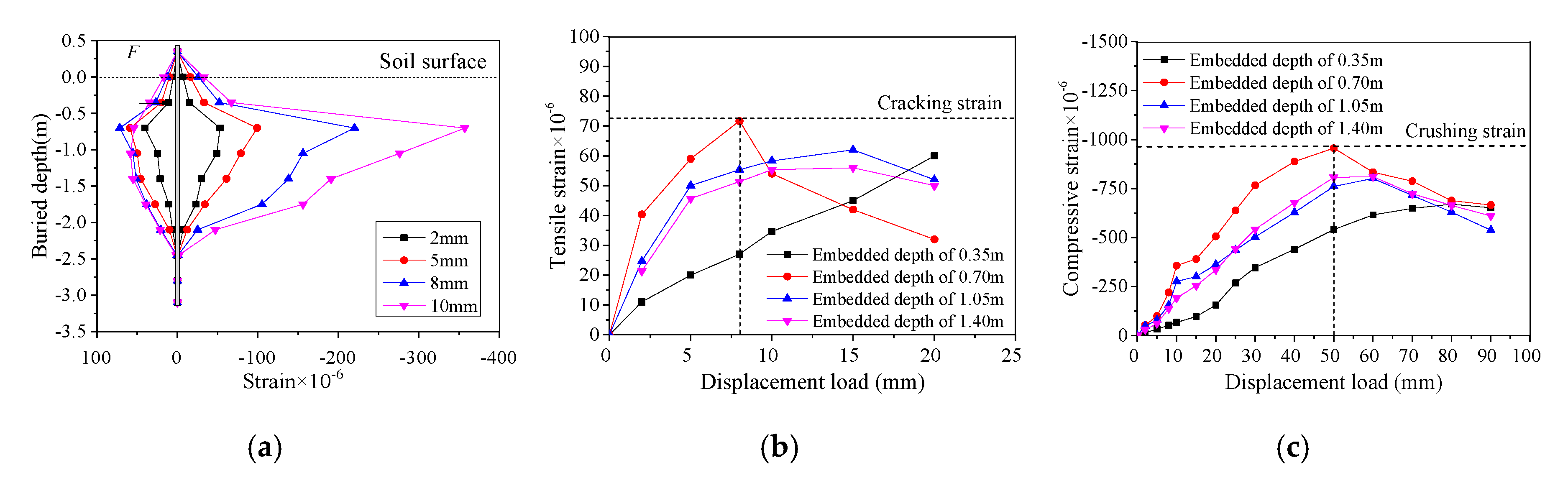
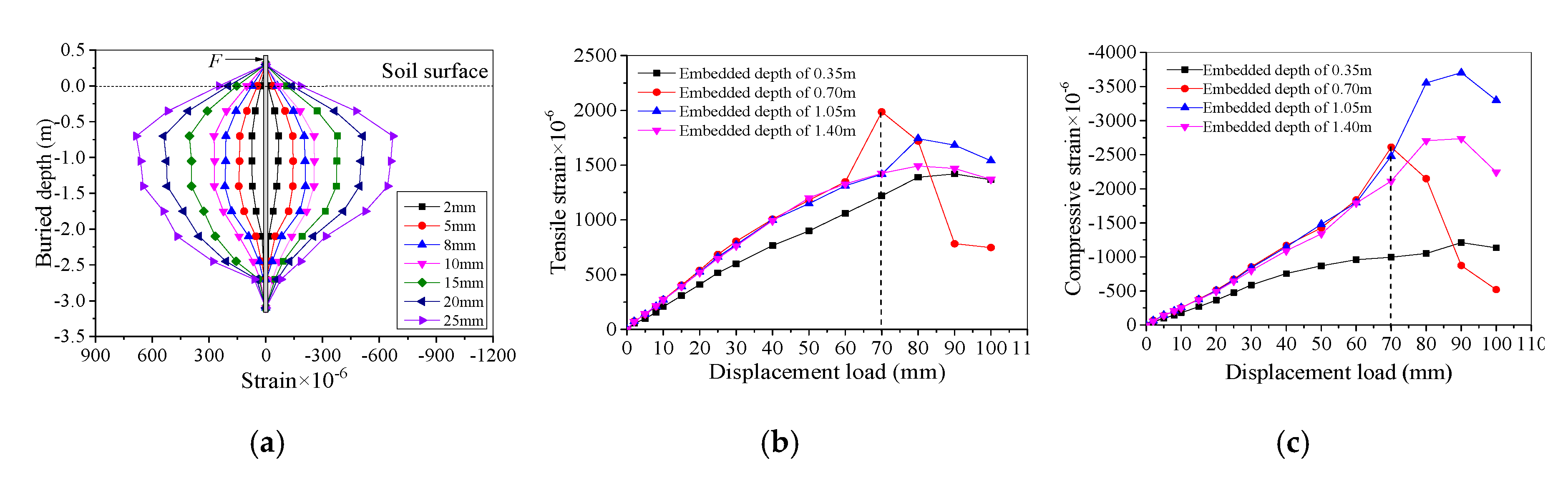
3.3. Strain Distributions
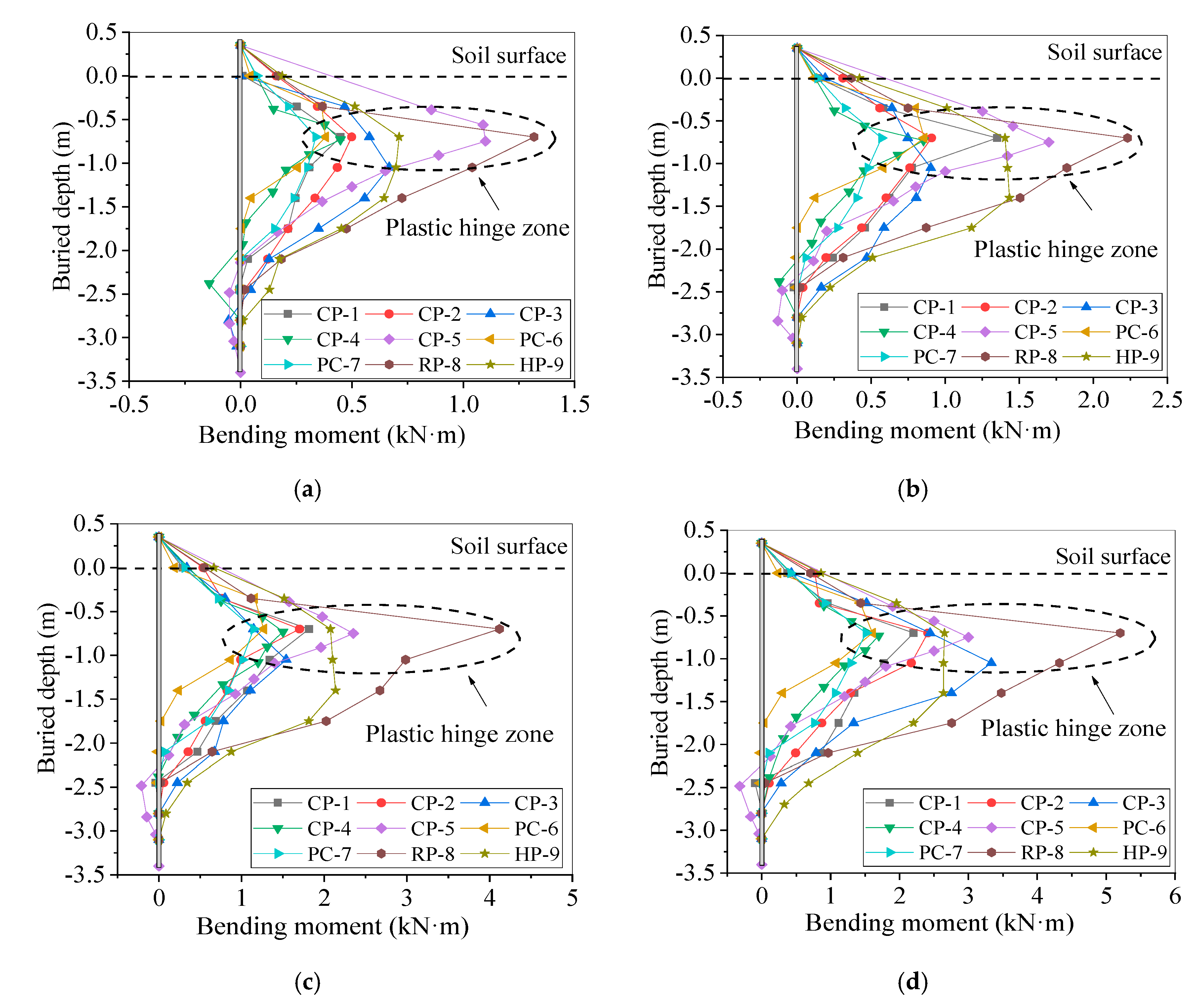
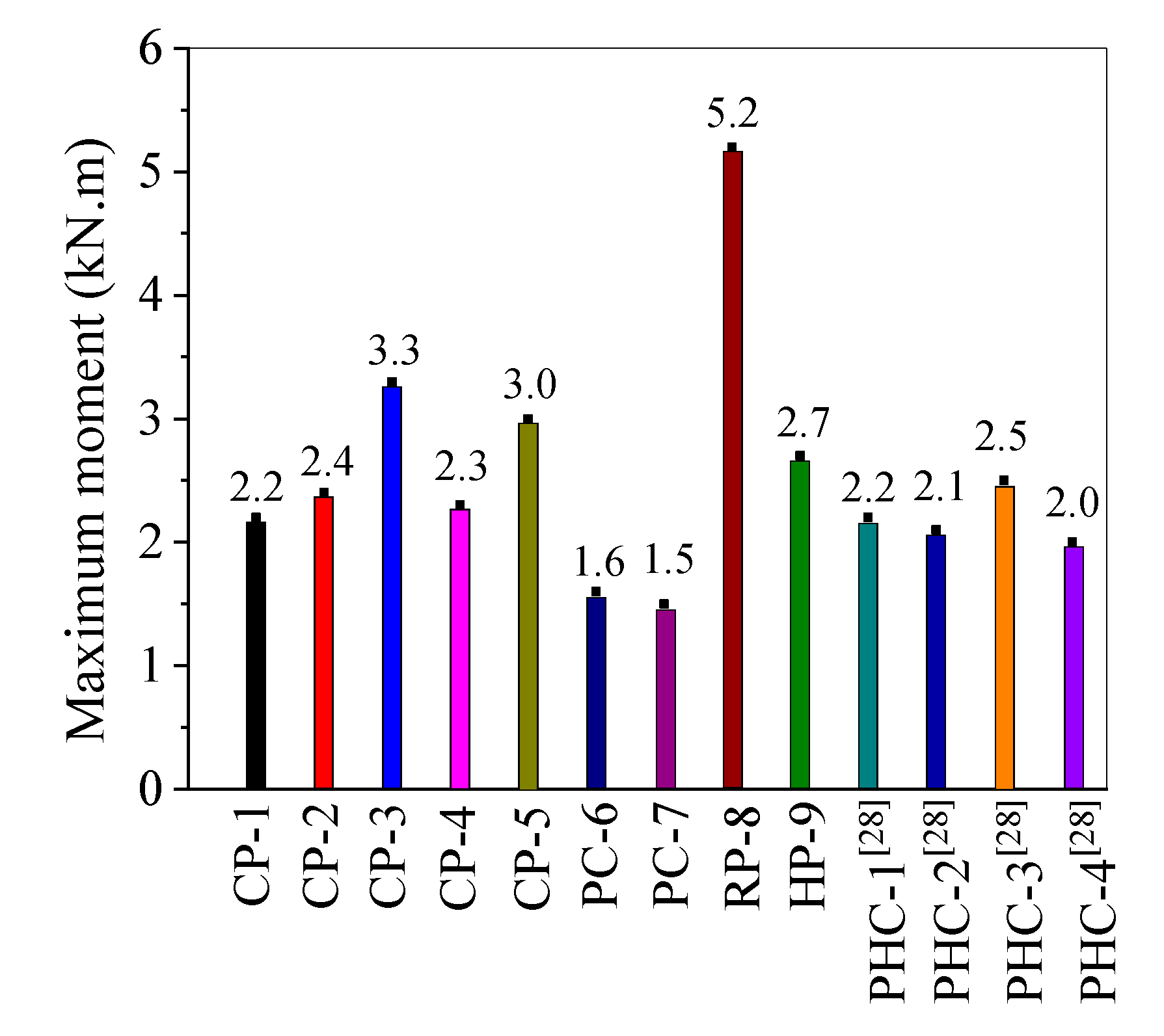
3.4. Bending Moment of Piles
3.4.1. Calculation of Bending Moment
3.4.2. The Analyses of Bearing Ratio
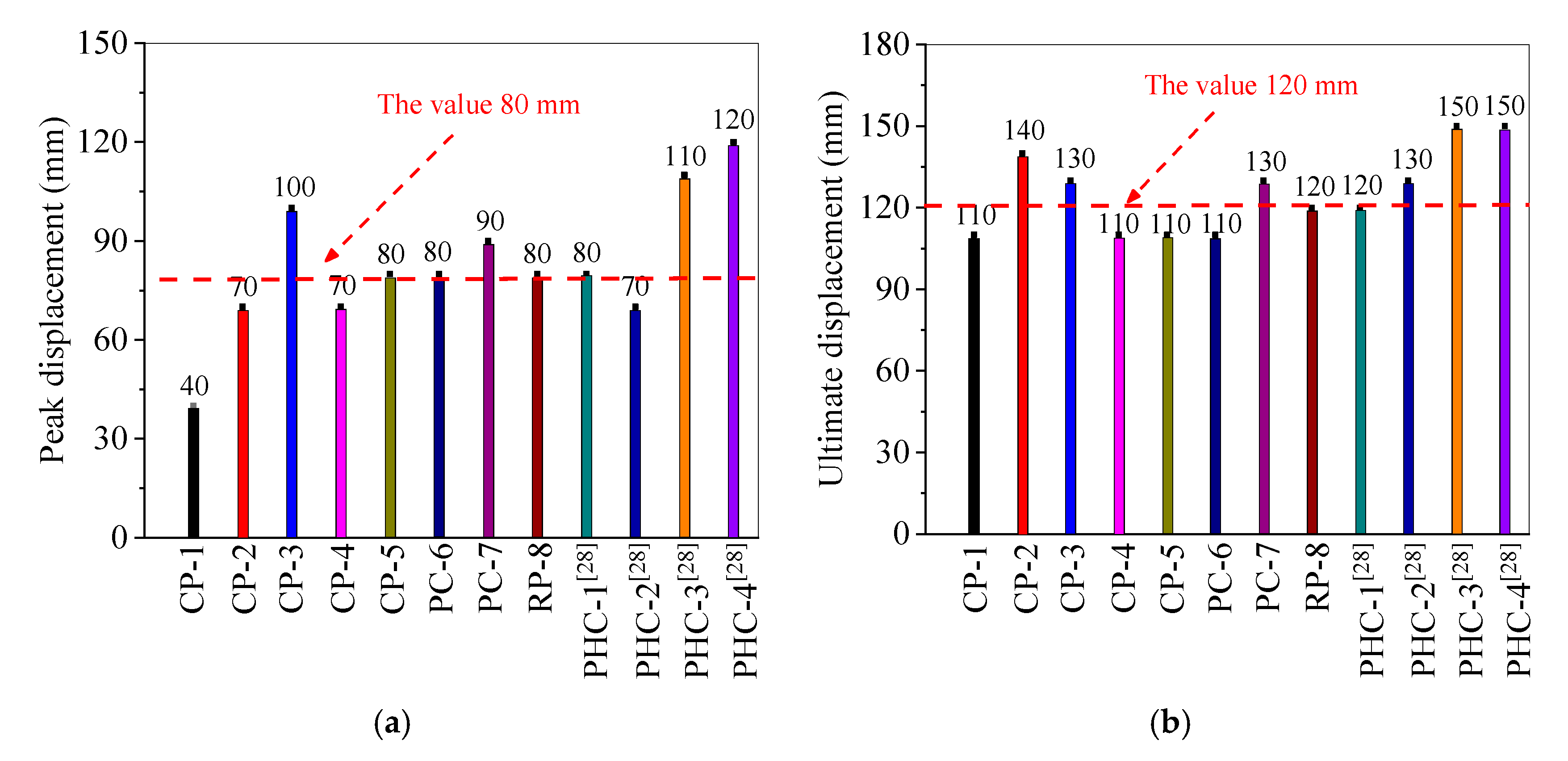
3.5. Hysteresis and Backbone Curves
3.5.1. Hysteresis Curves
3.5.2. Backbone Curves
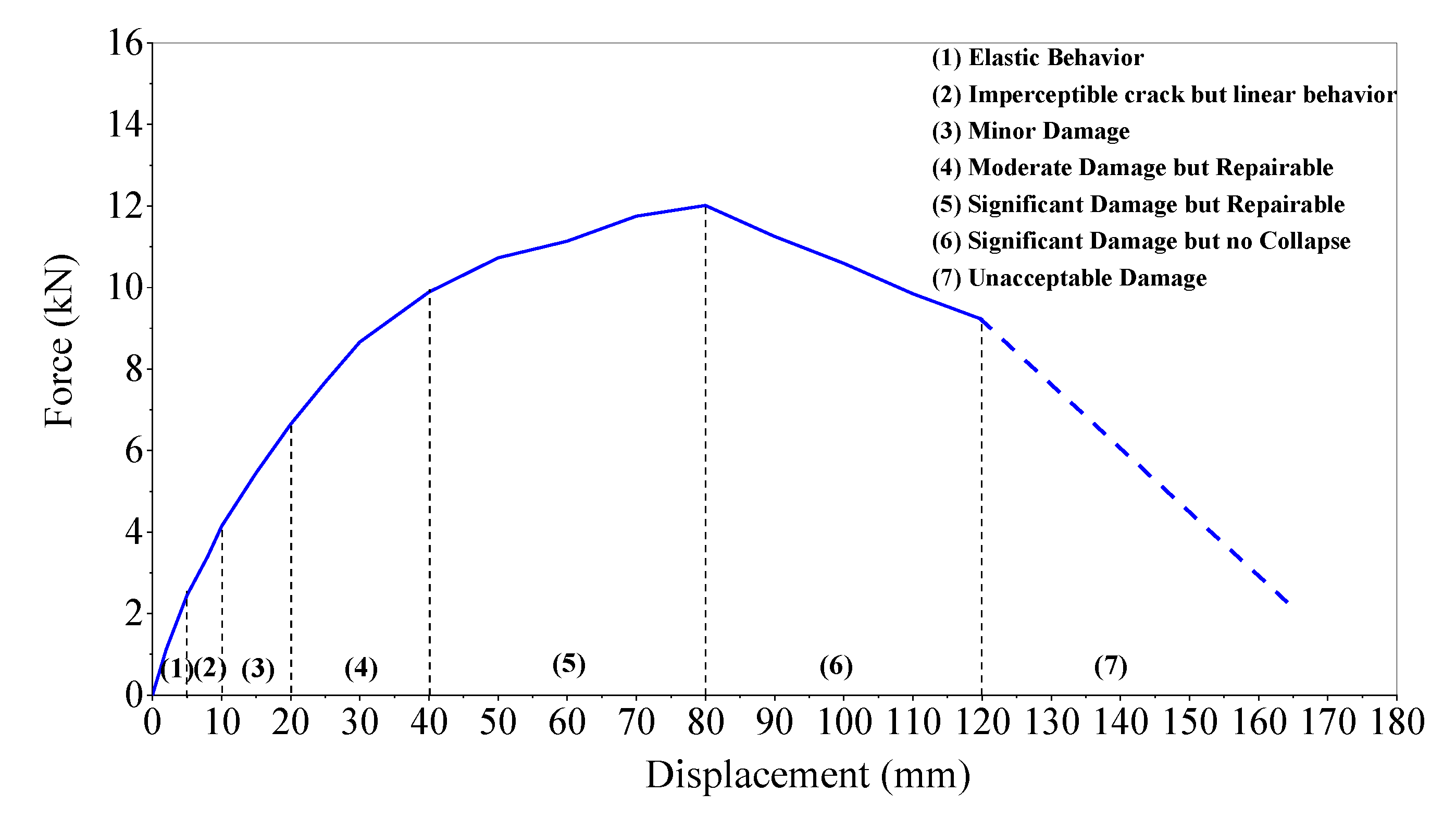
4. Displacement-Based Seismic Design of Pile
5. Conclusions
- (1)
- With the increase of reinforcement ratio, buried pile depth and prestressing level, the pile damage depth shifted to a deeper depth of the pile and also showed a better pile–soil interaction. Moreover, the rectangular pile had a larger soil–pile interaction than the circular pile. The H-shaped steel pile showed a better elastic-plastic deformation capacity, ductility and energy dissipation capacity as compared to the concrete pile.
- (2)
- The inflection point of pile deformations shifted deeper with the increase of reinforcement ratio, buried pile depth and prestressing level, which increased the effective length and horizontal deformation capacity of the pile. The deformation inflection point of the PHC pipe piles was at a deeper buried depth as compared to the reinforced concrete piles.
- (3)
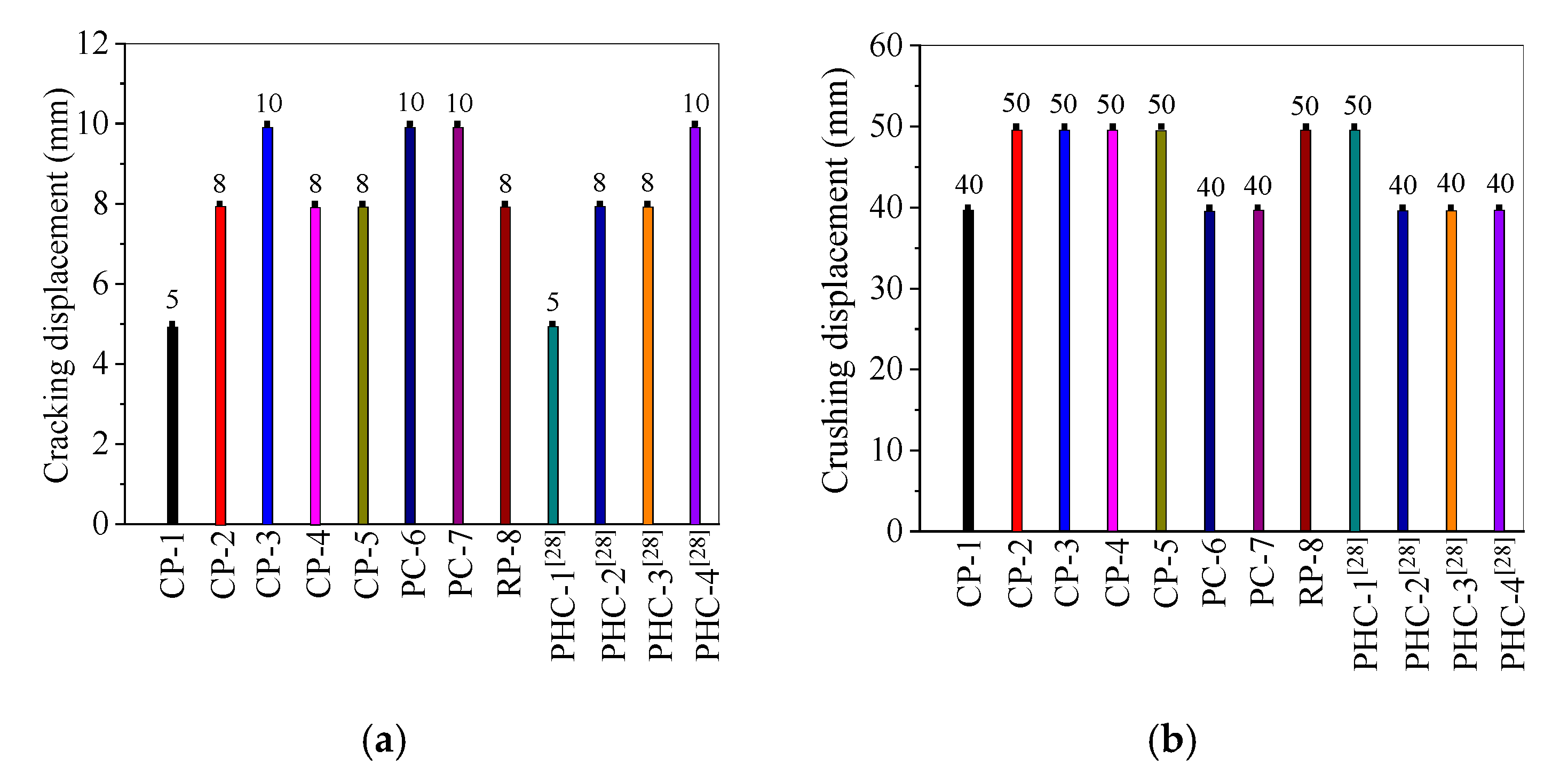
- The crack resistance of concrete piles was improved with the increase of reinforcement ratio and prestressing level, which is advantageous for the crack resistance design of the reinforced concrete, prestressed and PHC pipe pile foundations in IAJBs. The effect of the larger reinforcement ratio and prestressing level on the concrete crushing was insignificant.
- (4)
- The hysteresis area of the H-shaped steel pile was larger than the concrete pile which demonstrated a greater energy dissipation capacity. Moreover, the pile foundation with larger buried depth, prestressing level and cross-section had a better energy dissipation capacity.
- (5)
- The pile with larger bearing ratio can sustain more bearing capacity whereas the surrounding soil may be subject to larger loads.
- (6)
- The seismic design criteria of three-stage seismic fortification and five damage levels of the concrete piles can be used as a design reference for IAJBs. Currently, considering that the pile foundations are susceptible to earthquake damage, studies on the restoration and reinforcement of pile foundations do not go into sufficient detail following earthquake events.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Erhan, S.; Diclell, M. Effect of dynamic soil–bridge interaction modeling assumptions on the calculated seismic response of integral bridges. Soil Dyn. Earthq. Eng. 2014, 66, 42–55. [Google Scholar] [CrossRef]
- Peric, D.; Miletic, M.; Shah, B.R.; Esmaeily, A.; Wang, H. Thermally Induced Soil Structure Interaction in the Existing Integral Bridge. Eng. Struct. 2016, 106, 484–494. [Google Scholar] [CrossRef]
- Cheng, J.F.; Luo, X.F.; Zhuang, Y.Z.; Xu, L.; Luo, X.Y. Experimental Study on Dynamic Response of Characteristics of RPC and RC Micro Piles in SAJBs. Appl. Sci. 2019, 9, 2644. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.C.; Zhuang, Y.Z.; Huang, F.Y.; Briseghella, B. Jointless Bridges, 2nd ed.; China Communication Press: Beijing, China, 2019. [Google Scholar]
- Su, D.; Huang, J.J.; Yan, W.M. Parametric Investigation on the Responses of Laterally Loaded Piles in Overconsolidated Clay Using Nondimensional Solutions Addressing Nonlinear Soil-Pile Interaction. Comput. Geotech. 2018, 96, 203–214. [Google Scholar] [CrossRef]
- Arsoy, S.; Duncan, J.M.; Barker, R.M. Performance of Piles Supporting Integral Bridges. J. Transp. Res. Board 2002, 1808, 162–167. [Google Scholar] [CrossRef]
- Huang, F.Y.; Shan, Y.L.; Chen, G.D.; Lin, Y.W.; Tabatabai, H.; Briseghella, B. Experiment on Interaction of Abutment, Steel H-pile and Soil in Integral Abutment Jonitless Bridges (IAJBs) under Low-Cycle Pseudo-Static Displacement Loads. Appl. Sci. 2020, 10, 1358. [Google Scholar] [CrossRef] [Green Version]
- Kalaycı, E.; Civjan, S.A.; Breña, S.F.; Allen, C.A. Load Testing and Modeling of Two Integral Abutment Bridges in Vermont, US. Struct. Eng. Int. 2011, 21, 181–188. [Google Scholar] [CrossRef]
- Civjan, S.A.; Bonczar, C.; Brena, S.F.; DeJong, J.; Crovo, D. Integral Abutment Bridge Behavior: Parametric Analysis of a Massachusetts Bridge. J. Bridge Eng. 2007, 12, 64–71. [Google Scholar] [CrossRef]
- Sherafati, A.; Azizinamini, A. Flexible Pile Head in Jointless Bridges: Experimental Investigation. J. Bridge Eng. 2014, 20, 04014071-1–04014071-12. [Google Scholar] [CrossRef]
- Lafave, J.M.; Fahnestock, L.A.; Jarrett, M.; Wright, B.; Riddle, J.; Svatora, J. Numerical Simulations and Field Monitoring of Integral Abutment Bridges. Struct. Congress 2015, 561–572. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, L. Behavior of Model Steel H-Pile-to-Pile-Cap Connections. J. Constr. Steel Res. 2013, 80, 53–162. [Google Scholar] [CrossRef]
- Karalar, M.; Dicleli, M. Fatigue in Jointless Bridge H-piles under Axial Load and Thermal Movements. J. Constr. Steel Res. 2018, 147, 504–522. [Google Scholar] [CrossRef]
- Far, N.E.; Maleki, S.; Barghian, M. Design of Integral Abutment Bridges for Combined Thermal and Seismic Loads. Earthq. Struct. 2015, 9, 415–430. [Google Scholar] [CrossRef]
- White, H.; Petursson, H.; Collin, P. Integral Abutment Bridges: The European Way. Pract. Period. Struct. Des. Constr. 2010, 15, 201–208. [Google Scholar] [CrossRef]
- Chen, B.C.; Fu, C.; Zhuang, Y.Z.; Briseghella, B. Application Status and Development Strategies of Jointless Bridge in China. J. China Foreign Highw. 2018, 38, 87–95. (In Chinese) [Google Scholar]
- Kong, B.; Cai, C.S.; Zhang, Y. Parametric Study of an Integral Abutment Bridge Supported by Prestressed Precast Concrete Piles. Eng. Struct. 2016, 120, 37–48. [Google Scholar] [CrossRef]
- Kong, B.; Cai, C.S.; Kong, X. Field Monitoring Study of An Integral Abutment Bridge Supported by Prestressed Precast Concrete Piles on Soft Soils. Eng. Struct. 2015, 104, 18–31. [Google Scholar] [CrossRef]
- Gama, D.; Almeida, J.F. Concrete Integral Abutment Bridges with Reinforced Concrete Piles. Struct. Concr. 2014, 15, 292–304. [Google Scholar] [CrossRef]
- Kamel, M.R.; Benak, J.V.; Tadros, M.K. Application of Precast, Prestressed Concrete Piles in Integral Abutment Bridges. In Proceedings of the Fourth International Bridge Engineering Conference, San Francisco, CA, USA, 28–30 August 1995; pp. 146–157. [Google Scholar]
- Chen, B.C.; Luo, X.Y.; Huang, F.Y.; Dong, R.; Xue, J.Q. Displacement-Based Simplified Calculation for Pile-Soil Interaction under Reciprocating Low-Cycle Pseudo-Static Loads. J. Test. Eval. 2019, 49. [Google Scholar] [CrossRef]
- Luo, X.Y.; Huang, F.Y.; Zhuang, Y.Z.; Wu, S.W.; Qian, H.M. Modified Calculations of Lateral Displacement and Soil Pressure of Pile Considering Pile—Soil Interaction under Cyclic Loads. J. Test. Eval. 2019, 49. [Google Scholar] [CrossRef]
- Burdette, E.G.; Howard, S.C.; Ingram, E.E.; David, W. Behavior of prestressed concrete piles supporting integral abutment. In Proceedings of the 2004 Structures Congress: Building on the Past, Securing the Future, Nashville, TN, USA, 22–26 May 2004; pp. 213–218. [Google Scholar]
- Harries, K.A.; Petrou, M.F. Behavior of Precast, Prestressed Concrete Pile to Cast-in- Place Pile Cap Connections. PCI J. 2001, 46, 82–92. [Google Scholar] [CrossRef]
- Burdette, E.G.; Tidwell, J.B.; Ingram, E.E.; Goodpasture, D.W.; Howard, S.C.; Wasserman, E.P.; Deatherage, J.H. Lateral Load Tests on Prestressed Concrete Piles Supporting Integral Abutments. PCI J. 2004, 49, 70–77. [Google Scholar] [CrossRef]
- Abendroth, R.E.; Greimann, L.F.; LaViolette, M.D. An Integral Abutment Bridge with Precast Concrete Piles; Iowa State University: Ames, IA, USA, 2007. [Google Scholar]
- Hong, J.X.; Peng, D.W. Design of Shangban integral abutment bridge—Engineering application of jointless bridge. Fujian Archit. Constr. 2004, 5, 50–52. (In Chinese) [Google Scholar]
- Huang, F.Y.; Wu, S.W.; Luo, X.Y.; Chen, B.C.; Lin, Y.W. Pseudo-static Test on Mechanic Behavior of PHC Piles with Soil-Pile Interaction. Eng. Struct. 2018, 171, 992–1006. [Google Scholar] [CrossRef]
- Rollins, K.; Sparks, A.; Peterson, K. Lateral Load Capacity and Passive Resistance of Full-Scale Pile Group and Cap. Transportation Research Record. J. Transp. Res. Board 2000, 1736, 24–32. [Google Scholar] [CrossRef]
- Rollins, K.M.; Gerber, T.M.; Lane, J.D.; Ashford, S.A. Lateral Resistance of a Full-Scale Pile Group in Liquefied Sand. J. Geotech. Geoenviron. Eng. 2005, 131, 115–125. [Google Scholar] [CrossRef]
- Nimityongskul, N.; Kawamata, Y.; Rayamajhi, D.; Ashford, S.A. Full-Scale Tests on Effects of Slope on Lateral Capacity of Piles Installed in Cohesive Soils. J. Geotech. Geoenviron. Eng. 2018, 144, 04017103. [Google Scholar] [CrossRef]
- ASTM D2487–17e1. Standard Practice for Classification of Soils for Engineering Purposes; (Unified Soil Classification System); ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- Zhao, M.H.; Xiao, Y.; Chen, C.F.; He, W. Analysis of Deformation on Soft Subsoil Around Bridge Abutment Considering Soil Creep Property. China J. Highw. Transp. 2006, 19, 56–61. (In Chinese) [Google Scholar]
- Lou, M.L.; Wang, W.J.; Zhu, T.; Mang, H.C. Soil lateral boundary effect in shaking table model test of soil-structure system. Earthq. Eng. Eng. Dyn. 2000, 20, 30–36. [Google Scholar]
- AASHTO. Guide Specifications for LRFD Seismic Bridge Design, 7th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2014. [Google Scholar]





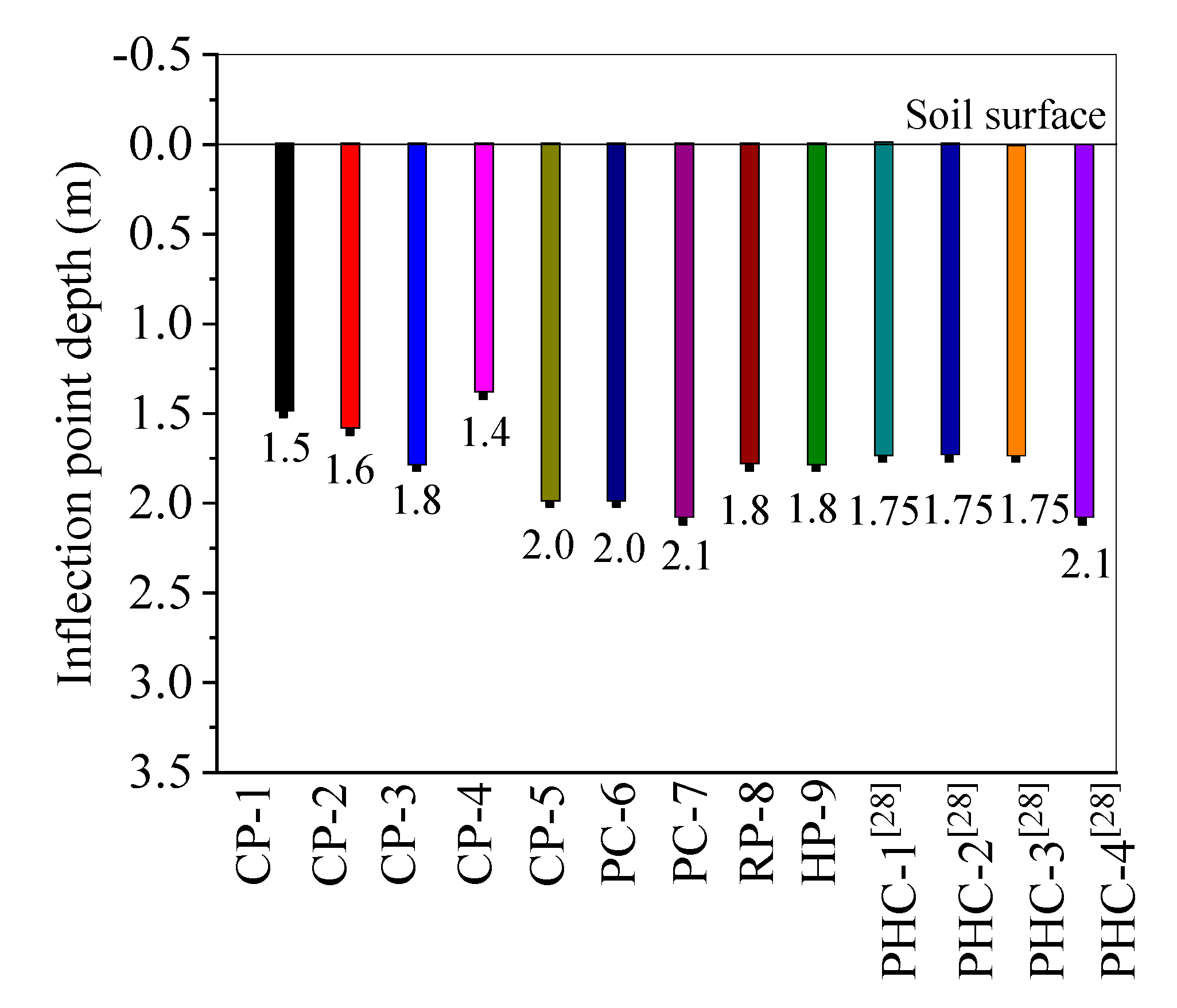



| Quantities | Scales | Scaled Relationships | Scaled Ratios | |
|---|---|---|---|---|
| Geometrical properties | Length/L | SL | [L] | SL = 0.31 |
| Modulus/E | SE | [E] | SE = 1.0 | |
| Density/ρ | Sρ | [ρ] | Sρ = 3.23 | |
| Stress/σ | Sσ | [E] | Sσ = SESε = 1.0 | |
| Strain/ε | Sε | -- | Sε = 1.0 | |
| Deformation/δ | SL | [L] | SL = 0.31 | |
| Dynamic characteristics | Acceleration/a | Sa | [Eρ−1L−1] | Sa1 = 1.0 |
| Acceleration/g | Sg | -- | Sg = 1.0 | |
| Time/T | ST | [E−0.5ρ0.5L] | ST = 0.56 | |
| Frequency/ω | Sω | [E0.5ρ−0.5L−1] | Sω = 1/ST = 1.79 | |
| Internal force | Bending moment/M | SM | [EL3] | SM = 0.03 |
| Shear force/F | SF | [EL2] | SF = 0.10 | |
| Inertia moment/I | SI | [L4] | SI = SL4 = 0.009 |
| Specimen | Section Type (Abbr.) | Material Type | D or W (mm) | H (m) | r | P (kN) | EI (kN·m2) |
|---|---|---|---|---|---|---|---|
| CP-1 | Circular section (CP) | C40 Concrete | 155 | 3.50 | 0.80% | 0.0 | 920.40 |
| CP-2 | 1.60% | 0.0 | 920.40 | ||||
| CP-3 | 3.20% | 0.0 | 920.40 | ||||
| CP-4 | 3.19(−2D) | 1.60% | 0.0 | 920.40 | |||
| CP-5 | 3.81(+2D) | 1.60% | 0.0 | 920.40 | |||
| PC-6 | Circular section (PC) | 3.50 | 1.60% | 45.0 | 920.40 | ||
| PC-7 | 1.60% | 90.0 | 920.40 | ||||
| RP-8 | Rectangular (RP) | 1.60% | 0.0 | 2187.25 | |||
| HP-9 | H section (HP) | Q235 steel | - | 0.0 | 777.09 | ||
| PHC-1 [28] | Circular section (PHC) | C80 Concrete | 2.75 | 1.50% | 0.0 | 859.7 | |
| PHC-2 [28] | 1.50% | 60.75 | 859.7 | ||||
| PHC-3 [28] | 1.50% | 121.5 | 859.7 | ||||
| PHC-4 [28] | 2.50% | 121.5 | 818.4 |
| Water Content ω (%) | Density ρ (g/cm3) | Porosity Ratio e | Internal Friction Angle Φ (°) | Compression Modulus (MPa) | Average SPT Blow Count |
|---|---|---|---|---|---|
| 4.6 | 1.90 | 0.59 | 35 | 12.9 | 11 |
| Specimen | CP-1 | CP-2 | CP-3 | CP-4 | CP-5 | PC-6 | PC-7 |
| Lci | 3.5 D | 3.6 D | 5.4 D | 3.4 D | 4.3 D | 4.4 D | 4.6 D |
| Lci/Lc1 | 100% | 103% | 154% | 97% | 123% | 126% | 131% |
| Specimen | RP-8 | HP-9 | PHC-1 [28] | PHC-2 [28] | PHC-3 [28] | PHC-4 [28] | |
| Lci | 6.2 D | -- | 4.5 D | 4.2 D | 5.2 D | 7.7 D | |
| Lci/Lc1 | 177% | -- | 129% | 120% | 149% | 220% |
| Specimen | 5 mm Loading | 8 mm Loading | 10 mm Loading | 15 mm Loading | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M (kN·m) | M0 (kN·m) | v5 | M (kN·m) | M0 (kN·m) | v8 | M (kN·m) | M0 (kN·m) | v10 | M (kN·m) | M0 (kN·m) | v15 | |
| CP-1 | 1.35 | 2.32 | 58% | 1.82 | 2.93 | 62% | 2.20 | 3.65 | 60% | 2.52 | 4.70 | 54% |
| CP-2 | 0.91 | 2.35 | 39% | 1.70 | 2.97 | 57% | 2.41 | 3.51 | 69% | 2.99 | 5.45 | 55% |
| CP-3 | 0.75 | 2.49 | 30% | 1.14 | 3.25 | 35% | 2.44 | 4.15 | 59% | 3.32 | 5.88 | 56% |
| CP-4 | 0.85 | 2.05 | 41% | 1.5 | 3.0 | 50% | 1.7 | 3.55 | 48% | 2.0 | 4.4 | 45% |
| CP-5 | 1.7 | 2.57 | 66% | 2.3 | 4.01 | 57% | 3.0 | 4.55 | 66% | 3.67 | 5.8 | 63% |
| PC-6 | 0.86 | 1.53 | 56% | 1.46 | 2.42 | 60% | 1.91 | 3.12 | 61% | 2.83 | 4.50 | 63% |
| PC-7 | 0.57 | 1.09 | 52% | 1.35 | 2.36 | 57% | 1.91 | 3.31 | 58% | 3.12 | 5.16 | 60% |
| RP-8 | 2.23 | 4.31 | 52% | 4.12 | 5.99 | 69% | 5.21 | 6.96 | 75% | 6.08 | 8.95 | 68% |
| HP-9 | 1.40 | 3.08 | 45% | 2.07 | 4.68 | 44% | 2.65 | 6.10 | 43% | 3.92 | 8.98 | 43% |
| PHC-1 | 1.53 | 2.25 | 68% | 2.22 | 3.20 | 69% | 2.19 | 3.62 | 60% | 2.91 | 4.73 | 62% |
| PHC-2 | 1.64 | 2.57 | 64% | 1.76 | 4.53 | 39% | 2.05 | 4.81 | 43% | 3.08 | 6.04 | 51% |
| PHC-3 | 1.92 | 3.37 | 67% | 2.31 | 5.12 | 45% | 2.53 | 5.68 | 45% | 3.19 | 6.48 | 49% |
| PHC-4 | 1.10 | 1.75 | 63% | 1.59 | 4.60 | 35% | 1.97 | 5.72 | 34% | 2.56 | 5.34 | 48% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, F.; Shan, Y.; Javanmardi, A.; Luo, X.; Chen, B. Seismic Performance of Various Piles Considering Soil–Pile Interaction under Lateral Cycle Loads for Integral Abutment Jointless Bridges (IAJBs). Appl. Sci. 2020, 10, 3406. https://doi.org/10.3390/app10103406
Huang F, Shan Y, Javanmardi A, Luo X, Chen B. Seismic Performance of Various Piles Considering Soil–Pile Interaction under Lateral Cycle Loads for Integral Abutment Jointless Bridges (IAJBs). Applied Sciences. 2020; 10(10):3406. https://doi.org/10.3390/app10103406
Chicago/Turabian StyleHuang, Fuyun, Yulin Shan, Ahad Javanmardi, Xiaoye Luo, and Baochun Chen. 2020. "Seismic Performance of Various Piles Considering Soil–Pile Interaction under Lateral Cycle Loads for Integral Abutment Jointless Bridges (IAJBs)" Applied Sciences 10, no. 10: 3406. https://doi.org/10.3390/app10103406
APA StyleHuang, F., Shan, Y., Javanmardi, A., Luo, X., & Chen, B. (2020). Seismic Performance of Various Piles Considering Soil–Pile Interaction under Lateral Cycle Loads for Integral Abutment Jointless Bridges (IAJBs). Applied Sciences, 10(10), 3406. https://doi.org/10.3390/app10103406







