Optimal Design of a Plenum Fan with Three-Dimensional Blades
Abstract
:1. Introduction
2. Numerical Investigation
2.1. Numerical Methods
2.2. Governing Equations
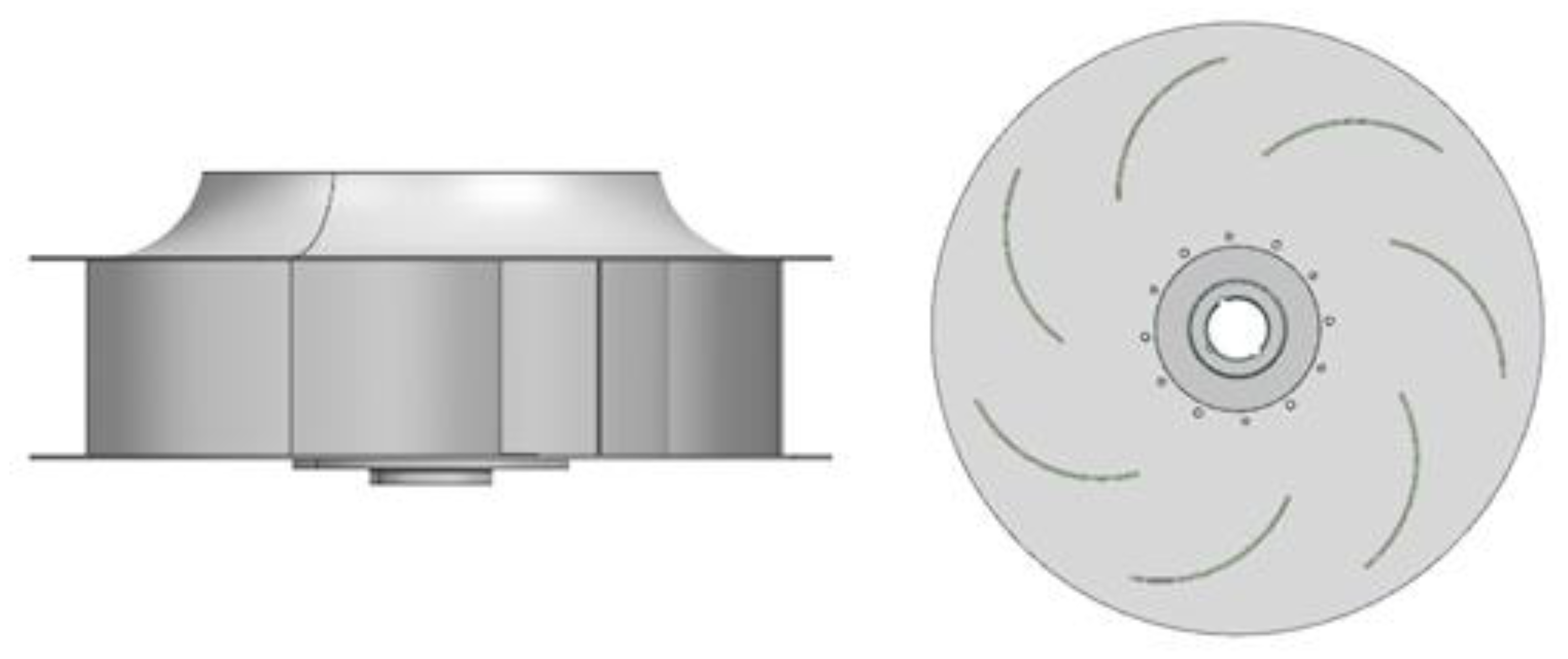
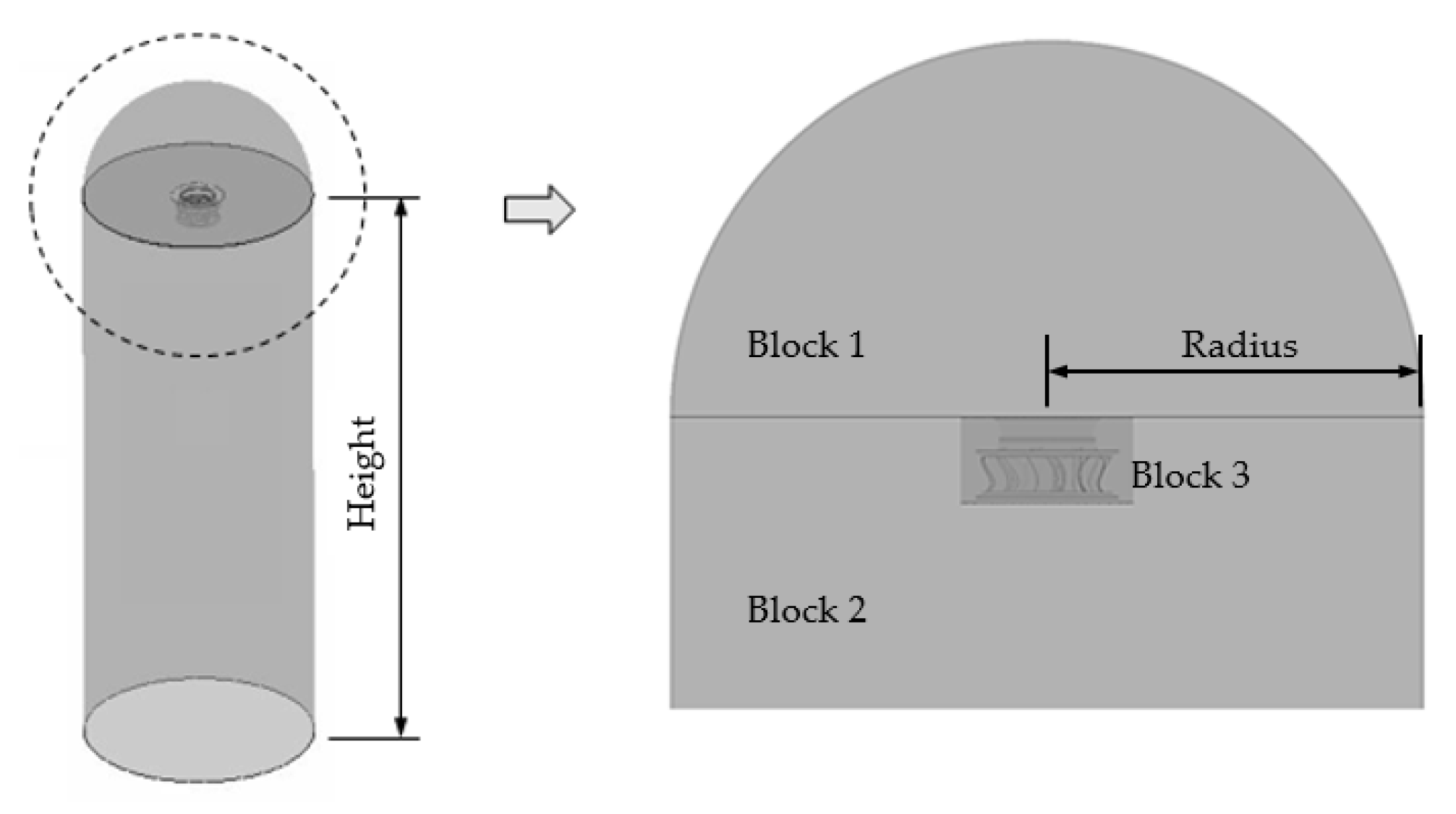
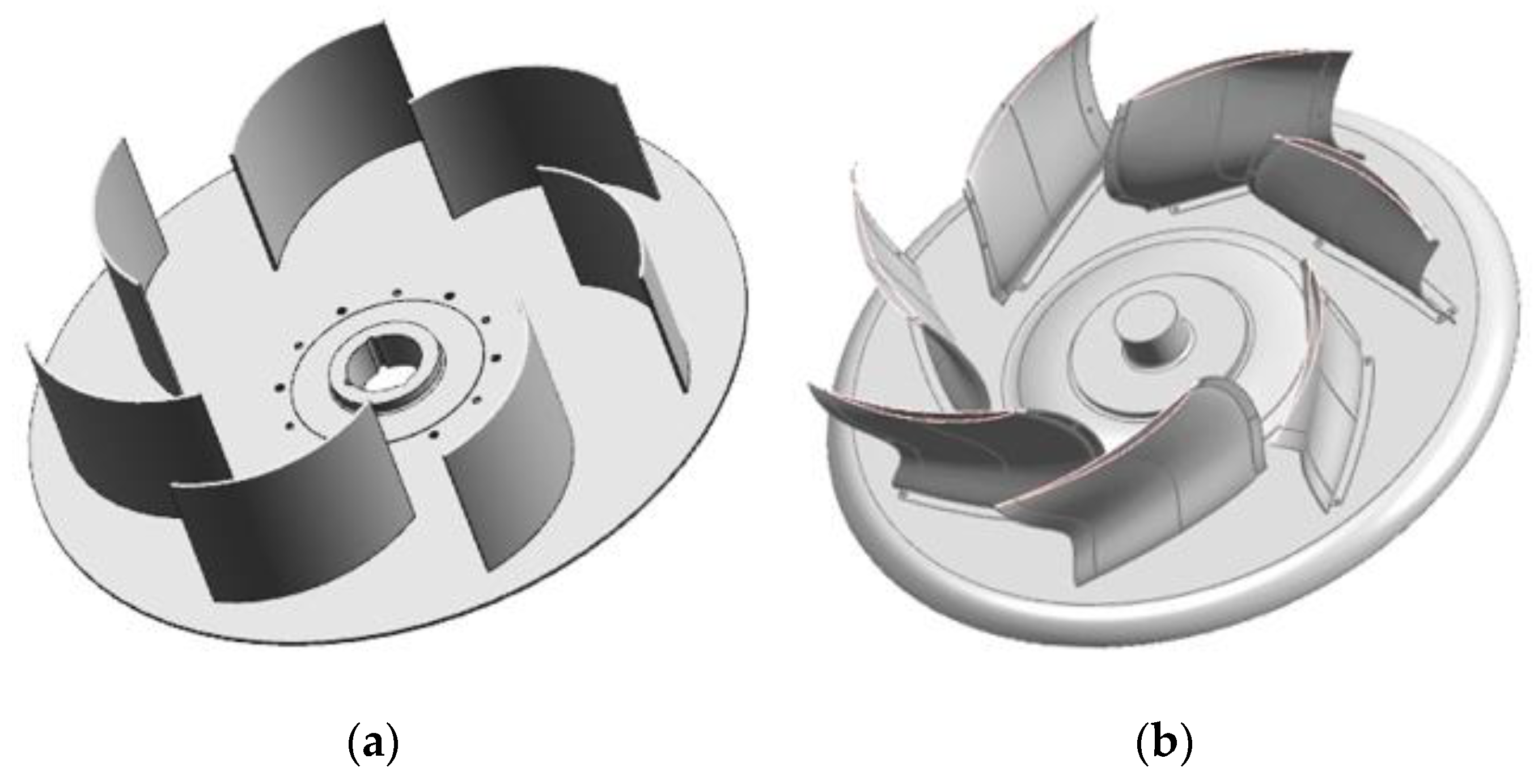
2.3. Geometrical Model and Mesh
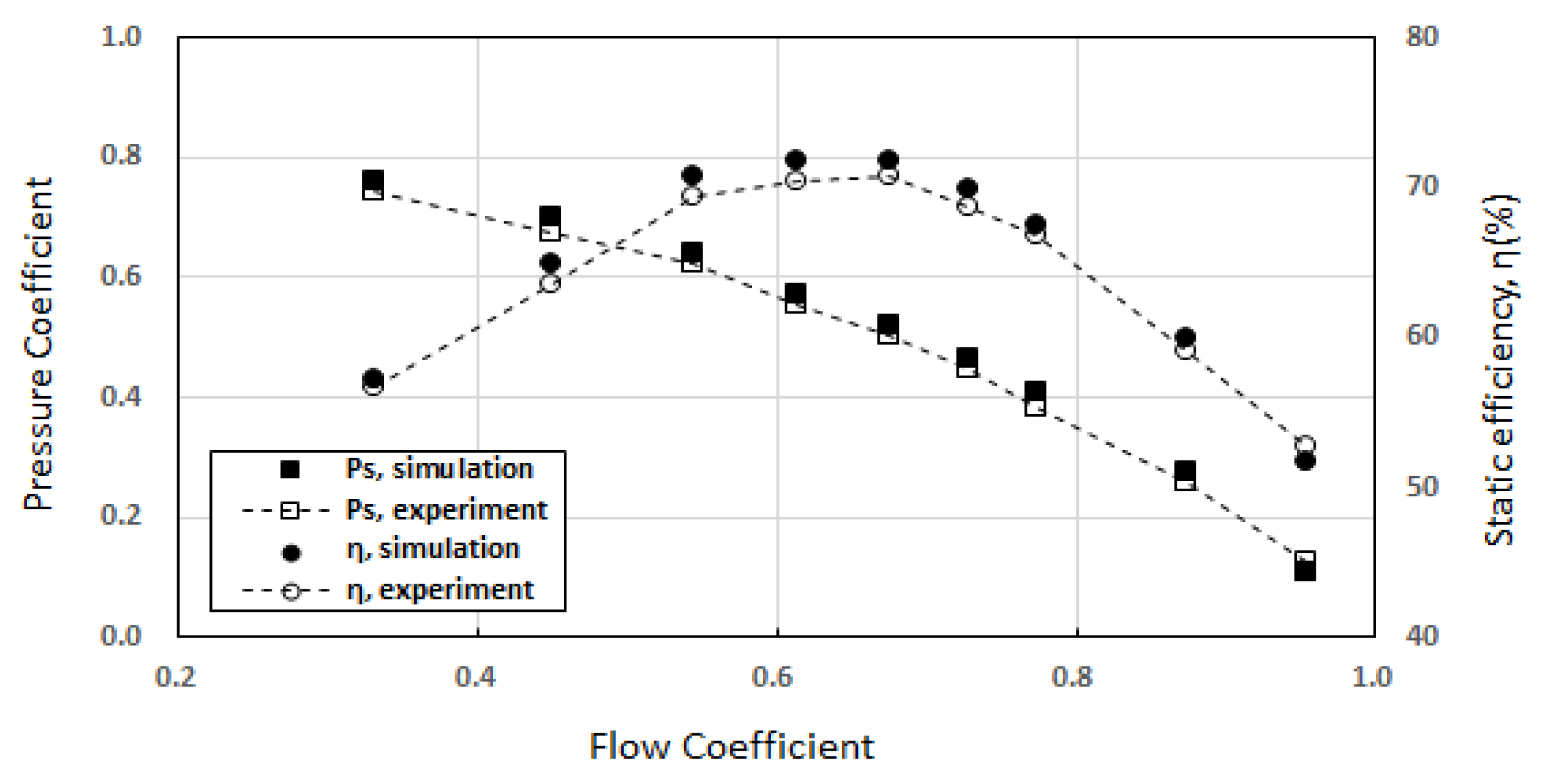
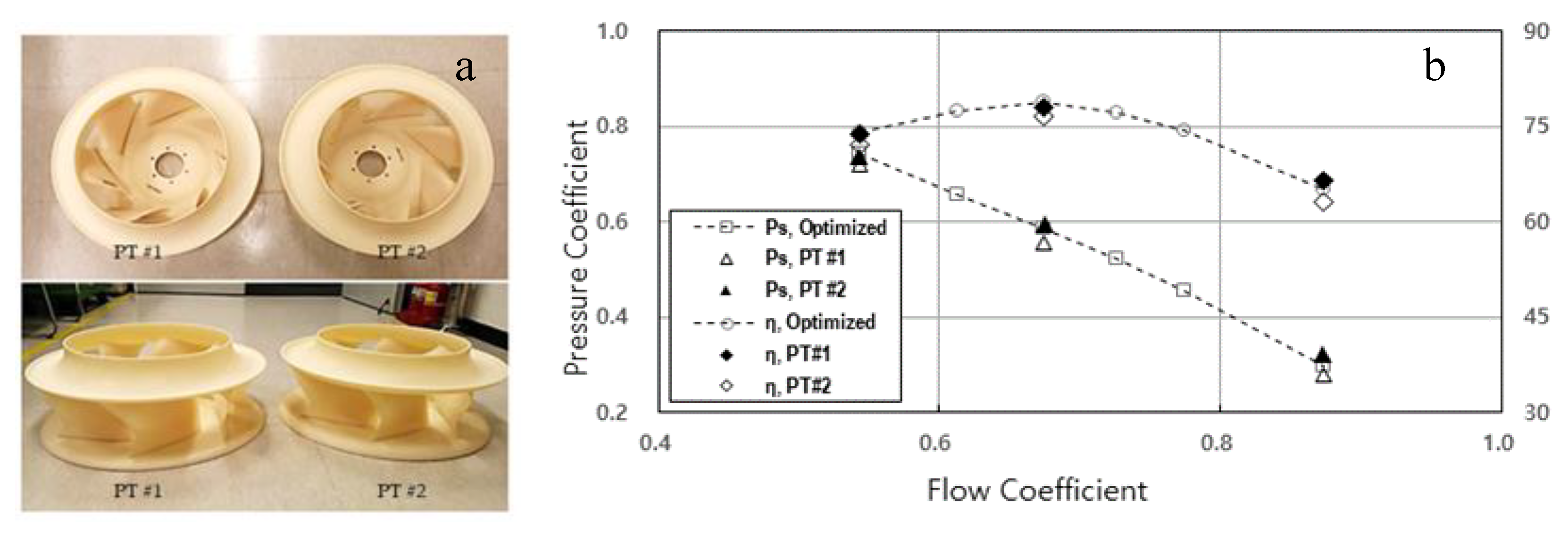
2.4. Experimental Results and Comparison with the Numerical Simulation
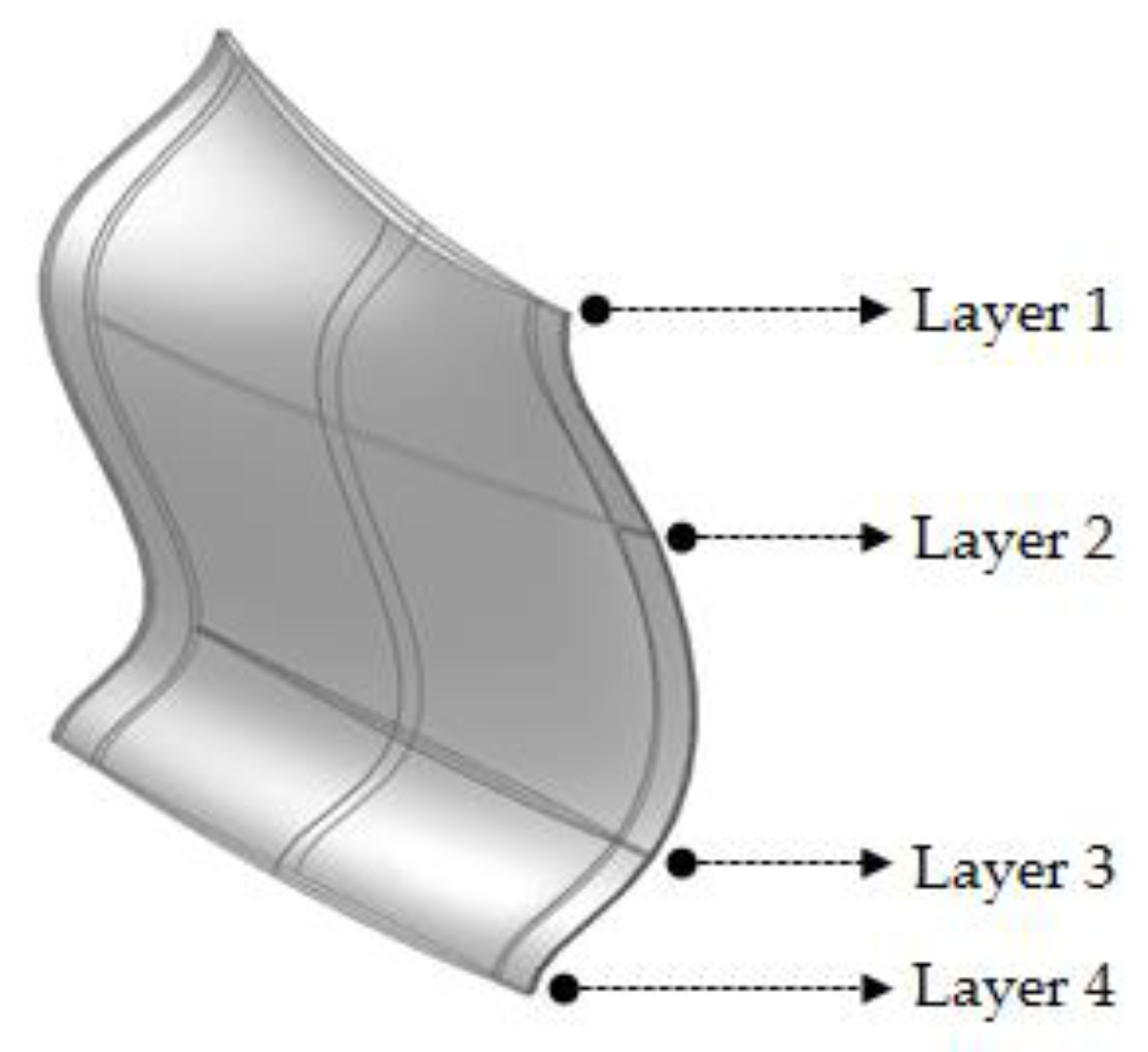
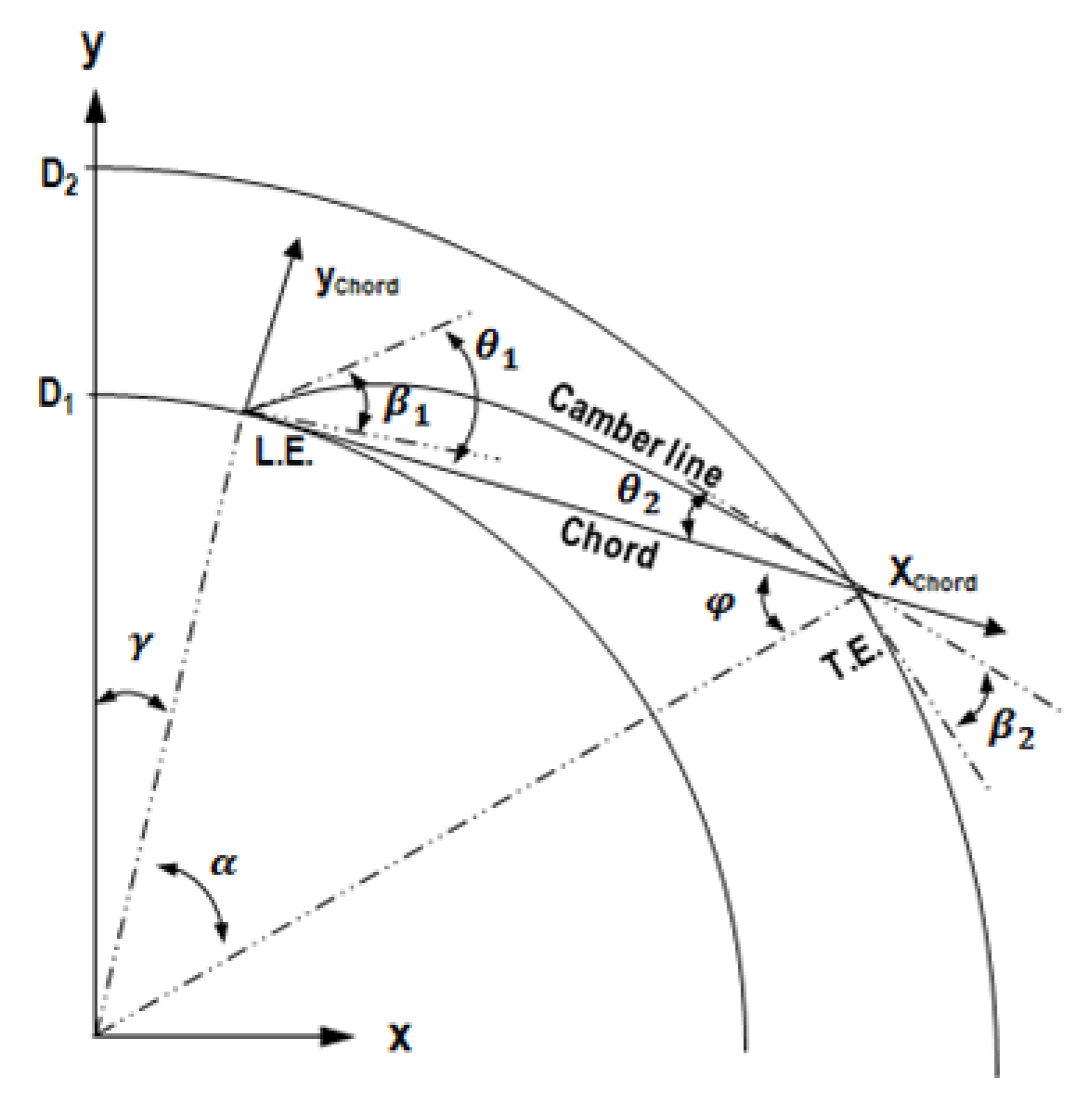
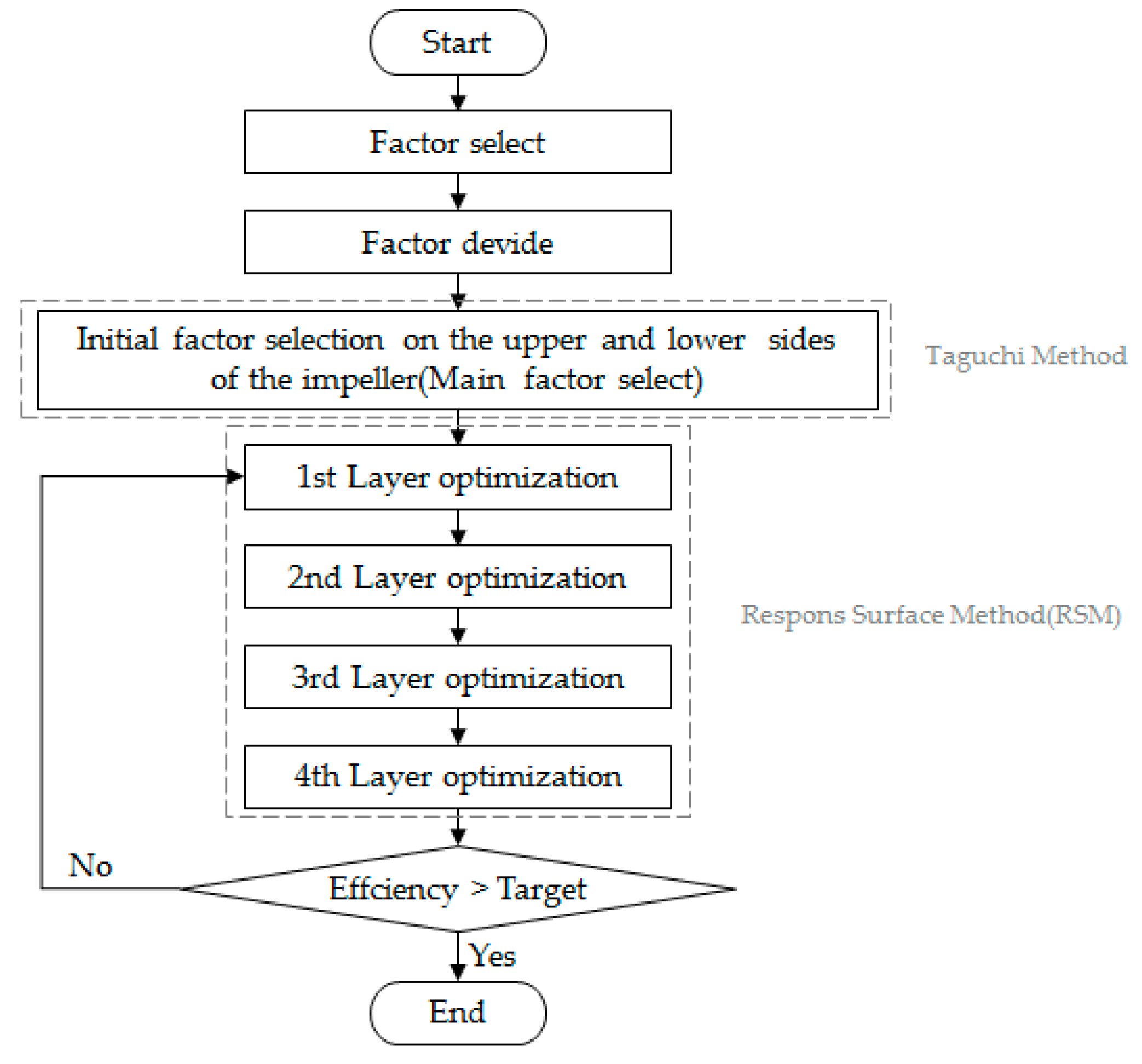
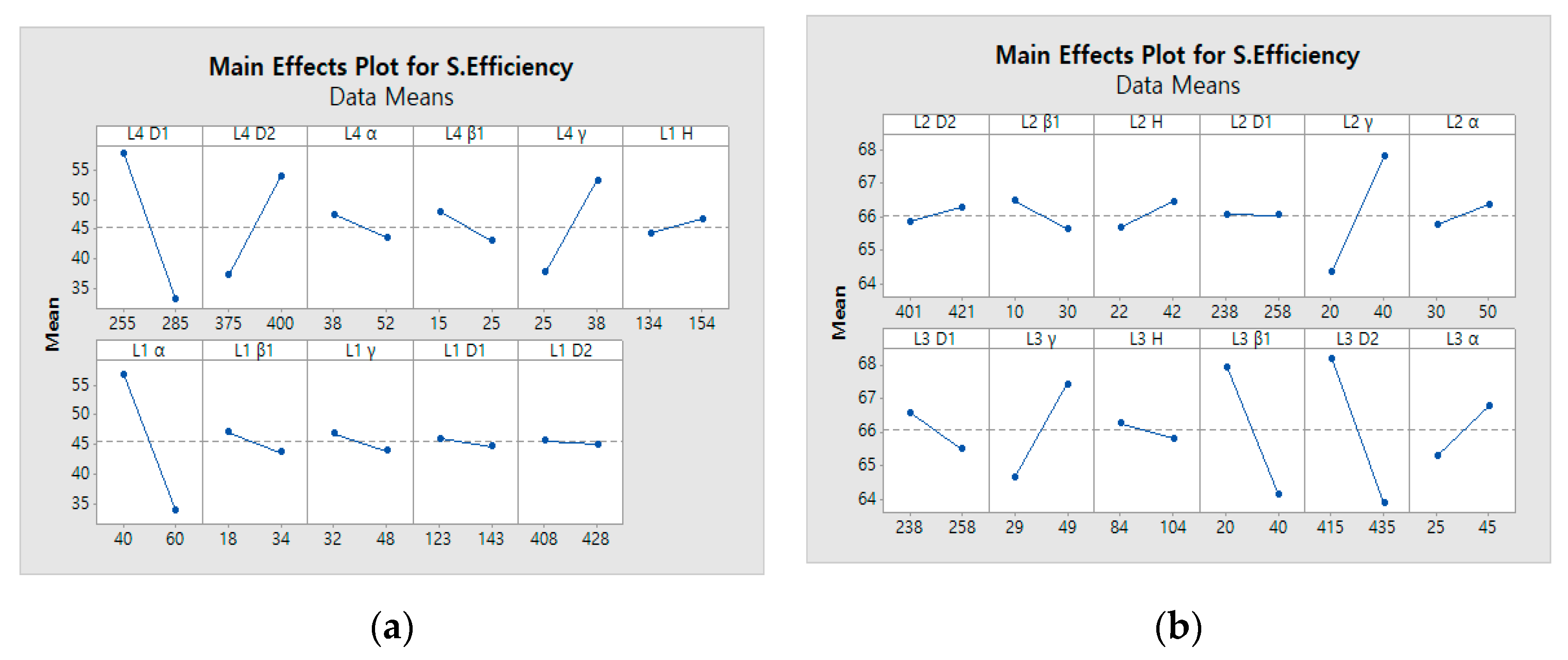
3. Optimization of the Blade Profile
4. Numerical Results and Discussion
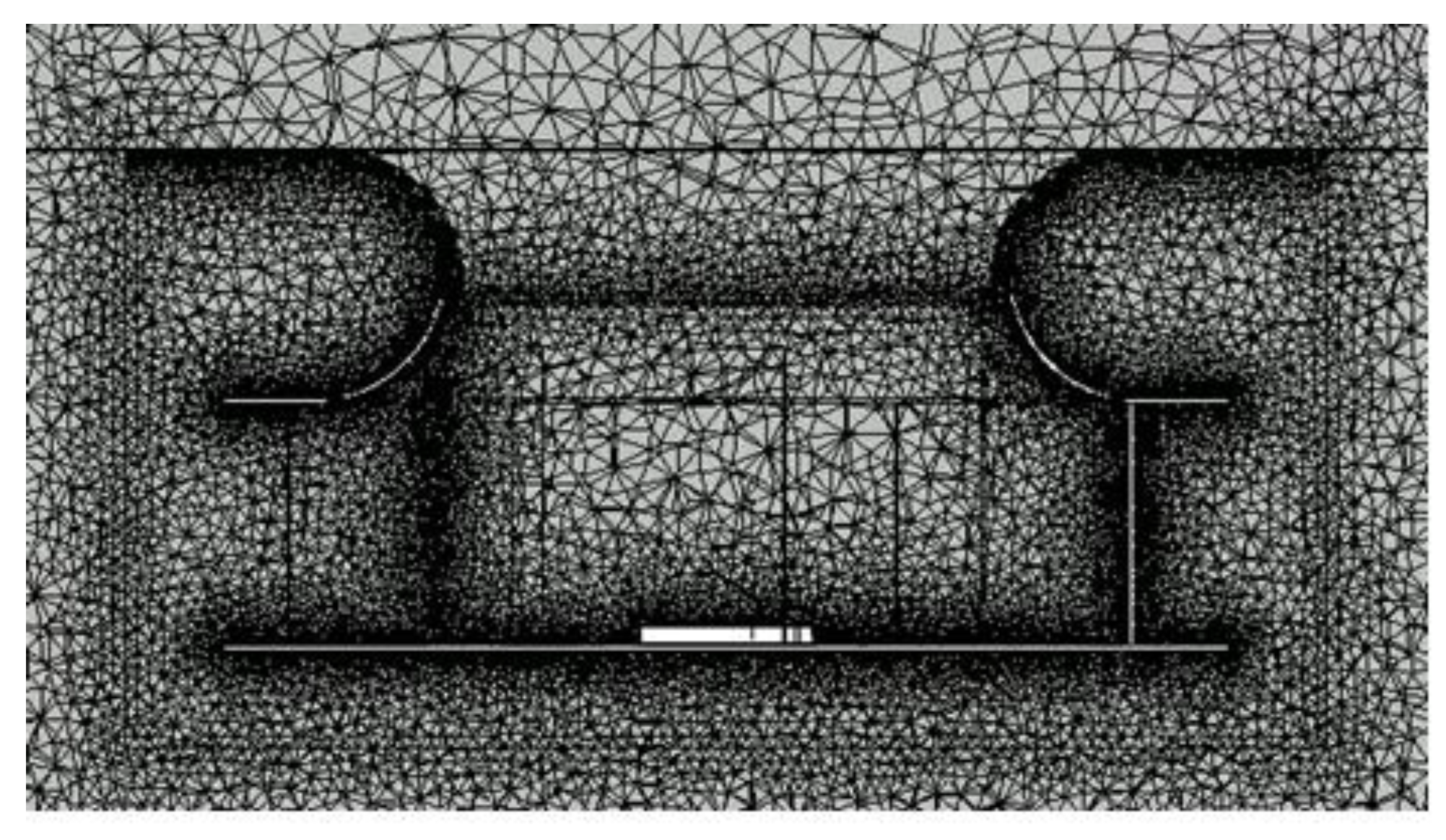
4.1. Mesh Independence Verification
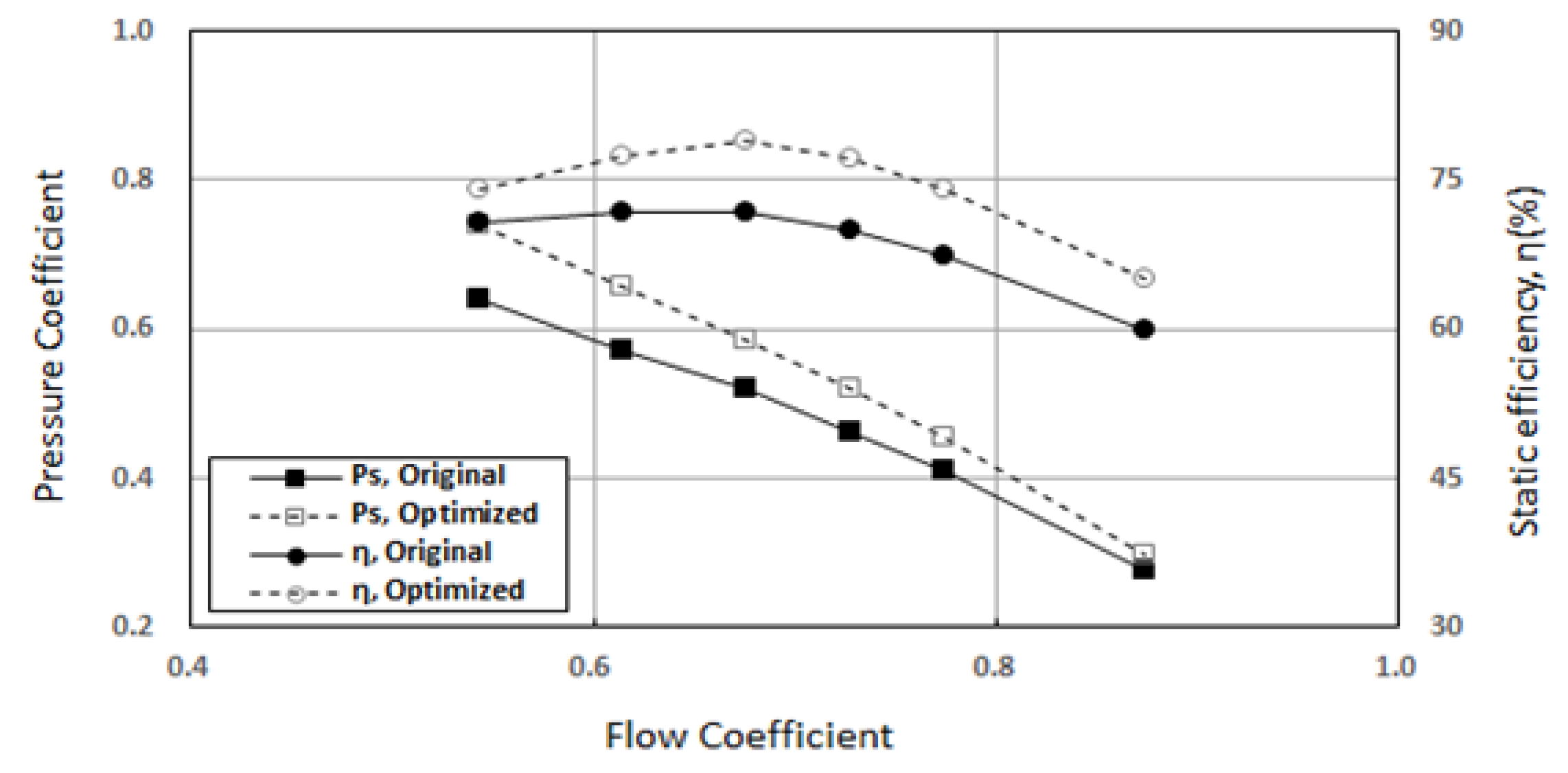
4.2. Comparison of the Performances of the Original and Optimized Models
5. Conclusions
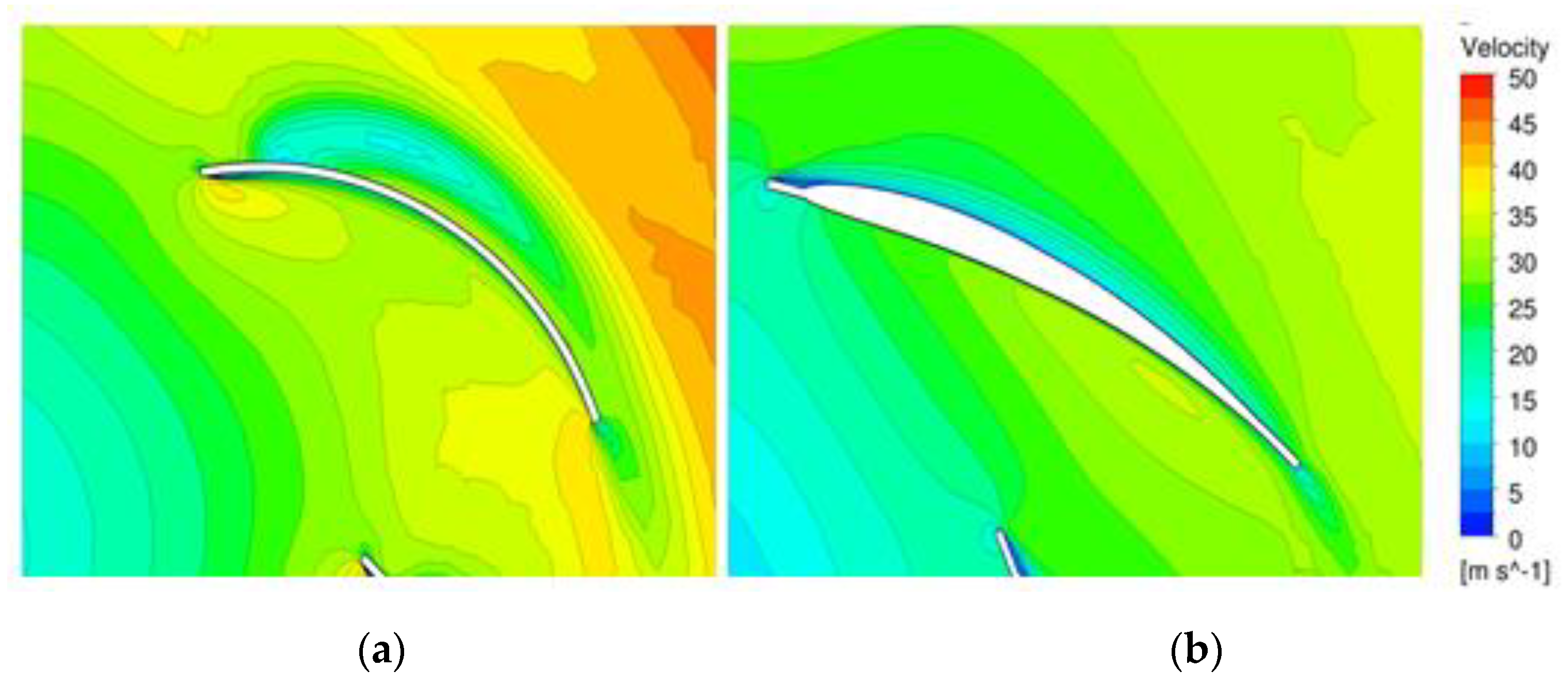
- The smooth, curved surface of the three-dimensional blade of the optimized model stabilized the flow and reduced the flow friction by restraining the flow separation as much as possible. The results show that both static pressure and static efficiency were improved in the optimized model compared with the original model. The static efficiency of the optimized model was improved by more than 6.3% compared with that of the original model at its peak.
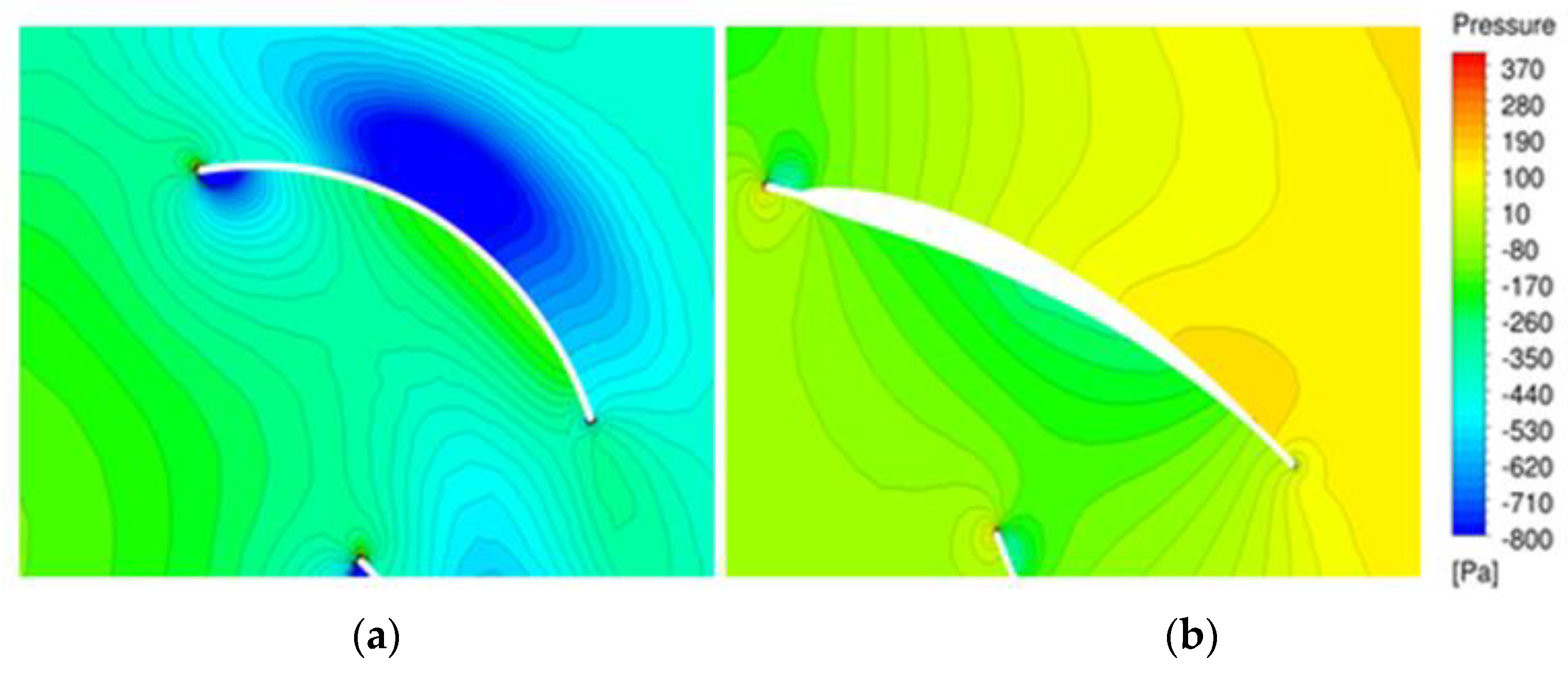
- In the original model, a relatively large loss occurred at the blade outlet. Additionally, in the original model, it was confirmed that turbulence grew because of flow separation from the leading edge. However, in the optimized model, the static pressure in the channel increased uniformly and stably. The flow separation at the leading edge was significantly reduced, which made the flow stable.
Author Contributions
Funding
Conflicts of Interest
References
- Wu, L.; Dou, H.; Wei, Y.; Chen, Y.; Cao, W.; Ying, C. Optimization of blade profile of a plenum fan. Int. J. Fluid Mach. Syst. 2016, 9, 95–106. [Google Scholar] [CrossRef] [Green Version]
- Dou, H.; Wu, L.; Wek, Y.; Chen, Y.; Cao, W.; Ying, C. Employing rotating vaneless diffuser to enhance the performance of plenum fan. Int. J. Fluid Mach. Syst. 2017, 10, 9–18. [Google Scholar] [CrossRef]
- Lee, J.; Jeon, H.; Jang, C. Performance characteristics according to the outlet impeller blade shape of a centrifugal blower. KSFM J. Fluid Mach. 2013, 16, 12–18. [Google Scholar] [CrossRef]
- Park, K.; Park, C. Application of airfoil impeller for enhancement of aerodynamic performance of high speed centrifugal fan. Trans. Korean Soc. Mech. Eng. 2016, 40, 321–327. [Google Scholar] [CrossRef] [Green Version]
- Siwek, T.; Gorski, J.; Fortuna, S. Numerical and experimental study of centrifugal fan flow structures and their relationship with machine efficiency. Pol. J. Environ. Stud. 2014, 23, 2359–2364. [Google Scholar]
- Kim, J.; Cha, K.; Kim, K.; Jang, C. Numerical investigation on aerodynamic performance of a centrifugal fan with splitter blades. Int. J. Fluid Mach. Syst. 2012, 5, 168–173. [Google Scholar] [CrossRef]
- Li, C.; Wang, S.L.; Jia, Y. The performance of a centrifugal fan with enlarged impeller. Energy Convers. Manag. 2012, 52, 2902–2910. [Google Scholar]
- Lin, S.; Tsai, M. An integrated performance analysis for a backward-inclined centrifugal fan. Comput. Fluids 2012, 56, 24–38. [Google Scholar] [CrossRef]
- Ni, S.; Cao, W.; Xu, J.; Wang, Y.; Zhang, W. Effects of an inclined blade on the performance of a sirocco fan. Appl. Sci. 2019, 9, 3154. [Google Scholar] [CrossRef]
- Xu, C.; Mao, Y. Experimental investigation of metal foam for controlling centrifugal fan noise. Appl. Acoust. 2016, 104, 182–192. [Google Scholar] [CrossRef]
- Baloni, B.; Pathak, Y.; Channiwala, S. Centrifugal blower volute optimization based on Taguchi method. Comput. Fluids 2015, 112, 72–78. [Google Scholar] [CrossRef]
- Heo, S.; Cheong, C.; Kim, T. Development of low-noise centrifugal fans for a refrigerator using inclined S-shaped trailing edge. Int. J. Refrig. 2011, 34, 2076–2091. [Google Scholar] [CrossRef]
- Park, S.; Ryu, S.; Cheong, C.; Kim, J.; Park, B.; Ahn, Y.; Oh, S. Optimization of the orifice shape of cooling fan units for high flow rate and low-level noise in outdoor air conditioning units. Appl. Sci. 2019, 9, 5207. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Chu, W.; Yi, L. Vibroacoustic optimization study for the volute casing of a centrifugal fan. Appl. Sci. 2019, 9, 859. [Google Scholar] [CrossRef] [Green Version]
- ANSYS CFX 17.0, ANSYS CFX Tutorials, ANSYS Inc. 2016. Available online: https://www.ansys.com/-/media/Ansys/en-gb/presentations/17x-update-seminar/fluent-cfx-simulation-showcase.pdf?la=en (accessed on 1 February 2020).
- Menter, F.R. Two-Equation Eddy-Viscosity turbulence models for engineering applications. AIAA-J. 1994, 32, 269–289. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.S.; Ziaul, H.; Han, S.E. A Study on the y+ Effects on Turbulence Model of Unstructured Grid for CFD Analysis of Wind Turbine. J. KASS 2015, 15, 75–84. [Google Scholar]
- ANSI/AMCA Standard 210, Laboratory Methods of Testing Fans for Aerodynamic Performance Rating, Air Movement and Control Association International, Inc. 2016. Available online: https://www.amca.org/publications-and-standards/standards/amca-standard-210-07-laboratory-methods-of-testing-fans-for-certified-aerodynamic-performance-rating.html (accessed on 10 December 2019).
- ANSI/ASHRAE Standard 51, Laboratory Methods of Testing Fans for Ratings, American Society of Heating, Refrigerating, and Air-Conditioning Engineers, Inc. 2016. Available online: https://www.techstreet.com/ashrae/standards/ashrae-amca-51-2016?gateway_code=ashrae&product_id=1929730 (accessed on 10 December 2019).
- Taguchi, G. Introduction to Quality Engineering; Asian Productivity Organization: Tokyo, Japan, 1990. Available online: https://archive.org/details/introductiontoqu0000tagu/ (accessed on 15 October 2019).
- Phadke, M.S. Quality Engineering Using Robust Design; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. Available online: https://dl.acm.org/doi/book/10.5555/525794 (accessed on 10 October 2019).
- Box, G.E.P.; Wilson, K.B. On the Experimental Attainment of Optimum Conditions. J. Royal Stat. Soc. 1951, 13, 1–45. [Google Scholar] [CrossRef]



| Variables | Units | Value |
|---|---|---|
| Flow coefficient | - | 0.675 |
| Static pressure | Pa | 392 |
| Static pressure efficiency | % | 71.8 |
| Impeller diameter | mm | 640 |
| Impeller outlet breadth | mm | 167 |
| Number of blades | - | 7 |
| Revolving speed | rpm | 1100 |
| Layer | Factor | Level | Layer | Factor | Level | ||||
|---|---|---|---|---|---|---|---|---|---|
| −1 | 0 | 1 | −1 | 0 | 1 | ||||
| Layer 1 and 4 | (Layer 1) | 20 | 35 | 50 | Layer 2 and 3 | (Layer 2) | 20 | 35 | 50 |
| D1 (Layer 4) | 200 | 300 | 400 | (Layer 3) | 5 | 15 | 30 | ||
| D2 (Layer 4) | 450 | 500 | 550 | D2 (Layer 3) | 450 | 500 | 550 | ||
| (Layer 4) | 20 | 35 | 50 | (Layer 3) | 20 | 35 | 50 | ||
| Part | Parameters | Unit | Value | Part | Parameters | Unit | Value |
|---|---|---|---|---|---|---|---|
| Layer 1 | D1 | mm | 340.0 | Layer 3 | D1 | mm | 330.0 |
| D2 | mm | 475.0 | D2 | mm | 527.0 | ||
| degrees | 42.5 | degrees | 45.0 | ||||
| degrees | 6.4 | degrees | 30.6 | ||||
| degrees | 45 | degrees | 35.4 | ||||
| Layer 2 | D1 | mm | 298.0 | H | mm | 130.0 | |
| D2 | mm | 444.0 | Layer 4 | D1 | mm | 343.0 | |
| degrees | 47.5 | D2 | mm | 478.0 | |||
| degrees | 6.8 | degrees | 45.0 | ||||
| degrees | 41.7 | degrees | 15.0 | ||||
| H | mm | 42.0 | degrees | 31.2 |
| No. | Mesh | Static Pressure (Pa) |
|---|---|---|
| 1 | 7,432,111 | 418 |
| 2 | 8,184,320 | 415 |
| 3 | 8,954,841 | 410 |
| 4 | 9,461,970 | 398 |
| 5 | 9,806,594 | 397 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.J.; Park, I.W.; Bang, K.S.; Kim, Y.M.; Ahn, Y.C. Optimal Design of a Plenum Fan with Three-Dimensional Blades. Appl. Sci. 2020, 10, 3460. https://doi.org/10.3390/app10103460
Lee KJ, Park IW, Bang KS, Kim YM, Ahn YC. Optimal Design of a Plenum Fan with Three-Dimensional Blades. Applied Sciences. 2020; 10(10):3460. https://doi.org/10.3390/app10103460
Chicago/Turabian StyleLee, Kyung Jung, Il Wung Park, Ki Suk Bang, Yeong Min Kim, and Young Chull Ahn. 2020. "Optimal Design of a Plenum Fan with Three-Dimensional Blades" Applied Sciences 10, no. 10: 3460. https://doi.org/10.3390/app10103460
APA StyleLee, K. J., Park, I. W., Bang, K. S., Kim, Y. M., & Ahn, Y. C. (2020). Optimal Design of a Plenum Fan with Three-Dimensional Blades. Applied Sciences, 10(10), 3460. https://doi.org/10.3390/app10103460





