A Helmholtz Resonator with Spiral Neck for Analyte Concentration Measurement in Low Frequency Range
Abstract
:1. Introduction
2. Material and Methods
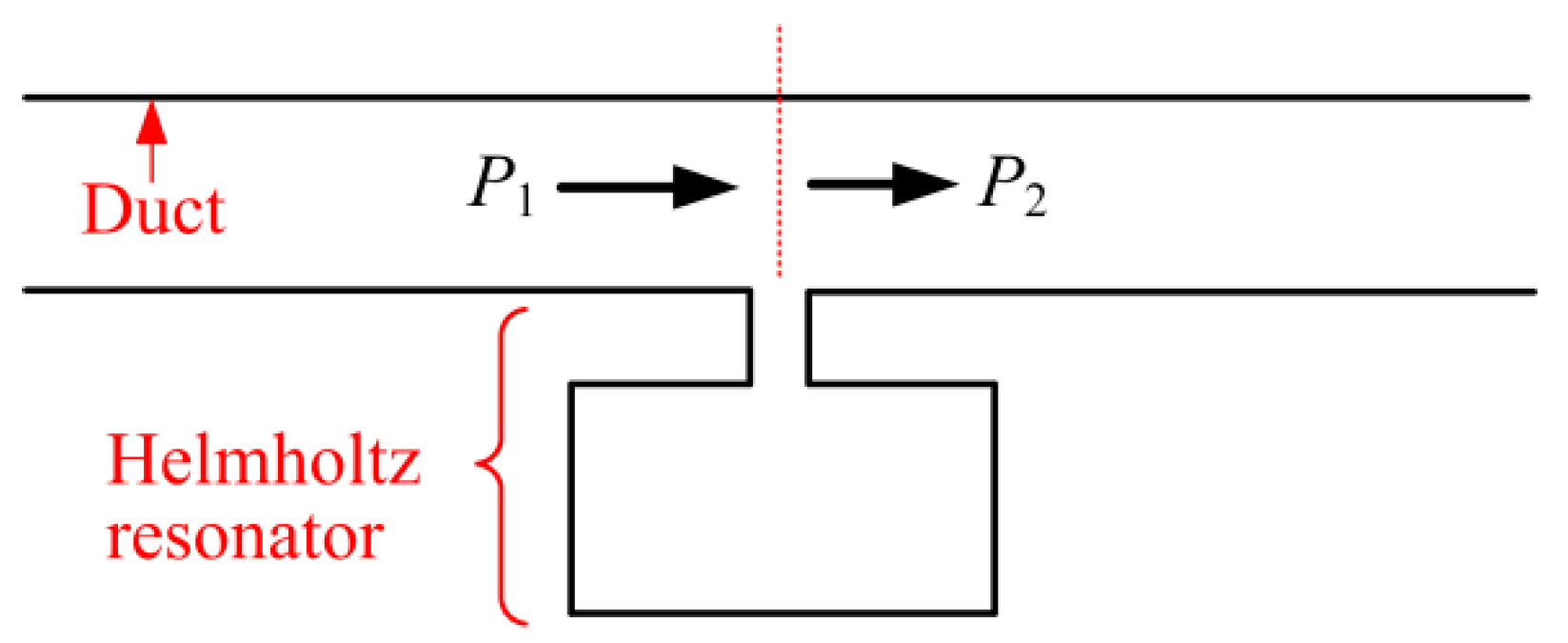
2.1. The Underlying Theory
2.2. Effects of the Analyte Concentration on Density and Sound Speed
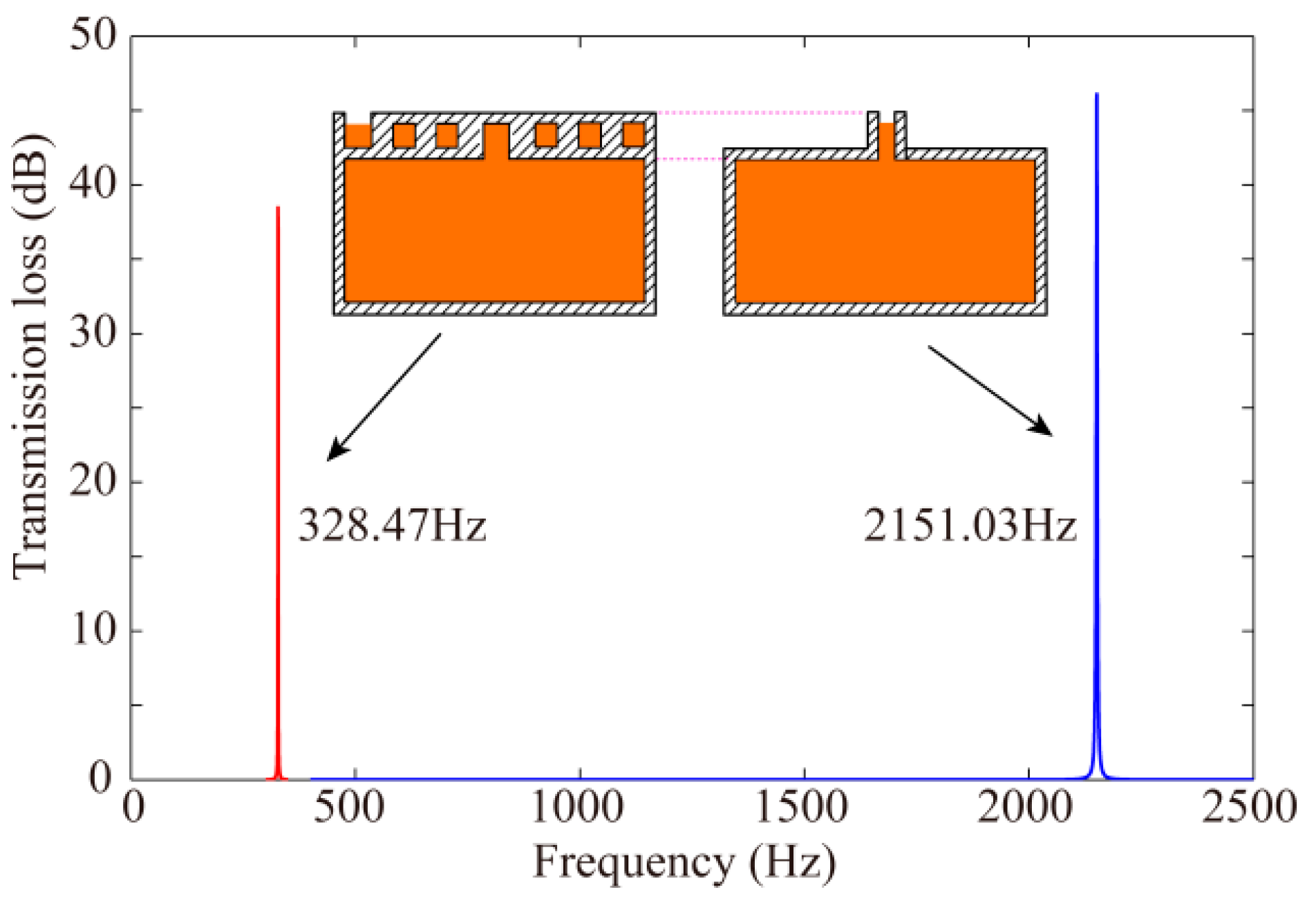
2.3. Analytical Example and Finite Element Method(FEM) Simulation
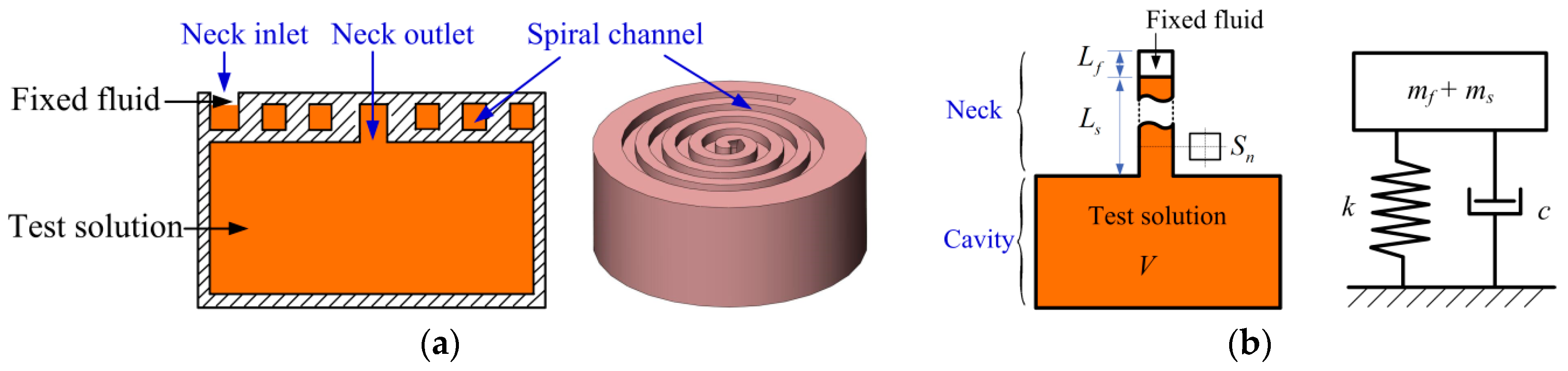
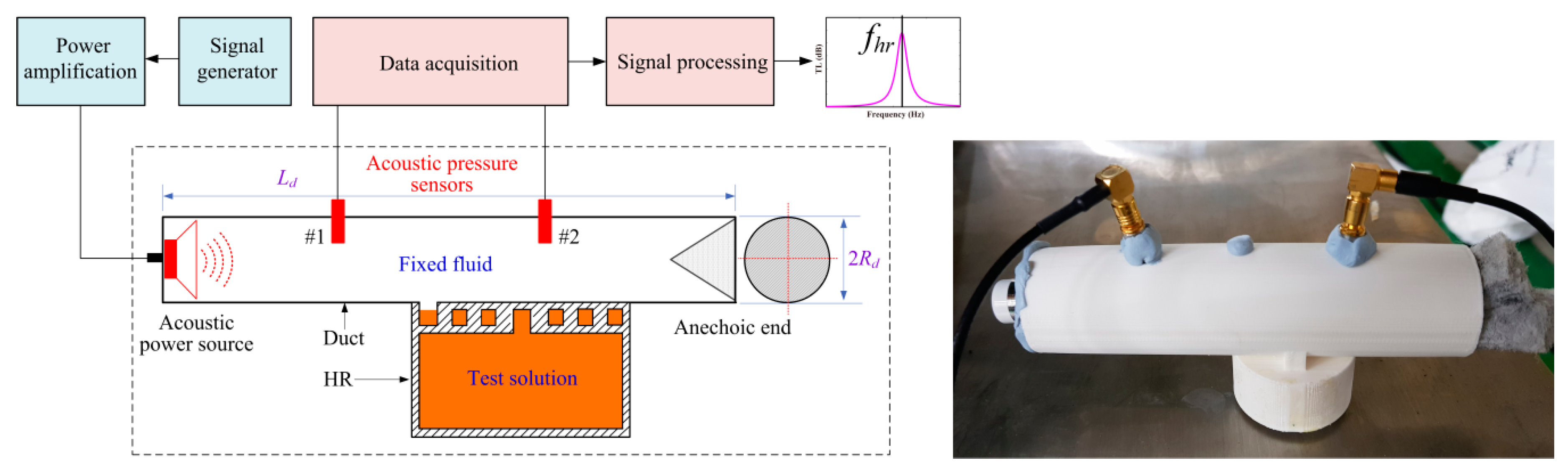
2.4. Measurement Principle and Device Architecture
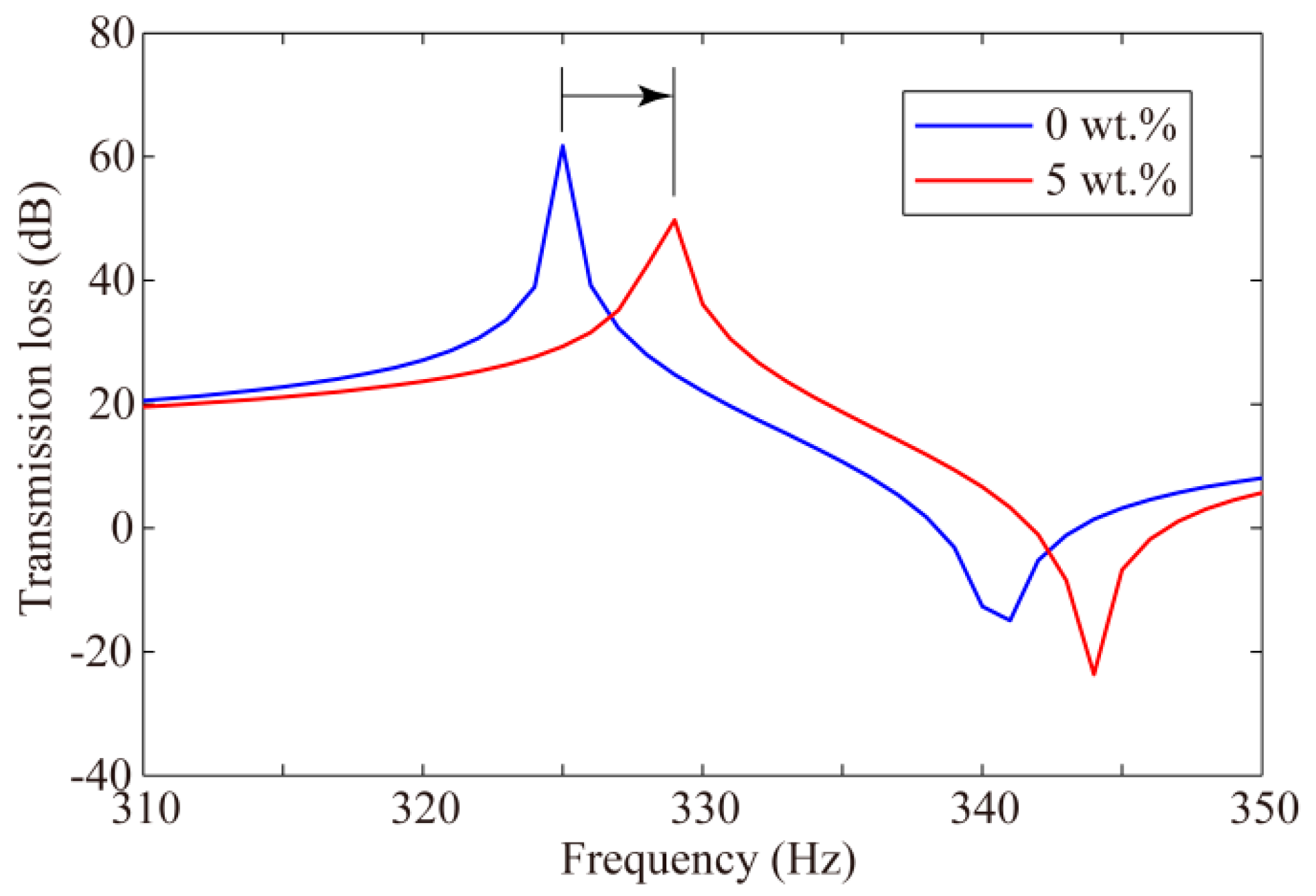
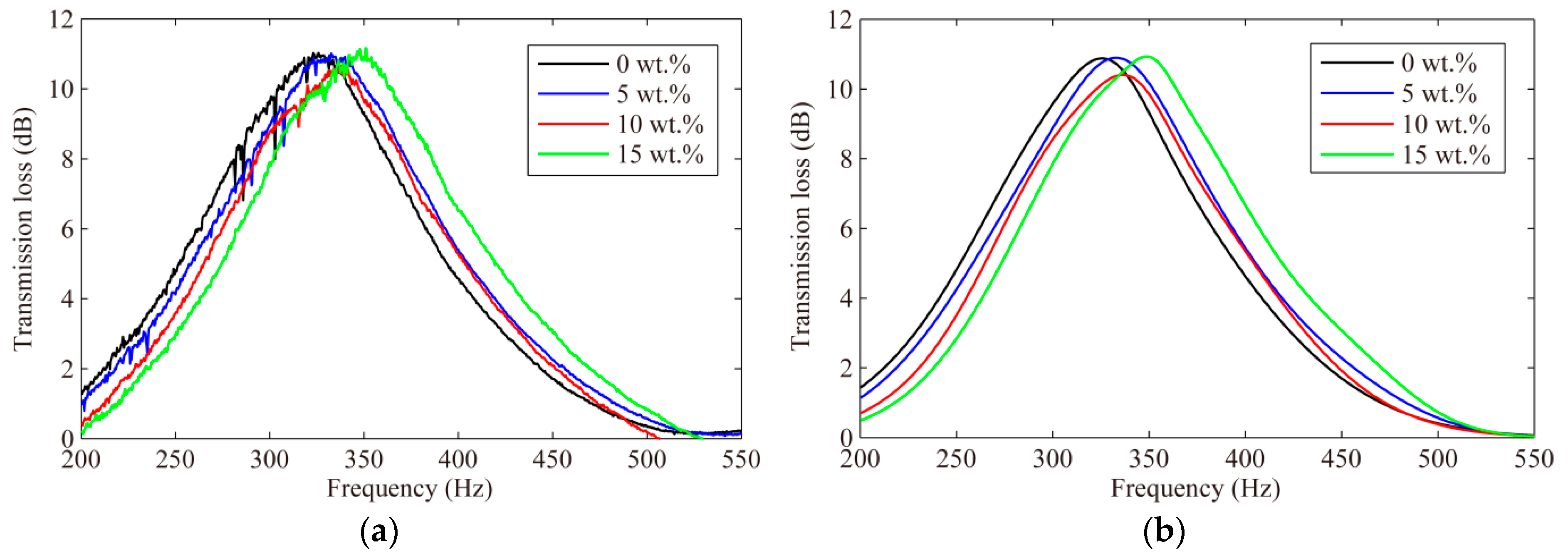
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alvarez, M.; Lechuga, L.M. Microcantilever-based platforms as biosensing tools. Analyst 2010, 135, 827–836. [Google Scholar] [CrossRef] [PubMed]
- Ricciardi, C.; Fiorilli, S.; Bianco, S.; Canavese, G.; Castagna, R.; Ferrante, I.; Digregorio, G.; Marasso, S.L.; Napione, L.; Bussolino, F. Development of microcantilever-based biosensor array to detect angiopoietin-1, a marker of tumor angiogenesis. Biosens. Bioelectron. 2010, 25, 1193–1198. [Google Scholar] [CrossRef] [PubMed]
- Okan, M.; Sari, E.; Duman, M. Molecularly imprinted polymer based micromechanical cantilever sensor system for the selective determination of ciprofloxacin. Biosens. Bioelectron. 2017, 88, 258–264. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Park, Y.-H. Measurement of an Analyte Concentration in Test Solution by Using Helmholtz Resonator for Biosensor Applications. Sensors 2019, 19, 1127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Selamet, A.; Lee, I. Helmholtz resonator with extended neck. J. Acoust. Soc. Am. 2003, 113, 1975–1985. [Google Scholar] [CrossRef] [PubMed]
- Selamet, A.; Xu, M.B.; Lee, I.J.; Huff, N.T. Helmholtz resonator lined with absorbing material. J. Acoust. Soc. Am. 2005, 117, 725–733. [Google Scholar] [CrossRef] [Green Version]
- Cheng, X.; Chen, X.; Rong, J.; Fan, B. Low-Frequency Noise Reduction of Rocket Fairings Using Horn-Shaped-Neck Helmholtz Resonators. J. Spacecr. Rocket. 2018, 56, 273–282. [Google Scholar] [CrossRef]
- Shi, X.; Mak, C.M. Helmholtz resonator with a spiral neck. Appl. Acoust. 2015, 99, 68–71. [Google Scholar] [CrossRef]
- Cai, C.; Mak, C.M.; Shi, X. An extended neck versus a spiral neck of the Helmholtz resonator. Appl. Acoust. 2017, 115, 74–80. [Google Scholar] [CrossRef]
- Nudehi, S.S.; Duncan, G.S.; Farooq, U. Modeling and experimental investigation of a Helmholtz resonator with a flexible plate. J. Vib. Acoust.-Trans. ASME 2013, 135, 041102. [Google Scholar] [CrossRef]
- Kurdi, M.H.; Duncan, G.S.; Nudehi, S.S. Optimal design of a Helmholtz resonator with a flexible end plate. J. Vib. Acoust. 2014, 136, 031004. [Google Scholar] [CrossRef]
- Li, Y.; Assouar, B.M. Acoustic metasurface-based perfect absorber with deep subwavelength thickness. Appl. Phys. Lett. 2016, 108, 063502. [Google Scholar] [CrossRef]
- Chen, Y.; Park, Y.-H. A Helmholtz resonator on elastic foundation for measurement of the elastic coefficient of human skin. J. Mech. Behav. Biomed. Mater. 2020, 101, 103417. [Google Scholar] [CrossRef] [PubMed]
- Spiral. Available online: https://en.wikipedia.org/wiki/Spiral#Two-dimensional,Wikipedia (accessed on 10 November 2019).
- Hooker, J.; Ramaswamy, V.; Arora, R.; Edison, A.; Withers, R.; Nast, R.; Brey, W. An empirical expression to predict the resonant frequencies of archimedean spirals. IEEE Trans. Microw. Theory Tech. 2015, 63, 2107–2114. [Google Scholar] [CrossRef]
- Maleeva, N.; Averkin, A.; Abramov, N.N.; Fistul, M.V.; Karpov, A.; Zhuravel, A.P.; Ustinov, A.V. Electrodynamics of planar Archimedean spiral resonator. J. Appl. Phys. 2015, 118, 033902. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J. A new calculation for designing multilayer planar spiral inductors. EDN (Electr. Des. News) 2010, 55, 37–40. [Google Scholar]
- Schweizer, B. The low-frequency spectrum of small Helmholtz resonators. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2015, 471, 20140339. [Google Scholar] [CrossRef]
- Kela, L. Resonant frequency of an adjustable Helmholtz resonator in a hydraulic system. Arch. Appl. Mech. 2009, 79, 1115–1125. [Google Scholar] [CrossRef]
- Zhao, S.; Tao, W.; He, Q.; Zhao, H.; Cao, W. A non-invasive photoacoustic and ultrasonic method for the measurement of glucose solution concentration. AIP Adv. 2017, 7, 035313. [Google Scholar] [CrossRef] [Green Version]
- Pryor, A.W.; Roscoe, R. The velocity and absorption of sound in aqueous sugar solutions. Proc. Phys. Soc. 1954, 67, 70–81. [Google Scholar] [CrossRef]
- Pritz, B.; Magagnato, F.; Gabi, M. Investigation of the Effect of Surface Roughness on the Pulsating Flow in Combustion Chambers with LES; Springer Proceedings in Physics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Yuvaraj, L.; Jeyanthi, S.; Chinnapandi, M.; Babu, L. Sound Absorption of Multilayer Micro Perforated Panel with Helmholtz Resonator Mount. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Madrid, Spain, 16–19 June 2019; Volume 259, pp. 4002–4009. [Google Scholar]
- Zhao, L.; Hu, Y.; Hebibul, R.; Xia, Y.; Huang, L.; Zhao, Y.; Jiang, Z. Density measurement sensitivity of micro-cantilevers influenced by shape dimensions and operation modes. Sens. Actuator B Chem. 2017, 245, 574–582. [Google Scholar] [CrossRef]
- Zhao, C.; Montaseri, M.H.; Wood, G.S.; Pu, S.H.; Seshia, A.A.; Kraft, M. A review on coupled MEMS resonators for sensing applications utilizing mode localization. Sens. Actuator A Phys. 2016, 249, 93–111. [Google Scholar] [CrossRef]

| Glucose Concentration | Density (kg/m3) | Sound Speed (m/s) |
|---|---|---|
| 0 wt.% (Water) | 998 | 1481.5 |
| 5 wt.% | 1010.5 | 1498.1 |
| 10 wt.% | 1023.8 | 1518.5 |
| 15 wt.% | 1038.0 | 1543.6 |
| Glucose Concentration | 0 wt.% | 5 wt.% | 10 wt.% | 15 wt.% |
|---|---|---|---|---|
| Analytical results (A) | 328.5 Hz | 332.1 Hz | 336.6 Hz | 342.1 Hz |
| Experiment results (B) | 326.5 Hz | 332.9 Hz | 336.3 Hz | 348.7 Hz |
| Standard deviations (C) | 1.13 | 1.21 | 1.15 | 1.32 |
| Relative error (|A − B|/B ∗ 100%) | 0.61% | 0.24% | 0.09% | 1.89% |
| Test Sample Amount | 0.1 mL | 0.1 mL | 0.01 mL |
|---|---|---|---|
| This Paper | Reference [4] | This Paper | |
| Resonant frequency | 3377.4 Hz | 134.8 kHz | 28.5 kHz |
| Sensitivity | 3.02 | 299.2 | 25.52 |
| Cantilever sensor [24] | Rectangle 1.9 mm (1st mode) | Trapezoid 1.5 mm (2nd mode) | |
| Resonant frequency | 3747.245 Hz | 29.1 kHz | |
| Sensitivity | 2.154 | 13.801 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Lee, B.; Park, Y.-H. A Helmholtz Resonator with Spiral Neck for Analyte Concentration Measurement in Low Frequency Range. Appl. Sci. 2020, 10, 3676. https://doi.org/10.3390/app10113676
Chen Y, Lee B, Park Y-H. A Helmholtz Resonator with Spiral Neck for Analyte Concentration Measurement in Low Frequency Range. Applied Sciences. 2020; 10(11):3676. https://doi.org/10.3390/app10113676
Chicago/Turabian StyleChen, Yugang, Bomi Lee, and Yong-Hwa Park. 2020. "A Helmholtz Resonator with Spiral Neck for Analyte Concentration Measurement in Low Frequency Range" Applied Sciences 10, no. 11: 3676. https://doi.org/10.3390/app10113676
APA StyleChen, Y., Lee, B., & Park, Y.-H. (2020). A Helmholtz Resonator with Spiral Neck for Analyte Concentration Measurement in Low Frequency Range. Applied Sciences, 10(11), 3676. https://doi.org/10.3390/app10113676





