Nonlinear Vibration Mitigation of a Beam Excited by Moving Load with Time-Delayed Velocity and Acceleration Feedback
Abstract
:1. Introduction
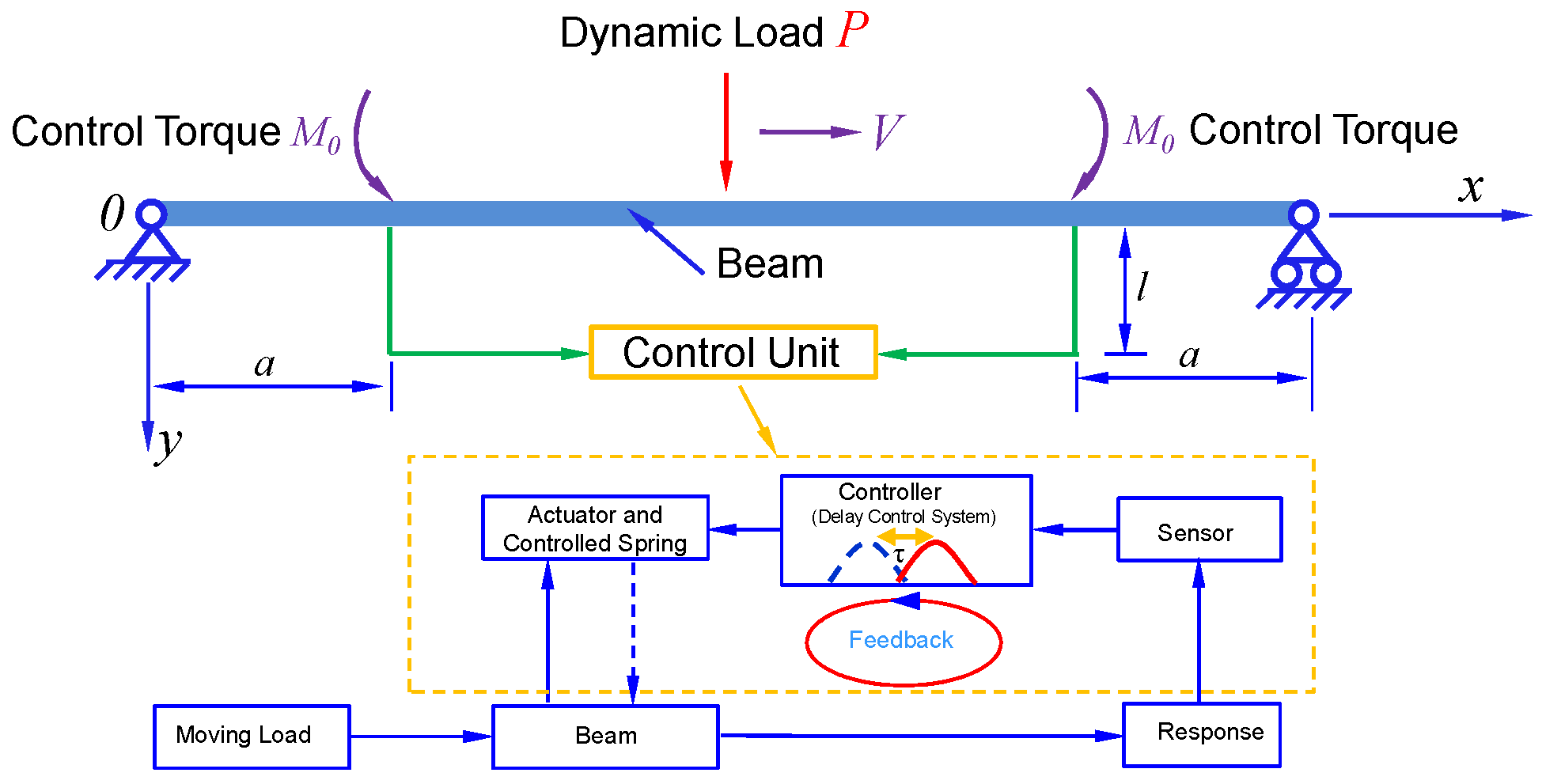
2. Controlled Beam Model and Equations of Motion
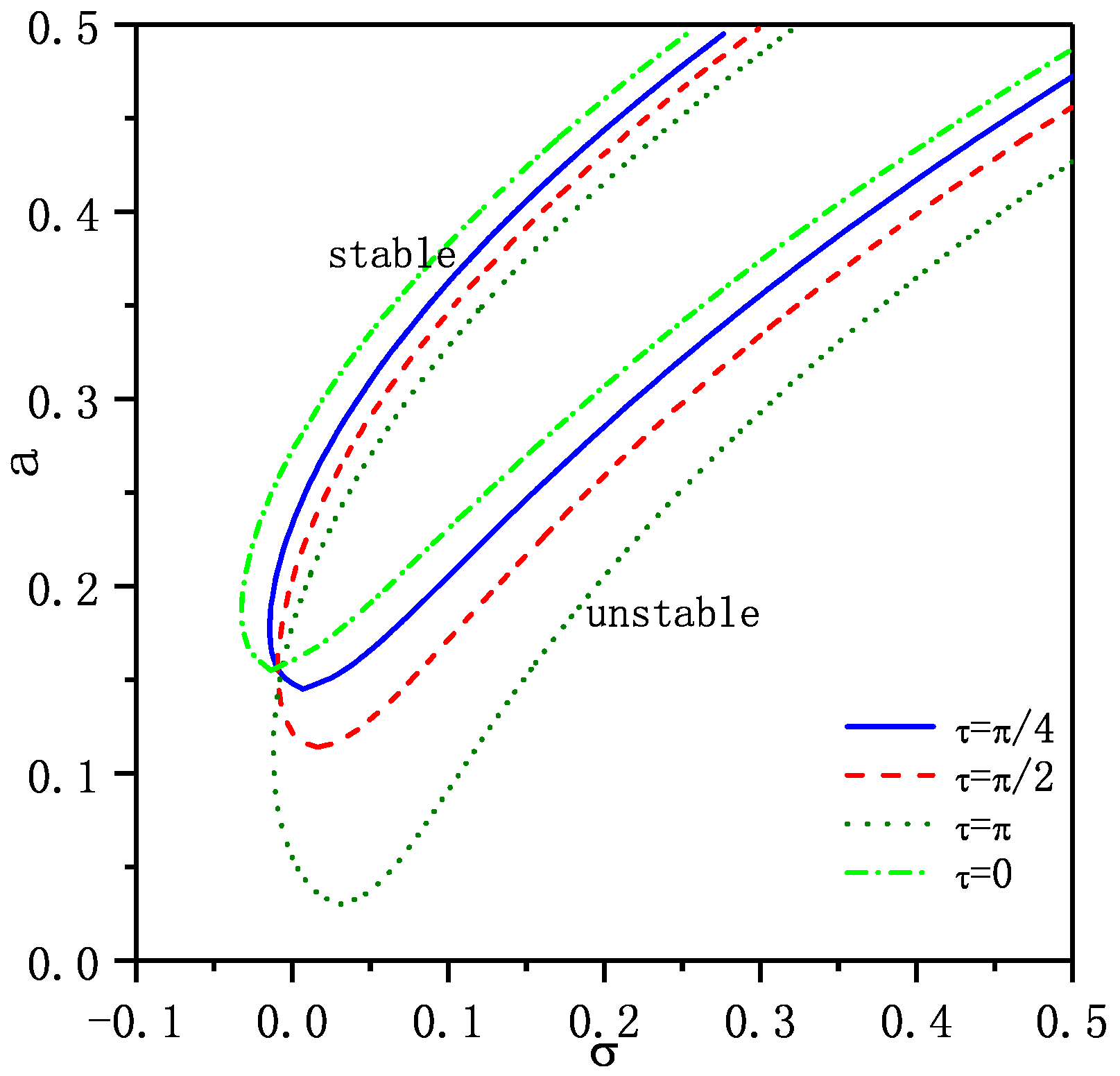
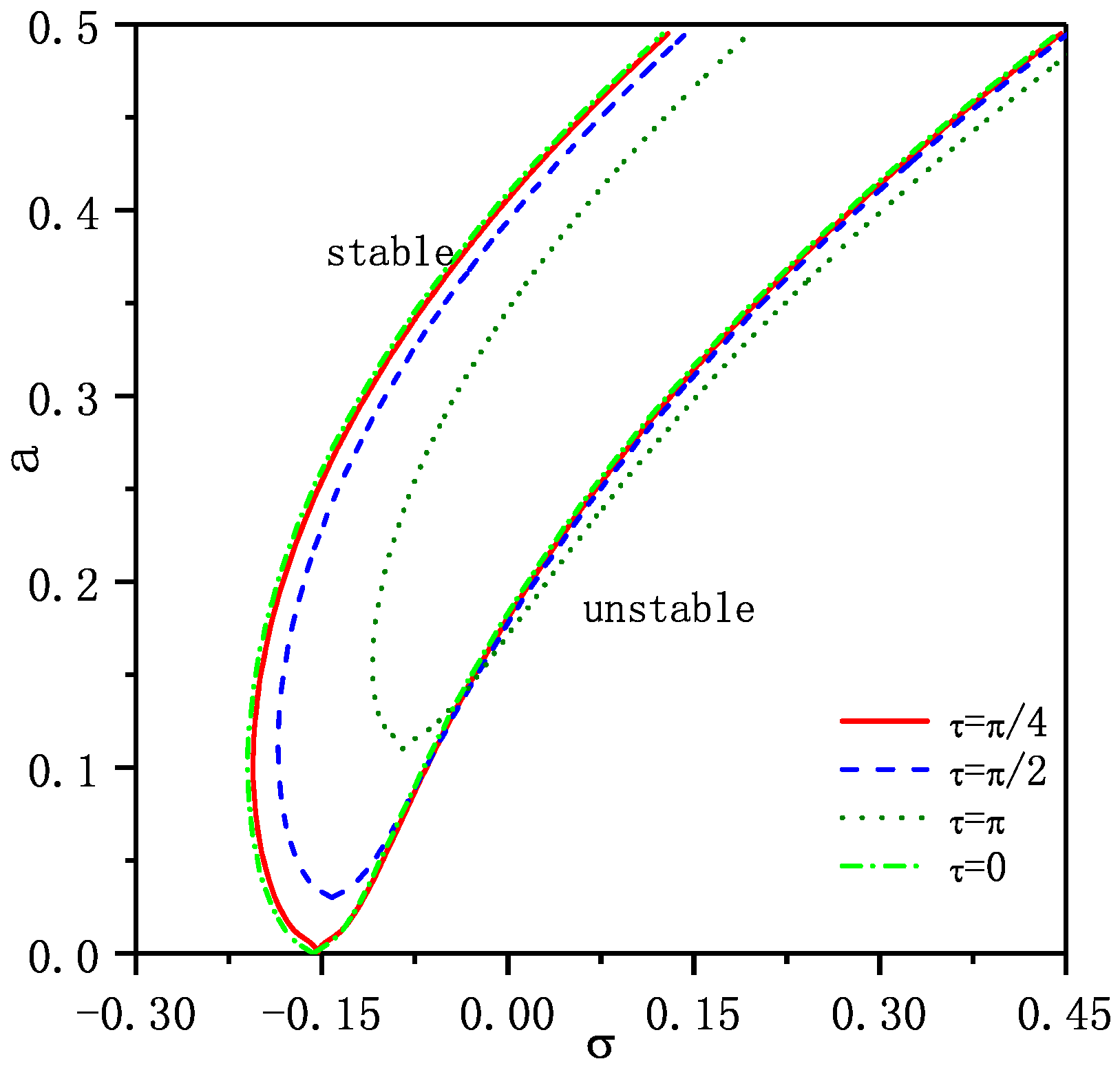
3. Time Delayed Velocity Feedback Control
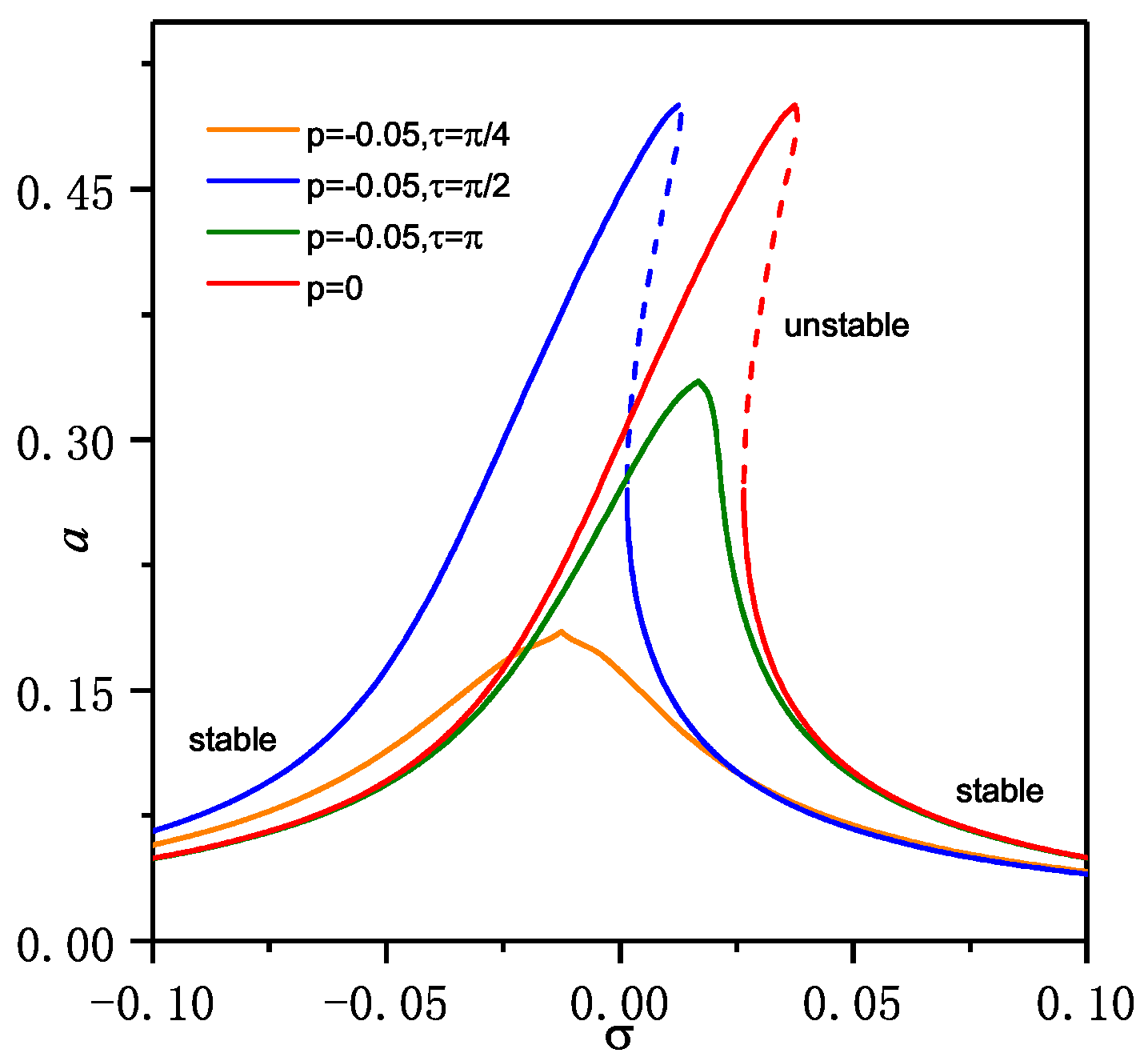
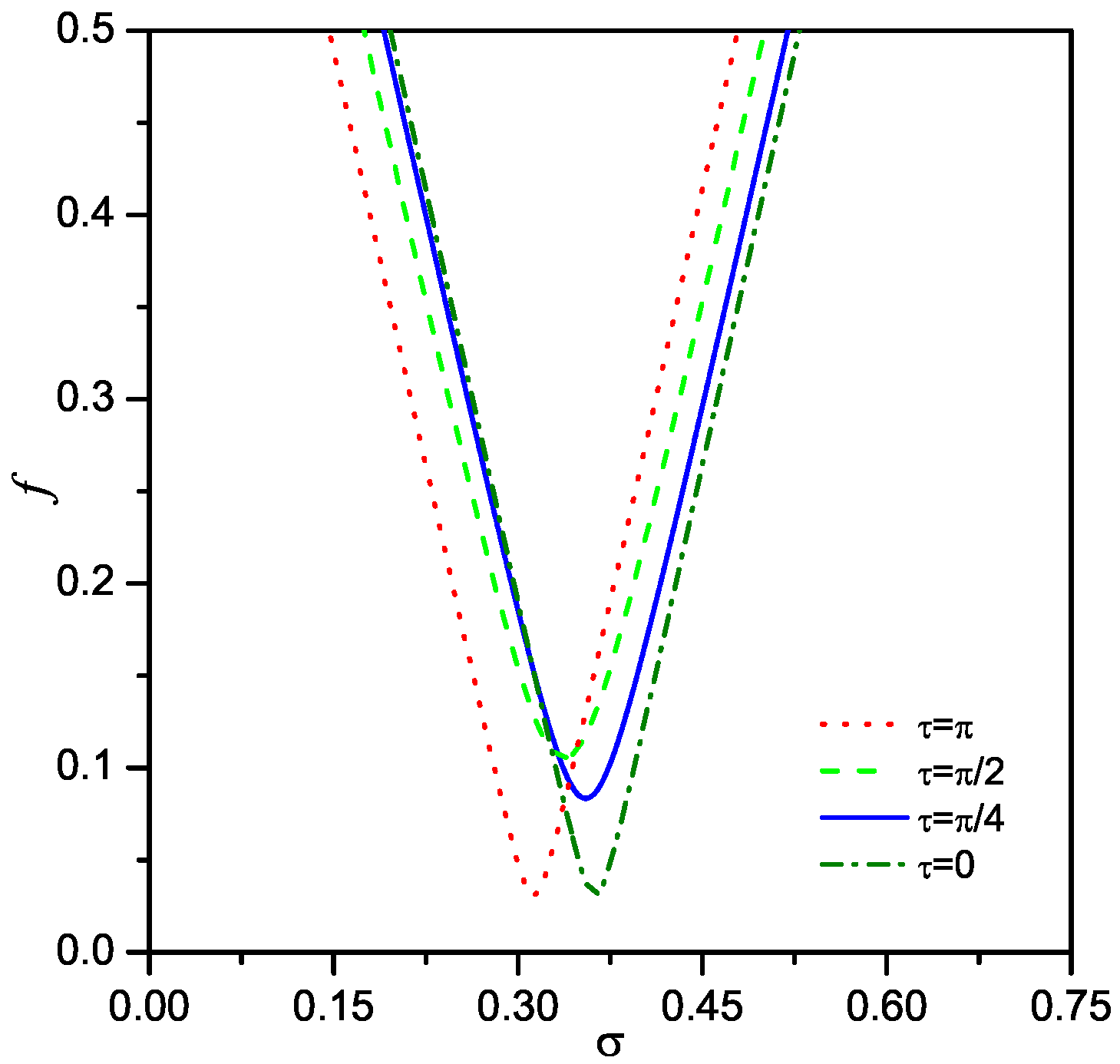
3.1. Nonlinear Primary Resonance Response
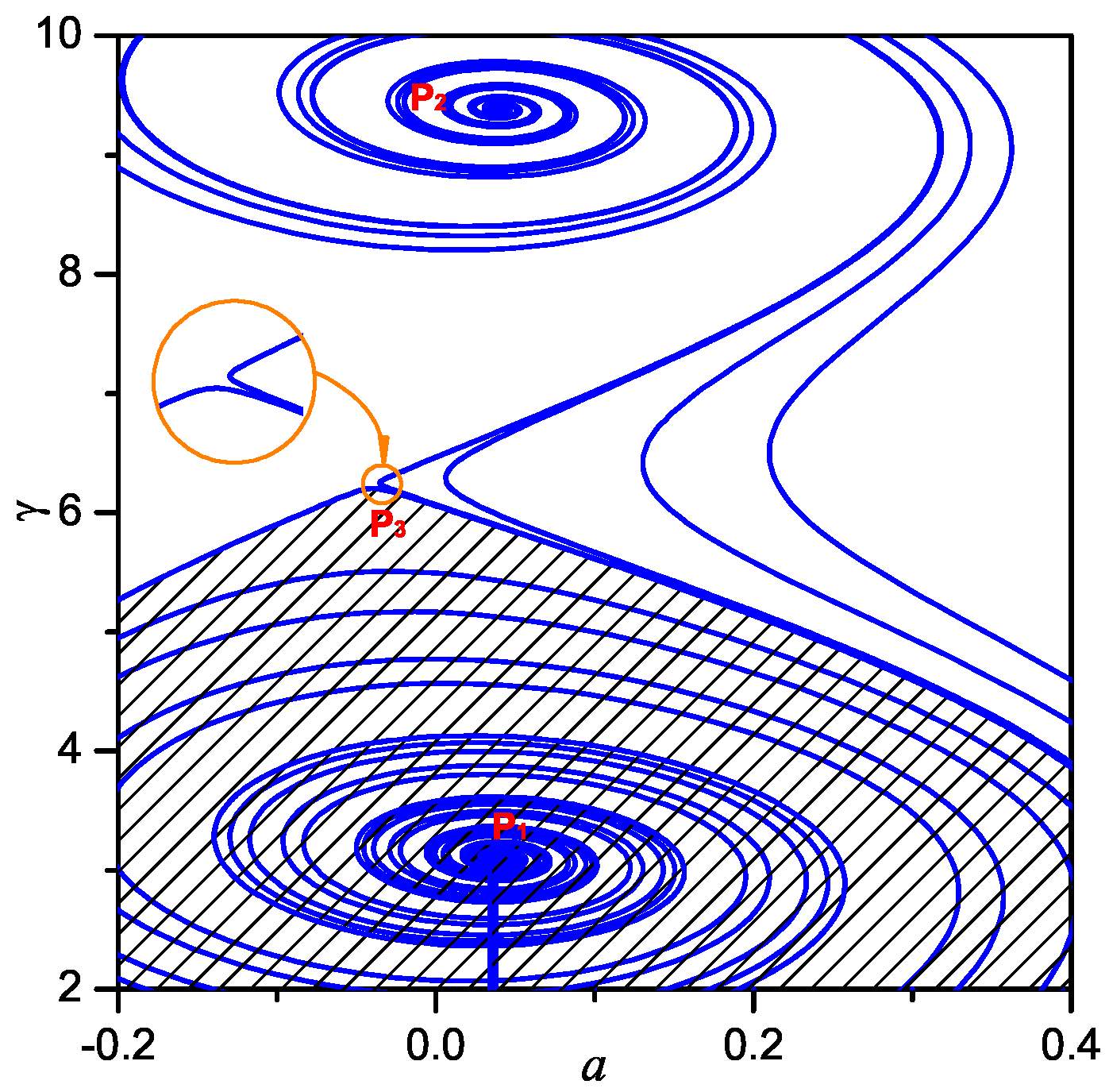
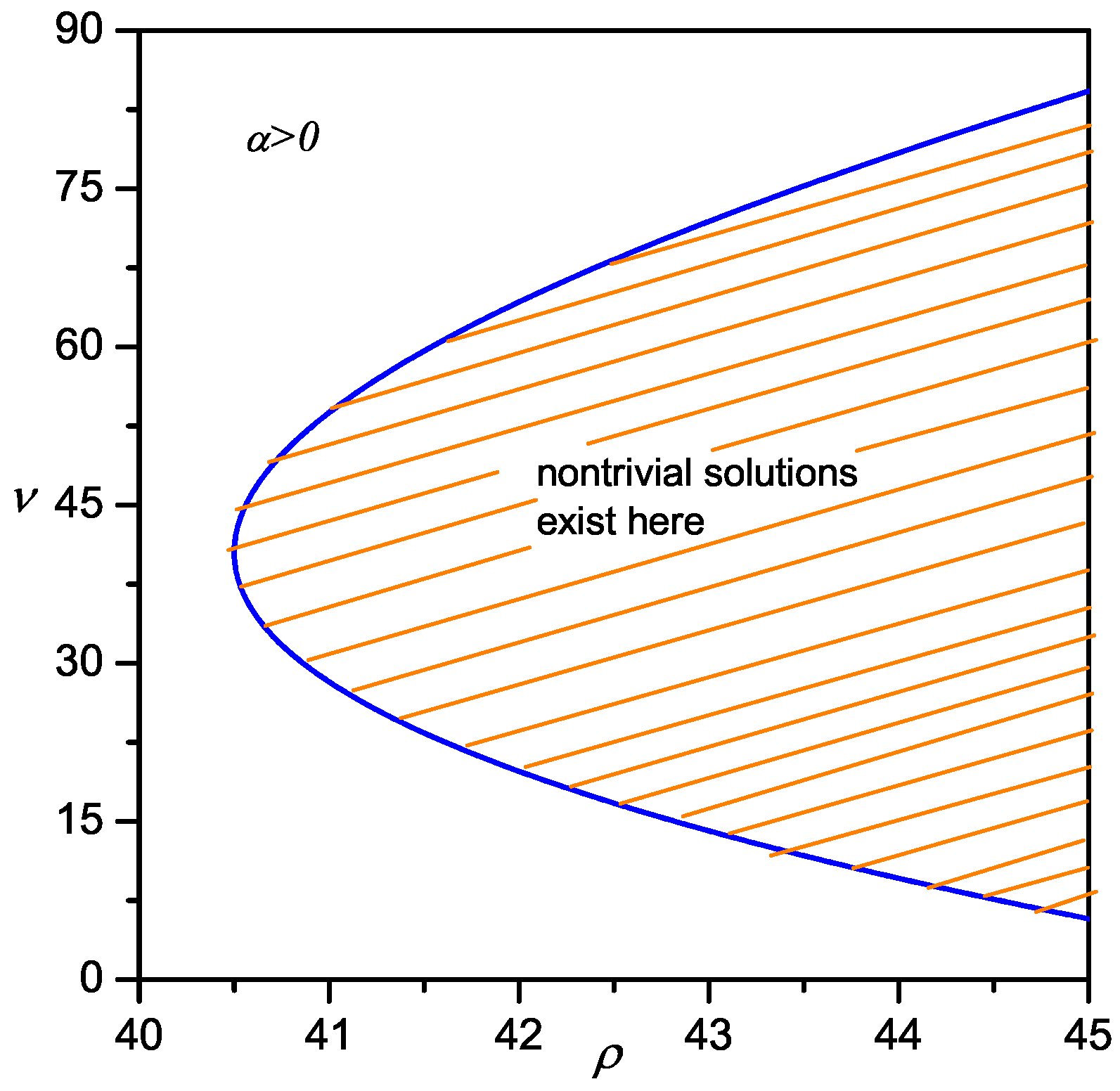
3.2. 1/3 Subharmonic Resonance
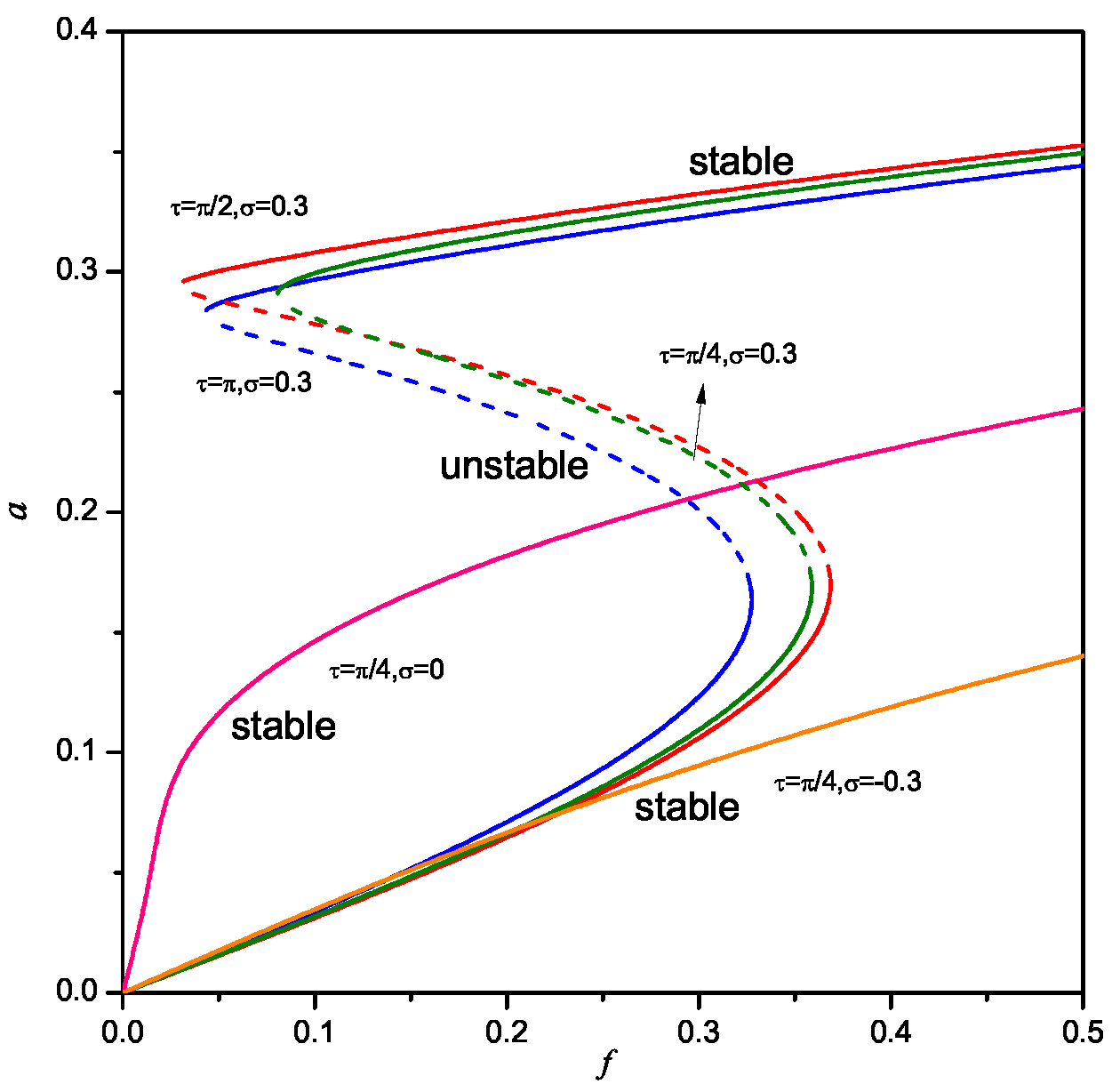
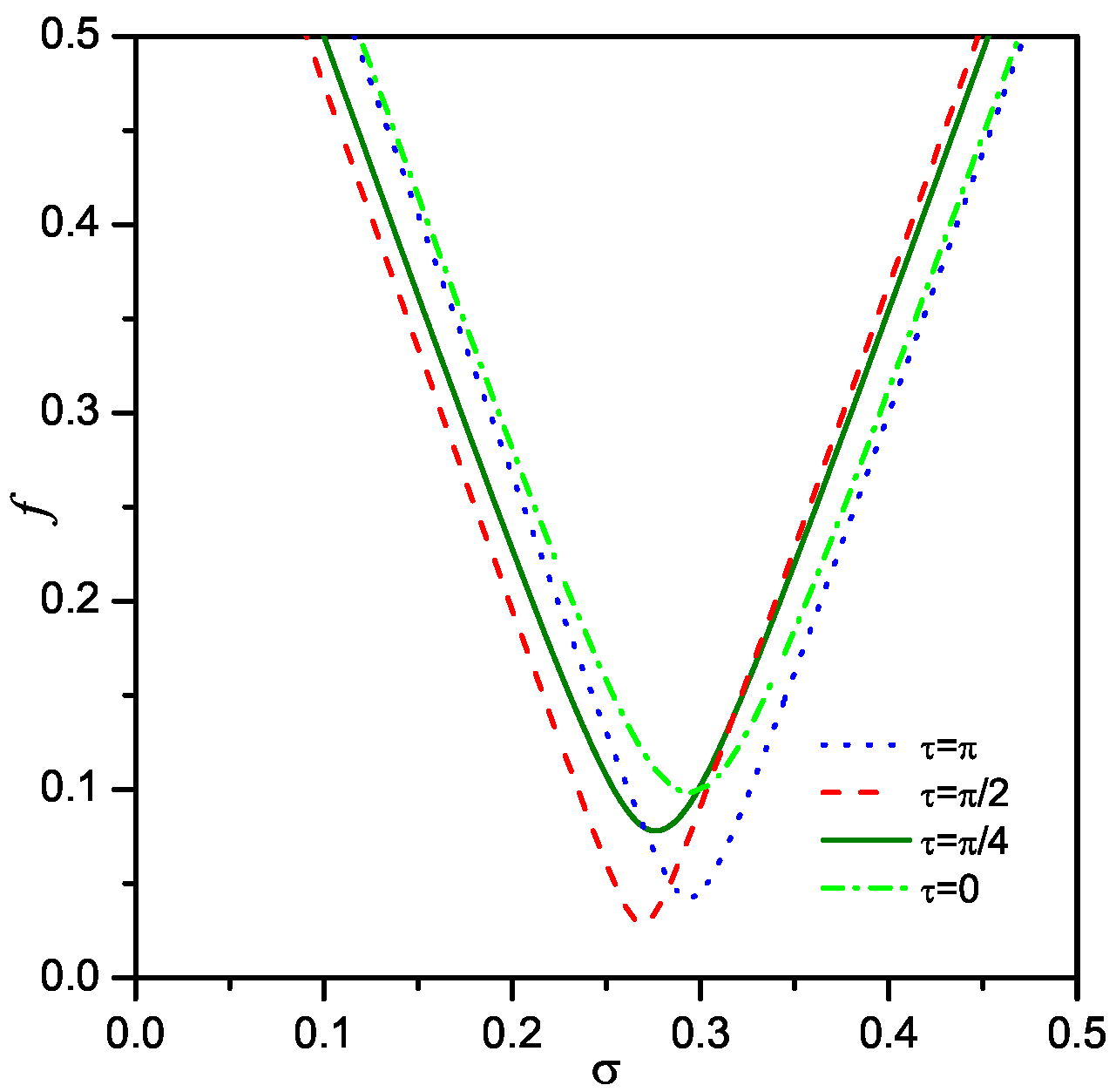
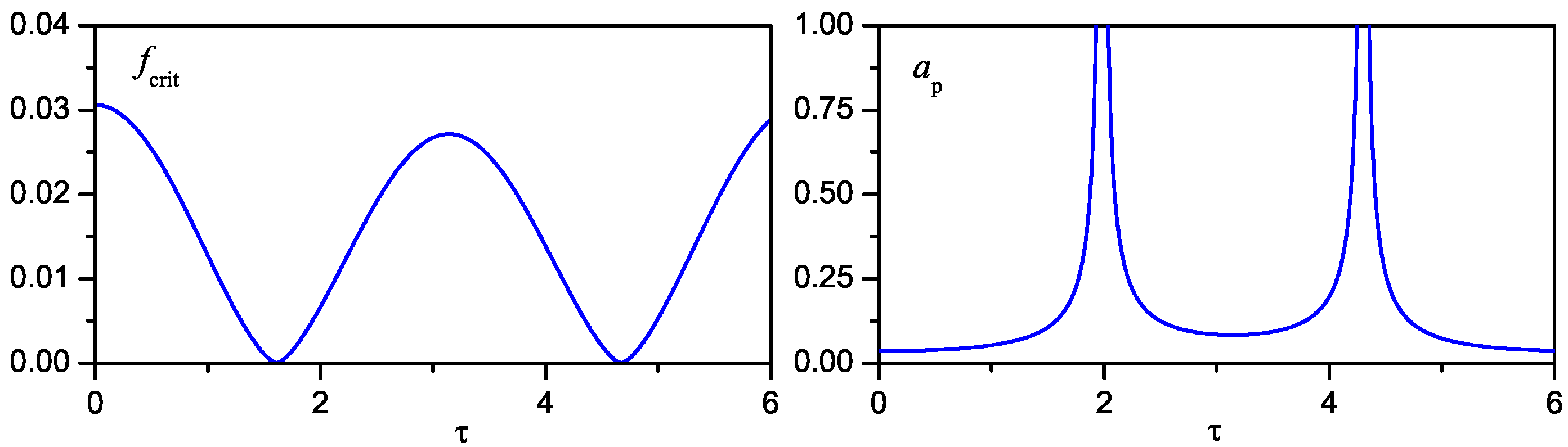
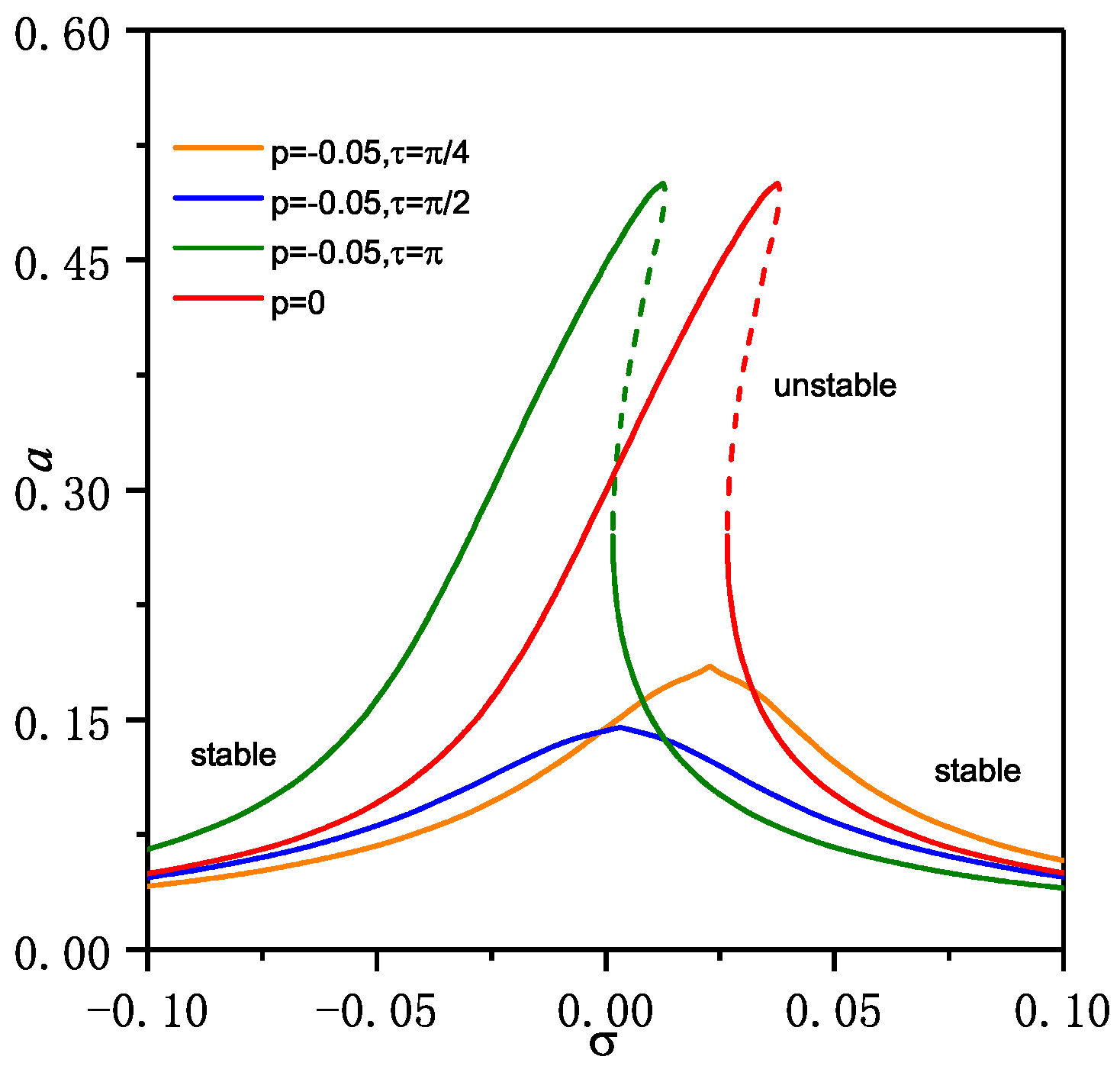
4. Time Delayed Acceleration Feedback Control
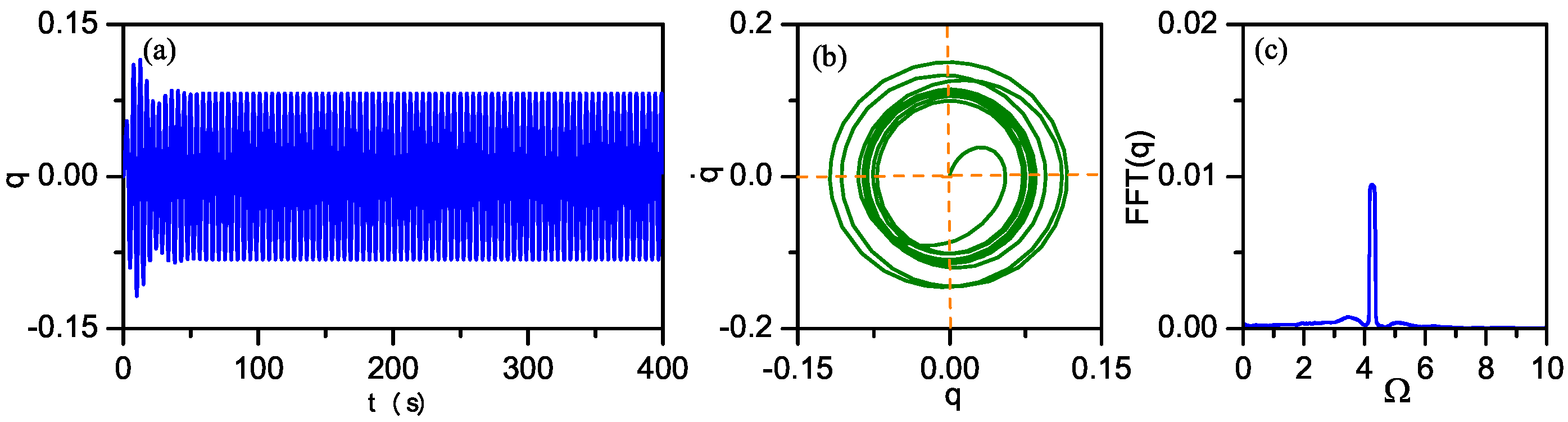
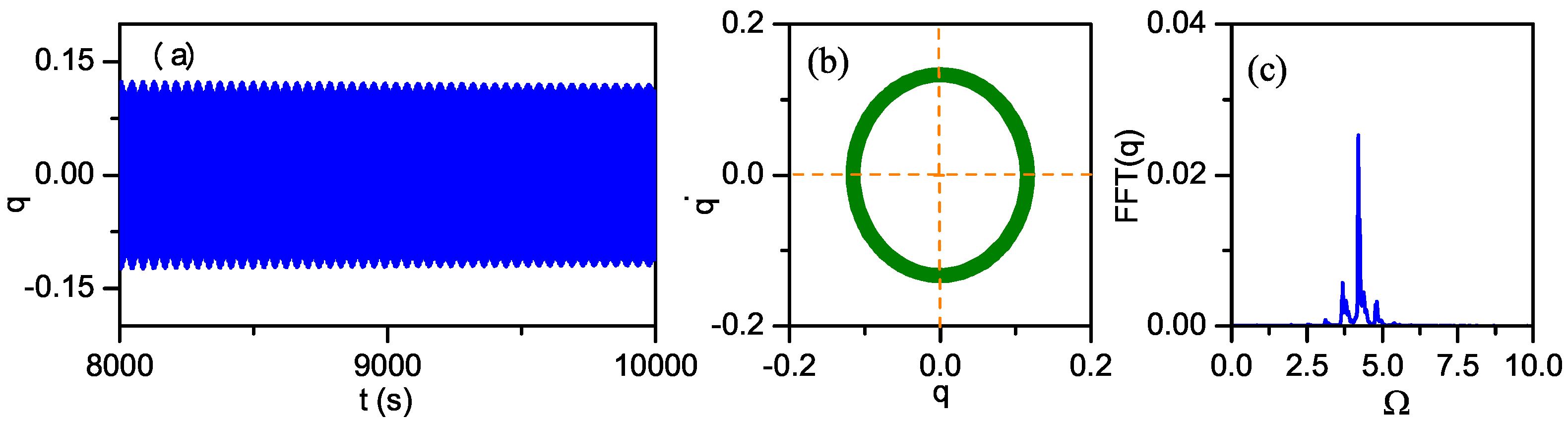
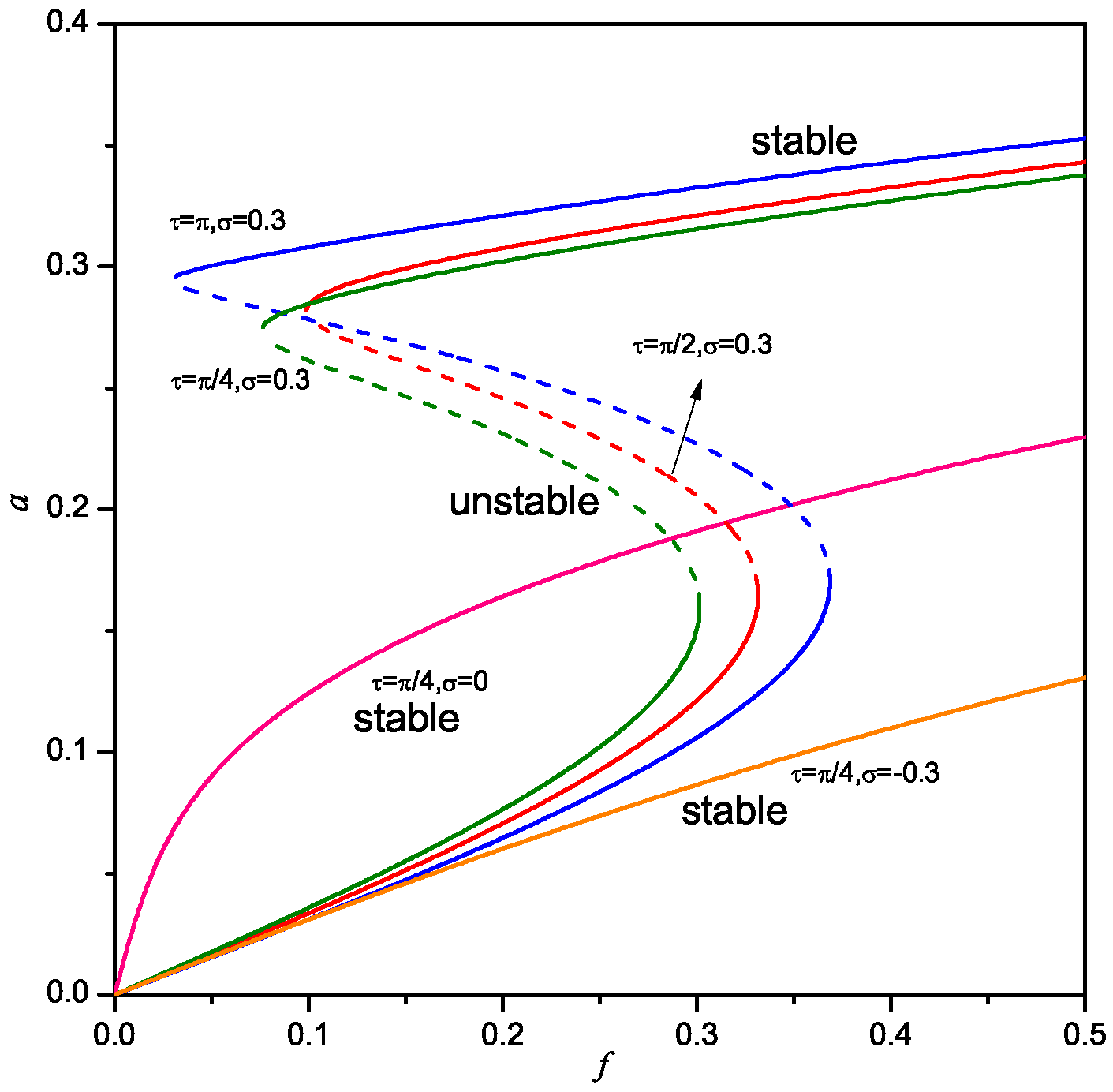
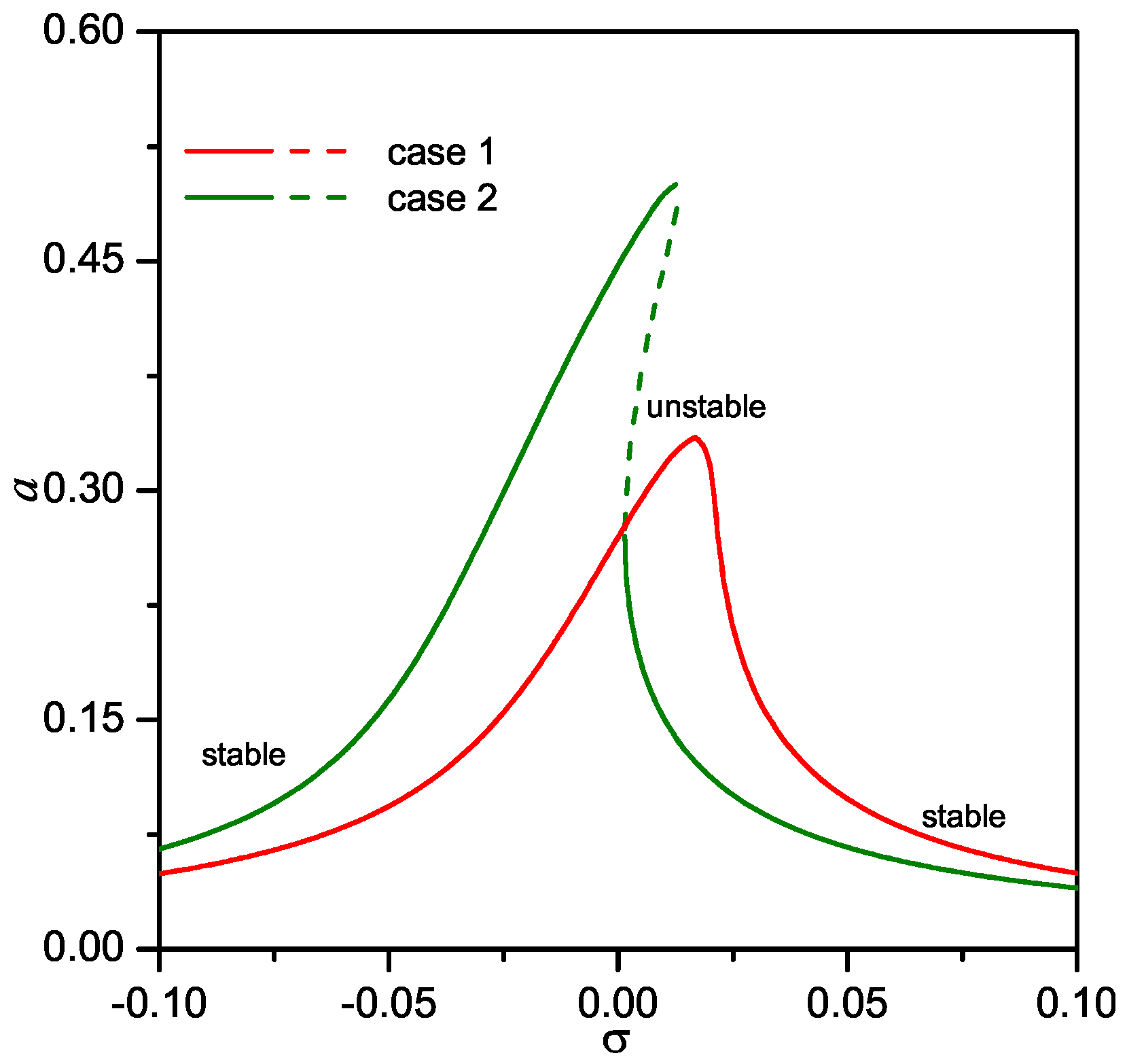
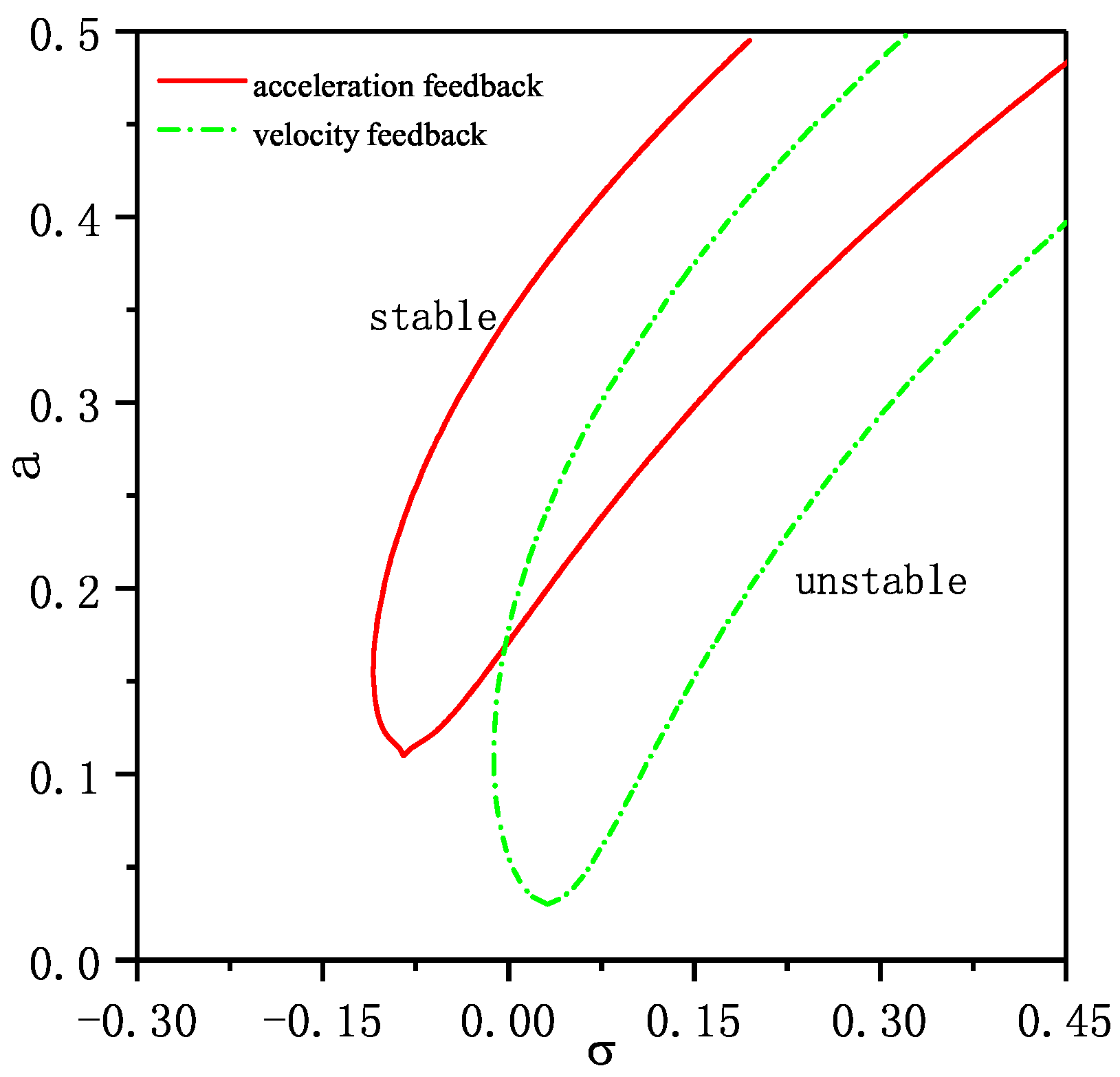
5. Discussion on Comparing the Velocity and Acceleration Feedback
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Discrete Model
References
- McDonald, P.H. Nonlinear motion of a beam. Nonlinear Dyn. 1991, 2, 187–198. [Google Scholar] [CrossRef]
- Ma, J.J.; Gao, X.J.; Liu, F.J. Nonlinear lateral vibrations and two-to-one resonant responses of a single pile with soil-structure interaction. Meccanica 2017, 52, 3549–3562. [Google Scholar] [CrossRef]
- Ma, J.J.; Liu, F.J.; Nie, M.Q.; Wang, J.B. Nonlinear free vibration of a beam on Winkler foundation with consideration of soil mass motion of finite depth. Nonlinear Dyn. 2018, 92, 429–441. [Google Scholar] [CrossRef]
- Sudheesh Kumar, C.P.; Sujatha, C.; Shankar, K. Vibration of simply supported beams under a single moving load: A detailed study of cancellation phenomenon. Int. J. Mech. Sci. 2015, 99, 40–47. [Google Scholar] [CrossRef]
- Fiorillo, G.; Ghosn, M. Application of influence lines for the ultimate capacity of beams under moving loads. Eng. Struct. 2015, 103, 125–133. [Google Scholar] [CrossRef]
- Soong, T.T.; Spencer, B.F., Jr. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2003, 24, 243–259. [Google Scholar] [CrossRef]
- Lin, W.; Song, G.B.; Chen, S.H. PTMD control on a benchmark tv tower under earthquake and wind load excitations. Appl. Sci. 2017, 7, 425. [Google Scholar] [CrossRef]
- Sun, H.; Zuo, L.; Wang, X.; Peng, J.; Wang, W. Exact H2 optimal solutions to inerter-based isolation systems for building structures. Struct. Control Health Monit. 2019, 26, e2357. [Google Scholar] [CrossRef]
- Liao, J.J.; Wang, A.P.; Ho, C.M.; Hwang, Y.D. A robust control of a dynamic beam structure with time delay effect. J. Sound Vib. 2002, 252, 835–847. [Google Scholar] [CrossRef]
- Qian, C.Z.; Tang, J.S. A time delay control for a nonlinear dynamic beam under moving load. J. Sound Vib. 2008, 309, 1–8. [Google Scholar] [CrossRef]
- Ji, J.C.; Leung, A.Y.T. Resonances of a non-linear s.d.o.f. system with two time-delays in linear feedback control. J. Sound Vib. 2002, 253, 985–1000. [Google Scholar] [CrossRef]
- Sadek, I.S.; Sloss, J.M.; Bruch, J.C., Jr.; Adali, S. Dynamically loaded beam subject to time-delayed active control. Mech. Res. Commun. 1989, 16, 73–81. [Google Scholar] [CrossRef]
- Koumene Taffo, G.I.; Siewe Siewe, M. Parametric resonance, stability and heteroclinic bifurcation in a nonlinear oscillator with time-delay: Application to a quarter-car model. Mech. Res. Commun. 2013, 52, 1–10. [Google Scholar] [CrossRef]
- Li, X.Y.; Ji, J.C.; Hansen, C.H. Dynamics of two delay coupled van der Pol oscillators. Mech. Res. Commun. 2006, 33, 614–627. [Google Scholar] [CrossRef]
- Hu, H.Y.; Dowell, E.H.; Virgin, L.N. Resonances of a harmonically forced duffing oscillator with time delay state feedback. Nonlinear Dyn. 1998, 15, 311–327. [Google Scholar] [CrossRef]
- Wang, Z.H.; Hu, H.Y. Stabilization of vibration systems via delayed state difference feedback. J. Sound. Vib. 2006, 296, 117–129. [Google Scholar] [CrossRef]
- Maccari, A. Vibration control for the primary resonance of a cantilever beam by a time delay state feedback. J. Sound Vib. 2003, 259, 241–251. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Xu, J. Effects of delayed feedback control on nonlinear vibration absorber system. J. Sound Vib. 2007, 308, 212–230. [Google Scholar] [CrossRef]
- Alhazza, K.A.; Daqaq, M.F.; Nayfeh, A.H.; Inman, D.J. Non-linear vibrations of parametrically excited cantilever beams subjected to non-linear delayed-feedback control. Int. J. Nonlin. Mech. 2007, 43, 801–812. [Google Scholar] [CrossRef]
- Peng, J.; Xiang, M.J.; Wang, L.H.; Xie, X.Z.; Sun, H.X.; Yu, J.D. Nonlinear primary resonance in vibration control of cable-stayed beam with time delay feedback. Mech. Syst. Signal Process. 2020, 137, 106488. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, G.; Xiang, M.J.; Sun, H.X.; Wang, X.W.; Xie, X.Z. Vibration control for the nonlinear resonant response of a piezoelectric elastic beam via time-delayed feedback. Smart. Mater. Struct. 2019, 28, 095010. [Google Scholar] [CrossRef]
- Peng, J.; Xiang, M.; Li, L.; Sun, H.; Wang, X. Time-Delayed Feedback Control of Piezoelectric Elastic Beams under Superharmonic and Subharmonic Excitations. Appl. Sci. 2019, 9, 1557. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.F.; Wang, Y.F.; Liu, X.R.; Liu, Y.X. Delay-induced dynamics of an axially moving string with direct time-delayed velocity feedback. J. Sound Vib. 2010, 329, 5434–5451. [Google Scholar] [CrossRef]
- Zhao, Y.B.; Huang, C.H.; Chen, L.C.; Peng, J. Nonlinear vibration behaviors of suspended cables under two-frequency excitation with temperature effects. J. Sound Vib. 2018, 416, 279–294. [Google Scholar] [CrossRef]
- Zhao, Y.B.; Huang, C.H.; Chen, L.C. Nonlinear planar secondary resonance analyses of suspended cables with thermal effects. J. Therm. Stress. 2019, 42, 1515–1534. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Turchin, P. Complex Population Dynamics: A Theoretical/Empirical Synthesis; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Scafetta, N.; Atmos, J. Empirical evidence for a celestial origin of the climate oscillations and its implications 2010,72, 951. J. Atmos. Sol.-Terr. Phys. 2010, 72, 951. [Google Scholar] [CrossRef] [Green Version]
- Salgado Sánchez, P.; Porter, J.; Tinao, I.; Laverón-Simavilla, A. Dynamics of weakly coupled parametrically forced oscillators. Phys. Rev. 2016, 94, 022216. [Google Scholar] [CrossRef] [Green Version]
- Buks, E.; Roukes, M.L. Electrically tunable collective response in a coupled micromechanical array. J. Microelectomech. Syst. 2002, 11, 802. [Google Scholar] [CrossRef]
- Lifshitz, R.; Cross, M.C. Response of parametrically-driven nonlinear coupled oscillators with application to micro- and nanomechanical resonator arrays. Phys. Rev. B 2003, 67, 134302. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.J.; Liu, F.J.; Gao, X.J.; Nie, M.Q. Buckling and free vibration of a single pile considering the effect of soil-structure interaction. Int. J. Struct. Stab. Dyn. 2017, 18, 1850061. [Google Scholar] [CrossRef]
- Ma, J.J.; Peng, J.; Gao, X.J.; Xie, L. Effect of soil-structure interaction on the nonlinear response of an inextensional beam on elastic foundation. Arch. Appl. Mech. 2014, 85, 273–285. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Peng, J.; Li, L.; Sun, H. Nonlinear Vibration Mitigation of a Beam Excited by Moving Load with Time-Delayed Velocity and Acceleration Feedback. Appl. Sci. 2020, 10, 3685. https://doi.org/10.3390/app10113685
Tang Y, Peng J, Li L, Sun H. Nonlinear Vibration Mitigation of a Beam Excited by Moving Load with Time-Delayed Velocity and Acceleration Feedback. Applied Sciences. 2020; 10(11):3685. https://doi.org/10.3390/app10113685
Chicago/Turabian StyleTang, Yiwei, Jian Peng, Luxin Li, and Hongxin Sun. 2020. "Nonlinear Vibration Mitigation of a Beam Excited by Moving Load with Time-Delayed Velocity and Acceleration Feedback" Applied Sciences 10, no. 11: 3685. https://doi.org/10.3390/app10113685




