Next Article in Journal
Highly Efficient Implementation of Block Ciphers on Graphic Processing Units for Massively Large Data
Next Article in Special Issue
Conversation-Based School Building Inspection Support System
Previous Article in Journal
Grapevine Phenology in Four Portuguese Wine Regions: Modeling and Predictions
Previous Article in Special Issue
Mine Fire Behavior under Different Ventilation Conditions: Real-Scale Tests and CFD Modeling
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 10
Issue 11
10.3390/app10113710
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Novel Ensemble Landslide Predictive Models Based on the Hyperpipes Algorithm: A Case Study in the Nam Dam Commune, Vietnam

by
Quoc Cuong Tran
1,*,
Duc Do Minh
2,
Abolfazl Jaafari
3,
Nadhir Al-Ansari
4,*,
Duc Dao Minh
1,5,
Duc Tung Van
1,
Duc Anh Nguyen
1,
Trung Hieu Tran
1,
Lanh Si Ho
6,
Duy Huu Nguyen
7,
Indra Prakash
8,
Hiep Van Le
9,* and
Binh Thai Pham
10,*
1
Institute of Geological Sciences, Vietnam Academy of Science and Technology, 84 Chua Lang Street, Dong Da, Hanoi 100000, Vietnam
2
VNU University of Science, Vietnam National University, 334 Nguyen Trai, Hanoi 100000, Vietnam
3
Research Institute of Forests and Rangelands, Agricultural Research, Education, and Extension Organization (AREEO), P.O. Box 64414-356, Tehran 64414, Iran
4
Department of Civil, Environmental and Natural Resources Engineering, Lulea University of Technology, 971 87 Lulea, Sweden
5
Vietnam Academy of Sciences and Technology, Graduate University of Science and Technology, 18 Hoang Quoc Viet, Hanoi 100000, Vietnam
6
Civil and Environmental Engineering Program, Graduate School of Advanced Science and Engineering, Hiroshima University, 1-4-1, Kagamiyama, Higashi-Hiroshima, Hiroshima 739-527, Japan
7
Faculty of Geography, VNU University of Science, Vietnam National University, 334 Nguyen Trai, Hanoi 100000, Vietnam
8
Department of Science & Technology, Bhaskarcharya Institute for Space Applications and Geo-Informatics (BISAG), Government of Gujarat, Gandhinagar 382002, India
9
Institute of Research and Development, Duy Tan University, Da Nang 550000, Vietnam
10
University of Transport Technology, Hanoi 100000, Vietnam
*
Authors to whom correspondence should be addressed.
Appl. Sci. 2020, 10(11), 3710; https://doi.org/10.3390/app10113710
Submission received: 27 April 2020 / Revised: 22 May 2020 / Accepted: 25 May 2020 / Published: 27 May 2020
(This article belongs to the Special Issue New Directions in Hazard and Disaster Science: Advances in Applied Sciences)
Browse Figures
Versions Notes

Abstract

:
Development of landslide predictive models with strong prediction power has become a major focus of many researchers. This study describes the first application of the Hyperpipes (HP) algorithm for the development of the five novel ensemble models that combine the HP algorithm and the AdaBoost (AB), Bagging (B), Dagging, Decorate, and Real AdaBoost (RAB) ensemble techniques for mapping the spatial variability of landslide susceptibility in the Nam Dan commune, Ha Giang province, Vietnam. Information on 76 historical landslides and ten geo-environmental factors (slope degree, slope aspect, elevation, topographic wetness index, curvature, weathering crust, geology, river density, fault density, and distance from roads) were used for the construction of the training and validation datasets that are the prerequisites for building and testing the proposed models. Using different performance metrics (i.e., the area under the receiver operating characteristic curve (AUC), negative predictive value, positive predictive value, accuracy, sensitivity, specificity, root mean square error, and Kappa), we verified the proficiency of all five ensemble learning techniques in increasing the fitness and predictive powers of the base HP model. Based on the AUC values derived from the models, the ensemble ABHP model that yielded an AUC value of 0.922 was identified as the most efficient model for mapping the landslide susceptibility in the Nam Dan commune, followed by RABHP (AUC = 0.919), BHP (AUC = 0.909), Dagging-HP (AUC = 0.897), Decorate-HP (AUC = 0.865), and the single HP model (AUC = 0.856), respectively. The novel ensemble models proposed for the Nam Dan commune and the resultant susceptibility maps can aid land-use planners in the development of efficient mitigation strategies in response to destructive landslides.

1. Introduction

Landslides are global geohazards that are responsible for substantial death and injury [1], as well as damage to the natural and built environment [2]. Previous studies reported that landslides annually cause more than 4300 fatalities and global economic losses of tens of billions of USD [3]. The distribution maps of landslide susceptibilities are essential tools for mitigating the devastating effects of landslides. These maps provide engineers and managers with operational guidance and reference for making timely decisions to proactively manage unstable terrain and mitigate the effects of potential landslides [4]. However, the preparation of reliable maps remains challenging because landslides are influenced by an interplay of different climate, geologic, geographic, and anthropogenic factors [5].
Landslide susceptibility can be modeled using a variety of GIS-aided methods, including regression logistics [6], simplified statistical/probabilistic frequency ratios [7], analytical hierarchy process [8], statistical indices [9], weight of evidence [10], evidential belief functions [11], certainty factors [12], and geographically weighted regression [13]. Another suite of approaches is machine learning methods, which are known as methods with an advantage for processing large datasets that exhibit non-linear and complex relationships, and that are typically associated with environmental problems, particularly natural hazard issues such as floods [14], wildfires [15], sinkholes [16], drought [17], earthquakes [18], gully erosion [19], and land subsidence [20,21]. The methods can recognize the discrepancy between historical records and different landscape-level variables to predict future events [22].
The models derived from machine learning that have been tried for modeling and mapping landslide susceptibility include artificial neural networks (ANN) [23], neuro-fuzzy [24,25,26], support vector machines (SVM) [22], decision trees [14,27], index of entropy [28,29], fuzzy Shannon entropy [30], logistic model trees (LMT) [31], Bayesian logistic regression (BLR) [32], reduced error pruning trees [33], classification and regression trees [34], kernel logistic regression [35,36], Naïve Bayes trees (NBT) [37], and alternating decision trees [20,38]. The methods differ in the matter of the input process, modeling, output process, and prediction success, and all of them involve uncertainties in the modeling process [39,40].
Another approach that has been proven effective in many fields of science, including landslide modeling and mapping, is ensemble modeling [41], which emerged in the early 1990s [42]. In terms of accuracy and robustness, ensemble methods have outperformed single model methods [43]. Recent advances in machine learning algorithms and computational powers, coupled with an increase in the availability of high-resolution data, now allow a wider use of ensemble modeling in landslide prediction [44]. Examples of popular ensemble techniques include Bagging, Rotation Forest, Random Subspace and MultiBoost. These methods, in turn, have been used to enhance the performance of base NBT [45], BLR [32], LMT [37], ANN [46], random forest [47], J48 decision tree [48], SVM [49], stochastic gradient descent [41], and alternating decision tree [50] methods.
Because landslides have such serious impacts on society, there is a need to continually improve the predictability of landslide susceptibility models for different environmental settings. The key objective of our modeling research is to improve the reliability of landslide modeling and the effectiveness of landslide susceptibility maps for land-use planners and decision makers. To achieve this, we use a Hyperpipes (HP) model in an ensemble learning framework to predict landslide susceptibility in the Ha Giang province, Vietnam. We couple the HP model with AdaBoost, Real AdaBoost, Bagging, Dagging, and Decorate ensemble learners. To the best of our knowledge, HP has not yet been employed as a base method for developing ensemble models for the prediction of natural hazards. HP is a straightforward, fast-executing algorithm that performs well on different datasets, and tailor its process to extend the scope of the dataset upon which it is effective. Here, we first formulate the likelihood of landslide occurrences as a binary classification problem. We next propose multiple copies of the HP model trained by different ensemble learning techniques. Lastly, we verify and compare the models in terms of their fitness and predictive powers, and generate distribution maps of landslide susceptibility by each model.

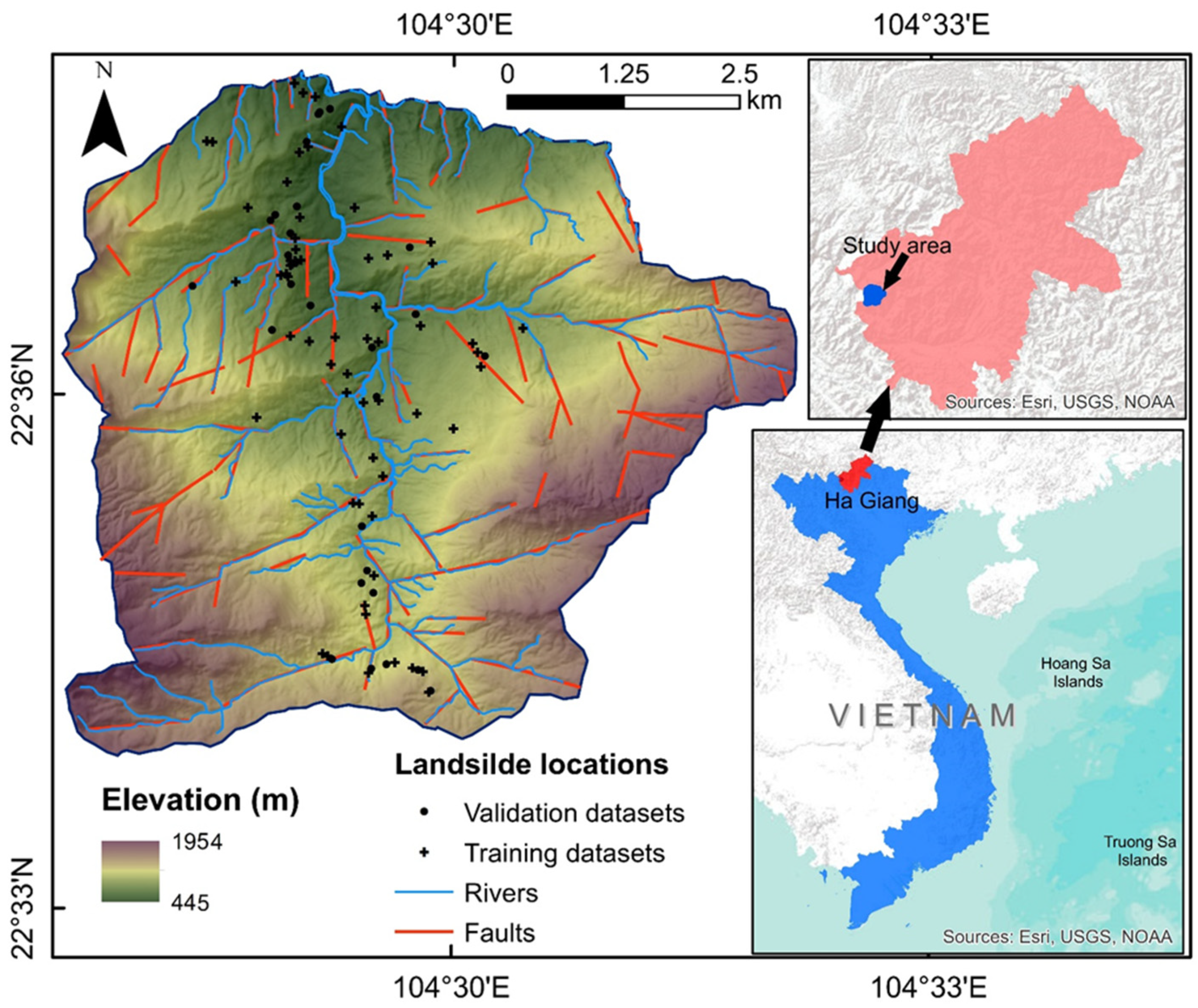
2. Description of the Study Area

Nam Dan commune is situated in the southern part of the Xin Man district, Ha Giang province, Vietnam (Figure 1). With a relatively complex terrain and an average altitude of 1000 m, the region has been visibly divided by high mountains. The climate of the area is tropical monsoon, so it often gets stormy in summer with an annual rainfall of about 2300–2400 mm. The area is dominated by two separate seasons that include rainy season and dry season. While the rainy season typically extends between 5 and 10 months, the dry season starts from November and ends in April of the next year. Forests cover most parts of the Nam Dan commune. However, over the recent years, the area of forests has been reduced due to the development of farmlands and fire occurrences that intensified the risk of landslides, which, in turn, causes significant damage to equipment and people. Through a field survey, over 71 landslide sites in the Nam Dan commune have been detected, which occurred from 2011 to 2019, and are mostly concentrated along provincial road No. 178. Local people are living on the slope and foot of the landslides, which can be extremely dangerous.

3. Modeling Methodology

In this paper, the prediction of landslide susceptibility for the Nam Dan commune was modeled in four main steps that are shown in Figure 2 and described as follows: (1) data collection and preparation; (2) development and validation of the models using the Weka software [51]; (3) generation susceptibility maps using ArcGIS (https://desktop.arcgis.com/en/); and (4) reliability analysis of the generated susceptibility maps.

3.1. Data Collection and Preparation

3.1.1. Generation of an Inventory Map of Historical Landslides

A map of the landslides that have occurred in the recent past is an important component for modeling of the landslide susceptibility using machine learning methods [52]. To generate such a map for the Nam Dan commune, the records for historical landslides were obtained from the SRV-10/0026 project that had been conducted in the study area. These records were verified and updated via visualization interpretation of remotely sensed data and field surveys (October 2018 and August 2019), also adding the recently occurred landslide locations at the talus provincial road No 178, in August 2019, to the initial records. In total, 76 locations of landslide events were identified across the Nam Dan commune. Most of the slides were of the shallow landslide type. Dividing the detected landslides into separate sets, the training and validation datasets that respectively comprised 53 (~70%) and 23 (~30%) landslides, were generated.

3.1.2. Landslide Conditioning Factors

Modeling of landslide susceptibility is the process of investigating the associations between historical landslides and a suit of explanatory variables known as landslide conditioning factors that typically characterize the geomorphology, hydrology, climate, and anthropogenic conditions of the research area [49,53]. For modeling the landslide susceptibility in the Nam Dan commune, ten conditioning factors were selected and used: slope aspect, slope degree, elevation, curvature, topographic wetness index (TWI), weathering crust, river density, fault density, distance from roads, and geomorphology. Maps of these factors are presented in Figure 3 and Figure 4. Currently, the development of data processing techniques and the data-sharing policies of companies, such as NASA, has facilitated the collection of such conditioning factors. Slope aspect is a widely used topography factor for landslide susceptibility mapping because this factor has a relationship with many other factors, such as solar radiation and rainfall amount, that affect landsliding [54]. Slope degree is a significant factor for modeling landslide susceptibility due to its weighty effects on the sliding of material and flow of water [55]. Elevation characterizes local climate condition and the resistance of the slope-forming materials to failure [56]. Curvature affects the accumulation and flow of water on terrain surface, thus influencing the probability of landslide occurrences [57]. TWI was selected as another conditioning factor because this factors in the relationships between topography and moisture [58]. The thematic map for these five topography factors was derived from a 10-m Digital Elevation Model (DEM) that was constructed using 1:10,000 topographic maps. A weathering crust was selected in this study to represent the difference between the weathering conditions of the rocks that in turn influence the probability of landsliding [59]. Data for the weathering crust were derived from the 1:10,000 geomorphology map, prepared by the SRV-10/0026 project. Rivers generally adversely affect the stability of slopes due to erosion and scouring of the side slopes of the valley and saturation of the groundmass within flood height [60,61]. Therefore, the inclusion of the information related to rivers is vital for landslide modeling and mapping. In this study, the rivers of the Nam Dan commune were derived from the DEM and used to generate a thematic map of river density. Faults induce instability in the ground and rock mass that typically lead to landslides [62,63]. In this study, faults were interpolated from the SAR images (Cosmos Skymed with descending orbit, band X, 3m resolution) and used to generate a thematic map of fault density for the Nam Dan commune. Road construction is the main causes of landslide occurrences in many regions [64]. A thematic map of distance to roads is usually used as a proxy for explaining the effects of human activities on landsliding. In this study, the road networks of the Nam Dan commune were derived from a topographic map with a scale of 1:10,000. Geology is another important factor for landslide susceptibility modeling because this factor reflects the rockmass/groundmass condition of the Nam Dan commune for the stability analysis [65]. In this study, geological units of the Nam Dan commune were identified using the geological map of the General Department of Geology and Minerals of Vietnam.

3.1.3. Factors Importance

To check for the significance of the factors identified for landslide modeling in the Nam Dan commune, we used the One-R feature selection technique [66]. The One-R technique works based on correlation analysis among the conditioning factors and the historical landslides to select the most significant factors for the modeling process [66]. Using the One-R technique, each factor is assigned a weight that indicate the average merit (AM) of the factor in landslide modeling. Based on the AM, one can more accurately focus on the crucial factors and remove unnecessary factors to increase the predictive performance of the models.

3.2. Methods Used

3.2.1. Hyperpipes (HP) Algorithm

HP is a very straightforward and fast classification algorithm that can deal with a large number of attributes [67,68,69]. The HP algorithm works as follows: (1) from the original training dataset, a single pipe for each particle class was created, and each pipe is marked corresponding to the class; (2) the dataset is analyzed instance-by-instance; (3) for every value in the instance, if the attribute value has not occurred yet in a dataset, it will be added to the pipe; (4) each instance is compared to the current attribute values in the pipes for every lass; and (5) the instance is then chosen with the class of pipe corresponding to the optimal match. The HP algorithm has been mostly used in medical science [67,68]. However, this algorithm can also be suggested for landslide modeling due to its several advantages [70].

3.2.2. AdaBoost

AdaBoost, proposed by Freund and Schapire [71], is known as a boosting ensemble technique developed for improving the performance of weak classifiers. Using an adaptive boosting approach, AdaBoost successively generates one classifier at a time; each classifier is trained on a dataset produced selectively from the initial dataset by progressively increasing at each step the likelihood of difficult data samples [57,72]. Therefore, this technique can control not only the bias but also the variance among the data. Generally, an initial classifier is built from a subset that was formed from the initial dataset. The initial classifier-based model is then utilized to predict all samples in the original dataset. Afterwards, a new subset is generated after the classification and evaluation of the error. This process is repeated until reaching the optimum performance for the base classifier. AdaBoost has been frequently used in combination of various classifiers, such as logistic regression [57], functional tree [73], and neural network [74], for landslide prediction.

3.2.3. Bagging

As one of the primary ensemble techniques that was developed by Breiman [75], Bagging is a component of various learners that is used to decrease the variance of the base classifiers, leading to an increase in prediction accuracy. Bagging utilizes a random bootstrap replacement method to generate multiple training subsets with sizes equivalent to the initial training dataset [76]. Each subset is then used to construct multiple classifiers. Finally, all the classifiers are aggregated by a majority vote for classification. Using this methodology, Bagging can mitigate the faults of component learners and improve the recognition performance of the unstable classifiers. Bagging has been frequently used in combination of various classifiers, such as alternating decision tree [38], Credal decision tree [77], kernel logistic regression [78], functional tree [73], and random forest [79], for landslide susceptibility mapping.

3.2.4. Dagging

Originally developed by Ting and Witten [80], Dagging is known as an ensemble learning technique that integrates various classifiers on different samples of training dataset in order to enhance predictive accuracy [81]. Normally, the structure for the training and classification phases of the Dagging ensemble is similar to that of the Bagging algorithm. Nevertheless, the Dagging ensemble generates several disjointed and stratified samples that insert each part of the data to a copy of the base classifier [80]. Finally, all the classifiers are aggregated by a majority vote for classification. Combined with models such as alternating decision tree [82] and functional tree [83], this technique has been frequently used for the prediction of landslides.

3.2.5. Decorate

The Diverse Ensemble Creation by Oppositional Relabeling of Artificial Training Examples method, also called Decorate, was introduced by Melville and Mooney [84]. Decorate is a straightforward meta-learner that can create diverse classifiers from the distribution characteristic of the original training dataset. While Bagging and AdaBoost generate classifiers from the training dataset, Decorate augments the training dataset by generating and adding base classifiers into the original training dataset, and an ensemble is then generated iteratively. In each iteration, the new created artificial training examples are added to the current ensemble. The procedure is repeated until obtaining the favorite size for the committee. For the Decorate algorithm, two key phases are (1) generating and adding the artificial training examples; and (2) evaluating the accuracy of the augmented training dataset. Among the different ensemble learning techniques, Decorate is the only technique that utilizes artificially generated samples to improve prediction quality [85].

3.2.6. Real AdaBoost

Based on the AdaBoost ensemble technique, Schapire and Singer [86] proposed the Real AdaBoost ensemble technique. Real AdaBoost, which combines adaptive and boosting, is an attractive technique that has been widely employed in many fields related to statistics and machine learning [87]. Real AdaBoost uses local optimum criteria that often yields better convergence than the AdaBoost technique [88]. Real AdaBoost has been used in combination with classifiers such as alternating decision tree [82] for landslide prediction.

3.3. Validation Methods

To assess and compare the ability of the six models proposed in this study, the following quantitative statistic measures were used: positive predictive value (PPV), negative predictive value (NPV), sensitivity (SST), specificity (SPF), accuracy (ACC), Kappa index, root mean square error (RMSE), and area under the receiver operating characteristic (ROC) curve (AUC). A full description on these methods and their corresponding formula can be found in the literature [89,90,91].

3.4. Susceptibility Mapping

When the HP models and its five ensemble models were successfully trained and validated using the training and verified datasets, they were used to generate the landslide susceptibility maps. To do so, we first computed the landslide susceptibility indices for all pixels of the study area, and then categorized the indices into different classes that depicted very low, low, moderate, high, and very high susceptibility to landslide occurrence within the Nam Dam commune [5].

4. Results and Discussion

4.1. Analysis of Factor Significance

The relevance of conditioning factors to landslide occurrence exerts a significant effect on the quality of the prediction output [92]. However, no universal method has yet been suggested for the best selection of conditioning factors [93]. Here, we used the One-R technique for quantifying the significance of the factor selected. The results revealed that distance from roads with AM = 82.379 was the most useful variable for describing the distribution of landslide susceptibility in the Nam Dan commune, followed by elevation (AM = 80.552), river density (AM = 72.915), weathering crust (AM = 68.75), and fault density (AM = 67.186) (Table 1). Since all ten factors showed AM ≠ 0, they need to be included in the modeling process [91,94]. From another point of view, the factor analysis revealed that, in our study area, landslides are mostly associated with road networks, demonstrating the impact of human activities on slope instabilities, and thereby intensifying the landslide susceptibilities [95].

4.2. Evaluation of Models Performance

The models were trained using the training dataset and after that were validated using the validation dataset. In the training phase (Table 2), the single HP and ensemble Decorate-HP models achieved the highest possible value of the PPV metric (100%), which indicated that the values of these two models had the highest capability to distinguish between landslide pixels and other pixels across the area. In terms of the NPV metric, the ensemble RABHP model with a value of 85.94% performed the best in distinguishing between non-landslide pixels and other pixels across the area. For the SST metric that measures the model’s ability to correctly assign the landslide pixels to the landslide class, the RABHP model with a value of 87.50% was the best model. Regarding the SPF metric that measures the model’s ability to correctly classify the non-landslide pixels in the non-landslide class, the single HP and ensemble Decorate-HP models with a value of 100% were dominant over the other models. In terms of the ACC metric that indicates the overall model accuracy, the RABHP model (92.19%) was identified as the most precise model over the training phase. Further, this model achieved the highest agreement (Kappa = 0.844) between observations and predictions.
To evaluate the practicability of the six proposed models, they need to be tested with the unseen data (i.e., validation dataset), resulting in computing the prediction rate of the models. In the validation phase (Table 3), while the single HP and ensemble Decorate-HP models reached the maximum values of the PPV (92.86%) and SPF (88.24%) indices, the ensemble BHP model gained the maximum values of NPV (85.71%), SST (85.19%), ACC (83.93%), and Kappa (0.679). Many machine learning researchers have previously reported the asymmetric performances of different models when applied to the different training and validation datasets [24,96]. The most logical explanation for these different performances is that different methods were developed based upon different computational algorithms, and therefore show different performances dealing with different datasets. For example, Quinlan [97] suggested that the main reason for AdaBoost’s failure is overfitting. According to Breiman [75], Bagging perform the best if the base model is unstable.
In the matter of the magnitude of the training and validation error, the ensemble ABHP and Decorate-HP models with the lowest and highest RMSEs were identified as the most and least accurate models, respectively. The RMSEs ranged from 0.334 (ABHP) to 0.495 (Decorate-HP) in the training phase and from 0.362 (ABHP) to 0.496 (Decorate-HP) in the validation phase of the modeling process (Figure 5).
The overall performance of the models proposed for the for the Nam Dan commune was evaluated by the ROC method that showed that all six models had excellent training and validation performances. More specifically, a comparative analysis of the AUC values derived from the models indicated that the ensemble RABHP model with an AUC of 0.968 had the best training performance (i.e., fitness to the training data), followed by the BHP, Dagging-HP, ABHP, Decorate-HP, and HP models that achieved the AUC values of 0.95, 0.937, 0.933, 0.895, and 0.895, respectively (Figure 6a). In the matter of the predictive power (i.e., validation performance) (Figure 6b), the ROC-AUC method exhibited that the ABHP model with an AUC of 0.922 was the best model for predicting future landslide susceptibilities, followed by the RABHP, BHP, Dagging-HP, Decorate-HP, and HP that achieved AUC values of 0.919, 0.909, 0.897, 0.865, and 0.856, respectively. Although the models ranked differently in the training and validation phases, and the ROC-AUC method clearly demonstrated that the ensemble models successfully outperformed the single HP model. Integrating the single HP model with the ensemble learning techniques, the generalization and predictive power of the HP model improved by up to 8% and 7%, respectively. In agreement with our results, several previous research reported on the superiority of ensemble modeling over single modeling approaches [79,98].

4.3. Evaluation of Susceptibility Maps

Using the models’ outputs, the distribution maps of landslide susceptibilities were constructed for the Nam Dan commune in favor of proper land-use planning for the development of infrastructure across the area. The distribution maps of landslide susceptibility were prepared to show very low, low, moderate, high, and very high susceptibilities to landslide occurrence within the commune (Figure 7). In the map produced using the ABHP model, approximately 5% and 15% of the land area fall in the very high and high susceptibility zones, respectively. In the map generated by the BHP model, approximately 12% of the Nam Dan commune is located in the high susceptibility zone and 5% in the very high susceptibility zone. In the map generated by the Dagging-HP model, 17% of the land area is affected by high susceptibility and 10% by very high susceptibility. In the map generated by the Decorate-HP model, 65% of the land area is hit by high susceptibility and 15% by very high susceptibility. The RABHP model locates approximately 27% of the land area in the high susceptibility zone and 10% in the very high susceptibility zone. In the map generated by the HP model, approximately 50% of the land area is in the high susceptibility zone and 12% in the very high susceptibility zone (Figure 8a).
The frequency ratio analysis of the susceptibility maps revealed that the map derived from the ABHP model was the most trustworthy map in comparison with the other maps derived from the other five models. The percentage and frequency of landslide pixels in the ABHP maps for the high and very high susceptibility classes were higher than the other models (Figure 8b,c).

5. Conclusions

Development of landslide predictive models with strong prediction power has become a major focus of many researchers. At present, attempts are in progress to develop reliable, accurate landslide models for different environmental settings worldwide. Here, we described the first attempt to model landslide susceptibilities for the Nam Dan commune of Vietnam using five novel ensemble models that integrated the HP algorithm with the AdaBoost, Bagging, Dagging, Decorate, and Real AdaBoost ensemble techniques. Several performance metrics were utilized to measure the fitness (i.e., training performance) and predictive power (i.e., validation performance) of the models over the training and testing phases using information from 76 historical landslides and 10 geo-environmental variables. The results showed that all five ensemble models performed excellently for landslide susceptibility mapping and for improving the fitness and predictive powers of the base HP model. These improvements underscore the effectiveness of ensemble learning techniques to overcome the variance, bias, and noise problems that are permanently associated with the landslide modeling process. Among the developed models, the ABHP model nominated by the highest AUC value (0.922) showed the best performance for predicting landslide susceptibility across the Nam Dan commune. The landslide susceptibility maps produced within this case study, particularly the map produced by the ABHP model, can guide land-use planners and decision-makers to make more informed and efficient decisions in response to future landslides.

Author Contributions

Conceptualization, Q.C.T., H.V.L., N.A.-A. and B.T.P; methodology, B.T.P., Q.C.T., A.J., I.P. and N.A.-A; validation, B.T.P., Q.C.T., N.A.-A., L.S.H. and I.P; formal analysis, Q.C.T., D.D.M. (Duc Dao Minh), D.D.M. (Duc Do Minh), T.T.H., D.T.V. and D.H.N.; data curation, D.D.M. (Duc Dao Minh), D.A.N., D.D.M. (Duc Do Minh), T.H.T. and D.T.V.; writing—original draft preparation, all authors; writing—review and editing, Q.C.T., L.S.H., B.T.P., A.J., N.A.-A. and I.P; visualization, L.S.H., H.V.L. and D.H.N; supervision, Q.C.T., B.T.P., N.A.-A. and I.P; project administration, Q.C.T., B.T.P. and N.A.-A.; funding acquisition, Q.C.T., N.A.-A. and B.T.P. All authors have read and agreed to the published version of the manuscript.

Funding

This study was conducted within the implementation of research project VT-UD.05/18-20 funded by the Vietnam Academy of Science and Technology (VAST). Thanks also to the project coded SRV-10/0026 (2013–2017) from the VNU University of Science for support data and co-operation.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
  2. Geertsema, M.; Highland, L.; Vaugeouis, L. Environmental impact of landslides. In Landslides–Disaster Risk Reduction; Springer: Berlin/Heidelberg, Germany, 2009; pp. 589–607. [Google Scholar]
  3. Intrieri, E.; Carlà, T.; Gigli, G. Forecasting the time of failure of landslides at slope-scale: A literature review. Earth Sci. Rev. 2019, 193, 333–349. [Google Scholar] [CrossRef]
  4. Piciullo, L.; Calvello, M.; Cepeda, J.M. Territorial early warning systems for rainfall-induced landslides. Earth Sci. Rev. 2018, 179, 228–247. [Google Scholar] [CrossRef]
  5. Shafizadeh-Moghadam, H.; Minaei, M.; Shahabi, H.; Hagenauer, J. Big data in geohazard; pattern mining and large scale analysis of landslides in Iran. Earth Sci. Inform. 2019, 12, 1–17. [Google Scholar] [CrossRef]
  6. Mousavi, S.Z.; Kavian, A.; Soleimani, K.; Mousavi, S.R.; Shirzadi, A. GIS-based spatial prediction of landslide susceptibility using logistic regression model. Geomat. Nat. Hazards Risk 2011, 2, 33–50. [Google Scholar] [CrossRef]
  7. Sharma, S.; Mahajan, A. A comparative assessment of information value, frequency ratio and analytical hierarchy process models for landslide susceptibility mapping of a Himalayan watershed, India. Bull. Eng. Geol. Environ. 2019, 78, 2431–2448. [Google Scholar] [CrossRef]
  8. Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hashim, M. Landslide susceptibility mapping at central Zab basin, Iran: A comparison between analytical hierarchy process, frequency ratio and logistic regression models. Catena 2014, 115, 55–70. [Google Scholar] [CrossRef]
  9. Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern Iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
  10. Ilia, I.; Tsangaratos, P. Applying weight of evidence method and sensitivity analysis to produce a landslide susceptibility map. Landslides 2016, 13, 379–397. [Google Scholar] [CrossRef]
  11. Chen, Z.; Liang, S.; Ke, Y.; Yang, Z.; Zhao, H. Landslide susceptibility assessment using evidential belief function, certainty factor and frequency ratio model at Baxie River basin, NW China. Geocarto Int. 2019, 34, 348–367. [Google Scholar] [CrossRef]
  12. Wang, Q.; Li, W.; Wu, Y.; Pei, Y.; Xie, P. Application of statistical index and index of entropy methods to landslide susceptibility assessment in Gongliu (Xinjiang, China). Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
  13. Li, Y.; Liu, X.; Han, Z.; Dou, J. Spatial Proximity-Based Geographically Weighted Regression Model for Landslide Susceptibility Assessment: A Case Study of Qingchuan Area, China. Appl. Sci. 2020, 10, 1107. [Google Scholar] [CrossRef] [Green Version]
  14. Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Bui, D.T. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
  15. Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wildfire probability. Agric. For. Meteorol. 2019, 266, 198–207. [Google Scholar] [CrossRef]
  16. Taheri, K.; Shahabi, H.; Chapi, K.; Shirzadi, A.; Gutiérrez, F.; Khosravi, K. Sinkhole susceptibility mapping: A comparison between Bayes-based machine learning algorithms. Land Degrad. Dev. 2019, 30, 730–745. [Google Scholar] [CrossRef]
  17. Choubin, B.; Soleimani, F.; Pirnia, A.; Sajedi-Hosseini, F.; Alilou, H.; Rahmati, O.; Melesse, A.M.; Singh, V.P.; Shahabi, H. Effects of drought on vegetative cover changes: Investigating spatiotemporal patterns. In Extreme Hydrology and Climate Variability; Elsevier: Amsterdam, The Netherlands, 2019; pp. 213–222. [Google Scholar]
  18. Alizadeh, M.; Alizadeh, E.; Asadollahpour Kotenaee, S.; Shahabi, H.; Beiranvand Pour, A.; Panahi, M.; Bin Ahmad, B.; Saro, L. Social vulnerability assessment using artificial neural network (ANN) model for earthquake hazard in Tabriz city, Iran. Sustainability 2018, 10, 3376. [Google Scholar] [CrossRef] [Green Version]
  19. Azareh, A.; Rahmati, O.; Rafiei-Sardooi, E.; Sankey, J.B.; Lee, S.; Shahabi, H.; Ahmad, B.B. Modelling gully-erosion susceptibility in a semi-arid region, Iran: Investigation of applicability of certainty factor and maximum entropy models. Sci. Total Environ. 2019, 655, 684–696. [Google Scholar] [CrossRef]
  20. Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Pradhan, B.; Chen, W.; Khosravi, K.; Panahi, M.; Bin Ahmad, B.; Saro, L. Land subsidence susceptibility mapping in south korea using machine learning algorithms. Sensors 2018, 18, 2464. [Google Scholar] [CrossRef] [Green Version]
  21. Rahmati, O.; Samadi, M.; Shahabi, H.; Azareh, A.; Rafiei-Sardooi, E.; Alilou, H.; Melesse, A.M.; Pradhan, B.; Chapi, K.; Shirzadi, A. SWPT: An automated GIS-based tool for prioritization of sub-watersheds based on morphometric and topo-hydrological factors. Geosci. Front. 2019, 10, 2167–2175. [Google Scholar] [CrossRef]
  22. Abedini, M.; Ghasemian, B.; Shirzadi, A.; Bui, D.T. A comparative study of support vector machine and logistic model tree classifiers for shallow landslide susceptibility modeling. Environ. Earth Sci. 2019, 78, 560. [Google Scholar] [CrossRef]
  23. Chen, W.; Yan, X.; Zhao, Z.; Hong, H.; Bui, D.T.; Pradhan, B. Spatial prediction of landslide susceptibility using data mining-based kernel logistic regression, naive Bayes and RBFNetwork models for the Long County area (China). Bull. Eng. Geol. Environ. 2019, 78, 247–266. [Google Scholar] [CrossRef]
  24. Jaafari, A.; Panahi, M.; Pham, B.T.; Shahabi, H.; Bui, D.T.; Rezaie, F.; Lee, S. Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 2019, 175, 430–445. [Google Scholar] [CrossRef]
  25. Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
  26. Wang, Y.; Hong, H.; Chen, W.; Li, S.; Panahi, M.; Khosravi, K.; Shirzadi, A.; Shahabi, H.; Panahi, S.; Costache, R. Flood susceptibility mapping in dingnan county (China) using adaptive neuro-fuzzy inference system with biogeography based optimization and imperialistic competitive algorithm. J. Environ. Manag. 2019, 247, 712–729. [Google Scholar] [CrossRef] [PubMed]
  27. Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
  28. Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid integration approach of entropy with logistic regression and support vector machine for landslide susceptibility modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef] [Green Version]
  29. Chen, W.; Xie, X.; Peng, J.; Shahabi, H.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.-X. GIS-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. Catena 2018, 164, 135–149. [Google Scholar] [CrossRef]
  30. Shadman Roodposhti, M.; Aryal, J.; Shahabi, H.; Safarrad, T. Fuzzy shannon entropy: A hybrid GIS-based landslide susceptibility mapping method. Entropy 2016, 18, 343. [Google Scholar] [CrossRef]
  31. Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khosravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Model. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
  32. Abedini, M.; Ghasemian, B.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Pham, B.T.; Bin Ahmad, B.; Tien Bui, D. A novel hybrid approach of bayesian logistic regression and its ensembles for landslide susceptibility assessment. Geocarto Int. 2018, 34, 1427–1457. [Google Scholar] [CrossRef]
  33. Ghasemain, B.; Asl, D.T.; Pham, B.T.; Avand, M.; Nguyen, H.D.; Janizadeh, S. Shallow landslide susceptibility mapping: A comparison between classification and regression tree and reduced error pruning tree algorithms. Vietnam J. Earth Sci. 2020. [Google Scholar] [CrossRef]
  34. Shafizadeh-Moghadam, H.; Valavi, R.; Shahabi, H.; Chapi, K.; Shirzadi, A. Novel forecasting approaches using combination of machine learning and statistical models for flood susceptibility mapping. J. Environ. Manag. 2018, 217, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.-X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 4397–4419. [Google Scholar] [CrossRef]
  36. Pham, B.T.; Prakash, I. Machine learning methods of kernel logistic regression and classification and regression trees for landslide susceptibility assessment at part of Himalayan area, India. Indian J. Sci. Technol. 2018, 11, 1–11. [Google Scholar] [CrossRef] [Green Version]
  37. Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve Bayes tree classifiers for a landslide susceptibility assessment in Langao County, China. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef] [Green Version]
  38. Pham, B.T.; Bui, D.T.; Prakash, I. Landslide susceptibility assessment using bagging ensemble based alternating decision trees, logistic regression and J48 decision trees methods: A comparative study. Geotech. Geol. Eng. 2017, 35, 2597–2611. [Google Scholar] [CrossRef]
  39. Shirzadi, A.; Solaimani, K.; Roshan, M.H.; Kavian, A.; Chapi, K.; Shahabi, H.; Keesstra, S.; Ahmad, B.B.; Bui, D.T. Uncertainties of prediction accuracy in shallow landslide modeling: Sample size and raster resolution. Catena 2019, 178, 172–188. [Google Scholar] [CrossRef]
  40. Jaafari, A. LiDAR-supported prediction of slope failures using an integrated ensemble weights-of-evidence and analytical hierarchy process. Environ. Earth Sci. 2018, 77, 42. [Google Scholar] [CrossRef]
  41. Tien Bui, D.; Shahabi, H.; Omidvar, E.; Shirzadi, A.; Geertsema, M.; Clague, J.J.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Chapi, K. Shallow landslide prediction using a novel hybrid functional machine learning algorithm. Remote Sens. 2019, 11, 931. [Google Scholar] [CrossRef] [Green Version]
  42. Nguyen, V.; Pham, B.; Vu, B.; Prakash, I.; Jha, S.; Shahabi, H.; Shirzadi, A.; Ba, D.; Kumar, R.; Chatterjee, J.; et al. Hybrid Machine Learning Approaches for Landslide Susceptibility Modeling. Forests 2019, 10. [Google Scholar] [CrossRef] [Green Version]
  43. Althuwaynee, O.F.; Pradhan, B.; Park, H.-J.; Lee, J.H. A novel ensemble decision tree-based CHi-squared Automatic Interaction Detection (CHAID) and multivariate logistic regression models in landslide susceptibility mapping. Landslides 2014, 11, 1063–1078. [Google Scholar] [CrossRef]
  44. Tien Bui, D.; Shirzadi, A.; Shahabi, H.; Geertsema, M.; Omidvar, E.; Clague, J.J.; Thai Pham, B.; Dou, J.; Talebpour Asl, D.; Bin Ahmad, B. New Ensemble Models for Shallow Landslide Susceptibility Modeling in a Semi-Arid Watershed. Forests 2019, 10, 743. [Google Scholar] [CrossRef] [Green Version]
  45. Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
  46. Nguyen, H.-D.; Pham, V.-D.; Nguyen, Q.-H.; Pham, V.-M.; Hai, P.; Manh, V.; Bui, Q.-T. An optimal search for neural network parameters by Salp swarm optimization algorithm: A landslide application. Remote Sens. Lett. 2020. [Google Scholar] [CrossRef]
  47. Miraki, S.; Zanganeh, S.H.; Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Pham, B.T. Mapping Groundwater Potential Using a Novel Hybrid Intelligence Approach. Water Resour. Manag. 2019, 33, 281–302. [Google Scholar] [CrossRef]
  48. Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.-X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using J48 Decision Tree with AdaBoost, Bagging and Rotation Forest ensembles in the Guangchang area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
  49. Hong, H.; Liu, J.; Zhu, A.-X.; Shahabi, H.; Pham, B.T.; Chen, W.; Pradhan, B.; Bui, D.T. A novel hybrid integration model using support vector machines and random subspace for weather-triggered landslide susceptibility assessment in the Wuning area (China). Environ. Earth Sci. 2017, 76, 652. [Google Scholar] [CrossRef]
  50. Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Thai Pham, B.; Pradhan, B. Novel GIS based machine learning algorithms for shallow landslide susceptibility mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef]
  51. Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. Acm Sigkdd Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
  52. Kavzoglu, T.; Colkesen, I.; Sahin, E.K. Machine learning techniques in landslide susceptibility mapping: A survey and a case study. In Landslides: Theory, Practice and Modelling; Springer: Berlin/Heidelberg, Germany, 2019; pp. 283–301. [Google Scholar]
  53. Tien Bui, D.; Tuan, T.; Hoang, N.-D.; Thanh, N.; Nguyen, D.; Liem, N.; Pradhan, B. Spatial Prediction of Rainfall-induced Landslides for the Lao Cai area (Vietnam) Using a Novel hybrid Intelligent Approach of Least Squares Support Vector Machines Inference Model and Artificial Bee Colony Optimization. Landslides 2016, 14. [Google Scholar] [CrossRef]
  54. Trigila, A.; Iadanza, C.; Esposito, C.; Scarascia-Mugnozza, G. Comparison of Logistic Regression and Random Forests techniques for shallow landslide susceptibility assessment in Giampilieri (NE Sicily, Italy). Geomorphology 2015, 249, 119–136. [Google Scholar] [CrossRef]
  55. Nicu, I.C.; Asăndulesei, A. GIS-based evaluation of diagnostic areas in landslide susceptibility analysis of Bahluieț River Basin (Moldavian Plateau, NE Romania). Are Neolithic sites in danger? Geomorphology 2018, 314, 27–41. [Google Scholar] [CrossRef]
  56. Bui, D.T.; Moayedi, H.; Kalantar, B.; Osouli, A.; Pradhan, B.; Nguyen, H.; Rashid, A.S.A. A novel swarm intelligence—Harris hawks optimization for spatial assessment of landslide susceptibility. Sensors 2019, 19, 3590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  57. Pham, B.T.; Tien Bui, D.; Indra, P.; Dholakia, M. Landslide susceptibility assessment at a part of Uttarakhand Himalaya, India using GIS–based statistical approach of frequency ratio method. Int. J. Eng. Res. Technol. 2015, 4, 338–344. [Google Scholar]
  58. Wang, G.; Lei, X.; Chen, W.; Shahabi, H.; Shirzadi, A. Hybrid Computational Intelligence Methods for Landslide Susceptibility Mapping. Symmetry 2020, 12, 325. [Google Scholar] [CrossRef] [Green Version]
  59. Van, N.T.H.; Van Son, P.; Khanh, N.H.; Binh, L.T. Landslide susceptibility mapping by combining the analytical hierarchy process and weighted linear combination methods: A case study in the upper Lo River catchment (Vietnam). Landslides 2016, 13, 1285–1301. [Google Scholar]
  60. Jaafari, A.; Najafi, A.; Rezaeian, J.; Sattarian, A. Modeling erosion and sediment delivery from unpaved roads in the north mountainous forest of Iran. GEM Int. J. Geomath. 2015, 6, 343–356. [Google Scholar] [CrossRef]
  61. Wang, Q.; Li, W.; Wu, Y.; Pei, Y.; Xing, M.; Yang, D. A comparative study on the landslide susceptibility mapping using evidential belief function and weights of evidence models. J. Earth Syst. Sci. 2016, 125, 645–662. [Google Scholar] [CrossRef] [Green Version]
  62. Zhang, G.; Cai, Y.; Zheng, Z.; Zhen, J.; Liu, Y.; Huang, K. Integration of the statistical index method and the analytic hierarchy process technique for the assessment of landslide susceptibility in Huizhou, China. Catena 2016, 142, 233–244. [Google Scholar] [CrossRef]
  63. Can, A.; Dagdelenler, G.; Ercanoglu, M.; Sonmez, H. Landslide susceptibility mapping at Ovacık-Karabük (Turkey) using different artificial neural network models: Comparison of training algorithms. Bull. Eng. Geol. Environ. 2019, 78, 89–102. [Google Scholar] [CrossRef]
  64. Jaafari, A.; Rezaeian, J.; Omrani, M.S. Spatial prediction of slope failures in support of forestry operations safety. Croat. J. For. Eng. 2017, 38, 107–118. [Google Scholar]
  65. Catani, F.; Lagomarsino, D.; Segoni, S.; Tofani, V. Landslide susceptibility estimation by random forests technique: Sensitivity and scaling issues. Nat. Hazards Earth Syst. Sci. 2013, 13, 2815–2831. [Google Scholar] [CrossRef] [Green Version]
  66. Holte, R.C. Very simple classification rules perform well on most commonly used datasets. Mach. Learn. 1993, 11, 63–90. [Google Scholar] [CrossRef]
  67. Randomized Decimation Hyperpipes. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.433.8586&rep=rep1&type=pdf (accessed on 27 July 2019).
  68. Smusz, S.; Kurczab, R.; Bojarski, A.J. A multidimensional analysis of machine learning methods performance in the classification of bioactive compounds. Chemom. Intell. Lab. Syst. 2013, 128, 89–100. [Google Scholar] [CrossRef]
  69. Mȩżyk, E.; Unold, O. Mining fuzzy rules using an Artificial Immune System with fuzzy partition learning. Appl. Soft Comput. 2011, 11, 1965–1974. [Google Scholar] [CrossRef]
  70. Kukreja, M.; Johnston, S.; Stafford, P. Comparative study of classification algorithms for immunosignaturing data. BMC Bioinform. 2012, 13, 139. [Google Scholar] [CrossRef] [Green Version]
  71. Freund, Y.; Schapire, R.E. A desicion-theoretic generalization of on-line learning and an application to boosting. In Proceedings of the European Conference on Computational Learning Theory, Barcelona, Spain, 13–15 March 1995; pp. 23–37. [Google Scholar]
  72. Sun, J.; Jia, M.-Y.; Li, H. AdaBoost ensemble for financial distress prediction: An empirical comparison with data from Chinese listed companies. Expert Syst. Appl. 2011, 38, 9305–9312. [Google Scholar] [CrossRef]
  73. Bui, D.T.; Ho, T.C.; Pradhan, B.; Pham, B.T.; Nhu, V.H.; Revhaug, I. GIS-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with AdaBoost, Bagging, and MultiBoost ensemble frameworks. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
  74. Pham, B.T.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
  75. Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
  76. Gong, B.; Ordieres-Meré, J. Prediction of daily maximum ozone threshold exceedances by preprocessing and ensemble artificial intelligence techniques: Case study of Hong Kong. Environ. Model. Softw. 2016, 84, 290–303. [Google Scholar] [CrossRef]
  77. He, Q.; Xu, Z.; Li, S.; Li, R.; Zhang, S.; Wang, N.; Pham, B.T.; Chen, W. Novel Entropy and Rotation Forest-Based Credal Decision Tree Classifier for Landslide Susceptibility Modeling. Entropy 2019, 21, 106. [Google Scholar] [CrossRef] [Green Version]
  78. Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.T.; Zhang, T.; Zhang, L.; Chai, H.; et al. Landslide susceptibility modeling based on GIS and Novel Bagging-based Kernel logistic regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef] [Green Version]
  79. Nhu, V.-H.; Shirzadi, A.; Shahabi, H.; Chen, W.; Clague, J.J.; Geertsema, M.; Jaafari, A.; Avand, M.; Miraki, S.; Asl, D.T. Shallow Landslide Susceptibility Mapping by Random Forest Base Classifier and its Ensembles in a Semi-Arid Region of Iran. Forests 2020, 11, 421. [Google Scholar] [CrossRef] [Green Version]
  80. Ting, K.M.; Witten, I.H. Stacking Bagged and Dagged Models; University of Waikato: Hamilton, New Zealand, 1997. [Google Scholar]
  81. Onan, A.; Korukoğlu, S.; Bulut, H. A multiobjective weighted voting ensemble classifier based on differential evolution algorithm for text sentiment classification. Expert Syst. Appl. 2016, 62, 1–16. [Google Scholar] [CrossRef]
  82. Nguyen, V.-T.; Tran, T.H.; Ha, N.A.; Ngo, V.L.; Nadhir, A.-A.; Tran, V.P.; Duy Nguyen, H.; MA, M.; Amini, A.; Prakash, I.; et al. GIS Based Novel Hybrid Computational Intelligence Models for Mapping Landslide Susceptibility: A Case Study at Da Lat City, Vietnam. Sustainability 2019, 11, 7118. [Google Scholar] [CrossRef] [Green Version]
  83. Zhao, X.; Chen, W. GIS-Based Evaluation of Landslide Susceptibility Models Using Certainty Factors and Functional Trees-Based Ensemble Techniques. Appl. Sci. 2020, 10, 16. [Google Scholar] [CrossRef] [Green Version]
  84. Melville, P.; Mooney, R.J. Creating diversity in ensembles using artificial data. Inf. Fusion 2005, 6, 99–111. [Google Scholar] [CrossRef]
  85. Adhvaryu, P.; Panchal, M. A review on diverse ensemble methods for classification. IOSR J. Comput. Eng. 2012, 1, 27–32. [Google Scholar] [CrossRef]
  86. Schapire, R.E.; Singer, Y. Improved boosting algorithms using confidence-rated predictions. Mach. Learn. 1999, 37, 297–336. [Google Scholar] [CrossRef] [Green Version]
  87. Liu, M.; Qiao, X.-q.; Xu, W.-l. Three categories customer churn prediction based on the adjusted real adaboost. Commun. Stat. Simul. Comput. 2011, 40, 1548–1562. [Google Scholar] [CrossRef]
  88. Xu, W.; Lee, E.-J. A Novel Multi-view Face Detection Method Based on Improved Real Adaboost Algorithm. KSII Trans. Internet Inf. Syst. 2013, 7. [Google Scholar] [CrossRef]
  89. Jaafari, A.; Zenner, E.K.; Pham, B.T. Wildfire spatial pattern analysis in the Zagros Mountains, Iran: A comparative study of decision tree based classifiers. Ecol. Inform. 2018, 43, 200–211. [Google Scholar] [CrossRef]
  90. Pham, B.T.; Phong, T.V.; Nguyen-Thoi, T.; Parial, K.; Singh, S.; Ly, H.-B.; Nguyen, K.T.; Ho, L.S.; Le, H.V.; Prakash, I. Ensemble modeling of landslide susceptibility using random subspace learner and different decision tree classifiers. Geocarto Int. 2020. [Google Scholar] [CrossRef]
  91. Nguyen, P.T.; Ha, D.H.; Avand, M.; Jaafari, A.; Nguyen, H.D.; Al-Ansari, N.; Phong, T.V.; Sharma, R.; Kumar, R.; Le, H.V.; et al. Soft Computing Ensemble Models Based on Logistic Regression for Groundwater Potential Mapping. Appl. Sci. 2020, 10, 2469. [Google Scholar] [CrossRef] [Green Version]
  92. Naghibi, S.; Dolatkordestani, M.; Rezaei, A.; Amouzegari, P.; Heravi, M.; Kalantar, B.; Pradhan, B. Application of rotation forest with decision trees as base classifier and a novel ensemble model in spatial modeling of groundwater potential. Environ. Monit. Assess. 2019, 191. [Google Scholar] [CrossRef]
  93. Pham, B.T.; Tien Bui, D.; Prakash, I. Landslide susceptibility modelling using different advanced decision trees methods. Civ. Eng. Environ. Syst. 2018, 35, 139–157. [Google Scholar] [CrossRef]
  94. Nguyen, P.T.; Ha, D.H.; Jaafari, A.; Nguyen, H.D.; Van Phong, T.; Al-Ansari, N.; Prakash, I.; Le, H.V.; Pham, B.T. Groundwater Potential Mapping Combining Artificial Neural Network and Real AdaBoost Ensemble Technique: The DakNong Province Case-study, Vietnam. Int. J. Environ. Res. Public Health 2020, 17, 2473. [Google Scholar] [CrossRef] [Green Version]
  95. Jaafari, A.; Najafi, A.; Rezaeian, J.; Sattarian, A.; Ghajar, I. Planning road networks in landslide-prone areas: A case study from the northern forests of Iran. Land Use Policy 2015, 47, 198–208. [Google Scholar] [CrossRef]
  96. Bayat, M.; Ghorbanpour, M.; Zare, R.; Jaafari, A.; Thai Pham, B. Application of artificial neural networks for predicting tree survival and mortality in the Hyrcanian forest of Iran. Comput. Electron. Agric. 2019, 164. [Google Scholar] [CrossRef]
  97. Quinlan, J.R. Bagging, boosting, and C4. 5. In Proceedings of the AAAI/IAAI, Portland, OR, USA, 4–8 August 1996; Volume 1, pp. 725–730. [Google Scholar]
  98. Nhu, V.-H.; Janizadeh, S.; Avand, M.; Chen, W.; Farzin, M.; Omidvar, E.; Shirzadi, A.; Shahabi, H.; Clague, J.J.; Jaafari, A. GIS-Based Gully Erosion Susceptibility Mapping: A Comparison of Computational Ensemble Data Mining Models. Appl. Sci. 2020, 10, 2039. [Google Scholar] [CrossRef] [Green Version]
Applsci 10 03710 g001 550
Figure 1. Study area (Nam Dan commune, Ha Giang province, Vietnam).
Figure 1. Study area (Nam Dan commune, Ha Giang province, Vietnam).
Applsci 10 03710 g001
Applsci 10 03710 g002 550
Figure 2. Flowchart of the modeling methodology proposed for the Nam Dan commune.
Figure 2. Flowchart of the modeling methodology proposed for the Nam Dan commune.
Applsci 10 03710 g002
Applsci 10 03710 g003 550
Figure 3. Thematic map of the landslide conditioning factors selected for the Nam Dan commune.
Figure 3. Thematic map of the landslide conditioning factors selected for the Nam Dan commune.
Applsci 10 03710 g003
Applsci 10 03710 g004 550
Figure 4. Geomorphology units Nam Dan commune.
Figure 4. Geomorphology units Nam Dan commune.
Applsci 10 03710 g004
Applsci 10 03710 g005 550
Figure 5. Training and validation errors of the modeling process.
Figure 5. Training and validation errors of the modeling process.
Applsci 10 03710 g005
Applsci 10 03710 g006 550
Figure 6. The AUC values derived from the models over (a) the training phase and (b) the validation phase.
Figure 6. The AUC values derived from the models over (a) the training phase and (b) the validation phase.
Applsci 10 03710 g006
Applsci 10 03710 g007a 550Applsci 10 03710 g007b 550
Figure 7. Landslide susceptibility maps (LSM) generated for the Nam Dan commune.
Figure 7. Landslide susceptibility maps (LSM) generated for the Nam Dan commune.
Applsci 10 03710 g007aApplsci 10 03710 g007b
Applsci 10 03710 g008 550
Figure 8. Frequency analysis of the landslide susceptibility maps: (a) percentage of class pixels, (b) percentage of landslide pixels, and (c) frequency ratio.
Figure 8. Frequency analysis of the landslide susceptibility maps: (a) percentage of class pixels, (b) percentage of landslide pixels, and (c) frequency ratio.
Applsci 10 03710 g008
Table
Table 1. Factor significance measured using the One-R technique.
Table 1. Factor significance measured using the One-R technique.
FactorAverage MeritError (AM)Average RankError (AR)
Distance from roads82.31.5041.20.4
Elevation80.5521.2831.80.4
River density72.9153.0723.30.64
Weathering crust68.750.9314.40.49
Fault density67.1863.5074.40.92
Geology57.2854.2786.71.27
TWI54.9462.6477.21.17
Slope52.083.5328.51.02
Aspect52.5953.4148.61.02
Curvature50.7823.7998.91.3
Table
Table 2. Model performance over the training phase.
Table 2. Model performance over the training phase.
MetricModel
HPABHPBHPDagging-HPDecorate-HPRABHP
PPV (%)100.0098.4492.1989.06100.0098.44
NPV (%)75.8170.3178.1381.5475.8185.94
SST (%)70.3376.8380.8282.6170.3387.50
SPF (%)100.0097.8390.9188.33100.0098.21
ACC (%)78.9184.3885.1685.2778.9192.19
Kappa 0.7580.6870.7030.7030.7580.844
Table
Table 3. Model performance over the validation phase.
Table 3. Model performance over the validation phase.
MetricModel
HPABHPBHPDagging-HPDecorate-HPRABHP
PPV (%)92.8689.2982.1482.1492.8685.71
NPV (%)75.5375.0085.7182.1475.5378.57
SST (%)66.6778.1385.1982.1466.6780.00
SPF (%)88.2487.5082.7682.1488.2484.62
ACC (%)73.2182.1483.9382.1473.2182.14
Kappa 0.4640.6430.6790.6430.4640.643

Share and Cite

MDPI and ACS Style

Tran, Q.C.; Minh, D.D.; Jaafari, A.; Al-Ansari, N.; Minh, D.D.; Van, D.T.; Nguyen, D.A.; Tran, T.H.; Ho, L.S.; Nguyen, D.H.; et al. Novel Ensemble Landslide Predictive Models Based on the Hyperpipes Algorithm: A Case Study in the Nam Dam Commune, Vietnam. Appl. Sci. 2020, 10, 3710. https://doi.org/10.3390/app10113710

AMA Style

Tran QC, Minh DD, Jaafari A, Al-Ansari N, Minh DD, Van DT, Nguyen DA, Tran TH, Ho LS, Nguyen DH, et al. Novel Ensemble Landslide Predictive Models Based on the Hyperpipes Algorithm: A Case Study in the Nam Dam Commune, Vietnam. Applied Sciences. 2020; 10(11):3710. https://doi.org/10.3390/app10113710

Chicago/Turabian Style

Tran, Quoc Cuong, Duc Do Minh, Abolfazl Jaafari, Nadhir Al-Ansari, Duc Dao Minh, Duc Tung Van, Duc Anh Nguyen, Trung Hieu Tran, Lanh Si Ho, Duy Huu Nguyen, and et al. 2020. "Novel Ensemble Landslide Predictive Models Based on the Hyperpipes Algorithm: A Case Study in the Nam Dam Commune, Vietnam" Applied Sciences 10, no. 11: 3710. https://doi.org/10.3390/app10113710

APA Style

Tran, Q. C., Minh, D. D., Jaafari, A., Al-Ansari, N., Minh, D. D., Van, D. T., Nguyen, D. A., Tran, T. H., Ho, L. S., Nguyen, D. H., Prakash, I., Le, H. V., & Pham, B. T. (2020). Novel Ensemble Landslide Predictive Models Based on the Hyperpipes Algorithm: A Case Study in the Nam Dam Commune, Vietnam. Applied Sciences, 10(11), 3710. https://doi.org/10.3390/app10113710

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop