A Simplified Calculation Method of Seepage Flux for Slope-Wall Rock-Fill Dams with a Horizontal Blanket
Abstract
:1. Introduction
2. Methods
2.1. Assumption
- (1)
- The groundwater level remains stable and the seepage process is in a steady state all the time.
- (2)
- The seepage behavior follows Darcy’s law.
- (3)
- Cracks in the horizontal blanket and slope wall are ignored.
- (4)
- Hysteresis in the soil–water characteristics is not considered.
- (5)
- The rock, soil, and water are not compressible, and the pore size and porosity of the soil remain unchanged during infiltration.
- (6)
- When there is water downstream, it is assumed that the seepage point, which is the intersection of the phreatic line and dam slope downstream, is flush with the downstream water level.
- (7)
- The horizontal blanket and slope wall are thin enough to assume that their hydraulic gradients along the seepage path remain constant.
2.2. Mathematical Formulation
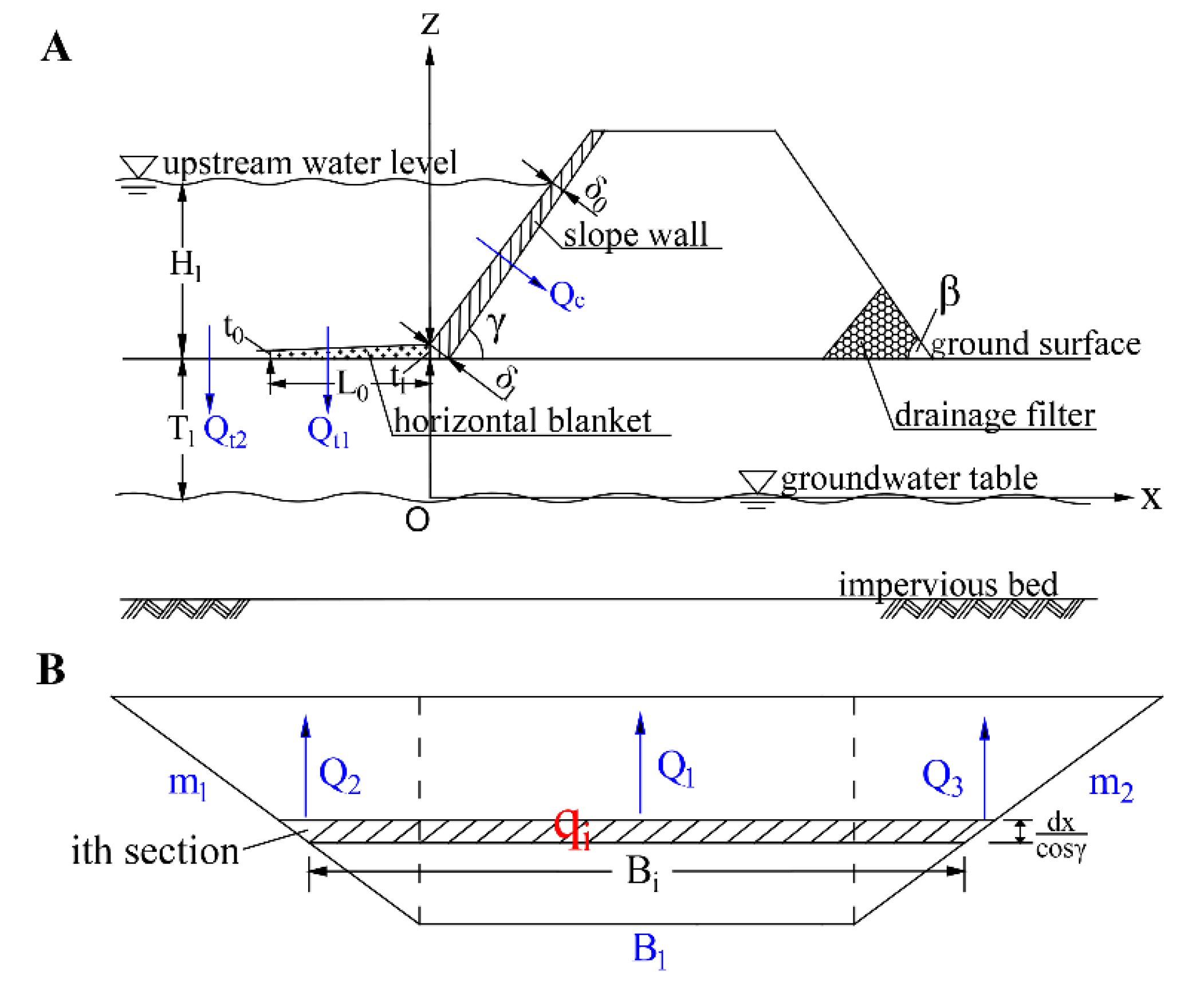
2.2.1. Dams with a Low Groundwater Level
Seepage through the Slope Wall
Seepage through the Horizontal Blanket
- At the steady ground water table, , the boundary condition can be written as
- The surface boundary is controlled by pore water pressure (which is the upstream water level constantly):
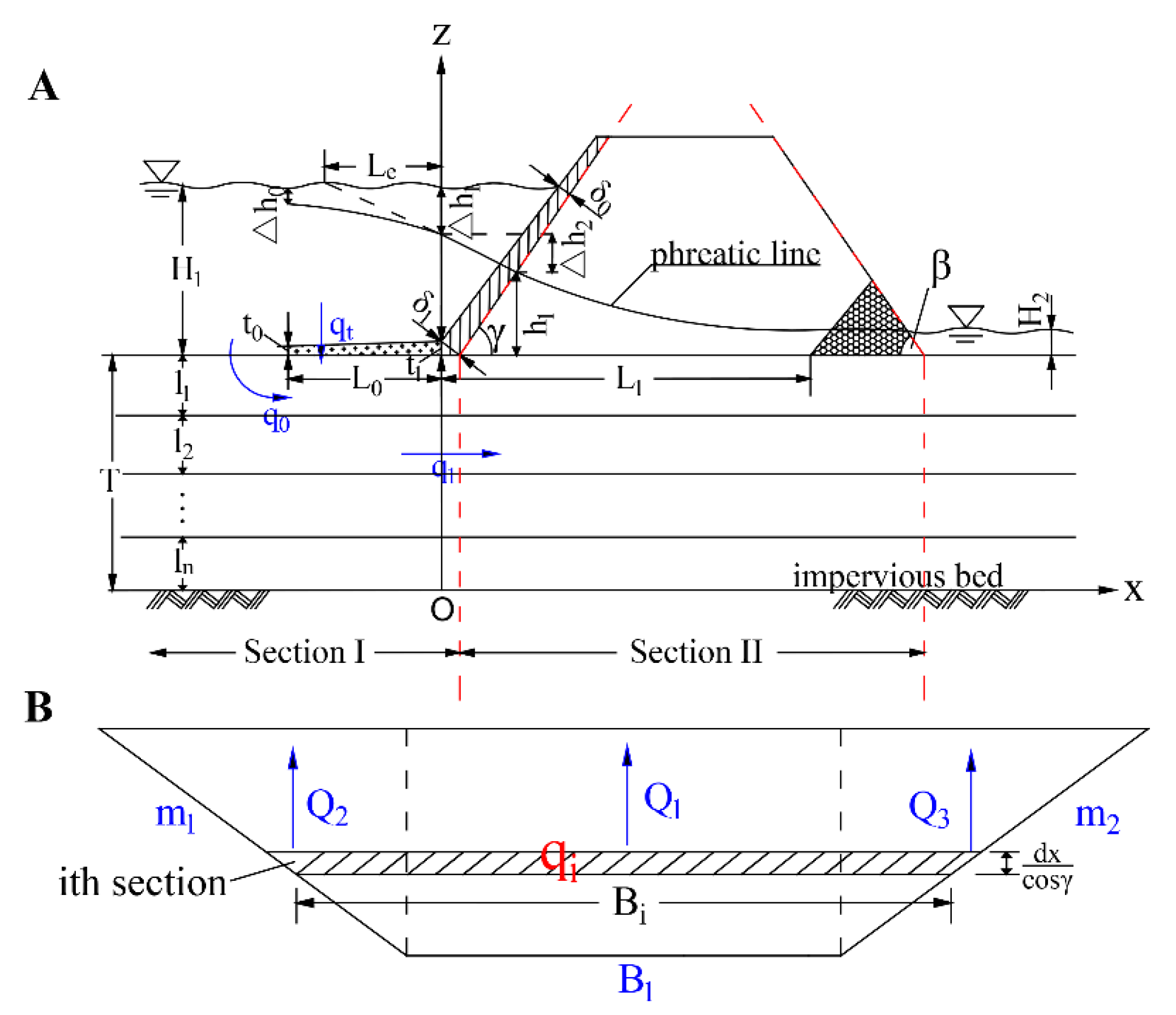
2.2.2. Dams with a High Groundwater Level
Seepage Flux Per Unit Width through Section I
- (1)
- Seepage flux per unit width of the foundation passing through the vertical section at the end of the blanket
- (2)
- The seepage flux per unit width through the slope wall
- (3)
- The seepage flux per unit width through Section II is calculated as:
3. Case Studies
3.1. Dams with a Low Groundwater Level
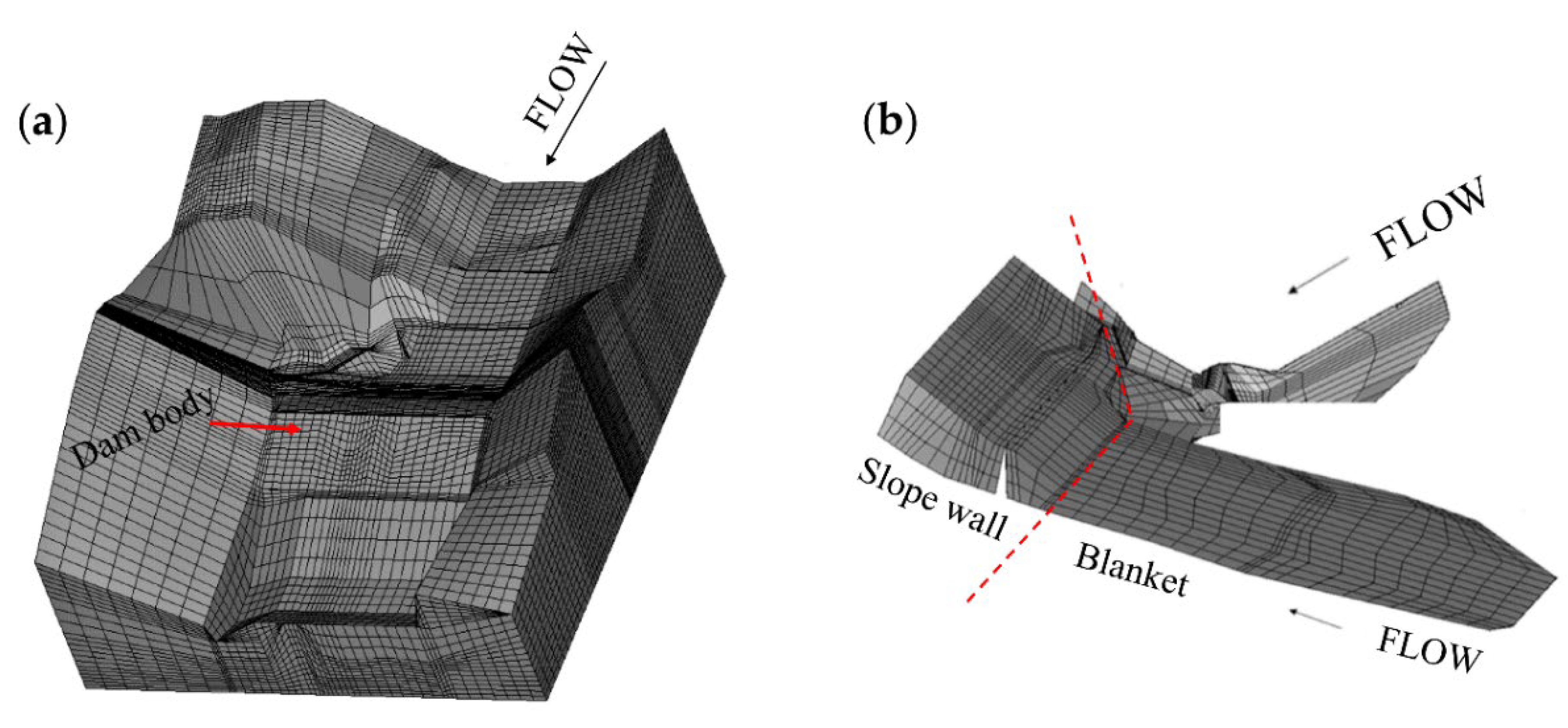
3.1.1. Numerical Simulation
3.1.2. Proposed Calculation Method
3.1.3. Comparison between the Calculation Results
3.2. Dams with High Groundwater Level
3.2.1. Numerical Simulation
3.2.2. Proposed Calculation Method
3.2.3. Comparison between the Calculation Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, M.-C.; Guo, X.-Y.; Shi, J.; Zhu, Z.-B. Seepage and stress analysis of anti-seepage structures constructed with different concrete materials in an RCC gravity dam. Water Sci. Eng. 2015, 8, 326–334. [Google Scholar] [CrossRef] [Green Version]
- Pedroso, D.M. A solution to transient seepage in unsaturated porous media. Comput. Methods Appl. Mech. Eng. 2015, 285, 791–816. [Google Scholar] [CrossRef] [Green Version]
- Fu, J.F.; Sheng, J.I.N. A study on unsteady seepage flow through dam. J. Hydrodyn. 2009, 4, 499–504. [Google Scholar] [CrossRef]
- Athani, S.S.; Solanki, C.; Dodagoudar, G. Seepage and stability analyses of earth dam using finite element method. Aquat. Procedia 2015, 4, 876–883. [Google Scholar] [CrossRef]
- Fukuchi, T. Numerical analyses of steady-state seepage problems using the interpolation finite difference method. Soils Found. 2016, 56, 608–626. [Google Scholar] [CrossRef]
- Lee, S.S.; Yamashita, T. Finite-Difference Method Three-Dimensional Model for Seepage Analysis Through Fordyce DAM. In Advances in Geosciences: Volume 6: Hydrological Science (HS); World Scientific: Singapore, 2007; pp. 171–180. [Google Scholar] [CrossRef]
- Rohaninejad, M.; Zarghami, M. Combining Monte Carlo and finite difference methods for effective simulation of dam behavior. Adv. Eng. Softw. 2012, 45, 197–202. [Google Scholar] [CrossRef]
- Hansen, D.; Roshanfekr, A. Assessment of potential for seepage-induced unraveling failure of flow-through rockfill dams. Int. J. Geomech. 2012, 12, 560–573. [Google Scholar] [CrossRef]
- Chang, C.S. Boundary element method in drawdown seepage analysis for earth dams. J. Comput. Civ. Eng. 1987, 1, 83–98. [Google Scholar] [CrossRef]
- Sánchez-Sesma, F.J.; Arellano-Guzmán, M.; Pérez-Gavilán, J.J.; Suarez, M.; Marengo-Mogollón, H.; Chaillat, S.; Jaramillo, J.D.; Gómez, J.; Iturrarán-Viveros, U.; Rodríguez-Castellanos, A. Seismic response of three-dimensional rockfill dams using the Indirect Boundary Element Method. In Proceedings of IOP Conference Series: Materials Science and Engineering; IOPscience: London, UK, 2010; p. 012167. [Google Scholar]
- Abou-Seeda, H.M. Nonlinear Seismic Response of Dams Using a Coupled Boundary Element-Finite Element Formulation; Rice University: Houston, TX, USA, 1996. [Google Scholar]
- Kai, C.; De-gao, Z.; Xian-jing, K.; Jing-mao, L. Novel nonlinear polygon scaled boundary finite element method and its application. J. Zhejiang Univ. (Eng. Sci.) 2017, 51, 1996–2004. [Google Scholar] [CrossRef]
- Hu, J.; Li, C. Numerical simulation of seepage stability of slab dam with sudden drop of reservoir water level based on face plate defect. Chin. J. Geol. Hazard Control 2019, 30, 129–136. [Google Scholar]
- Molla, D.A.E. Seepage through homogeneous earth dams provided with a vertical sheet pile and formed on impervious foundation. Ain Shams Eng. J. 2019, 10. [Google Scholar] [CrossRef]
- Calamak, M.; Yilmaz, A.N.; Yanmaz, A.M. Performance Evaluation of Internal Drains of Earthen Dams. J. Perform. Constr. Facil. 2018, 32, 10. [Google Scholar] [CrossRef]
- Chen, S.; He, Q.; Cao, J. Seepage simulation of high concrete-faced rockfill dams based on generalized equivalent continuum model. Water Sci. Eng. 2018, 11, 250–257. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D. Statistics of block conductivity through a simple bounded stochastic medium. Water Resour. Res. 1993, 29, 1825–1830. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, D.; Fenton, G.A. Seepage beneath water retaining structures founded on spatially random soil. Geotechnique 1993, 43, 577–587. [Google Scholar] [CrossRef] [Green Version]
- Fenton, G.A.; Griffiths, D. Statistics of free surface flow through stochastic earth dam. J. Geotech. Eng. 1996, 122, 427–436. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D. Extreme hydraulic gradient statistics in stochastic earth dam. J. Geotech. Geoenviron. Eng. 1997, 123, 995–1000. [Google Scholar] [CrossRef] [Green Version]
- Gui, S.; Zhang, R.; Turner, J.P.; Xue, X. Probabilistic slope stability analysis with stochastic soil hydraulic conductivity. J. Geotech. Geoenviron. Eng. 2000, 126, 1–9. [Google Scholar] [CrossRef]
- Srivastava, A.; Babu, G.S.; Haldar, S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis. Eng. Geol. 2010, 110, 93–101. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic analysis of seepage that considers the spatial variability of permeability for an embankment on soil foundation. Eng. Geol. 2012, 133, 30–39. [Google Scholar] [CrossRef]
- Chahar, B.R. Determination of length of a horizontal drain in homogeneous earth dams. J. Irrig. Drain. Eng. 2004, 130, 530–536. [Google Scholar] [CrossRef]
- Abdul Hussain, I.A.; Kashyap, D.; Hari Prasad, K. Seepage modeling assisted optimal design of a homogeneous earth dam: Procedure evolution. J. Irrig. Drain. Eng. 2007, 133, 116–130. [Google Scholar] [CrossRef]
- Fakhari, A.; Ghanbari, A. Note: A simple method for calculating the seepage from earth dams with clay core. J. Geoengin. 2013, 8, 27–32. [Google Scholar] [CrossRef]
- Bennett, P.T. The effect of blankets on seepage through pervious foundation. Trans. ASCE 1945, 111, 215–228. [Google Scholar]
- Uginchus, A. Seepage through Earth Dams.(Raschet Filtratsii Cherez Zemlyanye Plotiny); Israel Program for Scientific Translations: Jerusalem, Israel, 1966. [Google Scholar]
- Chugayev, P.P. Subsurface Loops in Hydraulic Engineering Structures: Design of the Subsurface Portion of the Dam on a Non-Rock Foundation (in Russian); Energy: Saint Petersburg, Russia, 1974. [Google Scholar]
- Changxi, M. Computation of seepage through earth dams with upstream blanket and sloping core (in Chinese). J. Hydraul. Eng. 1963, 1, 26–43. [Google Scholar] [CrossRef]
- U.S.B.R. Embankment Dams. In Chapter 5 Seepage Analysis; U.S. Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1987. [Google Scholar]
- Casinader, R.; Rome, G. Estimation of leakage through upstream concrete facings of rockfill dams. In Proceedings of the 16th International Congress on Large Dams, San Francisco, CA, USA, 13–17 June 1988. [Google Scholar]
- Wang, S. Theories and Methods of Hydraulic Design; China Water & Power Press: Beijing, China, 2000. [Google Scholar]
- Rezk, M.A.E.-R.M.; Senoon, A.E.-A.A.A. Analytical solution of seepage through earth dam with an internal core. Alex. Eng. J. 2011, 50, 111–115. [Google Scholar] [CrossRef] [Green Version]
- Kacimov, A.; Al-Maktoumi, A.; Obnosov, Y.V. Seepage through earth dam with clay core and toe drain: The Casagrande–Numerov analytical legacy revisited. ISH J. Hydraul. Eng. 2019. [Google Scholar] [CrossRef]
- Haitao, M. Study on Seepage Control Calculation Method and Anti-Seepage Measures of Earth-Rock Dam on the Infinite Deep Pervious Foundation (in Chinese); Xinjiang Agricultural University: Urumchi, China, 2010. [Google Scholar]
- Baozhong, Z. Seepage calculation of earth dam with impervious blanket and inclined wall on infinite deep permeable foundation (in Chinese). J. Hydraul. Eng. 1981, 5, 61–68. [Google Scholar] [CrossRef]
- Yoshitake, Y.; Kobayashi, N.; Fujihara, M.; Nishiyama, T. An analytical solution of seepage discharge from a reservoir of embankment dam with triangular soil blanket and its applicability. Trans. Jpn. Soc. Irrig. Drain. Rural Eng. 2011, 79, 109–115. [Google Scholar] [CrossRef]
- Deng, G.; Cao, K.; Chen, R.; Zhang, X.; Yin, Q.; Zhou, H. A simple approach to evaluating leakage through thin impervious element of high embankment dams. Environ. Earth Sci. 2018, 77, 25. [Google Scholar] [CrossRef]
- Gardner, W. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Polubarinova-Koch, P.I. Theory of Ground Water Movement; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Cui, B.; Kong, D.; Jia, W.; Yu, S. General layout and building design of Fukang Pumped Storage Power Station (in Chinese). In Proceedings of the China Society for Hydropower Engineering, Beijing, China, 19–21 May 2015; 2015; pp. 130–135. [Google Scholar]
- Ouyang, M.; Mu, Z. Analysis on Flood Impact Assessment of Fukang Pumped Storage Power Station Project. China Water Power Electrif. 2018, 33–37. [Google Scholar] [CrossRef]
- Fu, C.; Li, J.; Wang, Y. Research on seepage monitoring indicators for the reservoir basin of pumped storage power station. Dam Safe. 2011, 12–14, 18. [Google Scholar]
- Su, J. Study on the risk mitigation and reinforcement scheme for the flood cavern of the Shangmao water source project (in Chinese). Gansu Water Resource. Hydropower Technol. 2011, 47, 8–9, 20. [Google Scholar]
- Wang, Y. Shangma water source project of Tianshui city (in Chinese). Water Wastewater Eng. 2011, 49, 117. [Google Scholar] [CrossRef]
- Аравин, В.И.; Нумерoв, С.Н. Seepage Calculation of Hydraulic Structure (in Russian); USSR National Architectural Engineering and Architectural Art: Saint Petersburg, Russia, 1955. [Google Scholar]



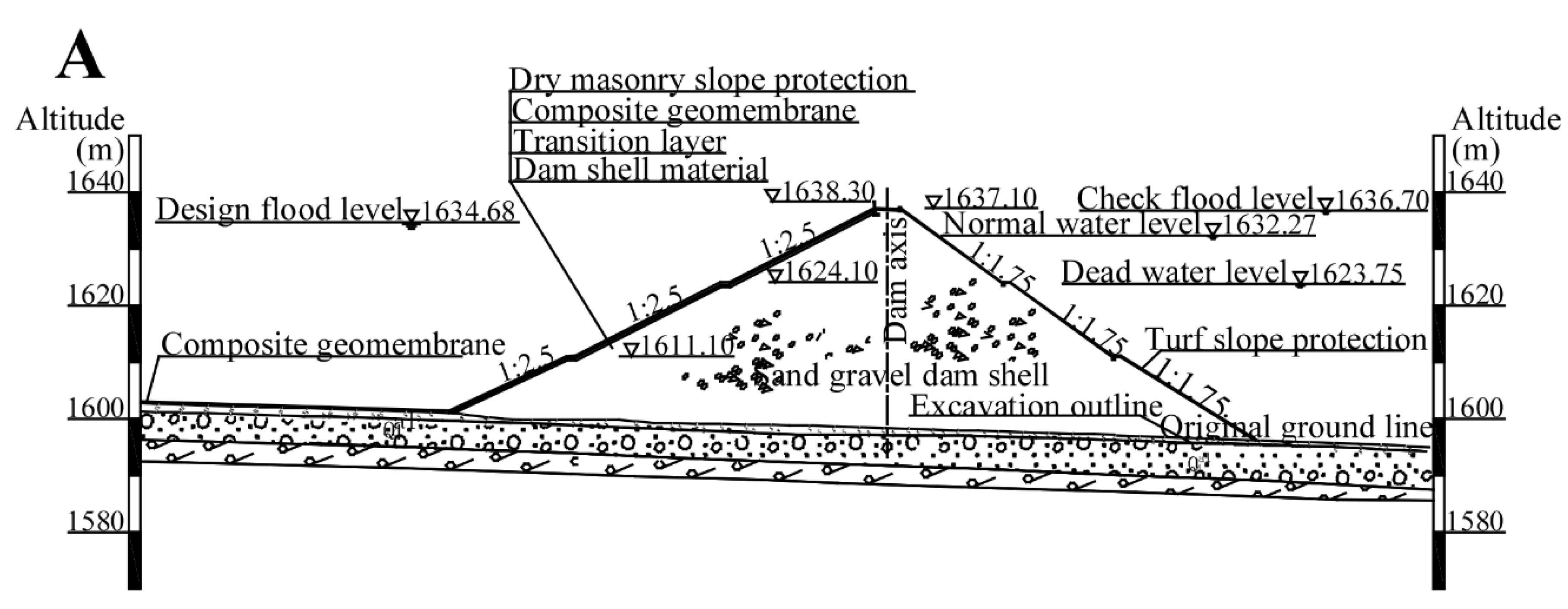

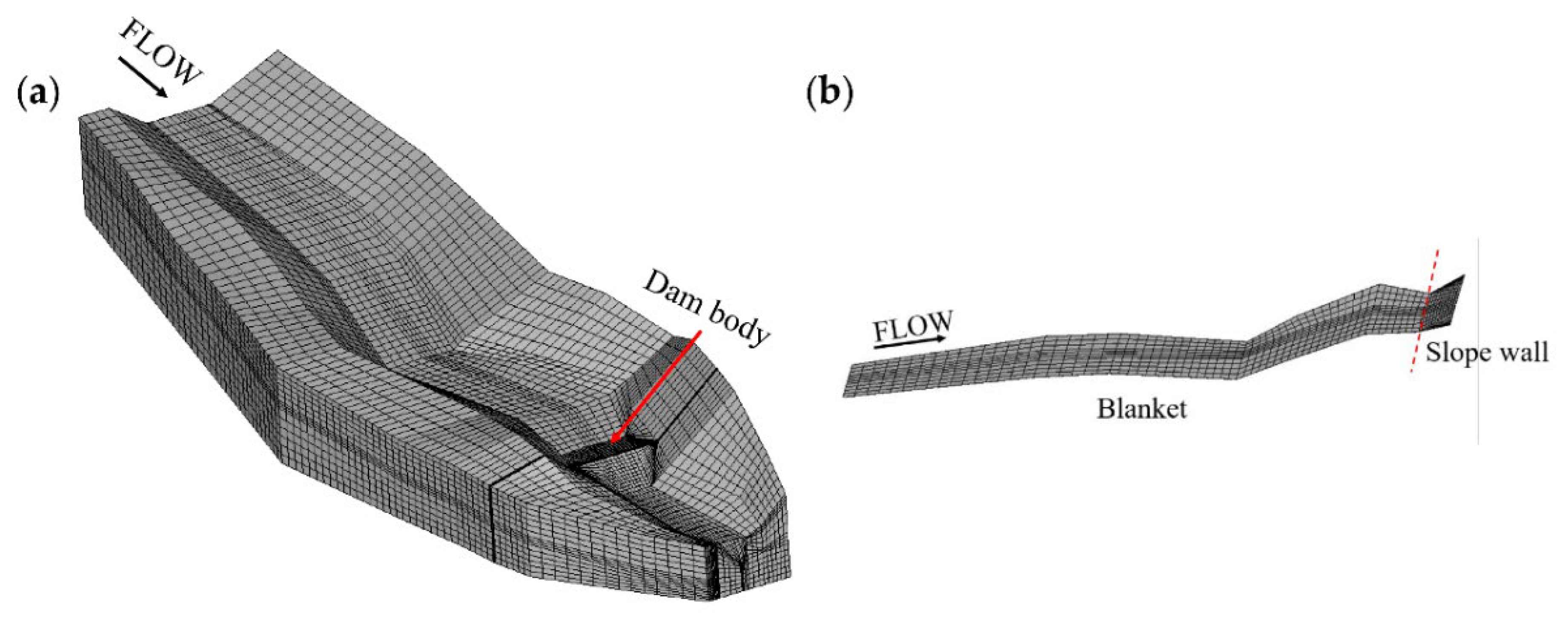
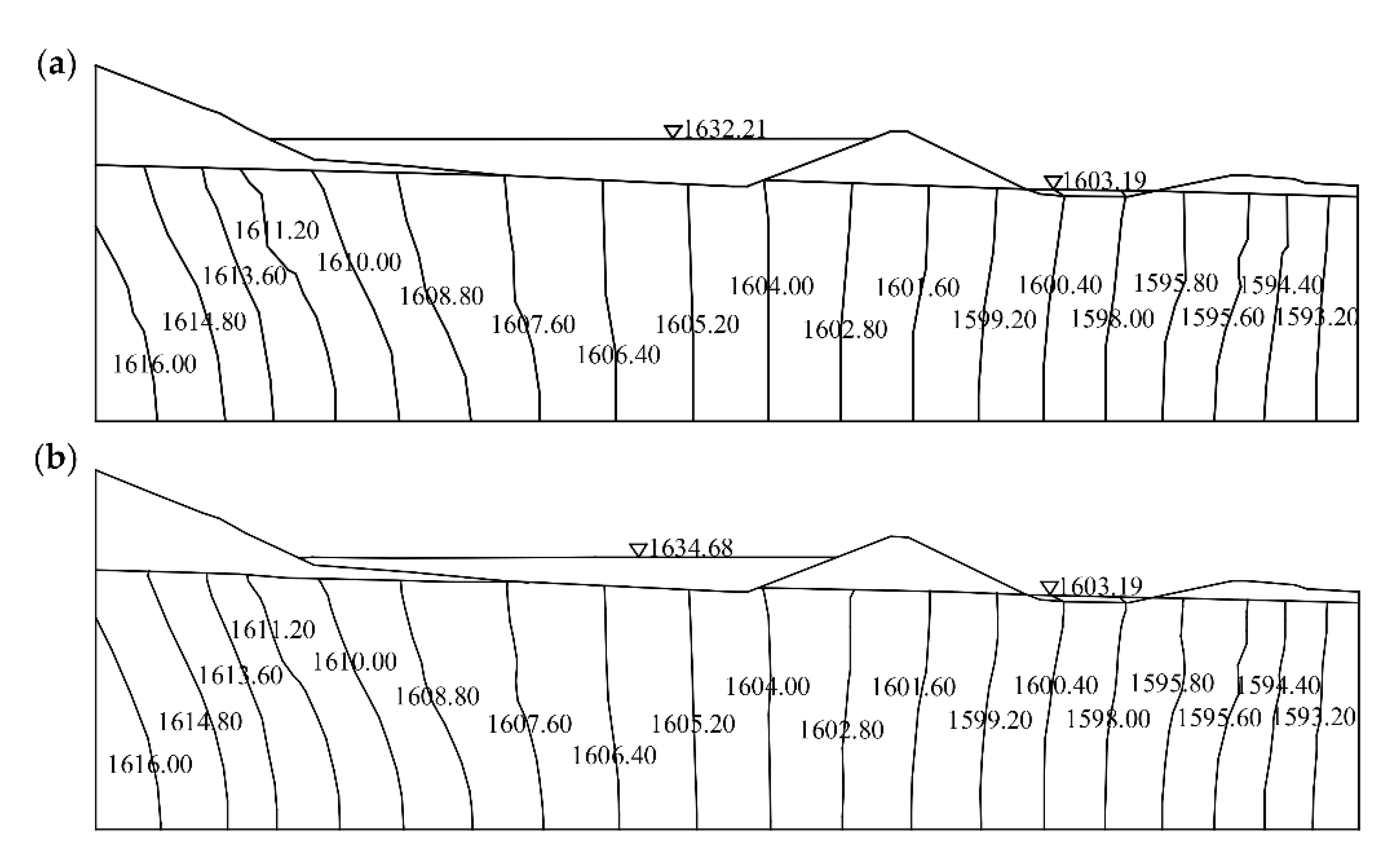

| Position | Material Partition | Permeability Coefficient (cm/s) |
|---|---|---|
| Foundation | sand gravel (upper) | 4.00 × 10−3 |
| sand gravel (lower) | 1.50 × 10−2 | |
| strong weathered rock | 1.00 × 10−4 | |
| week weathered rock | 1.00 × 10−5 | |
| overburden | 1.35 × 10−2 | |
| Dam | Composite geomembrane | 1.00 × 10−8 |
| Main rock-fill (dam body) | 1.00 × 10−1 | |
| cushion material | 5.00 × 10−2 | |
| berm | 1.35 × 10−2 |
| Positions | Methods | Design Flood Level | Check Flood Level | RMSE | ||
|---|---|---|---|---|---|---|
| Leakage (m3·d−1) | RE (%) | Leakage (m3·d−1) | RE (%) | |||
| Blanket | Proposed method | 2716.46 | 4.20 | 3896.64 | 4.36 | 138.73 |
| USBR method | 3173.71 | 21.7 | 4021.82 | 7.71 | 449.51 | |
| Numerical method | 2606.97 | / | 3733.84 | / | / | |
| Slope wall | Proposed method | 364.17 | 4.79 | 777.59 | 4.91 | 28.30 |
| Casinader method | 208.47 | 40.0 | 755.50 | 1.93 | 98.84 | |
| Chunjiang Fu method | 304.49 | 12.38 | 1275.07 | 72.02 | 378.73 | |
| Deng Gang method | 359.93 | 3.57 | 761.83 | 2.78 | 17.02 | |
| Numerical method | 347.52 | / | 741.20 | / | / | |
| Total | Proposed method | 3080.63 | 7.92 | 4674.23 | 6.84 | 265.19 |
| Numerical method | 2854.49 | / | 4375.04 | / | / | |
| Position | Material Partition | Permeability Coefficient (cm/s) |
|---|---|---|
| Foundation | Strong permeable layer 100Lu ≤ q | 2.0 × 10−3 |
| Medium permeable layer 10Lu ≤ q < 100Lu | 3.0 × 10−4 | |
| Weak permeable layer 5Lu ≤ q < 10Lu | 5.0 × 10−5 | |
| Relative impermeable layer q < 5Lu | 2.0 × 10−5 | |
| Dam | Composite geomembrane | 1.0 × 10−9 |
| Dam body | 2.0 × 10−1 | |
| Concrete slab | 1.0 × 10−7 |
| Positions | Methods | Normal Water Level | Design Flood Level | RMSE | ||
|---|---|---|---|---|---|---|
| Leakage (m3·d−1) | RE (%) | Leakage (m3·d−1) | RE (%) | |||
| Blanket | Proposed method | 1013.84 | 1.62 | 1097.28 | 3.61 | 29.41 |
| Аравин В.И., Нумерoв С.Н.’s method | 1029.46 | 3.19 | 1117.08 | 5.49 | 46.84 | |
| Wang’s method | 1027.40 | 2.98 | 1114.95 | 5.29 | 44.83 | |
| Numerical method | 997.68 | / | 1058.95 | / | / | |
| Slope wall | Proposed method | 265.93 | −1.59 | 313.19 | −2.14 | 5.72 |
| Gang’s method | 277.11 | 2.55 | 332.38 | 3.86 | 9.99 | |
| Аравин В.И., Нумерoв С.Н.’s method | 1344.15 | 397.41 | 1461.51 | 351.17 | 1108.21 | |
| Shixia Wang’s method | 298.70 | 10.54 | 324.78 | 1.48 | 20.41 | |
| Numerical method | 270.23 | / | 320.04 | / | / | |
| Total | Proposed method | 1209.6 | −4.60 | 1356.48 | 1.63 | 44.20 |
| Аравин В.И., Нумерoв С.Н.’s method | 2373.61 | 87.21 | 2578.59 | 86.99 | 1153.61 | |
| Wang’s method | 1326.11 | 4.59 | 1439.73 | 4.40 | 59.48 | |
| Numerical method | 1267.91 | / | 1378.99 | / | / | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Shen, Z.; Yang, C. A Simplified Calculation Method of Seepage Flux for Slope-Wall Rock-Fill Dams with a Horizontal Blanket. Appl. Sci. 2020, 10, 3848. https://doi.org/10.3390/app10113848
Li G, Shen Z, Yang C. A Simplified Calculation Method of Seepage Flux for Slope-Wall Rock-Fill Dams with a Horizontal Blanket. Applied Sciences. 2020; 10(11):3848. https://doi.org/10.3390/app10113848
Chicago/Turabian StyleLi, Gehang, Zhenzhong Shen, and Chao Yang. 2020. "A Simplified Calculation Method of Seepage Flux for Slope-Wall Rock-Fill Dams with a Horizontal Blanket" Applied Sciences 10, no. 11: 3848. https://doi.org/10.3390/app10113848
APA StyleLi, G., Shen, Z., & Yang, C. (2020). A Simplified Calculation Method of Seepage Flux for Slope-Wall Rock-Fill Dams with a Horizontal Blanket. Applied Sciences, 10(11), 3848. https://doi.org/10.3390/app10113848






