Novel Fault Injection Attack without Artificial Trigger
Abstract
:1. Introduction
2. Background
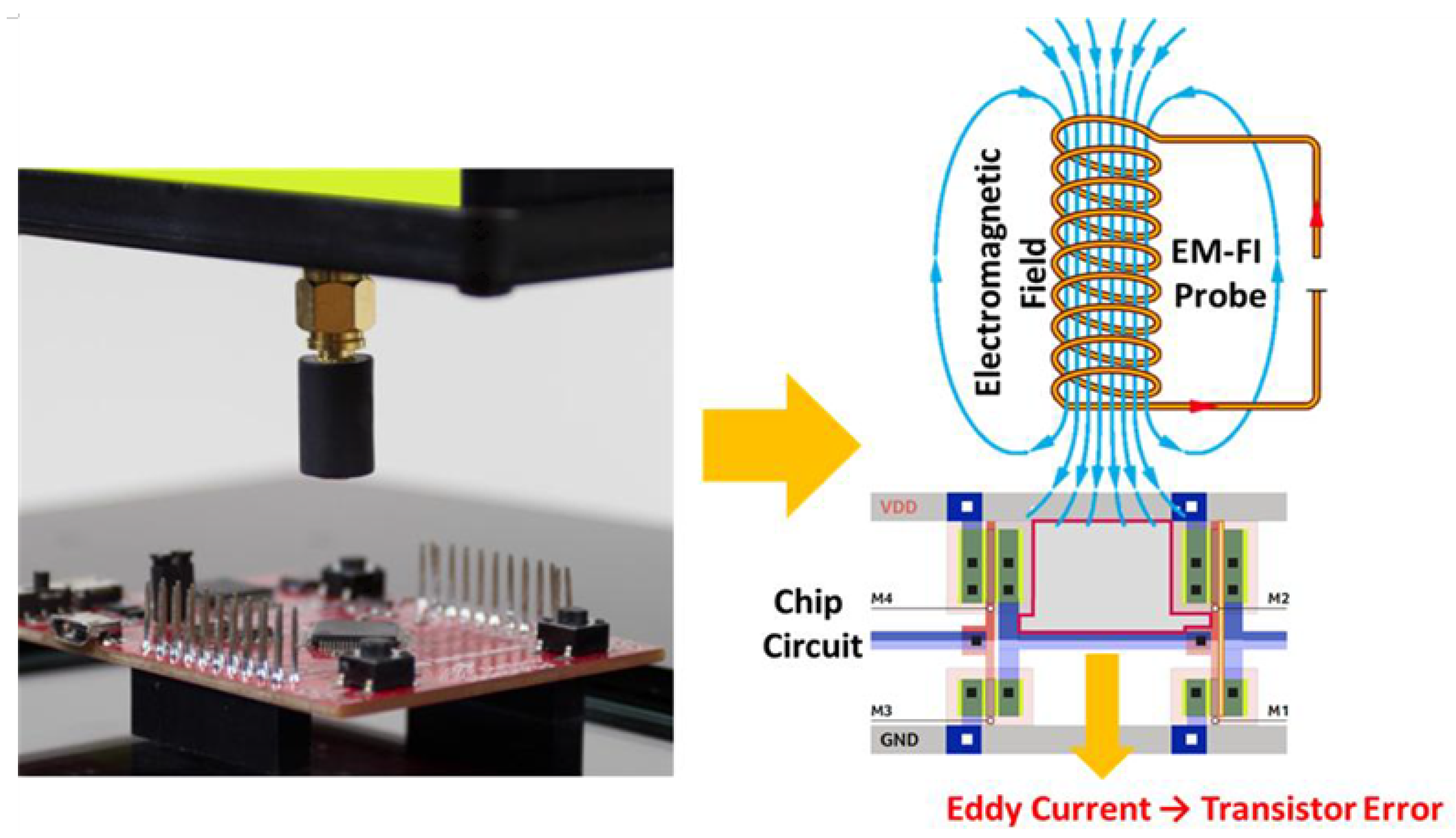
2.1. Electromagnetic Fault Injection Attack
2.2. PGO DFA Method
3. Novel Fault Injection Attack System for Relaxing the Fault Injection Attacker‘s Assumption
3.1. Fault Injection Attack System Using I/O Signals as Triggers
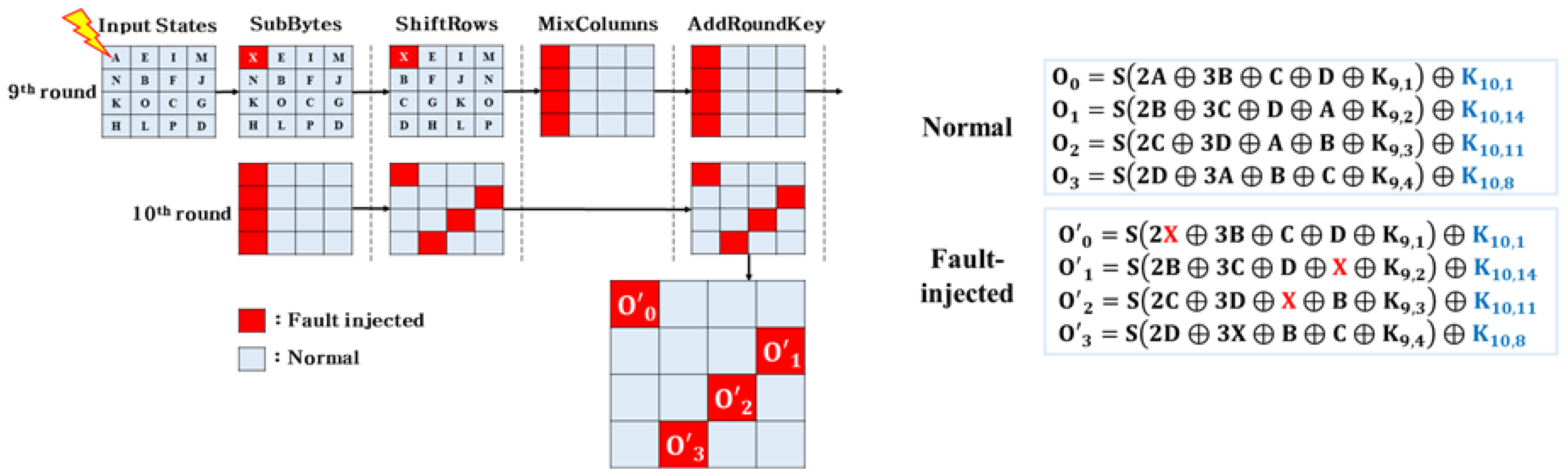
3.2. AES DFA Method
- Normal Ciphertext: Normal ciphertext used for analysis;
- Faulted Ciphertext: Fault-injected ciphertext used for analysis;
- Fault-Injected Byte: Analysis formulas according to an array with fault-injected input bytes corresponding Fault Type;
- Guessing Value: the and guessing pair to narrow.
| Algorithm 1 Key recovery algorithm |
| Input: sequence set of |
| Normal ciphertext |
| Fault-injected ciphertext of the same Fault Type |
| Fault Type: Fault Type |
| Fault-Injected Byte: Fault-injected input bytes corresponding Fault Type |
| Y: Possible Guessing Value, |
| Output: 4-byte 10th round keys |
| 1: procedure DFA Fault Type) |
| 2: initialize Y to all of guessing values |
| 3: Fault Type |
| 4: for to 3 do |
| 5: |
| 6: for to 3 do |
| 7: |
| 8: for to 3 do |
| 9: |
| 10: if NULL then |
| 11: xor |
| 12: xor |
| 13: xor |
| 14: xor |
| 15: return |
| 16: return FAILED |
| 17: end procedure |
4. Experiment
4.1. Experimental Setup
4.1.1. Specifying the Time of a Fault Injection Attack
4.1.2. Electromagnetic Fault Injection Attack
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kocher, P.C. Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In Annual International Cryptology Conference; Springer: Berlin/Heidelberg, Germany, 1996; pp. 104–113. [Google Scholar]
- Boneh, D.; DeMillo, R.A.; Lipton, R.J. On the importance of checking cryptographic protocols for faults. In International Conference on the Theory and Applications Of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1997; pp. 37–51. [Google Scholar]
- Dusart, P.; Letourneux, G.; Vivolo, O. Differential fault analysis on AES. In International Conference on Applied Cryptography and Network Security; Springer: Berlin/Heidelberg, Germany, 2003; pp. 293–306. [Google Scholar]
- Chen, C.N.; Yen, S.M. Differential fault analysis on AES key schedule and some countermeasures. In Australasian Conference on Information Security and Privacy; Springer: Berlin/Heidelberg, Germany, 2003; pp. 118–129. [Google Scholar]
- Blömer, J.; Seifert, J.P. Fault based cryptanalysis of the advanced encryption standard (AES). In International Conference on Financial Cryptography; Springer: Berlin/Heidelberg, Germany, 2003; pp. 162–181. [Google Scholar]
- Giraud, C. Dfa on aes. In International Conference on Advanced Encryption Standard; Springer: Berlin/Heidelberg, Germany, 2004; pp. 27–41. [Google Scholar]
- Arduino Uno Rev3. Available online: https://store.arduino.cc/usa/arduino-uno-rev3 (accessed on 30 May 2020).
- Hong, D.; Sung, J.; Hong, S.; Lim, J.; Lee, S.; Koo, B.S.; Lee, C.; Chang, D.; Lee, J.; Jeong, K.; et al. HIGHT: A new block cipher suitable for low-resource device. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 46–59. [Google Scholar]
- Lee, Y.; Kim, J.; Hong, S. A Differential Fault Attack against Block Cipher HIGHT. J. Korea Inst. Inf. Secur. Cryptol. 2012, 22, 485–494. [Google Scholar]
- Kwon, D.; Kim, J.; Park, S.; Sung, S.H.; Sohn, Y.; Song, J.H.; Yeom, Y.; Yoon, E.J.; Lee, S.; Lee, J.; et al. New block cipher: ARIA. In International Conference on Information Security and Cryptology; Springer: Berlin/Heidelberg, Germany, 2003; pp. 432–445. [Google Scholar]
- Lee, Y.; Jeong, K.; Sung, J.; Hong, S. Improved Differential Fault Analysis on ARIA using Small Number of Faults. IACR Cryptol. EPrint Arch. 2013, 2013, 191. [Google Scholar]
- Hong, D.; Lee, J.K.; Kim, D.C.; Kwon, D.; Ryu, K.H.; Lee, D.G. LEA: A 128-bit block cipher for fast encryption on common processors. In International Workshop on Information Security Applications; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3–27. [Google Scholar]
- Jap, D.; Breier, J. Differential fault attack on LEA. In Information and Communication Technology-EurAsia Conference; Springer: Berlin/Heidelberg, Germany, 2015; pp. 265–274. [Google Scholar]
- Beaulieu, R.; Shors, D.; Smith, J.; Treatman-Clark, S.; Weeks, B.; Wingers, L. The SIMON and SPECK Families of Lightweight Block Ciphers. IACR Cryptol. EPrint Arch. 2013, 2013, 404–449. [Google Scholar]
- Tupsamudre, H.; Bisht, S.; Mukhopadhyay, D. Differential fault analysis on the families of SIMON and SPECK ciphers. In Proceedings of the 2014 Workshop on Fault Diagnosis and Tolerance in Cryptography, Busan, Korea, 23 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 40–48. [Google Scholar]
- Koo, B.; Roh, D.; Kim, H.; Jung, Y.; Lee, D.G.; Kwon, D. CHAM: A family of lightweight block ciphers for resource-constrained devices. In International Conference on Information Security and Cryptology; Springer: Berlin/Heidelberg, Germany, 2017; pp. 3–25. [Google Scholar]
- Kwon, H.; Ha, J. Fault Injection Attack on Lightweight Block Cipher CHAM. J. Korea Inst. Inf. Secur. Cryptol. 2018, 28, 1071–1078. [Google Scholar]
- Derouet, O. Secure smartcard design against laser fault injection. In Proceedings of the 4th Workshop on Fault Diagnostic and Tolerance in Cryptography, Vienne, Autriche, 10 September 2007; p. 87. [Google Scholar]
- Spider. Available online: https://getquote.riscure.com/en/quote/2101116/spider.htm (accessed on 30 May 2020).
- EM-FI Transient Probe. Available online: https://getquote.riscure.com/en/quote/2101068/em-fi-transient-probe.htm (accessed on 30 May 2020).
- Inspector Subscription FI Professional. Available online: https://getquote.riscure.com/en/quote/2101094/inspector-subscription-fi-professional.htm (accessed on 30 May 2020).
- XYZ Stage. Available online: https://getquote.riscure.com/en/quote/2101124/xyz-stage-emps-em-fi-and-compact-laser.htm (accessed on 30 May 2020).



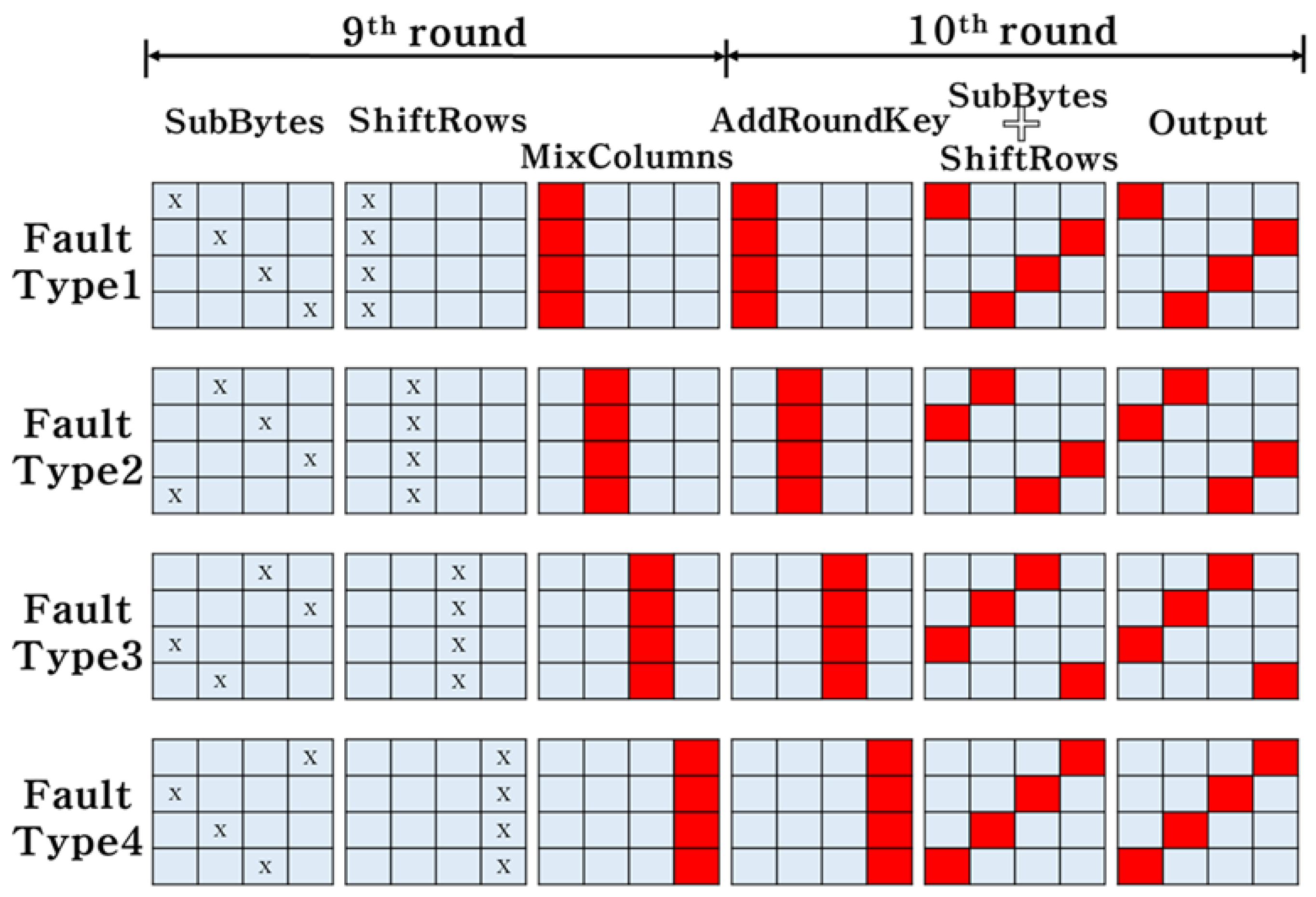


| Fault Byte | Formula Type |
|---|---|
| 1 | |
| 6 | |
| 11 | |
| 16 | |
| Number | Index of Byte | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| ➀ | 39 | 25 | 84 | 1D | 02 | DC | 09 | FB | DC | 11 | 85 | 97 | 19 | 6A | 0B | 32 |
| ➁ | 39 | 25 | 84 | 88 * | 02 | DC | D9 * | FB | DC | 11 * | 85 | 97 | E8 * | 6A | 0B | 32 |
| ➂ | 39 | 25 | B4 * | 1D | 02 | E0 * | 09 | FB | 64 * | 11 | 85 | 97 | 19 | 6A | 0B | 59 * |
| ➃ | 39 | B0 * | 84 | 1D | BC * | DC | 09 | FB | DC | 11 | 85 | F6 * | 19 | 6A | 27 * | 32 |
| ➄ | 89 * | 25 | 84 | 1D | 02 | DC | 09 | 68 * | DC | 11 | 55 * | 97 | 19 | A8 * | 0B | 32 |
| ➅ | 74 * | 25 | 9D * | 1D | 02 | 5C * | 09 | 97 * | 05 * | 11 | 01 * | 97 | 19 | 2D * | 0B | FB * |
| ➆ | 44 * | 8B * | 4F * | 1D | A9 * | 73 * | 09 | E6 * | 77 * | 11 | 82 * | 2B * | 19 | 4A * | C4 * | FB * |
| ➇ | 3B * | 5E * | D4 * | 22 * | AF * | 52 * | 78 * | 12 * | AF * | 88 * | 9B * | A4 * | 74 * | 70 * | 1D * | 64 * |
| Fault Byte | Formula Type |
|---|---|
| ➀ | Normal Cipher |
| ➁ | Input Fault: 2, 7, 12, 13 |
| Output Fault: 4, 7, 10, 13 | |
| ➂ | Input Fault: 3, 8, 9, 14 |
| Output Fault: 3, 6, 9, 16 | |
| ➃ | Input Fault: 4, 5, 10, 15 |
| Output Fault: 2, 5, 12, 15 | |
| ➄ | Input Fault: 1, 6, 11, 16 |
| Output Fault: 1, 8, 11, 14 | |
| ➅ | two-column fault injection |
| ➆ | three-column fault injection |
| ➇ | four-column fault injection or malfunction due to error |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, H.; Lee, J.; Han, D.-G. Novel Fault Injection Attack without Artificial Trigger. Appl. Sci. 2020, 10, 3849. https://doi.org/10.3390/app10113849
Lim H, Lee J, Han D-G. Novel Fault Injection Attack without Artificial Trigger. Applied Sciences. 2020; 10(11):3849. https://doi.org/10.3390/app10113849
Chicago/Turabian StyleLim, HanSeop, JongHyeok Lee, and Dong-Guk Han. 2020. "Novel Fault Injection Attack without Artificial Trigger" Applied Sciences 10, no. 11: 3849. https://doi.org/10.3390/app10113849
APA StyleLim, H., Lee, J., & Han, D.-G. (2020). Novel Fault Injection Attack without Artificial Trigger. Applied Sciences, 10(11), 3849. https://doi.org/10.3390/app10113849





