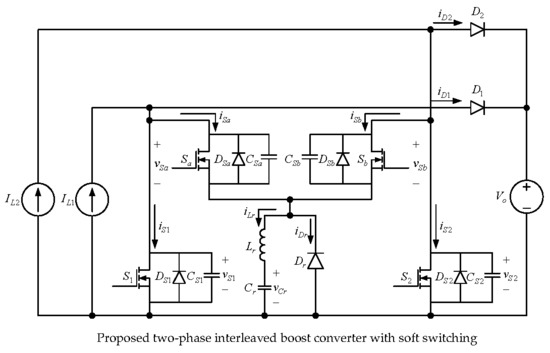
Two-Phase Interleaved Boost Converter with ZVT Turn-On for Main Switches and ZCS Turn-Off for Auxiliary Switches Based on One Resonant Loop
Abstract
:1. Introduction
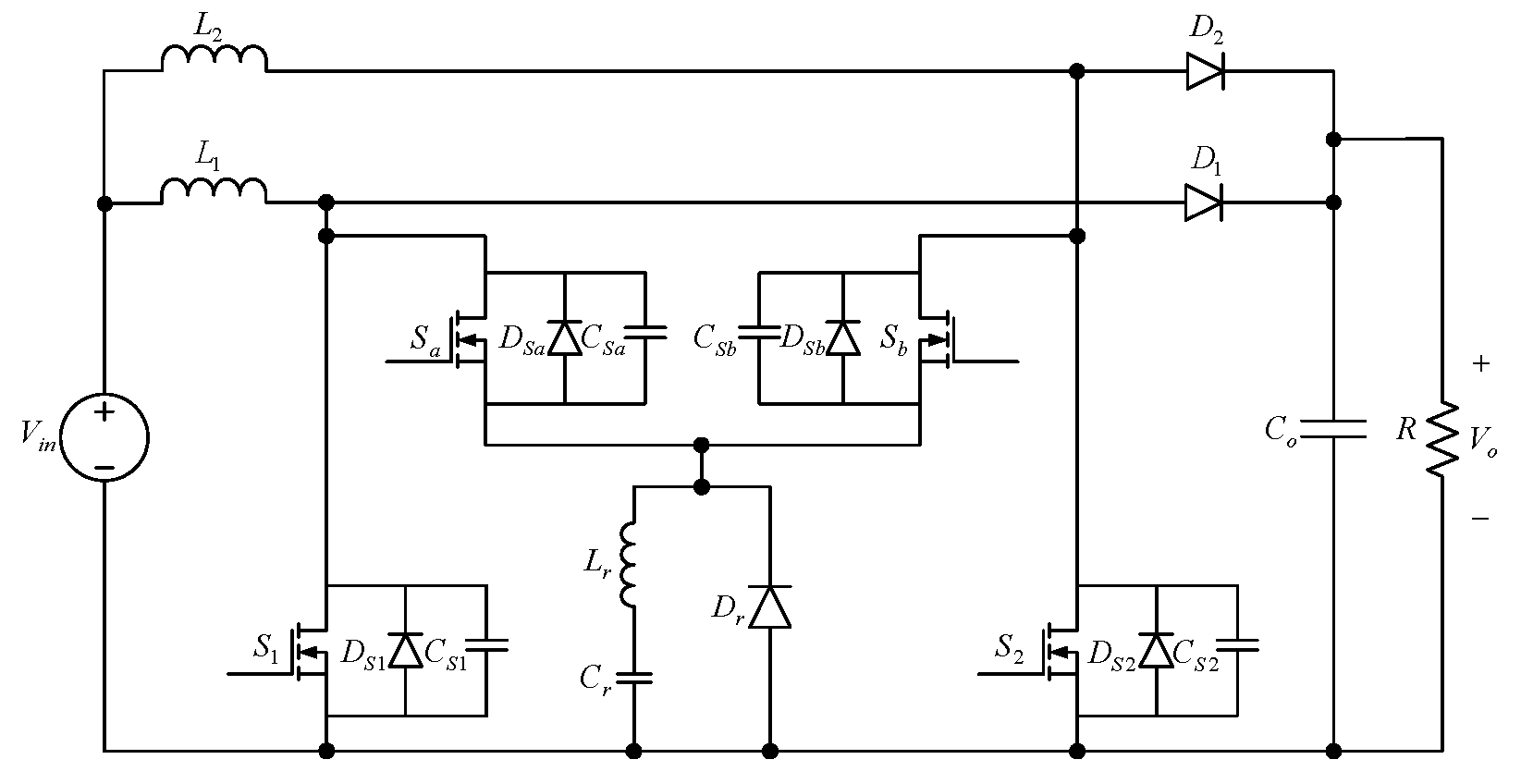
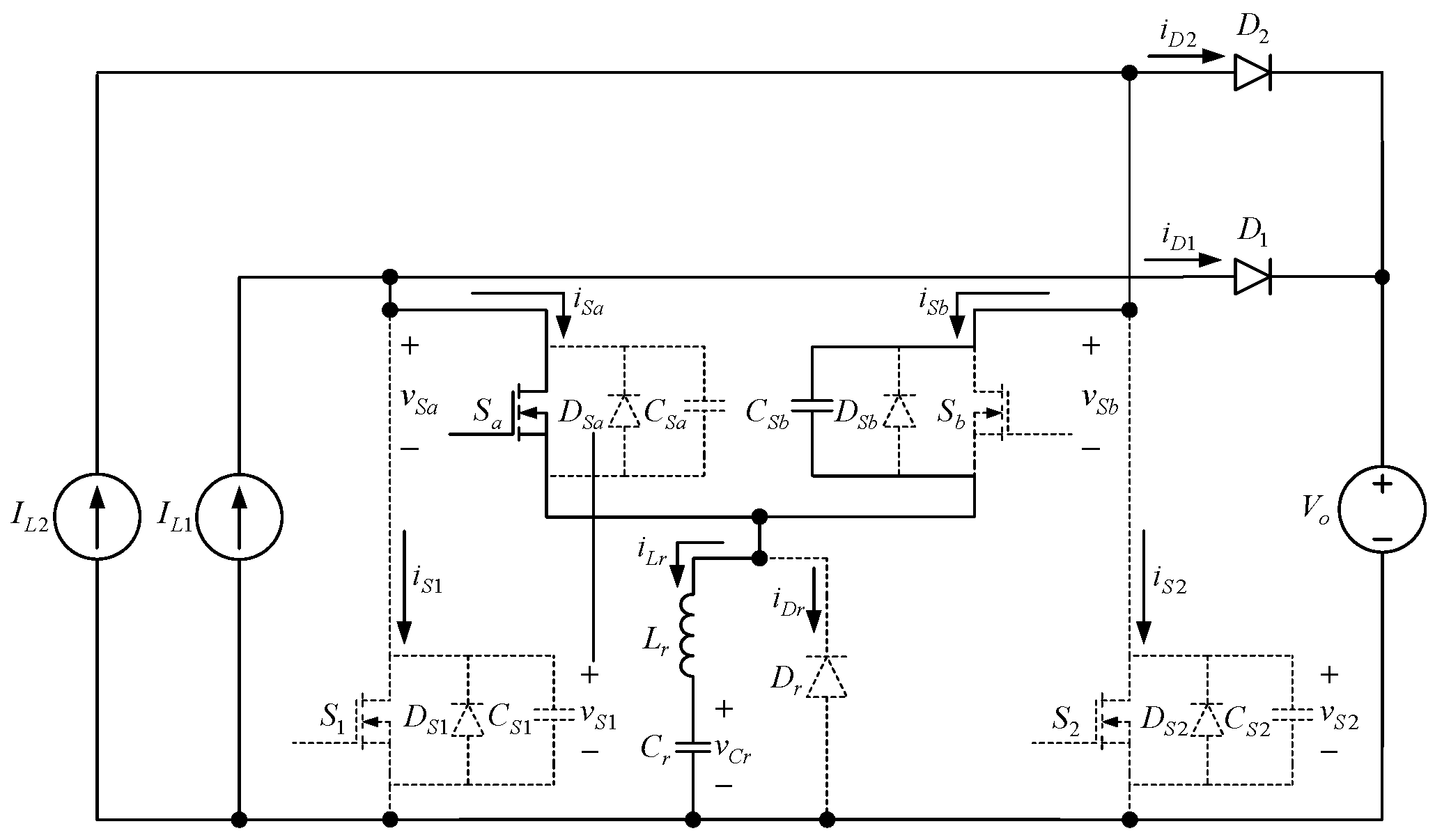
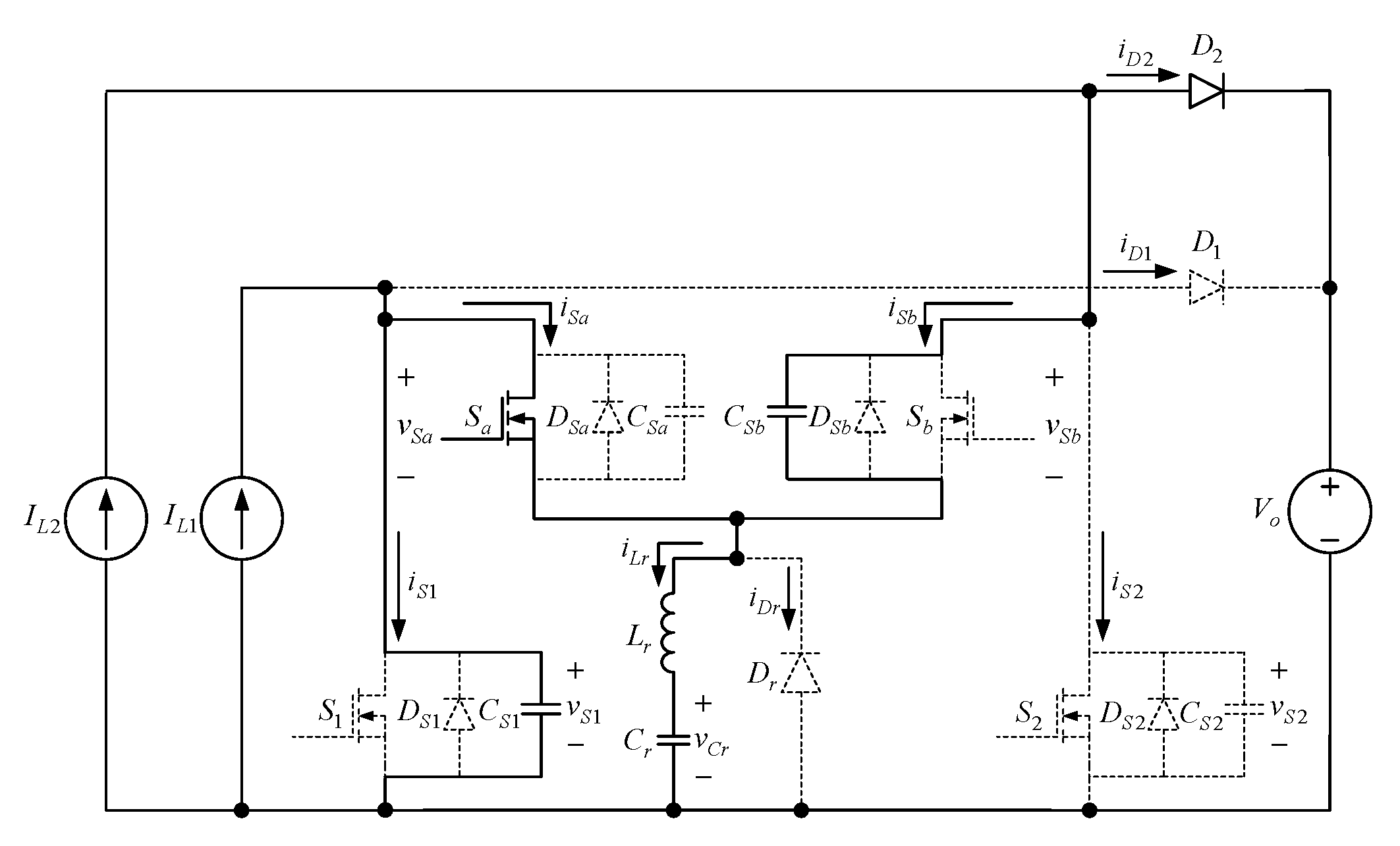
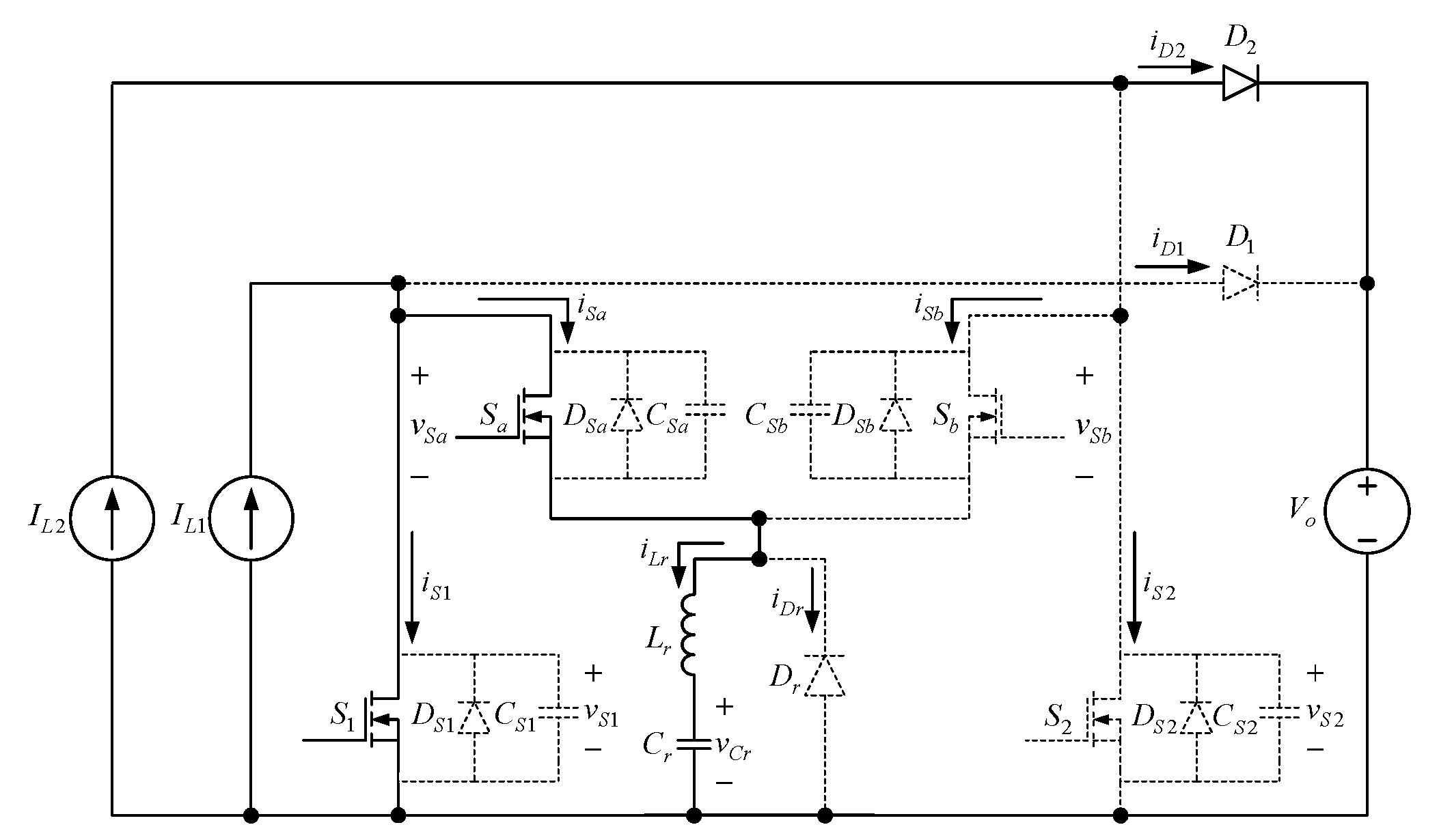
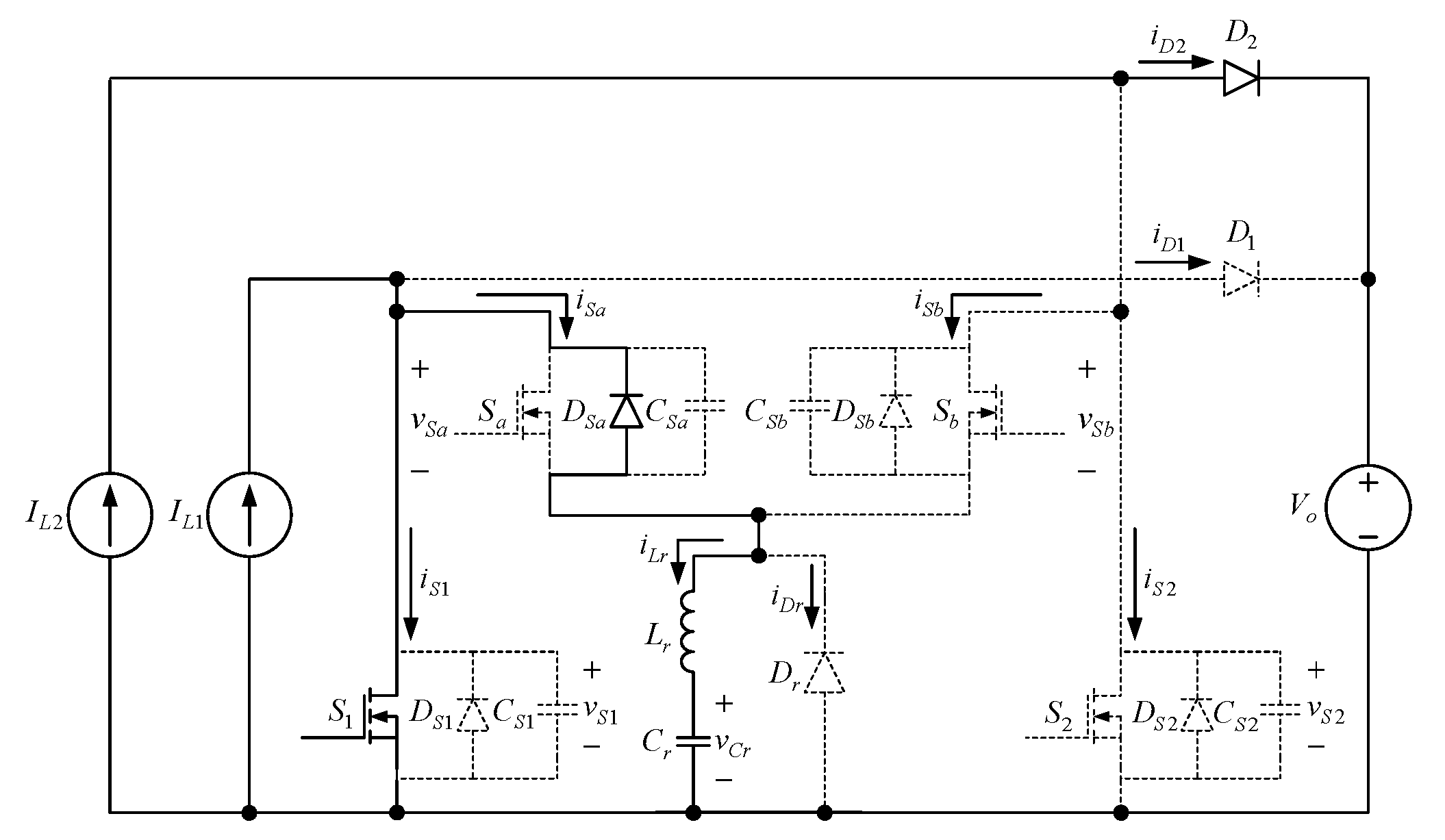
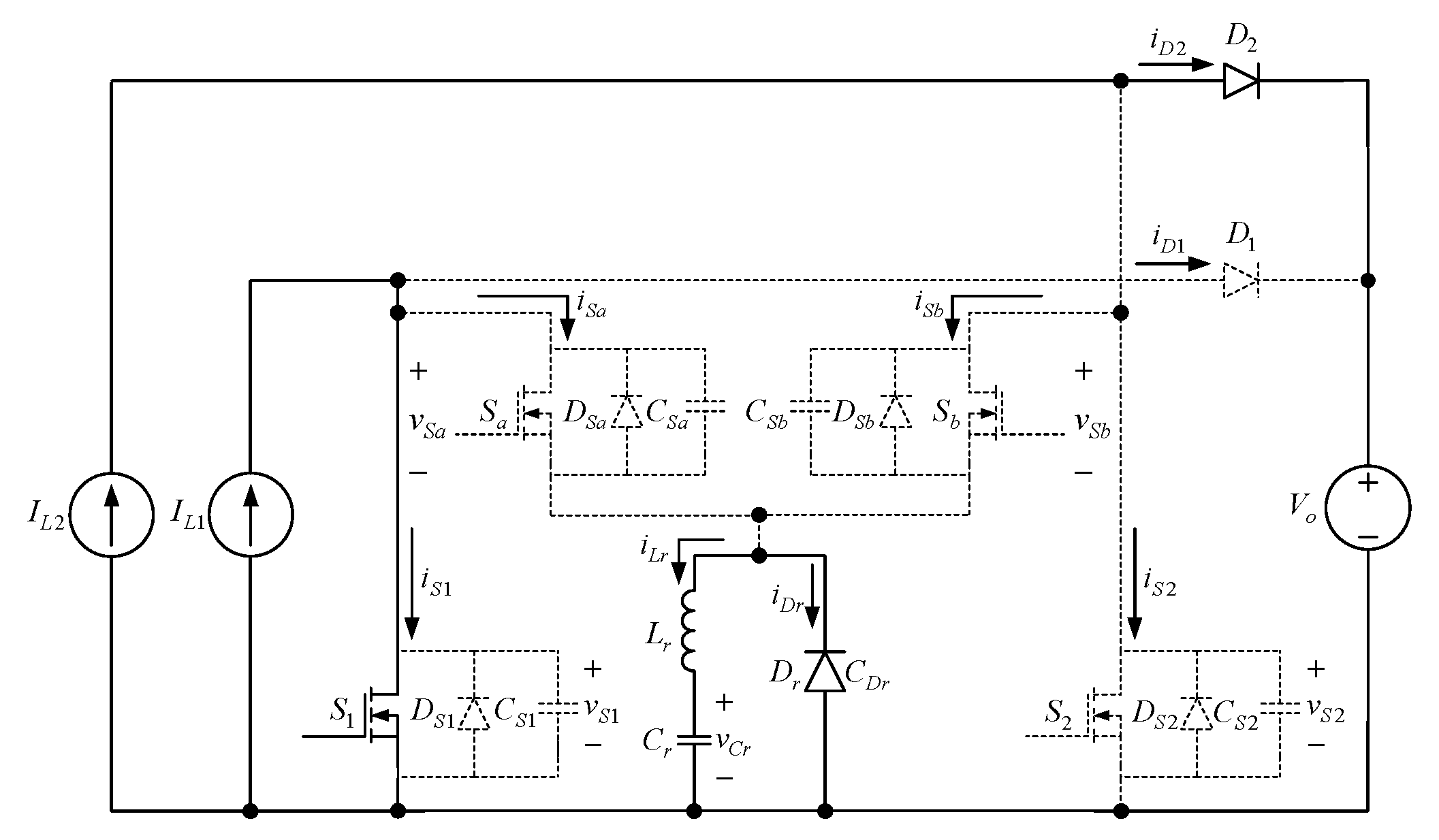
2. Proposed Converter
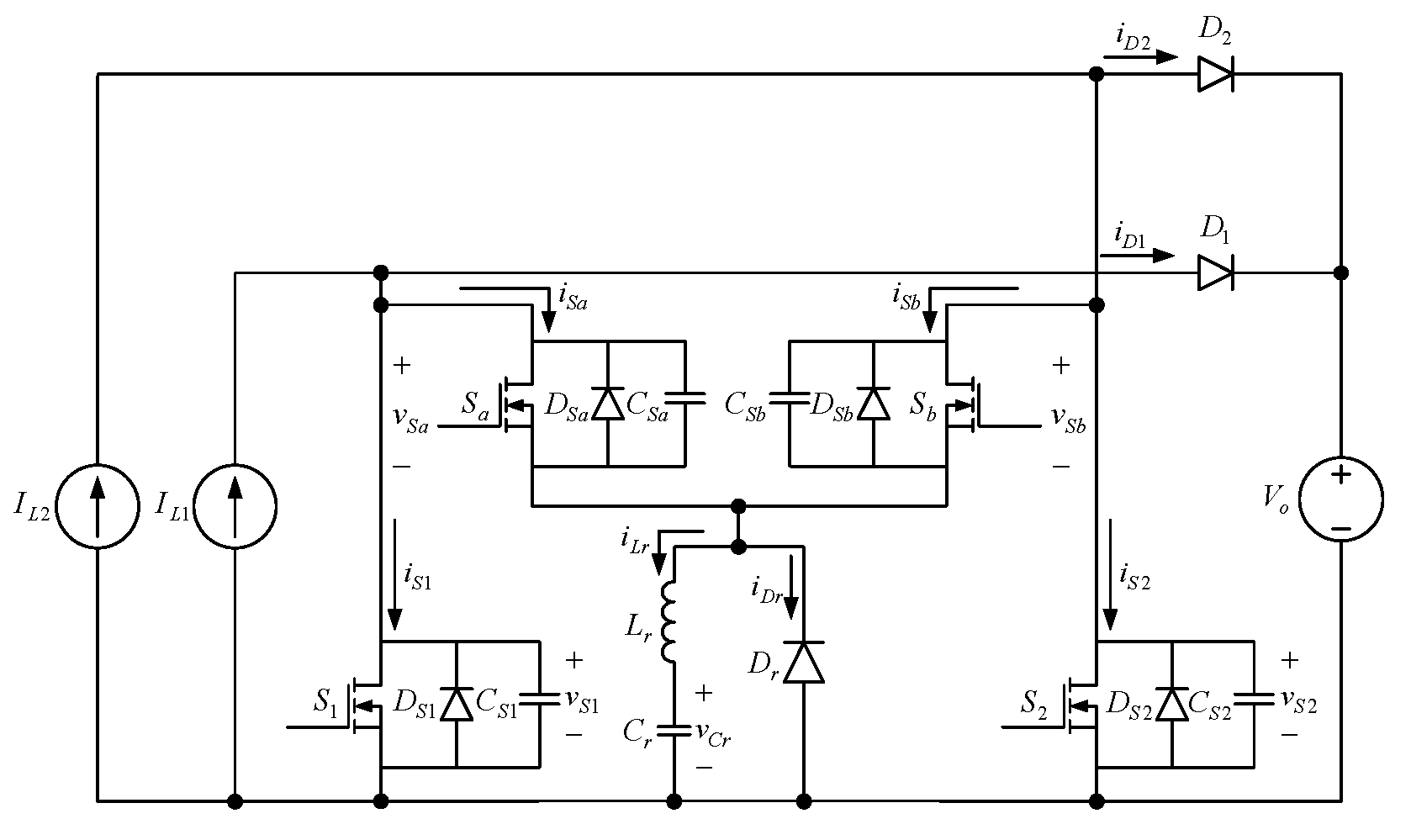
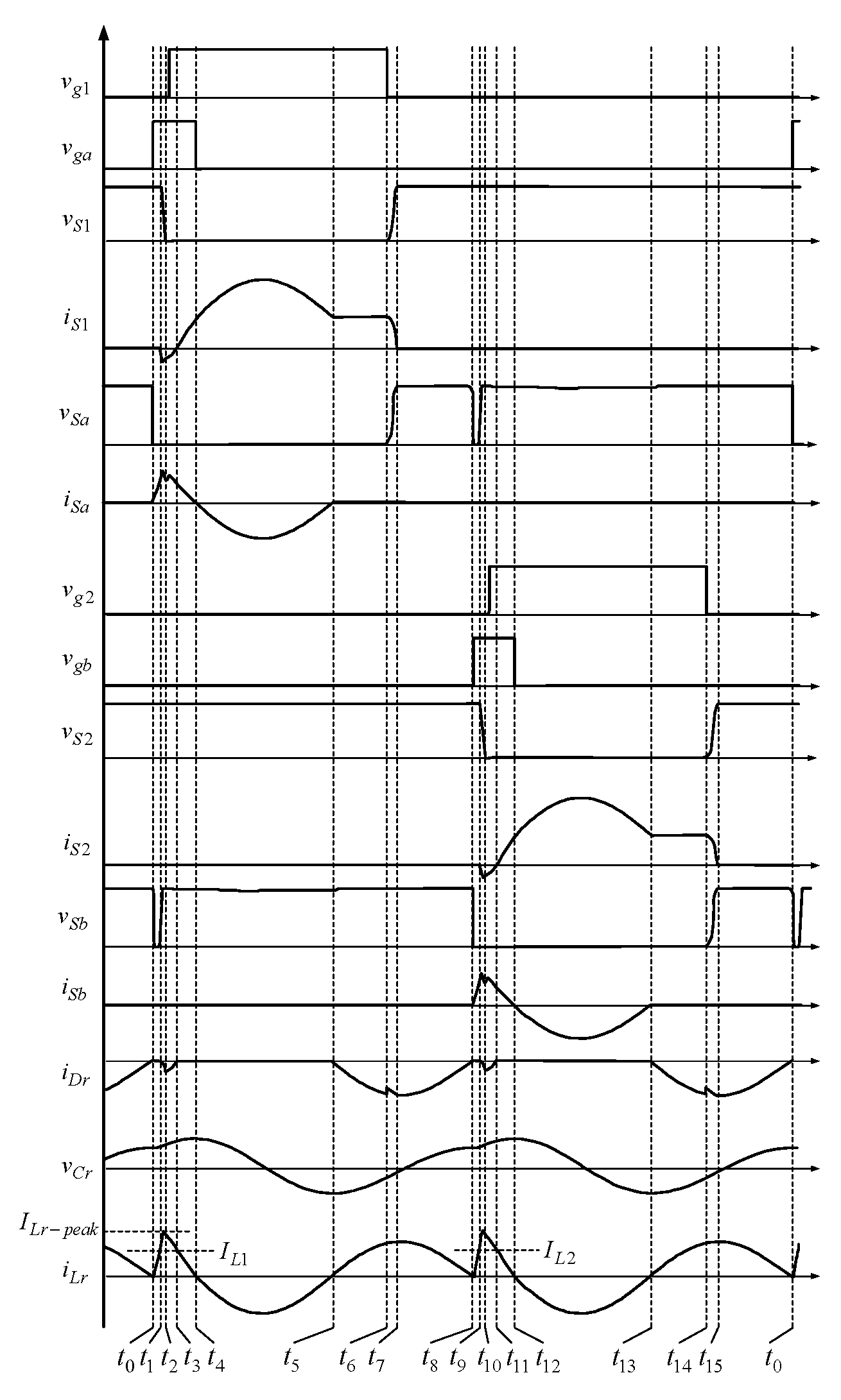
3. Operation Behavior
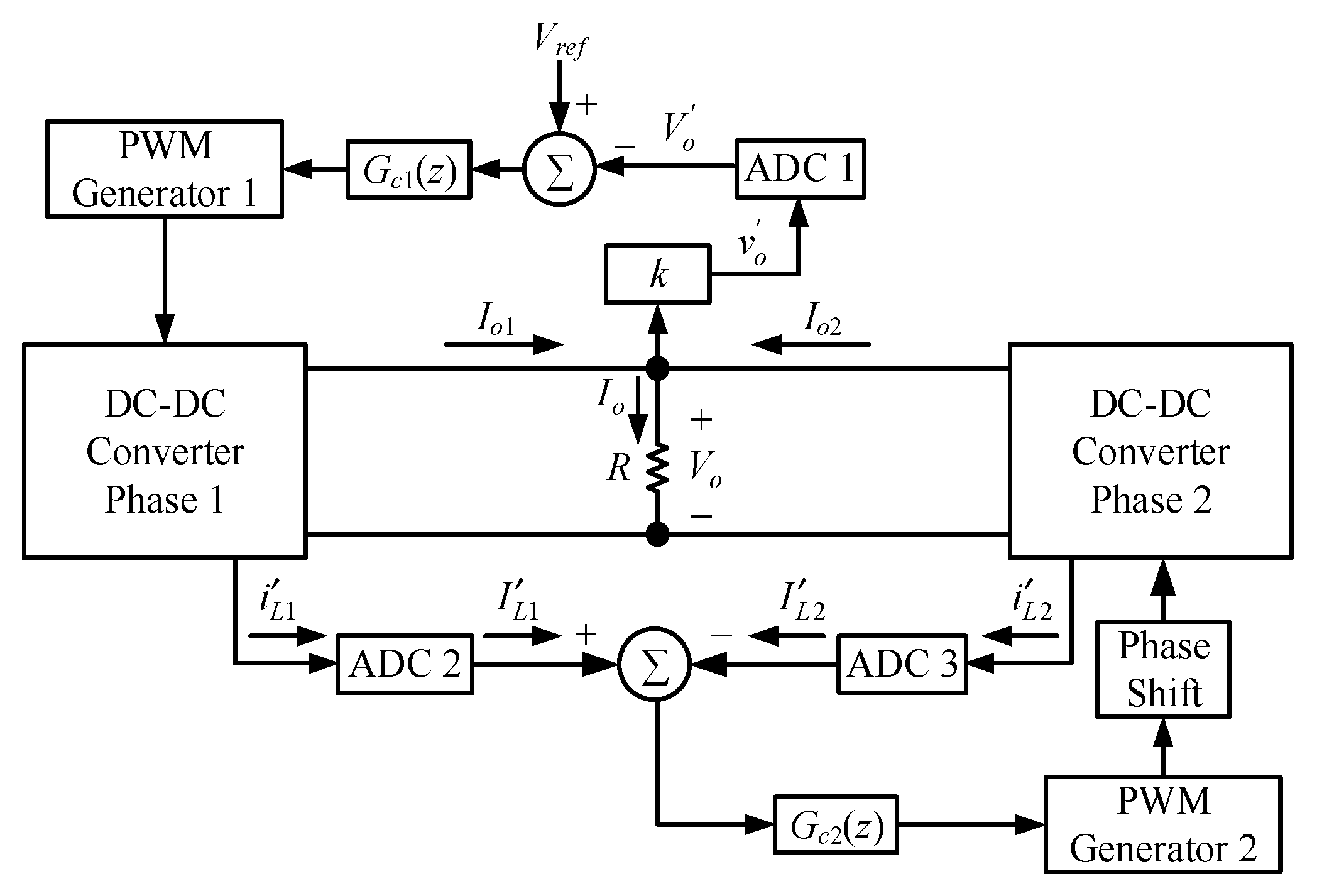
4. Current Control Strategy
5. Design Considerations
5.1. Design of L1 and L2
5.2. Design of Co
5.3. Design of Lr and Cr
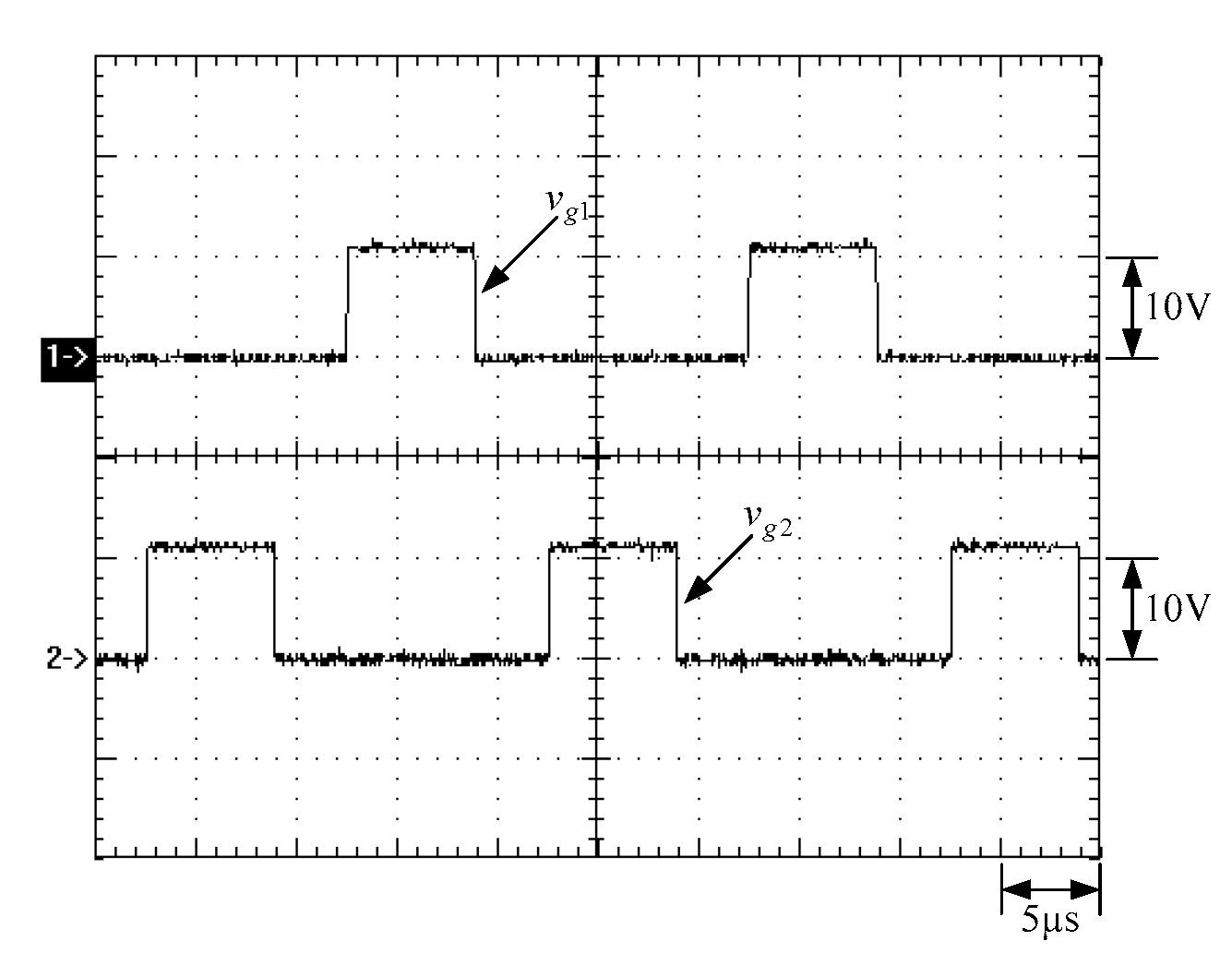
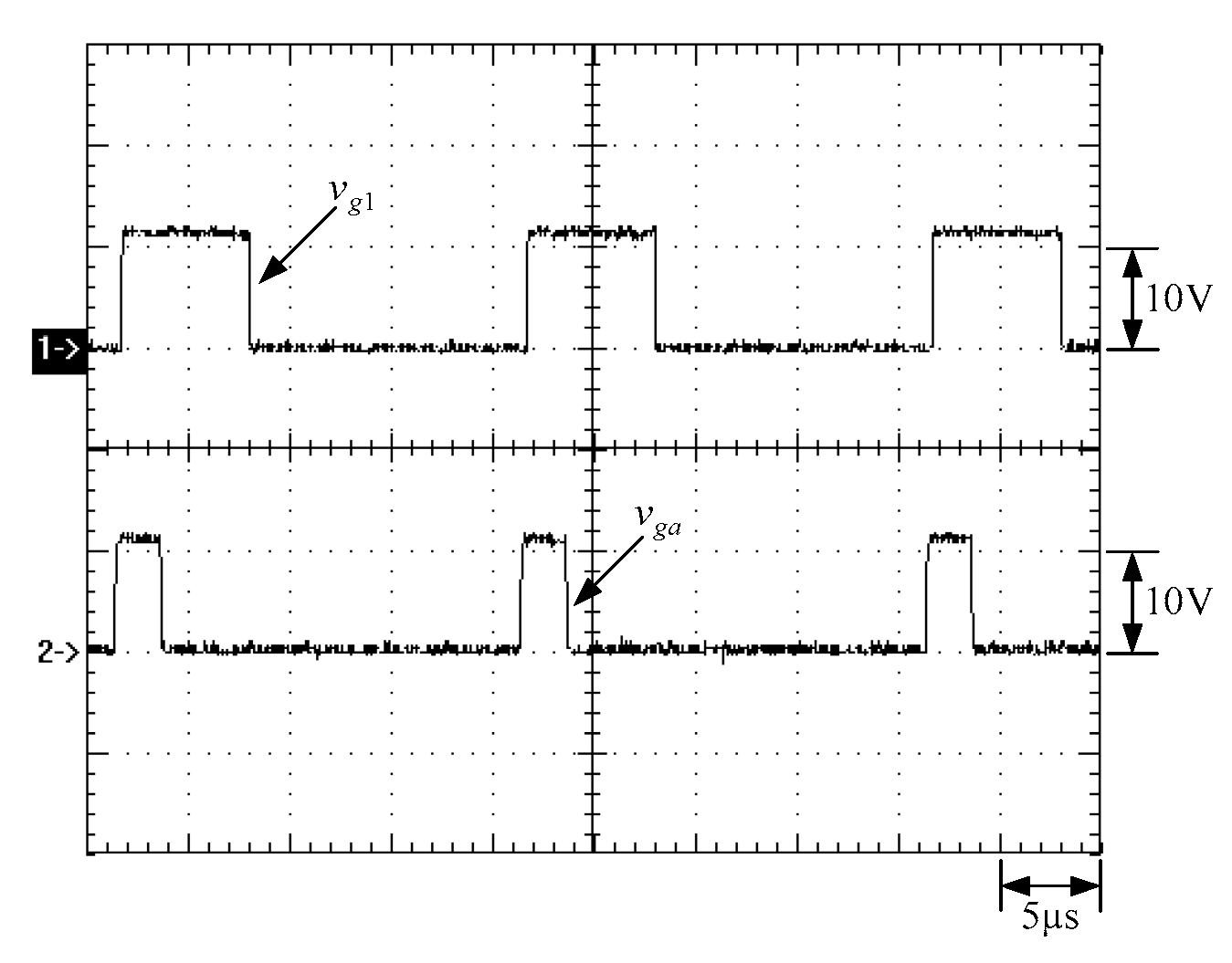
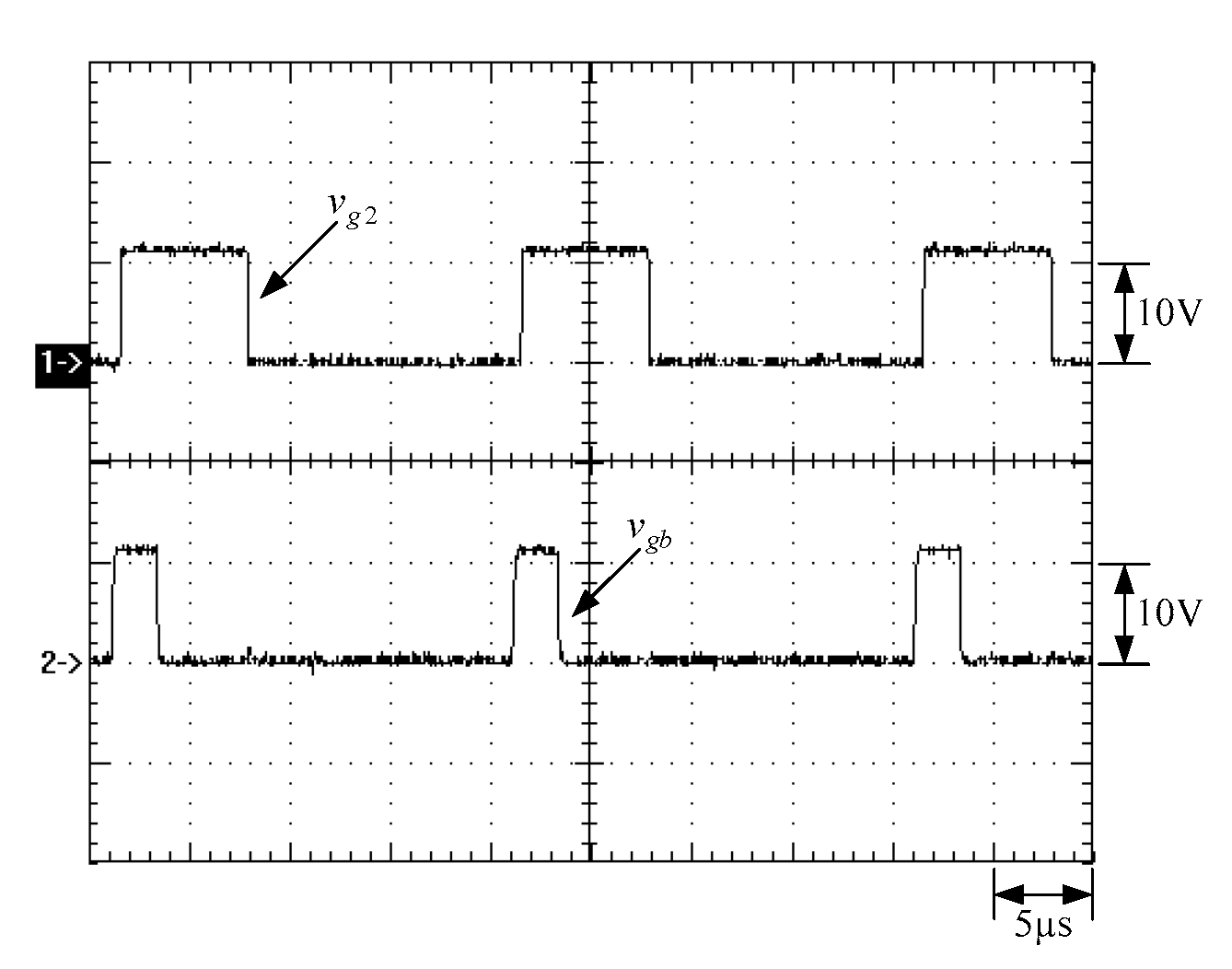
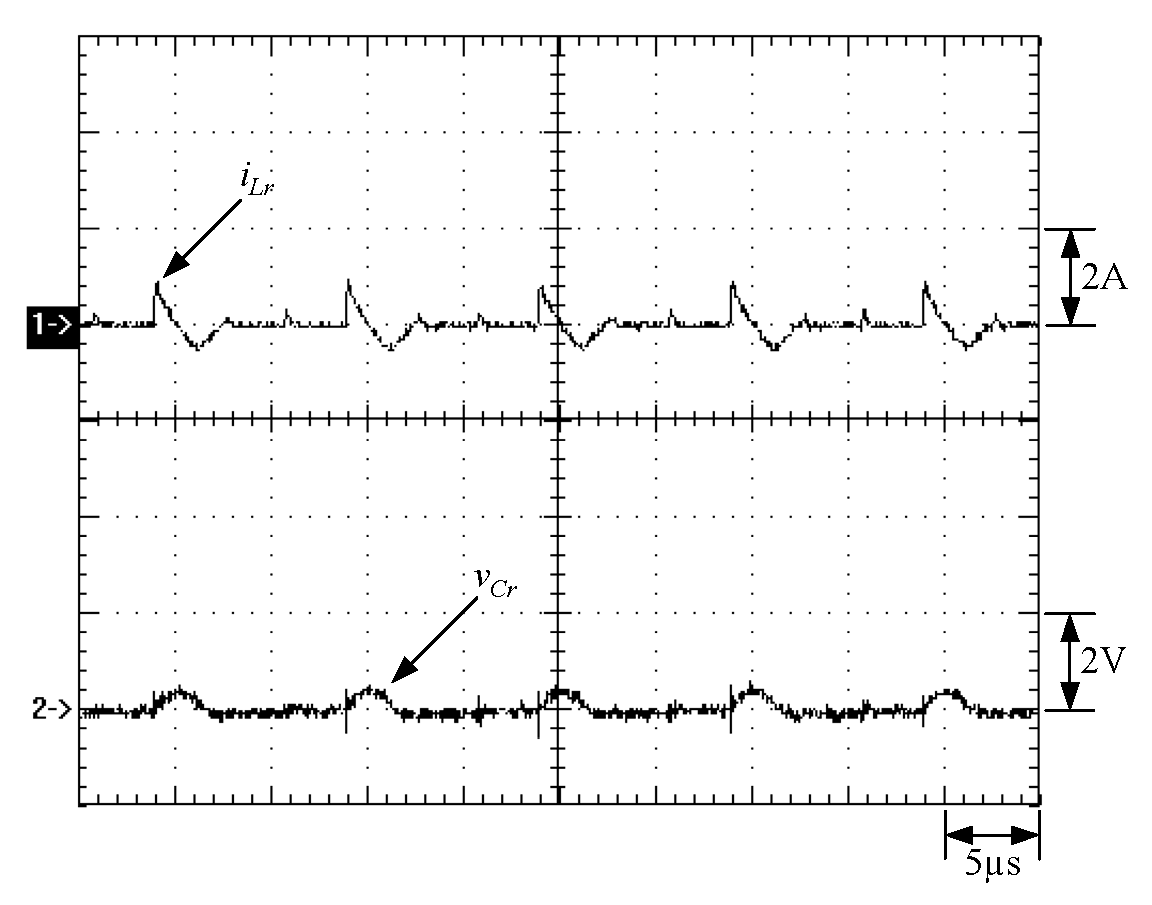
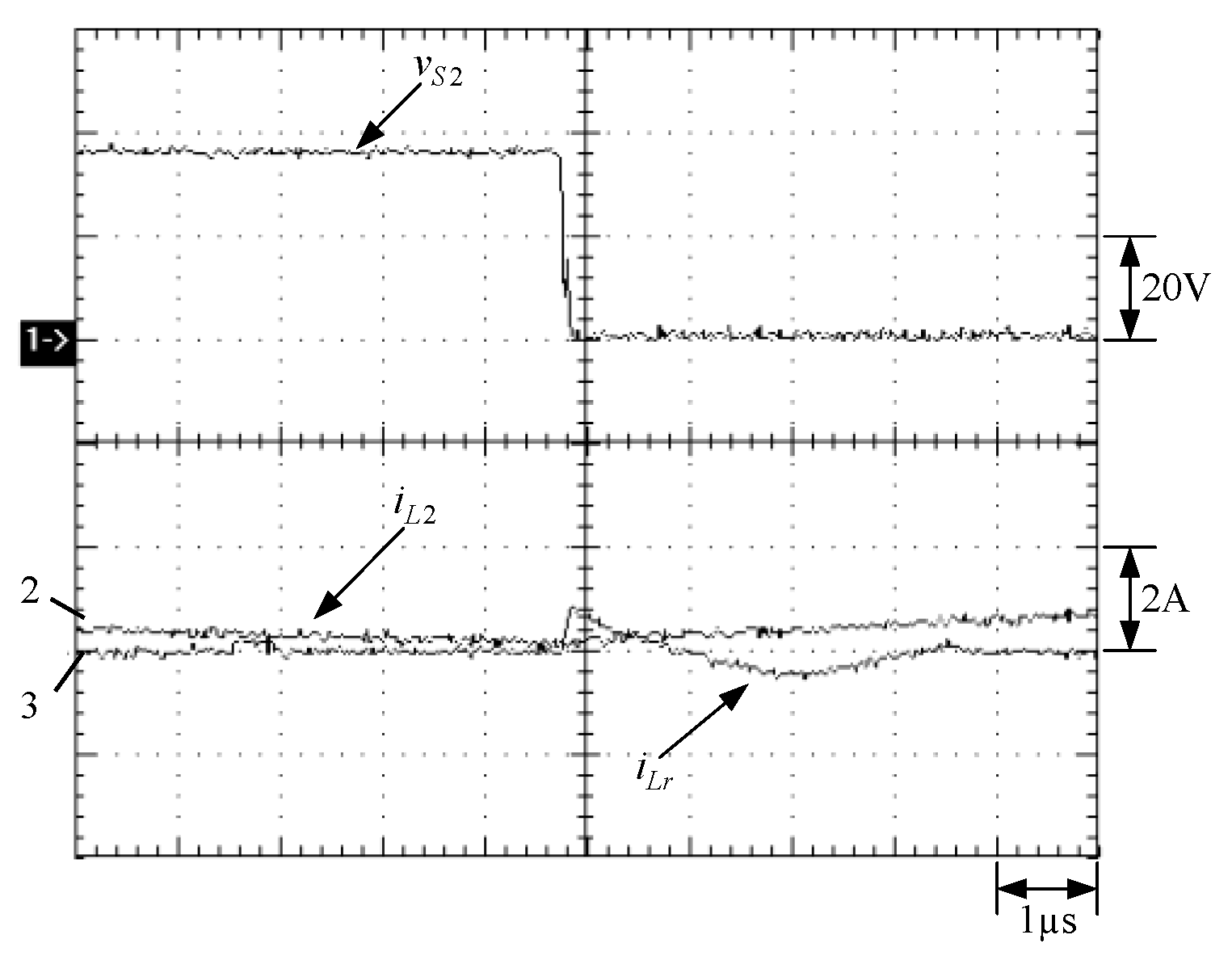
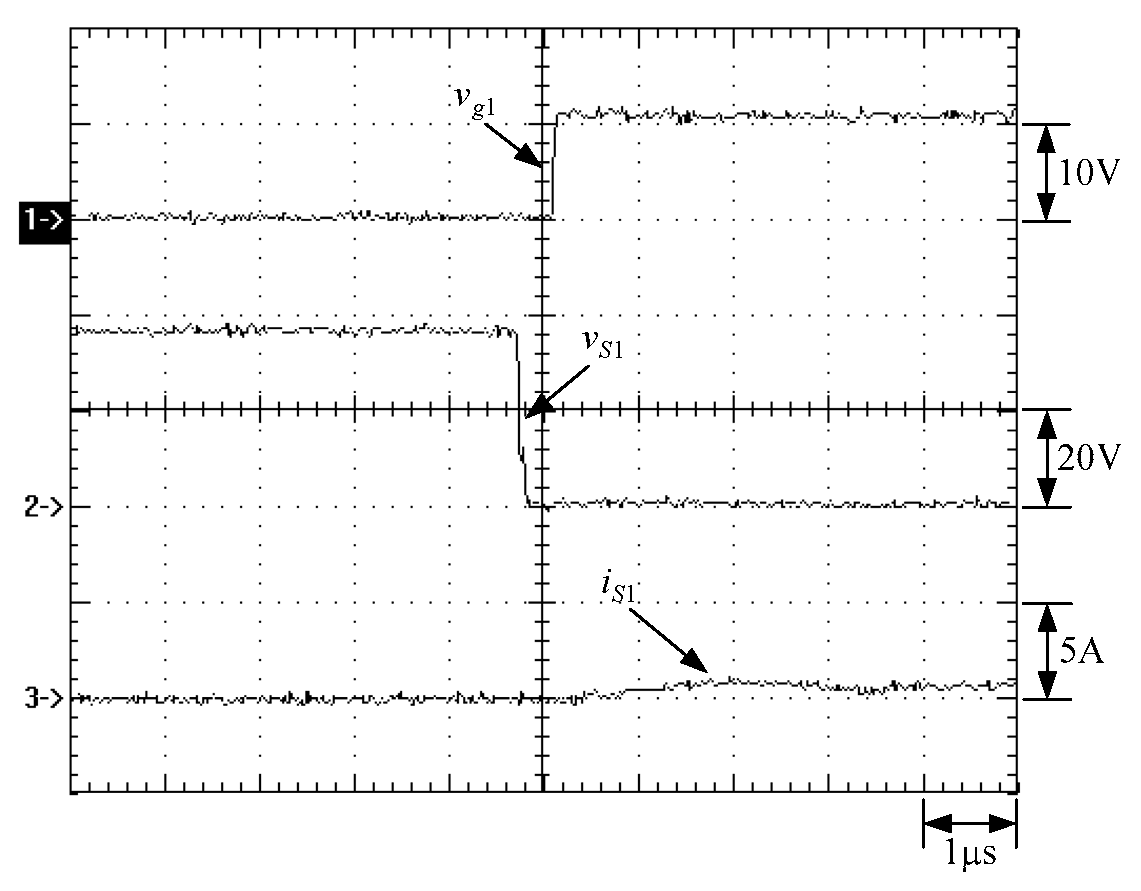
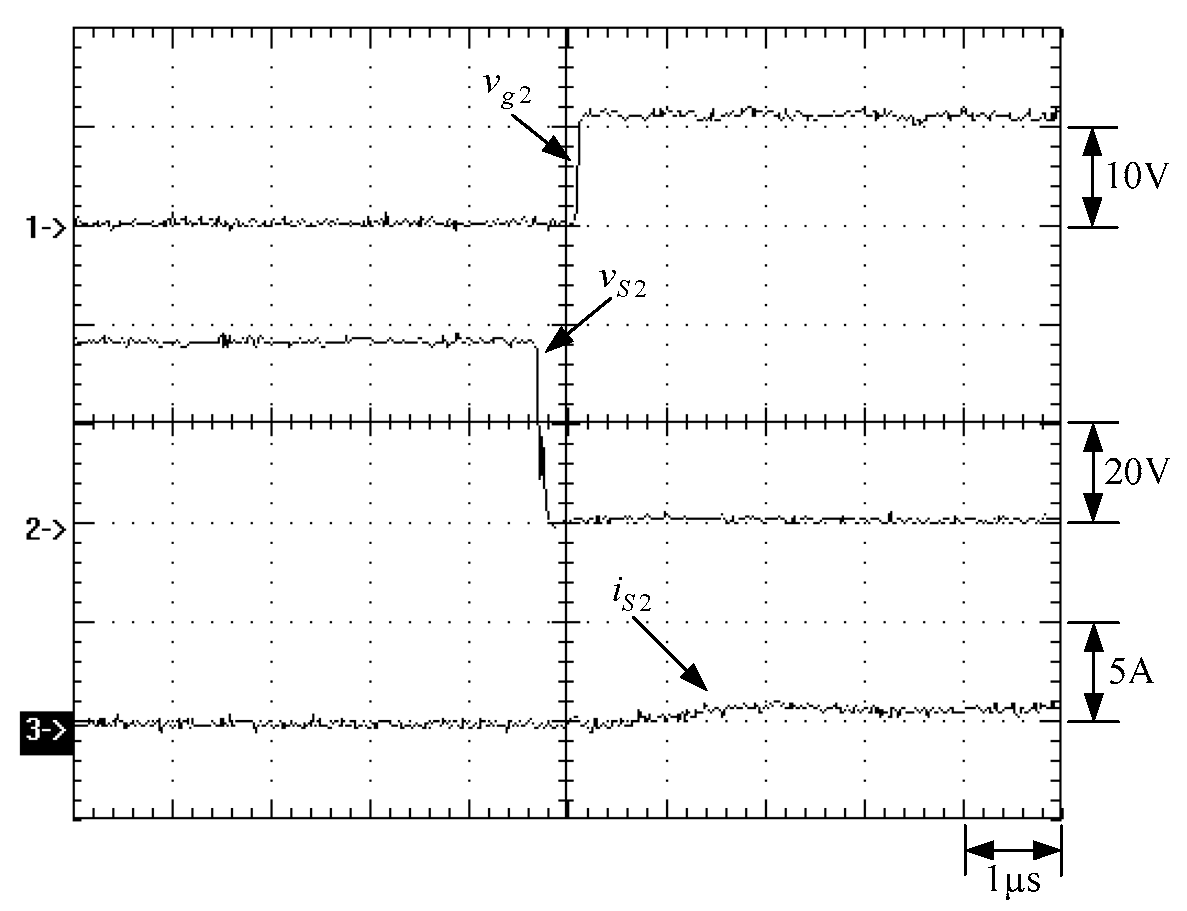
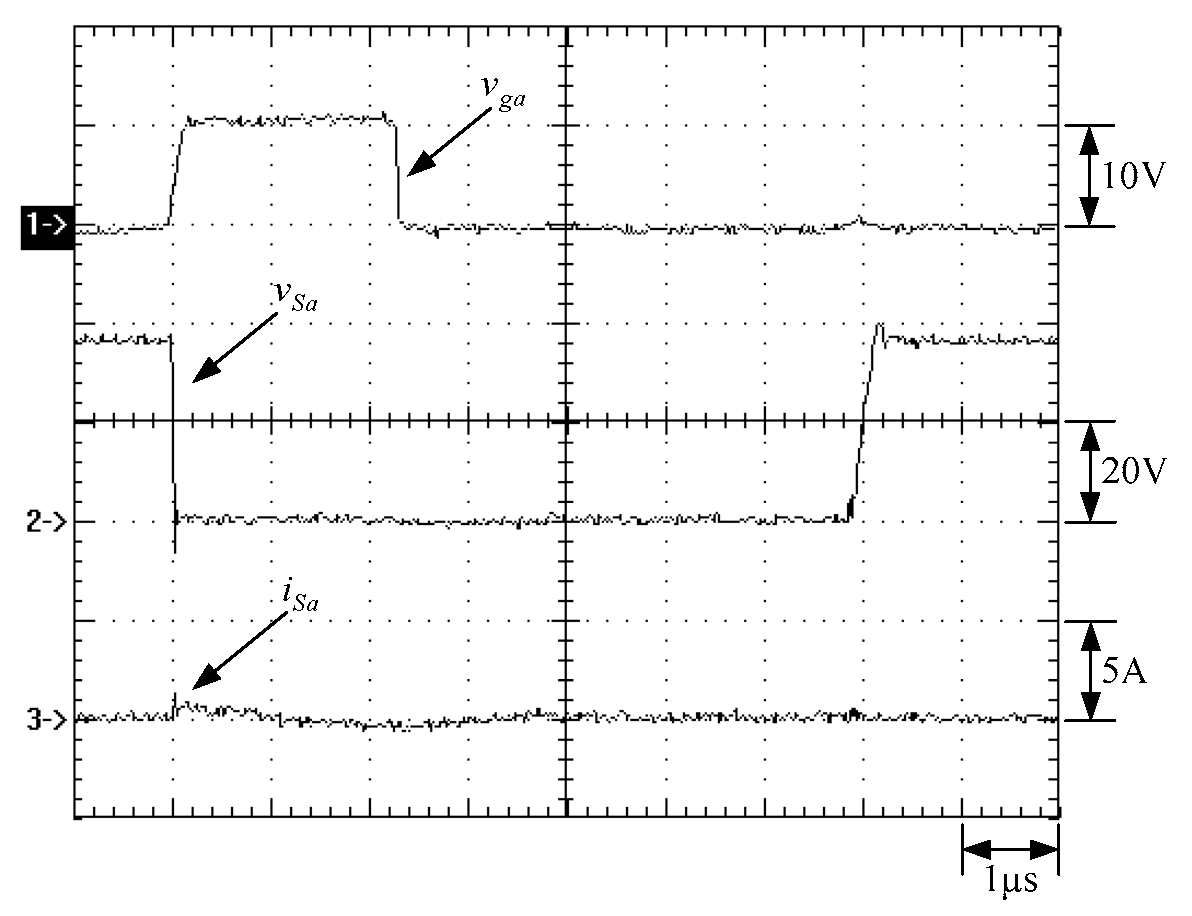
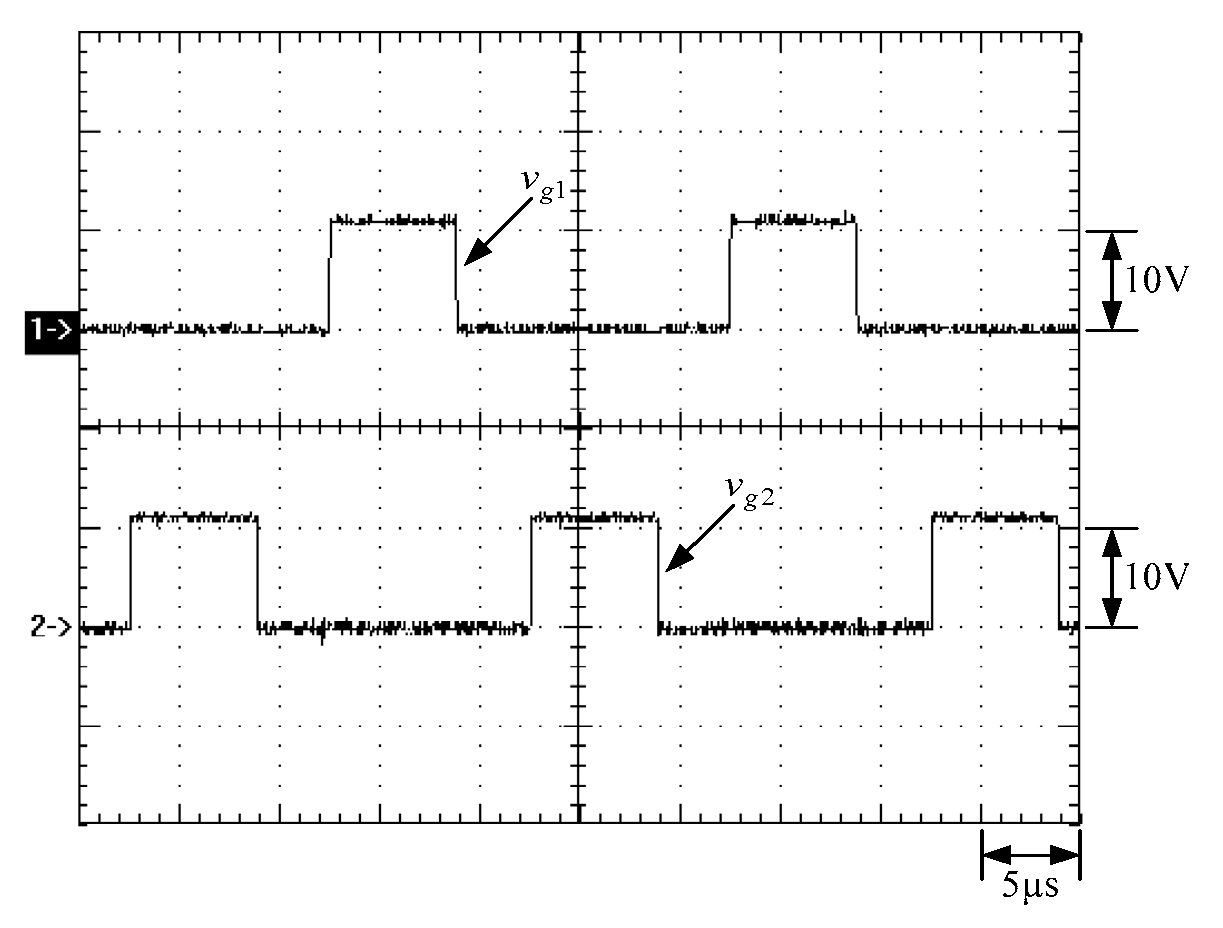
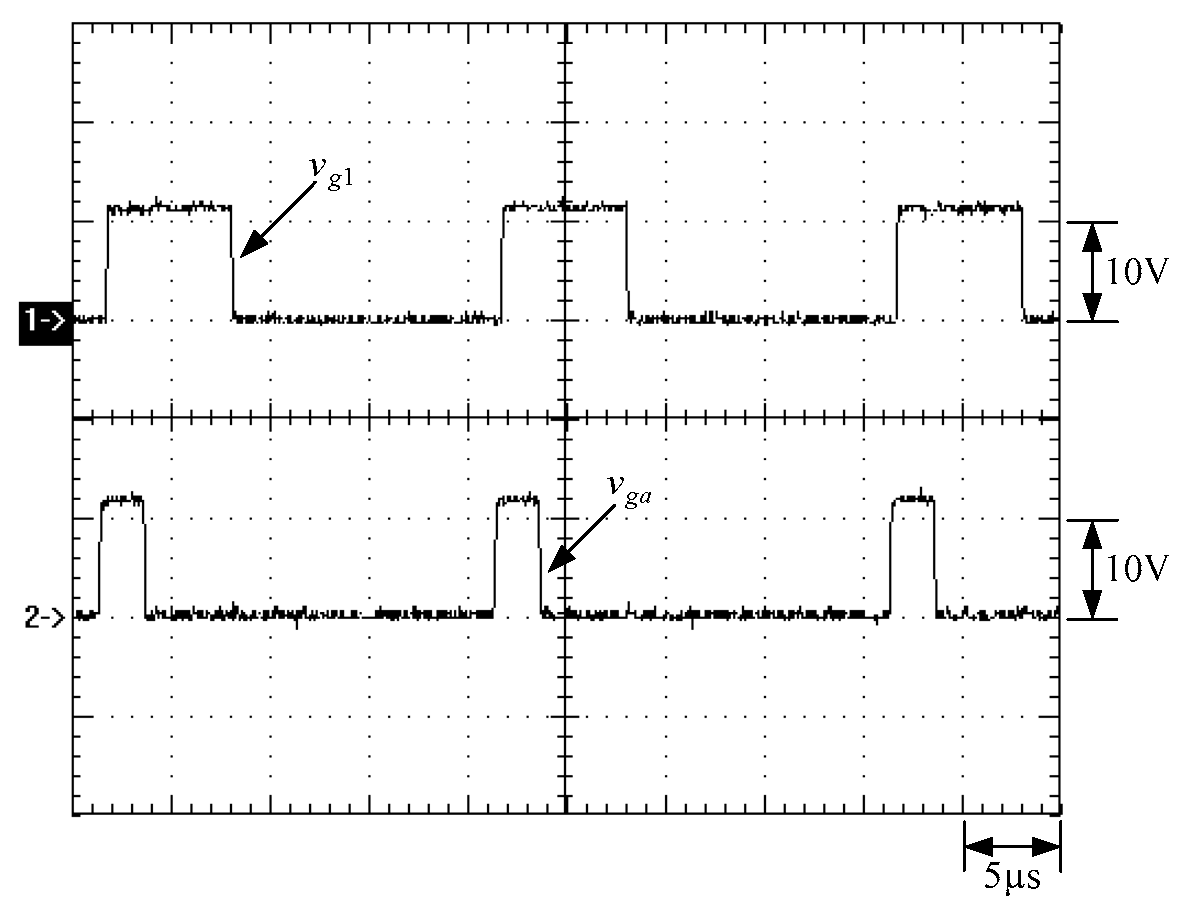
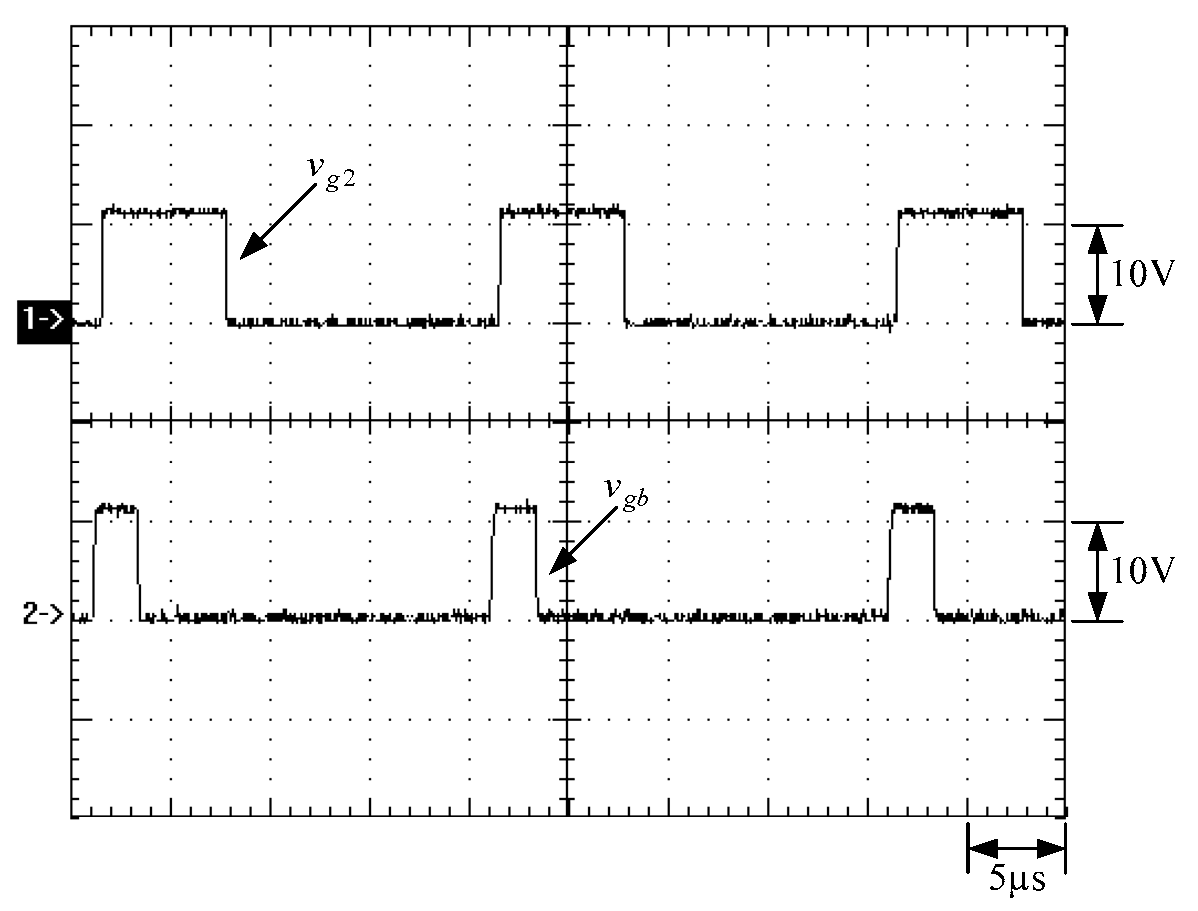
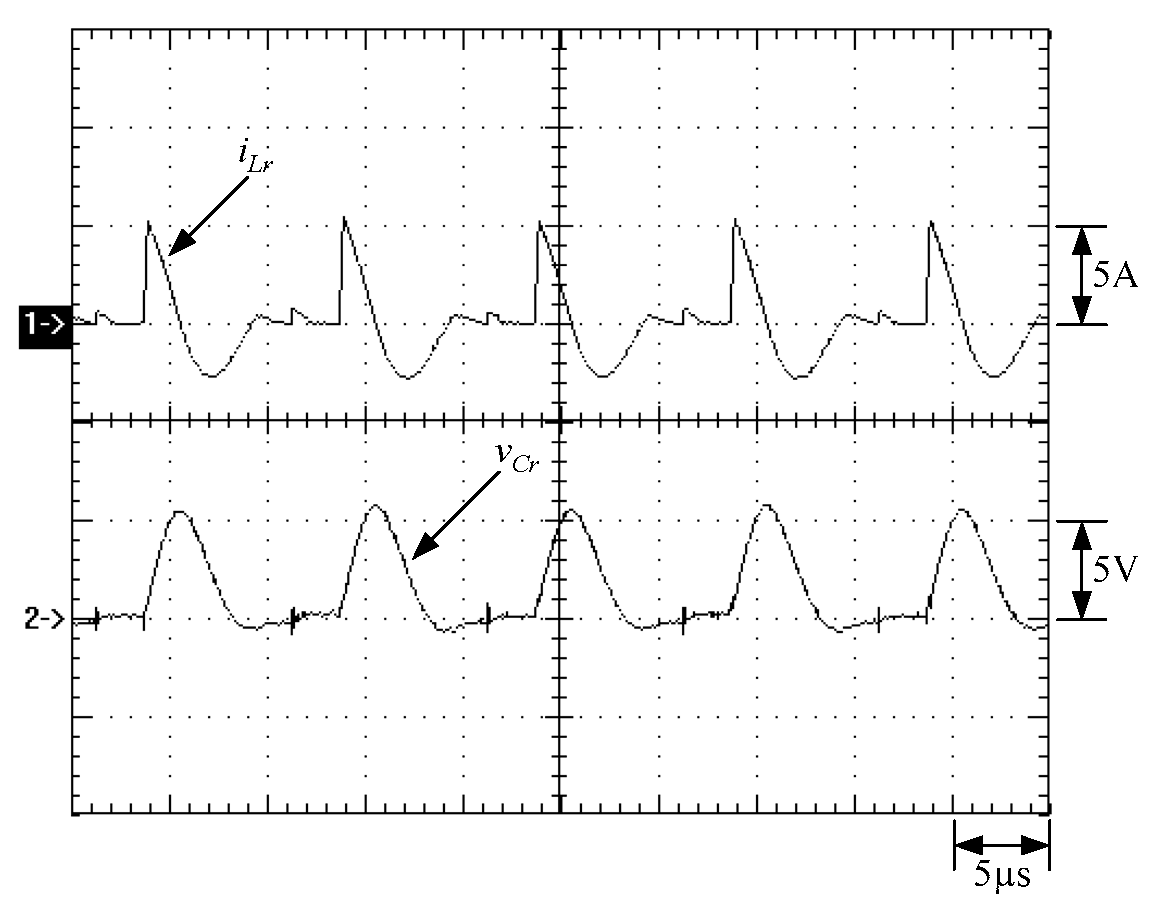
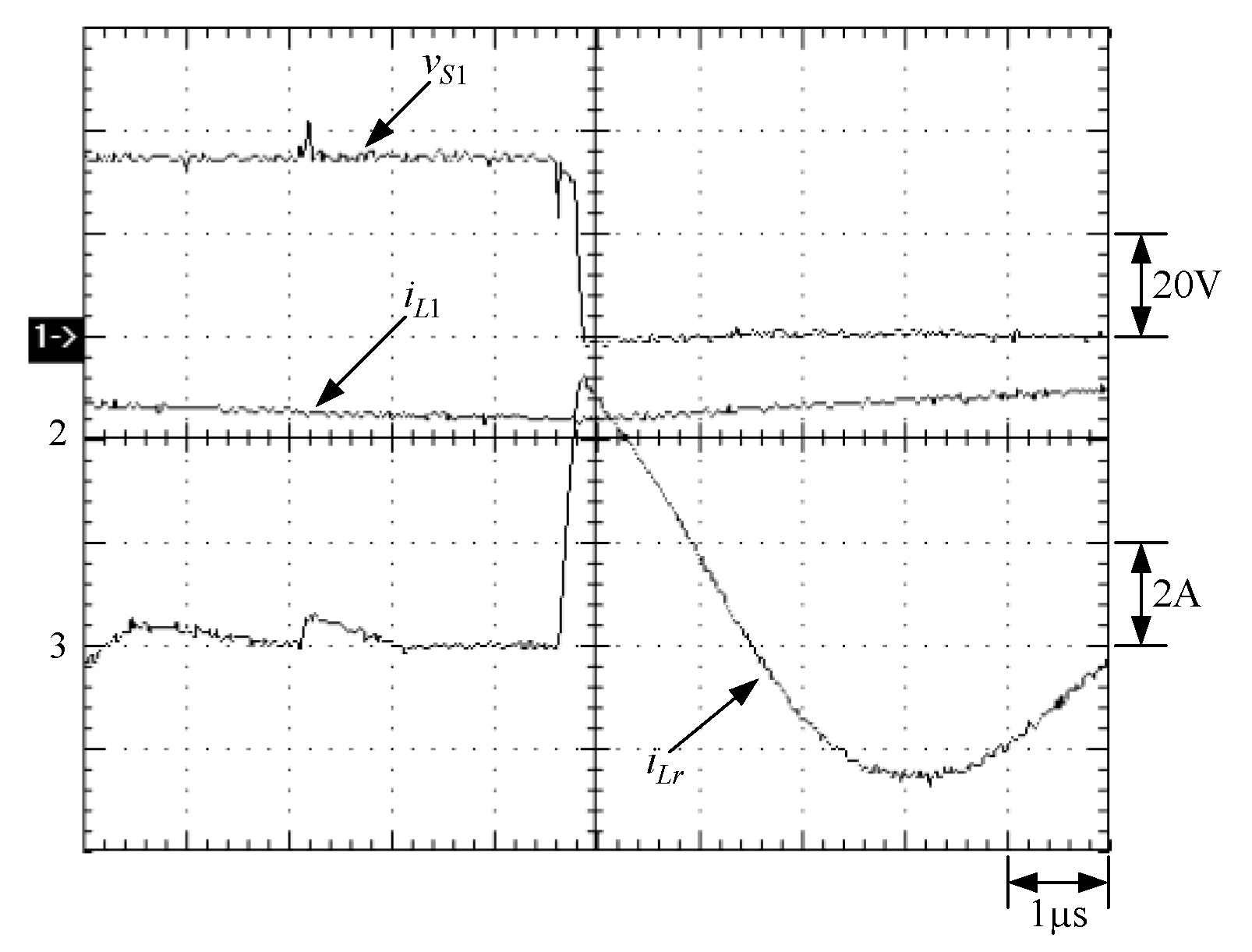
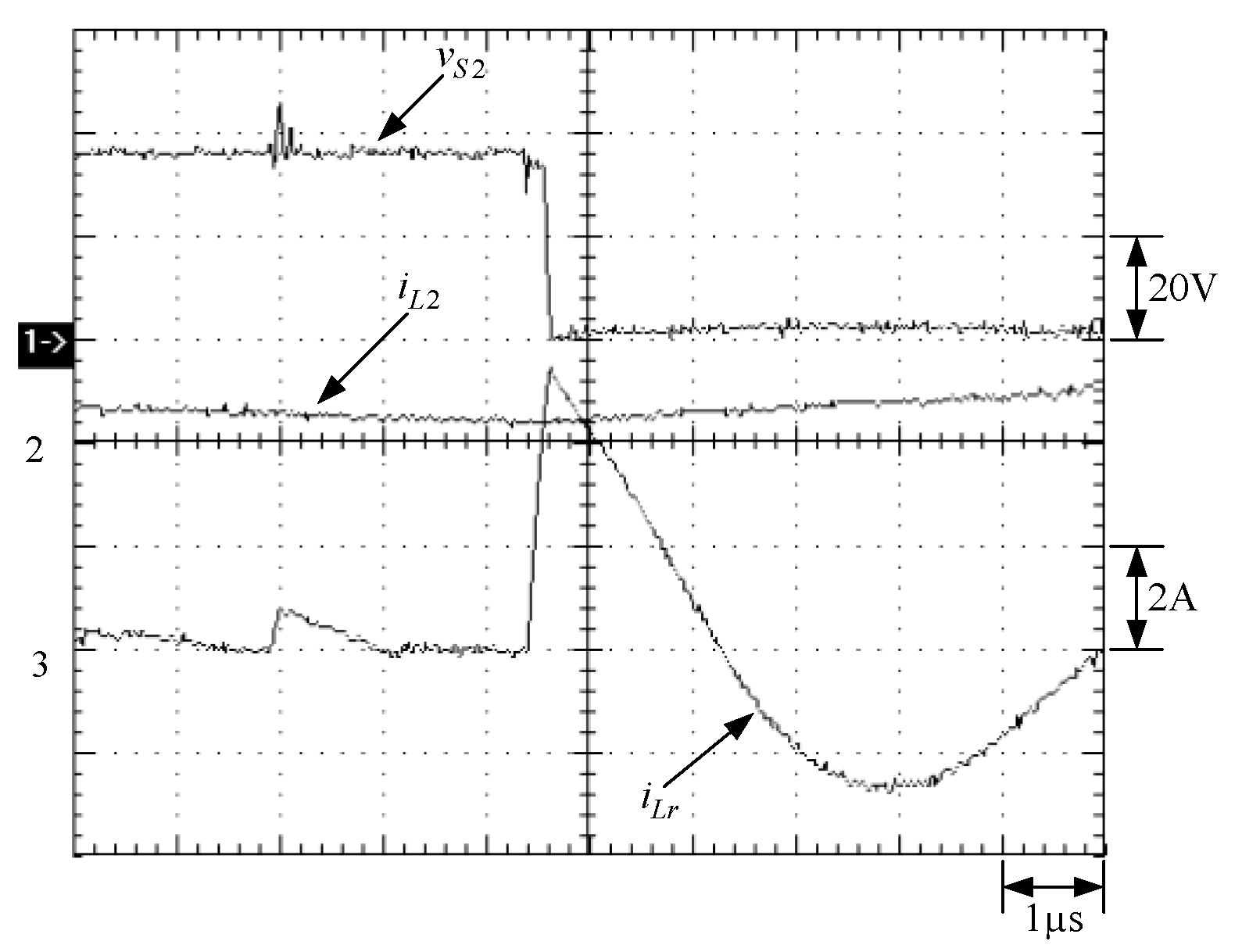
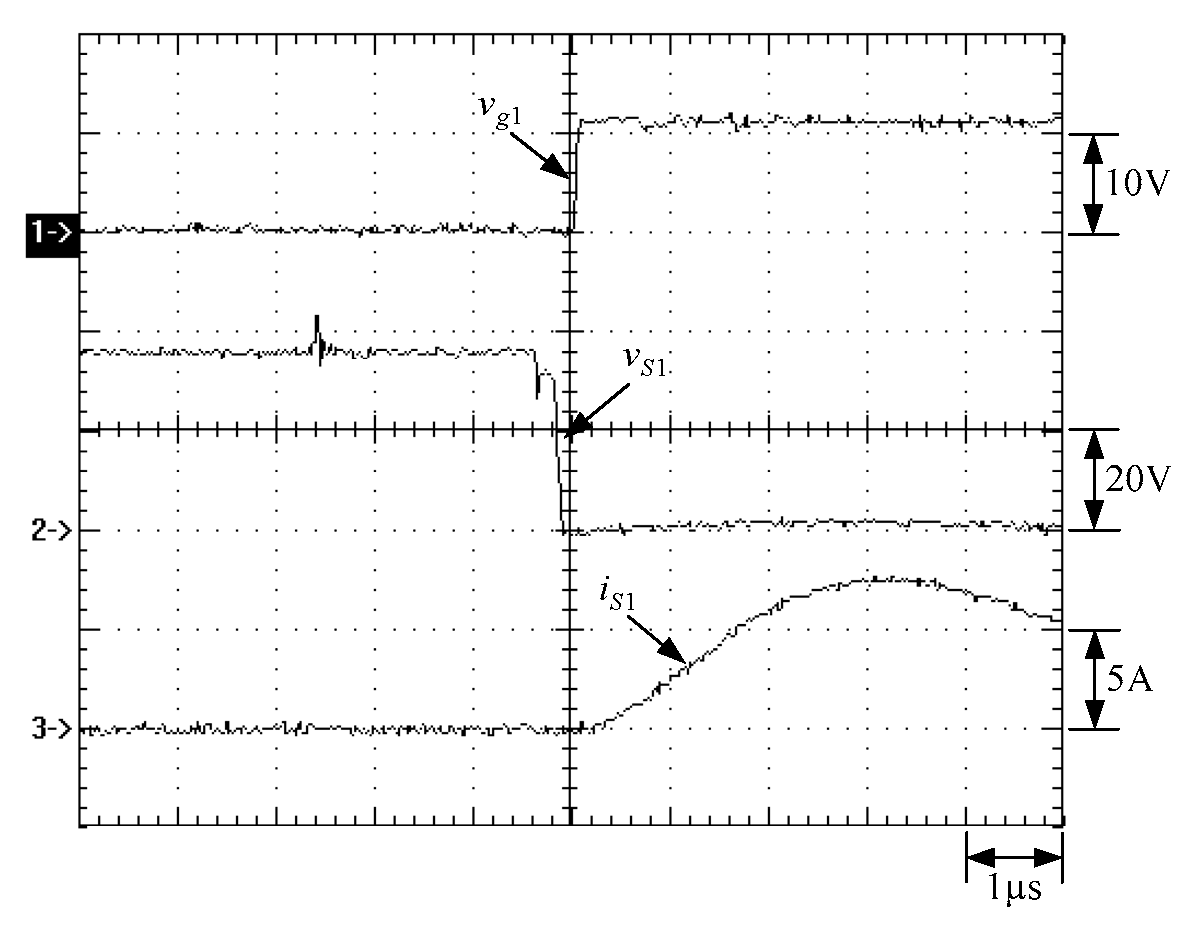
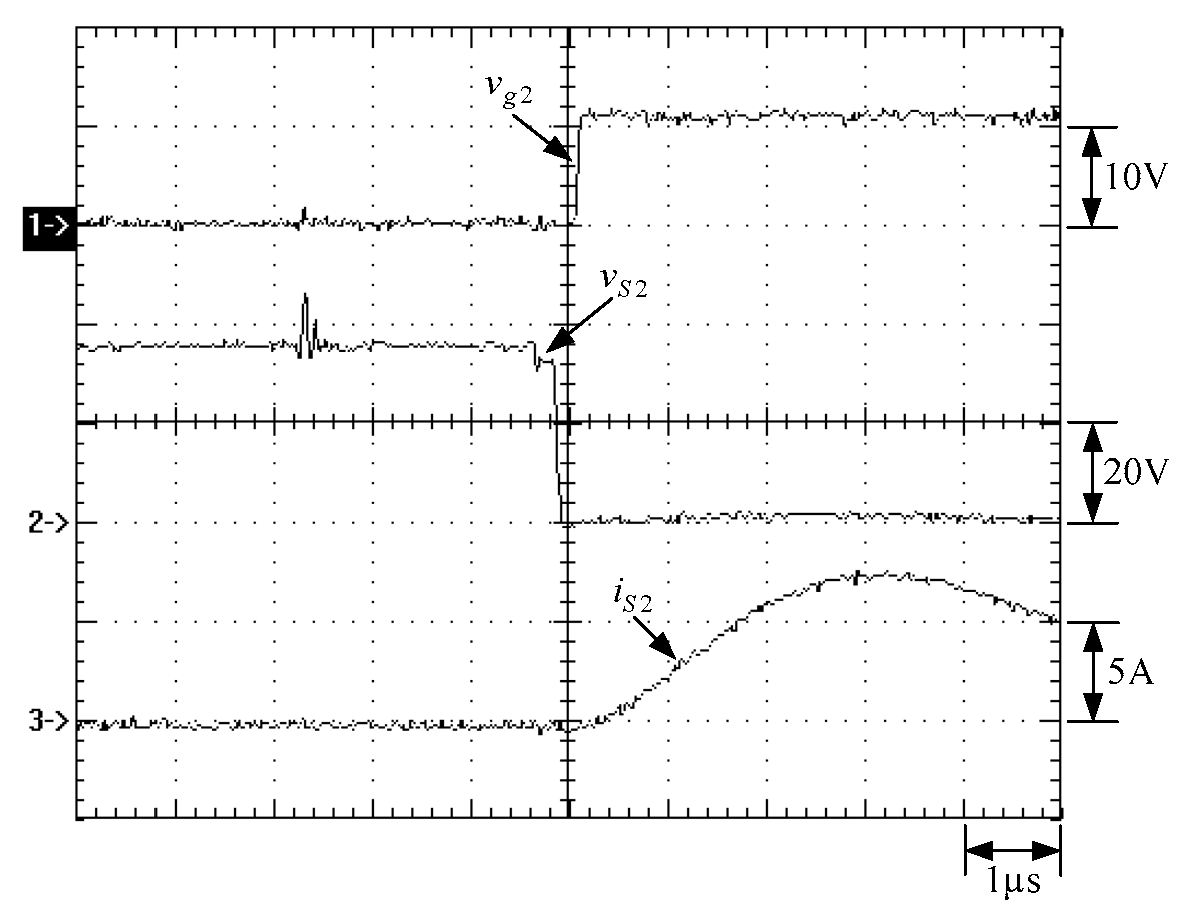
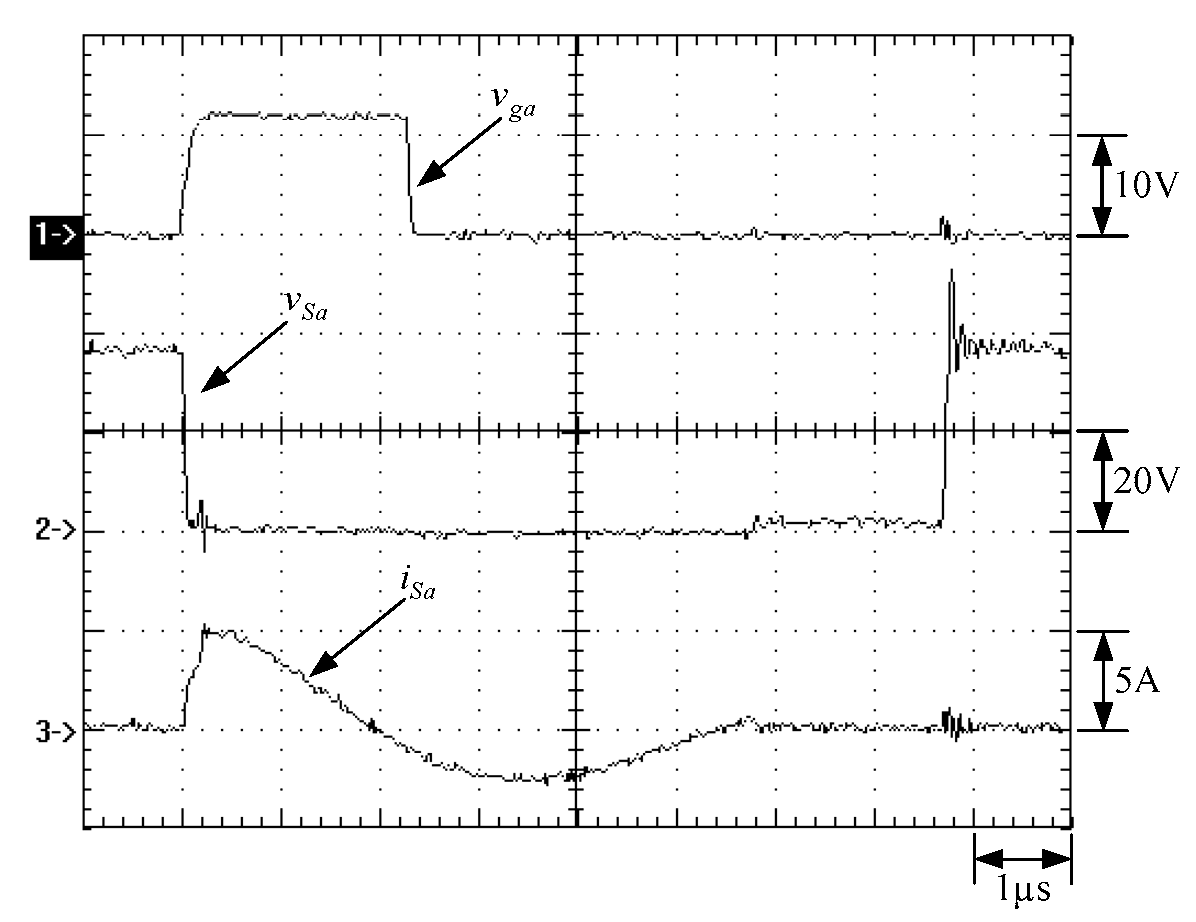
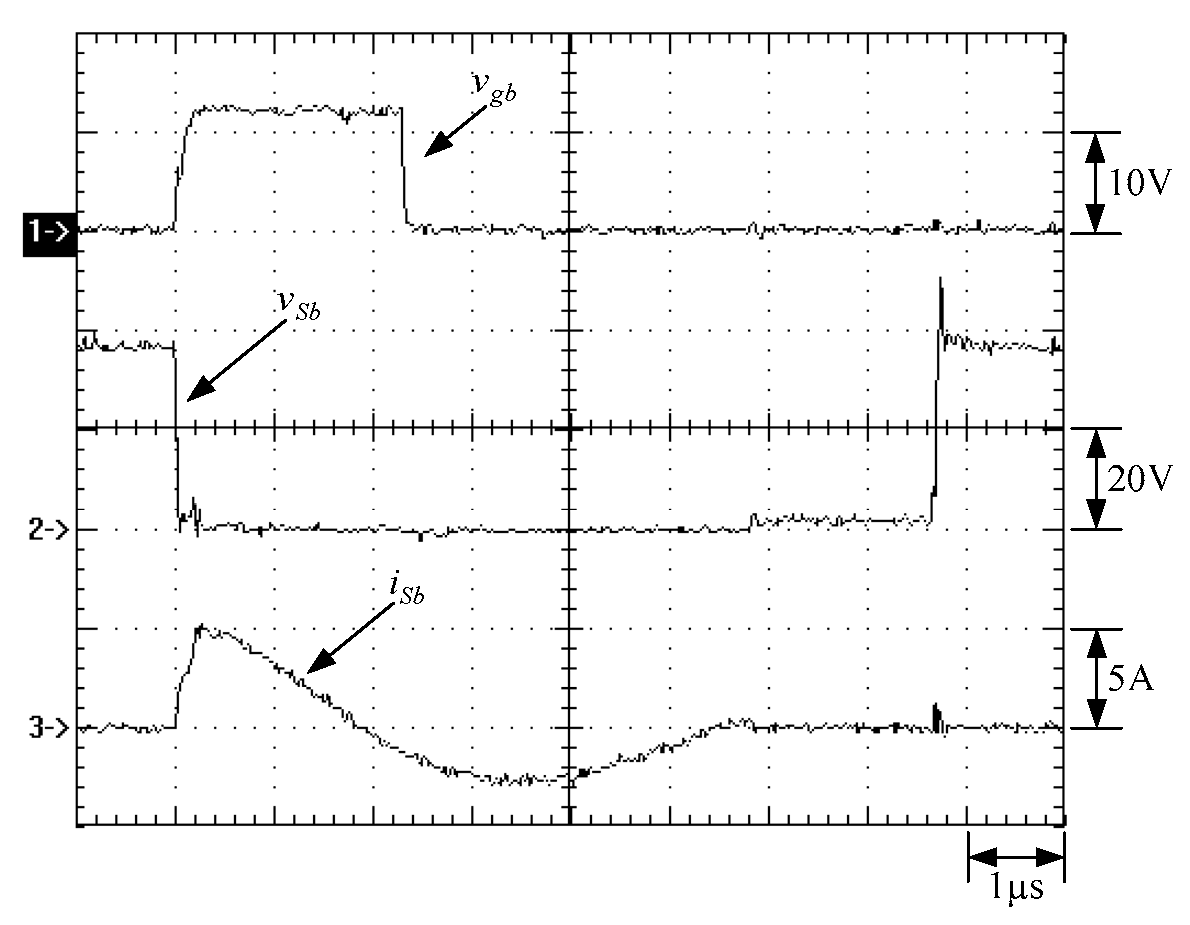
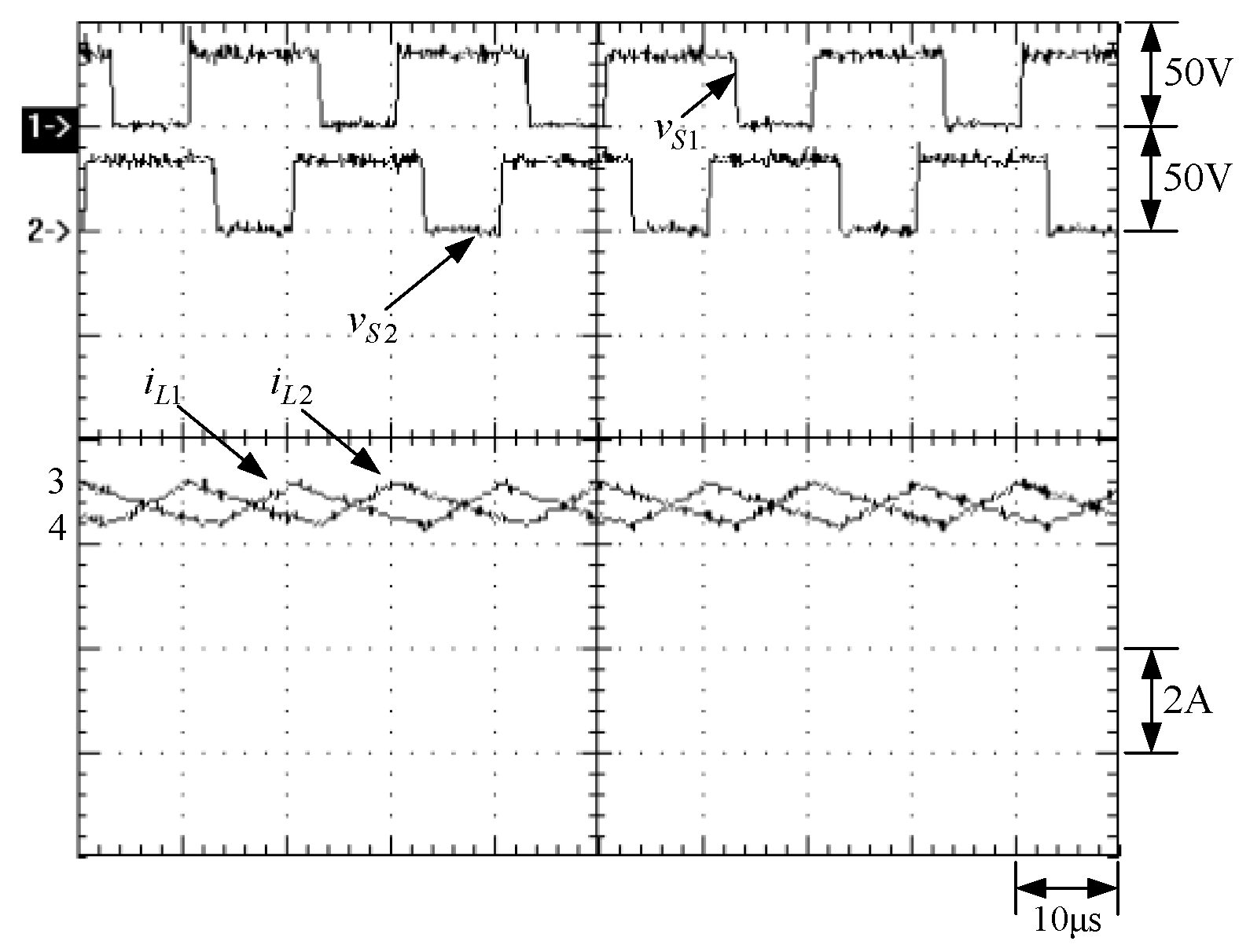
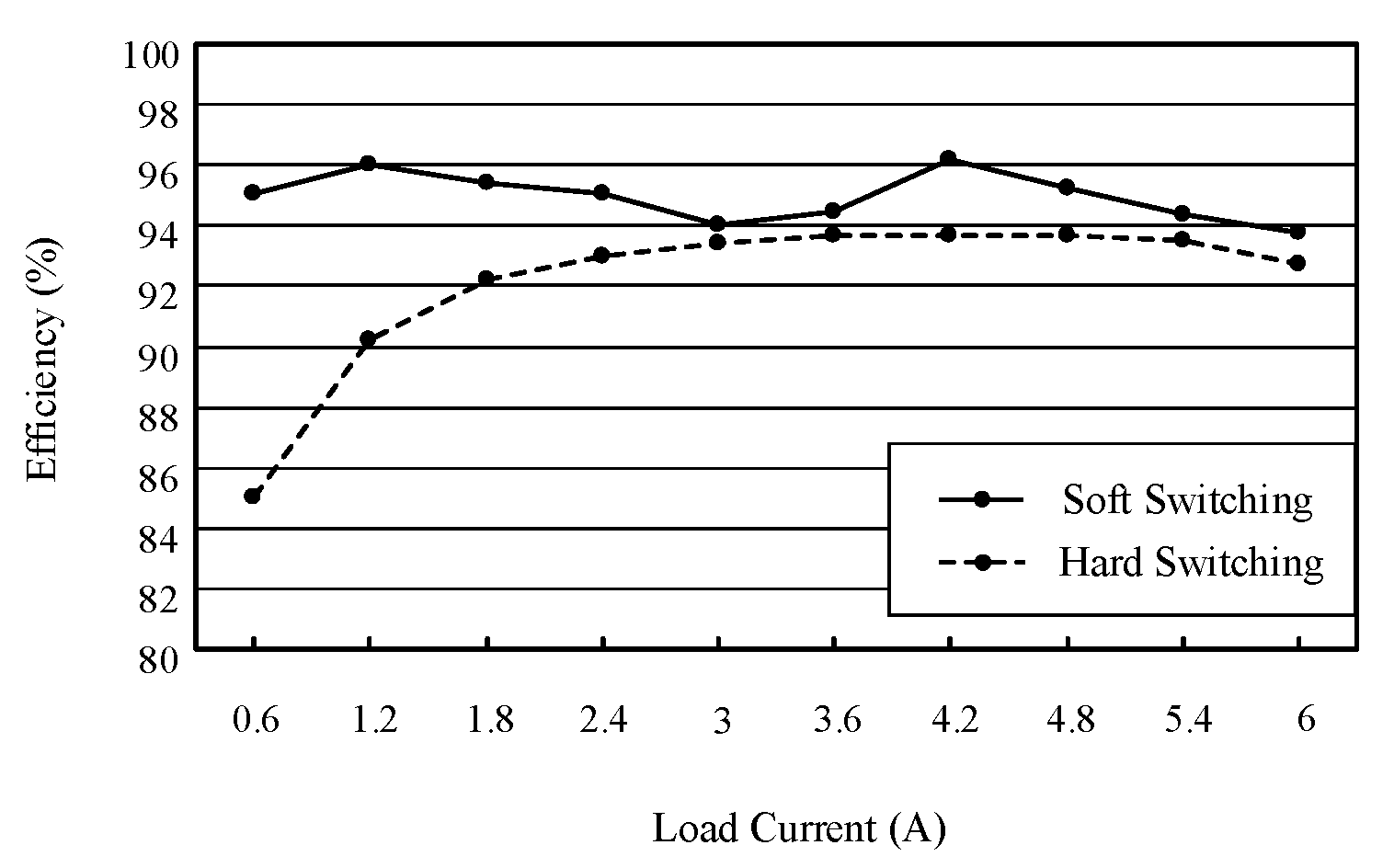
6. Experimental Results
7. Comparisons
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, F.C. High-frequency quasi-resonant converter technologies. Proc. IEEE 1988, 76, 377–390. [Google Scholar] [CrossRef]
- Lee, F.C. High-frequency quasi-resonant and multi-resonant converter technologies. In Proceedings of the IEEE IECON’88, Singapore, 24–28 October 1988; IEEE: New York, NY, USA; Volume 3, pp. 509–521. [Google Scholar]
- Vorperian, V. Quasi-square-wave converters: Topologies and analysis. IEEE Trans. Power Electron. 1988, 3, 183–191. [Google Scholar] [CrossRef]
- Hua, G.; Lee, F.C. Soft-switching techniques in PWM converters. IEEE Trans. Ind. Electron. 1995, 42, 595–603. [Google Scholar] [CrossRef]
- Chuang, Y.C.; Ke, Y.L. A novel high-efficiency battery charger with a buck zero-voltage-switching resonant converter. IEEE Trans. Energy Convers. 2007, 22, 848–854. [Google Scholar] [CrossRef]
- Hui, S.Y.R.; Cheng, K.W.E.; Prakash, S.R.N. A fully soft-switched extended-period quasi-resonant power-factor-correction circuit. IEEE Trans. Power Electron. 1997, 12, 922–930. [Google Scholar] [CrossRef]
- Watson, R.; Lee, F.C.; Hua, G.C. Utilization of an active-clamp circuit to achieve soft switching in flyback converters. IEEE Trans. Power Electron. 1996, 11, 162–169. [Google Scholar] [CrossRef]
- Watson, R.; Hua, G.C.; Lee, F.C. Characterization of an active clamp flyback topology for power factor correction applications. IEEE Trans. Power Electron. 1996, 11, 191–198. [Google Scholar] [CrossRef]
- Lee, Y.S.; Lin, B.T. Adding active clamping and soft switching to boost-flyback single-stage isolated power-factor-corrected power supplies. IEEE Trans. Power Electron. 1997, 12, 1017–1027. [Google Scholar]
- Duarte, C.M.C.; Barbi, I. A family of ZVS-PWM active-clamping DC-to-DC converters: Synthesis, analysis, design, and experimentation. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 698–704. [Google Scholar] [CrossRef]
- Zhao, Q.; Lee, F.C. High-efficiency, high step-up DC-DC converters. IEEE Trans. Power Electron. 2003, 18, 65–73. [Google Scholar] [CrossRef] [Green Version]
- Han, S.K.; Yoon, H.K.; Moon, G.W.; Youn, M.J.; Kim, Y.H.; Lee, K.H. A new active clamping zero-voltage switching PWM current-fed half-bridge converter. IEEE Trans. Power Electron. 2005, 20, 1271–1279. [Google Scholar] [CrossRef]
- Tuomainen, V.; Kyyra, J. Effect of resonant transition on efficiency of forward converter with active clamp and self-driven SRs. IEEE Trans. Power Electron. 2005, 20, 315–323. [Google Scholar] [CrossRef]
- Lo, Y.K.; Lin, J.Y. Active-clamping ZVS flyback converter employing two transformers. IEEE Trans. Power Electron. 2007, 22, 2416–2423. [Google Scholar] [CrossRef]
- Lin, B.R.; Hsieh, F.Y. Soft-switching zeta-flyback converter with a buck-boost type of active clamp. IEEE Trans. Ind. Electron. 2007, 54, 2813–2822. [Google Scholar]
- Chen, M.; Sun, J. Reduced-order averaged modeling of active-clamp converters. IEEE Trans. Power Electron. 2006, 21, 487–494. [Google Scholar] [CrossRef]
- Suryawanshi, H.M.; Ramteke, M.R.; Thakre, K.L.; Borghatem, V.B. Unity- power-factor operation of three-phase AC-DC soft switched converter based on boost active clamp topology in modular approach. IEEE Trans. Power Electron. 2008, 23, 229–236. [Google Scholar] [CrossRef]
- Wu, T.F.; Lai, Y.S.; Hung, J.C.; Chen, Y.M. Boost converter with coupled inductors and buck-boost type of active clamp. IEEE Trans. Ind. Electron. 2008, 55, 154–162. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, J.; Ye, X.; Qian, Z. Analysis and derivations for a family ZVS converter based on a new active clamp ZVS cell. IEEE Trans. Ind. Electron. 2008, 55, 773–781. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, J.; Ye, X.; Qian, Z. Analysis and design for a New ZVS DC-DC converter with active clamping. IEEE Trans. Power Electron. 2006, 21, 1572–1579. [Google Scholar] [CrossRef]
- Hua, G.; Leu, C.S.; Jiang, Y.; Lee, F.C.Y. Novel zero-voltage- transition PWM converters. IEEE Trans. Power Electron. 1994, 9, 213–219. [Google Scholar]
- Tseng, C.J.; Chen, C.L. Novel ZVT-PWM converters with active snubbers. IEEE Trans. Power Electron. 1998, 13, 861–869. [Google Scholar] [CrossRef] [Green Version]
- Cho, J.G.; Baek, J.W.; Yoo, D.W.; Lee, H.S. Reduced conduction loss zero-voltage-transition power factor correction converter with low cost. IEEE Trans. Ind. Electron. 1998, 45, 395–400. [Google Scholar]
- Tseng, C.J.; Chen, C.L. A novel ZVT PWM Cuk power-factor corrector. IEEE Trans. Ind. Electron. 1999, 46, 780–787. [Google Scholar] [CrossRef]
- Gurunathan, R.; Bhat, A.K.S. ZVT boost converter using a ZCS auxiliary circuit. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 889–897. [Google Scholar] [CrossRef]
- Gurunathan, R.; Bhat, A.K.S. A zero-voltage transition boost converter using a zero-voltage switching auxiliary circuit. IEEE Trans. Power Electron. 2002, 17, 658–668. [Google Scholar] [CrossRef]
- Bodur, H.; Bakan, A.F. A new ZVT-ZCT-PWM DC-DC converter. IEEE Trans. Power Electron. 2004, 19, 676–684. [Google Scholar] [CrossRef]
- Jain, N.; Jain, P.K.; Joos, G.A. Zero voltage transition boost converter employing a soft switching auxiliary circuit with reduced conduction losses. IEEE Trans. Power Electron. 2004, 19, 130–139. [Google Scholar] [CrossRef]
- Martins, M.L.D.S.; Hey, H.L. Self-commutated auxiliary circuit ZVT PWM converters. IEEE Trans. Power Electron. 2004, 19, 1435–1445. [Google Scholar] [CrossRef]
- Schuch, L.; Rech, C.; Hey, H.L.; Pinheiro, J.R. Integrated ZVT auxiliary commutation circuit for input stage of double-conversion UPSs. IEEE Trans. Power Electron. 2004, 19, 1486–1497. [Google Scholar] [CrossRef]
- Yang, S.P.; Lin, J.L.; Chen, S.J. A novel ZCZVT forward converter with synchronous rectification. IEEE Trans. Power Electron. 2006, 21, 912–922. [Google Scholar] [CrossRef]
- Chuang, Y.C.; Ke, Y.L. High-efficiency and low-stress ZVT-PWM DC-to-DC converter for battery charger. IEEE Trans. Ind. Electron. 2008, 55, 3030–3037. [Google Scholar] [CrossRef]
- Huang, W.; Gao, X.; Bassan, S.; Moschopoulos, G. Novel dual auxiliary circuits for ZVT-PWM converters. Can. J. Electr. Comput. Eng. 2008, 33, 153–160. [Google Scholar] [CrossRef]
- Carlos Marcelo de Oliveira Stein; Hey, H.L. A true ZCZVT commutation cell for PWM converters. IEEE Trans. Power Electron. 2000, 15, 185–193. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Zhang, B.; Deng, W.H. Study on novel ZVZCT PWM DC-DC converter family. In Proceedings of the IEEE IPEMC’04, Xi’an, China, 14–16 August 2004; IEEE: New York, NY, USA, 2004; Volume 1, pp. 154–159. [Google Scholar]
- Cho, J.G.; Baek, J.W.; Rim, G.H.; Kang, I. Novel zero-voltage-transition PWM multiphase converters. IEEE Trans. Power Electron. 1998, 13, 152–159. [Google Scholar]
- Tseng, S.Y.; Shiang, J.Z.; Chang, H.H.; Jwo, W.S.; Hsieh, C.T. A novel turn-on/off snubber for interleaved boost converters. In Proceedings of the IEEE PESC’07, Orlando, FL, USA, 17–21 June 2007; IEEE: New York, NY, USA, 2007; pp. 2341–2347. [Google Scholar]
- Hwu, K.I.; Tu, W.C.; Hon, M.J. A dimmable LED driver based on current balancing transformer with magnetizing energy recycling considered. IEEE J. Disp. Technol. 2014, 10, 388–395. [Google Scholar] [CrossRef]
- Hwu, K.I.; Jiang, W.Z.; Hsiao, C.W. Dimmable LED driver based on twin-bus converter and differential-mode transformer. IEEE J. Disp. Technol. 2016, 12, 1122–1129. [Google Scholar] [CrossRef]
- Qu, X.; Wong, S.C.; Tse, C.K. An improved LCLC current-source-output multistring LED driver with capacitive current balancing. IEEE Trans. Power Electron. 2015, 30, 5783–5791. [Google Scholar] [CrossRef]
- Hwu, K.I.; Tai, Y.K.; Tu, H.H. Implementation of a dimmable LED driver with extendable parallel structure and capacitive current sharing. Appl. Sci. 2019, 9, 5177. [Google Scholar] [CrossRef] [Green Version]
- Chiub, C.L.; Chen, K.H. A high accuracy current-balanced control technique for LED backlight. In Proceedings of the IEEE PESC’08, Rhodes, Greece, 15–19 June 2008; IEEE: New York, NY, USA, 2008; pp. 4202–4206. [Google Scholar]
- Yu, W.; Lai, J.S.; Ma, H.; Zheng, C. High-efficiency dc-dc converter with twin bus for dimmable LED lighting. IEEE Trans. Power Electron. 2011, 26, 2095–2100. [Google Scholar] [CrossRef]
- Lohaus, L.; Liao, L.; Strache, S.; Wunderlich, R.; Heinen, S. Energy efficient current control technique for driving high power LEDs. In Proceedings of the VDE PRIME’12, Aachen, Germany, 12–15 June 2012; pp. 1–4. [Google Scholar]
- Li, S.N.; Zhong, W.X.; Chen, W.; Hui, S.Y.R. Novel self-configurable current-mirror techniques for reducing current imbalance in parallel light-emitting diode (LED) strings. IEEE Trans. Power Electron. 2012, 27, 2153–2162. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.C.; Chen, C.L. A novel primary-side regulation scheme for single-stage high-power-factor ac-dc LED driving circuit. IEEE Trans. Ind. Electron. 2013, 60, 4978–4986. [Google Scholar] [CrossRef]
- Hwu, K.I.; Jenn, J.S.; Wen, Z.J. Interleaved boost converter with ZVT-ZCT for main switches and ZCS for auxiliary switch. Appl. Sci. 2019, 10, 2033. [Google Scholar] [CrossRef] [Green Version]
- Erickson, R.W. Fundamentals of Power Electronics, 2nd ed.; Kluwer Academic Publishers: Norwell, MA, USA, 2001. [Google Scholar]






| System Parameters | Specifications |
|---|---|
| Operating Mode | CCM |
| Input Voltage | 24 V |
| Switching Frequency | 50 kHz |
| Output Voltage | 36 V |
| Rated Output Power/Current | 216W/6A |
| Min. Output Power/Current | 21.6W/0.6A |
| Comparisons | Resonant Count | Soft Switching Type for Main Switches | Overall Efficiency | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Turn-On | Turn-Off | ||||||||||
| No. | ZVS | ZVT | ZCS | ZCT | ZVS | ZVT | ZCS | ZCT | Min. | Max. | |
| [37] | 5 | * | * | 84% | 90% | ||||||
| [47] | 7 | * | * | 91% | 93% | ||||||
| Proposed | 5 | * | 94% | 96% | |||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yau, Y.-T.; Hwu, K.-I.; Jiang, W.-Z. Two-Phase Interleaved Boost Converter with ZVT Turn-On for Main Switches and ZCS Turn-Off for Auxiliary Switches Based on One Resonant Loop. Appl. Sci. 2020, 10, 3881. https://doi.org/10.3390/app10113881
Yau Y-T, Hwu K-I, Jiang W-Z. Two-Phase Interleaved Boost Converter with ZVT Turn-On for Main Switches and ZCS Turn-Off for Auxiliary Switches Based on One Resonant Loop. Applied Sciences. 2020; 10(11):3881. https://doi.org/10.3390/app10113881
Chicago/Turabian StyleYau, Yeu-Torng, Kuo-Ing Hwu, and Wen-Zhuang Jiang. 2020. "Two-Phase Interleaved Boost Converter with ZVT Turn-On for Main Switches and ZCS Turn-Off for Auxiliary Switches Based on One Resonant Loop" Applied Sciences 10, no. 11: 3881. https://doi.org/10.3390/app10113881
APA StyleYau, Y.-T., Hwu, K.-I., & Jiang, W.-Z. (2020). Two-Phase Interleaved Boost Converter with ZVT Turn-On for Main Switches and ZCS Turn-Off for Auxiliary Switches Based on One Resonant Loop. Applied Sciences, 10(11), 3881. https://doi.org/10.3390/app10113881