Weak Signal Detection Method Based on the Coupled Lorenz System and Its Application in Rolling Bearing Fault Diagnosis
Abstract
:1. Introduction
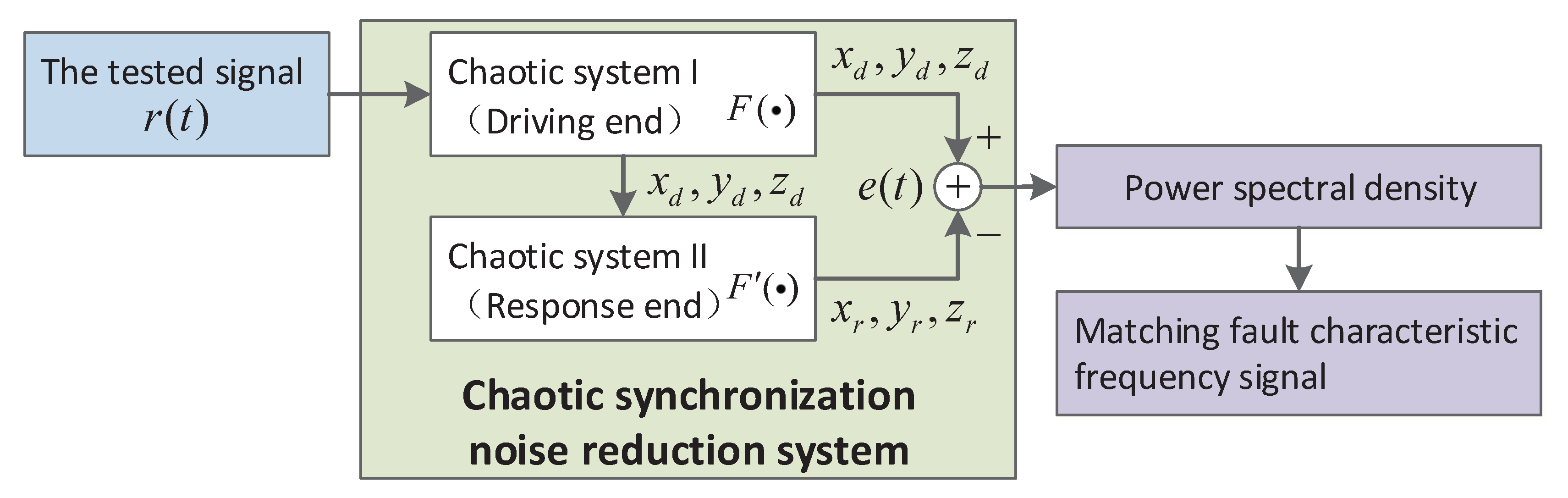
2. Noise Reduction Mechanism and Frequency Estimation Method Based on the Coupled Lorenz System
2.1. Theoretical Model and Working Mechanism
2.2. Selection and Configuration of Chaotic Model
2.3. Noise Reduction Model Based on the Coupled Lorenz System
3. Simulation Analysis and Method Comparison
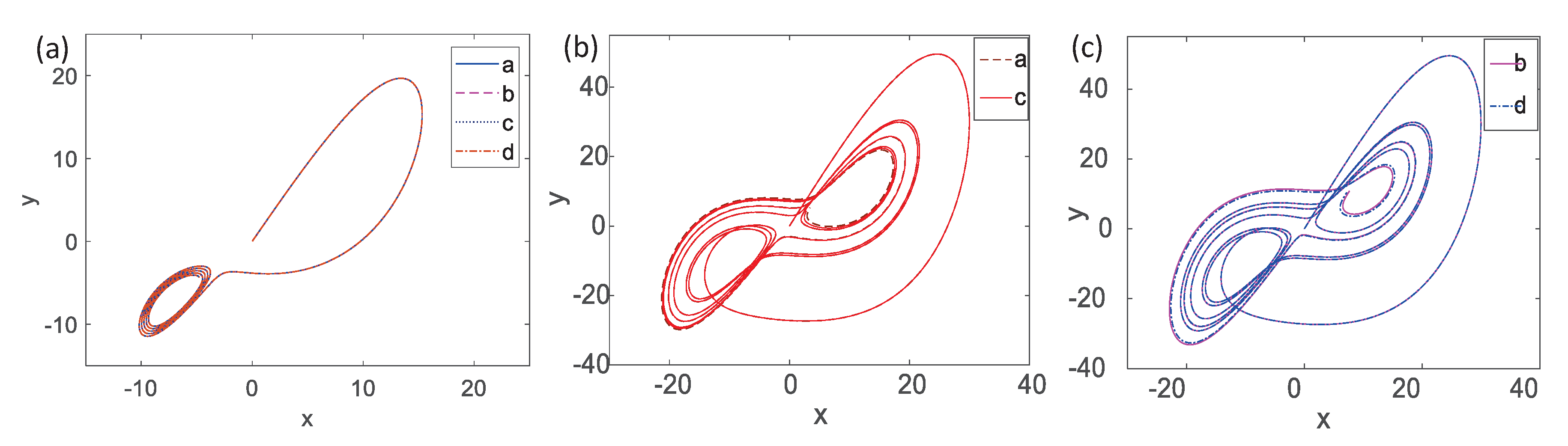
3.1. Simulation Analysis of the Coupled Lorenz System
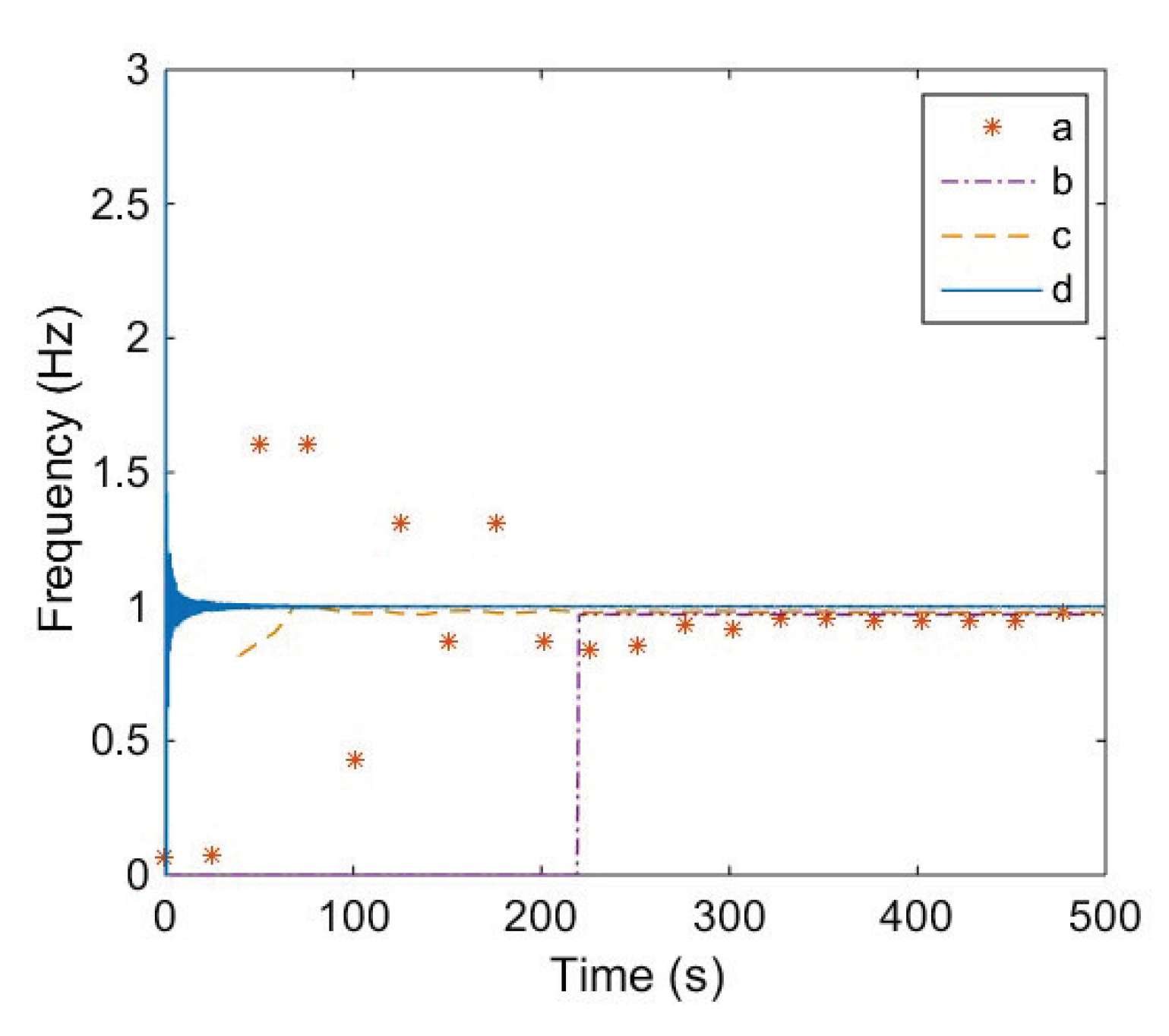
3.2. Effective Range of Frequency Detection
3.3. Comparison with Existing Chaotic Detection Methods
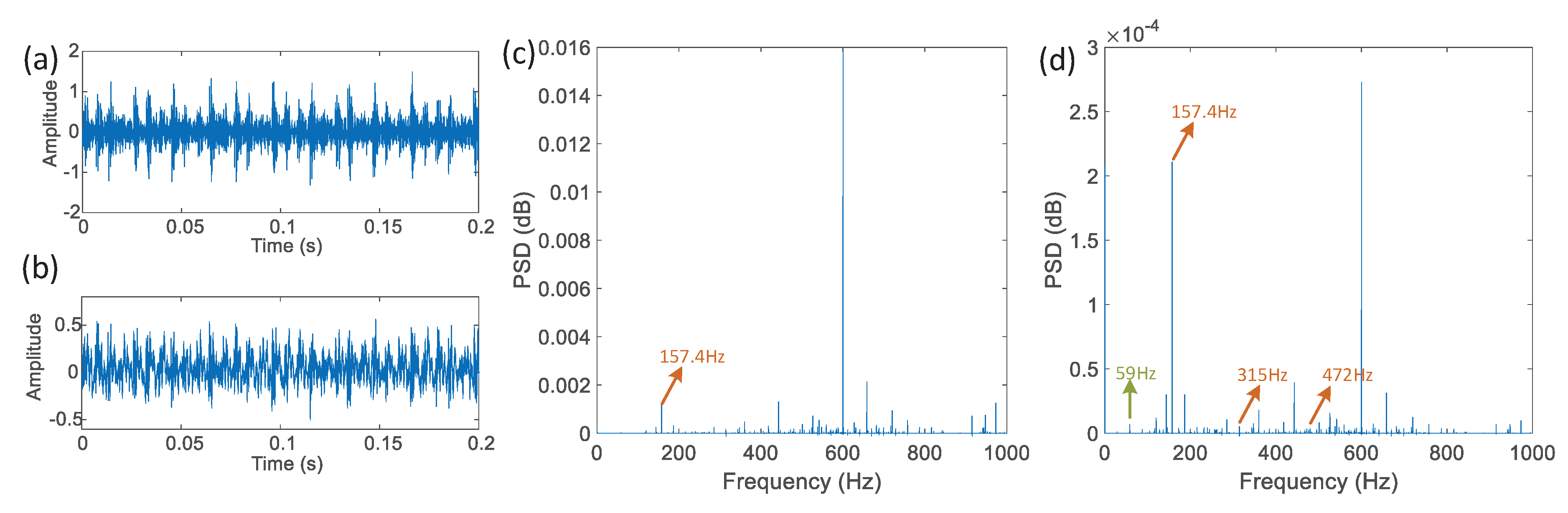
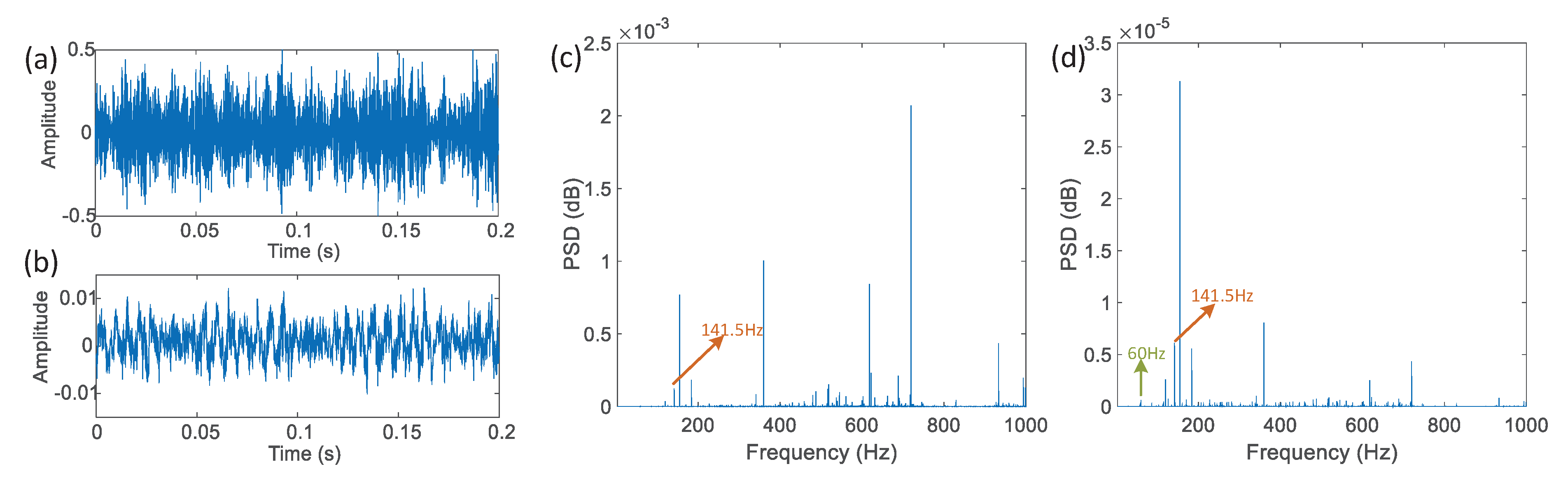
4. Application of the New Method in Fault Diagnosis of Rolling Bearing
4.1. Fault Mechanism and Characteristic Frequency
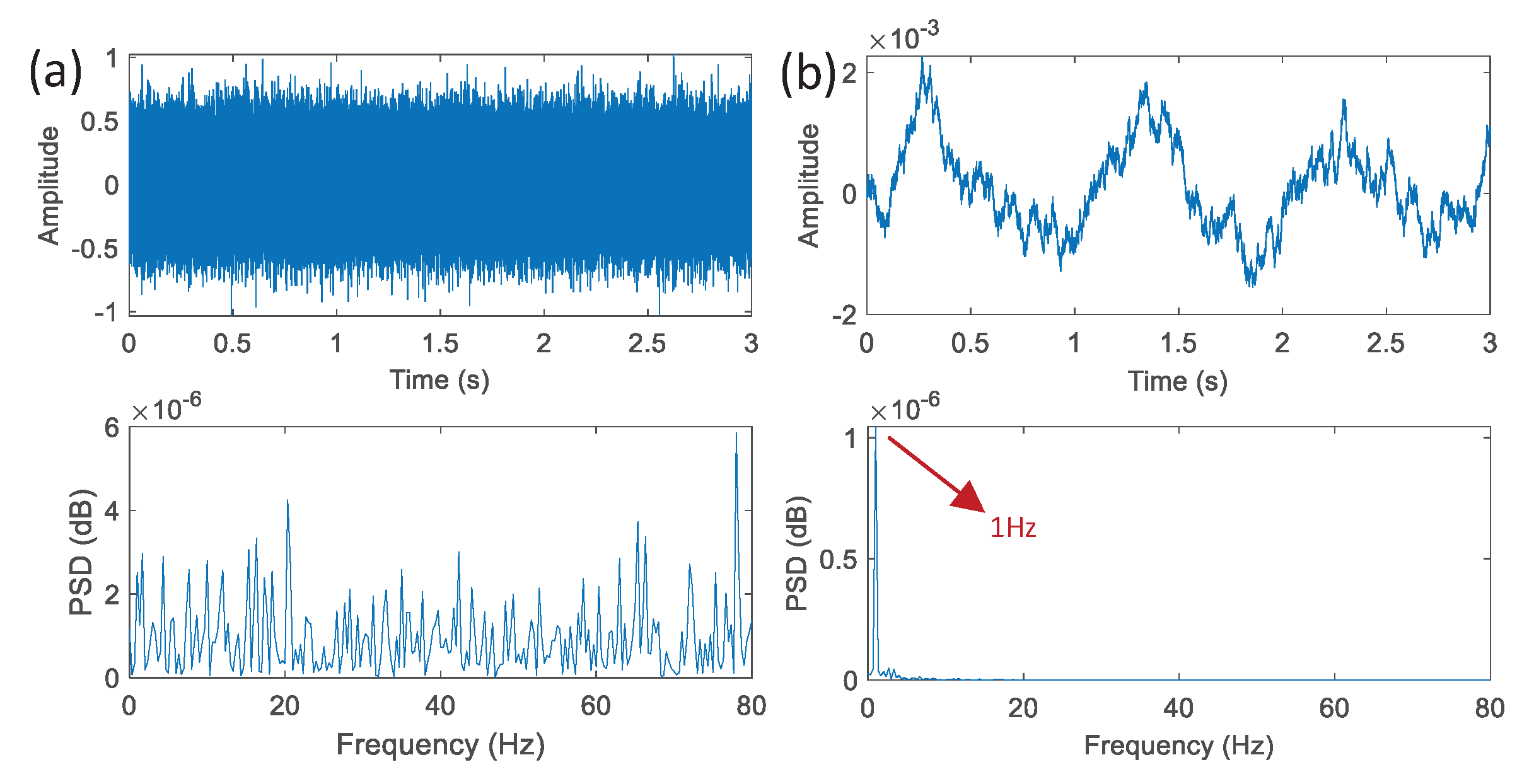
4.2. Experimental Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, Y.; Zhang, T.; Luo, Z.; Sun, K. A Novel Rolling Bearing Fault Diagnosis and Severity Analysis Method. Appl. Sci. 2019, 9, 2356. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y. A New Family of Model-Based Impulsive Wavelets and Their Sparse Representation for Rolling Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 2716–2726. [Google Scholar] [CrossRef]
- Wang, G.; He, S. A quantitative study on detection and estimation of weak signals by using chaotic Duffing oscillators. IEEE Trans. Circuits Syst. I-Regul. Pap. 2003, 50, 945–953. [Google Scholar] [CrossRef]
- Wang, G.Y.; Chen, D.J.; Lin, J.Y.; Chen, X. The application of chaotic oscillators to weak signal detection. IEEE Trans. Ind. Electron. 1999, 46, 440–444. [Google Scholar] [CrossRef]
- Zhang, S.; Rui, G.S. Chaotic detector for BPSK signals in very low SNR conditions. Int. J. Bifurc. Chaos 2012, 22, 1250144. [Google Scholar] [CrossRef]
- Xiang, X.; Shi, B. Weak signal detection based on the information fusion and chaotic oscillator. Chaos 2010, 20, 013104. [Google Scholar] [CrossRef]
- Faber, J.; Bozovic, D. Noise-induced chaos and signal detection by the nonisochronous Hopf oscillator. Chaos 2019, 29, 043132. [Google Scholar] [CrossRef]
- Rashtchi, V.; Nourazar, M. Detecting the stateof the duffing oscillator by phase space trajectory autocorrelation. Int. J. Bifurc. Chaos 2013, 23, 1350065. [Google Scholar] [CrossRef]
- Cong, C.; Li, X.K.; Song, Y. A method of detecting line spectrum of ship-radiated noise using a new intermittent chaotic oscillator. Acta Phys. Sin. 2014, 63, 064301. [Google Scholar]
- Li, G.; Zhang, B. Novel method for detecting weak signal with unknown frequency based on duffing oscillator. Yi Qi Yi Biao Xue Bao/Chin. J. Sci. Instrum. 2017, 38, 181–189. [Google Scholar]
- Zhao, Z.; Wang, F.L.; Jia, M.X.; Wang, S. Intermittent-Chaos-and-Cepstrum-Analysis-Based Early Fault Detection on Shuttle Valve of Hydraulic Tube Tester. IEEE Trans. Ind. Electron. 2009, 56, 2764–2770. [Google Scholar] [CrossRef]
- Rashtchi, V.; Aghmashe, R.; Ojaghi, M. Application of Duffing Oscillators to Dynamic Eccentricity Fault Detection in Squirrel Cage Induction Motors. Int. Rev. Electr. Eng. 2011, 6, 1196–1203. [Google Scholar]
- Bai, C.; Ren, H.P.; Grebogi, C.; Baptista, M.S. Chaos-Based Underwater Communication With Arbitrary Transducers and Bandwidth. Appl. Sci. 2018, 8, 162. [Google Scholar] [CrossRef] [Green Version]
- Acho, L. A Chaotic Secure Communication System Design Based on Iterative Learning Control Theory. Appl. Sci. 2016, 6, 311. [Google Scholar] [CrossRef] [Green Version]
- Ouannas, A.; Debbouche, N.; Wang, X.; Pham, V.T.; Zehrour, O. Secure Multiple-Input Multiple-Output Communications Based on F-M Synchronization of Fractional-Order Chaotic Systems with Non-Identical Dimensions and Orders. Appl. Sci. 2018, 8, 1746. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.K.; Chao, P.C.P. Trajectory Tracking between Josephson Junction and Classical Chaotic System via Iterative Learning Control. Appl. Sci. 2018, 8, 1285. [Google Scholar] [CrossRef] [Green Version]
- Hajipour, A.; Tavakoli, H. Dynamic Analysis and Adaptive Sliding Mode Controller for a Chaotic Fractional Incommensurate Order Financial System. Int. J. Bifurc. Chaos 2017, 27, 1750198. [Google Scholar] [CrossRef]
- Li, G.Z.; Zhang, B. A Novel Weak Signal Detection Method via Chaotic Synchronization Using Chua’s Circuit. IEEE Trans. Ind. Electron. 2017, 64, 2255–2265. [Google Scholar] [CrossRef]
- Cheng, C.K.; Chao, P.C.P. Chaotic Synchronizing Systems with Zero Time Delay and Free Couple via Iterative Learning Control. Appl. Sci. 2018, 8, 177. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Designing chaotic models. J. Atmos. Sci. 2005, 62, 1574–1587. [Google Scholar] [CrossRef]
- Salarieh, H.; Shahrokhi, M. Adaptive synchronization of two different chaotic systems with time varying unknown parameters. Chaos Solitons Fractals 2008, 37, 125–136. [Google Scholar] [CrossRef]
- Carroll, T.L.; Pecora, L.M. Synchronizing chaotic circuits. IEEE Trans. Circuits Syst. 1991, 38, 453–456. [Google Scholar] [CrossRef] [Green Version]
- Shevitz, D.; Paden, B. Lyapunov stability theory of nonsmooth systems. IEEE Trans. Autom. Control 1994, 39, 1910–1914. [Google Scholar] [CrossRef] [Green Version]




| Type | Mode | Measurable Range | Measurable Parameters | Time |
|---|---|---|---|---|
| Method I [8] | Duffing oscillator | A | ||
| Method II [10] | Duffing oscillator array | |||
| Method III [11] | Duffing oscillator array | |||
| Method IV [18] | Chua’s circuit | |||
| Proposed method | Lorenz system | S | T |
| Inside Diameter | Outside Diameter | Thickness | Ball Diameter | Pitch Diameter |
|---|---|---|---|---|
| 0.9843 | 2.0472 | 0.5906 | 0.3126 | 1.537 |
| Inner Ring | Outer Ring | Rolling Element |
|---|---|---|
| 5.4152 | 3.5848 | 4.7135 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Tan, N.; Li, X. Weak Signal Detection Method Based on the Coupled Lorenz System and Its Application in Rolling Bearing Fault Diagnosis. Appl. Sci. 2020, 10, 4086. https://doi.org/10.3390/app10124086
Li G, Tan N, Li X. Weak Signal Detection Method Based on the Coupled Lorenz System and Its Application in Rolling Bearing Fault Diagnosis. Applied Sciences. 2020; 10(12):4086. https://doi.org/10.3390/app10124086
Chicago/Turabian StyleLi, Guozheng, Nanlin Tan, and Xiang Li. 2020. "Weak Signal Detection Method Based on the Coupled Lorenz System and Its Application in Rolling Bearing Fault Diagnosis" Applied Sciences 10, no. 12: 4086. https://doi.org/10.3390/app10124086





