Fundamental Frequency Suppression for the Detection of Broken Bar in Induction Motors at Low Slip and Frequency †
Abstract
:1. Introduction
2. Theoretical Background
2.1. BRB Detection
2.2. Genetic Algorithm
3. Methodology
4. Experimental Setup
5. Results and Discussion
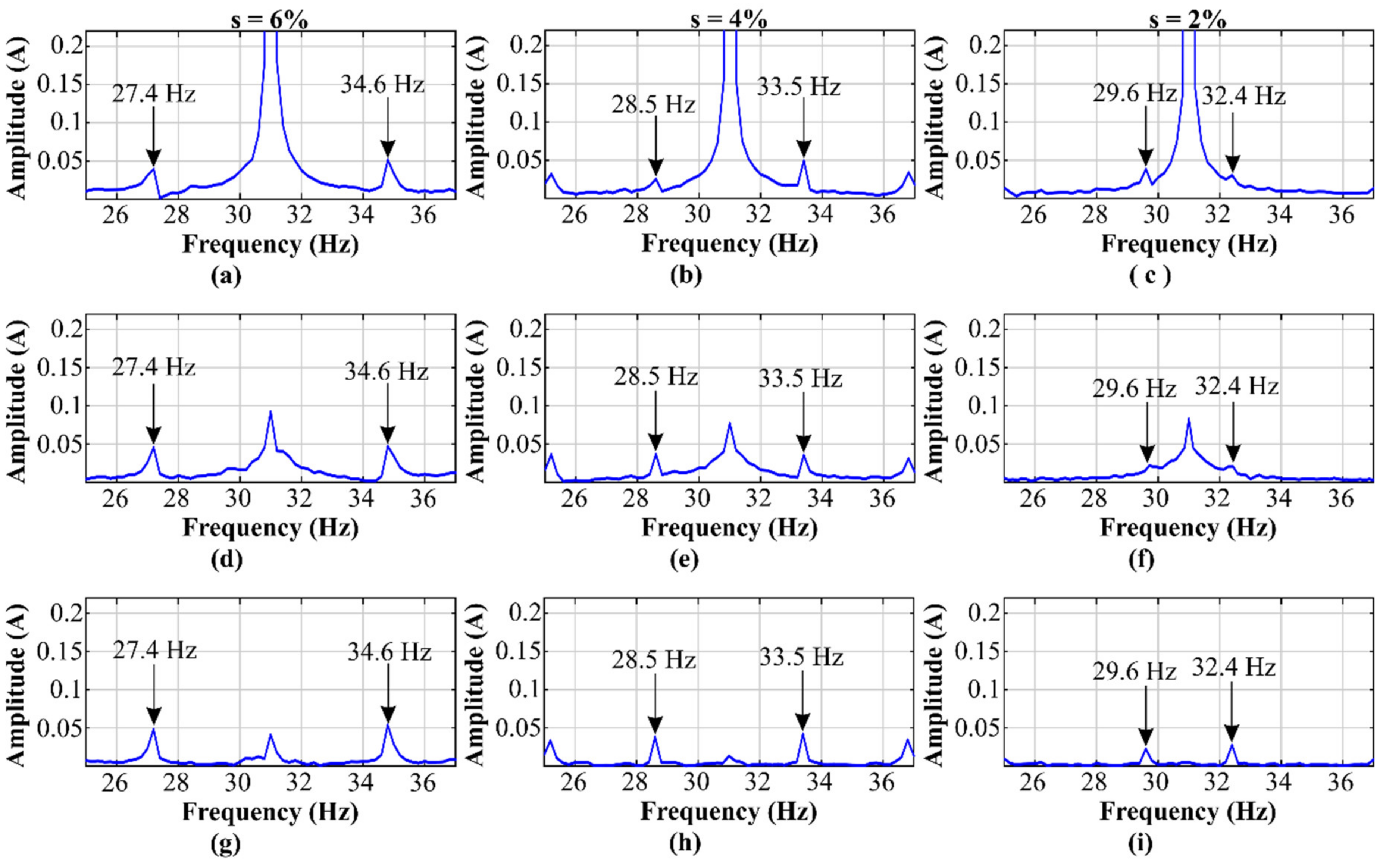
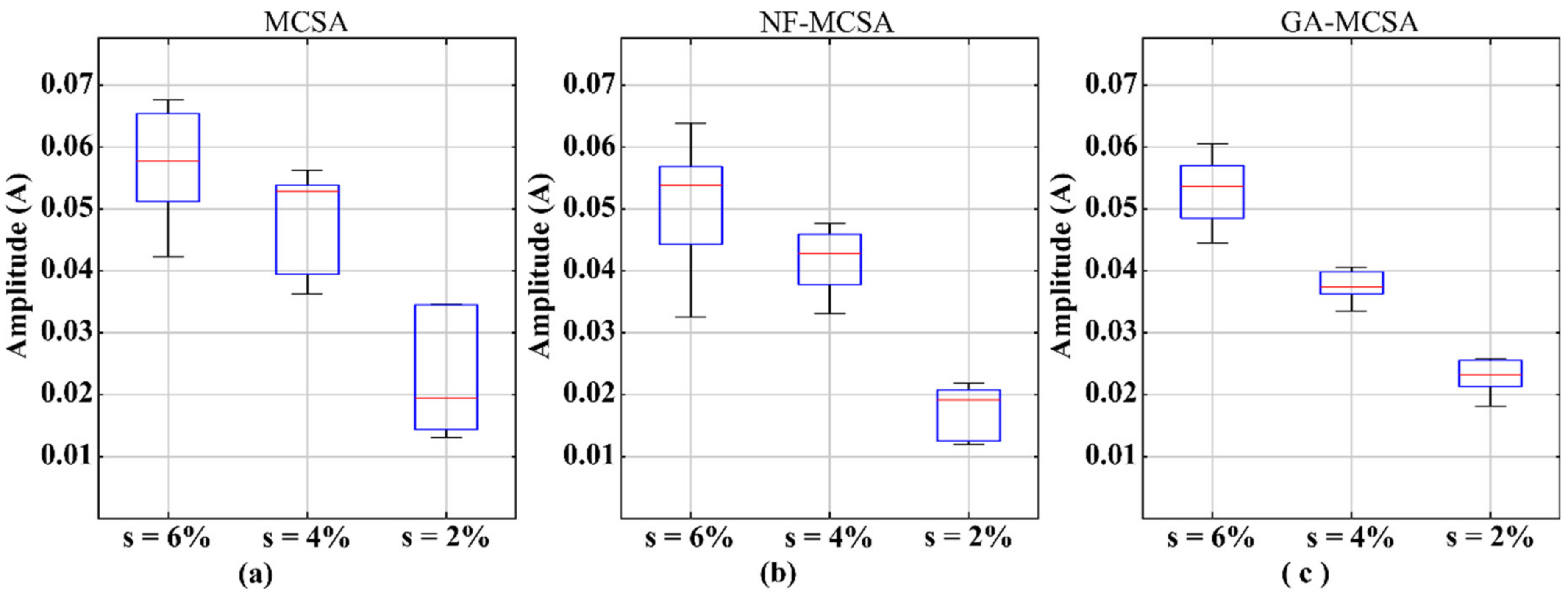
5.1. Results for the IM Operating at 31 Hz
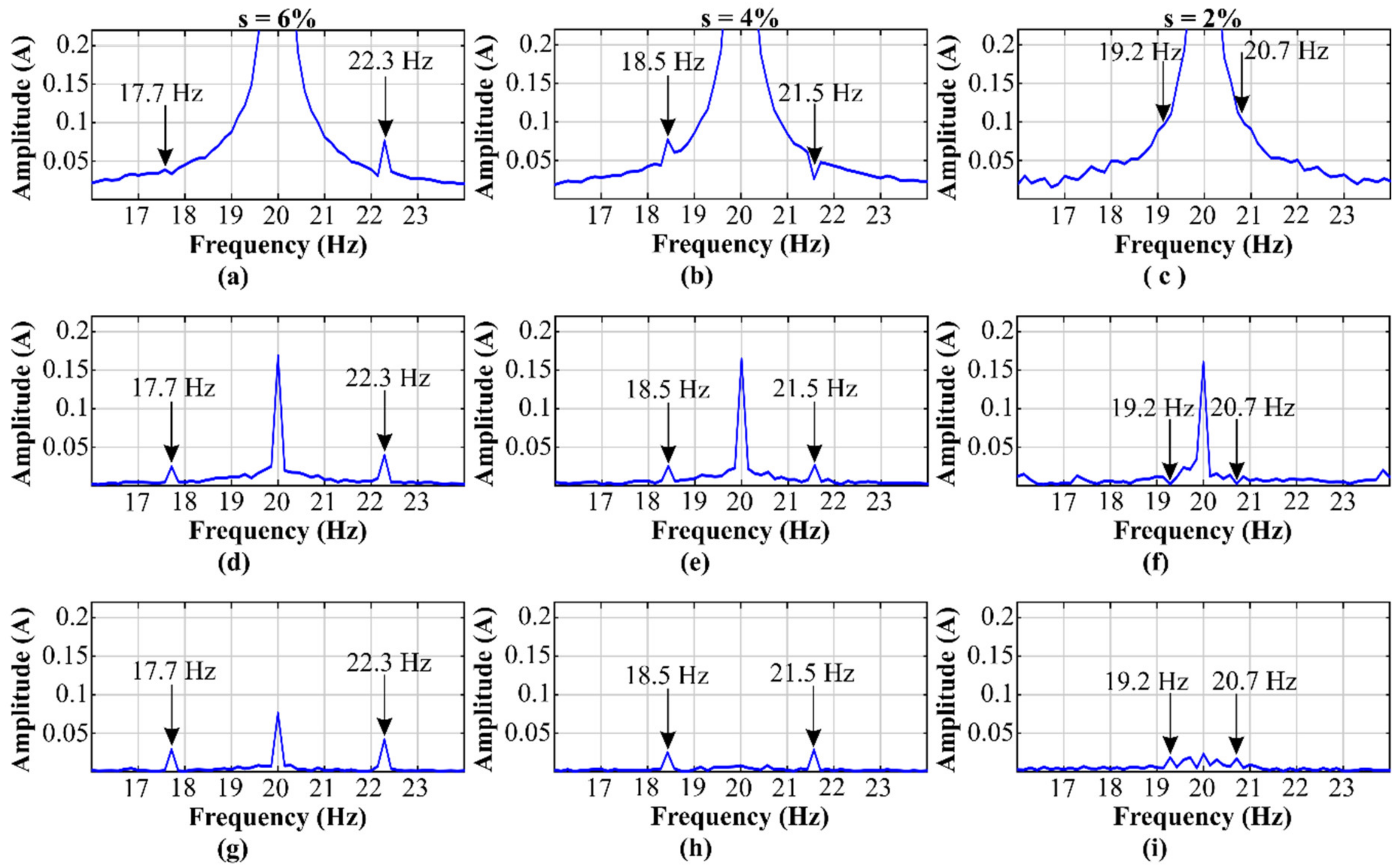
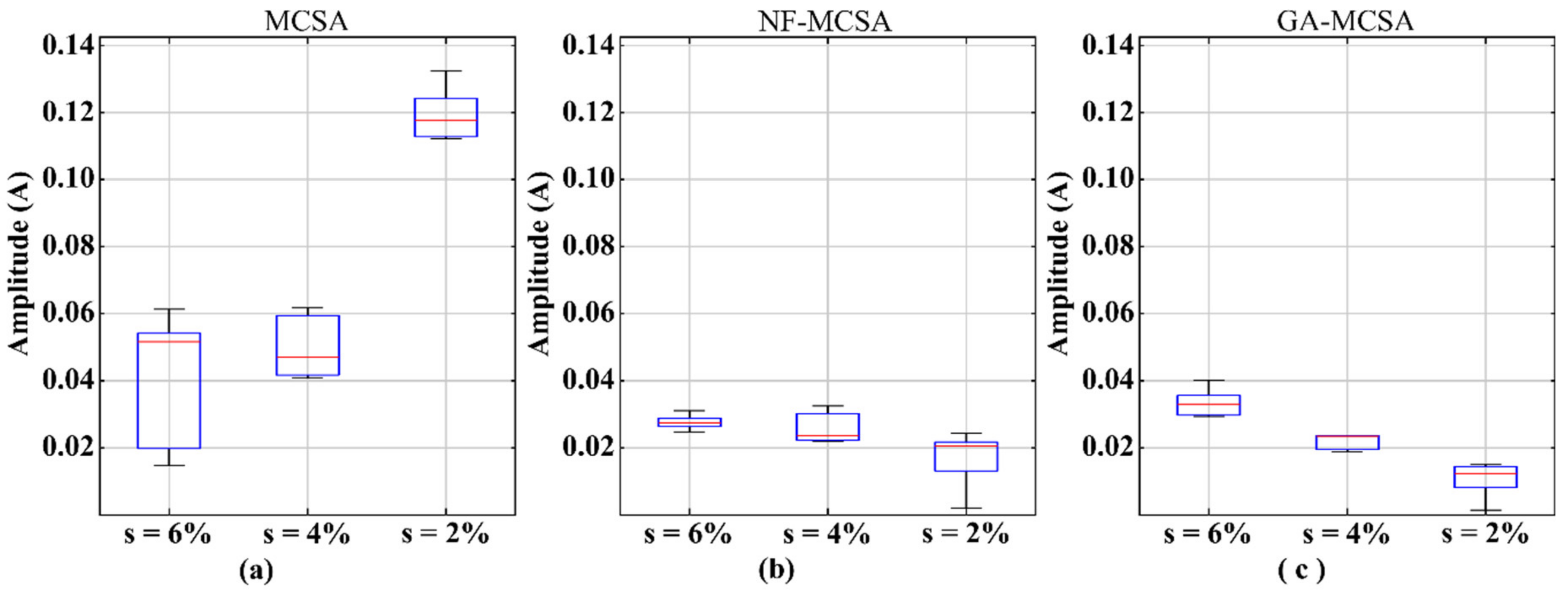
5.2. Results for the IM Operating at 20 Hz
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Signal Error | |
| Φ | Phase |
| Am | Amplitude |
| ANN | Artificial Neural Networks |
| BRB | Broken Rotor Bar |
| DAS | Data Acquisition System |
| f | Frequency |
| Estimated Fundamental Component | |
| Frequency of the Fundamental Component | |
| FFC | Fundamental Frequency Component |
| FFT | Fast Fourier Transform |
| Frequency of the Left Side Harmonic | |
| FPGA | Field Programmable Gate Array |
| Frequency of the Right Side Harmonic | |
| Best Member of the Current Population | |
| GA | Genetic Algorithms |
| i-th Individual of the Current Population | |
| i-th Individual of the Next Population | |
| Time Domain Current Signal | |
| Current from phase a | |
| IAE | Integral of the Absolute Error |
| Current from phase b | |
| Current from phase c | |
| IM | Induction Motors |
| Objective Function | |
| LSH | Left Side Harmonic |
| Maximum value of a fitness function | |
| MCSA | Motor Current Signature Analysis |
| MUSIC | Multiple Signal Classification |
| NF | Notch Filters |
| PLL | Phase-Locked Loop |
| Mutation Probability | |
| RS | Residual Signal |
| RSH | Right Side Harmonic |
| Induction Motor Slip | |
| VFD | Variable Frequency Drive |
References
- Aguilar, W.G.; Arcos-Avilés, D.; Sotomayor, D.; Granda, D. Broken Bar Diagnosis for Squirrel Cage Induction Motors Using Frequency Analysis Based on MCSA and Continuous Wavelet Transform. Math. Comput. Appl. 2017, 22, 30. [Google Scholar] [CrossRef] [Green Version]
- Guajardo, L.A.T.; Rodriguez-Maldonado, J.; Moonem, M.A.; Platas-Garza, M.A. A Multiresolution Taylor–Kalman Approach for Broken Rotor Bar Detection in Cage Induction Motors. IEEE Trans. Instrum. Meas. 2018, 67, 1317–1328. [Google Scholar] [CrossRef]
- Choudhary, A.; Goyal, D.; Shimi, S.L.; Akula, A. Condition Monitoring and Fault Diagnosis of Induction Motors: A Review. Arch. Comput. Methods Eng. 2018, 26, 1221–1238. [Google Scholar] [CrossRef]
- Singh, G.; Kumar, T.C.A.; Naikan, V. Efficiency monitoring as a strategy for cost effective maintenance of induction motors for minimizing carbon emission and energy consumption. Reliab. Eng. Syst. Saf. 2019, 184, 193–201. [Google Scholar] [CrossRef]
- Chang, H.-C.; Jheng, Y.-M.; Kuo, C.-C.; Hsueh, Y.-M. Induction Motors Condition Monitoring System with Fault Diagnosis Using a Hybrid Approach. Energies 2019, 12, 1471. [Google Scholar] [CrossRef] [Green Version]
- Ojaghi, M.; Sabouri, M.; Faiz, J. Performance Analysis of Squirrel-Cage Induction Motors Under Broken Rotor Bar and Stator Inter-Turn Fault Conditions Using Analytical Modeling. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Morinigo-Sotelo, D.; Romero-Troncoso, R.D.J.; Panagiotou, P.A.; Antonino-Daviu, J.; Gyftakis, K. Reliable Detection of Rotor Bars Breakage in Induction Motors via MUSIC and ZSC. IEEE Trans. Ind. Appl. 2017, 54, 1224–1234. [Google Scholar] [CrossRef]
- Panagiotou, P.A.; Arvanitakis, I.; Lophitis, N.; Antonino-Daviu, J.; Gyftakis, K. A New Approach for Broken Rotor Bar Detection in Induction Motors Using Frequency Extraction in Stray Flux Signals. IEEE Trans. Ind. Appl. 2019, 55, 3501–3511. [Google Scholar] [CrossRef] [Green Version]
- Bessam, B.; Menacer, A.; Boumehraz, M.; Cherif, H. Detection of broken rotor bar faults in induction motor at low load using neural network. ISA Trans. 2016, 64, 241–246. [Google Scholar] [CrossRef]
- Filho, P.C.M.L.; Baccarini, L.M.R.; Batista, F.B.; Alves, D.A. Broken rotor bar detection using empirical demodulation and wavelet transform: Suitable for industrial application. Electr. Eng. 2018, 100, 2253–2260. [Google Scholar] [CrossRef]
- Zhen, D.; Wang, Z.; Li, H.; Zhang, H.; Yang, J.; Gu, F. An Improved Cyclic Modulation Spectral Analysis Based on the CWT and Its Application on Broken Rotor Bar Fault Diagnosis for Induction Motors. Appl. Sci. 2019, 9, 3902. [Google Scholar] [CrossRef] [Green Version]
- Pineda-Sanchez, M.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Riera-Guasp, M.; Perez-Cruz, J. Partial Inductance Model of Induction Machines for Fault Diagnosis. Sensors 2018, 18, 2340. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quiroz, J.C.; Mariun, N.; Mehrjou, M.R.; Izadi, M.; Misron, N.; Radzi, M.M. Fault detection of broken rotor bar in LS-PMSM using random forests. Measurement 2018, 116, 273–280. [Google Scholar] [CrossRef]
- Cekic, Y.; Eren, L. Broken rotor bar detection via four-band wavelet packet decomposition of motor current. Electr. Eng. 2017, 100, 1957–1962. [Google Scholar] [CrossRef]
- Zolfaghari, S.; Noor, S.B.M.; Mehrjou, M.R.; Marhaban, M.H.; Mariun, N. Broken Rotor Bar Fault Detection and Classification Using Wavelet Packet Signature Analysis Based on Fourier Transform and Multi-Layer Perceptron Neural Network. Appl. Sci. 2017, 8, 25. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Calva, T.A.; Morinigo-Sotelo, D.; Romero-Troncoso, R.D.J. Non-Uniform Time Resampling for Diagnosing Broken Rotor Bars in Inverter-Fed Induction Motors. IEEE Trans. Ind. Electron. 2016, 64, 2306–2315. [Google Scholar] [CrossRef]
- Kia, S.; Henao, H.; Capolino, G.-A. A High-Resolution Frequency Estimation Method for Three-Phase Induction Machine Fault Detection. IEEE Trans. Ind. Electron. 2007, 54, 2305–2314. [Google Scholar] [CrossRef]
- Delgado-Arredondo, P.A.; Morinigo-Sotelo, D.; Osornio-Rios, R.A.; Avina-Cervantes, J.G.; Rostro-Gonzalez, H.; Romero-Troncoso, R.D.J. Methodology for fault detection in induction motors via sound and vibration signals. Mech. Syst. Signal Process. 2017, 83, 568–589. [Google Scholar] [CrossRef]
- Saucedo-Dorantes, J.J.; Delgado-Prieto, M.; Osornio-Rios, R.A.; Romero-Troncoso, R.D.J. Multifault Diagnosis Method Applied to an Electric Machine Based on High-Dimensional Feature Reduction. IEEE Trans. Ind. Appl. 2017, 53, 3086–3097. [Google Scholar] [CrossRef] [Green Version]
- Moussa, M.A.; Boucherma, M.; Khezzar, A. A detection method for induction motor bar fault using sidelobes leakage phenomenon of the sliding discrete Fourier transform. IEEE Trans. Power Electron. 2016, 32, 5560–5572. [Google Scholar] [CrossRef]
- Cruz, S.M.A.; Stefani, A.; Filippetti, F.; Cardoso, A.J.M. Diagnosis of rotor faults in traction drives for railway applications. In Proceedings of the 2008 18th International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008. [Google Scholar]
- Kim, J.; Shin, S.; Bin Lee, S.; Gyftakis, K.; Drif, M.; Cardoso, A.J.M. Power Spectrum-Based Detection of Induction Motor Rotor Faults for Immunity to False Alarms. IEEE Trans. Energy Convers. 2015, 30, 1123–1132. [Google Scholar] [CrossRef]
- Jiang, C.; Li, S.; Habetler, T.G. A review of condition monitoring of induction motors based on stray flux. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar]
- Bacha, K.; Ben Salem, S.; Chaari, A. An improved combination of Hilbert and Park transforms for fault detection and identification in three-phase induction motors. Int. J. Electr. Power Energy Syst. 2012, 43, 1006–1016. [Google Scholar] [CrossRef]
- Puche-Panadero, R.; Pineda-Sanchez, M.; Riera-Guasp, M.; Roger-Folch, J.; Hurtado-Pérez, E.; Perez-Cruz, J. Improved Resolution of the MCSA Method Via Hilbert Transform, Enabling the Diagnosis of Rotor Asymmetries at Very Low Slip. IEEE Trans. Energy Convers. 2009, 24, 52–59. [Google Scholar] [CrossRef]
- Malekpour, M.; Phung, B.T.; Ambikairajah, E. An envelope-based method with second order generalized integrator adaptive notch filter for diagnosis of rotor bar breakage at very low slips. In Proceedings of the IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017. [Google Scholar]
- Malekpour, M.; Phung, B.T.; Ambikairajah, E. Stator current envelope extraction for analysis of broken rotor bar in induction motors. In Proceedings of the IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017. [Google Scholar]
- Ince, T. Real-time broken rotor bar fault detection and classification by shallow 1D convolutional neural networks. Electr. Eng. 2019, 101, 599–608. [Google Scholar] [CrossRef]
- Asad, B.; Vaimann, T.; Belahcen, A.; Kallaste, A.; Rassolkin, A.; Iqbal, M.N. Broken rotor bar fault detection of the grid and inverter-fed induction motor by effective attenuation of the fundamental component. IET Electr. Power Appl. 2019, 13, 2005–2014. [Google Scholar] [CrossRef]
- Pineda-Sanchez, M.; Puche-Panadero, R.; Riera-Guasp, M.; Perez-Cruz, J.; Roger_Folch, J.; Pons-Llinares, J.; Climente-Alarcon, V.; Antonino-Daviu, J.A. Application of the Teager–Kaiser Energy Operator to the Fault Diagnosis of Induction Motors. IEEE Trans. Energy Convers. 2013, 28, 1036–1044. [Google Scholar] [CrossRef]
- Laala, W.; Guedini, S.; Zouzou, S. Novel approach for diagnosis and detection of broken bar in induction motor at low slip using fuzzy logic. In Proceedings of the 8th IEEE Symposium on Diagnostics for Electrical Machines, Power Electronics & Drives, Bologna, Italy, 5–8 September 2011; pp. 511–516. [Google Scholar]
- Zhang, W.; Jia, M.; Zhu, L.; Yan, X. Comprehensive Overview on Computational Intelligence Techniques for Machinery Condition Monitoring and Fault Diagnosis. Chin. J. Mech. Eng. 2017, 30, 782–795. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-H.; Pack, J.-H.; Lee, I.-S. Fault Diagnosis of Induction Motor Using Convolutional Neural Network. Appl. Sci. 2019, 9, 2950. [Google Scholar] [CrossRef] [Green Version]
- Elvira-Ortiz, D.A.; Morinigo-Sotelo, D.; Zorita-Lamadrid, A.L.; Osornio-Rios, R.A.; Romero-Troncoso, R.J. Genetic Algorithm Methodology for Broken Bar Detection in Induction Motor at Low Frequency and Load Operation. In Proceedings of the 2019 IEEE 12th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Toulouse, France, 27–30 August 2019. [Google Scholar]
- Rao, S.S. Engineering Optimization Theory and Practice, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2009; pp. 694–702. [Google Scholar]
- Mojiri, M.; Karimi-Ghartemani, M.; Bakhshai, A. Estimation of Power System Frequency Using an Adaptive Notch Filter. IEEE Trans. Instrum. Meas. 2007, 56, 2470–2477. [Google Scholar] [CrossRef]
- Karimi, H.; Karimi-Ghartemani, M.; Iravani, M.R. Estimation of frequency and its rate of change for applications in power systems. IEEE T Power Deliver 2004, 19, 472–480. [Google Scholar] [CrossRef]
- Zhang, Y.; Martínez-García, M.; Kalawsky, R.S.; Latimer, A. Grey-box modelling of the swirl characteristics in gas turbine combustion system. Measurement 2020, 151, 107266. [Google Scholar] [CrossRef]
- Zhang, Y.; Martinez-Garcia, M.; Latimer, A. Selecting Optimal Features for Cross-Fleet Analysis and Fault Diagnosis of Industrial Gas Turbines. In ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition; American Society of Mechanical Engineers Digital Collection: Oslo, Norway, 2018. [Google Scholar]


| Frequency | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 31 Hz | 3.8 × 10−3 | 5.0 × 10−3 | 4.7 × 10−4 | 2.0 × 10−3 | 1.1 × 10−3 | 3.2 × 10−3 | 2.5 × 10−4 | 2.9 × 10−4 | 8.0 × 10−4 |
| 20 Hz | 1.8 × 10−3 | 3.0 × 10−3 | 1.2 × 10−2 | 3.6 × 10−3 | 2.4 × 10−3 | 1.7 × 10−4 | 1.7 × 10−3 | 1.6 × 10−3 | 2.4 × 10−4 |
| Frequency | (MCSA) | (NF-MCSA) | (GA-MCSA) | |||
|---|---|---|---|---|---|---|
| 31 Hz | 3.3 × 10−2 | 5.0 × 10−3 | 2.4 × 10−2 | 1.1 × 10−2 | 1.4 × 10−2 | 1.6 × 10−2 |
| 20 Hz | 7.1 × 10−2 | 4.6 × 10−3 | 3.0 × 10−3 | 3.9 × 10−3 | 1.1 × 10−2 | 9.6 × 10−3 |
| Technique | Computational Cost (Seconds) | Acquisition Time (Seconds) |
|---|---|---|
| MCSA | 1.004 | 20 |
| NF-MCSA | 1.520 | 10 |
| GA-MCSA | 10.752 | 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elvira-Ortiz, D.A.; Morinigo-Sotelo, D.; Zorita-Lamadrid, A.L.; Osornio-Rios, R.A.; Romero-Troncoso, R.d.J. Fundamental Frequency Suppression for the Detection of Broken Bar in Induction Motors at Low Slip and Frequency. Appl. Sci. 2020, 10, 4160. https://doi.org/10.3390/app10124160
Elvira-Ortiz DA, Morinigo-Sotelo D, Zorita-Lamadrid AL, Osornio-Rios RA, Romero-Troncoso RdJ. Fundamental Frequency Suppression for the Detection of Broken Bar in Induction Motors at Low Slip and Frequency. Applied Sciences. 2020; 10(12):4160. https://doi.org/10.3390/app10124160
Chicago/Turabian StyleElvira-Ortiz, Daivd A., Daniel Morinigo-Sotelo, Angel L. Zorita-Lamadrid, Roque A. Osornio-Rios, and Rene de J. Romero-Troncoso. 2020. "Fundamental Frequency Suppression for the Detection of Broken Bar in Induction Motors at Low Slip and Frequency" Applied Sciences 10, no. 12: 4160. https://doi.org/10.3390/app10124160
APA StyleElvira-Ortiz, D. A., Morinigo-Sotelo, D., Zorita-Lamadrid, A. L., Osornio-Rios, R. A., & Romero-Troncoso, R. d. J. (2020). Fundamental Frequency Suppression for the Detection of Broken Bar in Induction Motors at Low Slip and Frequency. Applied Sciences, 10(12), 4160. https://doi.org/10.3390/app10124160







