Prediction of Opinion Keywords and Their Sentiment Strength Score Using Latent Space Learning Methods
Abstract
:1. Introduction
Related Work
2. Latent Space Based Learning
2.1. Opinion Dictionary Generation
- Rational sentiments, namely “rational reasoning, tangible beliefs, and utilitarian attitudes” [38]. An example of this category is given by the sentence ‘This camera is good”, which does not involve emotions like happiness at all. In this case, the opinion-word (the adjective “good”) fully reveals the user’s opinion on the phone.
- Emotional sentiments, described in [12] as “entities that go deep into people’s psychological states of mind”. For example, consider the sentence “I trust this camera”. Here, the opinion-word “trust” clearly conveys the emotional state of the writer.
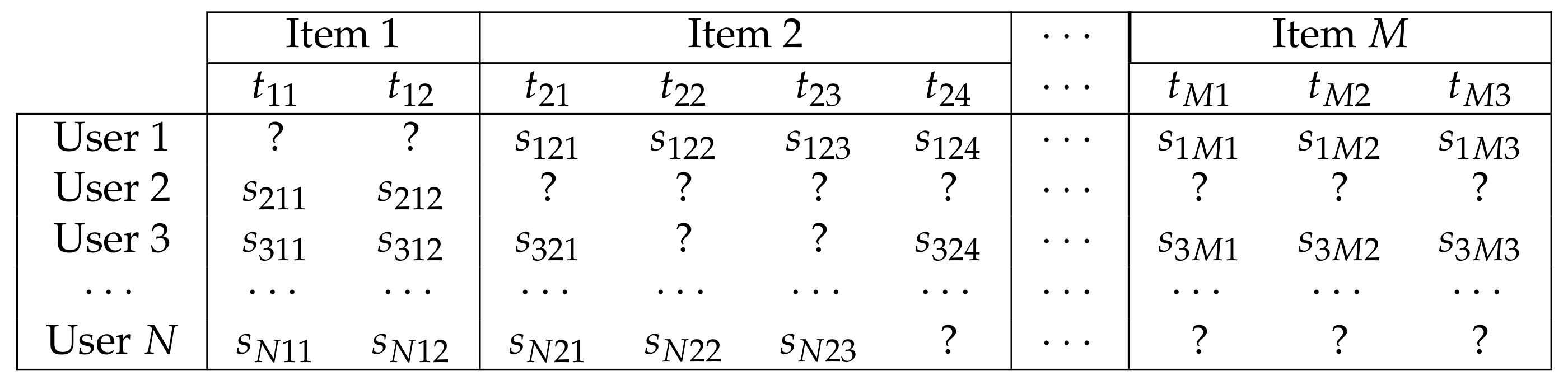
2.2. Notation and Input Matrix
2.3. Prediction Model
3. Experiments
3.1. Dataset
3.2. Technical Aspects
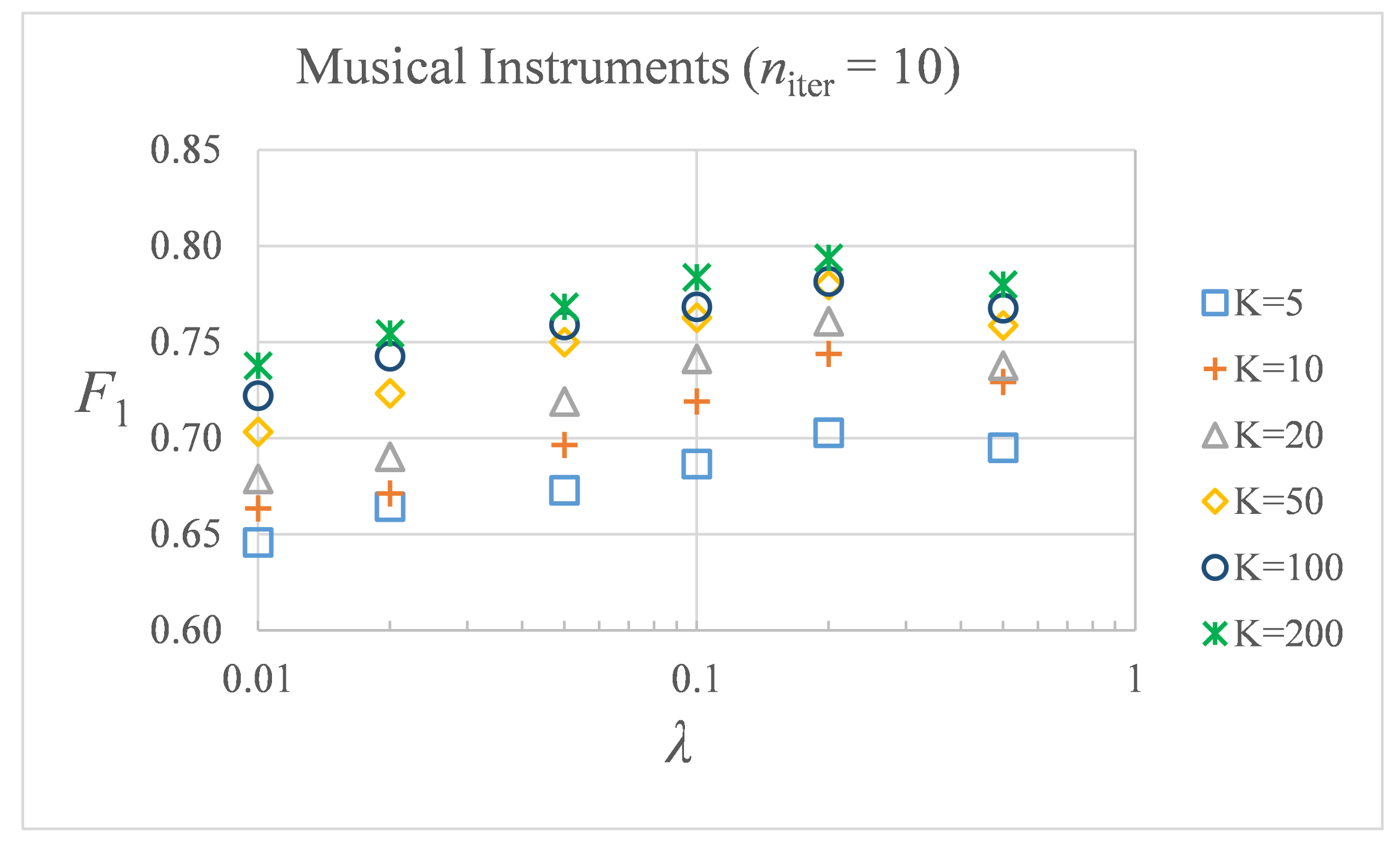
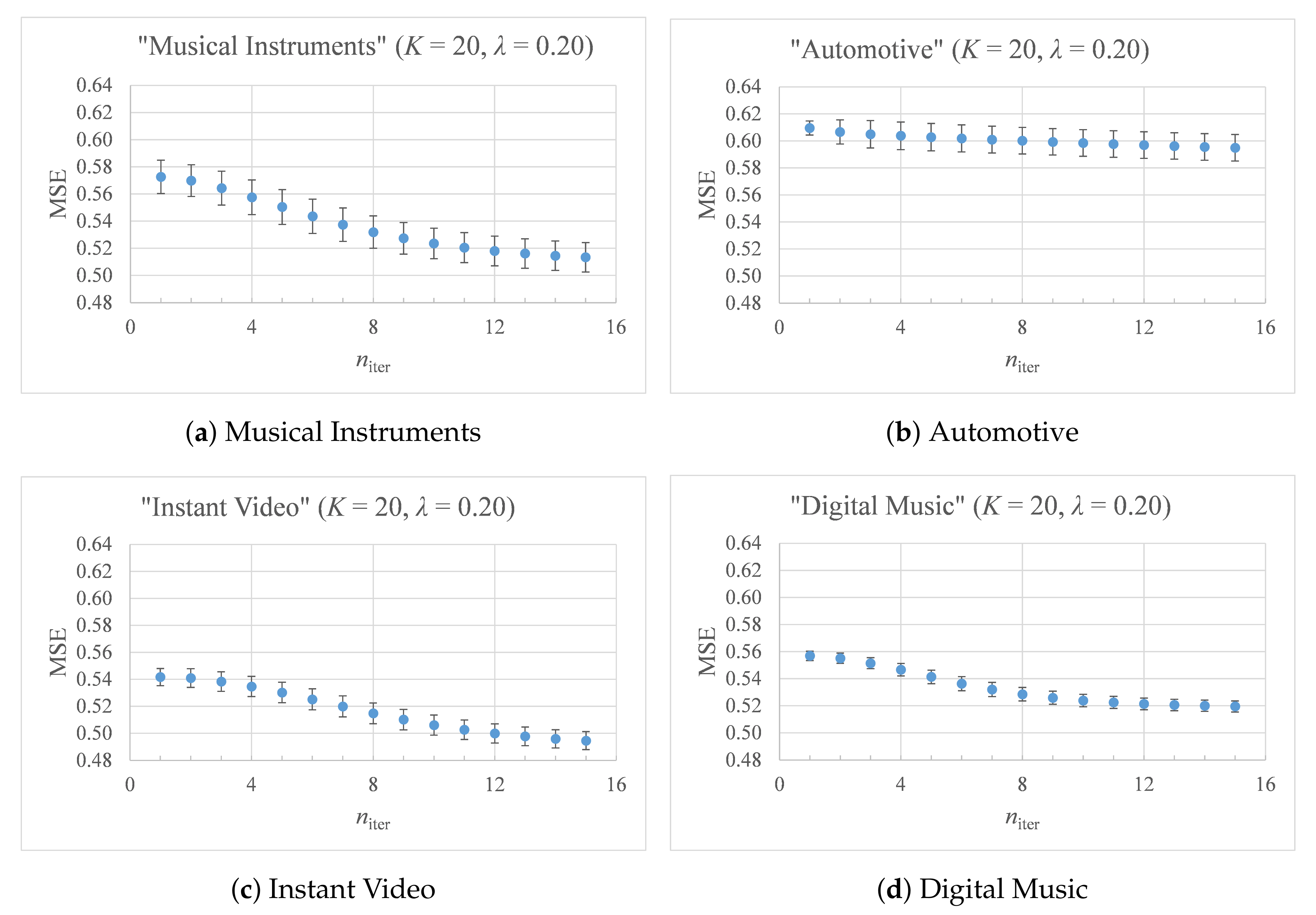
3.3. Experimental Design
- Combined analysis of and parameters to probe whether they can be set independently for each dataset.
- Analysis of the influence of the optimal K value on the model performance for different datasets and values.
- Analysis of the number of iterations needed until convergence is reached.
4. Results
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McAuley, J.; Leskovec, J. From amateurs to connoisseurs: Modeling the evolution of user expertise through online reviews. In Proceedings of the WWW, Rio de Janeiro, Brazil, 13–17 May 2013. [Google Scholar]
- Sharma, A.; Cosley, D. Do social explanations work? studying and modeling the effects of social explanations in recommender systems. In Proceedings of the WWW, Rio de Janeiro, Brazil, 13–17 May 2013. [Google Scholar]
- Ekstrand, M.D.; Riedl, J.T.; Konstan, J.A. Collaborative Filtering Recommender Systems, 2nd ed.; Foundations and Trends in Human-Computer Interaction; NowPublishers: Boston, MA, USA, 2012; Volume 4, pp. 81–173. [Google Scholar]
- de Lops, P.; Gemmis, M.; Semeraro, G. Content-based Recommender Systems: State of the Art and Trends. In Recommender Systems Handbook; Ricci, F., Rokach, L., Shapira, B., Kantor, P., Eds.; Springer: Boston, MA, USA, 2011. [Google Scholar]
- Fangtao, L.; Nathan, L.; Hongwei, J.; Zhao, K.; Yang, Q.; Zhu, X. Incorporating reviewer and item information for review rating prediction. In Proceedings of the 23rd IJCAI; AAAI Press: Palo Alto, CA, USA, 2011; pp. 1820–1825. [Google Scholar]
- Terzi, M.; Rowe, M.; Ferrario, M.A.; Whittle, J. Textbased User-KNN: Measuring User Similarity Based on Text Reviews; Adaptation and Personalization, Ed.; Springer: New York, NY, USA, 2011; pp. 195–206. [Google Scholar]
- Bell, R.M.; Koren, Y. Lessons from the Netflix prize challenge. SIGKDD Explor. Newsl. 2007, 9, 75–79. [Google Scholar] [CrossRef]
- Bennett, J.; Lanning, S. The netflix prize. In Proceedings of the KDD Cup and Workshop, San Jose, CA, USA, 12 August 2007; Volume 2007, p. 35. [Google Scholar]
- Luo, X.; Zhou, M.; Shang, M.; Li, S.; You, Z.; Xia, Y.; Zhu, Q. A nonnegative latent factor model for large-scale sparse matrices in recommender systems via alternating direction method. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 579–592. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Zhou, M.; Shang, M.; Li, S.; Xia, Y. A novel approach to extracting non-negative latent factors from non-negative big sparse matrices. IEEE Access 2016, 4, 2649–2655. [Google Scholar] [CrossRef]
- McAuley, J.; Leskovec, J. Hidden factors and hidden topics: Understanding rating dimension with review text. In Proceedings of the 7th ACM conference on Recommender Systems (RecSys), Hong Kong, China, 12–16 October 2013. [Google Scholar]
- Liu, B. Sentiment Analysis: Mining Opinions, Sentiments, and Emotions; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Hu, X.; Tang, J.; Gao, H.; Liu, H. Unsupervised sentiment analysis with emotional signals. In Proceedings of the WWW ’13, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 607–618. [Google Scholar] [CrossRef]
- Diao, A.; Qiu, M.; Wu, C.Y.; Smola, A.J.; Jiang, J.; Wang, C.G. Jointly modeling aspects, ratings and sentiments for movie recommendation (JMARS). In Proceedings of the KDD ’14, New York, NY, USA, 24–27 August 2014; pp. 193–202. [Google Scholar] [CrossRef]
- Ganu, G.; Elhadad, N.; Marian, A. Beyond the stars: Improving rating predictions using review text content. In Proceedings of the WebDB, Providence, RI, USA, 28 June 2009. [Google Scholar]
- Ling, G.; Lyu, M.R.; King, I. Ratings meet reviews, a combined approach to recommend. In Proceedings of the RecSys 14, Foster City, CA, USA, 6–10 August 2014; pp. 105–112. [Google Scholar] [CrossRef]
- McAuley, J.; Leskovec, J.; Jurafsky, D. Learning attitudes and attributes from multi-aspect reviews. In Proceedings of the ICDM, Brussels, Belgium, 10–13 December 2012. [Google Scholar]
- Zhang, W.; Wang, J. Integrating Topic and Latent Factors for Scalable Personalized Review-based Rating Prediction. IEEE Trans. Knowl. Data Eng. 2016, 28, 3013–3027. [Google Scholar] [CrossRef]
- Izard, C. The Psychology of Emotions; Springer: New York, NY, USA, 1991. [Google Scholar]
- Ekman, P.; Friesen, W. Constants across cultures in the face and emotion. J. Pers. Soc. Psychol. 1971, 17, 124–129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ekman, P. Basic emotions. In Handbook of Cognition and Emotion; Dalgleish, T., Power, M., Eds.; HarperCollins: Sussex, UK, 1999; pp. 45–60. [Google Scholar]
- Moshfeghi, Y.; Jose, J.M. Role of emotional features in collaborative recommendation. In Proceedings of the European Conference on Information Retrieval, Dublin, Ireland, 18–21 April 2011; Springer: Berlin/Heidelberg, Germany; pp. 738–742. [Google Scholar]
- Winoto, P.; Tang, T.Y. The role of user mood in movie recommendations. Exp. Syst. Appl. 2010, 8, 6086–6092. [Google Scholar] [CrossRef]
- McAuley, J.; Pandey, R.; Leskovec, J. Inferring networks of substitutable and complementary products. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015. [Google Scholar]
- Titov, I.; McDonald, R. A joint model of text and aspect ratings for sentiment summarization. In Proceedings of the ACL, Columbus, OH, USA, 15–20 June 2008. [Google Scholar]
- Wang, H.; Lu, Y.; Zhai, C. Latent aspect rating analysis on review text data: A rating regression approach. In Proceedings of the KDD, Washington, DC, USA, 25–28 July 2010. [Google Scholar]
- Markus, S.; Hamed, Z.; Ching-Wei, C.; Yashar, D.; Mehdi, E. Current Challenges and Visions in Music Recommender Systems Research. arXiv 2018, arXiv:1710.03208. [Google Scholar]
- Del Corso, G.M.; Romani, F. Adaptive nonnegative matrix factorization and measure comparisons for recommender systems. Appl. Math. Comput. 2019, 354, 164–179. [Google Scholar] [CrossRef] [Green Version]
- Gharibshah, J.; Jalili, M. Connectedness of users–items networks and recommender systems. Appl. Math. Comput. 2014, 243, 578–584. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Tintarev, N.; Masthoff, J. Survey of explanations in recommender systems. In Proceedings of the ICDE Workshops 2007, Istanbul, Turkey, 15–20 April 2007; pp. 801–810. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Riedl, J. Explaining collaborative filtering recommendations. In Proceedings of the CSCW’00, Philadelphia, PA, USA, 2–6 December 2000; pp. 241–250. [Google Scholar]
- Pu, P.; Chen, L.; Hu, R. A user-centric evaluation framework for recommender systems. In Proceedings of the Fifth ACM Conference on Recommender Systems (RecSys ’11), Chicago IL, USA, 23–27 October 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 157–164. [Google Scholar] [CrossRef] [Green Version]
- Shaikh, M.A.M.; Prendinger, H.; Ishizuka, M. A Linguistic Interpretation of the OCC Emotion Model for Affect Sensing from Text. In Affective Information Processing; Springer: London, UK, 2009. [Google Scholar]
- Pang, B.; Lee, L. Seeing stars: Exploiting class relationships for sentiment categorization with respect to rating scales. In Proceedings of the ACL’05, Ann Arbor, MI, USA, 25–30 June 2005. [Google Scholar]
- Goldberg, A.B.; Zhu, X. Seeing stars when there aren’t many stars: Graph-based semi-supervised learning for sentiment categorisation. In Proceedings of the First Workshop on Graph Based Methods for Natural Language Processing, New York, NY, USA, 9 June 2006; Association for Computational Linguistics: New York, NY, USA, 2006; pp. 45–52. [Google Scholar]
- Leung, C.; Chan, S.; Chung, F. Integrating collaborative filtering and sentiment analysis: A rating inference approach. In Proceedings of the ECAI’06, Riva del Garda, Italy, 29 August–1 September 2006. [Google Scholar]
- Almashraee, M.; Monett Díaz, D.; Paschke, A. Emotion Level Sentiment Analysis: The Affective Opinion Evaluation. In Proceedings of the 2th Workshop on Emotions Modality, Sentiment Analysis and the Semantic Web and the 1st International Workshop on Extraction and Processing of Rich Semantics from Medical Texts Co-Located with ESWC 2016, Heraklion, Greece, 29 May 2016. [Google Scholar]
- Hu, M.; Liu, B. Mining and summarizing customer reviews. In Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 168–177. [Google Scholar]
- Kamps, J.; Marx, M.; Mokken, R.J.; de Rijke, M. Using Wordnet to measure semantic orientations of adjectives. In Proceedings of the 4th International Conference on Language Resources and Evaluation, Lisbon, Portugal, 26–28 May 2004; pp. 1115–1118. [Google Scholar]
- Esuli, A.; Sebastiani, F. SENTIWORDNET: A Publicly Available Lexical Resource for Opinion Mining. In Proceedings of the 5th Conference on Language Resources and Evaluation (LREC’06), Genoa, Italy, 22–28 May 2006; pp. 417–422. [Google Scholar]
- García-Cuesta, E.; Gómez-Vergel, D.; Gracia-Expósito, L.; Vela-Pérez, M. Prediction of User Opinion for Products—A Bag of Words and Collaborative Filtering based Approach. In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM’2017), Porto, Portugal, 24–26 February 2017; pp. 233–238. [Google Scholar]
- Jakob, N.; Weber, S.H.; Muller, M.C.; Gurevych, I. Beyond the stars: Exploiting free-text user reviews to improve the accuracy of movie recommendations. In Proceedings of the First International CIKM Workshop on Topic-Sentiment Analysis for Mass Opinion (TSA 2009), Hong Kong, China, 6 November 2009; pp. 57–64. [Google Scholar]
- Wyllys, R.E. Empirical and theoretical bases of Zipf’s law. Libr. Trends 1981, 30, 53–64. [Google Scholar]
- Zipf, G.K. Human Behaviour and the Principle of Least Effort; Addison-Wesley: Reading, MA, USA, 1949. [Google Scholar]
- Hu, Y.; Koren, Y.; Volinsky, C. Collaborative filtering for implicit feedback datasets. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 263–272. [Google Scholar]




| Opinion Keyword | Sentiment Text | Score | |
|---|---|---|---|
| Opinion 1 | “phone” | “awesome” | +4.0 |
| Opinion 2 | “phone” | “much too expensive” | −5.4 |
| Opinion 3 | “screen” | “not big” | −1.0 |
| Symbol | Description |
|---|---|
| u | user, reviewer |
| N | total number of users |
| i | item, product |
| M | total number of items |
| S | set of pairs of existing reviews |
| u-th user review (‘document’) on i-th item | |
| j-th sentiment keyword for the i-th item | |
| normalized sentiment strength score for the j-th keyword in | |
| predicted ALS-generated sentiment score | |
| vocabulary size of the i-th product dictionary | |
| D | sum of all dictionary lengths |
| input matrix in | |
| K | rank, number of latent dimensions |
| ALS’s regularization parameter | |
| number of ALS iterations |
| Reviews | Users | Products | Number of Entries | Ratio of Positive vs. Negative/neutral | Sparsity | |
|---|---|---|---|---|---|---|
| Musical Instruments | 10,261 | 1429 | 900 | 41,942/6158 | 87.1% | 97.5% |
| Automotive | 20,473 | 2929 | 1835 | 75,917/9835 | 82.0% | 98.9% |
| Instant Video | 37,126 | 5129 | 1685 | 165,989/34,802 | 78.8% | 97.8% |
| Digital Music | 64,706 | 5536 | 3568 | 483,232/91,801 | 77.1% | 99.88% |
| Combined datasets | 132,566 | 14,809 | 7988 | 767,080/142,689 | 78.3% | 99.95% |
| Text Review ID | Extracted Opinion Dictionaries |
|---|---|
| B00CCOBOI4 (Automotive) | 3_month, car, instruction, job, layer, paint, problem, product, a result, stuff, surface, thing |
| B0002CZUUG (Musical Instruments) | action, finish, guitar, neck, pickup, sound, review, string, quality, way |
| B003VWJ2K8 (Musical Instruments) | battery, buy, clip, deal, display, design, color, guitar, head, item, job, price, problem, product, purchase, |
| quality, result, Snark, Snark_SN-1, spot, string, thing, time, tune, tuner, tuning, use, value, work |
| -Score | Accuracy | Precision | Recall | AUC | |
|---|---|---|---|---|---|
| Musical Instruments | 0.77(2) | 0.64(3) | 0.87(1) | 0.68(4) | 0.51(1) |
| Automotive | 0.667(8) | 0.544(8) | 0.826(9) | 0.56(1) | 0.516(9) |
| Instant Video | 0.730(4) | 0.615(4) | 0.814(7) | 0.663(7) | 0.551(4) |
| Digital Music | 0.728(8) | 0.611(8) | 0.790(2) | 0.67(1) | 0.54(1) |
| Combined datasets | 0.726(5) | 0.609(5) | 0.801(2) | 0.664(9) | 0.537(3) |
| Opinion | Sentiment Strength Score | ||||
|---|---|---|---|---|---|
| Opinions in the Review | Topic | Sentiment Text | Unprocessed | Normalized | Predicted |
| 1. “There isn’t much to get excited about in a guitar stand,” | - | - | - | - | - |
| 2. “however, it does its job and the price was right.” | “price” | “right” | |||
| 3. “I purchased four and they were all delivered on time.” | - | - | - | - | - |
| 4. “Each adjusted to, and held, its guitar securely.” | “guitar” | “securely” | |||
| 5. “I have found the stand to be very stable.” | “stand” | “very, stable” | |||
| 6. “The welds seem secure ad the materiel heavy enough to do the job.” | “weld” | “secure” | - | - | |
| 7. “My music teacher has a similar stand which cost him 4x as much.” | - | - | - | - | - |
| 8. “It does not appear to be of better quality.” | “quality” | “better” | - | - | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Cuesta, E.; Gómez-Vergel, D.; Gracia-Expósito, L.; López-López, J.M.; Vela-Pérez, M. Prediction of Opinion Keywords and Their Sentiment Strength Score Using Latent Space Learning Methods. Appl. Sci. 2020, 10, 4196. https://doi.org/10.3390/app10124196
García-Cuesta E, Gómez-Vergel D, Gracia-Expósito L, López-López JM, Vela-Pérez M. Prediction of Opinion Keywords and Their Sentiment Strength Score Using Latent Space Learning Methods. Applied Sciences. 2020; 10(12):4196. https://doi.org/10.3390/app10124196
Chicago/Turabian StyleGarcía-Cuesta, Esteban, Daniel Gómez-Vergel, Luis Gracia-Expósito, Jose M. López-López, and María Vela-Pérez. 2020. "Prediction of Opinion Keywords and Their Sentiment Strength Score Using Latent Space Learning Methods" Applied Sciences 10, no. 12: 4196. https://doi.org/10.3390/app10124196
APA StyleGarcía-Cuesta, E., Gómez-Vergel, D., Gracia-Expósito, L., López-López, J. M., & Vela-Pérez, M. (2020). Prediction of Opinion Keywords and Their Sentiment Strength Score Using Latent Space Learning Methods. Applied Sciences, 10(12), 4196. https://doi.org/10.3390/app10124196






