Numerical Analysis of Multi-Phase Flow around Supercavitating Body at Various Cavitator Angle of Attack and Ventilation Mass Flux
Abstract
:1. Introduction
2. Governing Equation and Numerical Method
2.1. Governing Equations
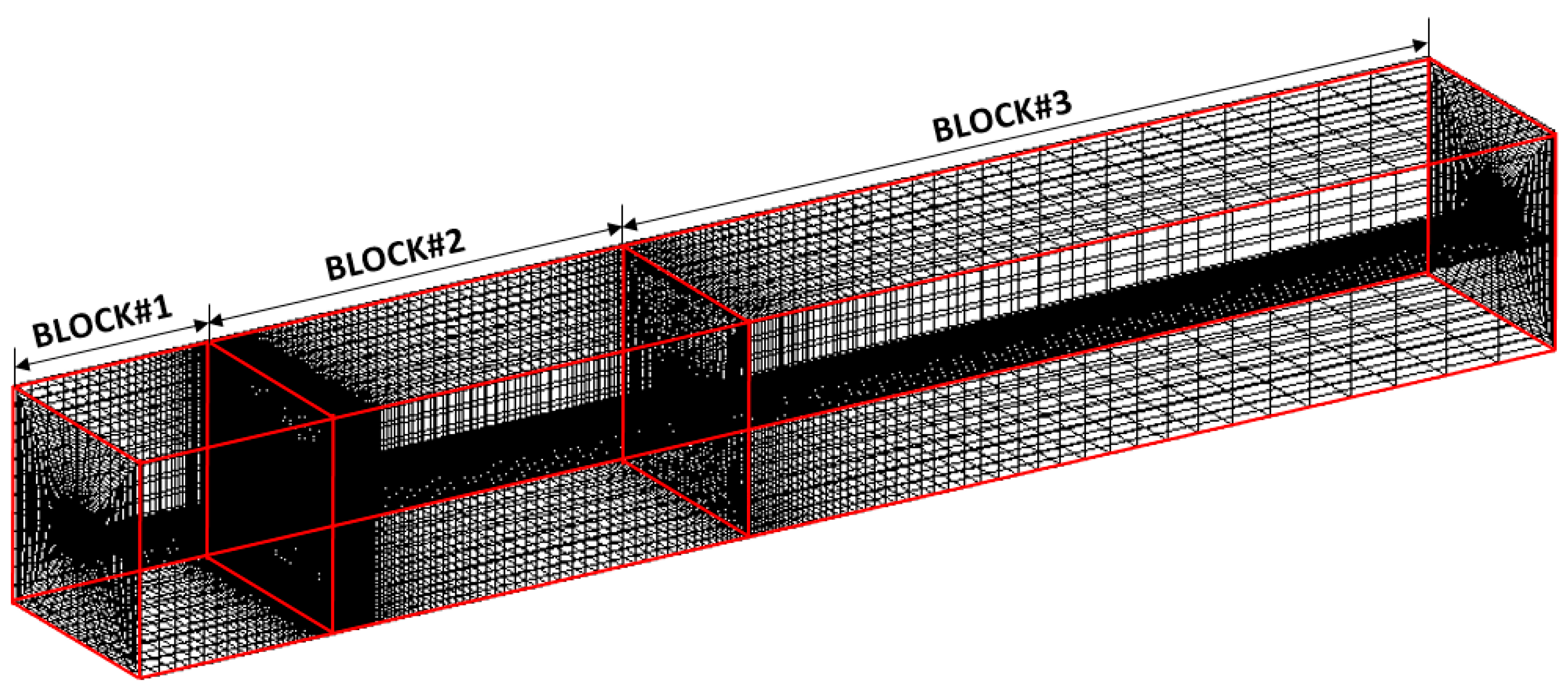
2.2. Numerical Method for Homogeneous Mixture Model
2.3. Turbulence Model
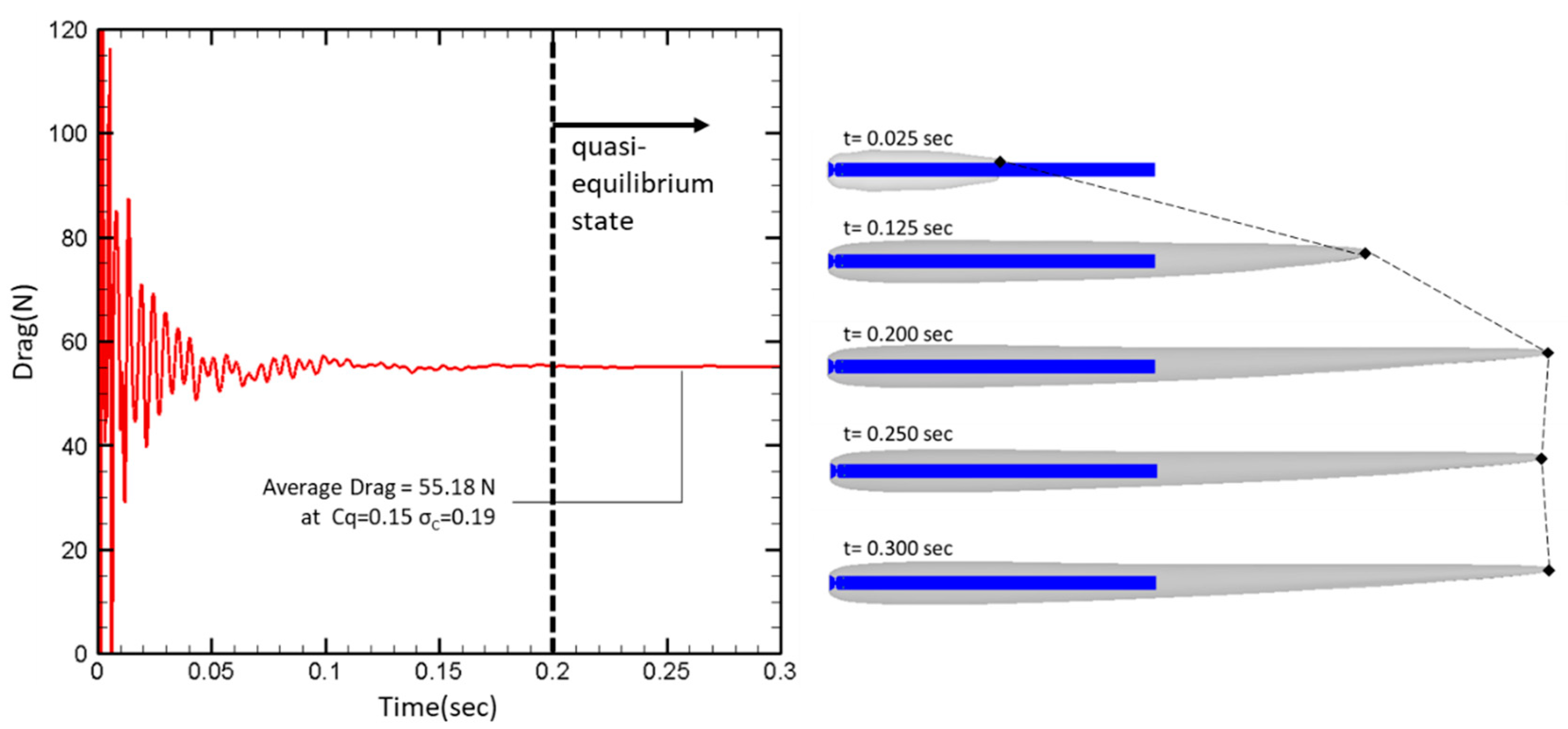
3. Ventilated Supercavitation Achievement
4. Numerical Results
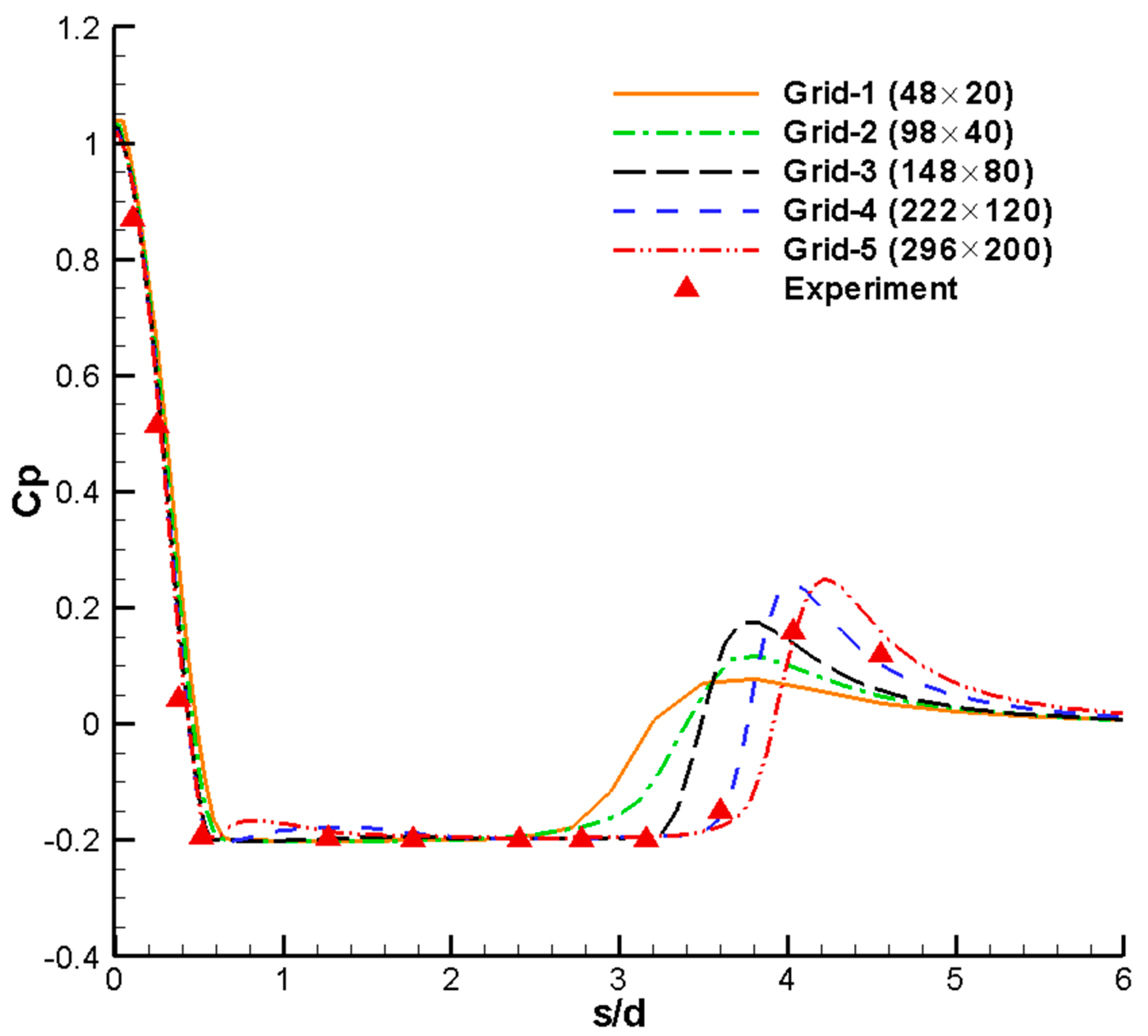
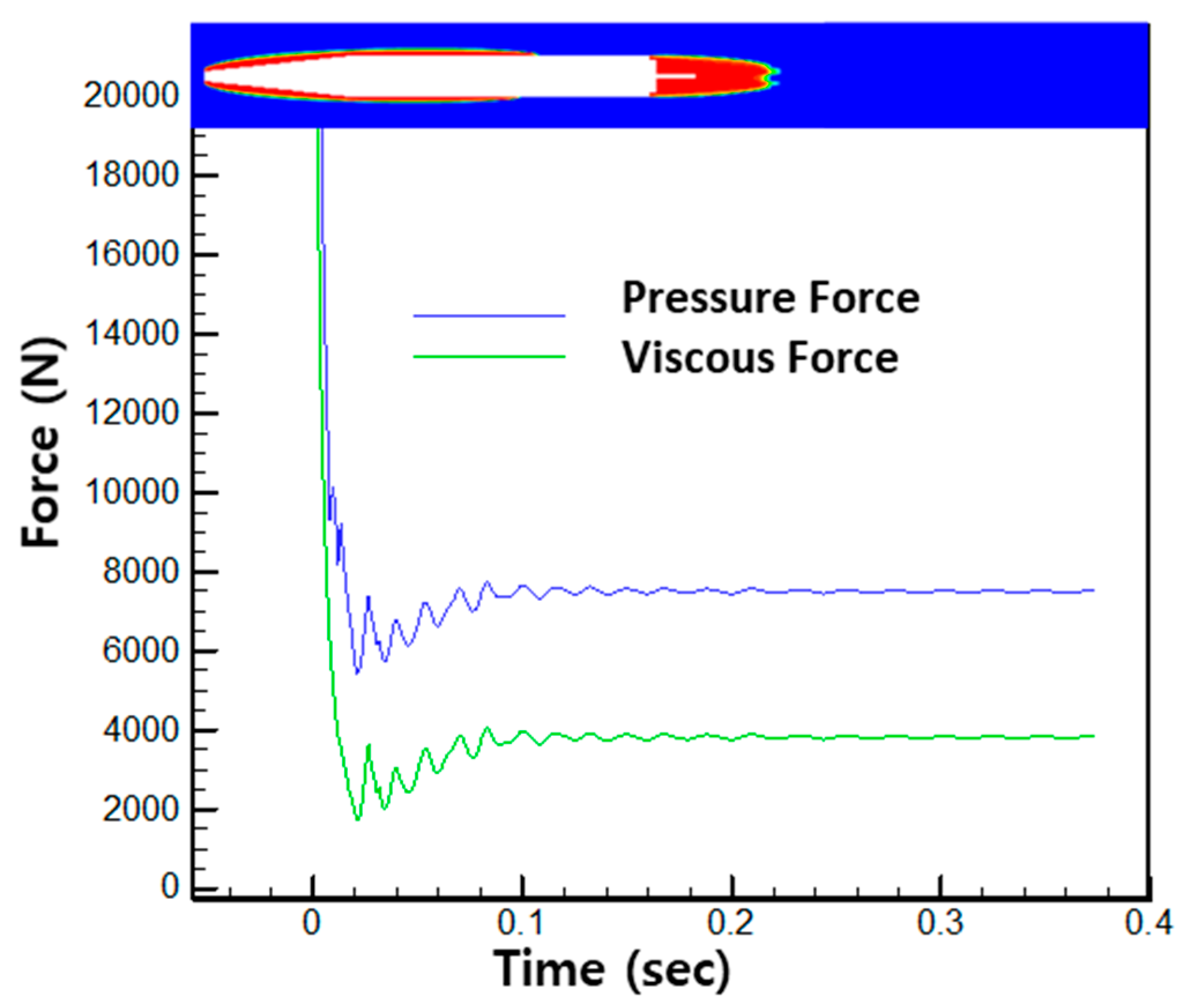
4.1. Natural Cavitation
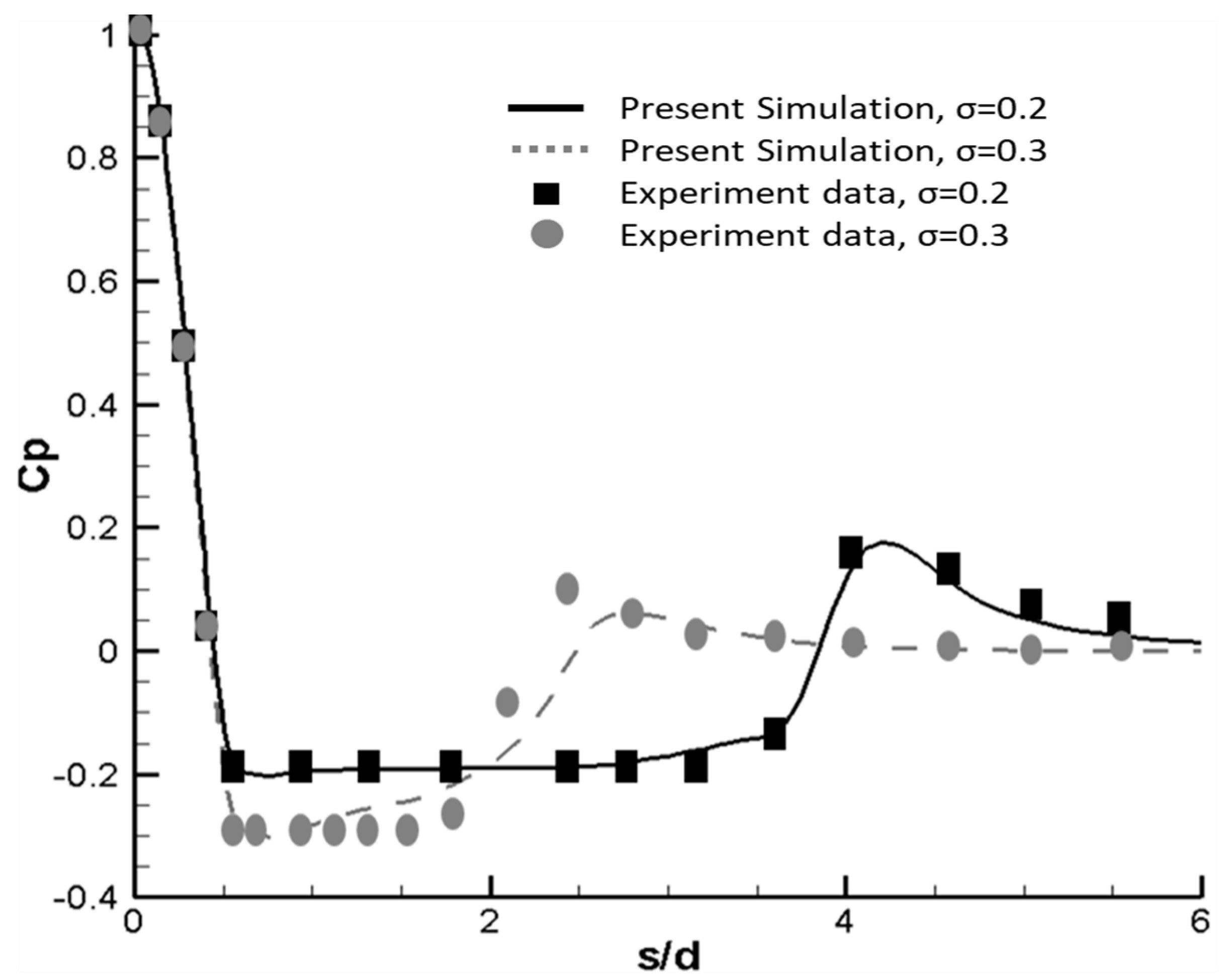
4.2. Ventilated Cavitation
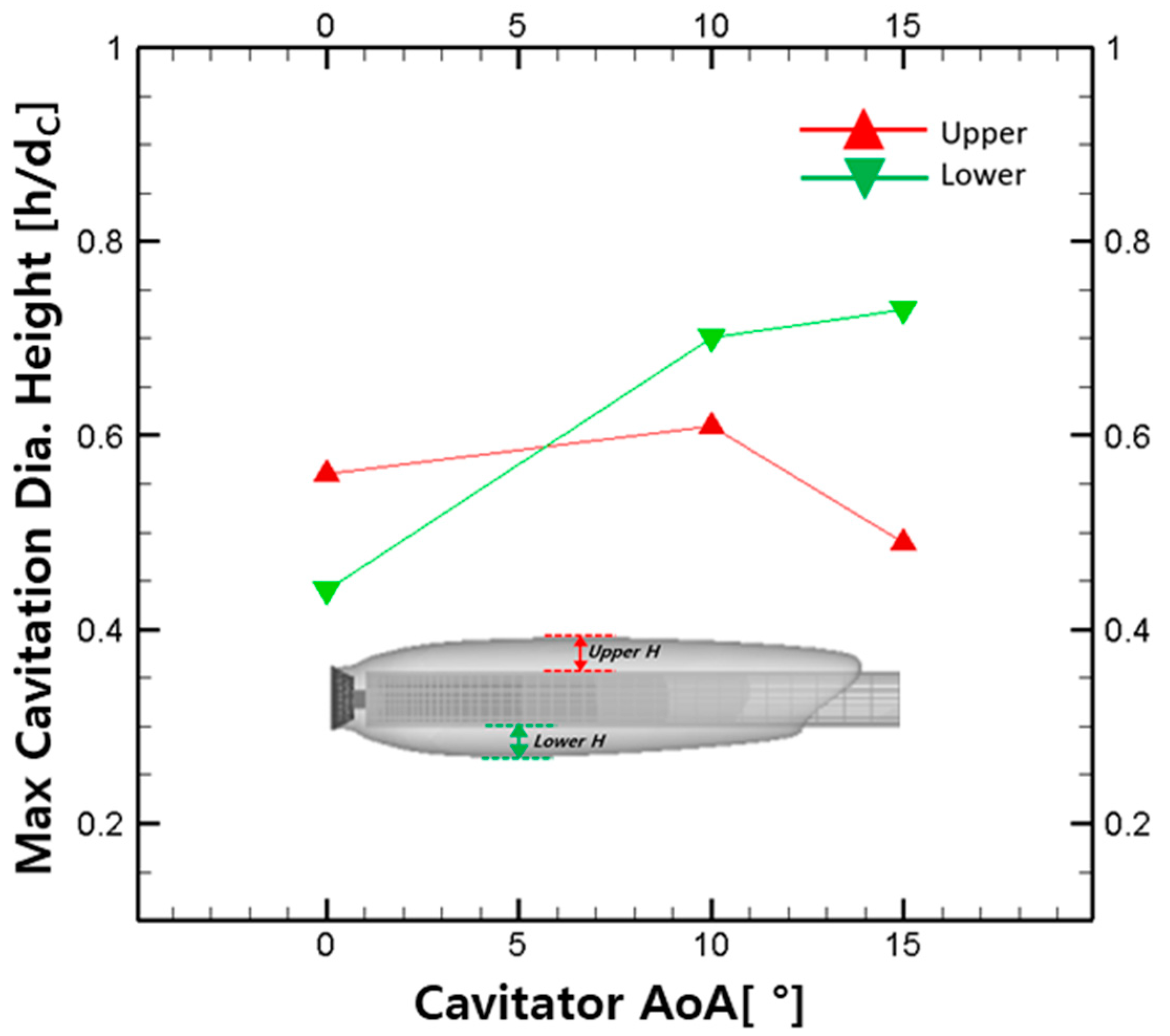
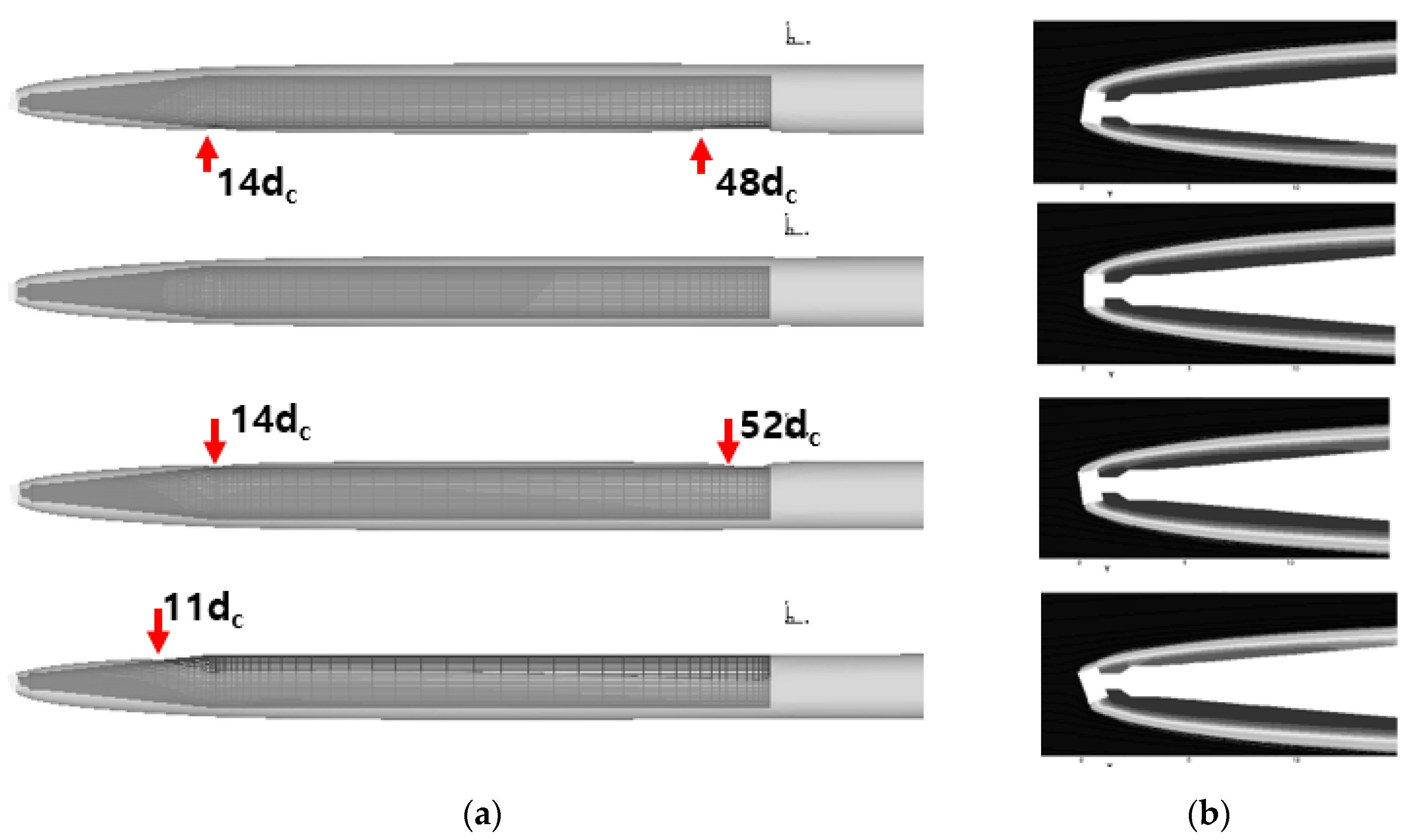
4.3. Cavitation Shape with Cavitator Angle of Attack
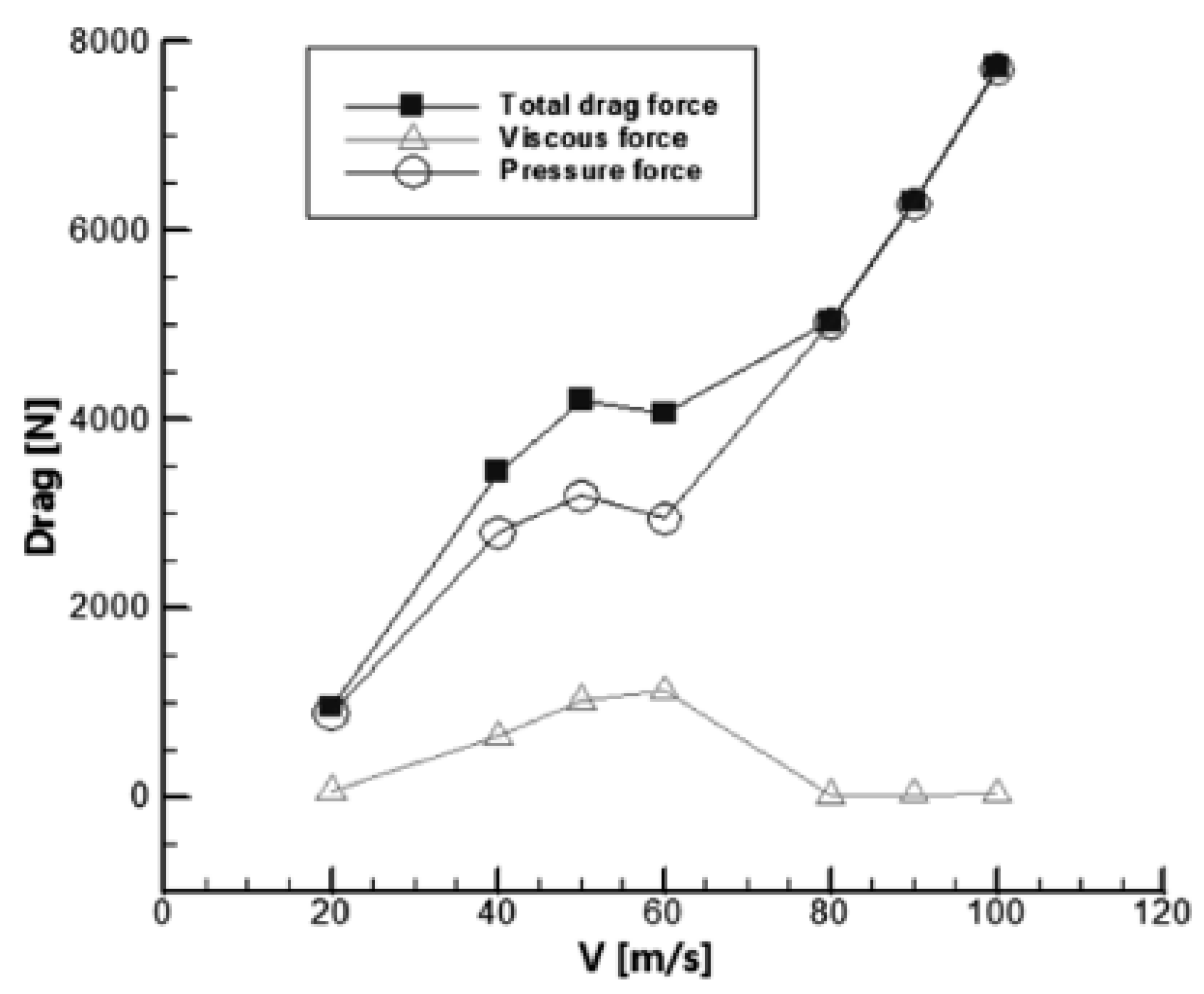
4.4. Cavitation and Drag Change According to Speed Variation
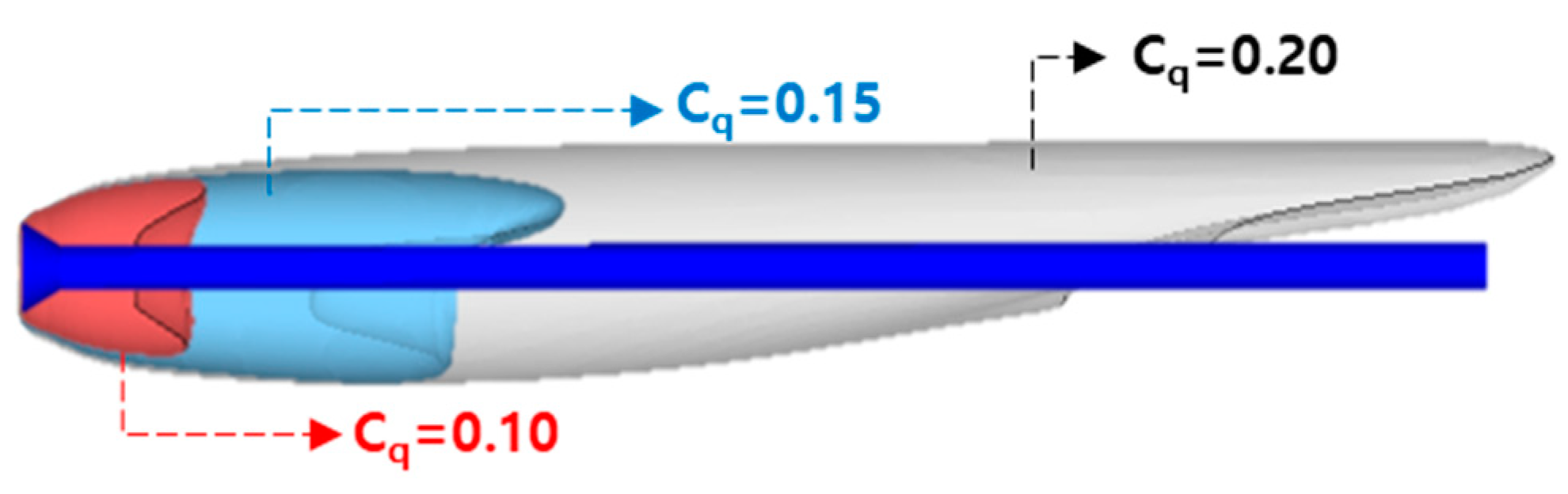
4.5. Ventilated Cavitation with High Speed Underwater Vehicle
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rouse, H.; McNown, J.S. Cavitation and Pressure Distribution: Head Forms at Zero Angle of Yaw; State University of Iowa: Iowa City, IA, USA, 1948. [Google Scholar]
- Kunz, R.F.; Lindau, J.W.; Billet, M.L.; Stinebring, D.R. Multiphase CFD Modeling of Developed and Supercavitaing Flows. In Proceedings of the Von Karman Institute, Special Course on Supercavitating Flows, Rhode-Saint-Genese, Belgium, 12–16 February 2001; RTO EN-013. pp. 12–16. [Google Scholar]
- Ahuja, V.; Hosangadi, A.; Arunajatesan, S. Simulation of cavitating flow using hybrid unstructured meshes. J. Fluids Eng. 2001, 123, 331–340. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Chyczewski, T.S.; Stinebring, D.R.; Gibeling, H.J.; Govindan, T.R. Multi-phase CFD analysis of natural and ventilated cavitation about submerged bodies. ASME Pap. FEDSM 1999, 99, 7364. [Google Scholar]
- Lindau, J.W.; Venkateswaran, S.; Kunz, R.F.; Merkle, C.L. Computation of compressible multiphase flows. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 1285. [Google Scholar]
- Lindau, J.W.; Kunz, L.F.; Venkateswaran, S.; Stinebring, D.R. Homogeneous multiphase CFD modeling of large scale cavities. In Proceedings of the ECCOMAS 2004, Jyväskylä, Finland, 24–28 July 2004. [Google Scholar]
- Merkle, C.L.; Feng, J.Z.; Buelow, P.E.O. Computational modeling of the dynamics of sheet cavitation. In Proceedings of the 3rd International Symposium on Cavitation, Grenoble, France, 7–10 April 1998; pp. 307–311. [Google Scholar]
- Owis, F.M.; Nayfeh, A.H. Computations of the compressible multiphase flow over the cavitating high-speed torpedo. J. Fluids Eng. 2003, 125, 459–468. [Google Scholar] [CrossRef]
- Kim, D.H.; Park, W.G.; Jung, C.M. Numerical simulation of cavitating flow past axisymmetric body. Int. J. Naval Archit. Ocean Eng. 2013, 4, 256–266. [Google Scholar] [CrossRef]
- Ha, C.T.; Park, W.G. Evaluation of a New Scaling Term in Preconditioning Schemes for Computations of Compressible Cavitating and Ventilated Flows. Ocean Eng. 2016, 126, 432–466. [Google Scholar] [CrossRef]
- Ahn, B.K.; Jeing, S.W.; Kim, J.H.; Shao, S.; Hong, J.; Arndt, R.E.A. An Experimental Investigation of Artificial Supercavitation Generated by Air Injection Behind Disk-shaped Cavitator. Int. J. Naval Archit. Ocean Eng. 2016, 9, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Paik, B.G.; Lee, S.J.; Ahn, J.W.; Kim, K.S.; Baek, B.K.; Jeong, Y.R.; Kim, K.Y.; Ahn, J.W.; Seol, H.S.; Ki, S.K. Fundamental Studies for Ventilated Supercavitation Experiments in New High-speed Cavitation Tunnel. J. Soc. Naval Archit. Korea 2018, 55, 330–340. [Google Scholar] [CrossRef]
- Ha, C.T.; Park, W.G. Application of preconditioning to compressible multi-phase mixture flow computation. In Proceedings of the 5th International Symposium on Fluids Machinery and Fluids Engineering, Jeju, Korea, 24–27 October 2012; pp. 24–27. [Google Scholar]
- Ha, C.T.; Kim, D.H.; Park, W.G. A compressive interface-capturing scheme for computation of compressible multi-fluid flows. Comput. Fluids 2017, 152, 164–181. [Google Scholar]
- Ha, C.T.; Park, W.G.; Merkle, C.K. Multiphase flow analysis of cylinder using a new cavitation model. In Proceedings of the 7th International Symposium on Cavitation, CAV2009, Ann Arbor, MI, USA, 16–18 August 2006; p. 99. [Google Scholar]
- Owis, F.; Nayfeh, A. Numerical simulation of super-and partially-cavitating flows over an axisymmetric projectile. In Proceedings of the 39th Aerospace Science Metting and Exhibit, Reno, NV, USA, 8–11 January 2001; p. 1042. [Google Scholar]
- Lindau, J.W.; Kunz, R.F.; Venkateswaran, S.; Merkle, C.L. Development of a fully—Compressible multiphase Reynolds Navier–Stokes model. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001; pp. 11–14. [Google Scholar]
- Johansen, S.T.; Wu, J.; Shyy, W. Filter-based unsteady RANS computations. Int. J. Heat Fluid Flow 2004, 25, 10–21. [Google Scholar] [CrossRef]
- Kinzel, M.P. Computational Techniques and Analysis of Cavitating-Fluidflows; The Pennsylvania State University: State College, PA, USA, 2008. [Google Scholar]












© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-H.; Paramanantham, S.S.; Park, W.-G. Numerical Analysis of Multi-Phase Flow around Supercavitating Body at Various Cavitator Angle of Attack and Ventilation Mass Flux. Appl. Sci. 2020, 10, 4228. https://doi.org/10.3390/app10124228
Kim D-H, Paramanantham SS, Park W-G. Numerical Analysis of Multi-Phase Flow around Supercavitating Body at Various Cavitator Angle of Attack and Ventilation Mass Flux. Applied Sciences. 2020; 10(12):4228. https://doi.org/10.3390/app10124228
Chicago/Turabian StyleKim, Dong-Hyun, SalaiSargunan S Paramanantham, and Warn-Gyu Park. 2020. "Numerical Analysis of Multi-Phase Flow around Supercavitating Body at Various Cavitator Angle of Attack and Ventilation Mass Flux" Applied Sciences 10, no. 12: 4228. https://doi.org/10.3390/app10124228
APA StyleKim, D.-H., Paramanantham, S. S., & Park, W.-G. (2020). Numerical Analysis of Multi-Phase Flow around Supercavitating Body at Various Cavitator Angle of Attack and Ventilation Mass Flux. Applied Sciences, 10(12), 4228. https://doi.org/10.3390/app10124228





