An Ordinary State-Based Peridynamic Model for Fatigue Cracking of Ferrite and Pearlite Wheel Material

Abstract

To deal with a new-developed ferrite and pearlite wheel material named D1, an alternative ordinary state-based peridynamic model for fatigue cracking is introduced due to cyclic loading. The proposed damage model communicates across the microcrack initiation to the macrocrack growth and does not require additional criteria. Model parameters are verified from experimental data. Each bond in the deformed material configuration is built as a fatigue specimen subjected to variable amplitude loading. Fatigue crack initiation and crack growth developed naturally over many loading cycles, which is controlled by the parameter “node damage” within a region of finite radius. Critical damage factors are also imposed to improve efficiency and stability for the fatigue model. Based on the improved adaptive dynamic relaxation method, the static solution is obtained in every loading cycle. Convergence analysis is presented in smooth fatigue specimens at different loading levels. Experimental results show that the proposed peridynamic fatigue model captures the crack sensitive location well without extra criteria and the fatigue life obtained from the simulation has a good correlation with the experimental results.

1. Introduction

Fatigue of metallic materials is a cumulative and irreversible process [1,2,3]. Under cyclic loading, the new dynamic balances are broken and the voids are generated, so that the damage will be initiated and accumulated [4,5,6]. The whole fatigue life is essentially a multiscale phenomenon [7,8,9,10,11], depending strongly on the material, geometry of the loaded body, the external loaded forces conditions, environmental factors, etc. The life prediction schemes of ferrite and pearlite wheel material under multiaxial loading have been through extensive research both in industry and scientific institution [12,13,14]. Modeling of fatigue crack growth in metallic materials encounters many problems [15,16,17]. Based on the framework of traditional continuum theory, the finite element method (FEM) models or various modified versions aim to find the kinetic relations among parameters near the fatigue crack tip that characterize the fatigue crack evolution [18,19,20]. By redefining the body, the crack is treated as a boundary so that extra criteria, such as fatigue crack growth speed and direction which guide the crack path, are necessary [21,22,23]. To solve these problems, Linear Elastic Fracture Mechanics (LEFM) use Cohesive Zone Elements (CZE) to deal with Mode-I crack mode and mixed-mode fracture [24,25,26,27]. The number of cohesive elements increases with decreasing mesh size, yet the size of the continuum region remains the same. Frequent redefining the body is difficult and costly, especially with multiple interacting cracks. The extended finite element method (XFEM), using the local enrich functions, permits the cracks to propagate on any element surface without remeshing in every incremental crack growth [28,29,30,31,32].Both the FEM model and the XFEM method need extra criteria such as the time of forming fatigue cracks, fatigue propagation speed, direction, branch, arrest, etc. The final fatigue fracture mechanisms are associated with grain boundaries, dislocations, microcracks, anisotropy, etc [33,34,35]. Each of them plays an important role at a specific length scale. It is difficult to obtain the location of fatigue initiation in advance, let alone the extra criteria from the experimental data [36,37,38].

In contrast, a peridynamic theory (PD) uses the spatial integral equations as opposed to derivatives of the displacement field to compute internal force acting on a material particle [39,40,41]. Material damage is part of the constitutive model. Without the need for some special crack growth criteria, peridynamics allows the cracks to propagate at multiple sites with natural paths not only along the element boundary in a consistent framework. Furthermore, the PD theory can link the micro to macro length scales [42,43,44].

The fatigue crack model with peridynamics was originally proposed by Oterkus, Guven, and Madenci [45] and substantially improved by and Askari [46]. Two phases of fatigue failure: crack initiation, fatigue propagation, are included in a consistent fatigue model and the parameters of the model are calibrated separately with experimental data. In ref [47]. the dynamic relaxation method is used to obtain the static solution. Nucleation and growth of a helical fatigue crack are demonstrated by using an aluminum alloy rod. Zhang [48] presented the conjugate gradient energy minimization method to obtain the static solution and applied this fatigue model to two-phase composite materials. The results show that the peridynamic fatigue crack model can deal with multiple crack without extra criteria to guide the crack path [49,50,51]. However, these peridynamic fatigue models are mainly focus on the simple linear elastic property. And the fatigue crack criteria just use the critical bond elongation technic so that it is difficulty to build effective links between the actual physical parameters and the current models. Moreover, few peridynamic fatigue models take into the cases of multiaxial fatigue failure.

To bridge the micro fatigue crack initiation to the macro fatigue crack growth, an alternative ordinary state-based peridynamic model for fatigue cracking is proposed. Based on the thermal disturbance of atomic motion, the theoretical foundation for the peridynamic fatigue model is built under cyclic loading. Fatigue model parameters are verified from S-N data of ferrite and pearlite wheel material. Each bond in the deformed material configuration is treated as a fatigue specimen subjected to variable amplitude loads. Bond damage accumulated over time, according to the cyclic strain in the bond that its progressive failure is characterized by a history variable called “wear-out life”. A bond will be broken when the variable reaches the entire life. Fatigue crack initiation and crack growth formulated naturally over many loading cycles which is controlled by the parameter “node damage” within a region of finite radius. Critical damage factors are also imposed to improve efficiency and stability for the fatigue model. Based on the improved adaptive dynamic relaxation method, the static solution is obtained in every loading cycle. Convergence analysis is presented in the smooth fatigue specimens at different loading levels. Experimental results show that the peridynamic results capture the crack sensitive location well without extra criteria. Fatigue lifetimes obtained from the simulation have a good correlation with the experimental results.

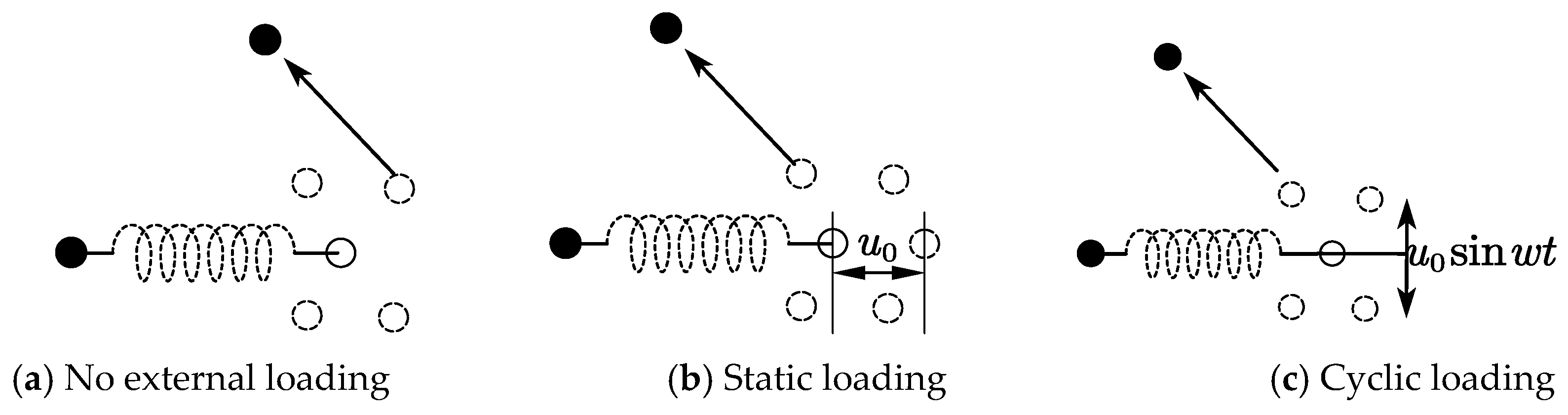
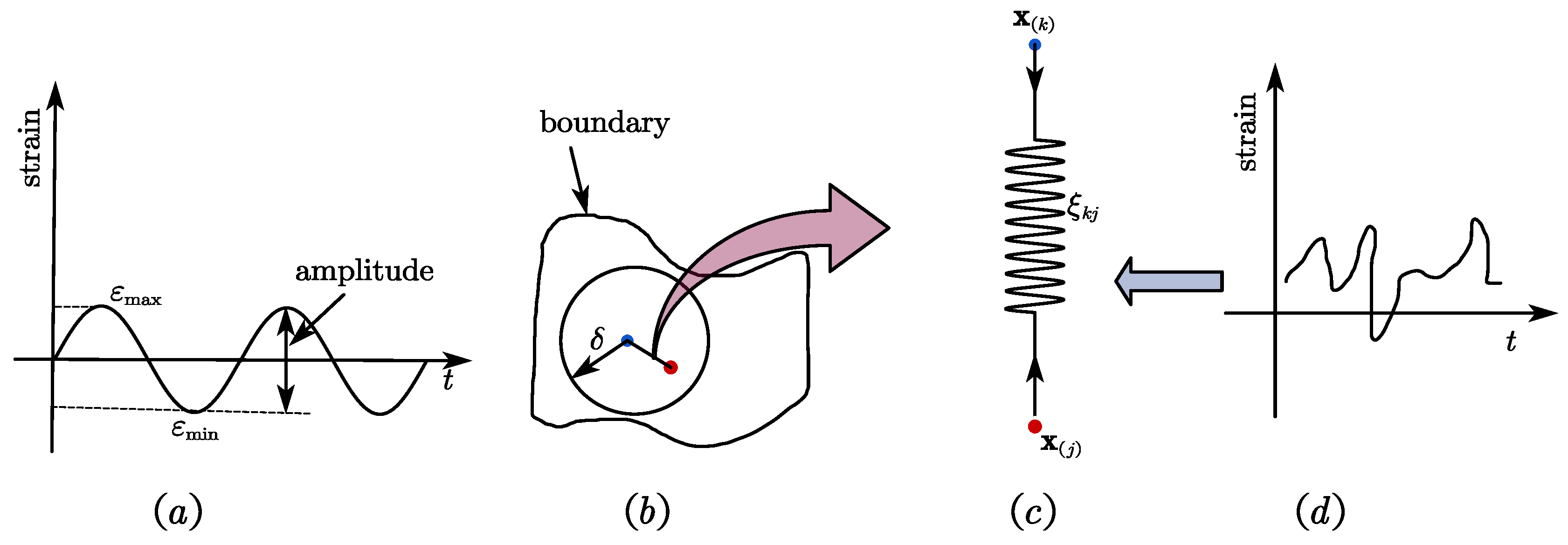
2. Mechanism of Fatigue Damage Evolution

2.1. Fatigue Damage Evolution

From the point of a material’s atomic structure, the atoms vibrate in high frequency (about 10¹²~10¹³ Hz) near the equilibrium position. Each atom in the material has certain energy whose value is random and different from other atoms. When the active energy of an atom exceeds a certain value, the atom will escape from its original equilibrium position and a void will be generated. The probability of an atom’s active energy above a certain value Q is described as follows:

$$P=\exp \left(-\frac{Q}{kT}\right)$$

(1)

where k is the Boltzmann constant, $T$ is thermodynamic temperature, $Q$ is the critical active energy that is the smallest value of an atom escaping from the equilibrium position.

As shown in Figure 1a, without external loading, although the critical energy $Q$ is larger than other loading condition, there is still some atoms escaping from the original equilibrium position and the escaped atoms reach to a new dynamic vacant site equilibrium state. Hence, in such a loading condition, damage evolution will be negligible.

As shown in Figure 1b, with the static loading, the critical active energy Q is described as follows:

$$Q=\frac{{\tau }_b+\alpha {\tau }_b\tau +\beta {\tau }^2}{2G}$$

(2)

where ${\tau }_b$ is ideal material shear strength, $\tau$ is the external shear stress, $G$ is the shear modulus, $\alpha$ is the constant associated with stress concentration factor, $\beta$ is the constant associated with the amplitude of the static loading. Combining Equations (1) and (2), the probability of an atom’s active energy above a certain value Q under static loading is described as follows:

$$P=\exp \left(-\frac{{\tau }_b+\alpha {\tau }_b\tau +\beta {\tau }^2}{2GkT}\right)$$

(3)

where it can be seen that the probability of an atom escaping from the equilibrium position under static loading increased compared with no external loading condition. The displacement u₀ of an atom away from the original equilibrium position is invariable. Therefore, the voids generated by the thermal disturbance can be annihilated.

As shown in Figure 1c, with the cyclic loading, the displacement of an atom away from the original equilibrium position is alternating. The voids generated by the thermal disturbance cannot be annihilated so that the damage will be initiated and accumulated.

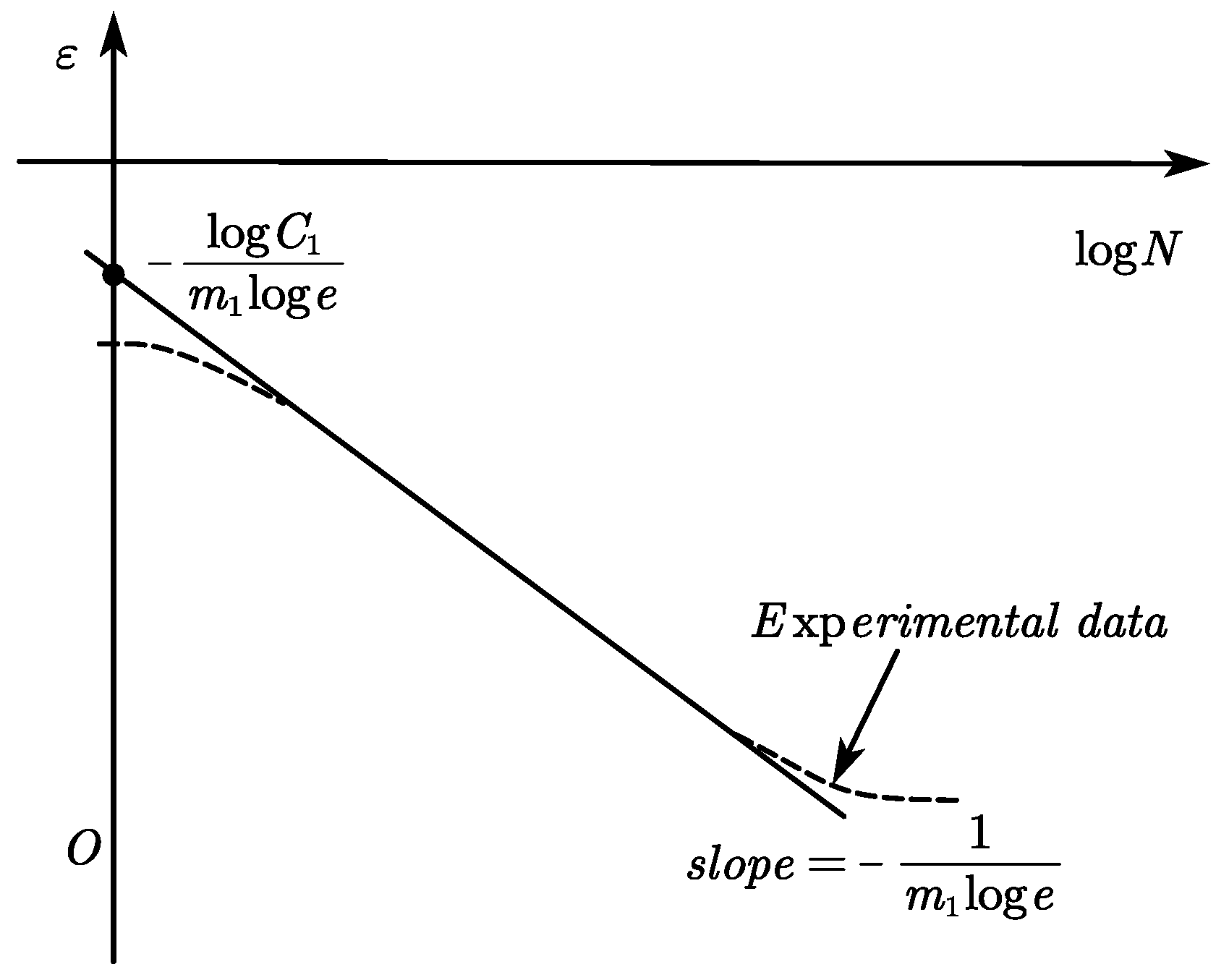
2.2. Fatigue Damage Evolution Law

The change rate caused by atomic escape is described as follows:

$$v=C\exp \left(-\frac{Q}{kT}\right)$$

(4)

where C is the material constant that contributes to the change rate caused by the probability of atomic escape.

There is a direct correlation between the current stress and the fatigue damage under cyclic loading for the critical energy The damage evolution rate of fatigue under such loading condition is described as follows [52]:

$$\frac{dD}{dN}=C\exp \left(-\frac{Q\left({\sigma }_a,{\sigma }_m,D\right)}{kT}\right)$$

(5)

where ${\sigma }_a$ is cyclic stress amplitude, ${\sigma }_m$ is mean stress, D is the current damage quantity.

3. Peridynamic Theory for Fatigue Cracking

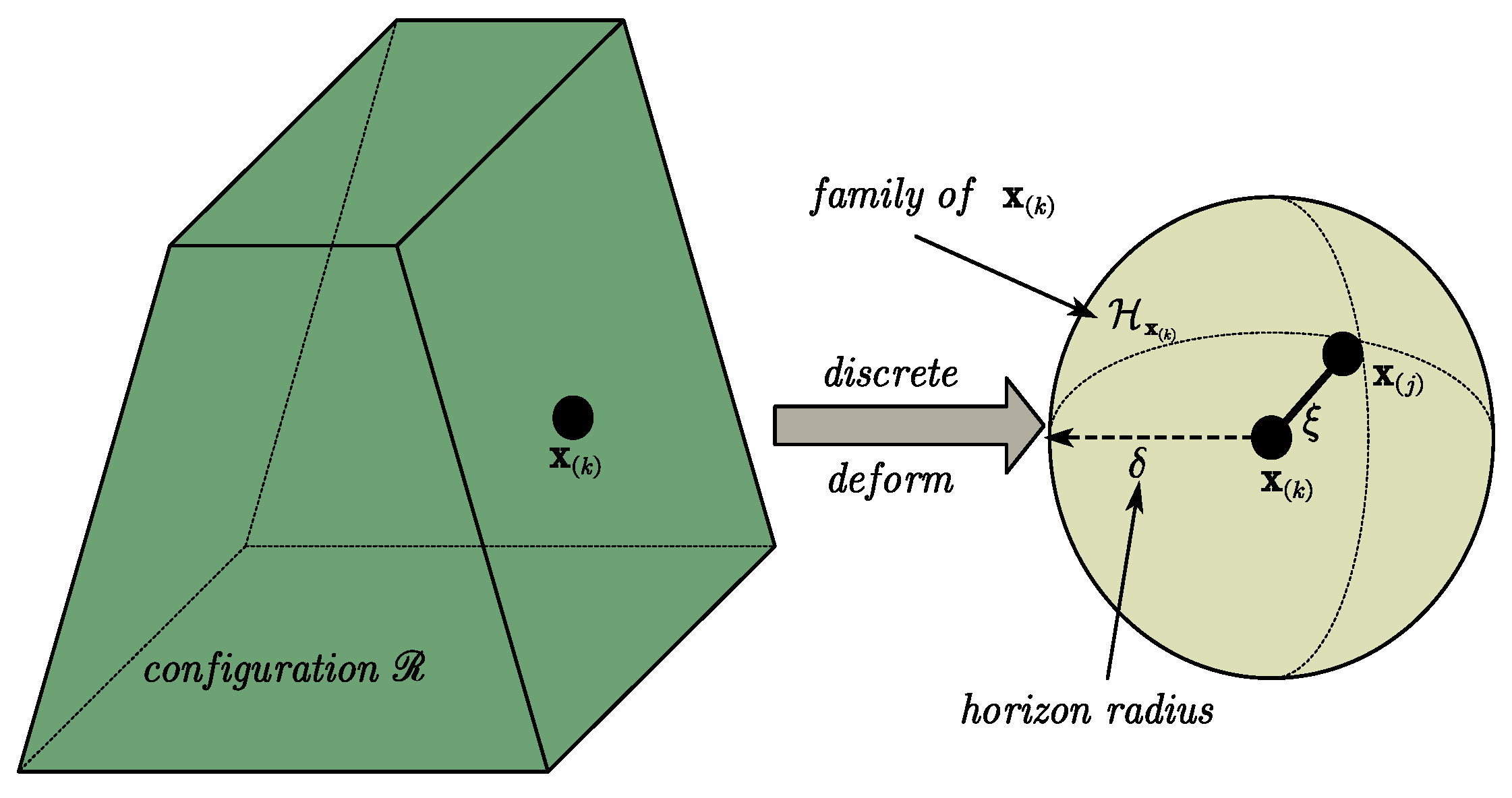
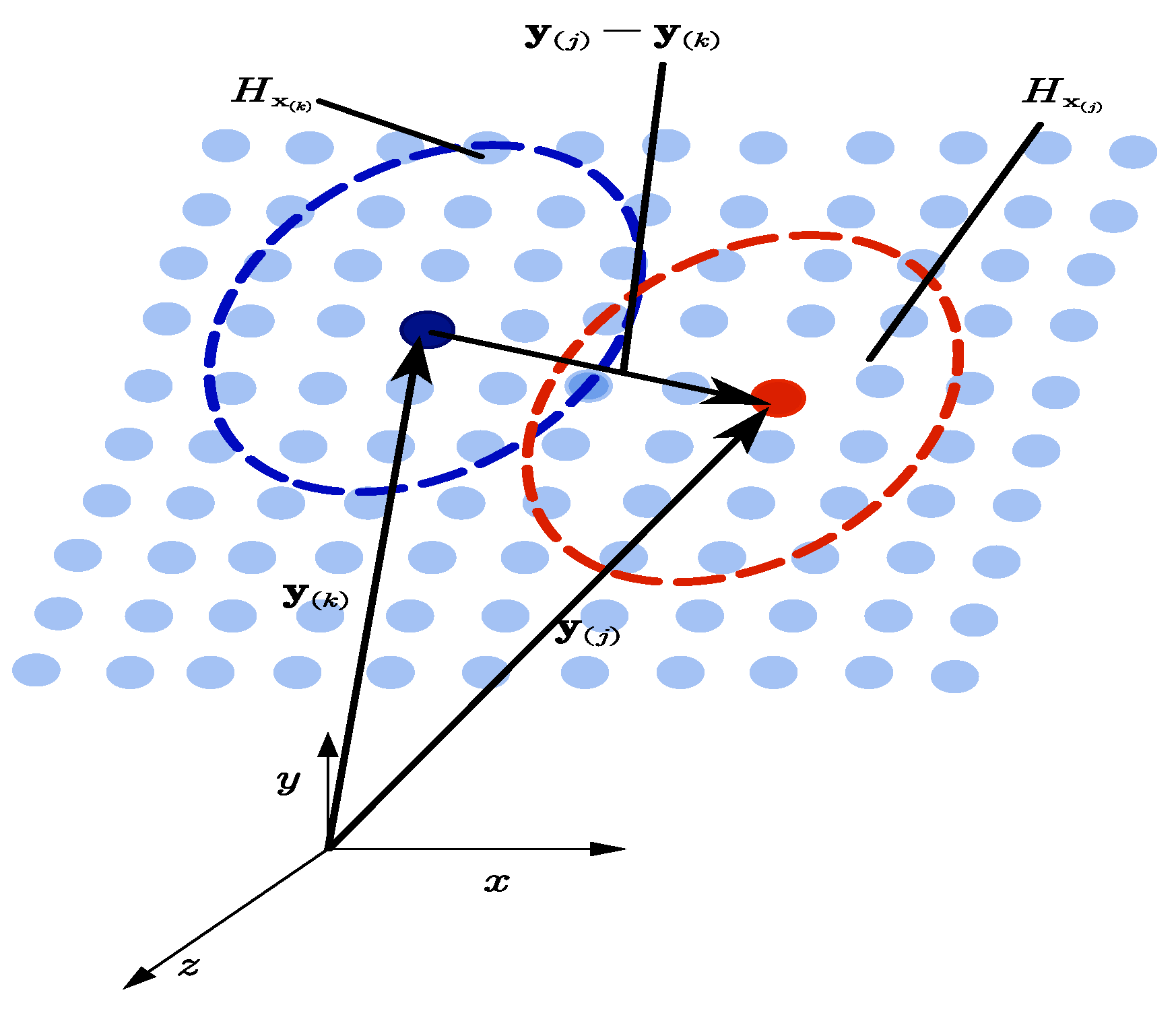
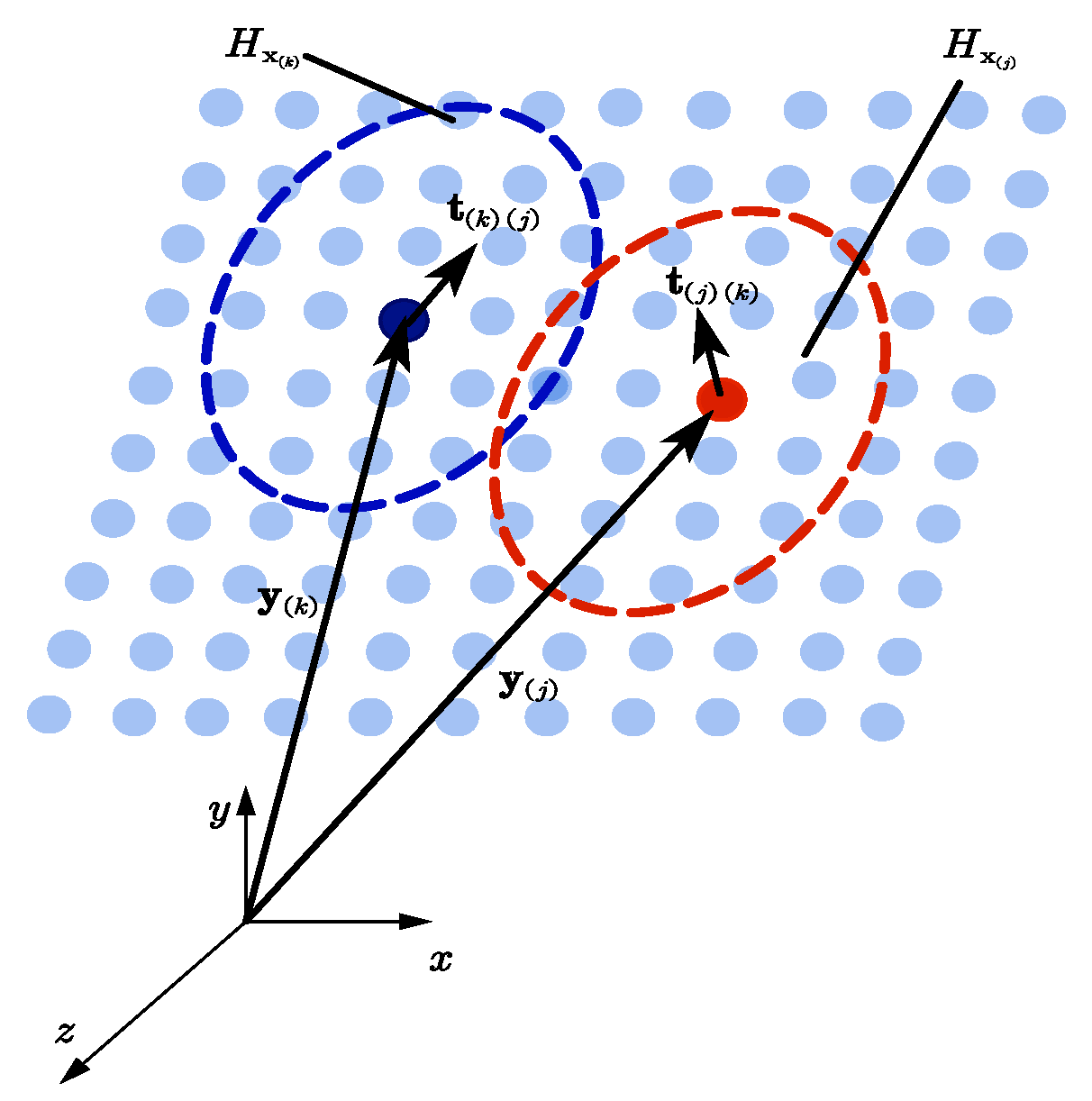
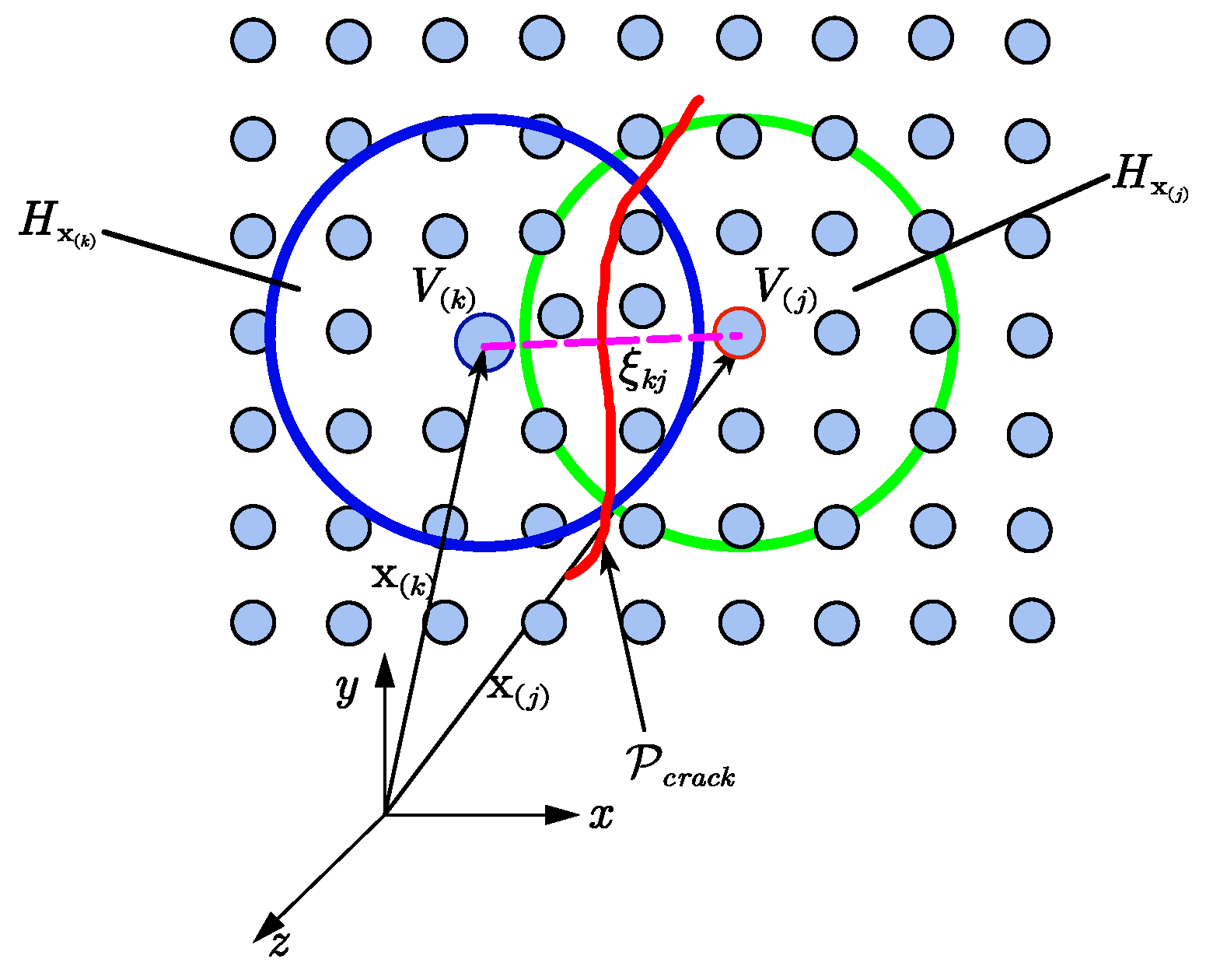
3.1. Basic Theory

According to peridynamic theory, the physics of a material body at a point interacts with all points within its horizon, as shown in Figure 2. The equation of motion of the material point $x_{\left(k\right)}$ in the deformed configuration is described as follows [53]:

$${\rho }_{\left(k\right)}\ddot{u}\left(x_{\left(k\right)},t\right)={{\displaystyle \int }}_{{\mathscr{H}}_{\left(x_{\left(k\right)}\right)}}(\underset{¯}{T}\left(x_{\left(k\right)},t\right)\langle x_{\left(j\right)}-x_{\left(k\right)}\rangle -\underset{¯}{T}\left(x_{\left(j\right)},t\right)\langle x_{\left(k\right)}-x_{\left(j\right)}\rangle )d{\mathscr{H}}_{\left(x_{\left(k\right)}\right)}+b\left(x_{\left(k\right)},t\right)$$

(6)

where $b\left(x_{\left(k\right)},t\right)$ is the body load vector, $\underset{¯}{T}\left(x_{\left(k\right)},t\right)$ and $\underset{¯}{T}\left(x_{\left(j\right)},t\right)$ are the force vector states, ${\mathscr{H}}_{\left(x_{\left(k\right)}\right)}$ is the horizon of point $x_{\left(k\right)}$, $u\left(x_{\left(k\right)},t\right)$ is the displacement vector at time t.

As shown in Figure 2, the bond ${\xi }_{kj}$ strain between material points $x_{\left(k\right)}$ and $x_{\left(j\right)}$ is described as follows:

$$s_{\left(k\right)\left(j\right)}=\frac{\left(\left|y_{\left(j\right)}-y_{\left(k\right)}\right|-\left|x_{\left(j\right)}-x_{\left(k\right)}\right|\right)}{\left|x_{\left(j\right)}-x_{\left(k\right)}\right|}$$

(7)

As shown in Figure 3, all of the relative position vectors in the horizon of point $x_{\left(k\right)}$, $\left(y_{\left(j\right)}-y_{\left(k\right)}\right)$ $\left(j=1,2,\dots ,\infty \right)$ is described as follows:

$$\{\begin{array}{c}\underset{¯}{Y}\left(x_{\left(k\right)},t\right)=\left\{\begin{array}{c}{y}_{\left(1\right)}-y_{\left(k\right)}\\ ⋮\\ y_{(\infty )}-y_{\left(k\right)}\end{array}\right\}\\ \left(y_{\left(j\right)}-y_{\left(k\right)}\right)=\underset{¯}{Y}\left(x_{\left(k\right)},t\right)\langle x_{\left(j\right)}-x_{\left(k\right)}\rangle \end{array}$$

(8)

where $\underset{¯}{Y}\left(x_{\left(k\right)},t\right)$ is the deformation vector state. Equation (8) means that the response of a material point $x_{\left(k\right)}$ depends collectively on the deformation of all bonds connected to the point.

As shown in Figure 4, the force vector state $\underset{¯}{T}\left(x_{\left(k\right)},t\right)$ including an infinite-dimension array force density vectors, $t_{\left(k\right)\left(j\right)}$, is described as follows:

$$\left\{z:\left|z-\alpha \right|<r\right\}$$

(9)

$$\underset{¯}{T}\left(x_{\left(k\right)},t\right)=\left\{\begin{array}{c}{t}_{\left(k\right)\left(1\right)}\\ ⋮\\ t_{\left(k\right)(\infty )}\end{array}\right\}$$

(10)

where the force density vector, $t_{\left(k\right)\left(j\right)}$, that the material point at location $x_{\left(j\right)}$ exerts on the material point at location $x_{\left(k\right)}$ can be expressed as:

$$t_{\left(k\right)\left(j\right)}\left(u_{\left(j\right)}-u_{\left(k\right)},x_{\left(j\right)}-x_{\left(k\right)},t\right)=\underset{¯}{T}\left(x_{\left(k\right)},t\right)\langle x_{\left(j\right)}-x_{\left(k\right)}\rangle$$

(11)

As for ordinary state-based peridynamic theory, the scalar state of the force density vector can be expressed as

$$\{\begin{array}{ccc}\{& \begin{array}{ll}\underset{¯}{t}=& 3k\theta \frac{\underset{¯}{\omega }\underset{¯}{x}}{A}+15G\frac{\underset{¯}{\omega }{\underset{¯}{e}}^d}{A}\\ & A=\left(\underset{¯}{\omega }\underset{¯}{x}\right)\cdot \underset{¯}{x}\\ & {\underset{¯}{e}}^d=\underset{¯}{e}-\frac{\theta \underset{¯}{x}}{3}\\ & \theta =3\frac{\underset{¯}{\omega }\underset{¯}{x}\cdot e}{A}\end{array}& for3D\\ & or& \\ \{& \begin{array}{ll}\underset{¯}{t}=& 2k^{\prime }\theta \frac{\underset{¯}{\omega }\underset{¯}{x}}{A}+8G\frac{\underset{¯}{\omega }{\underset{¯}{e}}^d}{A}\\ & A=\left(\underset{¯}{\omega }\underset{¯}{x}\right)\cdot \underset{¯}{x}\\ & {\underset{¯}{e}}^d=\underset{¯}{e}-\frac{\theta \underset{¯}{x}}{3}\end{array}& for2D\end{array}$$

(12)

where $\underset{¯}{\omega }$ is the influence function, $\theta$ is the volume dilatation, ${\underset{¯}{e}}^d$ is the deviatoric extension state and $\underset{¯}{e}$ is the extension scalar state, $k$ is the bulk modulus, $G$ is the shear modulus, $k^{\prime }$ can be expressed respectively as:

$$k^{\prime }=\{\begin{array}{ll}\frac{E}{2\left(1-\upsilon \right)}& planestress\\ \frac{E}{2\left(1+\upsilon \right)\left(1-2\upsilon \right)}& planestrain\end{array}$$

(13)

where $E$ is the elastic modulus, $\upsilon$ is the Poisson ratio.

For elastic solid material, the strain energy density of material point $x_{\left(k\right)}$ in the peridynamic state model can be expressed as

$$W=\frac{1}{2}B{\theta }^2+\frac{15G}{2A}\left(\underset{¯}{\omega }\underset{¯}{e}\right)\cdot e$$

(14)

where $B$ is defined as:

$$B=\{\begin{array}{c}k-\frac{15G}{9}for3D\\ k-\frac{15G}{4}for2D\end{array}$$

(15)

3.2. Energy-Based Failure Criterion

As shown in Figure 5, the force vector states $\underset{¯}{T}\left(x_{\left(k\right)},t\right)$ and $\underset{¯}{T}\left(x_{\left(j\right)},t\right)$ are opposite in direction and parallel to their deformed relative deformed position. However, their values are not equal.

As shown in Figure 6, the force density $f_{\left(kj\right)}=\left(\underset{¯}{t}\left[x_{\left(k\right)},t\right]-\underset{¯}{t}\left[x_{\left(j\right)},t\right]\right)$ exhibits non-linearity under cycle loading, therefore the total energy density stored in the bond $\xi$ can be expressed as follows.

$${\omega }_{\xi }={{\displaystyle \int }}_0^{{\epsilon }_{\xi }\left(\Delta t\right)}{\left(f_{\left(kj\right)}\right)}_{\xi }d\epsilon$$

(16)

As shown in Figure 7, all points $P_{down}$ along the dashed line $l$, connected to all points $P_{up}$ across fracture plane $\gamma$ of unit area and the volume above the fracture plane. The energy density required to open the plane $\gamma$ is as follows:

$$w_{\gamma }={{\displaystyle \int }}_0^{\delta }{{\displaystyle \int }}_0^{2\pi }{{\displaystyle \int }}_z^{\delta }{{\displaystyle \int }}_0^{{\cos }^{-1}\left(z/\xi \right)}{w}_c{\xi }^2\sin \varphi d\varphi d\xi d\theta dz$$

(17)

where $w_c$ is the critical energy density, $w_{\gamma }$ is the energy release rate defined in the continuum damage mechanics theory.

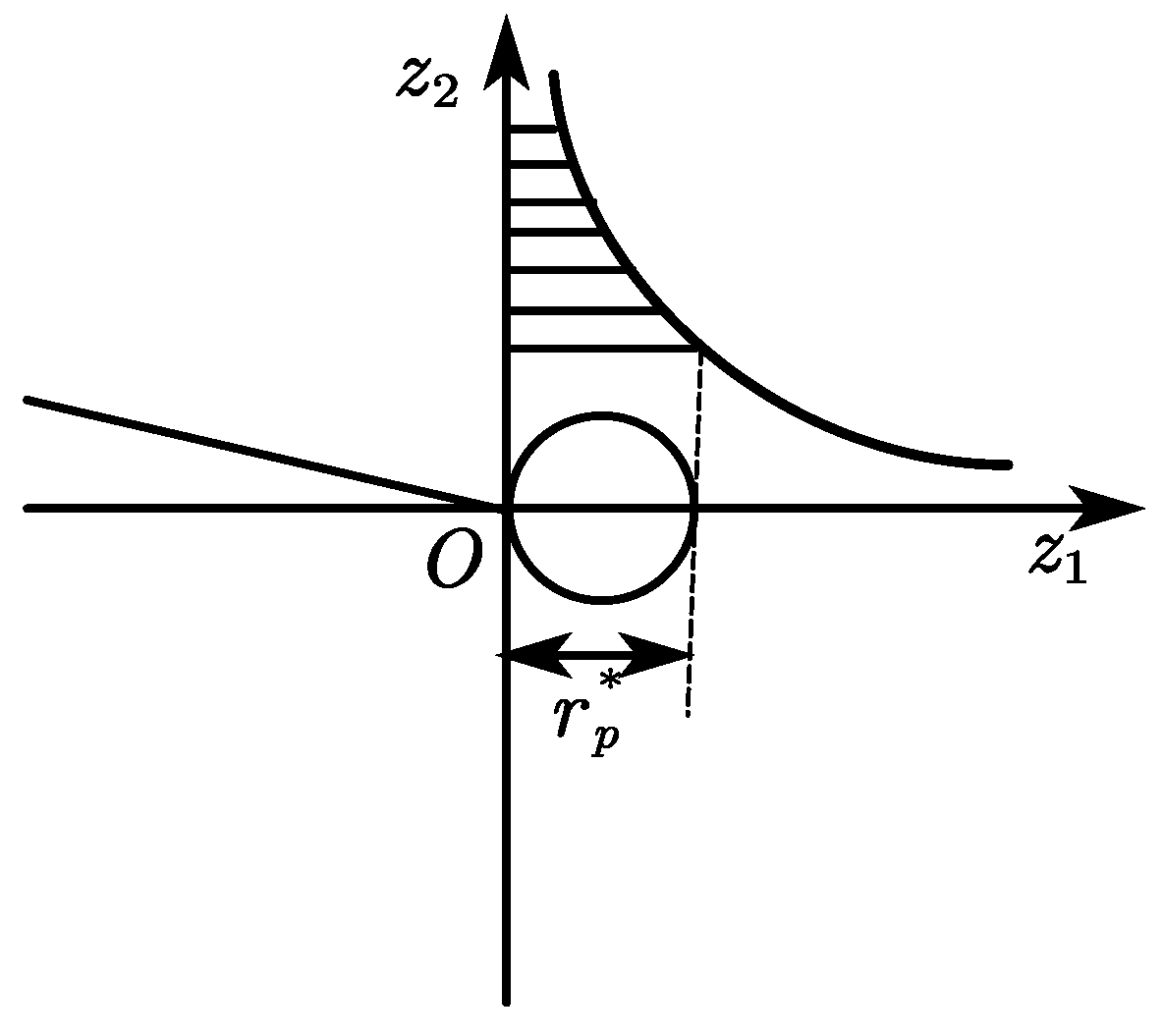
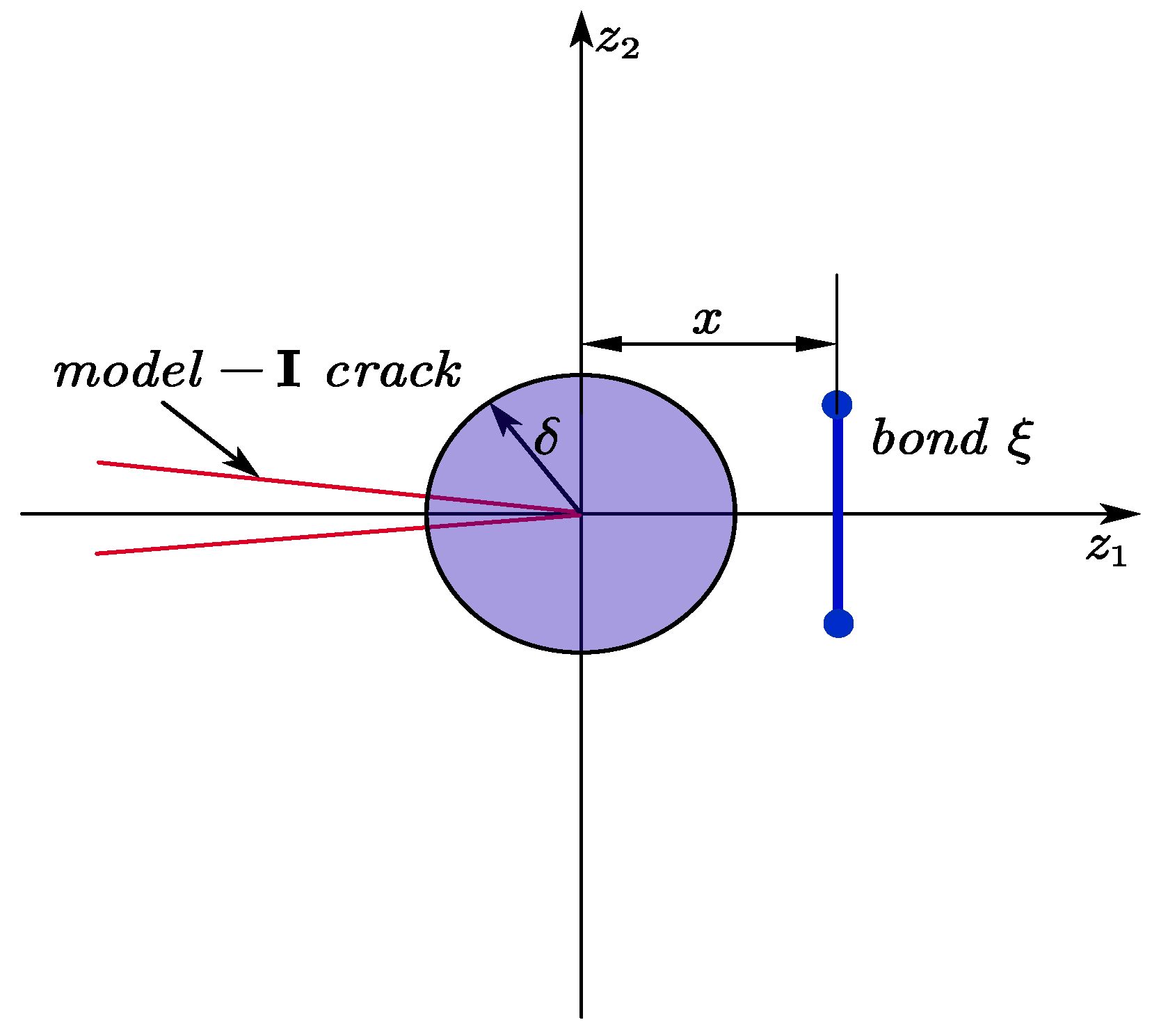
3.3. Fatigue Crack Tip Deformation Analysis

As shown in Figure 8, there are three kinds of bonds near the model-I crack tip: broken bonds, core bonds, and partially damaged bonds. For the core bonds, the bond strain $s_{core}^{*}$ is the largest compared with the partially damaged bonds [46]. Since the material is linear elastic-perfectly plasticity, the core bond strain can be described as:

$$s_{core}^{*}\left(\delta \right)={\widehat{s}}_{core}\frac{K}{E\sqrt{\delta }}$$

(18)

where $K$ is the stress intensity factor, $E$ is elastic modulus, ${\widehat{s}}_{core}$ is a dimensionless parameter.

As shown in Figure 9, there is a plastic zone near the crack tip, the length of the plastic zone is $r_p^{*}$. For the linear elastic fracture mechanics, the strain in the plastic zone can be described as:

$$s\left(z\right)~\frac{K}{E\sqrt{2\pi z}}0⩽z⩽r_p^{*}$$

(19)

Combining Equations (17) and (18), a function $\widehat{f}$ can be described as:

$$\widehat{f}\left(\frac{z}{\delta }\right)~\frac{1}{{\widehat{s}}_{core}\sqrt{2\pi z/\delta }}$$

(20)

4. Trans-Scale Peridynamic Fatigue Model

In ref. [46], Silling and Askari proposed a fatigue cracking model which can simulate two phases in fatigue failure: crack initiation, crack propagation. The evolution law for the bond “remaining life” is calibrated with S-N curve data during the fatigue crack nucleation phase and with Paris’ law during the fatigue crack growth phase. Inspired by this work, in this section, a trans-scale peridynamic fatigue model is built based on the mechanism of fatigue. Macroscale is directly depicted by the tans-scale peridyanmic model. Each bond in the body is defined as the ideal fatigue test specimen under variable loads.

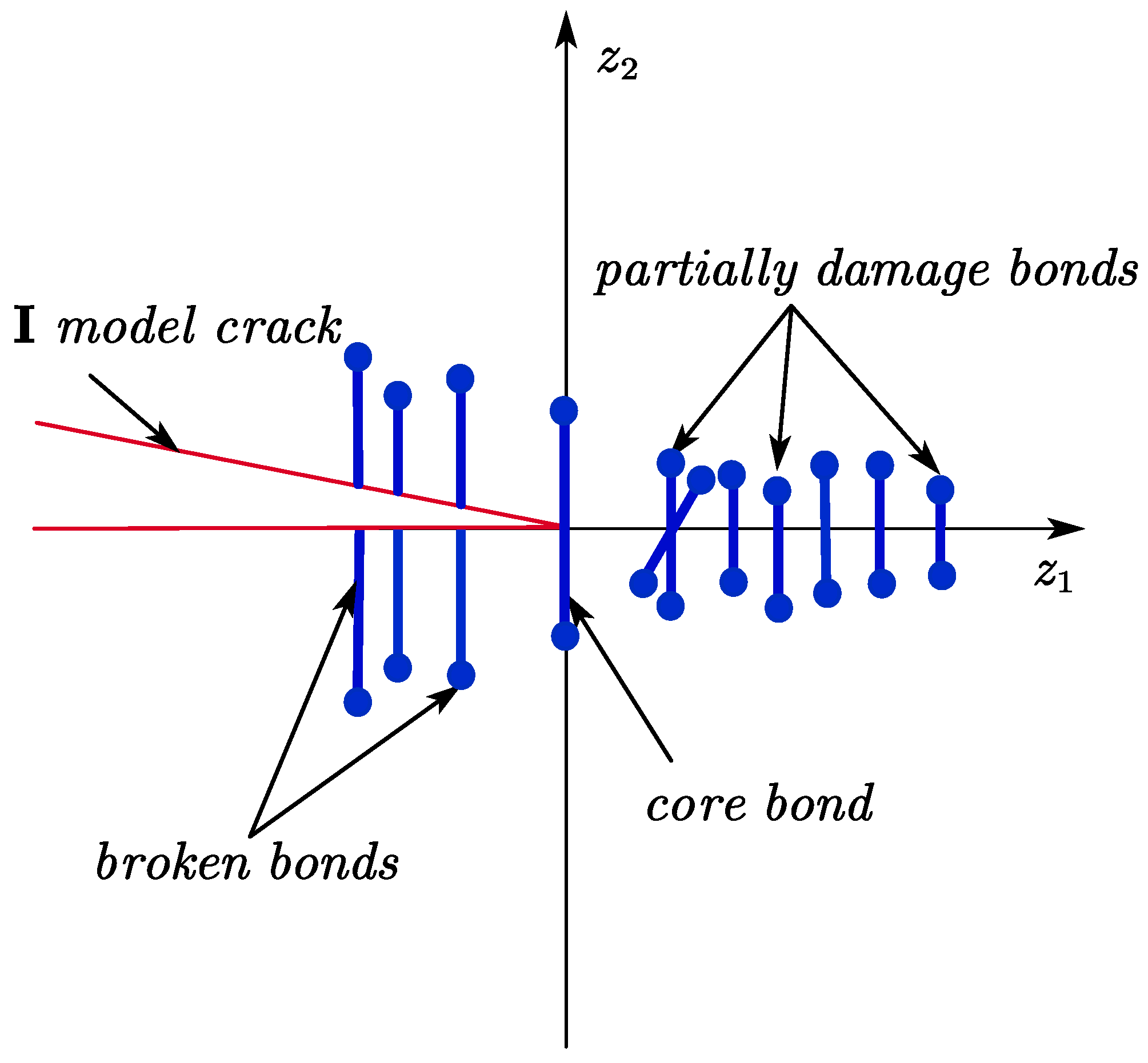
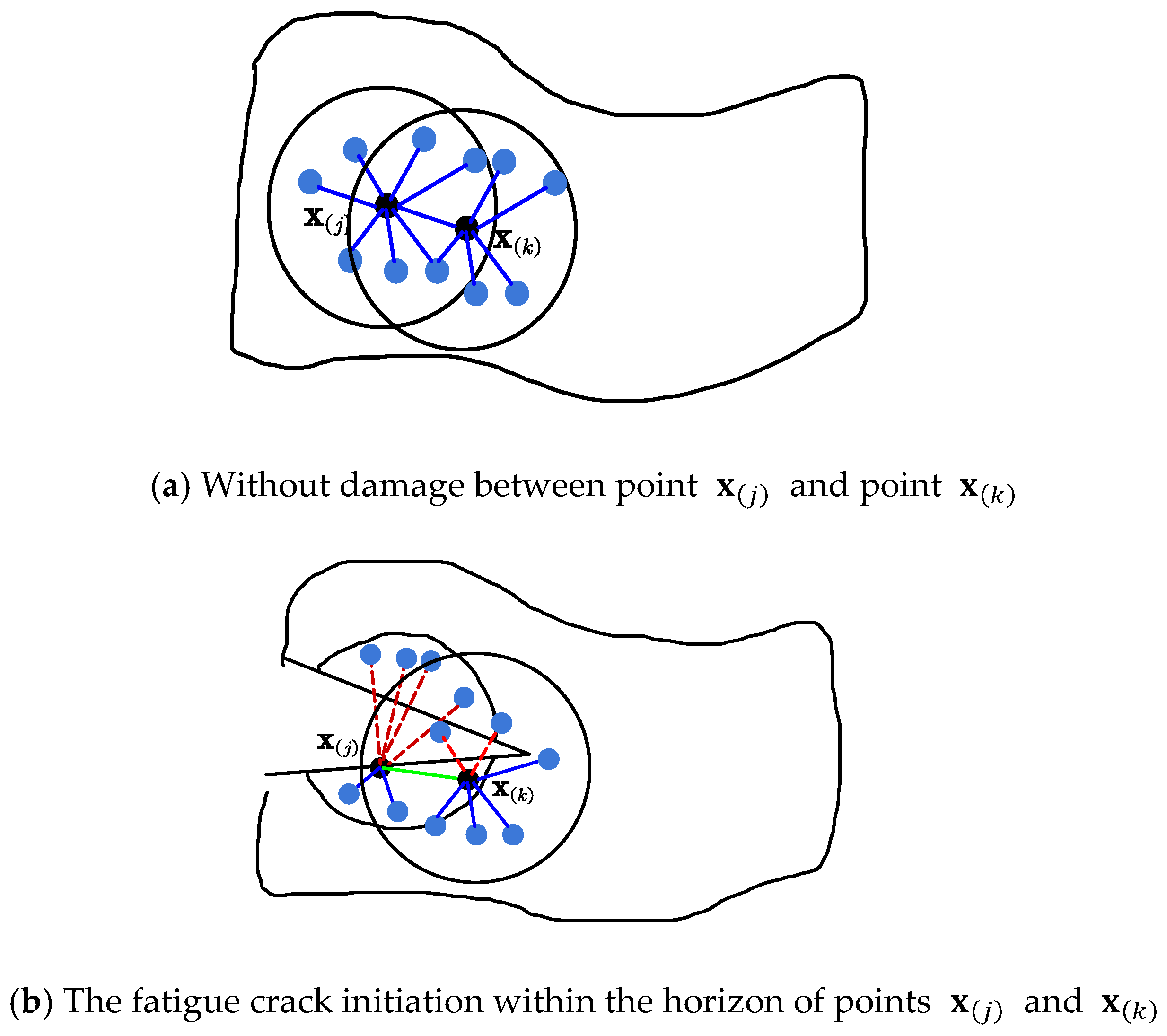
4.1. Bond Damage and Point Damage within the Horizon

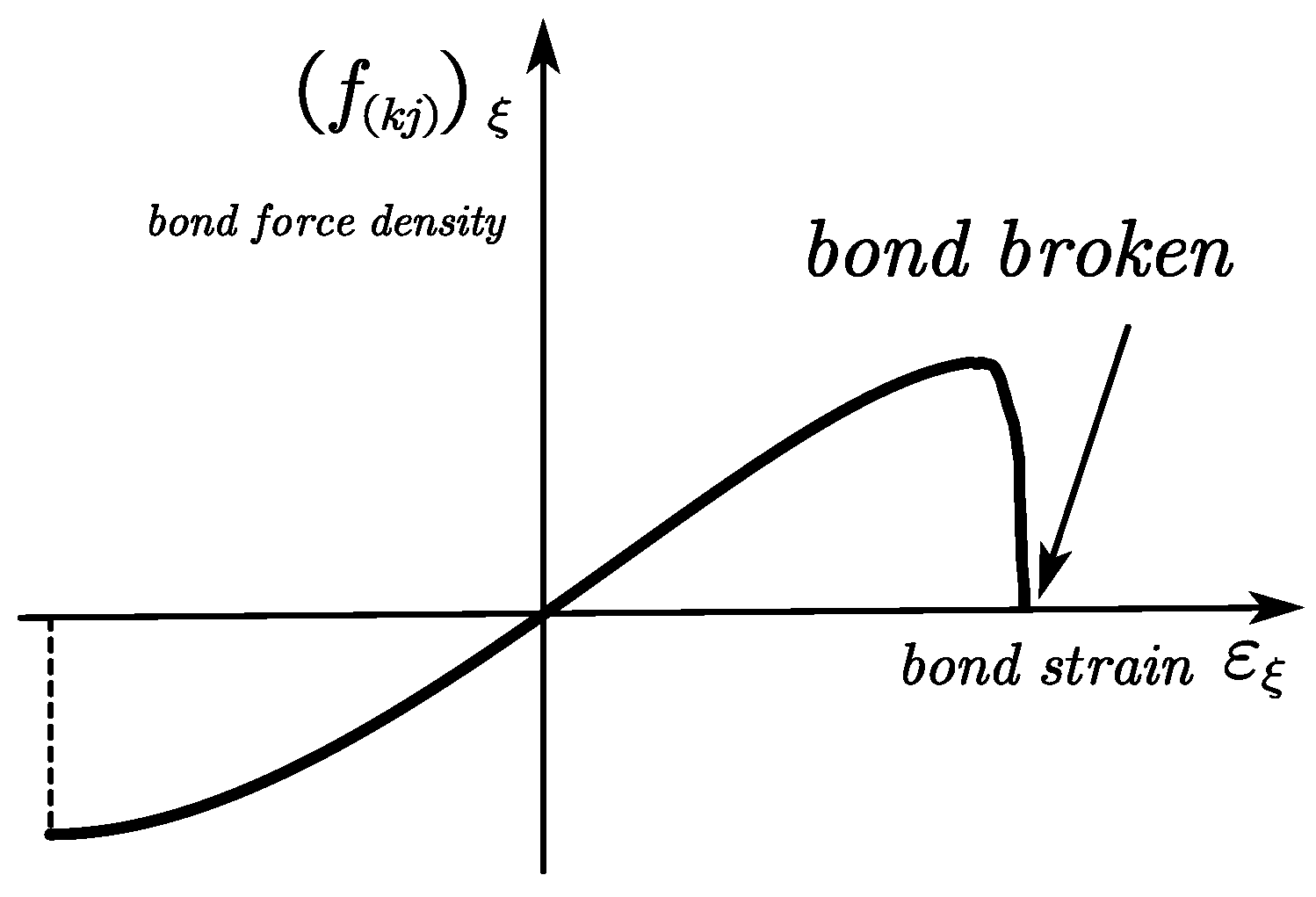
4.1.1. Bond Fatigue Damage and Failure

Bond damage in a peridynamic material body is defined by bond breakage. The simplest criterion is that when the bond strain, shown in Equation (21), exceeds the critical value, the micro-potential between two material points $x_{\left(k\right)}$ and $x_{\left(j\right)}$ will be removed away. As shown in Figure 5, the spring-like bond $\xi$ is subjected to variable force density in its two ends during each loading cycle exert on the body $ℛ$. Fatigue bond damage is tracked by a history-dependent variable $d_{kj}\left(\xi ,t\right)$.

$$d_{kj}\left(\xi ,t\right)=\{\begin{array}{c}1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}if \xi is broken\\ \phi \left(\xi ,s,t\right) otherwise\end{array}$$

(21)

where $\phi \left(\xi ,\epsilon ,t\right)$ is the normalized damage function, depending on the current bond strain $s$ and time t.

4.1.2. Point Damage and Fatigue Cracking

For a given material point, the point damage is defined as the weighted ratio of the number of eliminated bonds interactions to the total number of initial interactions within its family. The fatigue damage of a point $x_{\left(k\right)}$ during each loading cycle is described as:

$$\varphi \left(x_{\left(k\right)}\right)=\frac{{\int }_{{\mathscr{H}}_{x_{\left(k\right)}}}\phi \left(\xi ,s,t\right)d{V}^{\prime }}{{\int }_{{\mathscr{H}}_{x_{\left(k\right)}}}d{V}^{\prime }}$$

(22)

where $d{V}^{\prime }$ is an incremental volume for the material point connecting the point $x_{\left(k\right)}$ within the horizon ${\mathscr{H}}_{\left(x_{\left(k\right)}\right)}$. As shown in Figure 10, the failure of one bond ${\xi }_{kj}$ in the peridynamic body leads to the incremental point damage for $x_{\left(k\right)}$ and $x_{\left(j\right)}$. Therefore, the force density acting among the material points will be redistributed leading to the autonomous damage of neighboring bonds. The progressive failure of bond damage leads to the crack surface ${𝒫}_{crack}$ in the peridynamic material body.

4.2. Trans-Scale Fatigue Model

As shown in Figure 11a,b, The peridynamic solid undergoes cycle loading acting on the body boundary. For a given bond ${\xi }_{kj}$ within the horizon of point $x_{\left(k\right)}$, the force density acting on the spring-like bond varies in a noncyclic way. The spectrum loading of the bond strain ${\epsilon }_{kj}$, shown in Figure 11d, varies irregularly with every loading cycle acting on the body boundary. Defines the maximum and minimum bond strains in the current cycle $s_{\max }$ and $s_{\min }$.

As shown in Equation (5), to express the damage accumulation rate of a given bond explicitly, the concise representation of the critical active energy $Q\left({\sigma }_a,{\sigma }_m,D\right)$ is obtained by using inverse analysis through the damage fatigue failure process and damage fatigue law.

As shown in Figure 12, the normalized fatigue damage quantity can be expressed by fictitious time $t_f$ as follows:

$$\{\begin{array}{c}\lambda \left(x,\xi ,t_f\right)=NC\exp \left(m\epsilon \right)\\ t_f=\frac{N}{N_f}\end{array}$$

(23)

where $N_f$ is the cycle number to failure, $N$ is the current cycle number, $\epsilon =\left|s_{\max }-s_{\min }\right|$ is the current cycle bond strain in the bond, $C$ and $m$ are positive parameters corresponding to the material property. The normalized fatigue damage quantity $\lambda \left(x,\xi ,t_f\right)$ is defined as the consumption life of the bond. It involves the loading cycle $N$ increases.

$$\{\begin{array}{c}\frac{d\lambda }{dN}\left(N\right)=C\exp \left(m\epsilon \right)\\ \lambda \left(0\right)=0\end{array}$$

(24)

The bond breaks at the loading cycle $N$ that

$$\lambda \left(N\right)⩾1$$

(25)

For the fatigue crack initiation phase, parameter $C$ and $m$ are calibrated by the S-N curve expressed in exponent form, as shown in Figure 13. Equation (25) means that the cycle $N$ is the first bond breaks. Parameter $C$ and $m$ are set to

$$\{\begin{array}{c}C=C_1\\ m=m_1\end{array}$$

(26)

Combining Equations (23), (25) and (26), the first bond in the entire domain $\mathcal{R}$ breaks with ${\epsilon }_1$ is the cyclic strain range.

$$N_1{C}_1\exp \left(m_1{\epsilon }_1\right)=1$$

(27)

where $N_1$ is the smallest cycle at which this bond breaks and $\lambda \left(N_1\right)=1$. The first bond breaks in the fatigue crack initiation phase when its fatigue cycle number $N$ becomes larger than $N_1$.

$$N_1⩾\frac{1}{C_1\exp \left(m_1{\epsilon }_1\right)}$$

(28)

When the first bond breaks with the cyclic bond ${\epsilon }_1$ in fatigue crack initiation, new static solutions for other bonds are calculated in the same cycle. If those bonds strain ranges are larger than ${\epsilon }_1$, then the bonds break and new static solutions continue until no more bonds break at the same cycle. The largest bond strain is calculated for the next cycle number by using the static solution in the deformed peridynamic material configuration.

For the fatigue crack growth phase, parameter $C$ and $m$ are calibrated by the well-known Paris law. Parameter $C$ and $m$ are set to

$$\{\begin{array}{c}C=C_2\\ m=m_2\end{array}$$

(29)

As shown in Figure 14, a fixed bond $\xi$ normal to the axis of the growing model-I fatigue crack. During the cycle loading, the deformation in the vicinity of the crack tip is constant and the crack growth rate is defined as $da/dN$ in each loading cycle. The relative distance between the bond and the crack tip is expressed as follows.

$$z=x-\frac{da}{dN}N$$

(30)

where $z=0$ means that the crack tip is on the bond $\xi$, $x$ is the spatial coordinate along the crack axis. The bond consumption life at $z=0$ by integrating its first derivative to distance:

$$\lambda \left(\delta \right)=\lambda \left(0\right)+{{\displaystyle \int }}_0^{\delta }\frac{d\lambda }{dN}\frac{dN}{dz}dz$$

(31)

where $\lambda \left(\delta \right)=0$ and $\lambda \left(0\right)=1$, for the damage evolution law is effective within the horizon of the crack tip. Combing Equations (30) and (31) leads to

$$\frac{da}{dN}=C_2{{\displaystyle \int }}_0^{\delta }{e}^{m_2\epsilon }dz$$

(32)

Recall the well-known Paris law for fatigue crack growth:

$$\frac{da}{dN}=c{\left(\Delta k\right)}^M$$

(33)

where $c$ and $M$ are constant coefficients. Comparing Equations (32) and (33), two experimental data points are selected to determine the constants $C_2$ and $m_2$.

4.3. Transition from Fatigue Crack Initiation to Growth

As shown in Equation (24), the fatigue crack initiation and growth phase are depicted in a single model. The mechanism of fatigue initiation and growth are different. During the fatigue crack initiation, each bond strain is independent of the cycle number. However, a bond strain is changing over time as the bond transit to the fatigue crack growth phase. As shown in Figure 15, for the given point $x_{\left(j\right)}$, within the horizon of point $x_{\left(k\right)}$, the bond ${\xi }_{kj}$ (denoted as green) transit to the fatigue crack growth phase as the point damage $\varphi \left(x_{\left(j\right)}\right)$ satisfies the following conditions.

$$\varphi \left(x_{\left(j\right)}\right)⩾0.5$$

(34)

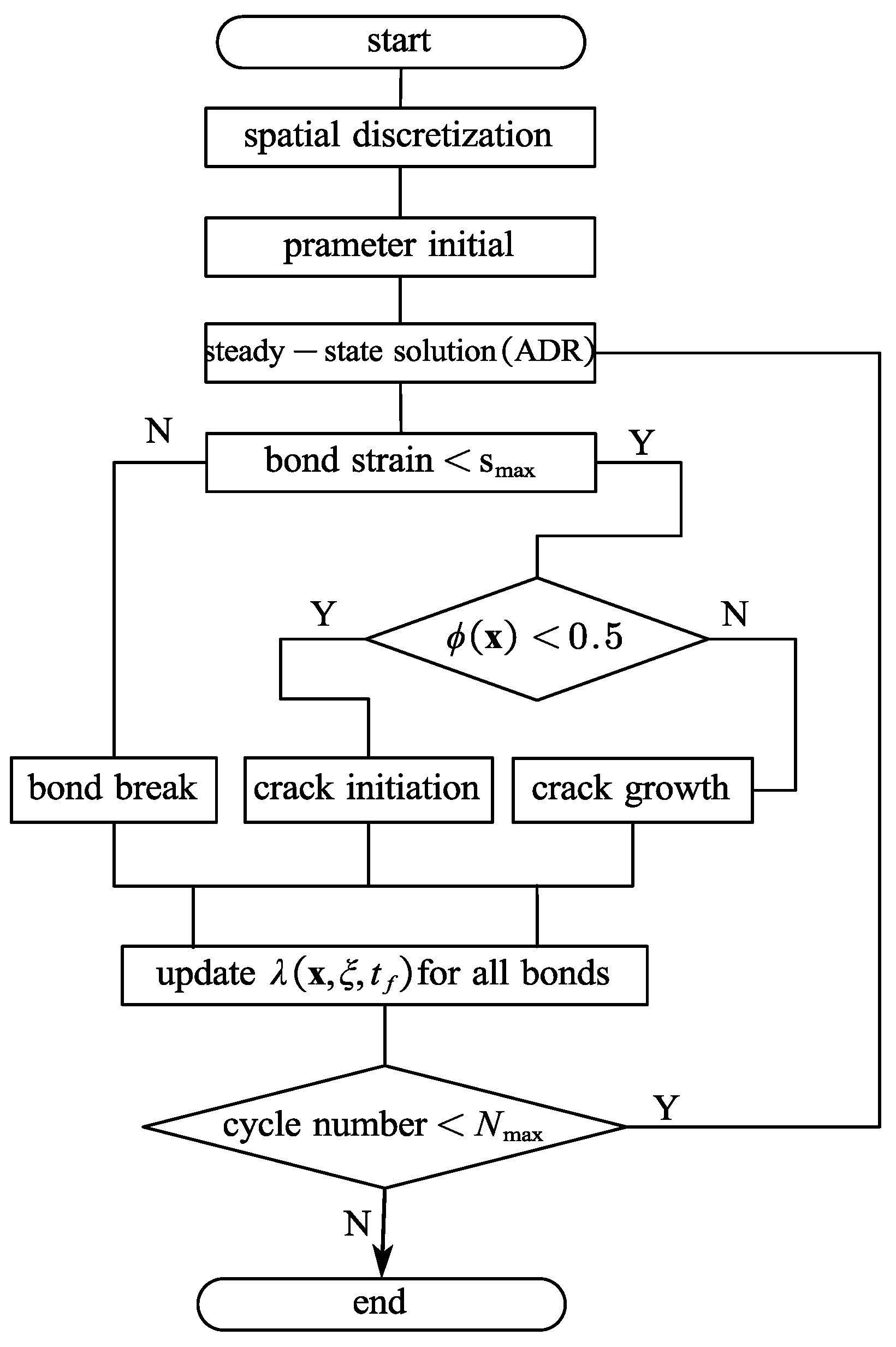
5. Numerical Solution Method

5.1. Adaptive Dynamic Relaxation for Static Solution

The peridynamic control equation for fatigue cracking is integral-different. As for cyclic loading simulation, only the maximal loading condition is necessary. Whenever some bonds break in a loading cycle, the new static solution is calculated at the same cycle until no bonds break. To solve quasi-static or static problems, the Adaptive Dynamic Relaxation is used for the fatigue crack simulation problems. The peridynamic equation of motion for all material points is expressed as follows

$$D\ddot{U}\left(X,t\right)+\zeta D\dot{U}\left(X,t\right)=F\left(U,U^{\prime },X,X^{\prime }\right)$$

(35)

where $D$ is the fictitious diagonal density matrix and $\zeta$ is the damping coefficient, $X$ and $U$ are initial position and displacement vector for all the material points in the configuration body.

$$\{\begin{array}{c}{X}^T=\left\{x_{\left(1\right)},x_{\left(2\right)},\dots ,x_{\left(N\right)}\right\}\\ U^T=\left\{u\left(x_{\left(1\right)},t\right),u\left(x_{\left(2\right)},t\right),\dots ,u\left(x_{\left(N\right)},t\right)\right\}\end{array}$$

(36)

where $N$ is the number of all the material points in the configuration body. Combing Equations (6) and (11), the vector $F$ can be expressed by its $k^{th}$ component.

$$F_{\left(k\right)}={\displaystyle \sum }_{j=1}^M\left(t_{\left(k\right)\left(j\right)}-t_{\left(j\right)\left(k\right)}\right)\left(v_{cj}{V}_{\left(j\right)}\right)+b_{\left(k\right)}$$

(37)

where $M$ is the total number of material points within the horizon of a material point $x_{\left(k\right)}$, $v_{cj}$ is the volume correction factor for the material point $x_{\left(j\right)}$. The velocities and displacements for the next time step are expressed as follows.

$$\{\begin{array}{c}{V}^{n+1/2}=\frac{\left(\left(2-{\zeta }^n\Delta t\right)V^{n-1/2}+2\Delta t{D}^{-1}{F}^n\right)}{2+{\zeta }^n\Delta t}\\ U^{n+1}=U^n+V^{n+1/2}\Delta t\end{array}$$

(38)

where $n$ is the $n^{th}$ iteration. The diagonal elements of the density matrix, $D$, can be expressed as:

$${\gamma }_{kk}⩾\frac{1}{4}\Delta t^2{\displaystyle \sum }_j\left|{\mathcal{J}}_{kj}\right|$$

(39)

where ${\mathcal{J}}_{ij}$ is the stiffness matrix of the current structure. As for the small displacement assumption.

$${\displaystyle \sum }_j\left|{\mathcal{J}}_{kj}\right|={\displaystyle \sum }_{j=1}^M\frac{\left|{\xi }_{\left(k\right)\left(j\right)}\cdot e\right|}{\left|{\xi }_{\left(k\right)\left(j\right)}\right|}\frac{4\delta }{\left|{\xi }_{\left(k\right)\left(j\right)}\right|}\{\frac{1}{2}\frac{a{d}^2\delta }{\left|{\xi }_{\left(k\right)\left(j\right)}\right|}(v_{ck}{V}_k+v_{cj}{V}_j)+b\}$$

(40)

where $e$ is a unit vector.

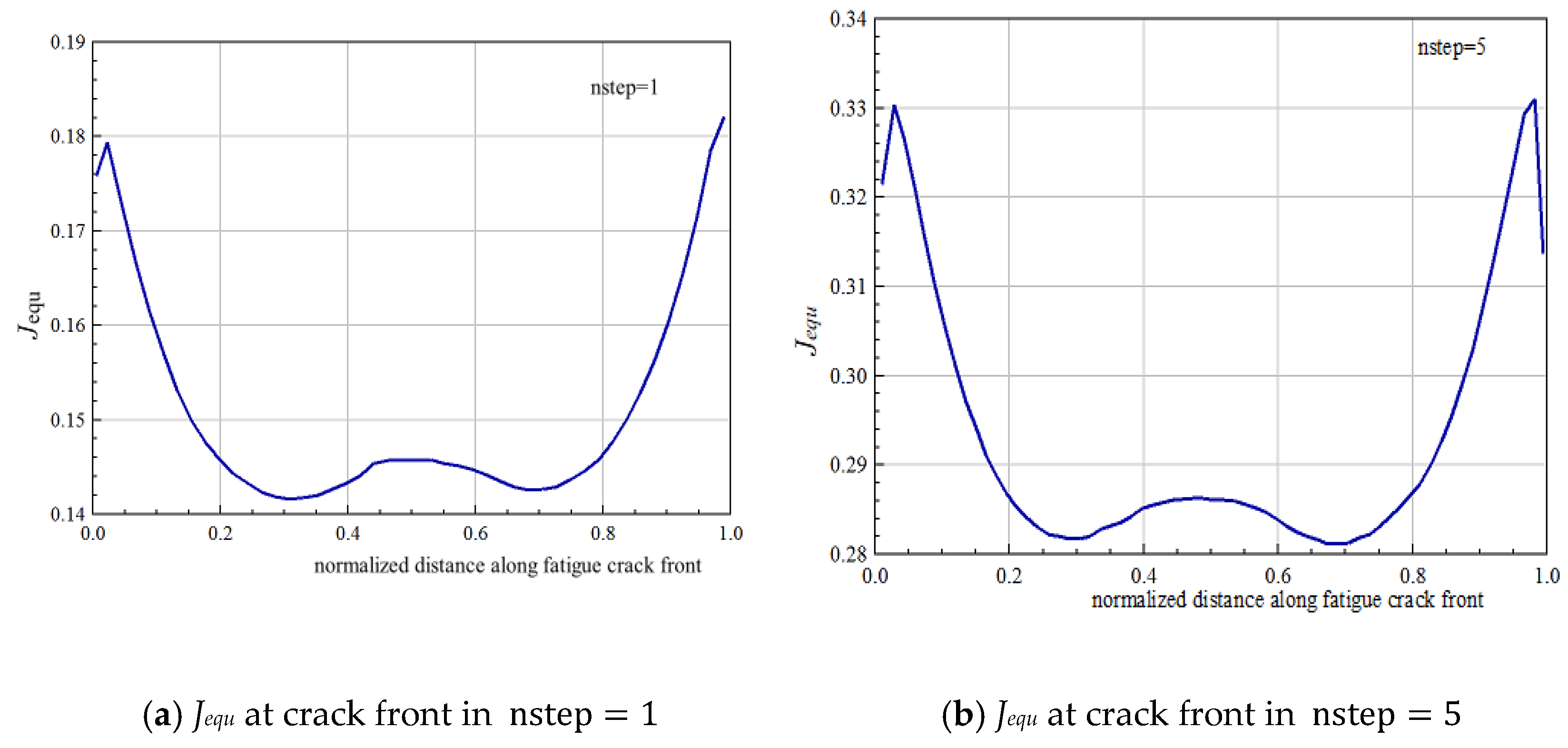
5.2. Equivalent Stress Intensity Factor

Each step of crack growth requires a driving force, which guides the fatigue crack path. Naturally, this driving force named stress intensity factor. Because of the complexity in mathematics and physics, solving the three-dimensional dynamic stress intensity factors is certainly limited in mechanics. In the state-based peridynamic theory, there is no concept of this driving force. To better characterize the propagating crack-tip fields, an equivalent stress intensity factor $J_{equ}$ can be expressed as follows [54]:

$$\begin{array}{c}{J}_{equ}={{\displaystyle \int }}_{\mathsf{\Gamma }}\left(Wdy-T_i\frac{\partial u_i}{\partial x}ds\right)\\ =\frac{2E}{\left(1-v^2\right)}{\displaystyle \sum _{i=I,II,II}}{{\displaystyle \int }}_i\left(W_{i}dy-w_{i}ds\right)\end{array}$$

(41)

where $x=x_1$, $y=x_2$ and $z=x_3$ are 3D Cartesian coordinates with origin at the fatigue crack tip, $J$ is a contour integral evaluated counterclockwise along a crack surface, $T_i={\sigma }_{ij}{n}_j$ is the traction vector along the crack surface, with the outward unit normal vector $n_j$ and ${\sigma }_{ij}$, $u_i$ is a displacement vector and $ds$ is an element of the crack surface. By taking the surface integration, the relationship between the displacement and fatigue crack criteria is built. Each step of crack growth can be obtained from the relationship.

5.3. Flowchart for the Fatigue Cracking Simulation

Based on the comparison and analysis of the classical fatigue crack simulation algorithm and the peridynamic one, the simulation process for the fatigue crack initiation and growth is deduced, as shown in Figure 16.

6. Experiment

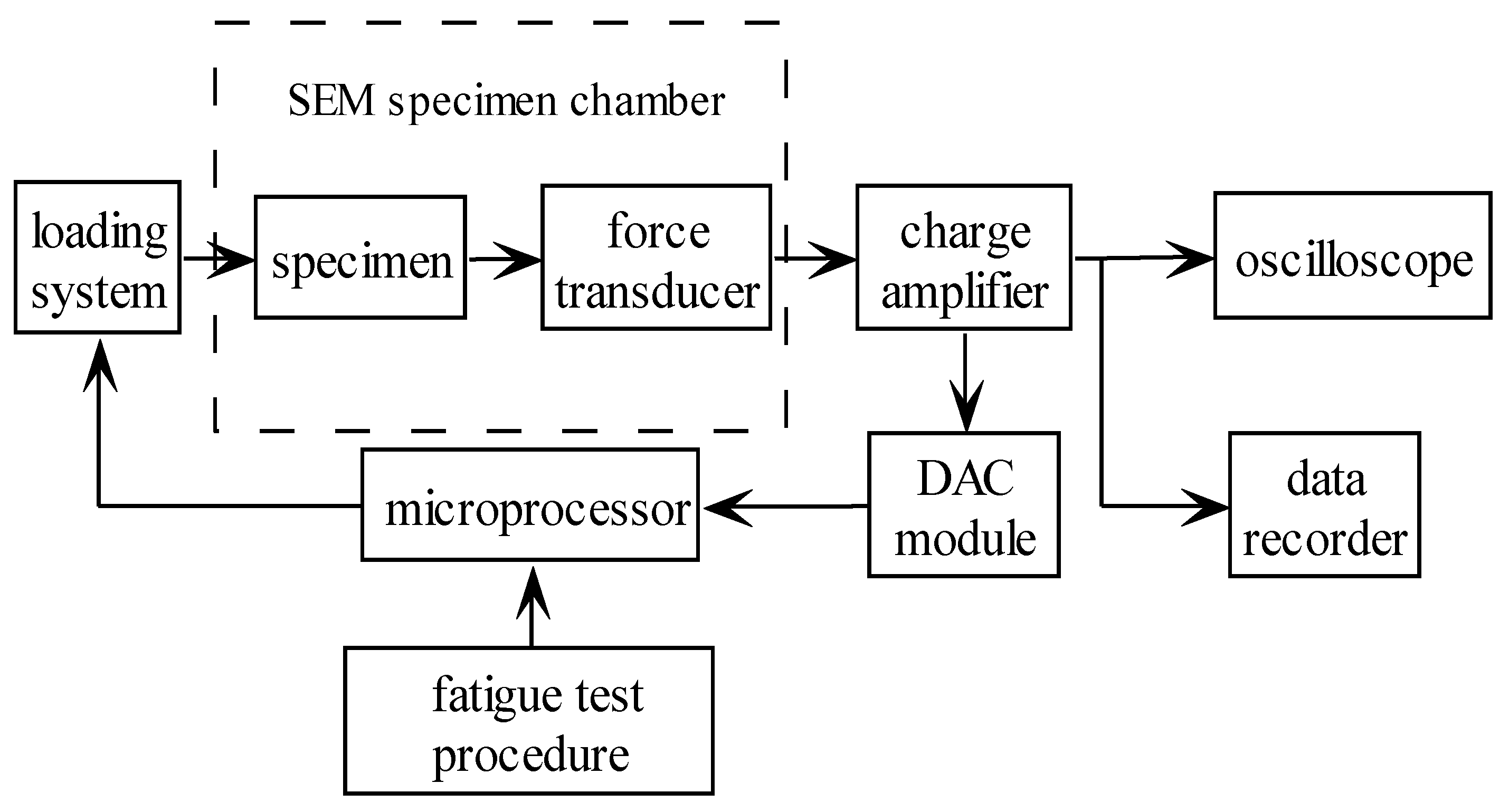
6.1. Experimental Equipment

As shown in Figure 17, the experiment was conducted on a fatigue test machine with a floor model biaxial servo-hydraulic dynamic test system, which provides axial and torsion load on a specimen in an integrated biaxial actuator. The system has an axial load capacity of ±250 KN (±56 kip) and a torque capacity of ±2000 Nm (±17700 in-lb), with an axial actuator stroke of 100 mm and a rotary stroke of 90°.

As shown in Figure 18, the loading system, which comes with console software to provide full system control from a personal computer (PC), including waveform generation in both axes, calibration, limit set up, and status monitoring. The loading waveform is sine and the loading frequency is 2HZ.

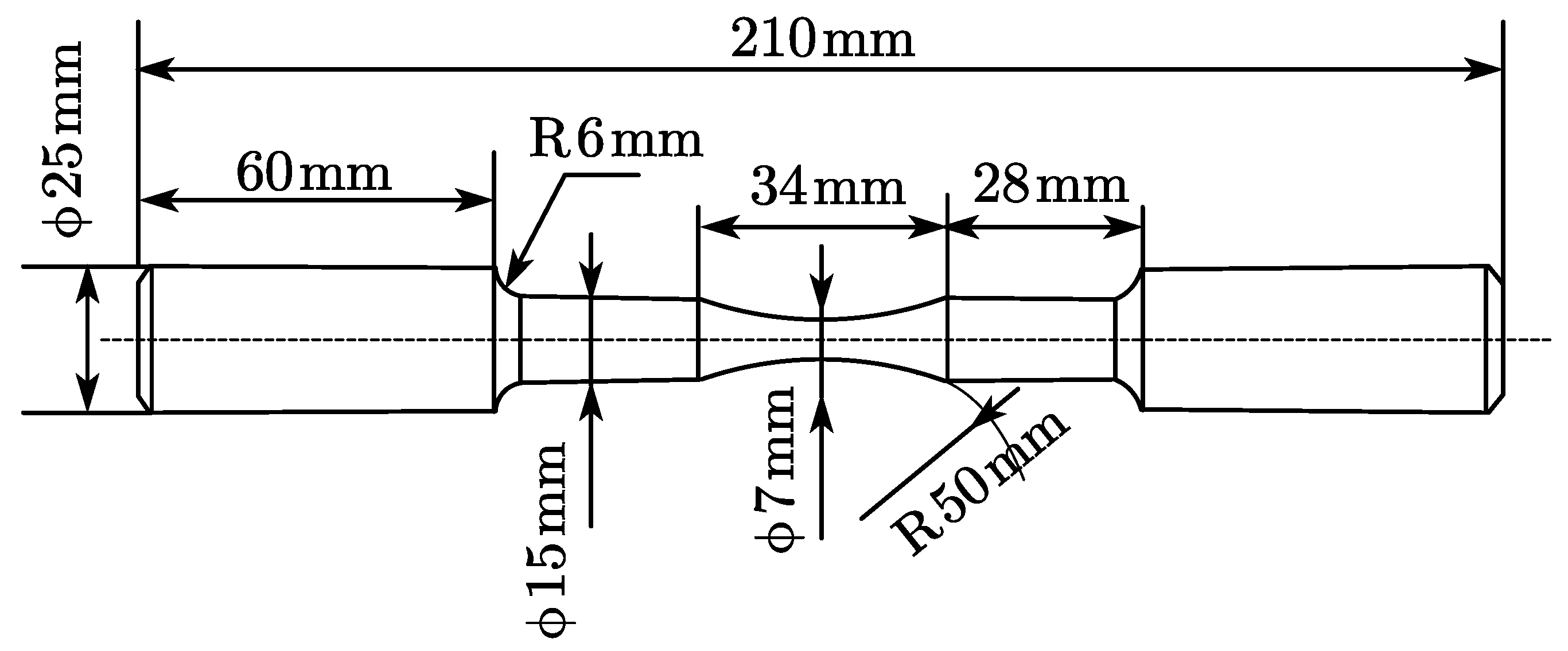
6.2. Specimen Size Requirements and Loading Parameters

As shown in Figure 19, a smooth specimen with a length of 210 mm is machined cutting from a high-speed wheel. The diameter of the grasping side is 25 mm. The minimum diameter of the test specimen is 7 mm, which also means that it is the weak part of the specimen without considering other factors. The maximum percentages of the various specified elements are shown in

Table 1. The maximum percentages of the various specified elements.

C%	Si%	Mn%	P%	S%	Cr%	Cu%	Mo%	Ni%	V%	(Cr + Mo + Ni)%
0.53	0.99	0.96	0.010	<0.002	0.03	0.036	<0.005	0.16	<0.005	<0.50

. The basic mechanical properties for the wheel material are shown in

Table 2. Basic properties of the wheel material at room temperature.

Name	E/GPa	σ0.2/MPa	σb/MPa	δ%	Ferrite Hardness/HV	Pearlite Hardness/HV
D1	178.530	553.230	956.380	16. 21	210	250

. The loading parameters are shown in

Table 3. Loading parameters.

σa/MPa	τa/MPa	σequ/MPa	Ra	Fmax/KN	Tmax/N.m	φ/°	f/HZ
340	196.3	480.83	$\sqrt{3}$	9.6	8.3	90	2

and the loading path is shown in Figure 20.

6.3. Fatigue Crack Path and Morphology

The fracture morphology and the angle between the fatigue crack path and the central axis are shown in Figure 21.

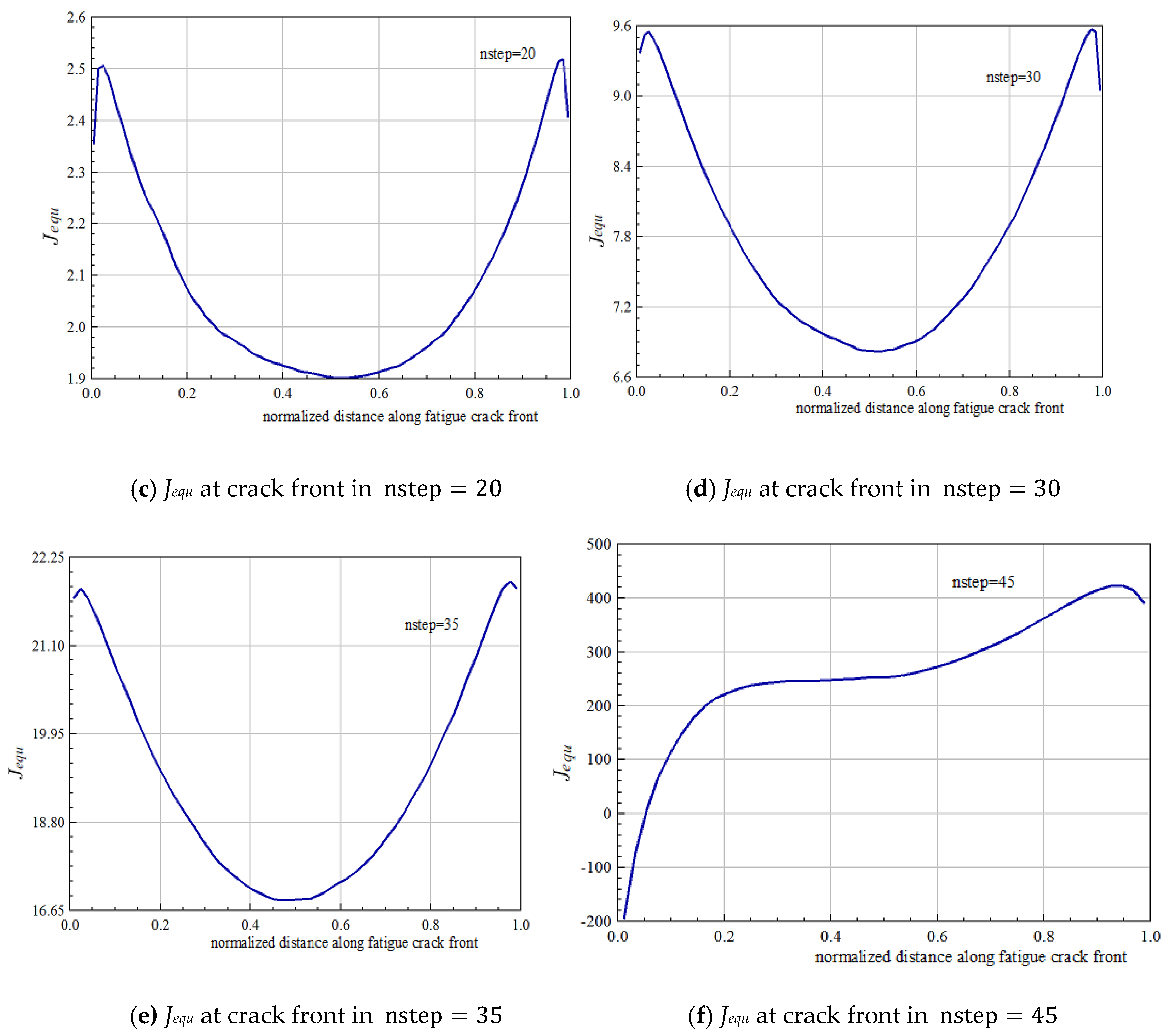
6.4. Results Analysis

As shown in Figure 22, using an electron microscope, it can be seen that the angle between the main long fatigue crack and cylinder axis line $l_c$ is about $\alpha =59.5$°.

As shown in

Table 4. Fatigue cycles and angles.

NO	N/Cycles	α/°
D1-1	16,239	57.8
D1-2	15,860	61.5
D1-3	17,963	70.1
D1-4	16,938	50.2
D1-5	15,608	53.6
D1-6	15,656	67.5
D1-7	15,320	62.8
D1-8	14,352	68.8

, the average fatigue cycle is 15,992 for the fatigue specimens, and the average angle between the main long fatigue crack and cylinder axis line $l_c$ is 61.54°.

As shown in Figure 23, the angle between the main long fatigue crack and cylinder axis line is about 58.5°. This simulation result has a good correlation with the average test result, as shown in Figure 22.

As shown in Figure 24, the value of the equivalent stress intensity factor $J_{equ}$ becomes larger as the number of iterations increases.

7. Conclusions

(1)

To evaluate and predict the fatigue life of specimens under combined tension and torsion, the peridynamic fatigue model was proposed and the fatigue cracks initiate and propagate naturally without extra criteria.

(2)

The proposed trans-scale fatigue model has no notion of scale, or it releases the scale constraints. The evolution of fatigue crack shows micro and macro scale including crack initiation, propagation, and fracture.

(3)

The short diffusion-generated and propagating crack converges and grows into the main crack, which expands to the macroscopic visible morphology.

(4)

The macroscopic morphology of fatigue was highly consistent with the actual experimental results and extended along the direction of 61.54° until the final fracture.

(5)

The natural propagation of the crack can be realized without the need for additional crack propagation criteria, and the distribution and quantitative analysis of the fatigue life can be obtained.