Effect of Liquid Viscosity and Flow Orientation on Initial Waves in Annular Gas–Liquid Flow
Abstract
:1. Introduction
2. Materials and Methods
3. Result
3.1. The Film Shape at the Initial Stage
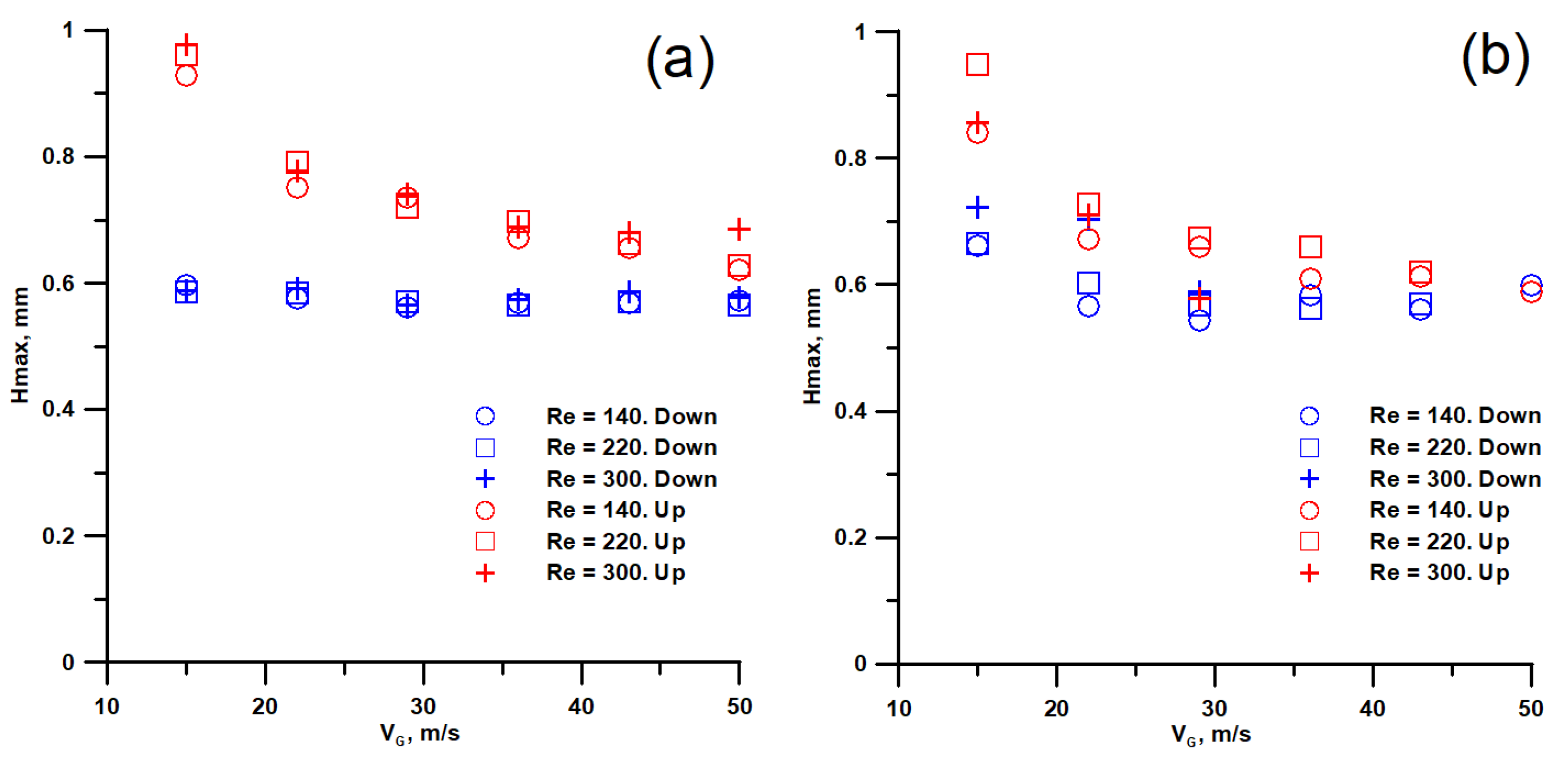
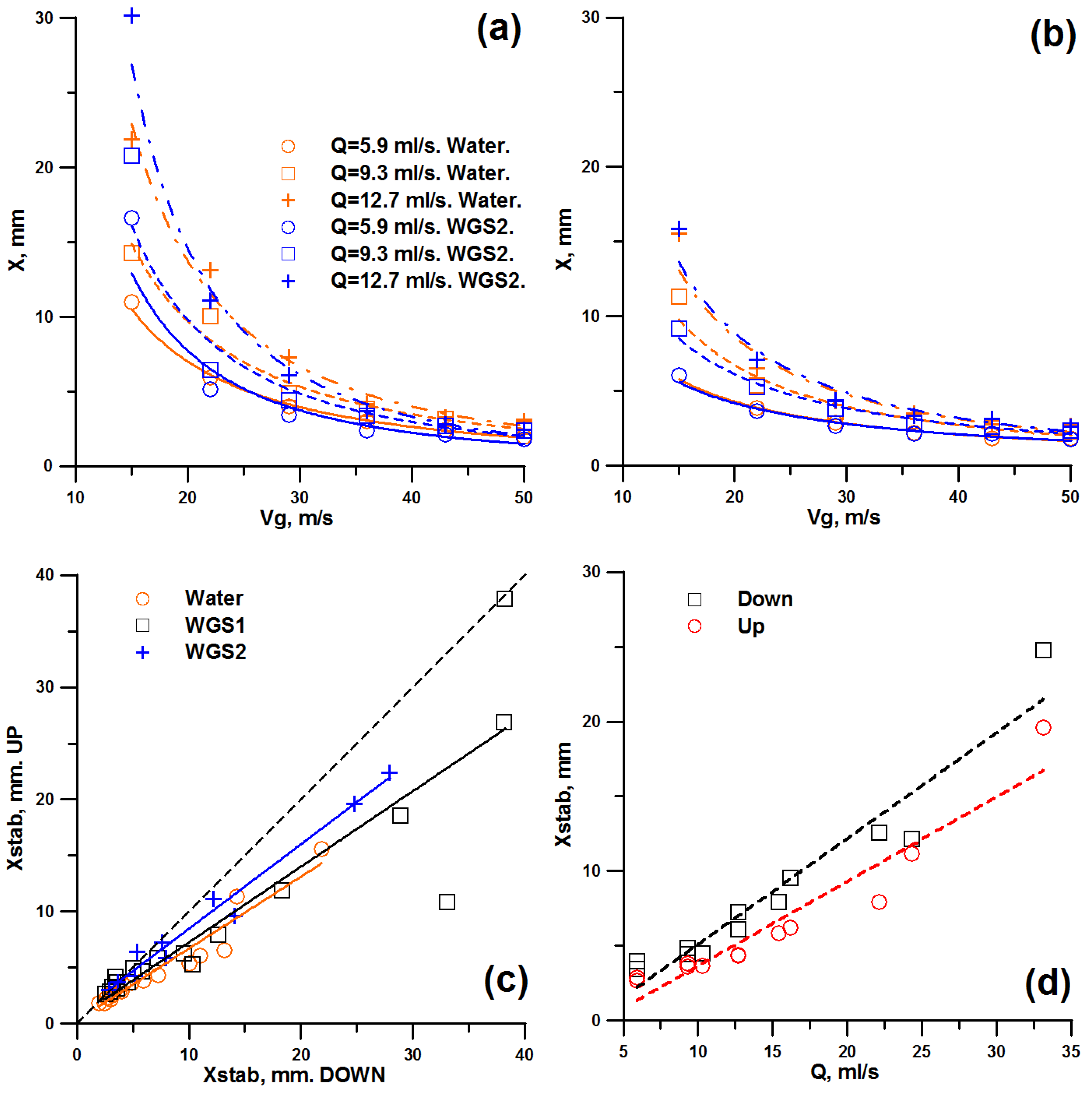
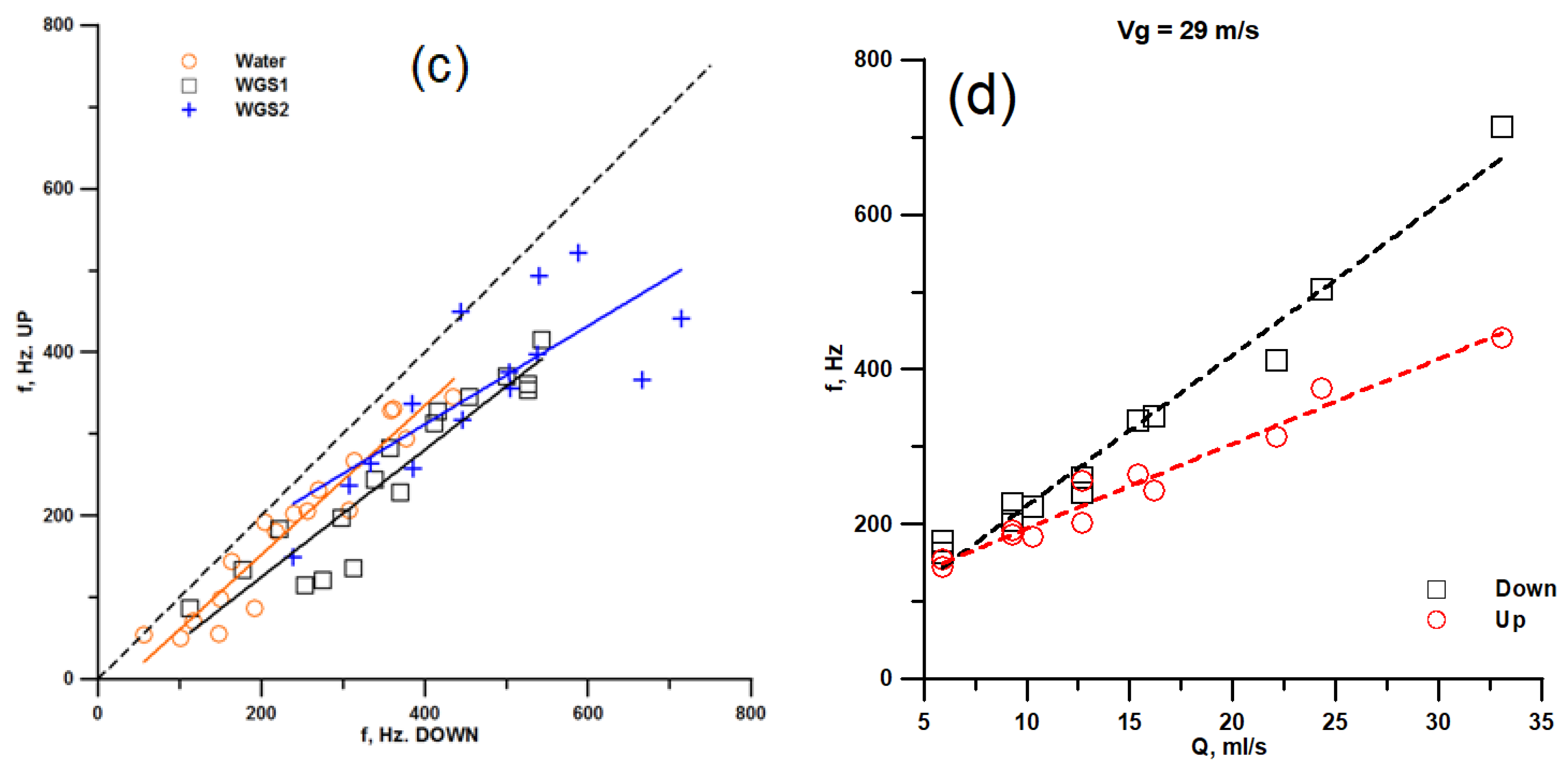
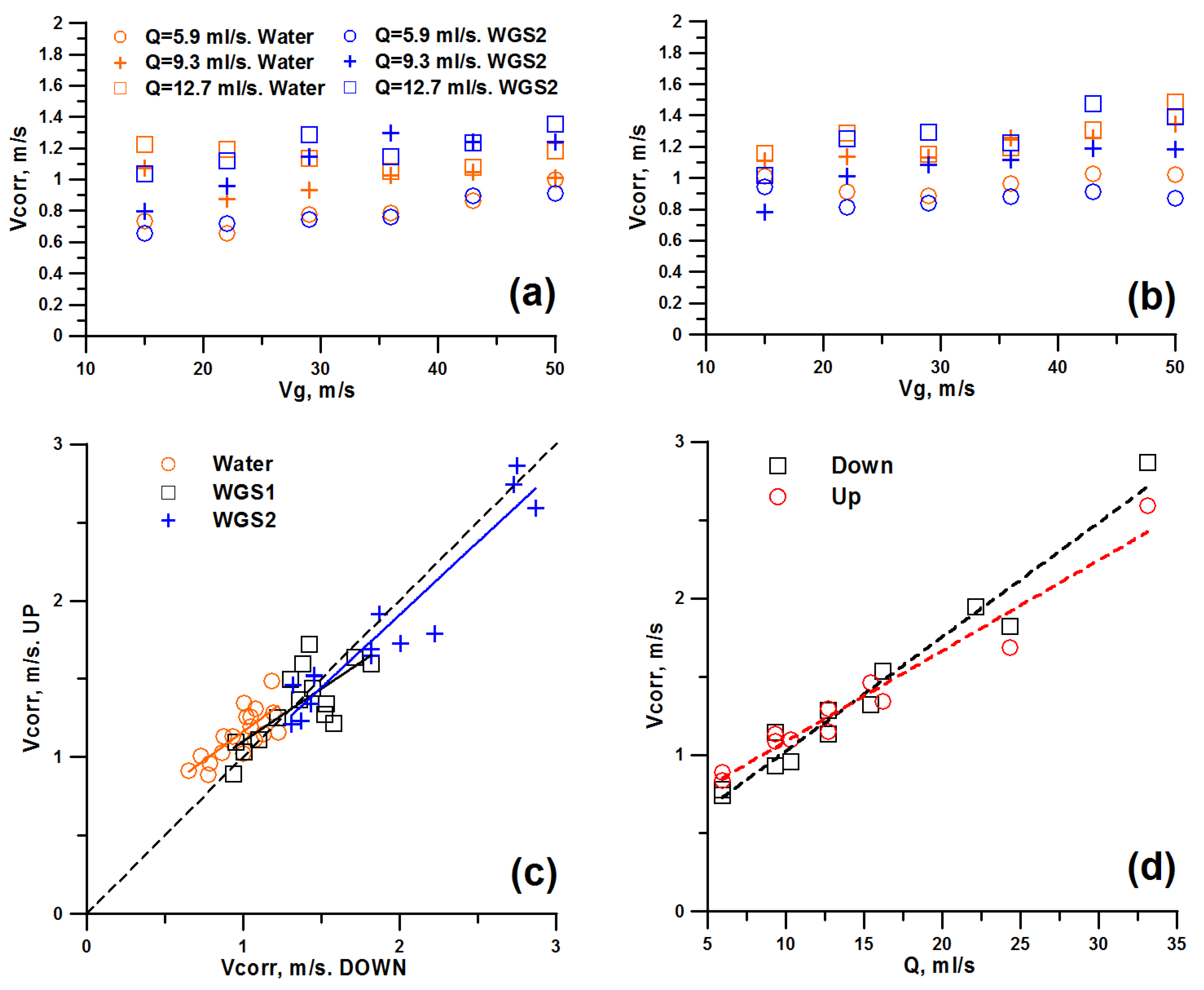
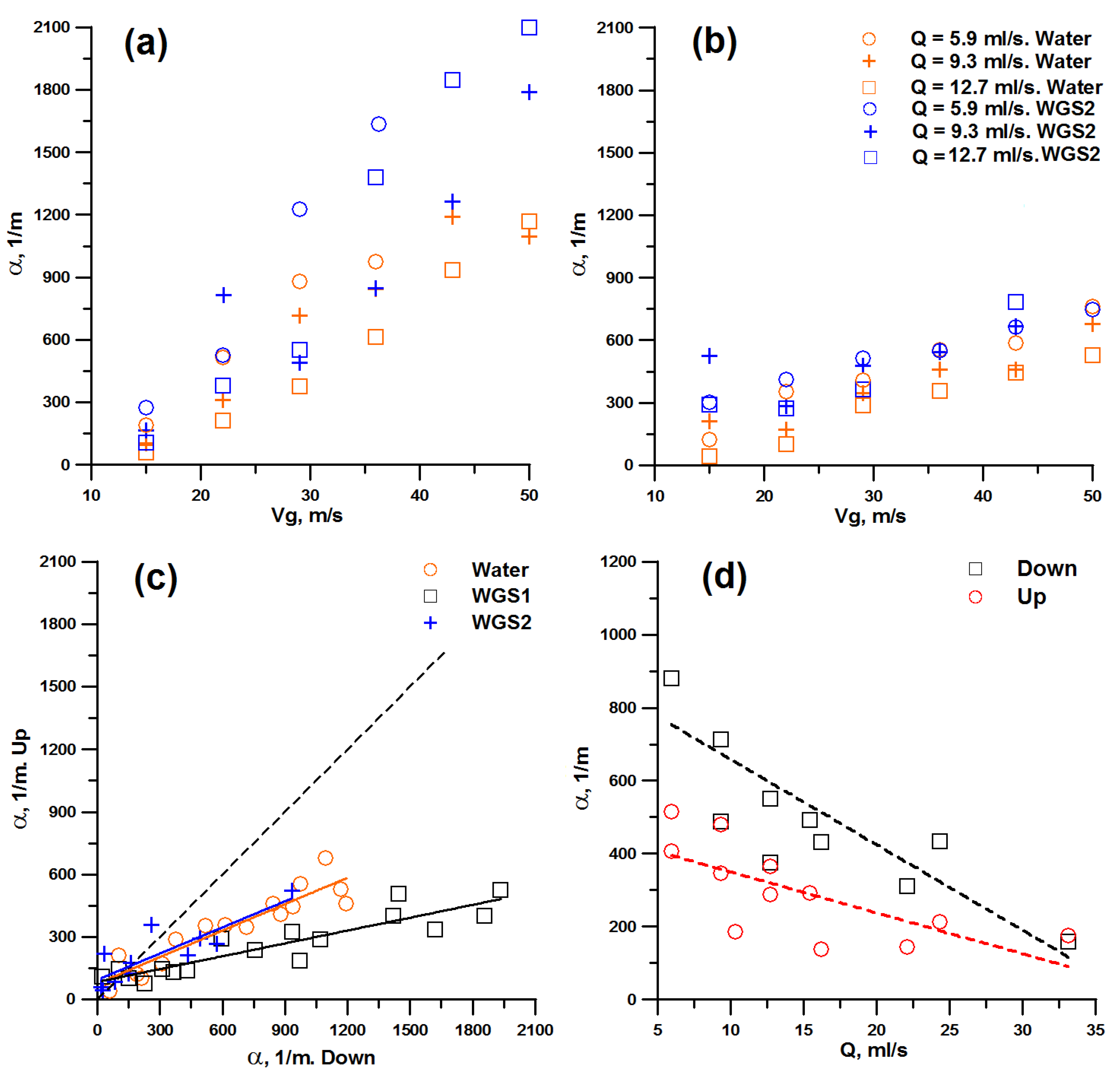
3.2. Characteristics of the Initial Waves
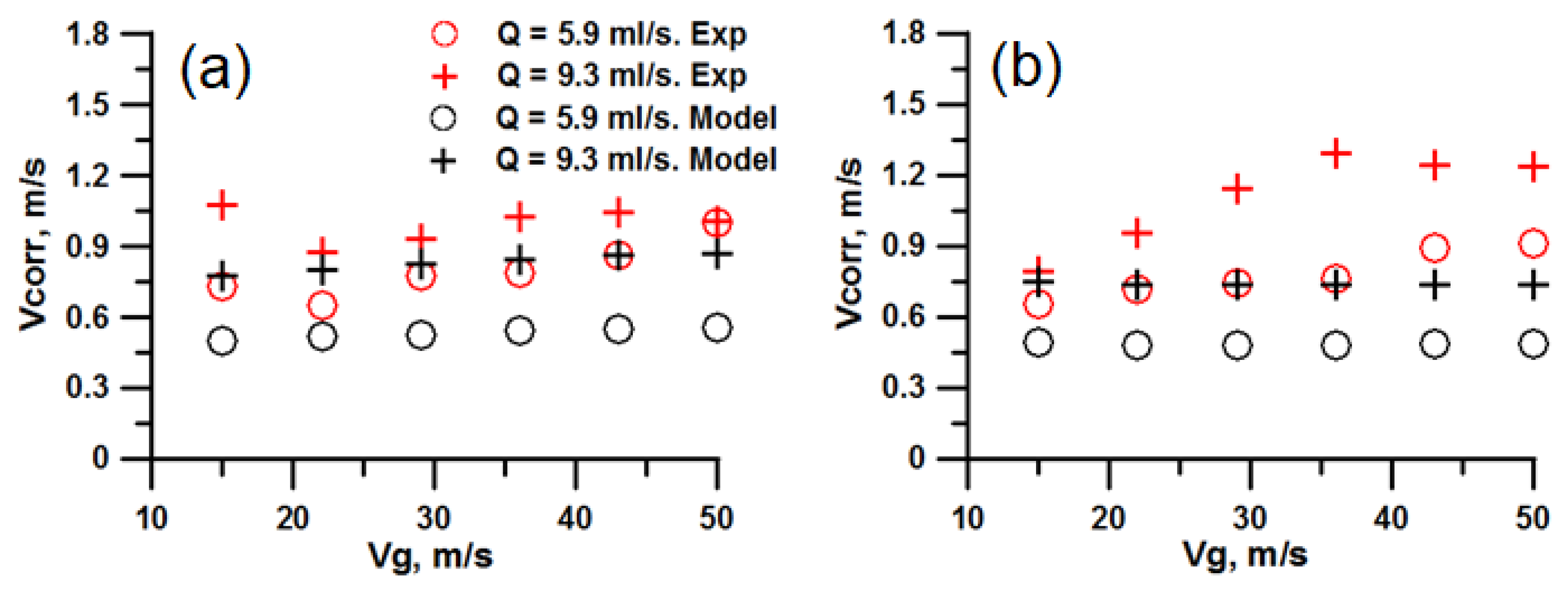
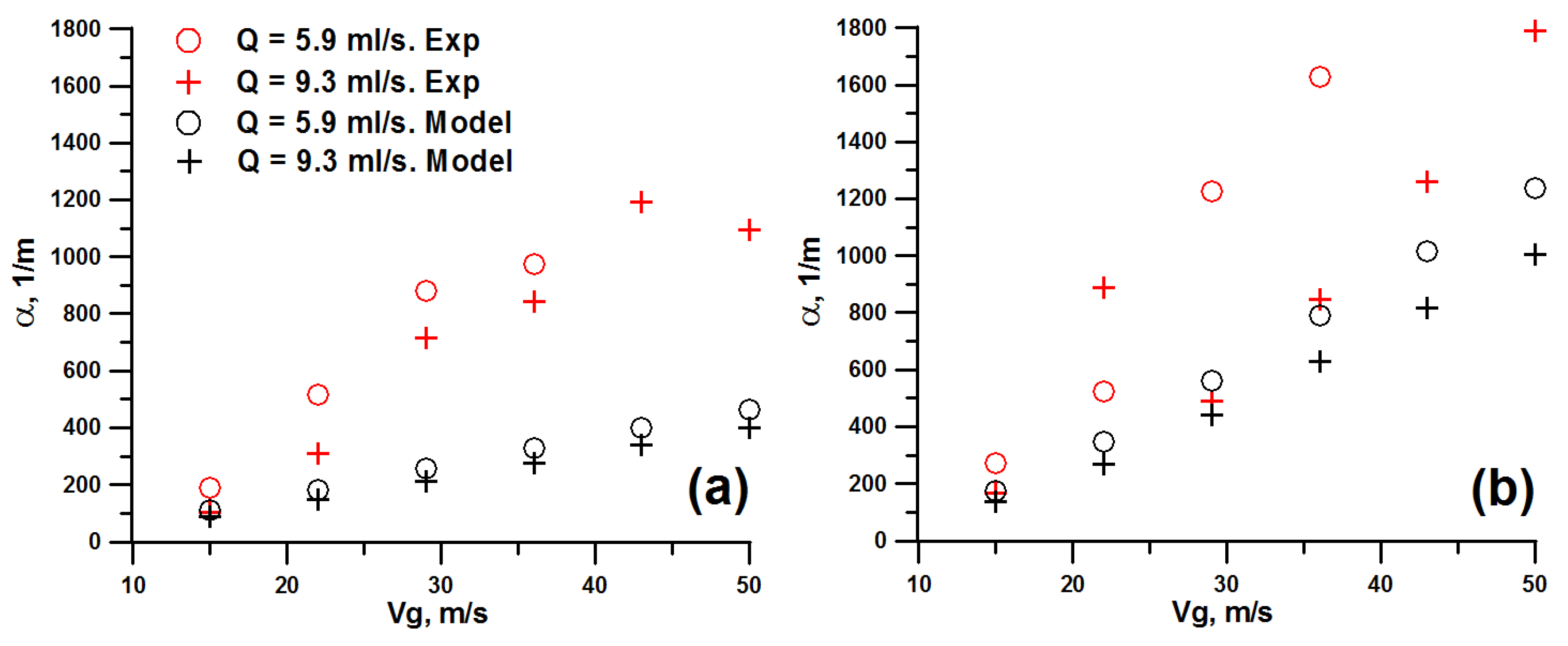
3.3. Modeling and Comparison
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Webb, D.R.; Hewitt, G.F. Downwards co-current annular flow. Int. J. Multiph. Flow 1975, 2, 35–49. [Google Scholar] [CrossRef]
- Azzopardi, B.J. Disturbance wave frequencies, velocities and spacing in vertical annular two-phase flow. Nucl. Eng. Des. 1986, 92, 121–133. [Google Scholar] [CrossRef]
- Han, H.; Zhu, Z.; Gabriel, K. A study on the effect of gas flow rate on the wave characteristics in two-phase gas–liquid annular flow. Nucl. Eng. Des. 2006, 236, 2580–2588. [Google Scholar] [CrossRef]
- Farias, P.S.C.; Martins, F.J.W.A.; Sampaio, L.E.B.; Serfaty, R.; Azevedo, L.F.A. Liquid film characterization in horizontal, annular, two-phase, gas–liquid flow using time-resolved laser-induced fluorescence. Exp. Fluids 2012, 52, 633–645. [Google Scholar] [CrossRef]
- Shedd, T.A.; Newell, T.A. Characteristics of the liquid film and pressure drop in horizontal, annular, two-phase flow through round, square and triangular tubes. J. Fluids Eng. 2004, 126, 807–817. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T.A. Wave behavior in horizontal annular air–water flow. Int. J. Multiph. Flow 2008, 34, 636–646. [Google Scholar] [CrossRef]
- Kaji, R.; Azzopardi, B.J. The effect of pipe diameter on the structure of gas/liquid flow in vertical pipes. Int. J. Multiph. Flow 2010, 36, 303–313. [Google Scholar] [CrossRef]
- Alamu, M.B.; Azzopardi, B.J. Wave and drop periodicity in transient annular flow. Nucl. Eng. Des. 2011, 241, 5079–5092. [Google Scholar] [CrossRef]
- Vasques, J.; Cherdantsev, A.; Cherdantsev, M.; Isaenkov, S.; Hann, D. Comparison of disturbance wave parameters with flow orientation in vertical annular gas-liquid flows in a small pipe. Exp. Therm. Fluid Sci. 2018, 97, 484–501. [Google Scholar] [CrossRef]
- Mori, K.; Kondo, Y.; Kaji, M.; Yagishita, T. Effects of Liquid Viscosity on Characteristics of Waves in Gas-Liquid Two-Phase Flow: Characteristics of Huge Waves and Disturbance Waves. JSME Int. J. Ser. B 1999, 42, 658–666. [Google Scholar] [CrossRef] [Green Version]
- Clark, W.W.; Campbell, G.B.; Hills, J.H.; Azzopardi, B.J. Viscous effects on the interfacial structure of falling liquid film/co-current gas systems. In Proceedings of the 4th International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Bousman, W.S. Studies of two-Phase Gas-Liquid Flow in Microgravity. Ph.D. Thesis, University of Houston, Houston, TX, USA, 1994. [Google Scholar]
- Mantilla, I. Mechanistic Modeling of Liquid Entrainment in Gas in Horizontal Pipes. Ph.D. Thesis, University of Tulsa, Tulsa, OK, USA, 2008. [Google Scholar]
- Setyawan, A.; Indarto; Deendarlianto. The effect of the fluid properties on the wave velocity and wave frequency of gas–liquid annular two-phase flow in a horizontal pipe. Exp. Therm. Fluid Sci. 2016, 71, 25–41. [Google Scholar] [CrossRef]
- Sekoguchi, K.; Nakazatomi, M.; Takeishi, M.; Shimizu, H.; Mori, K.; Miyake, G. Pressure Effect on Velocity of Liquid Lumps in Vertical Upward Gas-Liquid Two-Phase Flow. JSME Int. J. Ser. 2 1992, 35, 380–387. [Google Scholar] [CrossRef] [Green Version]
- Sawant, P.; Ishii, M.; Hazuku, T.; Takamasa, T.; Mori, M. Properties of disturbance waves in vertical annular two-phase flow. Nucl. Eng. Des. 2008, 238, 3528–3541. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, N.; Feng, Y.; Sun, H.; Fang, L. Interfacial wave velocity of vertical gas-liquid annular flow at different system pressures. Exp. Therm. Fluid Sci. 2018, 92, 20–32. [Google Scholar] [CrossRef]
- Berna, C.; Escrivá, A.; Muñoz-Cobo, J.L.; Herranz, L.E. Review of droplet entrainment in annular flow: Interfacial waves and onset of entrainment. Prog. Nucl. Energy 2014, 74, 14–43. [Google Scholar] [CrossRef]
- Dasgupta, A.; Chandraker, D.K.; Kshirasagar, S.; Reddy, B.R.; Rajalakshmi, R.; Nayak, A.K.; Hewitt, G.F. Experimental investigation on dominant waves in upward air-water two-phase flow in churn and annular regime. Exp. Therm. Fluid Sci. 2017, 81, 147–163. [Google Scholar] [CrossRef]
- Cuadros, J.L.; Rivera, Y.; Berna, C.; Escrivá, A.; Muñoz-Cobo, J.L.; Monrós-Andreu, G.; Chiva, S. Characterization of the gas-liquid interfacial waves in vertical upward co-current annular flows. Nucl. Eng. Des. 2019, 346, 112–130. [Google Scholar] [CrossRef]
- Lin, R.; Wang, K.; Liu, L.; Zhang, Y.; Dong, S. Application of the image analysis on the investigation of disturbance waves in vertical upward annular two-phase flow. Exp. Therm. Fluid Sci. 2020, 114, 110062. [Google Scholar] [CrossRef]
- Fan, W.; Li, H.; Anglart, H. Numerical investigation of spatial and temporal structure of annular flow with disturbance waves. Int. J. Multiph. Flow 2019, 110, 256–272. [Google Scholar] [CrossRef]
- Han, H.; Gabriel, K. A numerical study of entrainment mechanism in axisymmetric annular gas-liquid flow. J. Fluids Eng. 2007, 129, 293–301. [Google Scholar] [CrossRef]
- Yang, J.; Narayanan, C.; Lakehal, D. Large Eddy & Interface Simulation (LEIS) of disturbance waves and heat transfer in annular flows. Nucl. Eng. Des. 2017, 321, 190–198. [Google Scholar]
- Alekseenko, S.V.; Cherdantsev, A.V.; Cherdantsev, M.V.; Isaenkov, S.V.; Markovich, D.M. Study of formation and development of disturbance waves in annular gas–liquid flow. Int. J. Multiph. Flow 2015, 77, 65–75. [Google Scholar] [CrossRef]
- Hall Taylor, N.; Nedderman, R.M. The coalescence of disturbance waves in annular two phase flow. Chem. Eng. Sci. 1968, 23, 551–564. [Google Scholar] [CrossRef]
- Zhao, Y.; Markides, C.N.; Matar, O.K.; Hewitt, G.F. Disturbance wave development in two-phase gas–liquid upwards vertical annular flow. Int. J. Multiph. Flow 2013, 55, 111–129. [Google Scholar] [CrossRef] [Green Version]
- Wolf, A.; Jayanti, S.; Hewitt, G.F. Flow development in vertical annular flow. Chem. Eng. Sci. 2001, 56, 3221–3235. [Google Scholar] [CrossRef]
- Isaenkov, S.V.; Cherdantsev, A.V.; Vozhakov, I.S.; Cherdantsev, M.V.; Arkhipov, D.G.; Markovich, D.M. Study of primary instability of thick liquid films under strong gas shear. Int. J. Multiph. Flow 2019, 111, 62–81. [Google Scholar] [CrossRef]
- Pan, L.-M.; He, H.; Ju, P.; Hibiki, T.; Ishii, M. Experimental study and modeling of disturbance wave height of vertical annular flow. Int. J. Heat Mass Transfer. 2015, 89, 165–175. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Aktershev, S.P.; Cherdantsev, A.V.; Kharlamov, S.M.; Markovich, D.M. Primary instabilities of liquid film flow sheared by turbulent gas stream. Int. J. Multiph. Flow 2009, 35, 617–627. [Google Scholar] [CrossRef]
- Andreussi, P.; Asali, J.C.; Hanratty, T.J. Initiation of roll waves in gas-liquid flows. AIChE J. 1985, 31, 119–126. [Google Scholar] [CrossRef]
- Hewitt, G.F.; Hall-Taylor, N.S. Annular Two-Phase Flow; Pergamon Press: Oxford, UK, 1970. [Google Scholar]
- Asali, J.C.; Hanratty, T.J. Ripples generated on a liquid film at high gas velocities. Int. J. Multiph. Flow 1993, 19, 229–243. [Google Scholar] [CrossRef]
- Dontula, P.; Macosko, C.W.; Scriven, L.E. Does the viscosity of glycerin fall at high shear rates? Ind. Eng. Chem. Res. 1999, 38, 1729–1735. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isaenkov, S.V.; Vozhakov, I.S.; Cherdantsev, M.V.; Arkhipov, D.G.; Cherdantsev, A.V. Effect of Liquid Viscosity and Flow Orientation on Initial Waves in Annular Gas–Liquid Flow. Appl. Sci. 2020, 10, 4366. https://doi.org/10.3390/app10124366
Isaenkov SV, Vozhakov IS, Cherdantsev MV, Arkhipov DG, Cherdantsev AV. Effect of Liquid Viscosity and Flow Orientation on Initial Waves in Annular Gas–Liquid Flow. Applied Sciences. 2020; 10(12):4366. https://doi.org/10.3390/app10124366
Chicago/Turabian StyleIsaenkov, Sergey V., Ivan S. Vozhakov, Mikhail V. Cherdantsev, Dmitry G. Arkhipov, and Andrey V. Cherdantsev. 2020. "Effect of Liquid Viscosity and Flow Orientation on Initial Waves in Annular Gas–Liquid Flow" Applied Sciences 10, no. 12: 4366. https://doi.org/10.3390/app10124366
APA StyleIsaenkov, S. V., Vozhakov, I. S., Cherdantsev, M. V., Arkhipov, D. G., & Cherdantsev, A. V. (2020). Effect of Liquid Viscosity and Flow Orientation on Initial Waves in Annular Gas–Liquid Flow. Applied Sciences, 10(12), 4366. https://doi.org/10.3390/app10124366



