Novel Design Methodology for DC-DC Converters Applying Metaheuristic Optimization for Inductance Selection

Abstract

Nowadays in modern industrial applications, where the power supply efficiency is more important than the output noise performance, DC-DC converters are widely used in order to fulfill the requirements. Yet, component selection and precise estimation of parameters can improve the converter’s performance, leading to smaller and more efficient designs. Hence, metaheuristic optimization algorithms can be applied using the mathematical model of DC-DC converters, in order to optimize their performance through an optimal inductance selection. Therefore, this work presents a novel design methodology for DC-DC converters, where the inductance selection is optimized, in order to achieve an optimal relation between the inductance size and the required energy. Moreover, a multi-objective metaheuristic optimization is presented through the Earthquake Algorithm, for parameter estimation and component selection, using the inductance of a buck DC-DC converter as a case study. The experimental results validate the design methodology, showing ripple improvement and operating power range extension, which are key features to have an efficient performance in DC-DC converters. Results also confirm the Small-Signal Model of the circuit, as a correct objective function for the parameter optimization, achieving more than 90% of accuracy on the presented behavior.

1. Introduction

During the last few decades, power electronic devices are more often used at residential houses, industries, including electric vehicles, portable battery-operated electronic equipment, photovoltaic systems, energy storage systems, variable-speed air conditioners, etc., [1]. Therefore, increasing demand for power electronic devices also leads to new challenges to be solved or to solutions to be improved; such as power losses, power efficiency, voltage, current regulation, and high operating frequency.

Moreover, these power electronic devices with high-efficiency requirements and low noise dependence use DC-DC converters in order to satisfy the requirements. To fulfill these demands, DC-DC converters must operate at high efficiency over a wide load range. In other words, in order to achieve high power density, the high operating frequency is required. Thus, it is necessary to select the correct inductance and capacitance values, as explained in [2,3].

Yet, the higher and higher required response speed in DC-DC converters (as explored in [4]), lead to large overshoots in the inductance current at the initial state. Hence, Ref. [4] explains that the issue can be dealt through current limiter hardware elements, which adds cost to the converter implementation and adds parasitic elements that may reduce the efficiency of the circuit.

Nevertheless, knowing that for a DC-DC converter the resistance, inductance, and capacitance elements, are all key components for the ripple and efficiency performance of the converter, a correct inductance selection is the most critical part of designing switching converters; since, as discussed in [5], the inductor is the circuit element responsible of the operating mode in terms of the duty cycle and the switching frequency of the converter, where most of the applications require to operate in Continuous Conduction Mode (CCM), which implies that the inductor does not fully discharge during the switching-off time (as discussed in [5,6]).

Hence, in many of the typical design methodologies (as validated in [7]), the mathematical expressions for a correct inductor selection are focused on a given expression in the form of a mathematical inequality, which looks for the minimum value of the inductor without considering the one that would represent its optimal parameter. Nonetheless, the parameter selection is a contradictory optimization issue, because in order to work higher switching frequency, the inductor value should be lower, leading to lower design sizes and with lower Equivalent Resistance Value (ESR); which is the parasitic element referred to as $R_L$ in this work.

Additionally, as explained in [8], as the current in the load decreases the converter reduces the duty cycle, causing an undesired behavior when approaching the Discontinuous Conduction Mode (DCM). Therefore, when low currents are required, the inductor value must be bigger (as detailed in [6]). Thus, in order to reduce power losses, an efficiency optimization methodology is required to find achieve a correct design, as discussed in [9].

Notwithstanding, the novel designs studied in [8,10,11] show dynamic improvements in the performance and efficiency of energy conversion (focused in their particular applications); still, an optimal designing method of topologies is not specified, which is a constant even in classical topologies (as shown in [6]). The above, because DC-DC converters are usually designed thinking about fulfilling the operating mode requirements (CCM or DCM), power requirements, and even thinking about a maximum allowed ripple; however, there is no certainty of having an optimal design regarding the selection of the components (particularly the Inductance).

On the other hand, Ref. [12] shows a design methodology for a non-inverting DC-DC converter, with the objective of charging a supercapacitor using the energy flow from the Inductance. In spite of it being an effective method, it is only focused on the energy of the supercapacitor neglecting the energy from the inductor, which leads to a non-optimal solution.

Additionally, Ref. [13] shows an application where a DC-DC converter is used for Maximum Power Point Tracking (MPPT), which is an application that continually requires duty cycle changes in the converter, in order to perturb the actual state and observe the resultant behavior. Hence, in applications with periodic perturbations, an inefficient inductance selection may complicate the MPPT calibration, regarding unexpected or aggressive responses against the induced perturbations.

Thus, addressing the issue, a novel design methodology is proposed in this paper, seeking to improve the design of DC-DC converters through the optimization of the inductor selection. As will be later detailed in this paper, the inductance selection is a multi-objective optimization problem; since, focusing only on the output voltage of the circuit may lead to unreal current peaks or impossible required behaviors, just as validated in [2]. Therefore, to achieve an efficient design with a low ripple performance and stable behavior, the proposal is to optimize the energy from the inductor, by also optimizing the output voltage in the circuit.

The optimization in this proposal is made through a metaheuristic approach, which allows implementing the multi-objective cost function in order to evaluate the performance of the circuit. Therefore, to obtain a correct representation of the system to evaluate, the Small-Signal Modeling from [14] is proposed due to its accuracy for a dynamic representation; since according to [10], the Small-Signal approach allows modeling and designing the circuit based on its dynamic behavior.

The metaheuristic algorithm implemented for this modeling approach, is the Earthquake Algorithm (EA) proposed in [15], which as explained in [16], is a geo-inspired algorithm based in the behavior of the velocities of earthquake waves. Moreover, the EA is the first metaheuristic algorithm geo-inspired, which has a great suitability for different optimization problems (as validated in [17]), provided by the fine and aggressive searching capabilities, provided by the behavior of the P and S wave velocities (as highlighted in [2]).

As cost function for the optimization, the Integral of Time Multiplied by Absolute Error (ITAE) performance index is taken as inspiration; where, as explained in [18] and validated in [15], the performance index may lead to small overshoots with damped oscillations profiles, which is exactly what the optimization is looking for. In terms of the current behavior of the circuit, a dampened profile is expected, in order to avoid the undesired large current overshoots, without neglecting the speed with which the converter voltage is expected to respond, which enables better and more efficient designs, as explained in [4].

Therefore, Section 2 deepens in the inductor behavior in basic converter topologies, to better understand the relevance of a correct inductance selection. Meanwhile, Section 3 explains the proposed design methodology for DC-DC converters based on multi-objective metaheuristic optimization. Later, the Earthquake Algorithm (EA) is explained in Section 4, where the key elements for the metaheuristic optimization through the EA are also summarized. Thus, a buck converter case study is presented in Section 5, in order to exemplify the novel design methodology, which is used for the experimental testbed designed in Section 6. Finally, Section 7 presents the results of this work, followed by the final conclusions in Section 8.

2. Basic DC/DC Converters

Typically, the classification of DC to DC converters is generally divided in two types, according to whether they increase (step-up) or decrease the voltage (step-down) (as disscused in [19]).

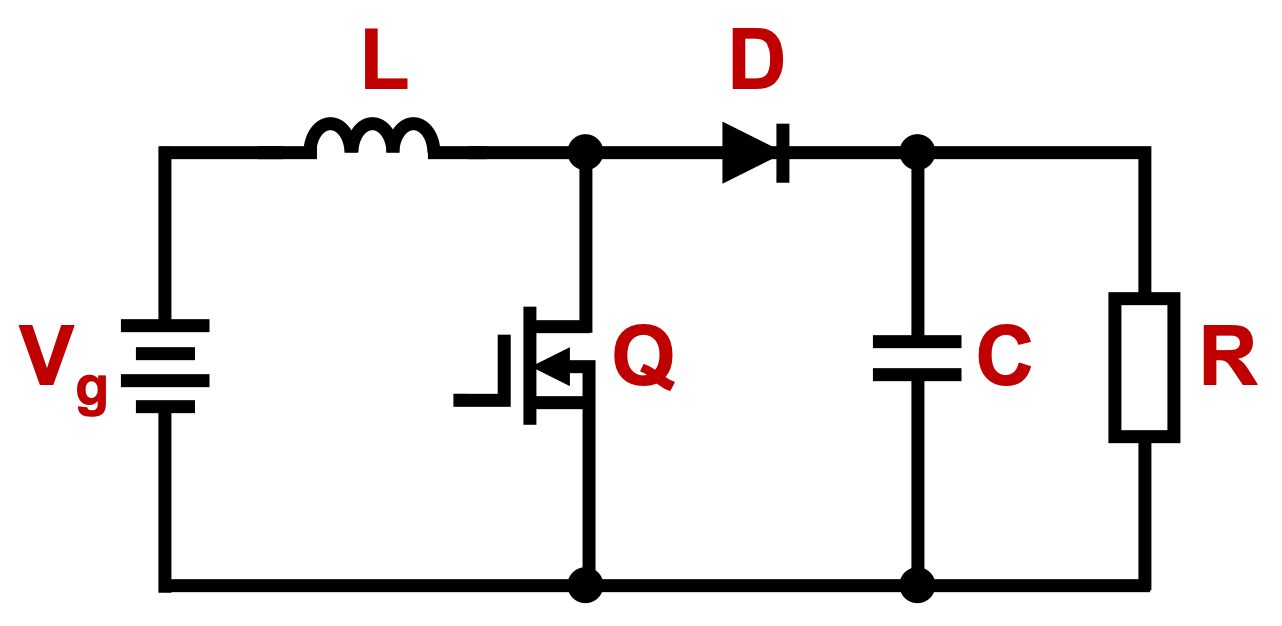
The step-up converter is usually known as boost converter (Figure 1), meanwhile the step-down converter is commonly known as buck converter (Figure 2). In both boost and buck topologies, the key elements for the power conversion are the input voltage $V_{\mathrm{g}}$, the L inductance, the output capacitance C, and the load of the system (resistance R).

The way the components interact between them leads to the power conversion, which directly depends on the configuration of the components and on their relation with the gates in the circuit. In the case of Figure 2 and Figure 1, the Diode D and the N-Channel MOSFET Q are the components that allow switching states between the charge and discharge of the inductance.

Hence, the inductor is the main element responsible of controlling energy flow to the output capacitor. Together, the output elements achieve a filter behavior that finally results in a “constant” output power to the load.

As explained in [6], the topologies of the buck and boost converters are the basis for the construction of many other topologies, since interconnecting series or parallel buck and/or boost converters give rise to other converters, such as the inverting and the non-inverting buck-boost converters.

Nevertheless, despite of the different configurations of the different converters, all the circuits have some common elements, such as the inductance L linked to the switch-node, and the inductance charging dependence on the control switches. Therefore, the correct selection of inductors remains a problem, whose solution leads to improve the efficiency of the performance of the converter.

Therefore, the main modeling approaches for DC/DC converters are the Average and the Small-Signal techniques. Nevertheless, both have different limitations, in the case of average state space model, according to [20] the approach is not able to simulate ripple effect on the inductance current and output voltage, due to the nonexistent switching frequency parameter; additionally, it does not allow an accurate closed-loop controller simulation, owing to the absence of a parameter involving the duty cycle of the switching device accurately.

Regardless, the Small-Signal analysis model used by [21] and also explained in [6], still has some of the limitations of the average model. Nevertheless, as explained in [22], the model approximates the dynamic behavior of the system around an initial steady-state, but again without considering the inductance current and output voltage ripple. Nevertheless, the introduction of the duty cycle term in the model allows to correctly study the behavior of the system around an operating point, and also the behavior of the circuit against disturbances.

3. Proposed Methodology

The proposed design methodology for the inductance selection, rescues basic concepts of metaheuristic optimization, adapted for the identification of an optimal inductance. The first approach of this method was discussed in [2], where the Earthquake Algorithm was implemented to optimize the inductance selection, in order to design a DC-DC converter for a supercapacitor charger application.

Nevertheless, the [2] proposal treated the design subject as a single objective optimization problem, taking the voltage at the supercapacitor as the optimization parameter. However, despite the fact that the capacity of nature-inspired metaheuristic algorithms for the design of DC-DC converters was demonstrated, it was left as future work to contemplate the current from the inductor as a second optimization objective.

This proposal, treats the inductance selection as a multi-objective optimization issue, regarding to the output voltage of the converter and the obtained current from the inductance.

Basically the proposal can be explained through the following steps:

• Converter modeling (objective functions).
• Cost functions selection for performance evaluation.
• Optimization through a metaheuristic algorithm.
• Results validation.

The converter modeling allows obtaining a transfer function per optimization objective, objectives whose performance can be later evaluated and classified, allowing the implementation of the metaheuristic algorithm. Therefore, each step will be detailed in the following subsections.

3.1. Converter Modeling

After obtaining the model of the converter to be designed, the transfer functions will work as the objective functions to be optimized, since they represent the performance of the circuit with the inductance values to be tested.

In the case of the Small-Signal analysis (detailed in [6]), the selected transfer functions are used to express the behavior of the output voltage and the inductance current, both related to the duty cycle. In order to validate the model regarding its experimental behavior, MATLAB/SImulink (MATLAB R2020a, MathWorks Inc.; Natick, MA, USA) can be used as the tool for the comparison with a more precise equivalent model, as discussed in [23].

According to [24], Simulink is a simulation tool created as a block-oriented environment for physical models of different systems. Therefore, the Simscape library of Simulink is proposed as the model validation tool for the dynamic behavior of the physical converter.

3.2. Cost Functions Selection

The next step, is to find proper criteria to evaluate the performance of the converter. Nevertheless, there are many possible cost functions that could be considered. Thus, the well known integral of square error (ISE), integral of absolute error (IAE), integral of time multiplied by square error (ITSE), and integral of time multiplied by absolute error (ITAE) performance indexes described in [25], are options that can be easily suited into the design application.

Henceforth, as described in [26], the main features that can be derived by the selection of the performance indexes are:

• Integral of the square of the error (ISE):

  $$\mathrm{ISE}={\int }_0^{\mathrm{T}}{e}^2\left(t\right)dt$$

  (1)

  where e is the error signal along to an evaluation period T. The ISE index is associated to the error energy, giving more importance to larger errors.
• Integral of the absolute magnitude of the error (IAE):

  $$\mathrm{IAE}={\int }_0^{\mathrm{T}}\left|e\left(t\right)\right|dt$$

  (2)
  The IAE index, is related to the cumulative error, giving more importance to the distance between the reference and the obtained response.
• Integral of time multiplied by absolute error (ITAE):

  $$\mathrm{ITAE}={\int }_0^{\mathrm{T}}t·\left|e\left(t\right)\right|dt$$

  (3)
  The ITAE index, is related to the absolute error value in time, giving more importance to the last errors than the initial ones.
• Integral of time multiplied by squared error, (ITSE):

  $$\mathrm{ITSE}={\int }_0^{\mathrm{T}}t·e^2\left(t\right)dt$$

  (4)
  The ITSE index, also associated to the error energy, is weighted by time, giving more importance to the most recent errors.

However, considering their main features and drawbacks, designing using the ITAE index may lead to small overshoots and damped oscillations (as explained in [15,18]). Therefore, it is highly recommended as a cost function for this methodology.

Moreover, since a fast voltage response is a priority for DC-DC converters design (as discussed in [4]), the ITAE allows an optimization that prioritizes the convergence and velocity of the converter, ensuring that the last errors will be weighted with greater importance.

3.3. Metaheuristic Optimization

With the objective function and the criteria to evaluate the performance of the converter, the following step is the implementation of the metaheuristic algorithm (Earthquake Algorithm for this paper).

The output voltage and the current from the inductor, can be optimized by simulating the response of the converter with the different inductor values, evaluated through the multi-objective function shown in Equation (5).

$$Err={\int }_0^{\mathrm{T}}t·|e_v\left(t\right)|dt+{\int }_0^{\mathrm{T}}t·\left|e_{i_L}\left(t\right)\right|dt$$

(5)

where $e_v\left(t\right)$ is the error of the output voltage through time, $e_{i_L}\left(t\right)$ the error of the current from the inductor in time, and $Err$ the total error to be minimized.

It can be clearly seen that Equation (5) is deduced from Equation (3), seeking to achieve small overshoots and damped oscillations equally in the output voltage and in the inductance current.

Nevertheless, in order to understand how the performance evaluation is made through the metaheuristic algorithm, Figure 3 and Figure 4 graphically show how the error is evaluated over time.

In the case of the voltage optimization shown in Figure 3, the reference voltage is taken as a step profile, due that the step is an instantaneous response without any overshoot. For a non-optimized behavior with over and undershoots (blue curve), taking the absolute value of the error in every sample allows weighting, in the same way, the oscillations below or above the reference, thus leading to a steady-state with dampened oscillations (as also explained in [18]).

Therefore, in the case of the output voltage, the expected behavior after the Optimization is shown in the green curve from Figure 3, where a smooth settlement without oscillations in the steady-state is shown (just as validated in [2]).

Nonetheless, a single-objective optimization directed only to the charge in the capacitor (output voltage), leads to the requirement of a greater initial current spike, which in some applications (such as [2]) makes it hardly possible to be implemented.

Consequently, the multi-objective optimization conducted to obtain the fast but possible response from the inductor, is developed through another step reference. Yet, the reference has to be estimated through the Ohm law, between the reference voltage and the resistive load of the circuit. Therefore, the expected behavior to be obtained after the optimization, should be similar to the green curve in Figure 4.

In other words, the current overshoot should be kept small in magnitude and with a non-aggressive slope, regarding to the properties of the ITAE performance index (as explained in [18]). Therefore, the shown profiles from Figure 3 and Figure 4 ensure the fastest voltage response with a low current slope, which is the best behavior to be obtained from the design, as discussed in [4].

3.4. Results Validation

The resulting inductor, is taken from the global best result found through the metaheuristic algorithm, even so as a “double-check” measure to be taken, the metaheuristic algorithm could be run more than once, and the final result can be taken as the statistical average value.

Accordingly, taking into consideration that the optimization was proposed to be made through the transfer functions from the small-signal model, the validation of the obtained results can be made through experimental implementations, or even through a Simscape simulation in MATLAB/Simulink as explored in [24].

4. Earthquake Algorithm

The optimization of the inductance selection in this paper is made through the first geo-inspired metaheuristic algorithm, called Earthquake Algorithm (EA), which is based on the behavior of the P and S waves existing in earthquakes (as explained in [16]).

The EA allows easy suitability to different kinds of optimization problems, since the combination of searching velocities given by the combination of the P and S velocities, provides to address both wide and fine searching paths; since, as discussed in [17], the EA require less parameters calibration to suite different optimization applications, compared to other metaheuristic algorithms. Hence, the EA allows suiting easily combining an aggressive searching behavior through the P-wave velocity with a smaller area optimization through the S-wave velocity.

The first complete version of the algorithm was delivered in [15], for the Optimization of the PID (Proportional Integrative Derivative) gains of a speed controller in a DC motor. The PID gains optimization showed the basic conceptualization of the ITAE performance index as cost function, which inspired the criteria utilization for this proposed methodology in DC-DC converters design, as explored in [2].

Summarizing the basic concepts for the deduction of the EA, the P-waves are faster and the S-waves are finer, which are the key elements that the algorithm takes advantage from. Consequently, as explained in [16], Equations (6) and (7) describe the estimation of P- and S-wave velocities.

$$v_p=\sqrt{\frac{\lambda +2\mu }{\rho }}$$

(6)

$$v_s=\sqrt{\frac{\mu }{\rho }}$$

(7)

where $v_p$ and $v_s$, are the P- and S-wave velocities, respectively, $\lambda$ and $\mu$ are the Lamé parameters, and $\rho$ is the density of the earth propagation material. Nevertheless, as explained in [15,16], the lamé parameters can be equal under some circumstances, maintaining then for this application that $\lambda =\mu =1.5$ GPa.

On the other hand, the density of the solids ($\rho$) is used as a random value, which gives the heuristic behavior to the algorithm, so as not to leave the geo-inspiration of the algorithm, the selected range for the density parameter is taken between 2200 and 3300 Kg/m${}^3$, inspired by the real geological properties of the materials described in

Table 1. Principal materials or geologic formation properties taken from [27].

Material	Density (Kg/m${}^3$)	Poisson’s Ratio	${\mathit{v}}_{\mathit{p}}/{\mathit{v}}_{\mathit{s}}$
Sandstone	2500	0.21	1.65
Salt	2200	0.17	1.59
Limestone	2700	0.19	1.62
Granite	2610	0.25	1.73
Basalt	2940	0.28	1.8
Peridotite	3300	0.29	1.8
Dunit	3300	0.29	1.8
Pyroxenite	3300	0.29	1.8

.

With all the main parameters of the algorithm already defined, the use of $v_s$ or $v_p$ is not yet clarified. Thus, it is crucial for the algorithm to define an operating range for the $v_s$ to be used, in order to define when to use a velocity or the other one; which, as explained in [15,16], is defined as the S-range or Sr.

The Sr, as shown in Figure 5, is always defined around the best solution; therefore the nearest particles (red epicenter in Figure 5) to the global solution (blue epicenter) will use the $v_s$ equation, meanwhile the epicenters out of the defined $Sr$ will take the $v_p$ equation.

Thus, it could be implied that the epicenters “orbit” around the global best solution, however, the Sr should be assigned (as explained in [16]) with the previous knowledge of the problem requirements. However, from [15,16] implementations, the Sr is recommended to be 2% from the best solution. It is important to highlight that since both speeds are calculated by a square root, the final result is a positive number. The architecture of the algorithm contemplates the random selection of a positive or a negative velocity value, regardless of whether it is $v_s$ or $v_p$, in order to select whether $\pm v_s$ or $\pm v_p$. Consequently, the position of the epicenters is updated through Equation (8).

$$X_i^t=X_i^{t-1}+V_i,$$

(8)

where $X_i^t$ and $X_i^{t-1}$ are the current and previous positions, respectively and $V_i$ is the current velocity ($v_s$ or $v_p$).

Finally, as another heuristic freedom degree for the Earthquake Algorithm, in [16] it is shown how a random selection for an exponential distribution reduces the probability of visiting points already visited for the epicenters. The implemented expression of the distribution is originally taken from [28] (attending to its relation with the Poisson distribution explained in [15]). Therefore, the random value is generated in a range of ± the maximum value of $v_p$/$v_s$, i.e., ± 1.91 (taken from Table 1), resulting in the relation described by Equation (9).

$$X_i^t=X_{best}+Ex{p}_{\mu }\left(s\right),$$

(9)

where $X_{best}$ is the global best solution and $Ex{p}_{\mu }\left(s\right)$ is the random value generated with the exponential distribution from the value of $\mu$.

After some iterations, all the epicenters begin to converge due to the small velocity around the global solution, when they enter the Sr. For that reason, Equation (9) allows some randomly selected epicenters to “escape” the Sr, in order to prevent to get trapped into a local minimum.

Details of the implementation of the Earthquake Algorithm for the inductance selection will be discussed in the following section. Additionally, Figure 6 shows the flow chart of the EA, adapted for the design application, where it is important to highlight that the $v_s$ and $v_p$ velocities selected through the Sr, represents the adaptability factor that allows optimizing solutions to problems that require both fine and aggressive searches, as explored in [17].

5. Case Study

In order to achieve the smart converter design, it is defined for this case study that the main purpose of the circuit to be designed, is to achieve an efficient 24 [V] to 5 [V] conversion, which is a typical conversion rate application. Therefore, a buck converter topology (as the one shown in Figure 2) is selected for the task.

Nevertheless, by the fact that a more precise model could lead to a better design in this proposed methodology, some of the parasitic elements from the inductor and capacitor are added into the modeling considerations. Thus, the ideal buck converter scheme from Figure 2, can be redrawn as shown in Figure 7; where the added $R_L$ and $R_C$, are the series parasitic elements of the inductance and capacitance, respectively.

Table 2. Buck converter initial parameters.

Variable	Parameter	Value
$V_g$	Input Voltage	24 [V]
f	Switching frequency	100 [kHz]
L	Inductor	330 [$\mathsf{\mu }$H]
$R_L$	L series Resistance	1.8 [$\Omega$]
C	Capacitor	220 [$\mathsf{\mu }$F]
$R_C$	C series Resistance	40 [m$\Omega$]
R	Load resistance	30–150 [$\Omega$]
$P_{out}$	Output power	0.167–0.833 [W]
$V_{out}$	Output voltage	5 [V]
$i_{out}$	Output current	33–167 [mA]

summarizes the initial parameters of the case study converter to be optimized. In the case of [2], the converter design was made through an open-loop model, unlike this case study where a closed-loop system is presented. Nevertheless, it is important to highlight that with the proposed methodology any of the parameters can be taken as optimization goals (even more than one of the parameters).

However, this optimization example enables the suitability of converters with fixed controllers, for different operating parameters. In other words, this case study takes as inspiration a typical issue in mass production elements, where a certain inductor is out of stock, and this methodology enables to find another inductance that could work even better, than the temporarily unavailable inductor. Additionally, this type of case study could enable the improvement of existing designs. Hence, the closed-loop system follows the blocks diagram shown in Figure 8, where a cascade scheme is presented for the inductance current ($i_L$) and the output voltage ($V_{out}$) parameters.

In both examples of application (the supercapacitor charger partially designed in [2] and the one presented in this work), the methodology allows selecting an optimal inductance without changing the calibration of the controllers or other circuit elements, which translates into economic benefits and into a viable solution for designers and manufacturers of electronic circuits.

Then, in Figure 8 can be seen two Proportional Integrative (PI) controllers in cascade, where the first one is tuned to compensate the error from the output voltage, and the second one tuned for the $i_L$ error compensation. In real applications, the output of both controllers has to be converted into the duty cycle, which is latter translated into the control signal for the transistor. Having already described the system to be optimized, the application of the proposed design methodology is presented below.

5.1. Converter Modeling

The basic operation of the circuit in Continuous Conduction Mode (CCM), can be described by two states: first when the transistor is ON (Figure 9) and when it is OFF (Figure 10).

In the ON state, the inductance is charged with the energy from the source, meanwhile in the OFF stage it is discharged, enabling the capacitor to be charged with the energy flow. Hence, as explained in [6], the converter has a linear control profile, considering its voltage conversion as $V=\left(D\right)\ast V_g$, where from this point in this paper D is the duty cycle of the PWM, which is the control signal of the converter.

Therefore, one of the most used and first-choice methods for the mathematical modeling of converters is the small-signal approach (Small-Signal Model), developed by S. Cúck and R.D. Middlebrook, where in [14] the work aims to describe the dynamics of the converter as a set of time-invariant equations, valid for the entire switching cycle.

Hence, the first step is to average all possible states (ON and OFF transistor states in this case) to obtain an average model, which removes variations over time but retains the non-linearities (described in [6]) of the system. As a second step, linearization is done by approximating the nonlinear relationships between the circuit variables under small-signal assumptions, which produces a dynamic model averaged over time in the presence of a small-signal excitation. Finally, the obtained model is transferred to the frequency domain, in order to obtain the transfer functions of the power stage dynamics as explained in [6].

Consequently, after applying the small-signal analysis to the states of the circuit, the transfer functions that represent the Output voltage and Inductance current behaviors against the control signal (Duty cycle), is given by Equations (10) and (11), respectively.

$$G_{vd}\left(s\right)=\frac{{\widehat{V}}_{out}}{\widehat{D}}=\frac{\left(C{R}_C{V}_{g}R\right)s+R{V}_g}{\mathrm{Den}}$$

(10)

$$G_{id}\left(s\right)=\frac{{\widehat{i}}_L}{\widehat{D}}=\frac{V_g(CR+C{R}_C)s+V_g}{\mathrm{Den}}$$

(11)

where in the denominator in both cases (Equations (10) and (11)), is given by the expression defined by Equation (12).

$$\mathrm{Den}=(CLR+CL{R}_C)s^2+(L+RC{R}_C+RC{R}_L+C{R}_C{R}_L)s+(R+R_L)$$

(12)

Henceforth, Equation (10) is defined as the objective function for the output voltage, and Equation (11) the objective function for the current in the inductor, which are the functions for the multi-objective optimization. Hence, Figure 8 can be redrawn as shown in Figure 11, where the buck converter block was substituted with the small-signal transfer functions.

Nevertheless, it is important to highlight that the input for the converter in Figure 8 was the PWM, with the duty cycle as control parameter. Yet, the duty cycle is still the input parameter for $G_{vd}$ and $G_{id}$, but the expected input is the duty cycle value, without any pulsing source for the transfer functions.

5.2. Model Validation

In order to ensure a correct optimization through the metaheuristic algorithm, the objective functions in Equations (10) and (11) have to be validated. Therefore, as explained above in Section 3, the MATLAB/Simulink simulation through its Simscape library is used for the model validation, since allows validating the dynamic performance of the converter.

It is important to highlight that the Simulink model is taken as reference for the mathematical equations validation, since it allows evaluating how the system dynamically reacts by also considering the ripple of the circuit. Nevertheless, the Simulink model is not taken as the simulating model for the optimization methodology regarding the computational cost of the simulation (which is higher than the transfer functions simulation), which would make it less efficient for the metaheuristic algorithm.

Thus, the simulations regarding the transfer functions and the circuit model, were performed using the parameters from Table 2. Then, Figure 12a shows the resultant curves for the output voltage, where it is clear the correct behavior of the transfer function compared against the circuit model.

To demonstrate a correct comparison against the real behavior of the system, the highlighted circled area is zoomed in, showing the performance of $G_{vd}$ against the ripple in the circuit.

Additionally, Figure 12b shows the validation of the $G_{id}$ transfer function, where it can be analyzed that the equation correctly represents the behavior of the current through the inductor. As in the previous case, a certain area, is highlighted and zoomed in, showing the behavior of the transfer function compared to the ripple of the current in the circuit.

As explained when the equations were obtained, $G_{vd}$ and $G_{id}$ represent the an average approach of the variables to be analyzed, therefore it is important to highlight from Figure 12, that the obtained curves represent the average behavior of the ripple in the real circuit model (exemplified by the Simscape model), validating then the behavior of both equations.

Even so, to quantify the model validation, the statistical mean can be computed to obtain a statistical comparison and therefore, to measure the accuracy of the models.

Table 3. Statistic mean of the inductor current.

Parameter	Value
Simscape Model	0.1669 [A]
$G_{id}$	0.1678 [A]
Accuracy	99.4636 [%]

shows the results for the $G_{id}$ objective function. Meanwhile,

Table 4. Statistic mean of the output voltage.

Parameter	Value
Simscape Model	4.8104 [V]
$G_{vd}$	4.8105 [V]
Accuracy	99.9990 [%]

shows the accuracy results for the $G_{vd}$ transfer function.

Finally, as a last double-check measure for the model validation, the ITAE performance index was computed for both voltage and current curves. The obtained $ITAE=0.0004$ between the Simscape vs $G_{vd}$ voltage curves, and the $ITAE=0.0017$ between the Simscape vs $G_{id}$ current curves, completely validated the objective functions.

5.3. Metaheuristic Optimization

As explained before, the metaheuristic optimization of the inductance selection is made through the geo-inspired Earthquake Algorithm. In this case, the $x_i$ positions represent the inductor values to be evaluated.

Therefore, Figure 6 shows the basic scheme of the EA, with the architecture adapted for the optimization through the $G_{vd}$ and $G_{id}$ transfer functions. Where the evaluation block in the flowchart corresponds to the simulation of the current and voltage performance with the inductor to be tested. After the simulation of both transfer functions, Equation (5) is applied in order to evaluate the performance through time.

The results of each position (each position from EA is an inductance value), are classified regarding their behavior against Equation (5). The classification leads to knowing which inductance achieved the better result and, therefore, to update the global best solution in case of having a new one.

The EA was implemented using 100 epicenters, for 100 iterations as the maximum number of iterations, the epicenters were initialized as a random population in the range between 0.1 [$\mathsf{\mu }$H] and 1000 [$\mathsf{\mu }$H], obeying the order of the initial value proposed for the inductor.

Additionally, to eliminate some of the uncertainty from the optimization process, the earthquake algorithm was performed four times, with the purpose of having three validation runs for the first response. Accordingly, Figure 13 shows the evolution of the error through the iterations, comparing the first obtained response with the validation trials.

Thus, the convergence plot in Figure 13 shows uniformity in all the trials, ensuring and validating accuracy and consistency of the results, therefore the selected inductor from the optimization process is taken from the average value of the four results.

Moreover, since this work presents a novel design methodology for the inductance selection in DC-DC converters, an experimental testbed was design for the validation of the proposal. Hence, the following section shows and details the schematic and the Printed Circuit Board (PCB) designed for the task.

6. Experimental Testbed Design

The control signal and data acquisition for this testbed application is given through a FRDM-K64F development board, which according to [29], has an MK64FN1M0VLL12 Microcontroller working at 120MHz, with 1024KB of Flash memory, 256KB of SRAM memory, and an integrated Floating Point Unit (FPU).

On the other hand, Figure 14 shows the complete schematic (in EAGLE (v.9.6.1)(Autodesk Inc.; San Rafael, CA, USA)) of the designed circuit for the experimental validation; where, for the gate activation of the MOSFET, a UCC27511A single-channel gate driver was selected since (according to [30]) its a high-speed compact gate driver perfectly suitable for DC-DC converters applications. Hence, the layout of the driver was made as recommended in [30], where the resistances are estimated in order to achieve a fast response from the driver with immunity against the parasitic Miller turn-on effect.

Additionally, it is important to highlight the implementation of the current sensor MAX44285H, which was selected due to the high-precision allowable from the Current-Sense Amplifier (as defined in [31]). Therefore, since [31] recommends for a better performance, to operate the sensing voltage difference around 25 mV for the 100 V/V gain amplifier, a 0.3 $\Omega$ shunt resistor was selected for the design.

Therefore, following the schematic design from Figure 14, Figure 15 shows the PCB designed (also through EAGLE (v.9.6.1)(Autodesk Inc.; San Rafael, CA, USA)) as testbed for the DC-DC converters evaluation; where it was sought to follow the arrangement pattern of the diagram of a classic buck converter model (as shown in Figure 2), in order to facilitate the location of the components presented in this work.

Moreover, it is critical for a correct evaluation of the converters to clarify the purpose of the LED indicators in the circuit, since the LED1 (left-side LED from Figure 15) is for the 24 V source power indicator; but LED2 is implemented for safety purposes in the circuit, since ensures a constant load in the circuit when there is no connection in $R_{LOAD}$ or $V_{OUT}$. Nevertheless, LED2 can be decoupled from the rest of the circuit by removing the header that connects the terminals to the circuit.

Accordingly, the testbed was designed for different applications, where a fixed load can be maintained by welding a resistive load in the $R_{LOAD}$ drills. In addition, a DC Electronic Load or any other load type can be connected for different tests in the $V_{OUT}$ terminals.

Henceforth, in order to properly evaluate the designed converter and compare it against the previous design, two identical PCBs were manufactured with the inductance value as the only difference between them. Then, Figure 16 shows the experimental testbeds designed for the converters evaluation, where it can be clearly seen that both boards are identical PCBs, except for the value of the inductors, where in the first plate there is a 472 inductor and in the second one an inductor 331. The precise values and features of the selected inductors will be explained and detailed in the following section.

7. Results

The metaheuristic optimization of the inductance selection, leaded to an average 5 [mH] inductor for the DC-DC converter. Therefore, in order to validate the results with an implementable value taken from an actual datasheet, Bourns^® Shielded Inductors where analyzed, due to their implementation capabilities for DC-DC converters. Therefore, taken from the [32] datasheet, the nearest inductor value to the optimized one is a 4.7 [mH], reason why the results presented in this section are made through that value.

Table 5. Inductor values comparative through [32] datasheet.

	Inductance	Test Frequency	${\mathit{R}}_{\mathit{L}}$
Initial	330 [$\mathsf{\mu }$H]	100 [kHz]	1.8 [$\Omega$]
Optimized	4.7 [mH]	100 [kHz]	13.9 [$\Omega$]

shows the main parameters of the inductors, with real data taken from [32].

To validate the results and compare the behavior of the optimized inductance selection, against the initial parameters of the buck converter, different simulated and experimental tests were performed.

7.1. Simulated Results

Therefore, to evaluate the behavior of the circuit in the proposed operating range from Table 2 (30 ≤ R ≤ 150), three simulated tests were performed for the comparison, the first one with R = 30, then with R = 90, and finally with R = 150.

All plots in this section have the same color code, the blue graphs are of the circuit with the 330 [$\mathsf{\mu }$H], and the orange ones are from the 4.7 [mH] inductance in the circuit. Additionally, all the current and voltage curves are presented with a zoomed-in area, in which the ripple reduction of the voltage and current are also shown.

In the case of the 30 [$\Omega$] load resistance, Figure 17a shows the inductor current and Figure 17b the output voltage profiles. Hence, Figure 17a clearly shows the ripple reduction in the current through the inductance, achieving a better steady-state.

Table 6. Integral of time multiplied by absolute error (ITAE) values under the 30 [$\Omega$] load test.

	${\mathit{i}}_{\mathit{L}}$	${\mathit{V}}_{\mathit{out}}$	Total
Initial	0.0023	0.0105	0.0127
Optimized	8.8038 × 10−4	0.0104	0.0113

shows the breakdown of the obtained error, evaluated through Equation (5). Therefore, it can be analyzed how the optimization affected in greater way the energy from the inductance, achieving a better output voltage with a more efficient current consumption.

On the other hand, Figure 18a,b shows the inductance current and output voltage curves, respectively, from the 90 [$\Omega$] load resistance test. In this performance evaluation, it can be clearly seen how the non-optimized circuit remains in Continuous Conduction Mode (CCM) in the inductance current curves. Nevertheless the ripple makes it be near the discontinuous mode, which seems still far from happening in the optimized circuit.

Thus,

Table 7. ITAE values under the 90 [$\Omega$] load test.

	${\mathit{i}}_{\mathit{L}}$	${\mathit{V}}_{\mathit{out}}$	Total
Initial	0.0025	0.0127	0.0153
Optimized	0.0013	0.0130	0.0143

quantifies the results from Figure 18, showing a 6.5359% improvement regarding the total estimated error, highlighting that the error in $i_L$ decreased by 48%. Yet, the output voltage did not show a did not show significant improvement, but the inductor current improvement showed to give the system a more accurate and more robust response since it would presumably be more easily maintained in the CCM zone thanks to the ripple reduction.

Finally, in the case where the 150 [$\Omega$] load resistance was taken for the test, the results are shown in Figure 19a,b for the current and voltage profiles. Consequently, the data quantification is shown in

Table 8. ITAE values under the 150 [$\Omega$] load test.

	${\mathit{i}}_{\mathit{L}}$	${\mathit{V}}_{\mathit{out}}$	Total
Initial	0.0024	0.0136	0.0160
Optimized	0.0013	0.0140	0.0153

, where the error reduction is validated as in the two cases before.

The results in this case, show the inductance current entering into the Discontinuous Conduction Mode in the non-optimized curve (blue plot in Figure 19a), which is an undesired behavior in this case study. Nevertheless, the same figure validates the consistency of the results from the optimized circuit, also achieving a stable behavior around the settling point, showing an extended operating rate for the converter.

Moreover, as shown by Table 6, Table 7 and Table 8, the greater error reduction was made in the current through the inductor, validating the relevance of the multi-objective optimization relevance, just as predicted from [2] application.

As a final measure to validate the implementation capabilities of the optimized converter, Figure 20 shows the control signals required by the optimized design, where it can be seen that the duty cycle in every instance of time remains in an allowable range (0 to 1), with non-aggressive changes.

Therefore, after the different load tests, the validation of the existing component (through the [32] datasheet), and the control signals analysis, it has been demonstrated the implementation capabilities of the optimized design. Henceforth, an experimental validation is presented in the following Subsection.

7.2. Experimental Validation

Finally, in order to validate the implementation capabilities of the proposed design methodology, where the performed tests are documented in the nominal operation values discussed in Table 2. Furthermore, it is important to highlight that as discussed in Section 6, all the control signals are given by the FRDM-K64F development board.

Moreover, Figure 21 shows how the testbeds from Figure 14 (with the optimized and the non optimized inductor values), were simultaneously tested using a constant nominal load (90 [$\Omega$]). The main objective of this test, is to validate the ripple reduction in the current of the optimized designed.

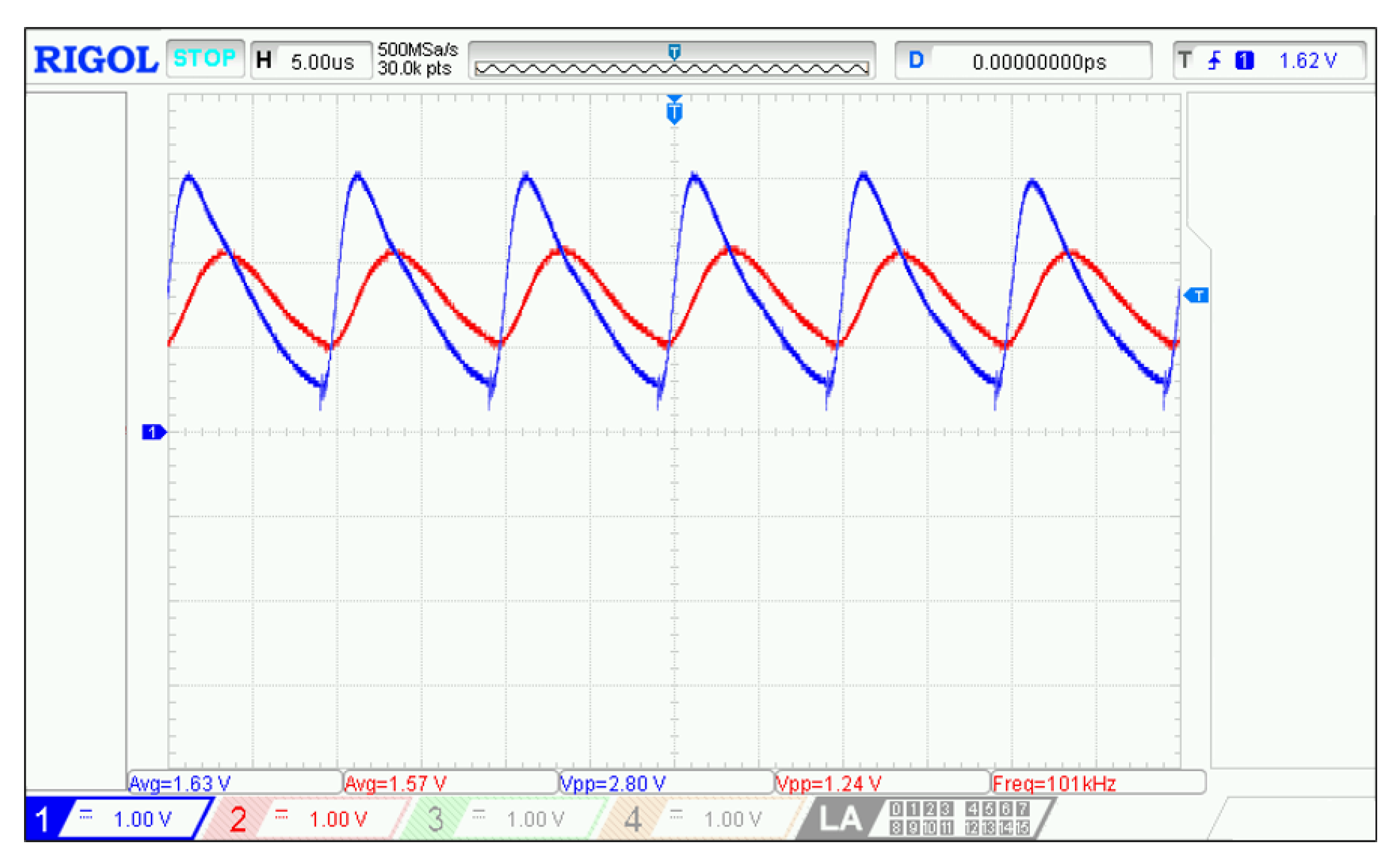
Therefore, Figure 22 shows the screenshot from the oscilloscope during the current evaluation, where it can be clearly seen the ripple reduction in the optimized design (Red Channel 2 in Figure 22). Nevertheless, since (as discussed in Section 6) the current profiles were obtained by measuring the analogic output in the Current-Sense amplifier (MAX44285H), post-processing of the acquired data is required for a correct evaluation in terms of [A].

Henceforth, after the data acquisition and voltage to current conversion (as recommended in [31]), Figure 23 shows the experimental results processed and plotted in MATLAB; where, the most important feature to be highlighted is the ripple reduction in the current of the optimized design compared to the non-optimized converter.

Therefore, the measured ripple of the optimized converter is 0.014 [A], meanwhile a 0.048 [A] ripple was achieved by the non-optimized design, which is traduced into a 70.833% of ripple reduction. Hence, the ripple reduction is validated as one of the main contributions of the proposed model.

On the other hand, each converter was individually tested in their nominal operation parameters, but this time seeking to acquire precise data regarding the output voltage performance of the converters through different control signals (duty cycle); where the duty cycle changes allow to evaluate how aggressive the output voltage changes, which allows evaluating the real achievable precision of the converter designs, since a more robust response can be achieved if the converter can make more precise adjustments in terms of its control signal.

Thus, Figure 24 shows how the testbeds were individually tested using a BK Precision 8601 (B&K Precision Corporation, Yorba Linda, CA, USA). DC Electronic Load, which allowed to safely manipulate the duty cycle of the converters in order to acquire precise voltage data regarding the duty cycle variations.

Hence, Figure 25 presents the experimental validation of the output voltage compared to the Simscape Simulink Model, which allows by inference to also validate that the mathematical models used for optimization were correctly developed, since the transfer functions model showed high fidelity compared to the Simscape model in Section 5.

Moreover, from the performed analysis through the simscape simulations, it was clear that the dynamic behavior of the output voltage of the converter did not have a significant change compared to the current ripple. Nevertheless, it is worth to analyze the performance of the converter through different duty cycle perturbations, since it allows to analyze the precision of the converter and how it will react against perturbations around nominal conditions (since the duty cycle is the control input of the system).

Thus, Figure 26 presents a comparative analysis of both designed converters (optimized and non-optimized), wherein both cases it is highlighted in black the profile that represents the nominal conditions of the converter. Hence the output voltage against different duty cycle curves were obtained with a 5% difference between each profile, in order to analyze a wider range of operation in both converters.

Therefore, comparing the optimized against the non-optimized design profiles from Figure 26, it can be clearly inferred that the optimized design provides a finer response against the duty cycle changes, since the non-optimized design proofs to have a more aggressive response against the duty cycle changes. Therefore, in addition to demonstrating the ability to carry out the proposed design methodology to a physical application, a better response was obtained in terms of precision, efficiency, and ripple in the circuit current.

8. Conclusions

The balance of the relation between the inductor size and the current that is used as an objective, is a contradictory design issue, due that if large thresholds are required between the minimum and maximum current, a large inductor value will be necessary. However, if the inductor value is increased, it grows with its Equivalent Series Resistance (ESR, $R_L$ in this work) which increases the losses in the inductor and therefore the efficiency of the converter will be compromised. On the other hand, if the switching frequency is increased to reduce the size of the inductor, the switching losses of the transistor and the diode begin to impact the efficiency of the converter. This is one of the most important disadvantages of the reducer converter. Therefore this work enabled to find the optimal relation between the size of the inductor and its performance.

This proposal achieves an optimal DC-DC converter design, regarding a fast voltage response with a low current slope, which enables designing based in the actual expected performance. Now then, it is clearly shown by the obtained results that the metaheuristic multi-objective optimization, directs the inductance selection to a low ripple design regarding the output voltage and the current through the inductor, achieving a behavior that it is also friendly with the required control signal. Therefore, with all the confidence provided by the simulation tests, the proposed methodology was validated to be an implementable solution through the designed experimental testbed, which allowed to physically demonstrate an almost 71% of current ripple through the inductance.

Henceforth, this work enables a methodology that allows achieving better and more efficient DC-DC converters design, not only optimizing the inductance selection but also through other parameters selection, since the methodology could be easily suited into other design applications that require improved performance, efficient designs, components substitutions (when out of stock), or just a particular behavior-oriented application.