Compressive Sensing Imaging Based on Modulation of Atmospheric Scattering Medium
Abstract
1. Introduction
2. Theoretical Basis and Imaging Model
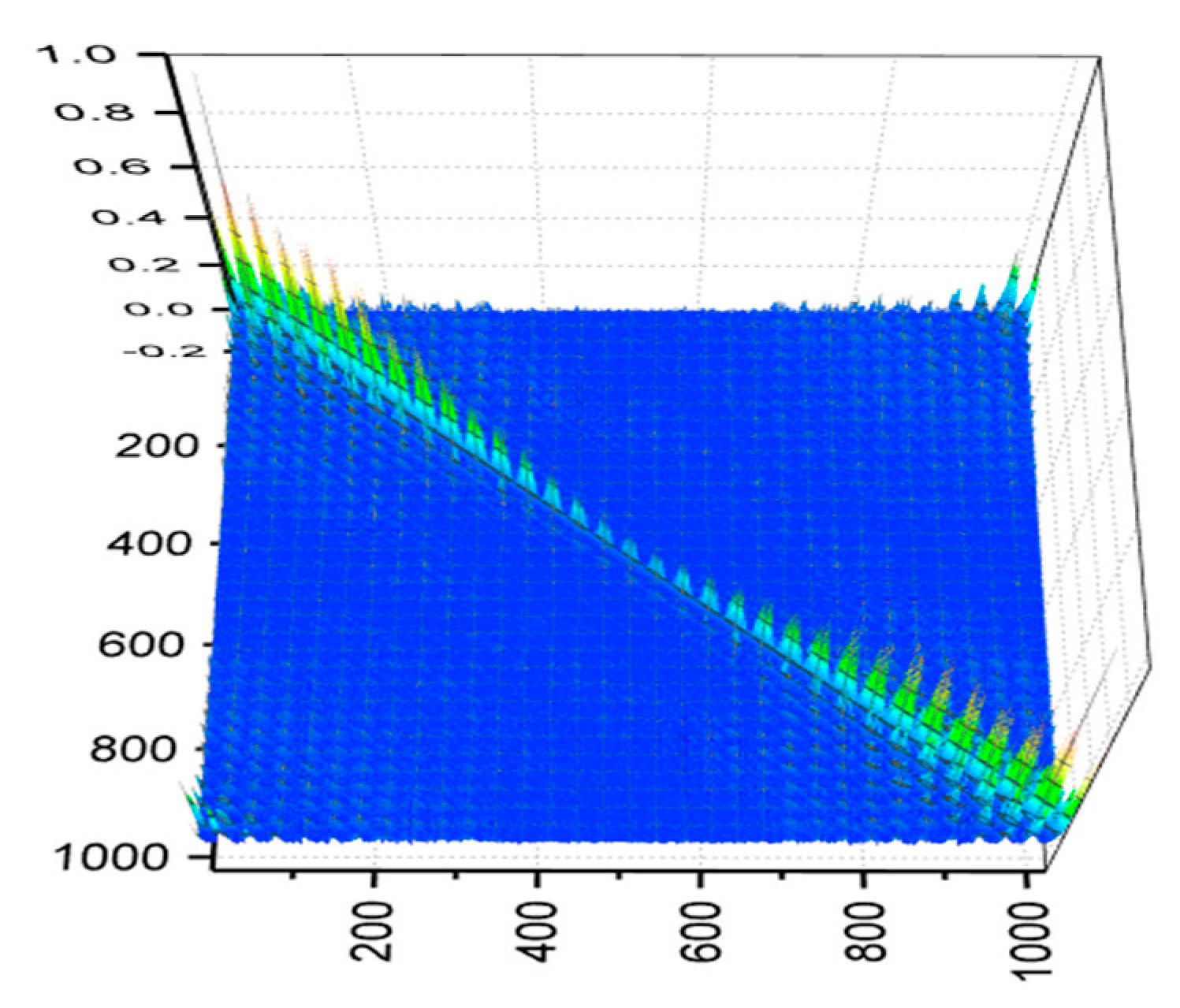
3. Numerical Simulation
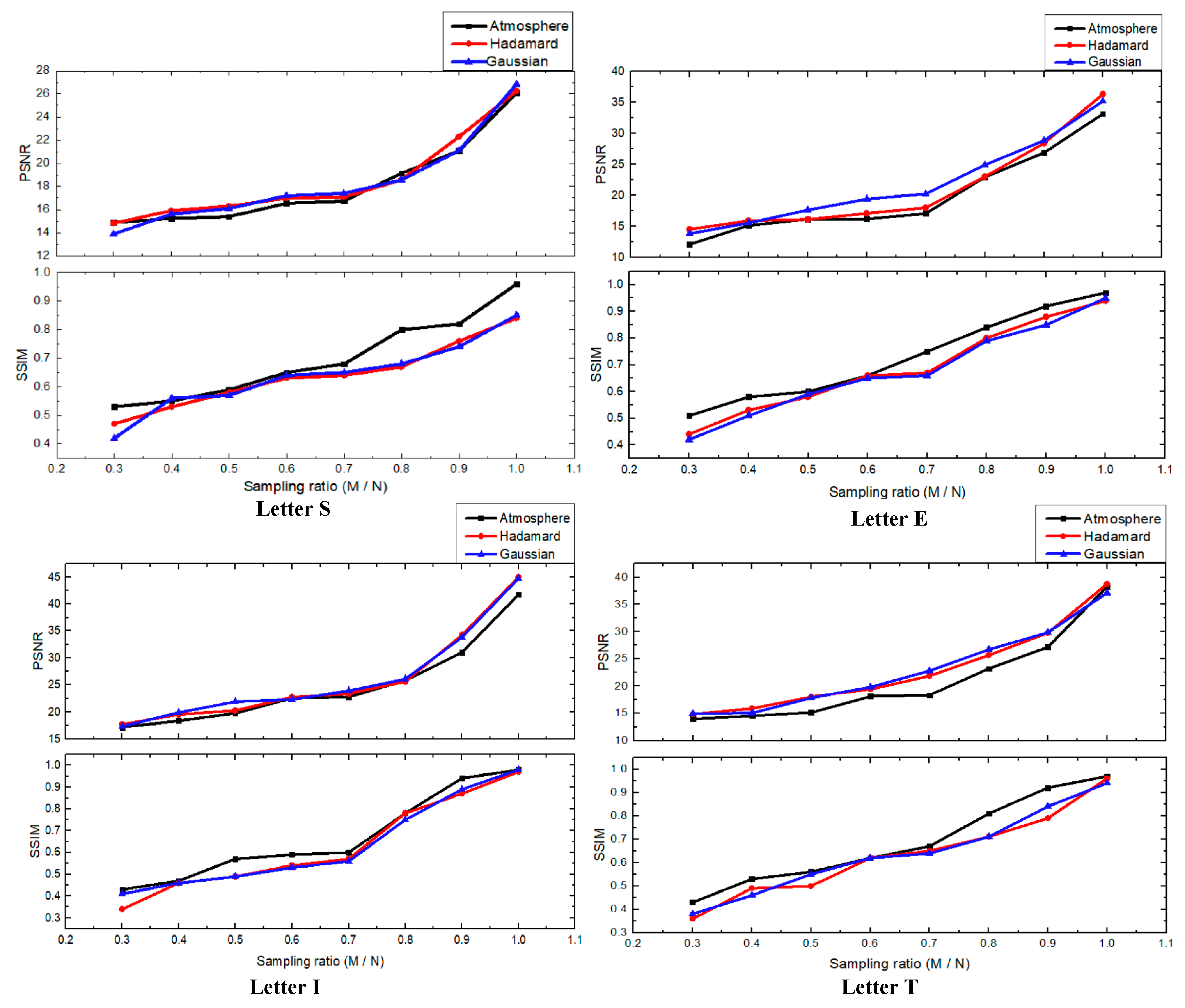
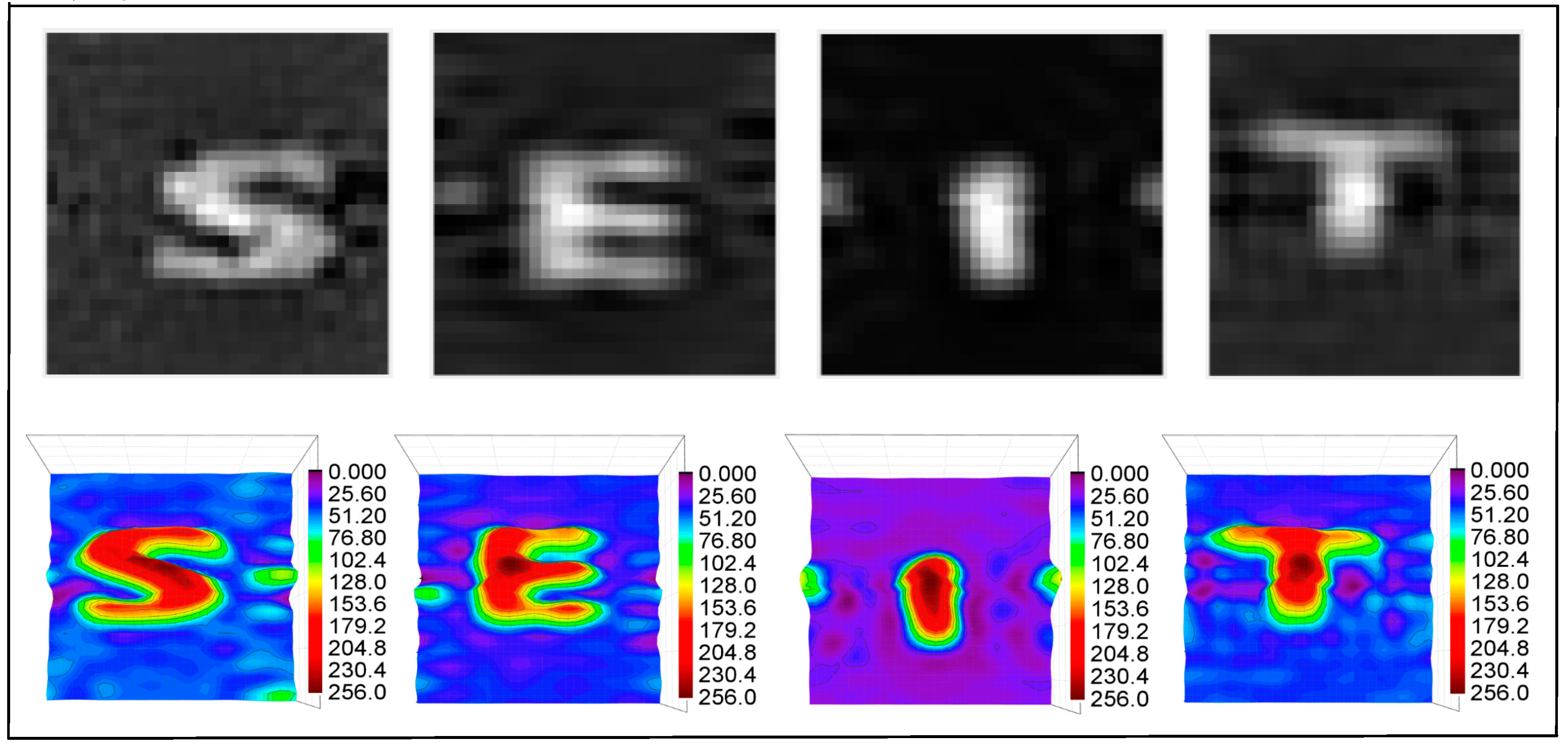
4. Experiment Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, L.; Ho, P.P.; Liu, C.; Zhang, G.; Alfano, R.R. Ballistic 2-D Imaging through Scattering Walls Using an Ultrafast Optical Kerr Gate. Science 1991, 253, 769–771. [Google Scholar] [CrossRef]
- Shiratori, A.; Obara, M. Photorefractive coherence-gated interferometry. Rev. Sci. Instrum. 1998, 69, 3741–3745. [Google Scholar] [CrossRef]
- Gong, W.L.; Han, S.H. Correlated imaging in scattering media. Opt. Lett. 2011, 36, 394–396. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theor. 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Durán, V.; Soldevila, F.; Irles, E.; Clemente, P.; Tajahuerce, E.; Andrés, P.; Lancis, J. Compressive imaging in scattering media. Opt. Express 2015, 23, 14424–14433. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.C.; Shi, J.H.; Liu, X.L.; Niu, Z.Z.; Zeng, G.H. Single-pixel non-imaging object recognition by means of Fourier spectrum acquisition. Opt. Commun. 2018, 413, 269–275. [Google Scholar] [CrossRef]
- Deng, H.X.; Gao, X.C.; Ma, M.C.; Yao, P.C.; Guan, Q.T.; Zhong, X.; Zhang, J. Fourier single-pixel imaging using fewer illumination patterns. Appl. Phys. Lett. 2019, 114, 5. [Google Scholar] [CrossRef]
- Freund, I.; Kaveh, M.; Rosenbluh, M. Dynamic Multiple-Scattering—Ballistic photons and the breakdown of the photon-diffusion approximation. Phys. Rev. Lett. 1988, 60, 1130–1133. [Google Scholar] [CrossRef]
- Freund, I.; Rosenbluh, M.; Berkovits, R.; Kaveh, M. Coherent backscattering of light in a quasi-2-dimensional system. Phys. Rev. Lett. 1988, 61, 1214–1217. [Google Scholar] [CrossRef]
- Freund, I.; Rosenbluh, M.; Feng, S. Memory effects in propagation of optical waves through disordered media. Phys. Rev. Lett. 1988, 61, 2328–2331. [Google Scholar] [CrossRef]
- Reijn, S.M.; Pinheiro, F.A.; Geskus, D.; Wetter, N.U. Enabling focusing around the corner in multiple scattering media. Appl. Opt. 2015, 54, 7740–7746. [Google Scholar] [CrossRef] [PubMed]
- Katz, O.; Small, E.; Silberberg, Y. Looking around corners and through thin turbid layers in real time with scattered incoherent light. Nat. Photonics 2012, 6, 549–553. [Google Scholar] [CrossRef]
- Frostig, H.; Small, E.; Daniel, A.; Oulevey, P.; Derevyanko, S.; Silberberg, Y. Focusing light by wavefront shaping through disorder and nonlinearity. Optica 2017, 4, 1073–1079. [Google Scholar] [CrossRef]
- Yu, H.; Lee, K.; Park, Y. Ultrahigh enhancement of light focusing through disordered media controlled by mega-pixel modes. Opt. Express 2017, 25, 8036–8047. [Google Scholar] [CrossRef] [PubMed]
- Li, H.J.; Wu, T.F.; Liu, J.T.; Gong, C.M.; Shao, X.P. Simulation and experimental verification for imaging of gray-scale objects through scattering layers. Appl. Opt. 2016, 55, 9731–9737. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.P.; Jin, X.; Dai, Q.H. Non-invasive imaging through strongly scattering media based on speckle pattern estimation and deconvolution. Sci. Rep. 2018, 8, 11. [Google Scholar]
- Liao, M.H.; Lu, D.J.; He, W.Q.; Pedrini, G.; Osten, W.; Peng, X. Improving reconstruction of speckle correlation imaging by using a modified phase retrieval algorithm with the number of nonzero-pixels constraint. Appl. Opt. 2019, 58, 473–478. [Google Scholar] [CrossRef]
- Stern, G.; Katz, O. Noninvasive focusing through scattering layers using speckle correlations. Opt. Lett. 2019, 44, 143–146. [Google Scholar] [CrossRef]
- Popoff, S.M.; Lerosey, G.; Carminati, R.; Fink, M.; Boccara, A.C.; Gigan, S. Measuring the Transmission Matrix in Optics: An approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 2010, 104, 100601. [Google Scholar] [CrossRef]
- Popoff, S.; Lerosey, G.; Fink, M.; Boccara, A.C.; Gigan, S. Image transmission through an opaque material. Nat. Commun. 2010, 1, 81. [Google Scholar] [CrossRef]
- Popoff, S.M.; Lerosey, G.; Fink, M.; Boccara, A.C.; Gigan, S. Controlling light through optical disordered media: Transmission matrix approach. New J. Phys. 2011, 13, 123021. [Google Scholar] [CrossRef]
- Liutkus, A.; Martina, D.; Popoff, S.; Chardon, G.; Katz, O.; Lerosey, G.; Gigan, S.; Daudet, L.; Carron, I. Imaging with nature: Compressive imaging using a multiply scattering medium. Sci. Rep. 2014, 4, 5552. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, B.; Xu, C.; Geng, Y.; Zhao, G.; Chen, H.; He, Z.; Wu, Z.; Ren, L. Round-trip imaging through scattering media based on optical transmission matrix. Chin. Opt. Lett. 2018, 16, 041102. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Mallat, S.G.; Zhang, Z.F. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Recht, B.; Fazel, M.; Parrilo, P.A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010, 52, 471–501. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Zayyani, H.; Babaie-Zadeh, M.; Jutten, C. Decoding real-field codes by an iterative expectation-maximization (em) algorithm. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008. [Google Scholar]
- Hongshun, L.; Wei, L. Analysis of the adjacency effect in satellite remote sensing by using backward Monte Carlo method. J. Huazhong Univ. Sci. Technol. 2004, 3201, 1–3. [Google Scholar]
- Modest, M.F. Backward Monte Carlo simulations in radiative heat transfer. J. Heat Trans. T. ASME 2003, 125, 57–62. [Google Scholar] [CrossRef]
- Reinersman, P.N.; Carder, K.L. Monte-Carlo simulation of the atmospheric point-spread function with an application to correction for the adjacency effect. Appl. Opt. 1995, 34, 4453–4471. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.S.; Wang, H.D.; Li, L.G.; Yang, Z.; Meng, X. Neural network simulation of the atmospheric point spread function for the adjacency effect research. In Proceedings of the SPIE Remote Sensing, Edinburgh, UK, 26–29 September 2016. [Google Scholar]
- Gordon, H.R.; Brown, J.W.; Evans, R.H. Exact Rayleigh Scattering calculations for use with the Nimbus-7 coastal zone color scanner. Appl. Opt. 1988, 27, 862–871. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.S.; Guo, X.Y.; Meng, X.; Yang, Z.; Peng, X.D.; Li, L.G.; Xie, W.M. Simulation and analysis of the adjacency effect in earth-imaging process of the optical remote sensing. J. Infrared Millim. Waves 2015, 34, 250–256. [Google Scholar]
- Candes, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Candès, E.J. The restricted isometry property and its implications for compressed sensing. Comptes Rendus Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via l(1) minimization. Proc. Natl. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef]
- Abolghasemi, V.; Ferdowsi, S.; Makkiabadi, B.; Sanei, S. On optimization of the measurement matrix for compressive sensing. In Proceedings of the 2010 18th European Signal Processing Conference, Aalborg, Denmark, 23–27 August 2010; Kleijn, B., Larsen, J., Eds.; European Assoc Signal Speech & Image Processing-Eurasip: Kessariani, Greece, 2010; pp. 427–431. [Google Scholar]
- Kocifaj, M. Ground albedo impacts on higher-order scattering spectral radiances of night sky. J. Quant. Spectrosc. Radiat. Transf. 2019, 239, 13. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, X.; Ma, X.; Yang, Z.; Peng, X.; Li, Y.; Ni, W. Compressive Sensing Imaging Based on Modulation of Atmospheric Scattering Medium. Appl. Sci. 2020, 10, 4466. https://doi.org/10.3390/app10134466
Lei X, Ma X, Yang Z, Peng X, Li Y, Ni W. Compressive Sensing Imaging Based on Modulation of Atmospheric Scattering Medium. Applied Sciences. 2020; 10(13):4466. https://doi.org/10.3390/app10134466
Chicago/Turabian StyleLei, Xuelin, Xiaoshan Ma, Zhen Yang, Xiaodong Peng, Yun Li, and Wei Ni. 2020. "Compressive Sensing Imaging Based on Modulation of Atmospheric Scattering Medium" Applied Sciences 10, no. 13: 4466. https://doi.org/10.3390/app10134466
APA StyleLei, X., Ma, X., Yang, Z., Peng, X., Li, Y., & Ni, W. (2020). Compressive Sensing Imaging Based on Modulation of Atmospheric Scattering Medium. Applied Sciences, 10(13), 4466. https://doi.org/10.3390/app10134466



