Τhe February-March 2019 Seismic Swarm Offshore North Lefkada Island, Greece: Microseismicity Analysis and Geodynamic Implications
Abstract
Featured Application
Abstract
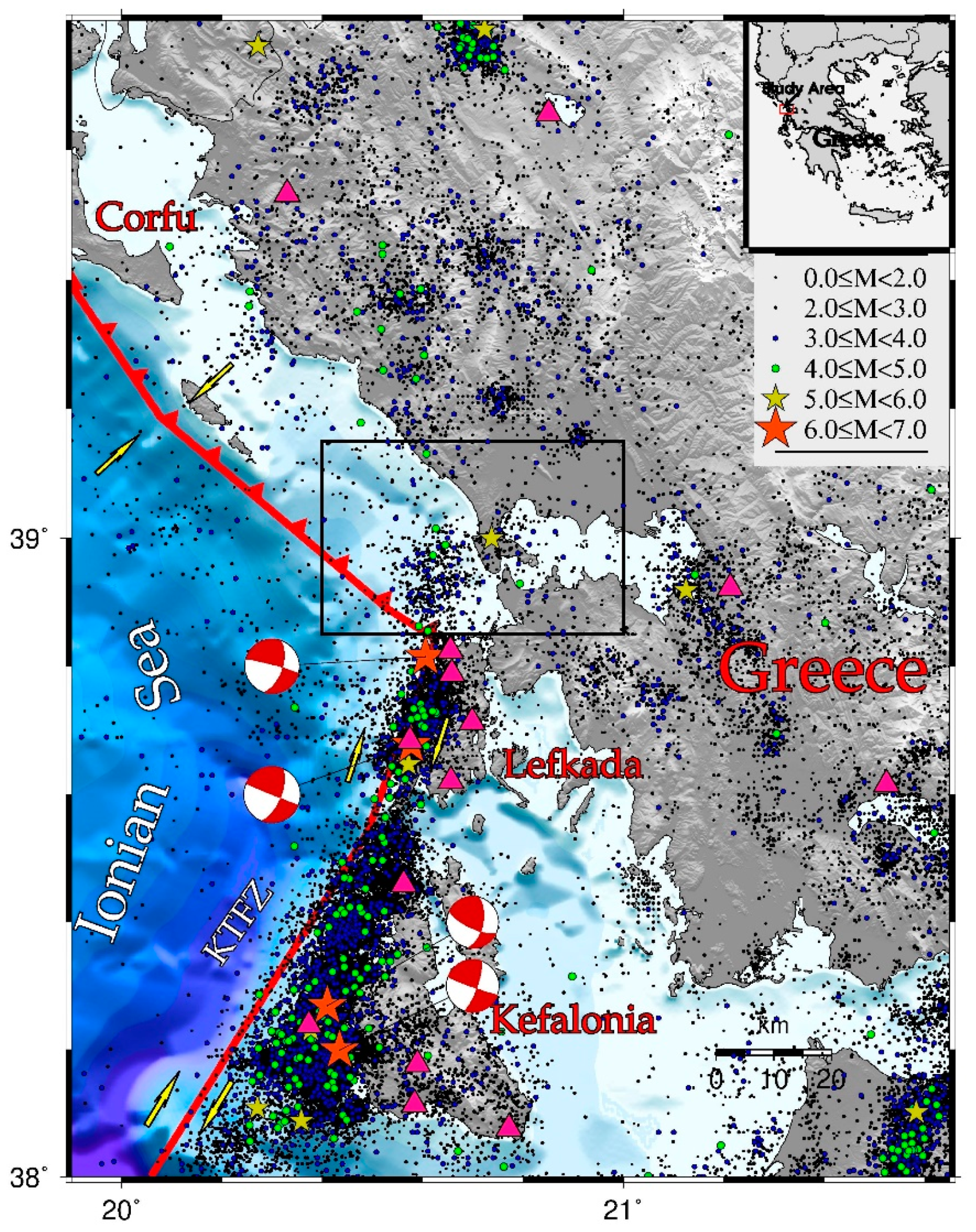
1. Introduction
2. Seismicity Relocation
2.1. Data Acquisition and Earthquake Relocation
2.2. Location Errors Estimation
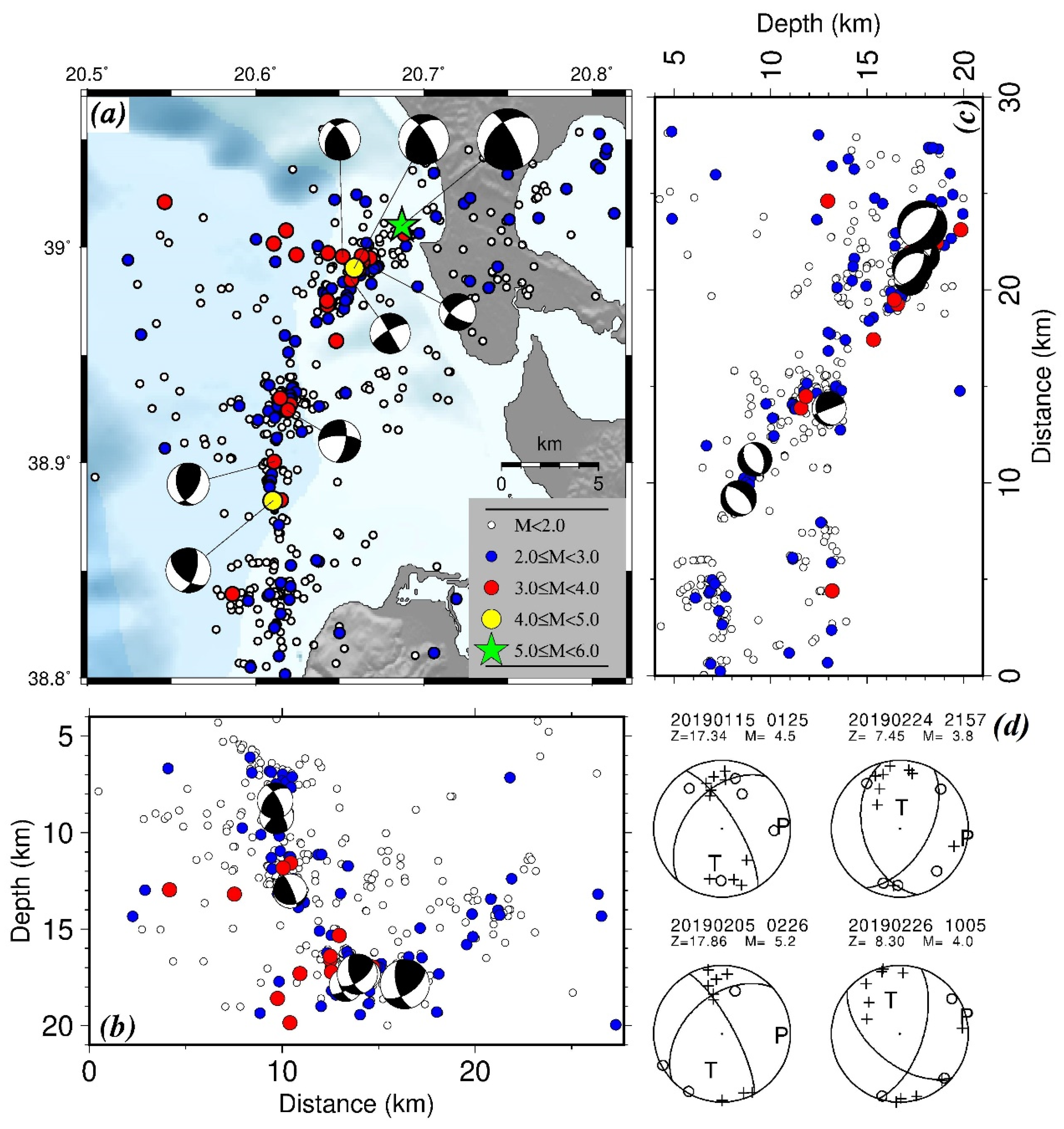
3. Fault Plane Solutions Determination
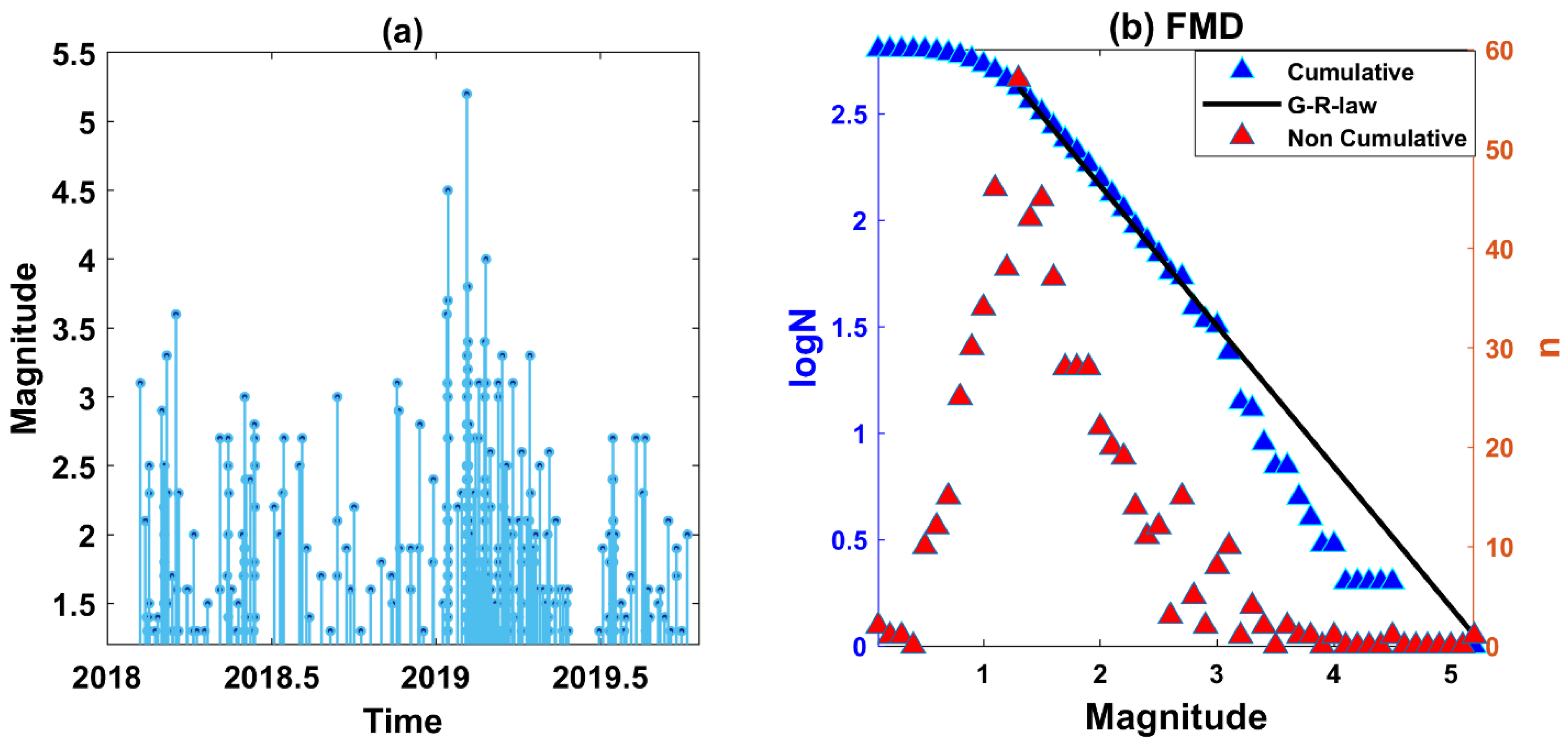
4. Seismicity Temporal and Spatial Characteristics
4.1. Temporal Distribution of Earthquakes
4.2. Spatial Distribution
5. Coulomb Stress Changes and Possible Triggering
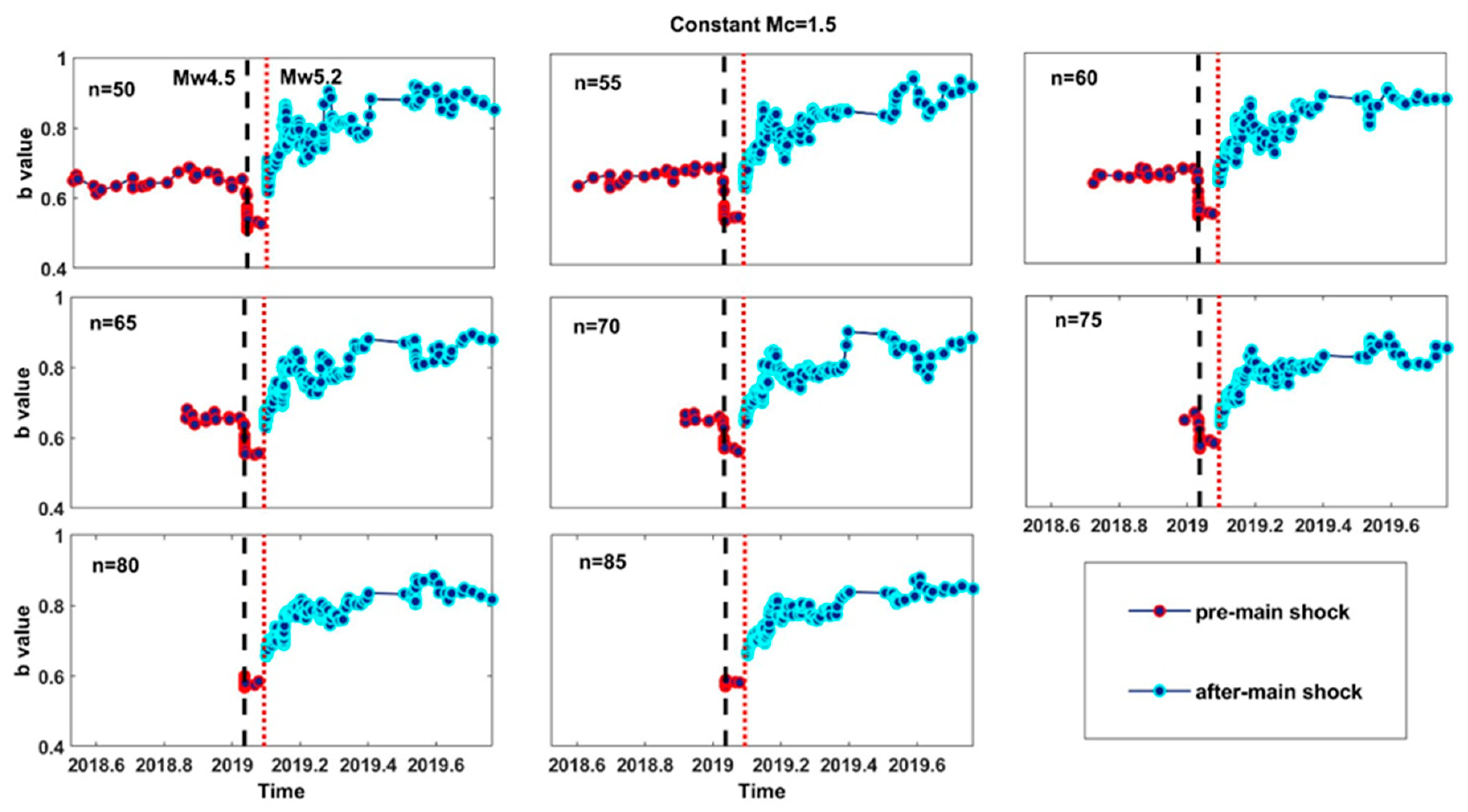
6. Aftershock Sequence Analysis in Relation with Temporal Variations of b Value
7. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Papadimitriou, E.E. Mode of strong earthquake recurrence in the central Ionian Islands (Greece): Possible triggering due to Coulomb stress changes generated by the occurrence of previous strong shocks. Bull. Seismol. Soc. Am. 2002, 92, 3293–3308. [Google Scholar] [CrossRef]
- Karakostas, V.G.; Papadimitriou, E.E.; Papazachos, C.B. Properties of the 2003 Lefkada, Ionian Islands, Greece, earthquake seismic sequence and seismicity triggering. Bull. Seismol. Soc. Am. 2004, 94, 1976–1981. [Google Scholar] [CrossRef]
- Goebel, T.H.; Schorlemmer, D.; Becker, T.W.; Dresen, G.; Sammis, C.G. Acoustic emissions document stress changes over many seismic cycles in stick-slip experiments. Geophys. Res. Lett. 2013, 40, 2049–2054. [Google Scholar] [CrossRef]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Permanent Regional Seismological Network operated by the Aristotle University of Thessaloniki. Available online: http://geophysics.geo.auth.gr/the_seisnet/WEBSITE_2005/station_index_en.html (accessed on 17 May 2020). [CrossRef]
- Klein, F.W. User’s Guide to HYPOINVERSE-2000, A Fortran Program to Solve Earthquake Locations and Magnitudes; U.S. Geological Survey Open File Report, 02-171 Version 1.0; U.S. Geological Survey: Reston, VA, USA, 2000.
- Papadimitriou, E.; Karakostas, V.; Mesimeri, M.; Ghouliaras, C.; Kourouklas, C. The Mw6.5 17 November 2015 Lefkada (Greece) Earthquake: Structural Interpretation by Means of the Aftershock Analysis. Pure Appl. Geophys. 2017, 174, 3869–3888. [Google Scholar] [CrossRef]
- Karakostas, V.G.; Papadimitriou, Ε.Ε.; Gospodinov, D. Modeling the 2013 North Aegean (Greece) seismic sequence: Geometrical and frictional constraints, and aftershock probabilities. Geophys. J. Int. 2014, 197, 525–541. [Google Scholar] [CrossRef]
- Waldhauser, F. HypoDD—A Program to Compute Double–Difference Hypocenter Locations; US Geological Survey Open File Report; U.S. Geological Survey: Reston, VA, USA, 2001; pp. 1–113.
- Paige, C.C.; Saunders, M.A. LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares. ACM Trans. Math. Softw. 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Schaff, D.P.; Bokelmann, G.H.R.; Ellsworth, W.L.; Zanzerkia, E.; Waldhauser, F.; Beroza, G.C. Optimizing correlation techniques for improved earthquake location. Bull. Seismol. Soc. Am. 2004, 94, 705–721. [Google Scholar] [CrossRef]
- Schaff, D.P.; Waldhauser, F. Waveform cross–correlation–based differential travel–time measurements at the northern California seismic network. Bull. Seism. Soc. Am. 2005, 95, 2446–2461. [Google Scholar] [CrossRef]
- Mesimeri, M.; Karakostas, V.; Papadimitriou, E.; Tsaklidis, G.; Jacobs, K. Relocation of recent seismicity and seismotectonic properties in the Gulf of Corinth (Greece). Geophys. J. Intern. 2018, 212, 1123–1142. [Google Scholar] [CrossRef]
- Efron, B. The Jackknife, the Bootstrap and Other Resampling Plans. Soc. Idustr. Appl. Math. Phila. 1982, 5–11. [Google Scholar] [CrossRef]
- Waldhauser, F.; Ellsworth, W.L. A double-difference earthquake location algorithm: Method and application to the Northern Hayward Fault, California. Bull. Seism. Soc. Am. 2000, 90, 1353–1368. [Google Scholar] [CrossRef]
- Reasenberg, P.; Oppenheimer, D.H. FPFIT, FPPLOT and FPPAGE; Fortran Computer Programs for Calculating and Displaying Earthquake Fault-Plane Solutions; Open-File Rep. 85-739; U.S. Geological Survey: Reston, VA, USA, 1985.
- Karakostas, V.G.; Papadimitriou, E.E. Fault complexity associated with the 14 August 2003 Mw6.2 Lefkada, Greece, aftershock sequence. Acta Geophys. 2010, 58, 838–854. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New Empirical Relationships among Magnitude, Rupture Length, Rupture width, Rupture Area, and Surface Displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Papazachos, B.C.; Scordilis, E.M.; Panagiotopoulos, D.G.; Papazachos, C.B.; Karakaisis, G.F. Global relations between seismic fault parameters and moment magnitude of earthquakes. In Proceedings of the 10th International Congress of the Geological Society, Thessaloniki, Greece, 14–17 April 2004; pp. 539–540. [Google Scholar] [CrossRef]
- Thingbaijam, K.K.S.; Mai, P.M.; Goda, K. New Empirical Earthquake Source-Scaling Laws. Bull. Seismol. Soc. Am. 2017, 107, 2225–2246. [Google Scholar] [CrossRef]
- Ganas, A.; Elias, P.; Bozionelos, G.; Papathanassiou, G.; Avallone, A.; Papastergios, A.; Valkaniotis, S.; Parcharidis, I.; Briole, P. Coseismic deformation, field observations and seismic fault of the 17 November 2015 M = 6.5, Lefkada Island, Greece earthquake. Tectonophysics 2016, 687, 210–222. [Google Scholar] [CrossRef]
- King, G.C.P.; Stein, R.S.; Jian, L. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar] [CrossRef]
- Harris, R.A. Introduction to Special Section: Stress Triggers, Stress Shadows, and Implications for Seismic Hazard. J. Geophys. Res. Solid Earth 1998, 103, 24347–24358. [Google Scholar] [CrossRef]
- Reasenberg, P.A.; Simpson, R.W. Response of regional seismicity to the static stress change produced by the Loma Prieta earthquake. Science 1992, 255, 1687–1690. [Google Scholar] [CrossRef]
- Rice, J.R.; Cleary, M.P. Some basic stress diffusion solutions for fluid–saturated elastic porous media with compressible constituents. Rev. Geophys. Space Phys. 1976, 14, 227–241. [Google Scholar] [CrossRef]
- Robinson, R.; McGinty, P.J. The enigma of the Arthur’s Pass, New Zealand, earthquake: 2. The aftershock distribution and its relation to regional and induced stress fields. J. Geophys. Res. 2000, 105, 16139–16150. [Google Scholar] [CrossRef]
- Karakostas, V.; Papadimitriou, E.; Mesimeri, M.; Gkarlaouni, C.; Paradisopoulou, P. The 2014 Kefalonia Doublet (Mw6.1 and Mw6.0), central Ionian Islands, Greece: Seismotectonic implications along the Kefalonia transform fault zone. Acta Geophys. 2015, 63, 1–16. [Google Scholar] [CrossRef]
- Karakostas, V.; Mirek, K.; Mesimeri, M.; Papadimitriou, E.; Mirek, J. The Aftershock Sequence of the 2008 Achaia, Greece, Earthquake: Joint Analysis of Seismicity Relocation and Persistent Scatterers Interferometry. Pure Appl. Geophys. 2017, 174, 151–176. [Google Scholar] [CrossRef]
- Lippiello, E.; Cirillo, A.; Godano, C.; Papadimitriou, E.; Karakostas, V. Post Seismic Catalog Incompleteness and Aftershock Forecasting. Geosciences 2019, 9, 355. [Google Scholar] [CrossRef]
- Gulia, L.; Wiemer, S. Real-time discrimination of earthquake foreshocks and aftershocks. Nature 2019, 574, 193–199. [Google Scholar] [CrossRef] [PubMed]
- Wiemer, S.; Wyss, M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seism. Soc. Am. 2002, 90, 859–869. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, S.; Zhuang, J. A test on methods for MC estimation based on earthquake catalog. Earth Planet. Phys. 2018, 2, 150–162. [Google Scholar] [CrossRef]
- Aki, K. Maximum likelihood estimate of b in the formula log N=a-bM and its confidence limits. Bull. Earthq. Res. Inst. 1965, 43, 237–239. [Google Scholar]
- Tormann, T.; Wiemer, S.; Mignan, A. Systematic survey of high-resolution b value imaging along Californian faults: Inference on asperities. J. Geophys. Res. Sol. Earth 2014, 119, 2029–2054. [Google Scholar] [CrossRef]
- Console, R.; Carluccio, R.; Papadimitriou, E.; Karakostas, V. Synthetic earthquake catalogs simulating seismic activity in the Corinth Gulf, Greece, fault system. J. Geophys. Res. Sol. Earth 2015, 120, 326–343. [Google Scholar] [CrossRef]
- Woessner, J.; Wiemer, S. Assessing the quality of earthquake catalogues: Estimating the magnitude of completeness and its uncertainty. Bull. Seismol. Soc. Am. 2005, 95, 684–698. [Google Scholar] [CrossRef]
- van Hinsbergen, D.J.J.; van der Meer, D.G.; Zachariasse, W.J.; Meulenkamp, J.E. Deformation of western Greece during Neogene clockwise rotation and collision with Apulia. Int. J. Earth Sci. (Geol. Rundsch.) 2006, 95, 463–490. [Google Scholar] [CrossRef]
- Vassilakis, E.; Royden, L.; Papanikolaou, D. Kinematic links between subduction along the Hellenic trench and extension in the Gulf of Corinth, Greece: A multidisciplinary analysis. Earth Planet. Sci. Lett. 2011, 303, 108–120. [Google Scholar] [CrossRef]
- Perouse, E.; Sebrier, M.; Braucher, R.; Chamot Rooke, N.; Bourles, D.; Briole, P.; Sorel, D.; Dimitrov, D.; Arsenikos, S. Transition from collision to subduction in western Greece: The katouna—Stamna active fault system and regional kinematics. Int. J. Earth Sci. (Geol. Rundsch.) 2017, 106, 967–989. [Google Scholar] [CrossRef]
- Haddad, A.; Ganas, A.; Kassaras, I.; Lupi, M. Seismicity and geodynamics of western Peloponnese and central Ionian Islands: Insights from a local seismic deployment. Tectonophysics 2020. [Google Scholar] [CrossRef]
- Baker, C.; Hatzfeld, D.; Lyon-Caen, H.; Papadimitriou, E.; Rigo, A. Earthquake mechanisms of the Adriatic Sea and Western Greece: Implications for the oceanic subduction-continental collision transition. Geophys. J. Int. 1997, 131, 559–594. [Google Scholar] [CrossRef]
- Louvari, E.; Kiratzi, A.A.; Papazachos, B.C. The Cephalonia Transform Fault and its extension to western Lefkada Island (Greece). Tectonophysics 1999, 308, 223–236. [Google Scholar] [CrossRef]
- Hatzfeld, D.; Kassaras, I.; Panagiotopoulos, D.; Amorese, D.; Makropoulos, K.; Karakaisis, G.; Coutant, O. Microseimicity and strain pattern in northwestern Greece. Tectonics 1995, 14, 773–785. [Google Scholar] [CrossRef]
- Benetatos, C.; Kiratzi, A.; Roumelioti, Z.; Stavrakakis, G.; Drakatos, G.; Latoussakis, I. The 14 August 2003 Lefkada Island (Greece) earthquake: Focal mechanisms of the mainshock and of the aftershock sequence. J. Seismol. 2005, 9, 171–190. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic Mapping Tools: Improved Version Released. EOS Trans. Am. 2013. [Google Scholar] [CrossRef]






| VP (km/s) | Depth (km) |
|---|---|
| 5.850 | 0.0 |
| 5.870 | 1.0 |
| 5.980 | 2.0 |
| 6.635 | 6.0 |
| 6.490 | 8.0 |
| 6.525 | 9.0 |
| 6.560 | 11.0 |
| 6.580 | 13.0 |
| 6.625 | 21.0 |
| 6.700 | 28.0 |
| 8.000 | 40.0 |
| Direction | W-E | N-S | Depth |
|---|---|---|---|
| Bootstrap Median error (m) | 1447 | 422 | 1806 |
| Jackknife Median St. Deviation Errors (m) | 1055 | 235 | 330 |
| n | Date | Occurrence Time | Lat (oN) | Lon (oE) | Depth (km) | ML | Nodal Plane I | Nodal Plane II | Az. Gap | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Strike (o) | Dip (o) | Rake (o) | Strike (o) | Dip (o) | Rake (o) | ||||||||
| 1 | 13/01/19 | 21:07:21.16 | 38.9849 | 20.6569 | 17.24 | 3.6 | 240 | 76 | 180 | 330 | 90 | 14 | 181 |
| 2 | 15/01/19 | 01:25:05.00 | 38.9904 | 20.6587 | 17.34 | 4.5 | 220 | 45 | 155 | 328 | 73 | 48 | 127 |
| 3 | 15/01/19 | 02:58:46.96 | 38.9957 | 20.6517 | 17.90 | 3.7 | 215 | 40 | 150 | 329 | 71 | 54 | 127 |
| 4 | 05/02/19 | 02:26:09.27 | 39.0101 | 20.6870 | 17.86 | 5.2 | 227 | 45 | 160 | 331 | 76 | 47 | 138 |
| 5 | 05/02/19 | 09:25:28.43 | 38.9931 | 20.6636 | 17.35 | 3.3 | 226 | 67 | −153 | 125 | 65 | −25 | 131 |
| 6 | 06/02/19 | 05:30:05.52 | 38.9242 | 20.6190 | 13.03 | 3.8 | 10 | 67 | −156 | 270 | 68 | −25 | 122 |
| 7 | 24/02/19 | 21:58:30.28 | 38.9005 | 20.6110 | 8.34 | 3.8 | 30 | 55 | 120 | 165 | 45 | 54 | 127 |
| 8 | 26/02/19 | 10:05:59.39 | 38.8823 | 20.6103 | 9.18 | 4.0 | 18 | 62 | 139 | 130 | 55 | 35 | 129 |
| Datasets | Time Interval | N | ||||
|---|---|---|---|---|---|---|
| Pre-main shock | 4/2/2018–5/2/2019 | 122 | 1.5 | 94 | 2.84 | 0.58 |
| After-main shock | 5/2/2019–8/10/2019 | 298 | 1.5 | 226 | 3.48 | 0.75 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kostoglou, A.; Karakostas, V.; Bountzis, P.; Papadimitriou, E. Τhe February-March 2019 Seismic Swarm Offshore North Lefkada Island, Greece: Microseismicity Analysis and Geodynamic Implications. Appl. Sci. 2020, 10, 4491. https://doi.org/10.3390/app10134491
Kostoglou A, Karakostas V, Bountzis P, Papadimitriou E. Τhe February-March 2019 Seismic Swarm Offshore North Lefkada Island, Greece: Microseismicity Analysis and Geodynamic Implications. Applied Sciences. 2020; 10(13):4491. https://doi.org/10.3390/app10134491
Chicago/Turabian StyleKostoglou, Anastasios, Vasileios Karakostas, Polyzois Bountzis, and Eleftheria Papadimitriou. 2020. "Τhe February-March 2019 Seismic Swarm Offshore North Lefkada Island, Greece: Microseismicity Analysis and Geodynamic Implications" Applied Sciences 10, no. 13: 4491. https://doi.org/10.3390/app10134491
APA StyleKostoglou, A., Karakostas, V., Bountzis, P., & Papadimitriou, E. (2020). Τhe February-March 2019 Seismic Swarm Offshore North Lefkada Island, Greece: Microseismicity Analysis and Geodynamic Implications. Applied Sciences, 10(13), 4491. https://doi.org/10.3390/app10134491







