Metallic Ribbon-Core Sandwich Panels Subjected to Air Blast Loading
Abstract
Featured Application
Abstract
1. Introduction
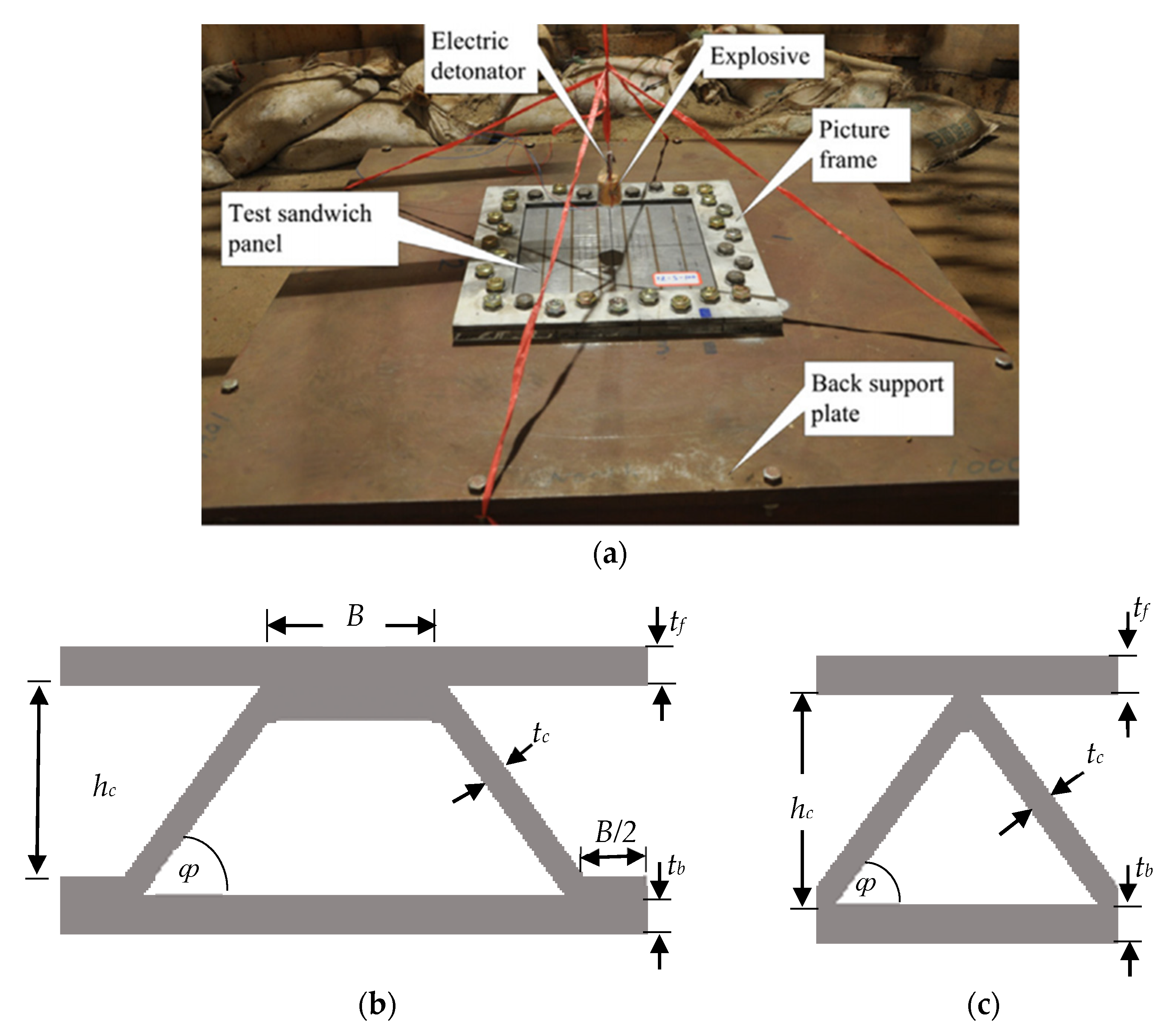
2. Structure Configuration and Finite Element Model Validation
2.1. Geometric Description
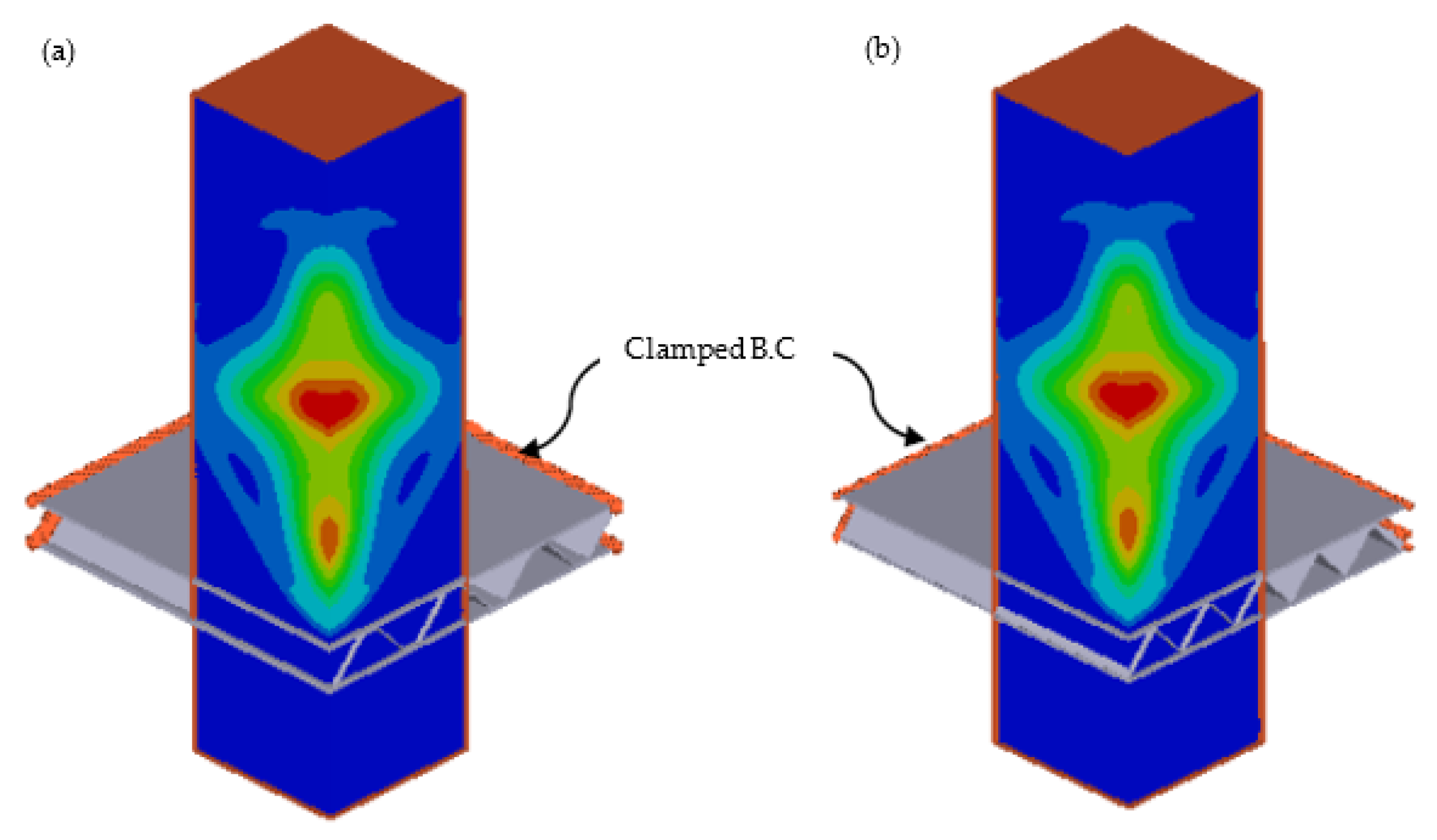
2.2. FE Modeling
2.3. Material Models
2.3.1. Air and TNT
2.3.2. Annealed 304 Stainless Steel
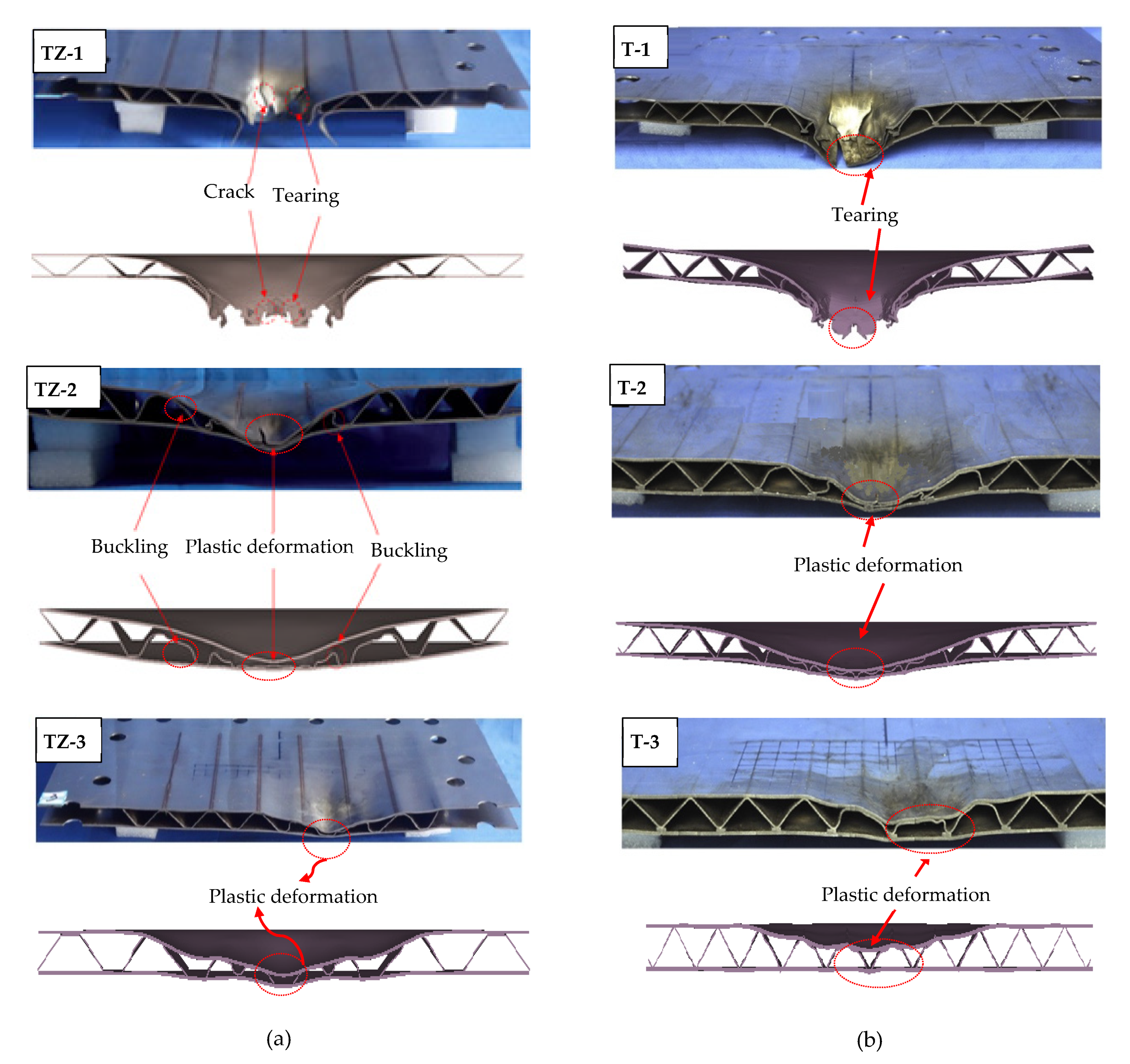
2.4. Results and Discussion
3. Proposed Sandwich Panels
4. Parametric Study
4.1. Influence of Varying Face Sheets Thickness on RCSPs’ Face Sheets Deformations
4.2. Influence of Face Sheets Thickness on Energy Dissipation
4.3. Variation of Core Parameters on the Blast Performance of the RCS
5. Conclusions
- The back-plate deflection decreases with increasing front-plate thickness due to the increased stiffness. When using a front sheet with 2.6 mm thickness, the deflection decreases by an average 70% for the rear face sheet.
- The back-plate thickness has a negligible effect on the front-layer deflection however, the back-plate deflection decreases upon increasing the back-plate thickness.
- The sandwich panel with the thinner front-face plate could improve the energy-absorbing capabilities of the structure. However, under large blast loading, tearing damage may take place on the thinner front face.
- Increasing the core thickness has a negative impact on the blast behavior of the structure and also increasing the angle of corrugation more than 45° reduces the efficiency of the structure under the impact of blast loading.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wiernicki, C.J.; Liem, F.; Woods, G.D.; Furio, A.J. Structural analysis methods for lightweight metallic corrugated core sandwich panels subjected to blast loads. Nav. Eng. J. 1991, 103, 192–202. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Lu, G.; Yu, T. Energy Absorption of Structures and Materials; Woodhead Publishing: Sawston, Cambridge, UK, 2003. [Google Scholar]
- Jing, L.; Wang, Z.; Ning, J.; Zhao, L. The dynamic response of sandwich beams with open-cell metal foam cores. Compos. Part B Eng. 2011, 42, 1–10. [Google Scholar] [CrossRef]
- Zhang, P.; Li, X.; Jin, T.; Wang, Z.; Zhao, L. Dynamic response of circular metallic sandwich panels under projectile impact. J. Sandw. Struct. Mater. 2017, 19, 572–594. [Google Scholar] [CrossRef]
- Palanivelu, S.; Van Paepegem, W.; Degrieck, J.; Reymen, B.; Ndambi, J.-M.; Vantomme, J. Close-range blast loading on empty recyclable metal beverage cans for use in sacrificial cladding structure. Eng. Struct. 2011, 33, 1966–1987. [Google Scholar] [CrossRef]
- Alberdi, R.; Przywara, J.; Khandelwal, K. Performance evaluation of sandwich panel systems for blast mitigation. Eng. Struct. 2013, 56, 2119–2130. [Google Scholar] [CrossRef]
- Abada, M.; Ibrahim, A. Hybrid multi-cell thin-walled tubes for energy absorption applications: Blast shielding and crashworthiness. Compos. Part B Eng. 2020, 183, 107720. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhu, F.; Wu, G.; Zhao, L. Response of aluminium corrugated sandwich panels under air blast loadings: Experiment and numerical simulation. Int. J. Impact Eng. 2014, 65, 79–88. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Hui, D. Blast resistance and parametric study of sandwich structure consisting of honeycomb core filled with circular metallic tubes. Compos. Part B Eng. 2018, 145, 261–269. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Liu, T.; Deng, Z.; Lu, T. Design optimization of truss-cored sandwiches with homogenization. Int. J. Solids Struct. 2006, 43, 7891–7918. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, T.; Wang, H.; Li, Y.; Liu, J.; Zhang, P. Numerical investigation on the dynamic response of foam-filled corrugated core sandwich panels subjected to air blast loading. J. Sandw. Struct. Mater. 2019, 21, 838–864. [Google Scholar] [CrossRef]
- Jing, L.; Zhao, L. Blast resistance and energy absorption of sandwich panels with layered gradient metallic foam cores. J. Sandw. Struct. Mater. 2019, 21, 464–482. [Google Scholar] [CrossRef]
- Kooistra, G.W.; Deshpande, V.; Wadley, H.N. Hierarchical Corrugated Core Sandwich Panel Concepts. J. Appl. Mech. 2007, 74, 259–268. [Google Scholar] [CrossRef]
- Ahmed, S.; Galal, K. Effectiveness of FRP sandwich panels for blast resistance. Compos. Struct. 2017, 163, 454–464. [Google Scholar] [CrossRef]
- Wei, Z.; Deshpande, V.; Evans, A.; Dharmasena, K.; Queheillalt, D.; Wadley, H. The resistance of metallic plates to localized impulse. J. Mech. Phys. Solids 2008, 56, 2074–2091. [Google Scholar] [CrossRef]
- Dharmasena, K.; Queheillalt, D.; Wadley, H.; Dudt, P.; Chen, Y.; Knight, D. Dynamic compression of metallic sandwich structures during planar impulsive loading in water. Eur. J. Mech. A/Solids 2010, 29, 56–67. [Google Scholar] [CrossRef]
- Liang, Y.; Spuskanyuk, A.V.; Flores, S.E.; Hayhurst, D.R.; Hutchinson, J.W.; McMeeking, R.M. The response of metallic sandwich panels to water blast. J. Appl. Mech. 2007, 74, 81–99. [Google Scholar] [CrossRef]
- Ahmed, S.; Galal, K. Response of Metallic Sandwich Panels to Blast Loads. J. Struct. Eng. 2019, 145, 04019145. [Google Scholar] [CrossRef]
- ASCE, Blast Protection of Buildings: ASCE/SEI 59-11. 2011. Available online: https://sp360.asce.org/PersonifyEbusiness/Merchandise/Product-Details/productId/232616700 (accessed on 4 February 2020).
- Autodyn, T. Theory Manual Revision 4.3; Century Dynamics Inc.: Concord, CA, USA, 2003. [Google Scholar]
- Zhang, P.; Liu, J.; Cheng, Y.; Hou, H.; Wang, C.; Li, Y. Dynamic response of metallic trapezoidal corrugated-core sandwich panels subjected to air blast loading–An experimental study. Mater. Des. (1980–2015) 2015, 65, 221–230. [Google Scholar] [CrossRef]
- Zhang, P.; Cheng, Y.; Liu, J.; Wang, C.; Hou, H.; Li, Y. Experimental and numerical investigations on laser-welded corrugated-core sandwich panels subjected to air blast loading. Mar. Struct. 2015, 40, 225–246. [Google Scholar] [CrossRef]
- Yuen, S.C.K.; Langdon, G.; Nurick, G.; Pickering, E.; Balden, V. Response of V-shape plates to localised blast load: Experiments and numerical simulation. Int. J. Impact Eng. 2012, 46, 97–109. [Google Scholar] [CrossRef]
- Autodyn, A. Theory Manual Revision 4.3; Century Dynamics: Concord, CA, USA, 2005. [Google Scholar]
- Zukas, J. Introduction to Hydrocodes; Elsevier Science: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Dobratz, B.M. Properties of Chemical Explosives and Explosive Simulants; Dobratz, B.M., Ed.; California University, Livermore (USA), Lawrence Livermore Lab: Livermore, CA, USA, 1972.
- Lee, S.; Barthelat, F.; Hutchinson, J.; Espinosa, H.D. Dynamic failure of metallic pyramidal truss core materials–experiments and modeling. Int. J. Plast. 2006, 22, 2118–2145.S. [Google Scholar] [CrossRef]
- Xiong, J.; Du, Y.; Mousanezhad, D.; Eydani Asl, M.; Norato, J.; Vaziri, A. Sandwich Structures with Prismatic and Foam Cores: A Review. Adv. Eng. Mater. 2019, 21, 1800036. [Google Scholar] [CrossRef]









| Panel | Explosive | Geometric Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|
| SoD (mm) | W (g) | tf (mm) | hc (mm) | tc (mm) | tb (mm) | B (mm) | ȹ (°) | (%) | |
| TZ-1 | 50 | 55 | 1.38 | 14 | 0.7 | 1.38 | 7 | 45 | 6.34 |
| TZ-2 | 100 | 55 | 1.38 | 14 | 0.7 | 1.38 | 7 | 45 | 6.34 |
| TZ-3 | 150 | 55 | 1.38 | 14 | 0.7 | 1.38 | 7 | 45 | 6.34 |
| T-1 | 50 | 55 | 1.38 | 14 | 0.7 | 1.38 | - | 45 | 6.6 |
| T-2 | 100 | 55 | 1.38 | 14 | 0.7 | 1.38 | - | 45 | 6.6 |
| T-3 | 150 | 55 | 1.38 | 14 | 0.7 | 1.38 | - | 45 | 6.6 |
| EOS | γ | Reference Density (g/cm3) | Reference Energy (μJ/mg) |
|---|---|---|---|
| Ideal gas | 1.4 | 1.225 × 10−3 | 2.068 × 105 |
| (GPa) | (GPa) | ||||
|---|---|---|---|---|---|
| 1.63 | 373.75 | 3.747 | 4.15 | 0.90 | 0.35 |
| Parameter | Unit | Value |
|---|---|---|
| Reference density | g/cm3 | 7.85 |
| EOS | - | Linear |
| Bulk modulus | kPa | 1.67 × 108 |
| Strength | - | Johnson Cook |
| Shear modulus | kPa | 6.69 × 107 |
| Yield stress, A | kPa | 3.10 × 105 |
| Hardening constant, B | kPa | 1.00 × 105 |
| Hardening, exponent, n | - | 0.65 |
| Strain rate constant, c | - | 0.07 |
| Ref. strain rate, | s−1 | 1.00 |
| Thermal softening exponent, m | - | 1.00 |
| Indoor temperature, Tm | K | 292 |
| Melting temperature, Tr | K | 1672 |
| Failure | - | Plastic strain |
| Plastic strain | - | 0.42 |
| Panel | Front-Plate Deflection δf (mm) | Discrepancy (%) | Back Plate Deflection δb (mm) | Discrepancy (%) | ||
|---|---|---|---|---|---|---|
| Experimental * | Numerical | Experimental * | Numerical | |||
| TZ-1 | Failure | Failure | - | Failure | Failure | - |
| TZ-2 | 28.89 | 29.42 | 1.83 | 14.14 | 14.64 | 3.54 |
| TZ-3 | 18.99 | 20.55 | 8.21 | 7.69 | 8.21 | 6.76 |
| T-1 | Failure | Failure | - | Failure | Failure | - |
| T-2 | 22.71 | 24.70 | 8.76 | 10.31 | 11.54 | 11.93 |
| T-3 | 12.91 | 14.11 | 9.31 | 5.18 | 5.63 | 8.69 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abada, M.; Ibrahim, A. Metallic Ribbon-Core Sandwich Panels Subjected to Air Blast Loading. Appl. Sci. 2020, 10, 4500. https://doi.org/10.3390/app10134500
Abada M, Ibrahim A. Metallic Ribbon-Core Sandwich Panels Subjected to Air Blast Loading. Applied Sciences. 2020; 10(13):4500. https://doi.org/10.3390/app10134500
Chicago/Turabian StyleAbada, Mahmoud, and Ahmed Ibrahim. 2020. "Metallic Ribbon-Core Sandwich Panels Subjected to Air Blast Loading" Applied Sciences 10, no. 13: 4500. https://doi.org/10.3390/app10134500
APA StyleAbada, M., & Ibrahim, A. (2020). Metallic Ribbon-Core Sandwich Panels Subjected to Air Blast Loading. Applied Sciences, 10(13), 4500. https://doi.org/10.3390/app10134500






