Novel Swarm Intelligence Algorithm for Global Optimization and Multi-UAVs Cooperative Path Planning: Anas Platyrhynchos Optimizer
Abstract
:1. Introduction
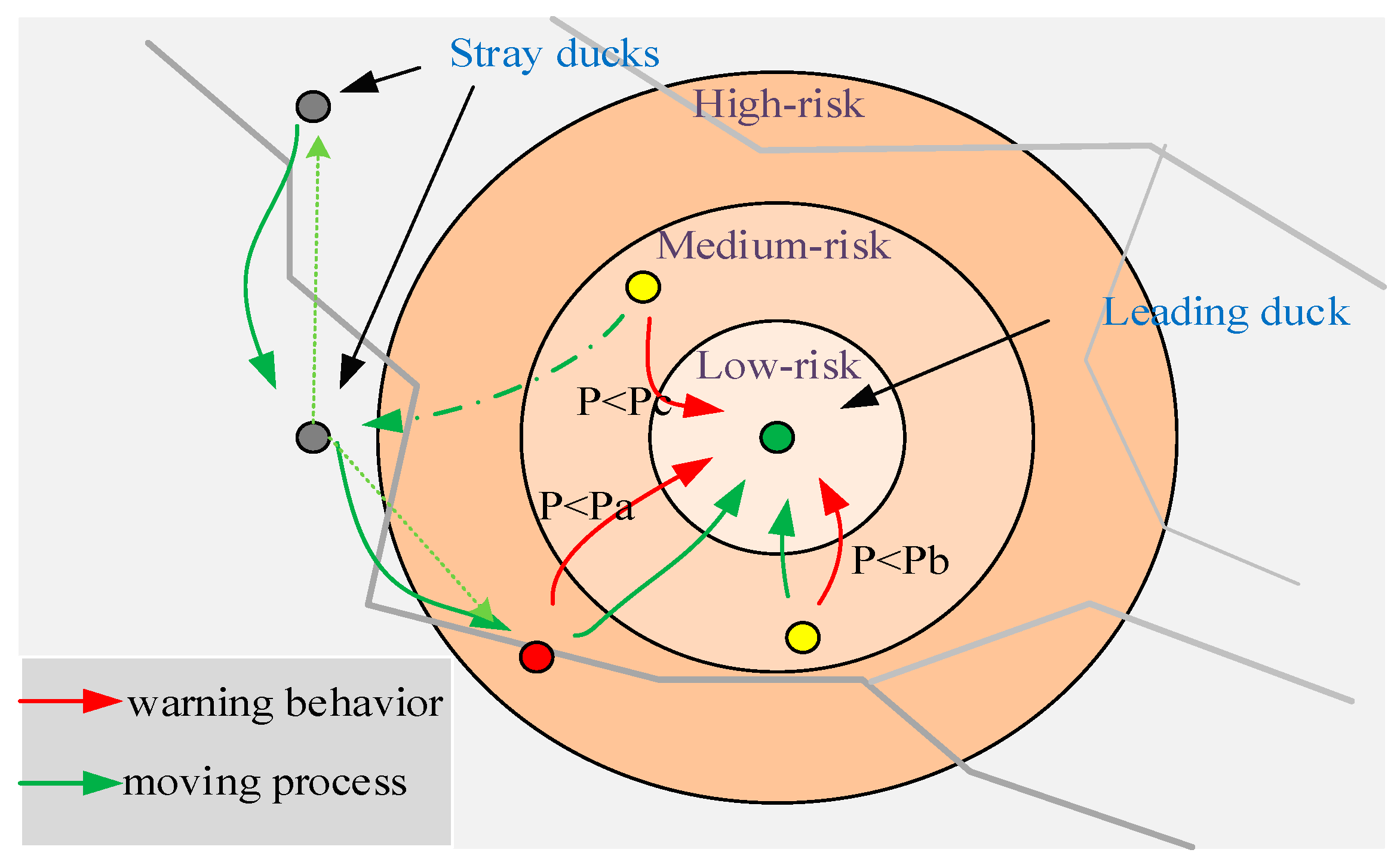
2. Anas Platyrhynchos Optimizer
2.1. Inspiration
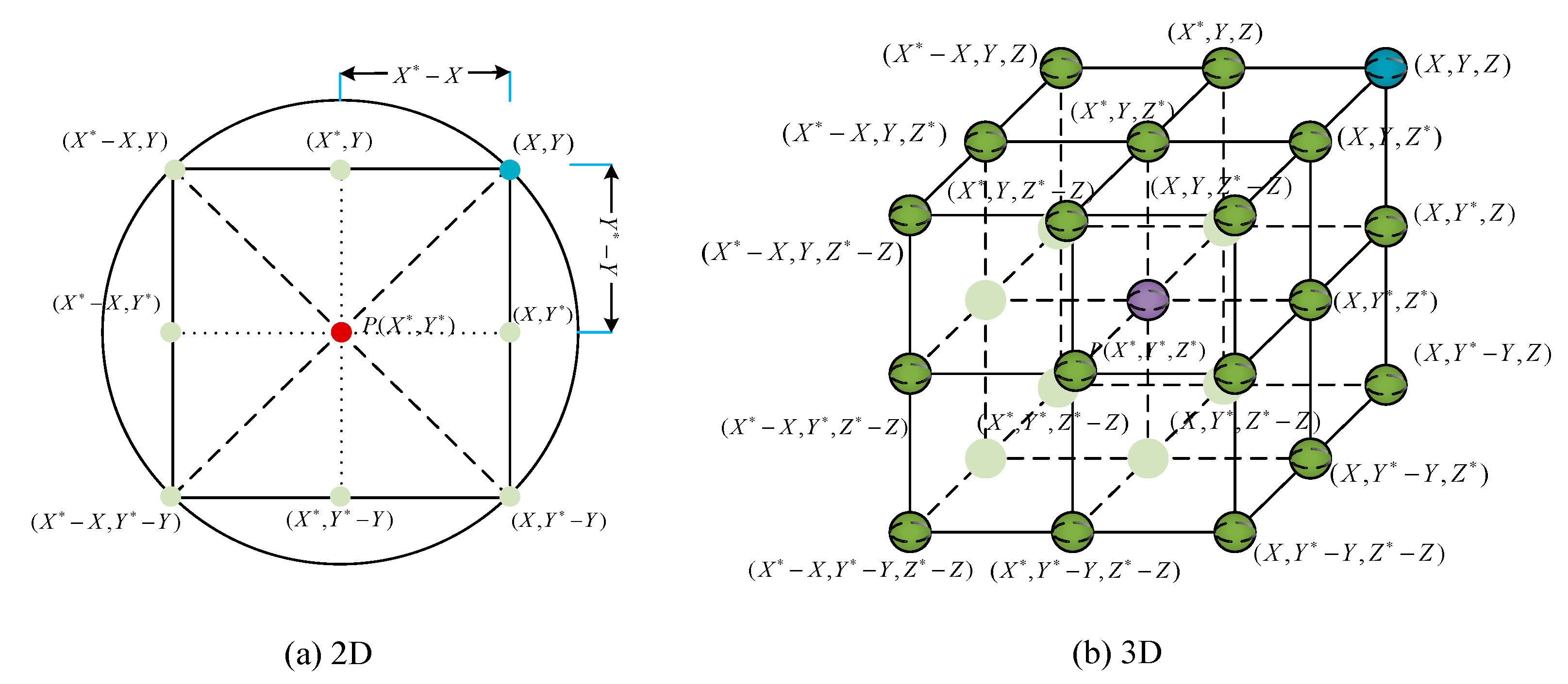
2.2. Mathematical Model and Algorithm
2.2.1. Warning Behavior
2.2.2. Moving Process
2.2.3. Flow of APO
3. Experiment and Application
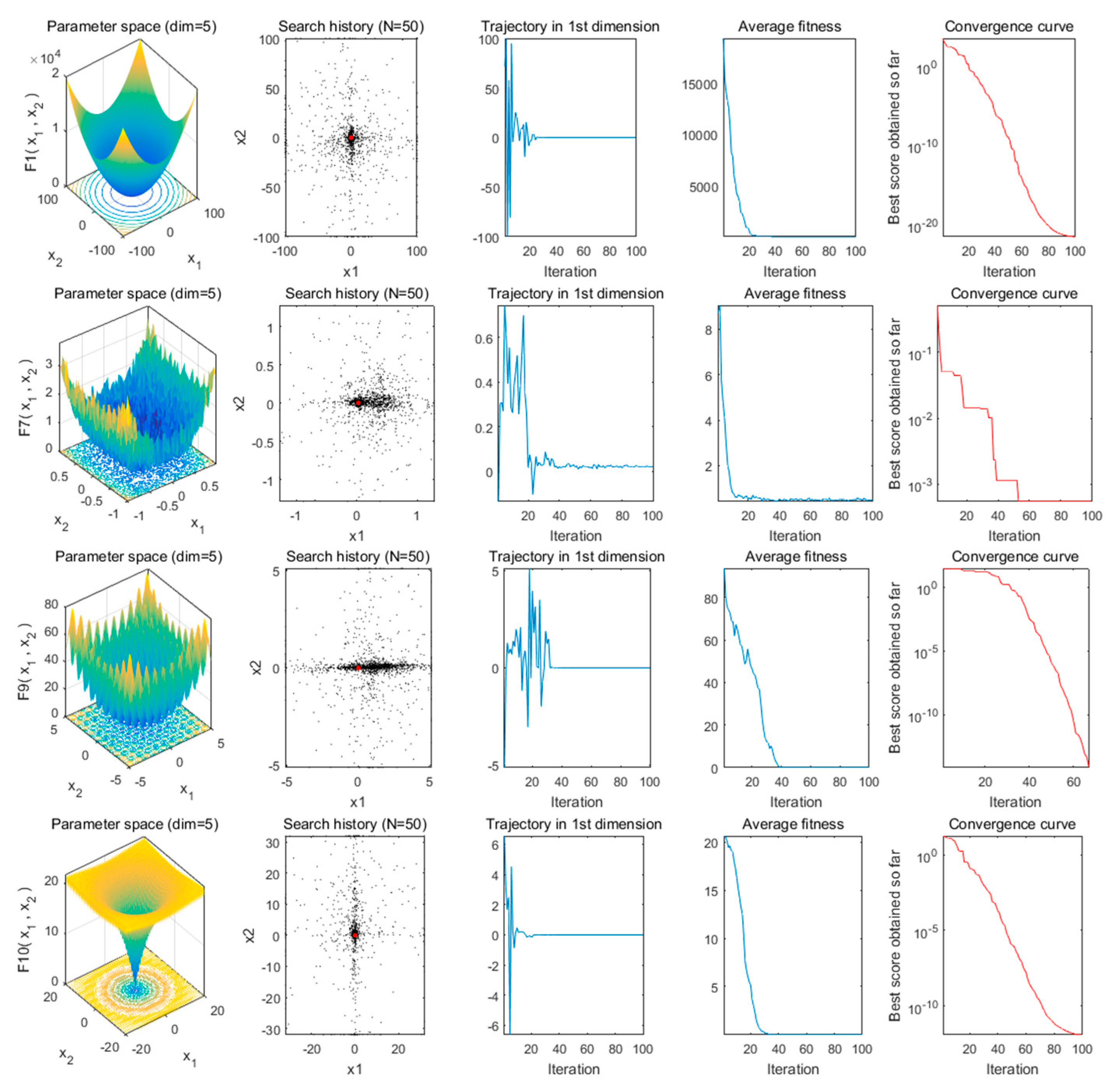
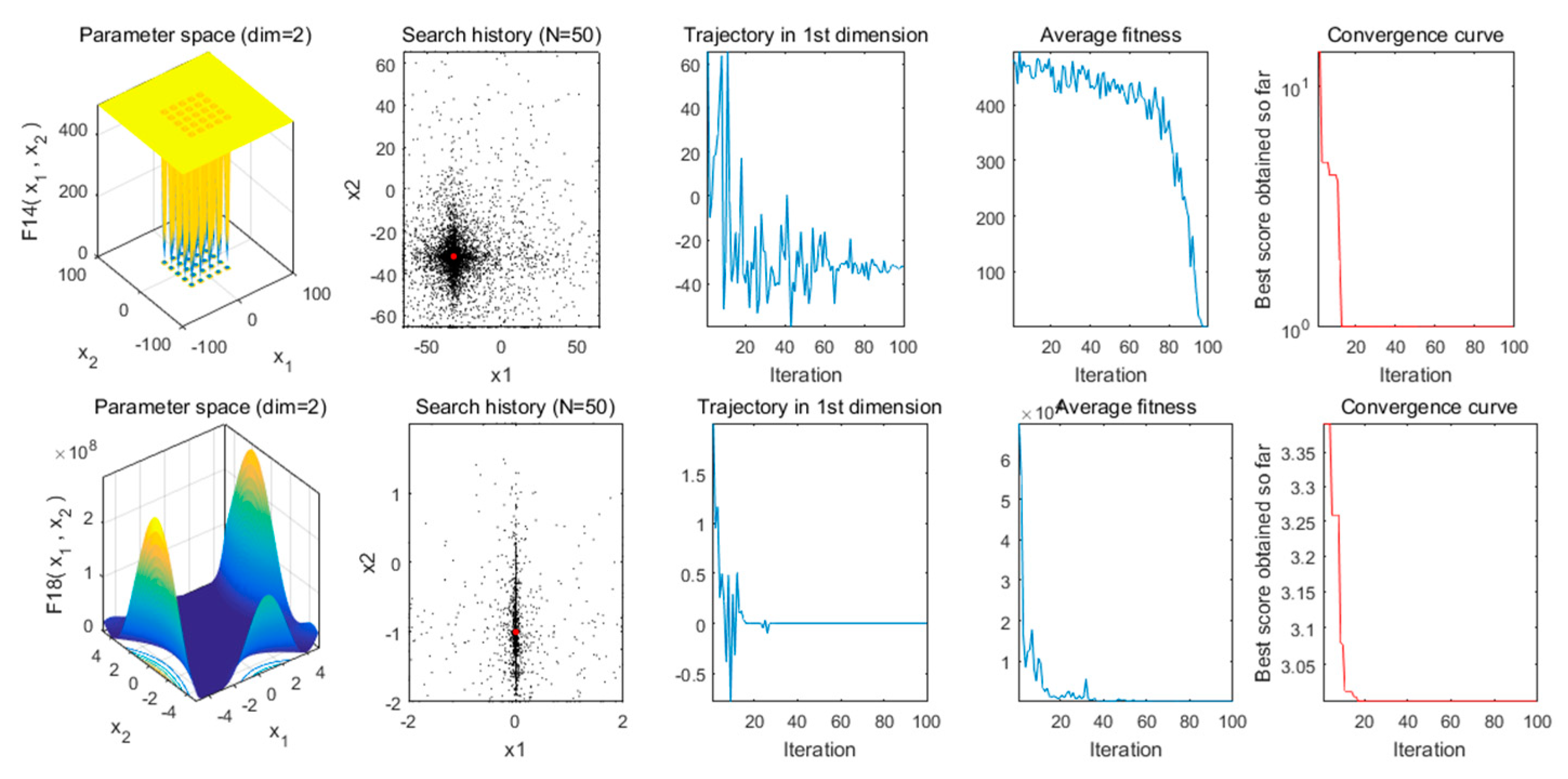
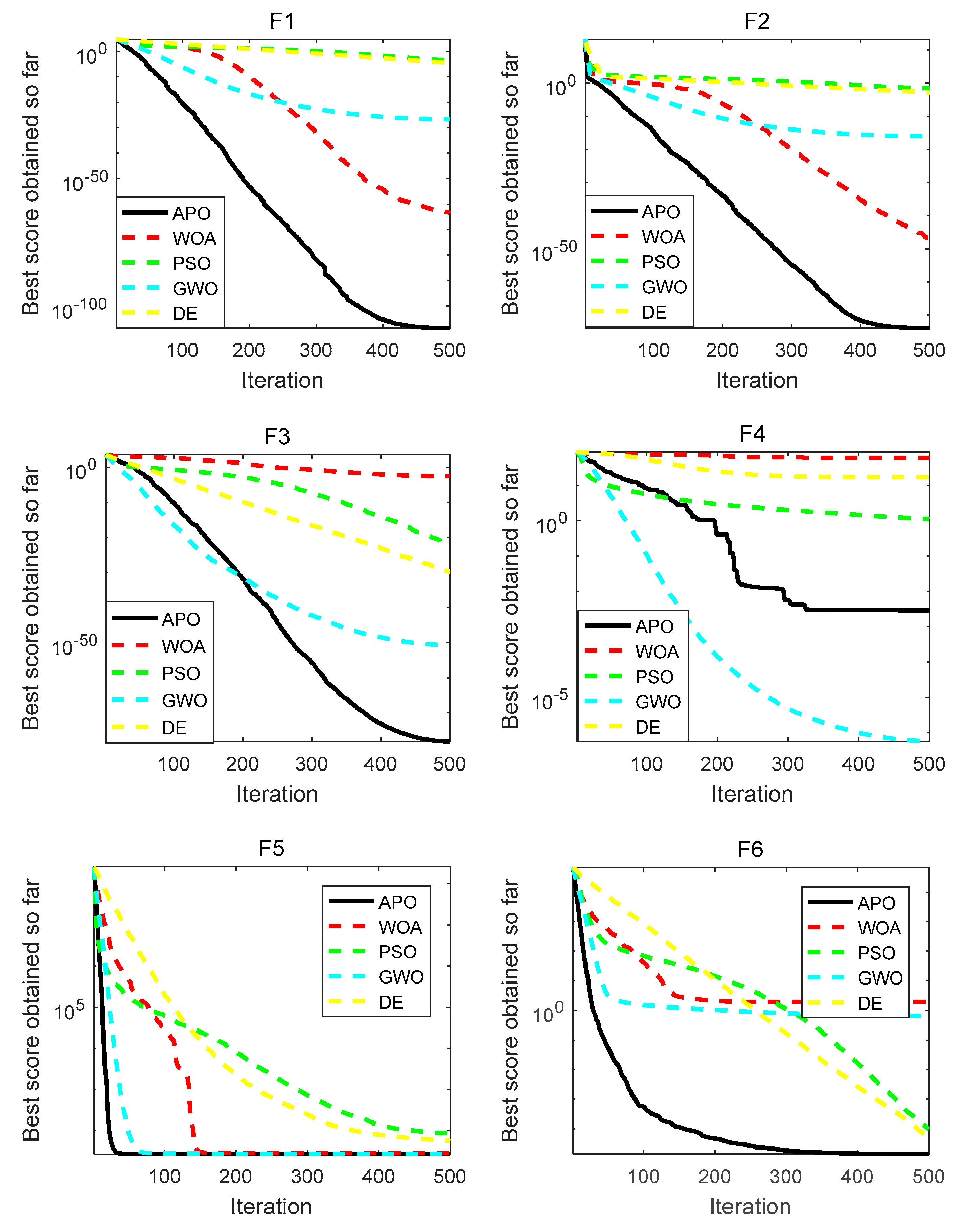
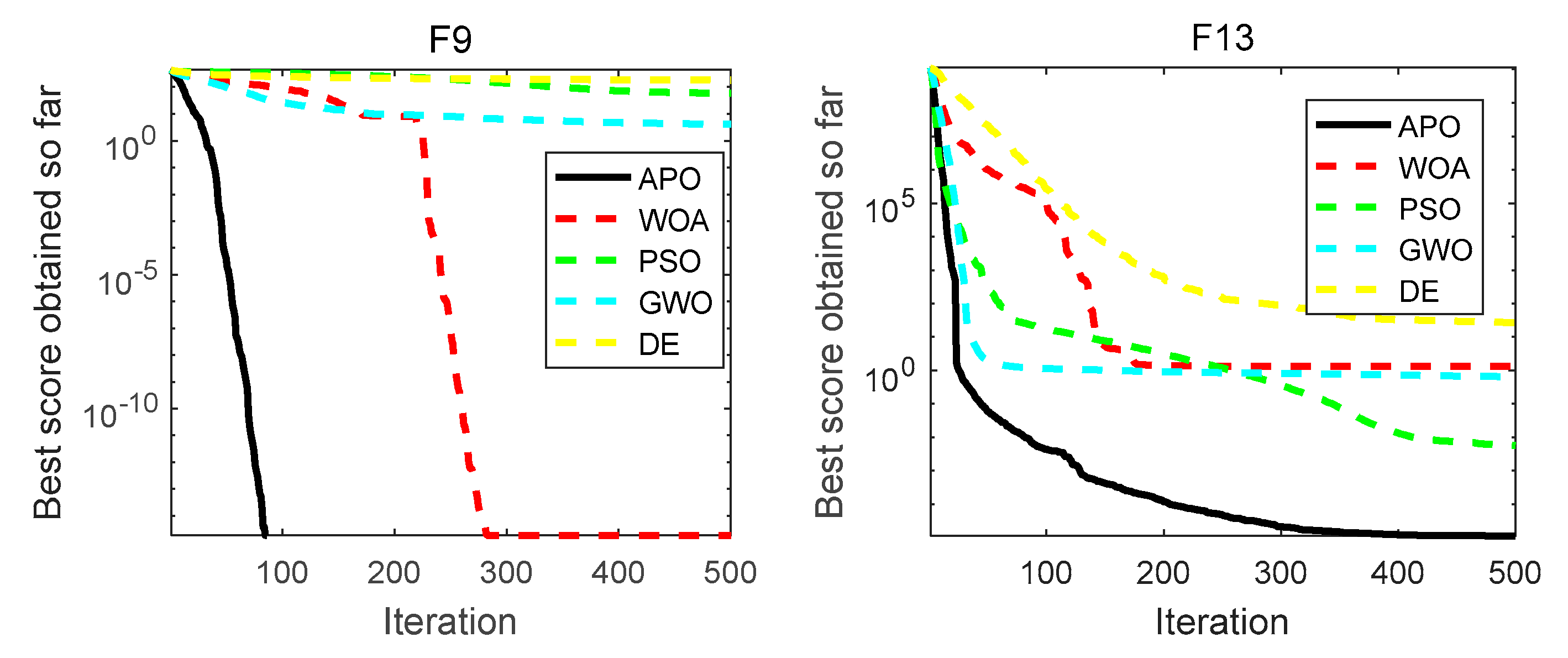
3.1. Performance Analysis: Classic Benchmark Functions
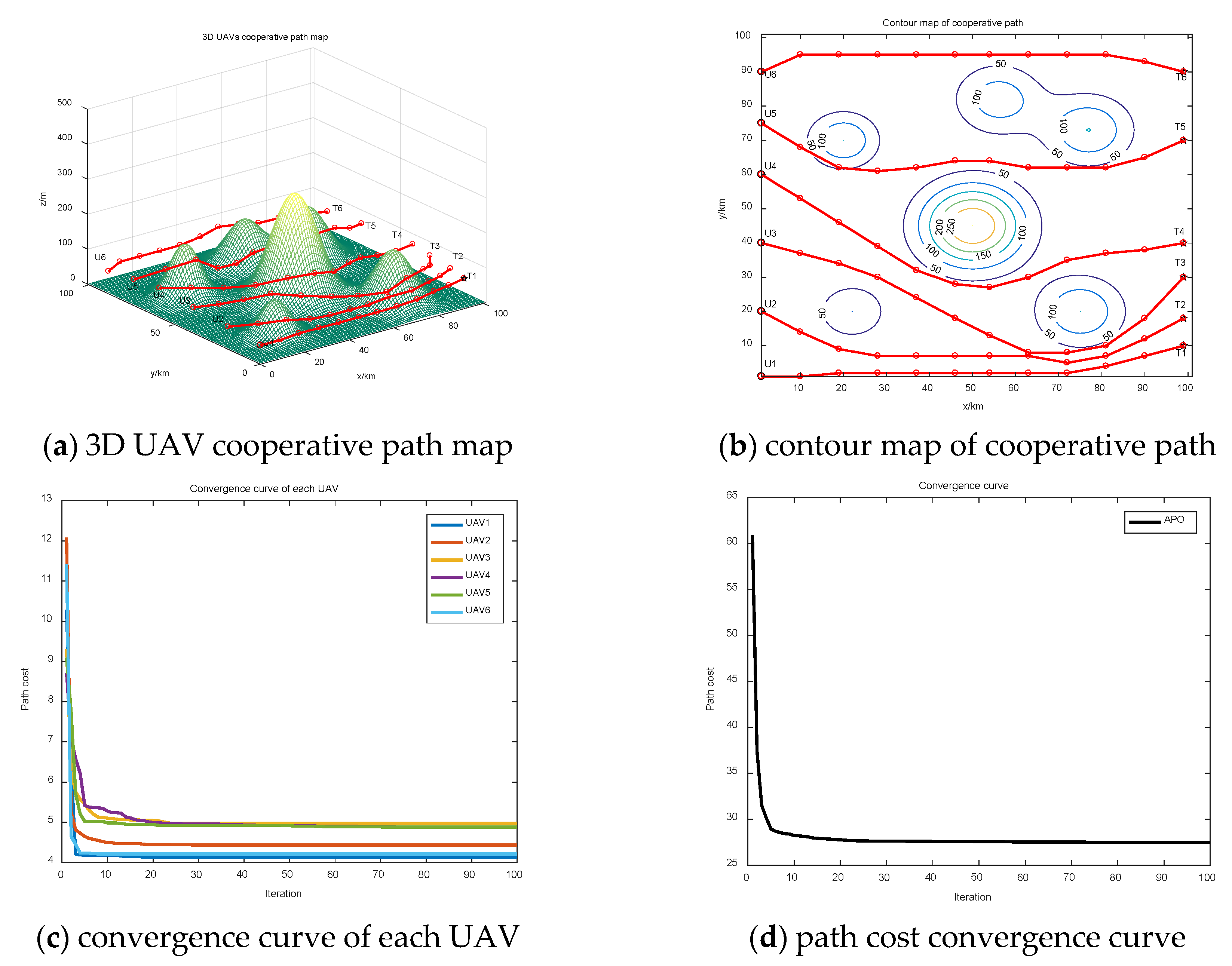
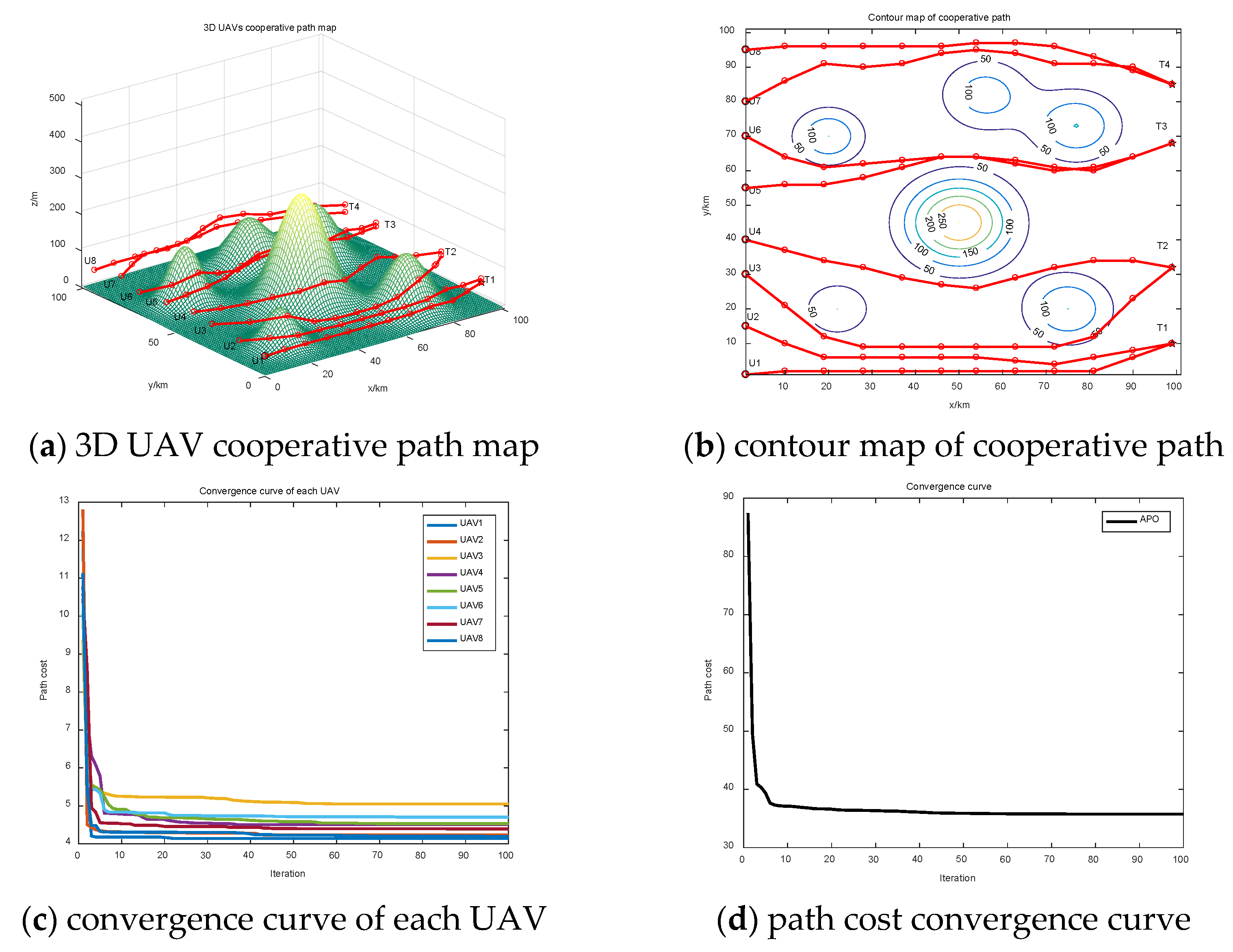
3.2. Engineering Application: Multi-UAVs Cooperative Path Planning
3.2.1. Modeling the UAV Cooperative Path Planning
3.2.2. Path Cost Function
3.2.3. Multi-Population Track Coding
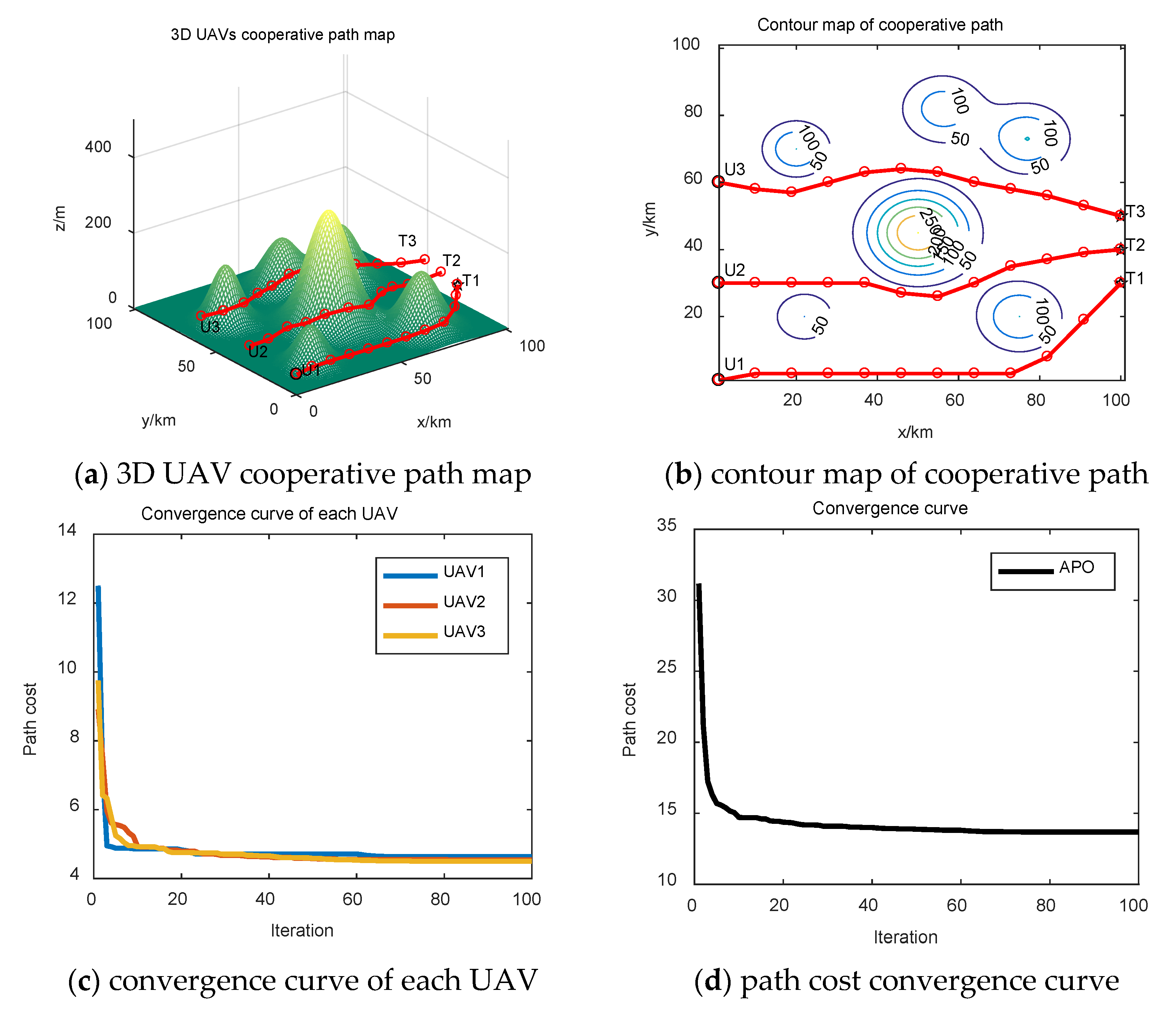
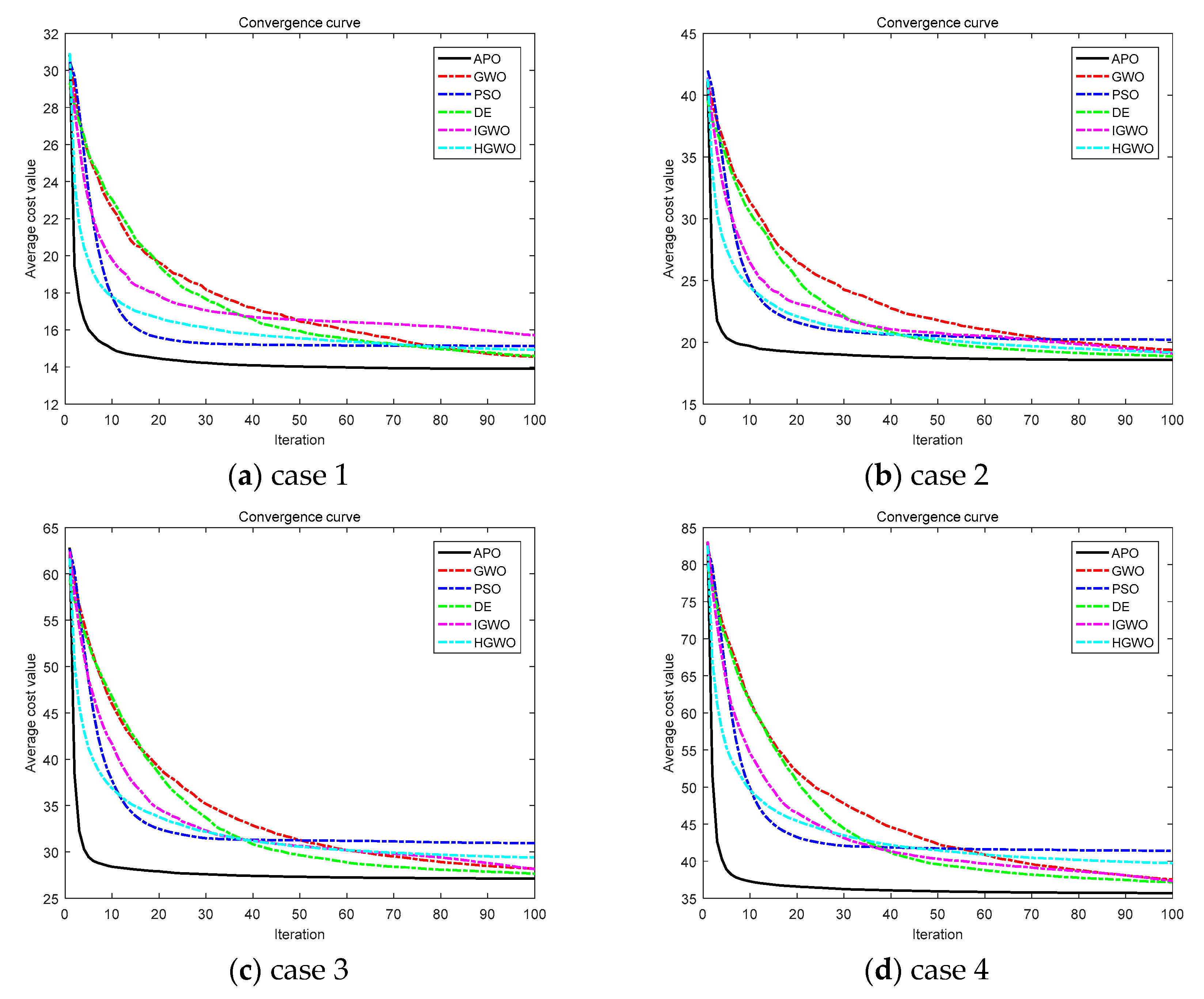
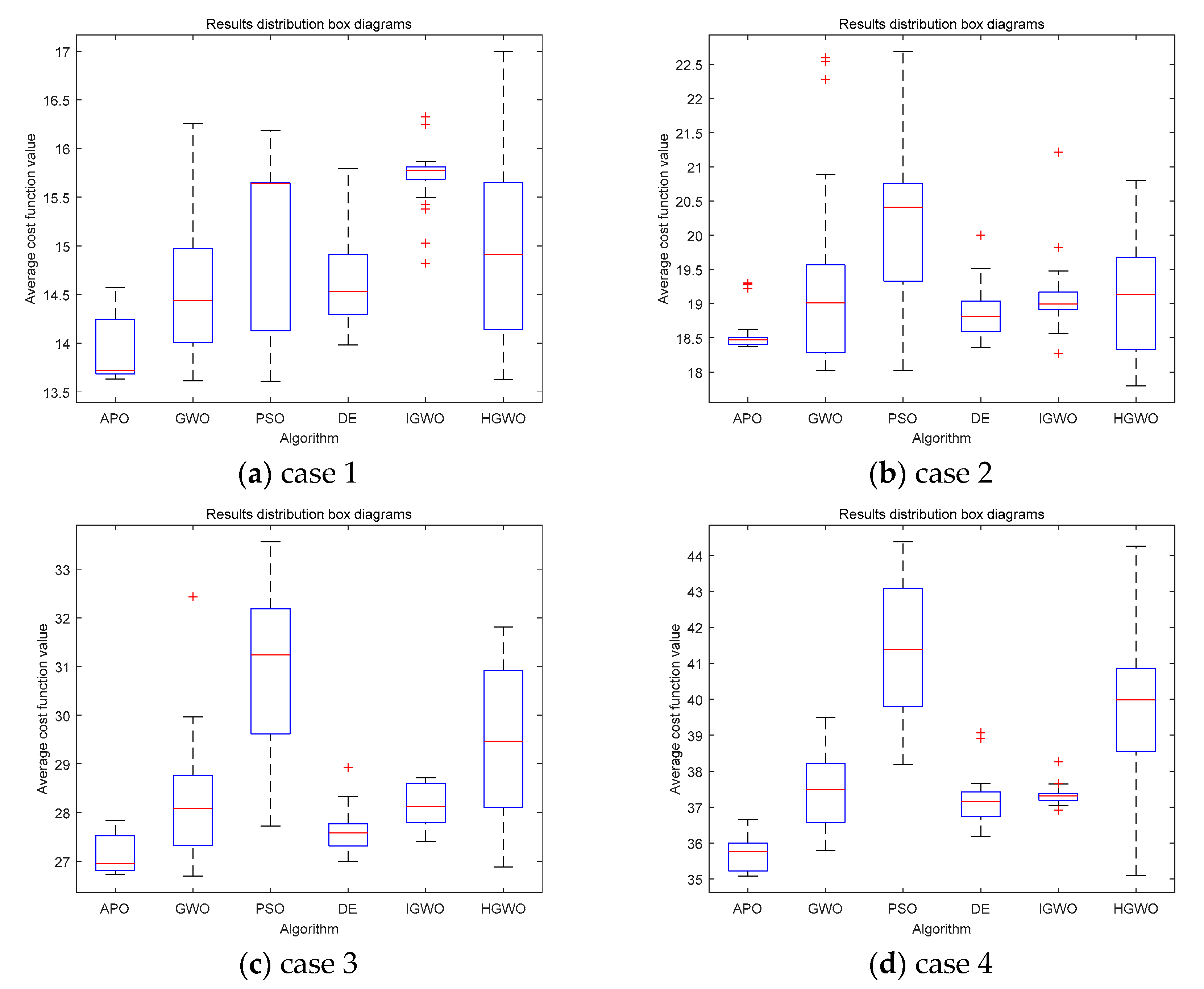
3.2.4. Simulation Validation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Branke, J.; Guntsch, M. Solving the probabilistic TSP with ant colony optimization. J. Math. Model. Algorithms 2004, 3, 403–425. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Mirjalili, S.Z.; Mirjalili, S.; Saremi, S.; Faris, H.; Aljarah, I. Grasshopper optimization algorithm for multi-objective optimization problems. Appl. Intell. 2018, 48, 805–820. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Chen, Y.; Vepa, R.; Shaheed, M.H. Enhanced and speedy energy extraction from a scaled-up pressure retarded osmosis process with a whale optimization based maximum power point tracking. Energy 2018, 153, 618–627. [Google Scholar] [CrossRef]
- Saha, A.; Saikia, L.C. Performance analysis of combination of ultra-capacitor and superconducting magnetic energy storage in a thermal-gas AGC system with utilization of whale optimization algorithm optimized cascade controller. J. Renew. Sustain. Energy 2018, 10, 014103. [Google Scholar] [CrossRef]
- Jadhav, A.R.; Shankar, T. Whale optimization based energy-efficient cluster head selection algorithm for wireless sensor networks. arXiv 2017, arXiv:1711.09389. [Google Scholar]
- Kumawat, I.R.; Nanda, S.J.; Maddila, R.K. Positioning LED panel for uniform illuminance in indoor VLC system using whale optimization. In Optical and Wireless Technologies; Springer: Berlin/Heidelberg, Germany, 2018; pp. 131–139. [Google Scholar]
- Sreenu, K.; Sreelatha, M. W-Scheduler: Whale optimization for task scheduling in cloud computing. Clust. Comput. 2019, 22, 1087–1098. [Google Scholar] [CrossRef]
- Mousavirad, S.J.; Ebrahimpour-Komleh, H. Multilevel image thresholding using entropy of histogram and recently developed population-based metaheuristic algorithms. Evol. Intell. 2017, 10, 45–75. [Google Scholar] [CrossRef]
- Hassan, G.; Hassanien, A.E. Retinal fundus vasculature multilevel segmentation using whale optimization algorithm. Signal Image Video Process 2018, 12, 263–270. [Google Scholar] [CrossRef]
- Yuan, P.; Guo, C.; Zheng, Q.; Ding, J. Sidelobe suppression with constraint for MIMO radar via chaotic whale optimisation. Electron. Lett. 2018, 54, 311–313. [Google Scholar] [CrossRef]
- Pathak, V.K.; Singh, A.K. Accuracy control of contactless laser sensor system using whale optimization algorithm and moth-flame optimization. TM-Tech. Mess. 2017, 84, 734–746. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, X.; Ligthart, L.P.; Peng, S.; Xie, M. Synthesis of broadside linear aperiodic arrays with sidelobe suppression and null steering using whale optimization algorithm. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 347–350. [Google Scholar] [CrossRef]
- Hegazy, A.E.; Makhlouf, M.A.; El-Tawel, G.S. Dimensionality reduction using an improved whale optimization algorithm for data classification. Int. J. Mod. Educ. Comput. Sci. 2018, 11, 37. [Google Scholar] [CrossRef] [Green Version]
- Zamani, H.; Nadimi-Shahraki, M.H. Feature selection based on whale optimization algorithm for diseases diagnosis. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 1243. [Google Scholar]
- Mafarja, M.; Mirjalili, S. Whale optimization approaches for wrapper feature selection. Appl. Soft Comput. 2018, 62, 441–453. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, H.; Li, N. Automatic carrier landing system based on active disturbance rejection control with a novel parameters optimizer. Aerosp. Sci. Technol. 2017, 69, 149–160. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Li, N. Path planning for solar-powered UAV in urban environment. Neurocomputing 2018, 275, 2055–2065. [Google Scholar] [CrossRef]
- Kaveh, A.; Ghazaan, M.I. Enhanced whale optimization algorithm for sizing optimization of skeletal structures. Mech. Based Des. Struct. Mach. 2017, 45, 345–362. [Google Scholar] [CrossRef]
- Kaveh, A. Sizing optimization of skeletal structures using the enhanced whale optimization algorithm. In Applications of Metaheuristic Optimization Algorithms in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2017; pp. 47–69. [Google Scholar]
- Wu, J.; Wang, H.; Li, N. Distributed trajectory optimization for multiple solar-powered UAVs target tracking in urban environment by Adaptive Grasshopper Optimization Algorithm. Aerosp. Sci. Technol. 2017, 70, 497–510. [Google Scholar] [CrossRef]
- Barman, M.; Choudhury, N.B.D.; Sutradhar, S. A regional hybrid GOA-SVM model based on similar day approach for short-term load forecasting in Assam, India. Energy 2018, 145, 710–720. [Google Scholar] [CrossRef]
- El-Fergany, A.A. Electrical characterisation of proton exchange membrane fuel cells stack using grasshopper optimiser. IET Renew. Power Gener. 2017, 12, 9–17. [Google Scholar] [CrossRef]
- Łukasik, S.; Kowalski, P.A.; Charytanowicz, M. Data clustering with grasshopper optimization algorithm. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems (FedCSIS), Prague, Czech Republic, 3–6 September 2017; pp. 71–74. [Google Scholar]
- Rajput, N.; Chaudhary, V.; Dubey, H.M. Optimal generation scheduling of thermal System using biologically inspired grasshopper algorithm. In Proceedings of the 2017 2nd International Conference on Telecommunication and Networks (TEL-NET), Noida, India, 10–11 August 2017; pp. 1–6. [Google Scholar]
- Zhang, X.; Miao, Q.; Zhang, H. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, H.; Guo, S. Short-term wind electric power forecasting using a novel multi-stage intelligent algorithm. Sustainability 2018, 10, 881. [Google Scholar] [CrossRef] [Green Version]
- Ahanch, M.; Asasi, M.S.; Amiri, M.S. A Grasshopper Optimization Algorithm to solve optimal distribution system reconfiguration and distributed generation placement problem. In Proceedings of the 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 659–666. [Google Scholar]
- Ibrahim, H.T.; Mazher, W.J.; Ucan, O.N. A grasshopper optimizer approach for feature selection and optimizing SVM parameters utilizing real biomedical data sets. Neural Comput. Appl. 2019, 31, 5965–5974. [Google Scholar] [CrossRef]
- Amaireh, A.A.; Alzoubi, A.; Dib, N.I. Design of linear antenna arrays using antlion and grasshopper optimization algorithms. In Proceedings of the 2017 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT), Aqaba, Jordan, 11–13 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Hamad, A.; Houssein, E.H.; Hassanien, A.E. Hybrid grasshopper optimization algorithm and support vector machines for automatic seizure detection in EEG signals. In International Conference on Advanced Machine Learning Technologies and Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 82–91. [Google Scholar]
- Hekimoğlu, B.; Ekinci, S. Grasshopper optimization algorithm for automatic voltage regulator system. In Proceedings of the 2018 5th International Conference on Electrical and Electronic Engineering (ICEEE), Istanbul, Turkey, 3–5 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 152–156. [Google Scholar]
- Heidari, A.A.; Faris, H.; Aljarah, I. An efficient hybrid multilayer perceptron neural network with grasshopper optimization. Soft Comput. 2019, 23, 7941–7958. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Mirjalili, S. Evolving radial basis function networks using moth–flame optimizer[M]. In Handbook of Neural Computation; Academic Press: Cambridge, MA, USA, 2017; pp. 537–550. [Google Scholar]
- Hassanin, M.F.; Shoeb, A.M.; Hassanien, A.E. Designing multilayer feedforward neural networks using multi-verse optimizer. In Handbook of Research on Machine Learning Innovations and Trends; IGI Global: Hershey, PA, USA, 2017; pp. 1076–1093. [Google Scholar]
- Benmessahel, I.; Xie, K.; Chellal, M. A new evolutionary neural networks based on intrusion detection systems using multiverse optimization. Appl. Intell. 2018, 48, 2315–2327. [Google Scholar] [CrossRef]
- Faris, H.; Hassonah, M.A.; Ala’M, A.Z. A multi-verse optimizer approach for feature selection and optimizing SVM parameters based on a robust system architecture. Neural Comput. Appl. 2018, 30, 2355–2369. [Google Scholar] [CrossRef]
- Rosenberg, A.; Hirschberg, J. V-measure, A conditional entropy-based external cluster evaluation measure. In Proceedings of the 2007 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning (EMNLP-CoNLL), Prague, Czech Republic, 28–30 June 2007; Association for Computational Linguistics: Stroudsburg, PA, USA, 2007; pp. 410–420. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Panwar, L.K.; Reddy, S.; Verma, A. Binary grey wolf optimizer for large scale unit commitment problem. Swarm Evol. Comput. 2018, 38, 251–266. [Google Scholar] [CrossRef]
- Jayabarathi, T.; Raghunathan, T.; Adarsh, B.R. Economic dispatch using hybrid grey wolf optimizer. Energy 2016, 111, 630–641. [Google Scholar] [CrossRef]
- Srikanth, K.; Panwar, L.K.; Panigrahi, B.K. Meta-heuristic framework, Quantum inspired binary grey wolf optimizer for unit commitment problem. Comput. Electr. Eng. 2018, 70, 243–260. [Google Scholar] [CrossRef]
- Liu, C.A.; Wang, X.P.; Liu, C.Y.; Wu, H. Three-dimensional route planning for unmanned aerial vehicle based on improved grey wolf optimizer. J. Huazhong Univ. Sci. Technol. 2017, 45, 38–42. [Google Scholar]
- Singh, N.; Singh, S.B. Hybrid algorithm of particle swarm optimization and grey wolf optimizer for improving convergence performance. J. Appl. Math. 2017, 2030489. [Google Scholar] [CrossRef]
- Ab Rashid, M.F.F. A hybrid Ant-Wolf Algorithm to optimize assembly sequence planning problem. Assem. Autom. 2017, 37, 238–248. [Google Scholar] [CrossRef] [Green Version]
- ElGayyar, M.; Emary, E.; Sweilam, N.H. A hybrid Grey Wolf-bat algorithm for global optimization. In International Conference on Advanced Machine Learning Technologies and Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–12. [Google Scholar]
- Pan, J.S.; Dao, T.K.; Chu, S.C. A novel hybrid GWO-FPA algorithm for optimization applications. In International Conference on Smart Vehicular Technology, Transportation, Communication and Applications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 274–281. [Google Scholar]
- Debnath, M.K.; Mallick, R.K.; Sahu, B.K. Application of hybrid differential evolution–grey wolf optimization algorithm for automatic generation control of a multi-source interconnected power system using optimal fuzzy–PID controller. Electr. Power Compon. Syst. 2017, 45, 2104–2117. [Google Scholar] [CrossRef]
- Singh, N.; Singh, S.B. A novel hybrid GWO-SCA approach for optimization problems. Eng. Sci. Technol. Int. J. 2017, 20, 1586–1601. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, Q.; Cheng, J.; Wang, X. A novel hybrid algorithm based on biogeography-based optimization and grey wolf optimizer. Appl. Soft Comput. 2018, 67, 197–214. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Jangir, P.; Kumar, A. A novel hybrid PSO–WOA algorithm for global numerical functions optimization. In Advances in Computer and Computational Sciences; Springer: Berlin/Heidelberg, Germany, 2018; pp. 53–60. [Google Scholar]
- Kaveh, A.; Rastegar Moghaddam, M. A hybrid WOA-CBO algorithm for construction site layout planning problem. Sci. Iran. 2018, 25, 1094–1104. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 210–214. [Google Scholar]
- Zelinka, I. SOMA—Self-Organizing Migrating Algorithm. In New Optimization Techniques in Engineering; Springer: Berlin/Heidelberg, Germany, 2004; pp. 167–217. [Google Scholar]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar]
- Digalakis, J.G.; Margaritis, K.G. On benchmarking functions for genetic algorithms. Int. J. Comput. Math. 2001, 77, 481–506. [Google Scholar] [CrossRef]
- Molga, M.; Smutnicki, C. Test functions for optimization needs. Test Funct. Optim. Needs 2005, 101, 48. [Google Scholar]
- Yang, X.S. Test problems in optimization. arXiv 2010, arXiv:1008.0549. [Google Scholar]
- Mirjalili, S.; Lewis, A. S-shaped versus V-shaped transfer functions for binary particle swarm optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.S. Binary bat algorithm. Neural Comput. Appl. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Price, K.V. Differential Evolution. In Handbook of Optimization; Springer: Berlin/Heidelberg, Germany, 2013; pp. 187–214. [Google Scholar]
- Van den Bergh, F.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Yang, L.; Guo, J.; Liu, Y. Three-Dimensional UAV Cooperative Path Planning Based on the MP-CGWO Algorithm. Int. J. Innov. Comput. Inf. Control 2020, 16, 991–1006. [Google Scholar]
- Cheng, Z.; Tang, X.Y.; Liu, Y.L. 3-D path planning for UAV based on chaos particle swarm optimization. Appl. Mech. Mater. 2012, 232, 625–630. [Google Scholar] [CrossRef]
- Hu, Z.H. Research on Some Key Techniques of UAV Path Planning Based on Intelligent Optimization algorithm; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2011. [Google Scholar]
- Ye, Y.Y.; Min, C.P. A co-evolutionary method for cooperative UAVs path planning. Comput. Simul. 2007, 24, 37–39. [Google Scholar]


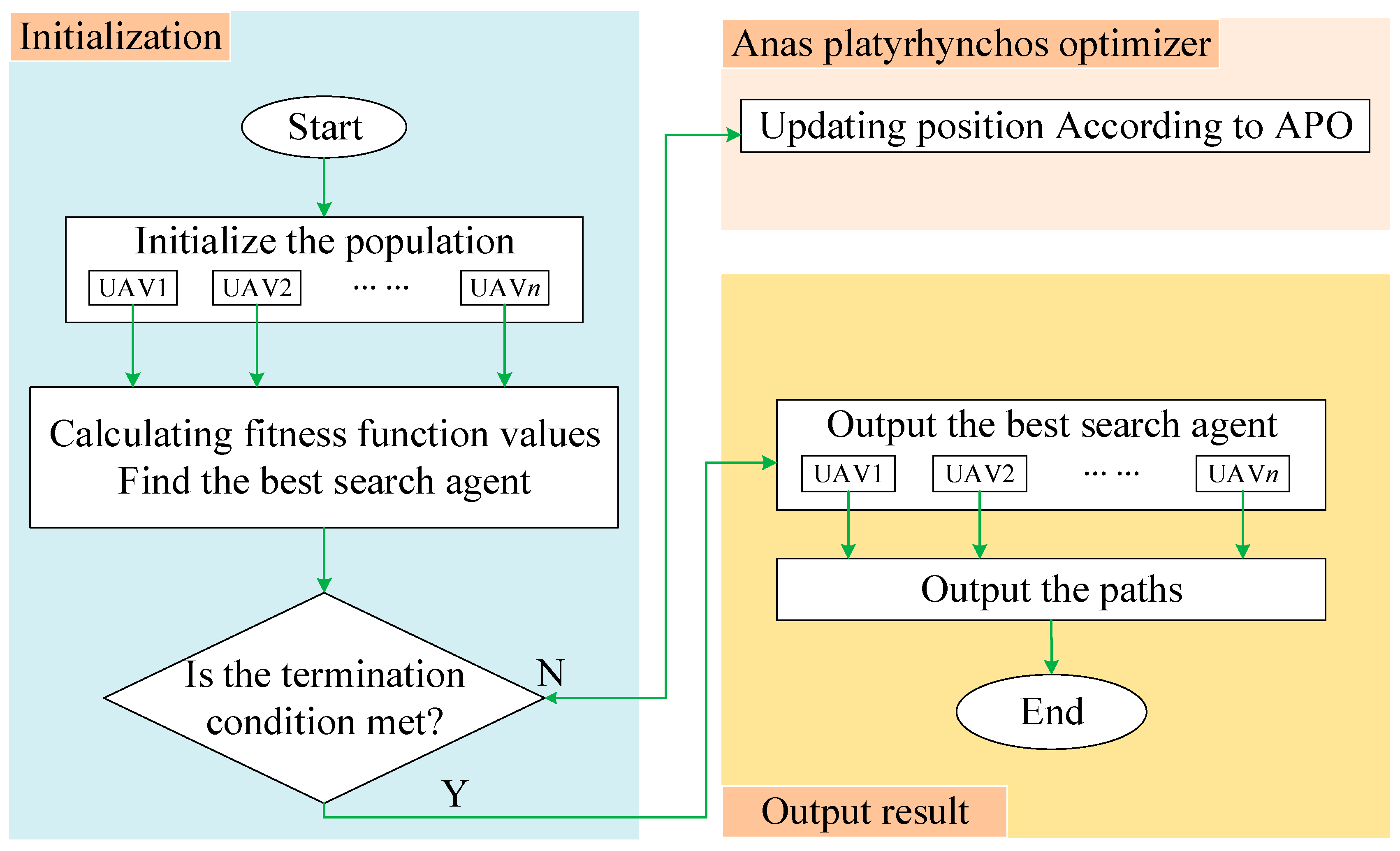

| Setting:low, up, N, D, ObjFun, and T |
| Initial population according to Equation (1) |
| Calculating fitness function of population by |
| Finding the leading duck |
| t = 1 |
| while (t < = T) |
| Calculating the Pc according to Equation (2)//warning behavior |
| for i from 1 to N do |
| if rand < Pc |
| Updating position according to Equation (3) |
| end if |
| Updating parameters A and C according to Equations (8) and (9)//moving process |
| Updating position according to Equation (7) |
| if //take the minimum as an example |
| Selecting another particle at random |
| if |
| Updating position according to Equation (11) |
| elseif |
| Keeping unchanged |
| elseif |
| Updating position according to Equation (12) |
| end if |
| end if |
| end for |
| Finding the leading duck |
| t = t + 1 |
| end while |
| return |
| Test Function | D | Range | Optimum |
|---|---|---|---|
| 30 | [−100,100] | 0 | |
| 30 | [−10,10] | 0 | |
| 30 | [−100,100] | 0 | |
| 30 | [−100,100] | 0 | |
| 30 | [−30,30] | 0 | |
| 30 | [−100,100] | 0 | |
| 30 | [−1.28,1.28] | 0 | |
| 30 | [−500,500] | −418.9825∗5 | |
| 30 | [−5.12,5.12] | 0 | |
| 30 | [−32,32] | 0 | |
| 30 | [−600,600] | 0 | |
| 30 | [−50,50] | 0 | |
| 30 | [−50,50] | 0 |
| 2 | [−65,65] | 1 | |
| 4 | [−5,5] | 0.00030 | |
| 2 | [−5,5] | −1.0316 | |
| 2 | [−5,5] | 0.398 | |
| 2 | [−2,2] | 3 | |
| 3 | [1,3] | −3.86 | |
| 6 | [0,1] | −3.32 | |
| 4 | [0,10] | −10.1532 | |
| 4 | [0,10] | −10.4028 | |
| 4 | [0,10] | −10.5363 |
| Algorithms | Parameter Settings |
|---|---|
| Gray wolf optimization (GWO) [8] | a = 2 − t*2/T |
| Whale optimization algorithm (WOA) [9] | a1 = 2 − t*2/T, a2 = −1 + t*(−1)/T |
| Particle swarm optimization (PSO) [2] | wmax = 0.9, wmin = 0.2, c1 = c2 = 2 |
| Differential evolution (DE) [68] | F = 0.5, CR = 0.9 |
| F | Result | APO | GWO | WOA | PSO | DE | Rank |
|---|---|---|---|---|---|---|---|
| f1 | Best | 7.8190 | 1.0102 | 1.9587 | 9.3358 | 2.3626 | 1 |
| Worst | 6.9690 | 1.6995 | 7.1646 | 0.0029 | 2.1183 | ||
| Mean | 2.3236 | 2.1408 | 2.8808 | 2.6064 | 3.3728 | ||
| Std | 1.2723 | 4.1907 | 1.3261 | 5.4256 | 4.4013 | ||
| f2 | Best | 5.5304 | 1.1204 | 2.0437 | 0.0036 | 5.1036 | 1 |
| Worst | 2.4478 | 3.6284 | 3.4372 | 0.1201 | 0.0033 | ||
| Mean | 1.3539 | 9.5431 | 2.0876 | 0.0309 | 0.0016 | ||
| Std | 5.2303 | 8.7339 | 7.4074 | 0.0268 | 6.9524 | ||
| f3 | Best | 1.5871 | 1.1907 | 4.7969 | 5.4371 | 2.2540 | 1 |
| Worst | 8.1085 | 5.6634 | 0.0293 | 5.0743 | 1.8224 | ||
| Mean | 6.0509 | 2.0580 | 0.0033 | 3.7279 | 1.6513 | ||
| Std | 1.7318 | 1.0323 | 0.0068 | 1.1100 | 3.9570 | ||
| f4 | Best | 1.2424 | 6.5653 | 5.3046 | 0.5731 | 5.7123 | 2 |
| Worst | 0.0312 | 1.9500 | 89.6219 | 1.5222 | 37.5491 | ||
| Mean | 0.0029 | 5.7114 | 59.6414 | 1.1226 | 16.8984 | ||
| Std | 0.0078 | 4.6159 | 29.3820 | 0.2522 | 7.2691 | ||
| f5 | Best | 0.0078 | 26.0434 | 27.1465 | 25.3115 | 19.0580 | 1 |
| Worst | 28.7807 | 28.7485 | 28.8434 | 188.8556 | 181.2647 | ||
| Mean | 26.6971 | 27.2864 | 28.3636 | 85.1733 | 56.5542 | ||
| Std | 7.2574 | 0.7167 | 0.4466 | 40.5425 | 40.1468 | ||
| f6 | Best | 1.2702 | 1.3209 | 0.7374 | 7.9911 | 3.6153 | 1 |
| Worst | 4.3859 | 1.5119 | 3.1981 | 4.1143 | 1.8978 | ||
| Mean | 1.3972 | 0.6602 | 1.9556 | 9.7234 | 4.7963 | ||
| Std | 9.8769 | 0.3692 | 0.6576 | 8.7218 | 4.8581 | ||
| f7 | Best | 1.9336 | 4.8037 | 6.4622 | 0.0804 | 0.0360 | 1 |
| Worst | 0.0077 | 0.0034 | 0.0194 | 0.3469 | 0.1085 | ||
| Mean | 8.5533 | 0.0019 | 0.0050 | 0.1729 | 0.0797 | ||
| Std | 0.0015 | 7.0049 | 0.0057 | 0.0584 | 0.0158 | ||
| f8 | Best | −12569 | −7250.9 | N/A | −8727.2 | −7317.7 | 1 |
| Worst | −12150 | −3727.9 | N/A | −2629.0 | −4691.7 | ||
| Mean | −12529 | −6129.3 | N/A | −4978.3 | −5946.6 | ||
| Std | 106.3406 | 767.8156 | N/A | 1569.8 | 667.0457 | ||
| f9 | Best | 0 | 5.6843 | 0 | 33.8862 | 1.4607 | 1 |
| Worst | 0 | 16.9267 | 5.6843 | 83.6992 | 2.1638 | ||
| Mean | 0 | 4.0526 | 1.8948 | 58.1507 | 1.8134 | ||
| Std | 0 | 4.5006 | 1.0378 | 14.4306 | 16.9916 | ||
| f10 | Best | 8.8818 | 5.7732 | 8.8818 | 0.0016 | 5.7932 | 1 |
| Worst | 7.9936 | 1.3589 | 7.9936 | 1.5175 | 0.0226 | ||
| Mean | 2.6645 | 1.0309 | 3.8488 | 0.1757 | 0.0024 | ||
| Std | 2.2372 | 1.7645 | 2.6526 | 0.4313 | 0.0040 | ||
| f11 | Best | 0 | 0 | 0 | 1.2377 | 1.5597 | 1 |
| Worst | 0 | 0.0384 | 0.1508 | 0.0246 | 0.0340 | ||
| Mean | 0 | 0.0030 | 0.0086 | 0.0071 | 0.0032 | ||
| Std | 0 | 0.0090 | 0.0333 | 0.0081 | 0.0072 | ||
| f12 | Best | 8.3024 | 0.0063 | 0.0295 | 1.3634 | 5.3389 | 1 |
| Worst | 0.0065 | 0.0939 | 0.7203 | 0.1037 | 8.3340 | ||
| Mean | 2.1901 | 0.0373 | 0.1473 | 0.0104 | 62.5083 | ||
| Std | 0.0012 | 0.0186 | 0.1722 | 0.0316 | 1.9621 | ||
| f13 | Best | 1.9591 | 0.2159 | 0.6067 | 1.8128 | 1.0309 | 1 |
| Worst | 4.1407 | 1.1442 | 1.9571 | 0.0178 | 7.4778 | ||
| Mean | 1.1372 | 0.6458 | 1.3359 | 0.0057 | 26.6912 | ||
| Std | 1.0199 | 0.2486 | 0.3731 | 0.0058 | 1.3623 |
| F | Result | APO | GWO | WOA | PSO | DE | Rank |
|---|---|---|---|---|---|---|---|
| f14 | Best | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 4 |
| Worst | 12.6705 | 12.6705 | 10.7632 | 10.7632 | 2.9821 | ||
| Mean | 4.2973 | 4.4937 | 2.0822 | 3.1636 | 1.0641 | ||
| Std | 4.0039 | 4.0086 | 2.1440 | 2.8550 | 0.3622 | ||
| f15 | Best | 3.1012 | 3.0749 | 3.2572 | 5.0404 | 3.0749 | 1 |
| Worst | 0.0023 | 0.0204 | 0.0043 | 0.0011 | 0.0204 | ||
| Mean | 5.2403 | 0.0037 | 0.0012 | 8.2951 | 0.0018 | ||
| Std | 5.1504 | 0.0076 | 8.6353 | 1.5813 | 0.0051 | ||
| f16 | Best | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | = |
| Worst | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | ||
| Mean | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | ||
| Std | 8.4272 | 1.7842 | 2.1111 | 6.3877 | 6.7752 | ||
| f17 | Best | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.3979 | = |
| Worst | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.3979 | ||
| Mean | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.3979 | ||
| Std | 9.2877 | 2.0274 | 1.4524 | 0 | 0 | ||
| f18 | Best | 3.0000 | 3.0000 | 3.0000 | 3.0000 | 3.0000 | ≈ |
| Worst | 30.0000 | 3.0000 | 30.0033 | 3.0000 | 3.0000 | ||
| Mean | 6.6000 | 3.0000 | 3.9003 | 3.0000 | 3.0000 | ||
| Std | 9.3351 | 4.3052 | 4.9301 | 1.6472 | 2.0301 | ||
| f19 | Best | −3.8628 | −3.8628 | −3.8628 | −3.8628 | −3.8628 | ≈ |
| Worst | −3.8549 | −3.8549 | −3.8445 | −3.8628 | −3.8628 | ||
| Mean | −3.8605 | −3.8613 | −3.8611 | −3.8628 | −3.8628 | ||
| Std | 0.0036 | 0.0027 | 0.0038 | 2.5829 | 2.7101 | ||
| f20 | Best | −3.3220 | −3.3220 | −3.3218 | −3.3220 | −3.3220 | ≈ |
| Worst | −3.0839 | −3.0499 | −3.1627 | −3.2031 | −3.2031 | ||
| Mean | −3.2599 | −3.2672 | −3.2599 | −3.2784 | −3.2507 | ||
| Std | 0.0838 | 0.0861 | 0.0651 | 0.0583 | 0.0592 | ||
| f21 | Best | −10.1532 | −10.1529 | −10.1526 | −10.1532 | −10.1532 | 1 |
| Worst | −0.8810 | −2.6302 | −2.6020 | −2.6305 | −2.6305 | ||
| Mean | −9.5341 | −8.8857 | −8.2591 | −7.0685 | −9.4850 | ||
| Std | 2.3522 | 2.3709 | 2.9335 | 3.1409 | 2.0722 | ||
| f22 | Best | −10.4029 | −10.4025 | −10.4009 | −10.4029 | −10.4029 | 1 |
| Worst | −10.3988 | −5.0876 | −1.8302 | −2.7519 | −3.7243 | ||
| Mean | −10.4015 | −10.2239 | −7.4542 | 3.1828 | −10.1803 | ||
| Std | 0.0011 | 0.9701 | 3.0686 | −8.2324 | 1.2193 | ||
| f23 | Best | −10.5364 | −10.5360 | −10.5363 | −10.5364 | −10.5364 | 1 |
| Worst | −10.5303 | −2.4217 | −1.6447 | −2.4217 | −2.8711 | ||
| Mean | −10.5348 | −10.2638 | −6.9538 | −9.5065 | −10.0575 | ||
| Std | 0.0015 | 1.4811 | 3.7470 | 2.3863 | 1.8268 |
| Functions | APO Versus GWO | APO Versus WOA | APO Versus PSO | APO Versus DE |
|---|---|---|---|---|
| f1 | 1.7344 | 1.7344 | 1.7344 | 1.7344 |
| f2 | 1.7344 | 1.7344 | 1.7344 | 1.7344 |
| f3 | 1.7344 | 1.7344 | 1.7344 | 1.7344 |
| f4 | 0.0039 | 1.7344 | 1.7344 | 1.7344 |
| f5 | 6.6392 | 0.1156 | 8.4661 | 0.0018 |
| f6 | 1.7344 | 1.7344 | 5.7517 | 1.6046 |
| f7 | 2.4118 | 1.6046 | 1.7344 | 1.7344 |
| f8 | 1.7344 | 1.7344 | 1.7344 | 1.7344 |
| f9 | 1.7224 | 1 | 1.7344 | 1.7344 |
| f10 | 1.6521 | 0.0623 | 1.7344 | 1.7344 |
| f11 | 0.5000 | 0.1250 | 1.7344 | 1.7344 |
| f12 | 1.7344 | 1.7344 | 0.0132 | 5.2165 |
| f13 | 1.7344 | 1.7344 | 2.1266 | 1.7344 |
| f14 | 0.5440 | 0.0519 | 0.2059 | 1.7344 |
| f15 | 0.0859 | 4.1955 | 0.0028 | 0.0859 |
| f16 | 1.0570 | 0.0786 | 1.7344 | 1.7344 |
| f17 | 8.9443 | 6.9838 | 1.7344 | 1.7344 |
| f18 | 1.9209 | 1.4936 | 1.7344 | 1.7344 |
| f19 | 0.8936 | 0.5577 | 1.7344 | 1.7344 |
| f20 | 0.5038 | 0.2134 | 0.0285 | 0.8130 |
| f21 | 0.0013 | 1.8910 | 0.0449 | 0.0018 |
| f22 | 0.0300 | 1.7344 | 0.6435 | 3.1123 |
| f23 | 0.0350 | 5.2165 | 0,0571 | 0.0350 |
| Number | Altitude (m) | Center Location (x,y)/(km) | Slope |
|---|---|---|---|
| 1 | 130 | (56,82) | (10,10) |
| 2 | 150 | (75,20) | (10,10) |
| 3 | 300 | (50,45) | (12,12) |
| 4 | 100 | (22,20) | (8,8) |
| 5 | 150 | (20,70) | (8,8) |
| 6 | 150 | (77,73) | (10,10) |
| Number | Start Point | Target Point |
|---|---|---|
| 1 | (1,1,0) | (100,30,70) |
| 2 | (1,30,0) | (100,40,70) |
| 3 | (1,60,0) | (100,50,70) |
| Number | Range (km) | Flight Time (s) |
|---|---|---|
| 1 | 110.9405 | [1849.0089, 2773.5134] |
| 2 | 102.1812 | [1703.0205, 2554.5307] |
| 3 | 102.259 | [1704.3164, 2556.4746] |
| Number | Start Point | Target Point |
|---|---|---|
| 1 | (1,1,0) | (90,40,100) |
| 2 | (1,30,0) | (95,40,100) |
| 3 | (1,55,0) | (95,85,100) |
| 4 | (1,90,0) | (80,85,100) |
| Number | Range (km) | Flight Time (s) |
|---|---|---|
| 1 | 117.7185 | [1961.975, 2942.9626] |
| 2 | 99.8391 | [1663.9855, 2495.9783] |
| 3 | 106.0902 | [1768.1699, 2652.2548] |
| 4 | 97.3108 | [1621.8469, 2432.7704] |
| Number | Start Point | Target Point |
|---|---|---|
| 1 | (1,1,0) | (99,10,70) |
| 2 | (1,20,0) | (99,18,70) |
| 3 | (1,40,0) | (99,30,70) |
| 4 | (1,60,0) | (99,40,70) |
| 5 | (1,75,0) | (99,70,70) |
| 6 | (1,90,0) | (99,90,70) |
| Number | Range (km) | Flight Time(s) |
|---|---|---|
| 1 | 99.2486 | [1654.1433, 2481.215] |
| 2 | 104.8832 | [1748.0538, 2622.0807] |
| 3 | 115.4467 | [1924.111, 2886.1664] |
| 4 | 110.7951 | [1846.5853, 2769.8779] |
| 5 | 104.5509 | [1742.5156, 2613.7734] |
| 6 | 100.002 | [1666.7006, 2500.0509] |
| Number | Start Point | Target Point |
|---|---|---|
| 1 | (1,1,0) | (99,10,70) |
| 2 | (1,15,0) | (99,10,70) |
| 3 | (1,30,0) | (99,32,70) |
| 4 | (1,40,0) | (99,32,70) |
| 5 | (1,55,0) | (99,68,70) |
| 6 | (1,70,0) | (99,68,70) |
| 7 | (1,80,0) | (99,85,70) |
| 8 | (1,95,0) | (99,85,70) |
| Number | Range (km) | Flight Time (s) |
|---|---|---|
| 1 | 99.7531 | [1662.5517, 2493.8276] |
| 2 | 100.9139 | [1681.8984, 2522.8476] |
| 3 | 115.3703 | [1922.8382, 2884.2573] |
| 4 | 101.3747 | [1689.5775, 2534.3663] |
| 5 | 101.0788 | [1684.6466, 2526.97] |
| 6 | 102.4978 | [1708.2963, 2562.4445] |
| 7 | 103.6654 | [1727.7567, 2591.635] |
| 8 | 100.3576 | [1672.6264, 2508.9396] |
| Algorithms | Parameter Settings |
|---|---|
| APO | a = 2 − t*2/T |
| GWO, HGWO, IGWO | a = 2 − t*2/T |
| PSO | wmax = 0.9, wmin = 0.2, c1 = c2 = 2 |
| DE | F = 0.5, CR = 0.9 |
| Case | APO | GWO | HGWO | IGWO | PSO | DE |
|---|---|---|---|---|---|---|
| 1 | 5.1268 | 5.6972 | 7.1175 | 56.6774 | 14.0171 | 27.2034 |
| 2 | 7.5716 | 8.1782 | 9.9407 | 64.2276 | 19.2131 | 38.6358 |
| 3 | 12.7386 | 12.4842 | 15.829 | 65.7687 | 33.3886 | 61.1923 |
| 4 | 18.7229 | 18.8581 | 21.8224 | 81.9172 | 45.57 | 81.6728 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, P.; Yang, L.; Liu, Y.; Lu, Y.; Zhu, X. Novel Swarm Intelligence Algorithm for Global Optimization and Multi-UAVs Cooperative Path Planning: Anas Platyrhynchos Optimizer. Appl. Sci. 2020, 10, 4821. https://doi.org/10.3390/app10144821
Zhang Y, Wang P, Yang L, Liu Y, Lu Y, Zhu X. Novel Swarm Intelligence Algorithm for Global Optimization and Multi-UAVs Cooperative Path Planning: Anas Platyrhynchos Optimizer. Applied Sciences. 2020; 10(14):4821. https://doi.org/10.3390/app10144821
Chicago/Turabian StyleZhang, Yong, Pengfei Wang, Liuqing Yang, Yanbin Liu, Yuping Lu, and Xiaokang Zhu. 2020. "Novel Swarm Intelligence Algorithm for Global Optimization and Multi-UAVs Cooperative Path Planning: Anas Platyrhynchos Optimizer" Applied Sciences 10, no. 14: 4821. https://doi.org/10.3390/app10144821
APA StyleZhang, Y., Wang, P., Yang, L., Liu, Y., Lu, Y., & Zhu, X. (2020). Novel Swarm Intelligence Algorithm for Global Optimization and Multi-UAVs Cooperative Path Planning: Anas Platyrhynchos Optimizer. Applied Sciences, 10(14), 4821. https://doi.org/10.3390/app10144821





