Reliability Evaluation of Hinged Slab Bridge Considering Hinge Joints Damage and Member Failure Credibility
Abstract
:1. Introduction
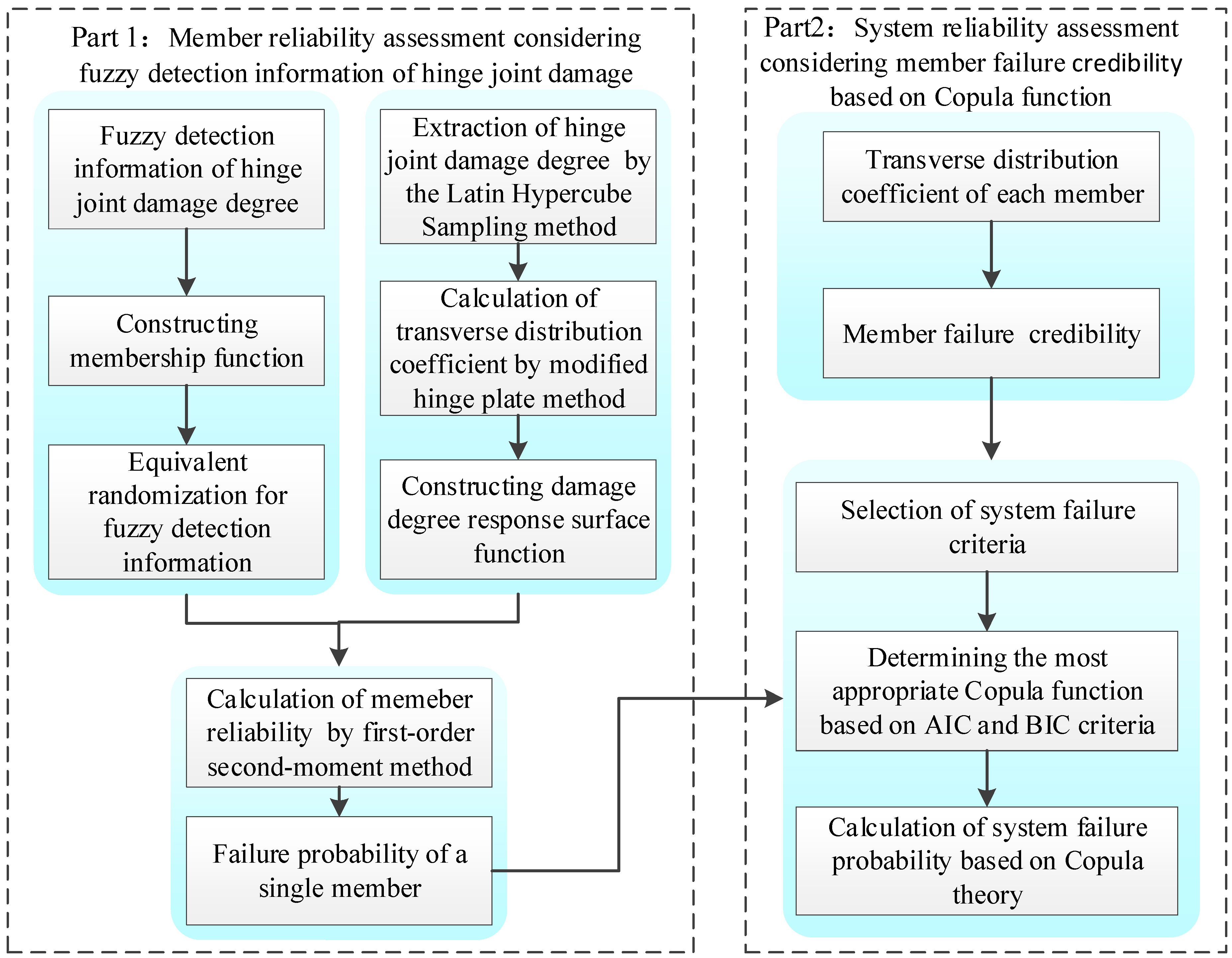
2. Member Reliability Evaluation Method of Considering Fuzzy Detection Information of Hinge Joints Damage
2.1. Fuzzy Detection Information Expression of Hinge Joints Damage Degree
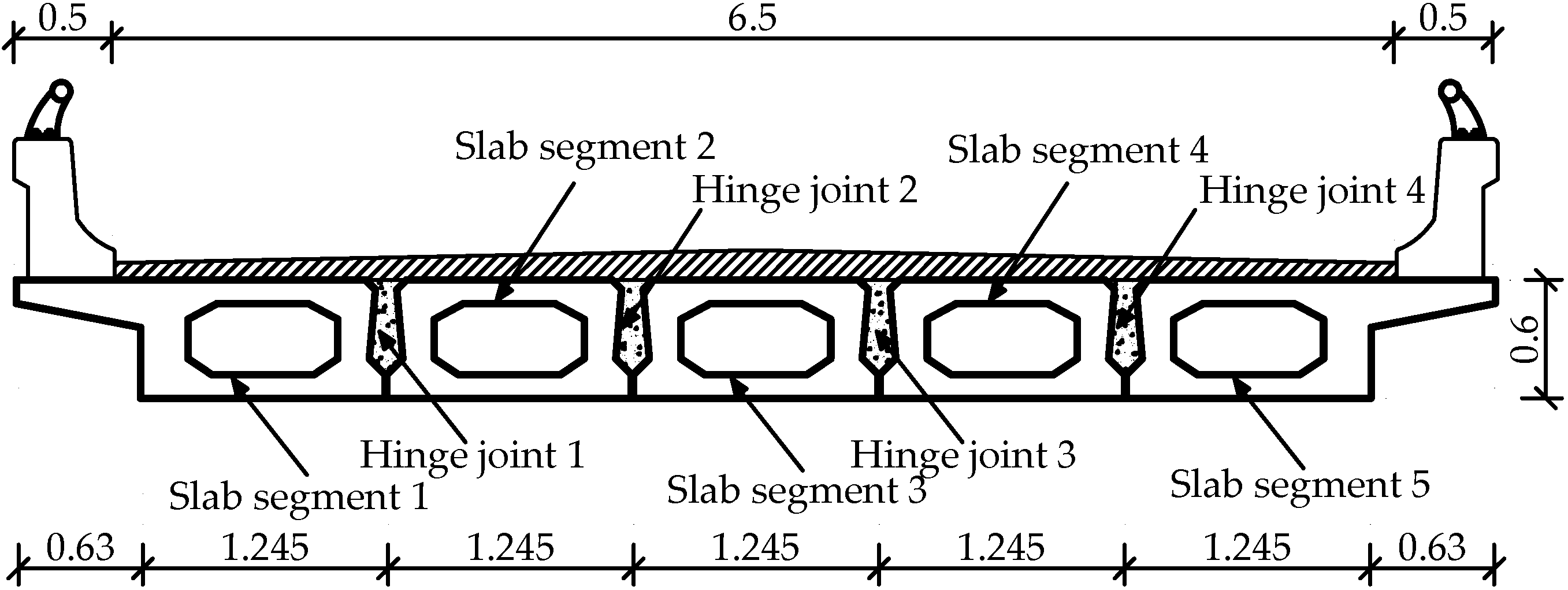
2.2. Calculation of Transverse Distribution Coefficient Based on Damage Degree Response Surface Function
2.3. Reliability Assessment of Individual Members
3. System Reliability Evaluation Method Considering Member Failure Credibility
4. Numerical Simulation
4.1. Member Reliability Analysis
4.2. System Reliability Analysis
5. Conclusions
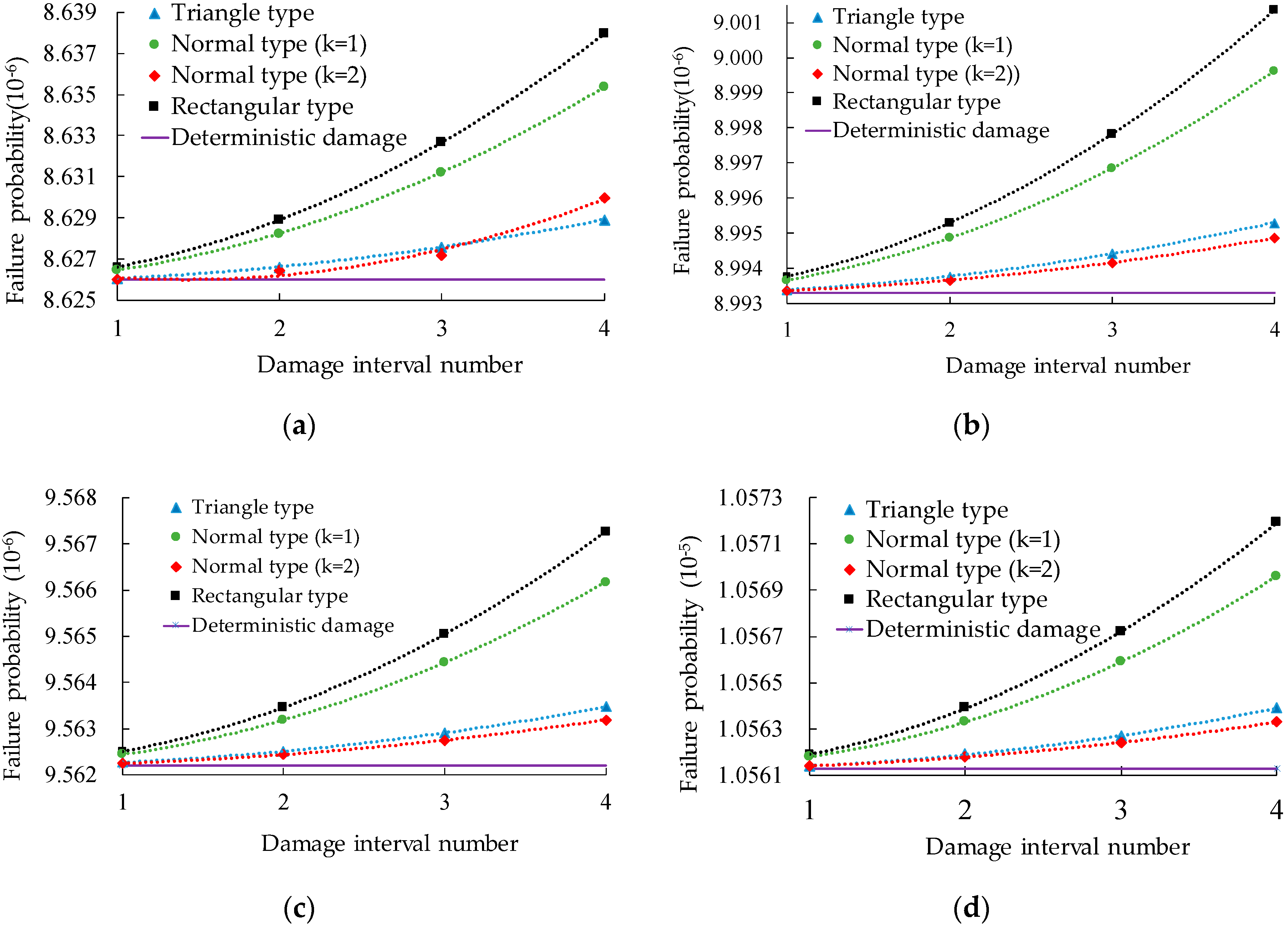
- Triangle, normal, and rectangle membership functions in fuzzy theory are used to express the damage degree of hinge joints in this paper, and the damage degree of hinge joints is transformed into a random variable. Numerical examples show that the equivalent randomization method of the membership function proposed is feasible.
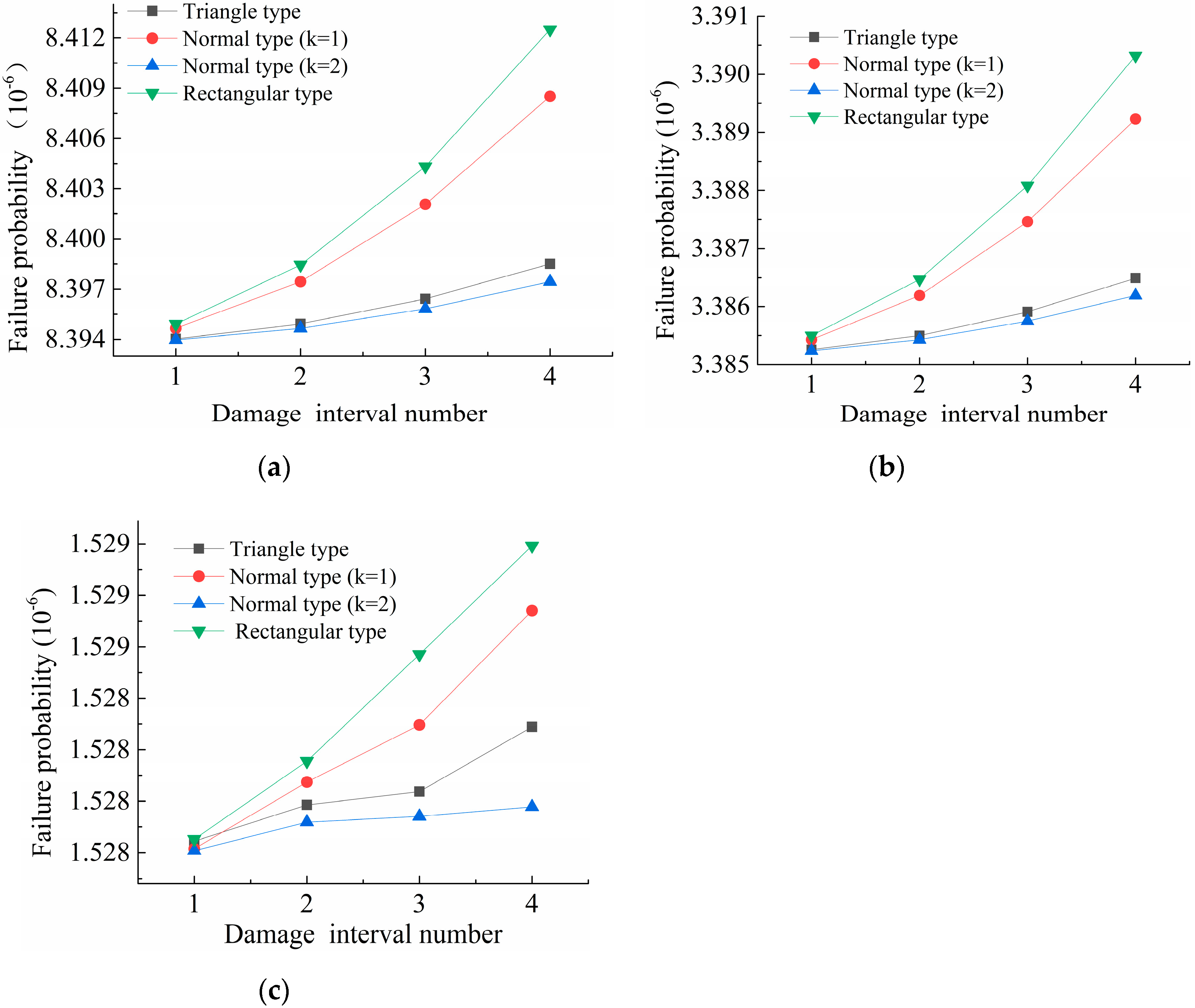
- When different membership functions are used to express the damage interval, the change rate of failure probability varies greatly with the increase in the damage interval. With the reduction in the damage interval, the failure probability corresponding to the three membership functions is closer to the failure probability corresponding to the deterministic hinge joint damage degree, which indicates that the reliability evaluation method considering the fuzzy detection information of hinge joint damage proposed in this paper conforms to the objective law, and the rationality and accuracy of the method are verified.
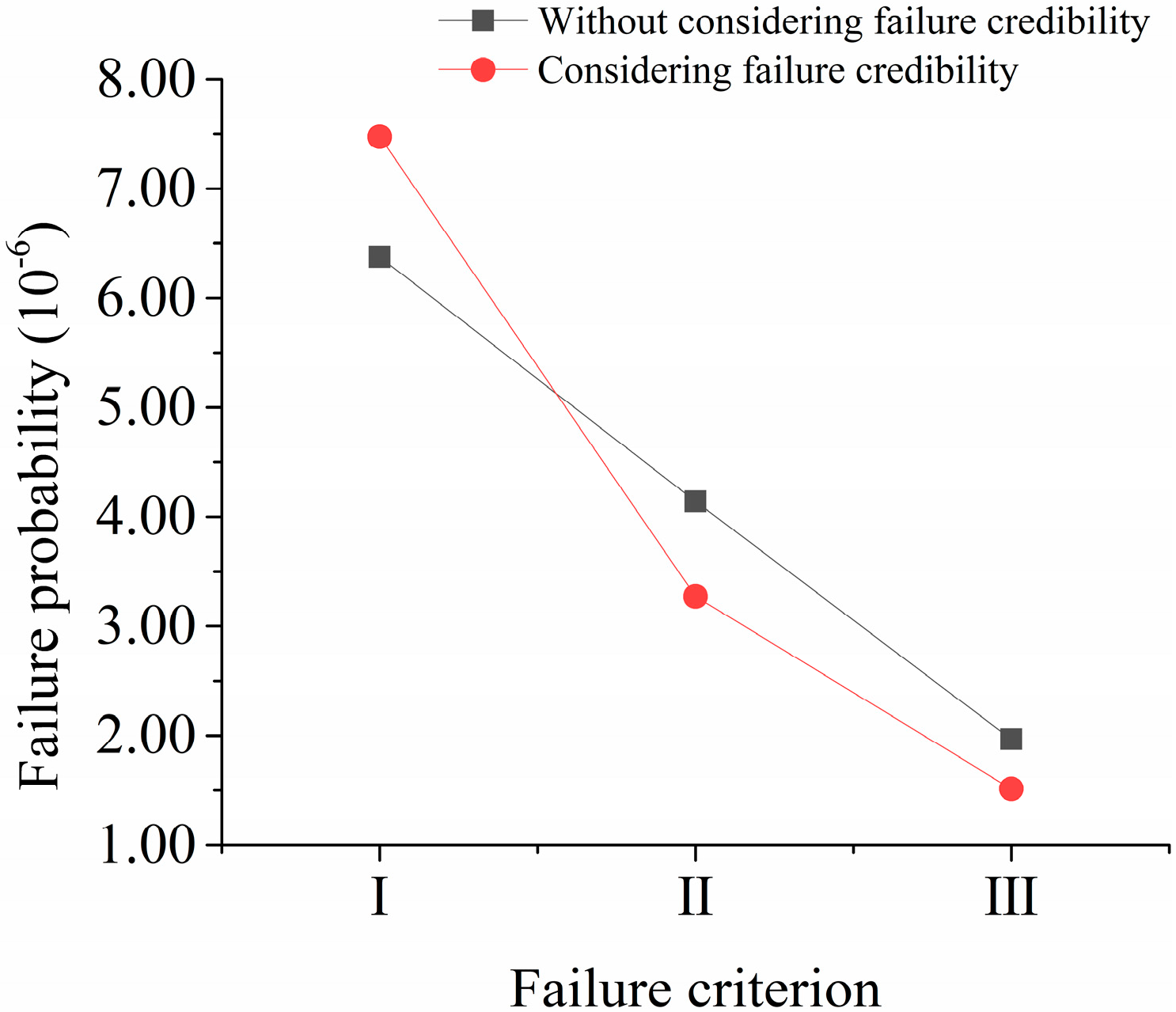
- There is a deviation in the joint failure probability between considering member failure credibility and without considering member failure credibility under different criteria calculated based on Copula theory, and member failure credibility has an impact on the system reliability. Therefore, it is meaningful to consider the failure credibility in the system reliability evaluation method.
- Furthermore, on the basis of this study, the authors will carry out the fragility analysis and reliability evaluation method of medium- and small-span bridges under natural disasters (earthquakes, floods).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dey, A.; Miyani, G.; Sil, A. Reliability assessment of reinforced concrete (RC) bridges due to service loading. Innov. Infrastruct. Solut. 2019, 4, 9. [Google Scholar] [CrossRef]
- Li, Q.; Wang, C.; Ellingwood, B.R. Time-dependent reliability of aging structures in the presence of non-stationary loads and degradation. Struct. Saf. 2015, 52, 132–141. [Google Scholar] [CrossRef]
- Pagnoncelli, A.P.; Miguel, L.F. Methodology to Obtain Dynamic Response of Road Bridges Considering Bridge–Vehicle Interactions. Pract. Period. Struct. Des. Constr. 2019, 24, 04019010. [Google Scholar] [CrossRef]
- Matin, A.; Elias, S.; Matsagar, V. Distributed multiple tuned mass dampers for seismic response control in bridges. Proc. Inst. Civ. Eng. -Struct. Build. 2020, 173, 217–234. [Google Scholar] [CrossRef]
- Hou, G.; Chen, S. Bent Connection Options for Curved and Skewed SMC Bridges in Low-to-Moderate Seismic Regions. Pract. Period. Struct. Des. Constr. 2017, 22, 04017011. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Effectiveness of tuned mass dampers in seismic response control of isolated bridges including soil-structure interaction. Lat. Am. J. Solids Struct. 2017, 14, 2324–2341. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Chen, G. Method to compute live-load distribution in bridge girders. Pract. Period. Struct. Des. Constr. 2011, 16, 191–198. [Google Scholar] [CrossRef]
- Saydam, D.; Frangopol, D.M. Risk-Based Maintenance Optimization of Deteriorating Bridges. J. Struct. Eng. 2015, 141, 04014120. [Google Scholar] [CrossRef]
- Xie, H.B.; Wu, W.J.; Wang, Y.F. Life-time reliability based optimization of bridge maintenance strategy considering LCA and LCC. J. Clean. Prod. 2018, 176, 36–45. [Google Scholar] [CrossRef]
- Ghodoosi, F.; Abu-Samra, S.; Zeynalian, M.; Zayed, T. Maintenance Cost Optimization for Bridge Structures Using System Reliability Analysis and Genetic Algorithms. J. Constr. Eng. Manag. 2018, 144, 04017116. [Google Scholar] [CrossRef]
- Pipinato, A.; Modena, C. Structural analysis and fatigue reliability assessment of the Paderno bridge. Pract. Period. Struct. Des. Constr. 2010, 15, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Mahamid, M.; Ozevin, D.; Torra-Bilal, I.; Kabir, M.; Mastny, S.; Khudeira, S.; Sauter, B.W.; Zroka, D. Structural Design and Inspectability of Highway Bridges. Pract. Period. Struct. Des. Constr. 2019, 24, 06019002. [Google Scholar] [CrossRef]
- Wang, H.; Xie, C.; Liu, D.; Qin, S. Continuous Reinforced Concrete Rigid-Frame Bridges in China. Pract. Period. Struct. Des. Constr. 2019, 24, 05019002. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, H.; Zuo, Z.; Sirotiak, T.L.; Yang, M. Optimal Steel Section Length of the Composite Rigid-Frame Bridge. Pract. Period. Struct. Des. Constr. 2018, 23, 05018001. [Google Scholar] [CrossRef]
- Schneider, R.; Thöns, S.; Straub, D. Reliability analysis and updating of deteriorating systems with subset simulation. Struct. Saf. 2017, 64, 20–36. [Google Scholar] [CrossRef] [Green Version]
- Ghasemi, S.H.; Nowak, A.S. Target reliability for bridges with consideration of ultimate limit state. Eng. Struct. 2017, 152, 226–237. [Google Scholar] [CrossRef]
- Brunesi, E.; Parisi, F. Progressive collapse fragility models of European reinforced concrete framed buildings based on pushdown analysis. Eng. Struct. 2017, 152, 579–596. [Google Scholar] [CrossRef]
- Carroll, C.; Juneau, A. Repair of Concrete Bridge Deck Expansion Joints Using Elastomeric Concrete. Pract. Period. Struct. Des. Constr. 2015, 20, 04014038. [Google Scholar] [CrossRef]
- Wei, Y.; Bai, G.; Song, L.; Bai, B. The Estimation of Reliability Probability of Structures based on Improved Iterative Response Surface Methods. KSCE J. Civ. Eng. 2019, 23, 4063–4074. [Google Scholar] [CrossRef]
- Lee, Y.J.; Lee, S.H.; Lee, H.S. Reliability Assessment of Tie-Down Cables for Cable-Stayed Bridges Subject to Negative Reactions: Case Study. J. Bridge Eng. 2015, 20, 04014108. [Google Scholar] [CrossRef]
- Cho, T.; Lee, J.B.; Kim, S.S. Probabilistic Risk Assessment for the Construction Phases of a PSC Box Girder Railway Bridge System with Six Sigma Methodology. KSCE J. Civ. Eng. 2011, 15, 119–130. [Google Scholar] [CrossRef]
- An, X.; Gosling, P.D.; Zhou, X. Analytical structural reliability analysis of a suspended cable. Struct. Saf. 2016, 58, 20–30. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Xiao, R.; He, L. Reliability assessment of large-span cable-stayed bridges based on artificial intelligence. China Civ. Eng. J. 2007, 40, 41–48. [Google Scholar]
- Gholipour, G.; Zhang, C.; Kang, W.-H.; Mousavi, A.A. Reliability analysis of girder bridge piers subjected to barge collisions. Struct. Infrastruct. Eng. 2019, 15, 1200–1220. [Google Scholar] [CrossRef]
- Castaldo, P.; Palazzo, B.; Mariniello, A. Effects of the axial force eccentricity on the time-variant structural reliability of aging r.c. cross-sections subjected to chloride-induced corrosion. Eng. Struct. 2017, 130, 261–274. [Google Scholar] [CrossRef]
- Fiorillo, G.; Ghosn, M. MPI Parallel Monte Carlo Framework for the Reliability Analysis of Highway Bridges. J. Comput. Civ. Eng. 2018, 32, 04017087. [Google Scholar] [CrossRef]
- Wong, F.S. Slope Reliability and Response Surface Method. J. Geotech. Eng. 1985, 111, 32–53. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, S.; Chakraborty, S. Seismic reliability analysis of reinforced concrete bridge pier using efficient response surface method-based simulation. Adv. Struct. Eng. 2018, 21, 2326–2339. [Google Scholar] [CrossRef]
- Yu, X.L.; Yan, Q.S. Reliability Analysis of Self-anchored Suspension Bridge by Improved Response Surface Method. Appl. Mech. Mater. 2011, 90–93, 869–873. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, S.; Jiang, F.; Soares, C.G. System Reliability Analysis of an Offshore Jacket Platform. J. Ocean Univ. China 2020, 19, 47–59. [Google Scholar] [CrossRef]
- Feng, Y. Enumerating significant failure modes of a structural system by using criterion methods. Comput Struct. 1988, 30, 1152–1157. [Google Scholar] [CrossRef]
- Lu, N.; Liu, Y.; Beer, M. System reliability evaluation of in-service cable-stayed bridges subjected to cable degradation. Struct. Infrastruct. Eng. 2018, 14, 1486–1498. [Google Scholar] [CrossRef]
- Gao, X.; Li, S.L. Dominant failure modes identification and structural system reliability analysis for a long-span arch bridge. Struct. Eng. Mech. 2017, 63, 799–808. [Google Scholar]
- Wang, H.; Zhang, X.; Li, Q.; Wang, G.; Jiang, H.; Peng, J. Recursive Method for Distribution System Reliability Evaluation. Energies 2018, 11, 2681. [Google Scholar] [CrossRef] [Green Version]
- Cornell, C.A. Bounds on the reliability of structural system. J. Struct. Div. 1967, 93, 171–200. [Google Scholar]
- Ditlevsen, O. Narrow reliability bounds for structural systems. Res Mech. 1979, 7, 453–472. [Google Scholar] [CrossRef]
- Ang, A.H.S.; Pires, J.A.; Villaverde, R. A model for the seismic reliability assessment of electric power transmission systems. Reliab. Eng. Syst. Saf. 1996, 51, 7–22. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, W.; Wang, B.; Han, X. Structural reliability analysis using a copula-function-based evidence theory model. Comput. Struct. 2014, 143, 19. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, X. Time-Independent Reliability Analysis of Bridge System Based on Mixed Copula Models. Math. Probl. Eng. 2016, 2016, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Anoop, M.B.; Rao, K.B. Performance evaluation of corrosion-affected reinforced concrete bridge girders using Markov chains with fuzzy states. Sādhanā 2016, 41, 887–899. [Google Scholar] [CrossRef] [Green Version]
- Andri, J.M.; Lu, D. Risk assessment of bridges under multiple hazards in operation period. Saf. Sci. 2016, 83, 80–92. [Google Scholar] [CrossRef]
- Wang, L.; Ma, Y.; Zhang, J.; Zhang, X.; Liu, Y. Uncertainty Quantification and Structural Reliability Estimation Considering Inspection Data Scarcity. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A: Civ. Eng. 2015, 1, 04015004. [Google Scholar] [CrossRef]
- Adam, C.; Heuer, R.; Ziegler, F. Reliable dynamic analysis of an uncertain compound bridge under traffic loads. Acta Mech. 2012, 223, 1567–1581. [Google Scholar] [CrossRef]
- Malekly, H.; Mousavi, S.M.; Hashemi, H. A fuzzy integrated methodology for evaluating conceptual bridge design. Expert Syst. Appl. 2010, 37, 4910–4920. [Google Scholar] [CrossRef]
- Lu, H.; Zhu, Z. A method for estimating the reliability of structural systems with moment-matching and copula concept. Mech. Based Des. Struct. Mach. 2018, 46, 196–208. [Google Scholar] [CrossRef]
- Liu, H.B.; He, X.; Jiao, Y.B. Damage Identification Algorithm of Hinged Joints for Simply Supported Slab Bridges Based on Modified Hinge Plate Method and Artificial Bee Colony Algorithms. Algorithms 2018, 11, 198. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.B.; Wang, X.R.; Tan, G.J.; He, X.; Luo, G.B. System Reliability Evaluation of Prefabricated RC Hollow Slab Bridges Considering Hinge Joint Damage Based on Modified AHP. Appl. Sci. 2019, 9, 4841. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.B.; Wang, X.R.; Tan, G.J.; He, X. System Reliability Evaluation of a Bridge Structure Based on Multivariate Copulas and the AHP–EW Method That Considers Multiple Failure Criteria. Appl. Sci. 2020, 10, 1399. [Google Scholar] [CrossRef] [Green Version]
- CCCC Highway Consultants CO., Ltd. General Specifications for Design of Highway Bridges and Culverts; Ministry of Communications of the People’s Republic of China: Beijing, China, 2015. (In Chinese) [Google Scholar]

| The Maximum Credibility is 20% | The Maximum Credibility is 40% | ||||
|---|---|---|---|---|---|
| Interval Number | Damage Range | Interval Number | Damage Range | Interval Number | Damage Range |
| 1 | [15–25%] | 1 | [35–45%] | 5 | [15–65%] |
| 2 | [10–30%] | 2 | [30–50%] | 6 | [10–70%] |
| 3 | [5–35%] | 3 | [25–55%] | 7 | [5–75%] |
| 4 | [0–40%] | 4 | [20–60%] | 8 | [0–80%] |
| Bel1 | Bel2 | Bel3 | Bel4 | Bel5 |
|---|---|---|---|---|
| 1.000 | 0.7793 | 0.7635 | 0.7793 | 1.000 |
| Gaussian | Clayton | Gumbel | Frank | |
|---|---|---|---|---|
| Z1Z2 | 0.9638 | 5.598 | 5.268 | 20.84 |
| Z1Z3 | 0.9635 | 5.567 | 5.319 | 20.72 |
| Z1Z4 | 0.9625 | 5.523 | 5.100 | 20.25 |
| Z1Z5 | 0.9567 | 5.22 | 4.84 | 19.13 |
| Z2Z3 | 0.9675 | 5.835 | 5.524 | 22.15 |
| Z2Z4 | 0.9673 | 6.02 | 5.484 | 21.58 |
| Z2Z5 | 0.9632 | 5.534 | 5.166 | 20.71 |
| Z3Z4 | 0.9664 | 5.76 | 5.516 | 21.64 |
| Z3Z5 | 0.9642 | 5.646 | 5.314 | 20.99 |
| Z4Z5 | 0.9647 | 6.011 | 5.23 | 21.00 |
| Z1Z2Z3 | 0.965 | 5.236 | 5.158 | 20.26 |
| Z2Z3Z4 | 0.9671 | 5.454 | 5.269 | 20.81 |
| Z3Z4Z5 | 0.9651 | 5.443 | 5.139 | 20.18 |
| Gaussian | Clayton | Gumbel | Frank | |||||
|---|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | AIC | BIC | |
| Z1Z2 | −2630.94 | −2626.03 | −2060.63 | −2055.73 | −2504.95 | −2500.04 | −2411.98 | −2407.07 |
| Z1Z3 | −2623.55 | −2618.64 | −2045.51 | −2040.60 | −2525.52 | −2520.62 | −2400.81 | −2395.90 |
| Z1Z4 | −2595.22 | −2590.31 | −2047.60 | −2042.70 | −2442.23 | −2437.33 | −2373.22 | −2368.32 |
| Z1Z5 | −2455.64 | −2450.73 | −1955.75 | −1950.84 | −2334.87 | −2329.96 | −2255.88 | −2250.97 |
| Z2Z3 | −2738.17 | −2733.26 | −2119.30 | −2114.39 | −2605.01 | −2600.11 | −2516.50 | −2511.59 |
| Z2Z4 | −2730.31 | −2725.40 | −2176.92 | −2172.01 | −2580.07 | −2575.16 | −2473.04 | −2468.13 |
| Z2Z5 | −2615.39 | −2610.48 | −2055.53 | −2050.62 | −2465.32 | −2460.41 | −2401.07 | −2396.16 |
| Z3Z4 | −2703.77 | −2698.86 | −2106.95 | −2102.05 | −2592.93 | −2588.02 | −2475.32 | −2470.41 |
| Z3Z5 | −2642.35 | −2637.45 | −2075.89 | −2070.98 | −2517.99 | −2513.08 | −2421.48 | −2416.57 |
| Z4Z5 | −2655.93 | −2651.02 | −2163.67 | −2158.76 | −2488.56 | −2483.65 | −2426.43 | −2421.52 |
| Z1Z2Z3 | −5603.47 | −5598.56 | −4338.82 | −4333.91 | −5315.29 | −5310.39 | −5121.51 | −5116.60 |
| Z2Z3Z4 | −5726.49 | −5721.59 | −4467.73 | −4462.83 | −5400.57 | −5395.66 | −5215.75 | −5210.84 |
| Z3Z4Z5 | −5611.87 | −5606.96 | −4455.50 | −4450.59 | −5280.78 | −5275.87 | −5106.59 | −5101.68 |
| Joint Failure Probability Pf,Bel | |||
|---|---|---|---|
| Z1Z2 | 1.069 × 10−6 | Z3Z4 | 5.604 × 10−7 |
| Z1Z3 | 9.316 × 10−7 | Z3Z5 | 9.347 × 10−7 |
| Z1Z4 | 1.062 × 10−6 | Z4Z5 | 1.074× 10−6 |
| Z1Z5 | 4.016 × 10−6 | Z1Z2Z3 | 5.438 × 10−7 |
| Z2Z3 | 5.679 × 10−7 | Z2Z3Z4 | 4.240 × 10−7 |
| Z2Z4 | 6.145 × 10−7 | Z3Z4Z5 | 5.445 × 10−7 |
| Z2Z5 | 1.066 × 10−6 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, G.; Kong, Q.; Wang, L.; Wang, X.; Liu, H. Reliability Evaluation of Hinged Slab Bridge Considering Hinge Joints Damage and Member Failure Credibility. Appl. Sci. 2020, 10, 4824. https://doi.org/10.3390/app10144824
Tan G, Kong Q, Wang L, Wang X, Liu H. Reliability Evaluation of Hinged Slab Bridge Considering Hinge Joints Damage and Member Failure Credibility. Applied Sciences. 2020; 10(14):4824. https://doi.org/10.3390/app10144824
Chicago/Turabian StyleTan, Guojin, Qingwen Kong, Longlin Wang, Xirui Wang, and Hanbing Liu. 2020. "Reliability Evaluation of Hinged Slab Bridge Considering Hinge Joints Damage and Member Failure Credibility" Applied Sciences 10, no. 14: 4824. https://doi.org/10.3390/app10144824





