A Novel Fiber Optic Sensor for Microparticle Velocity Measurement Using Multicore Fiber
Abstract
:1. Introduction
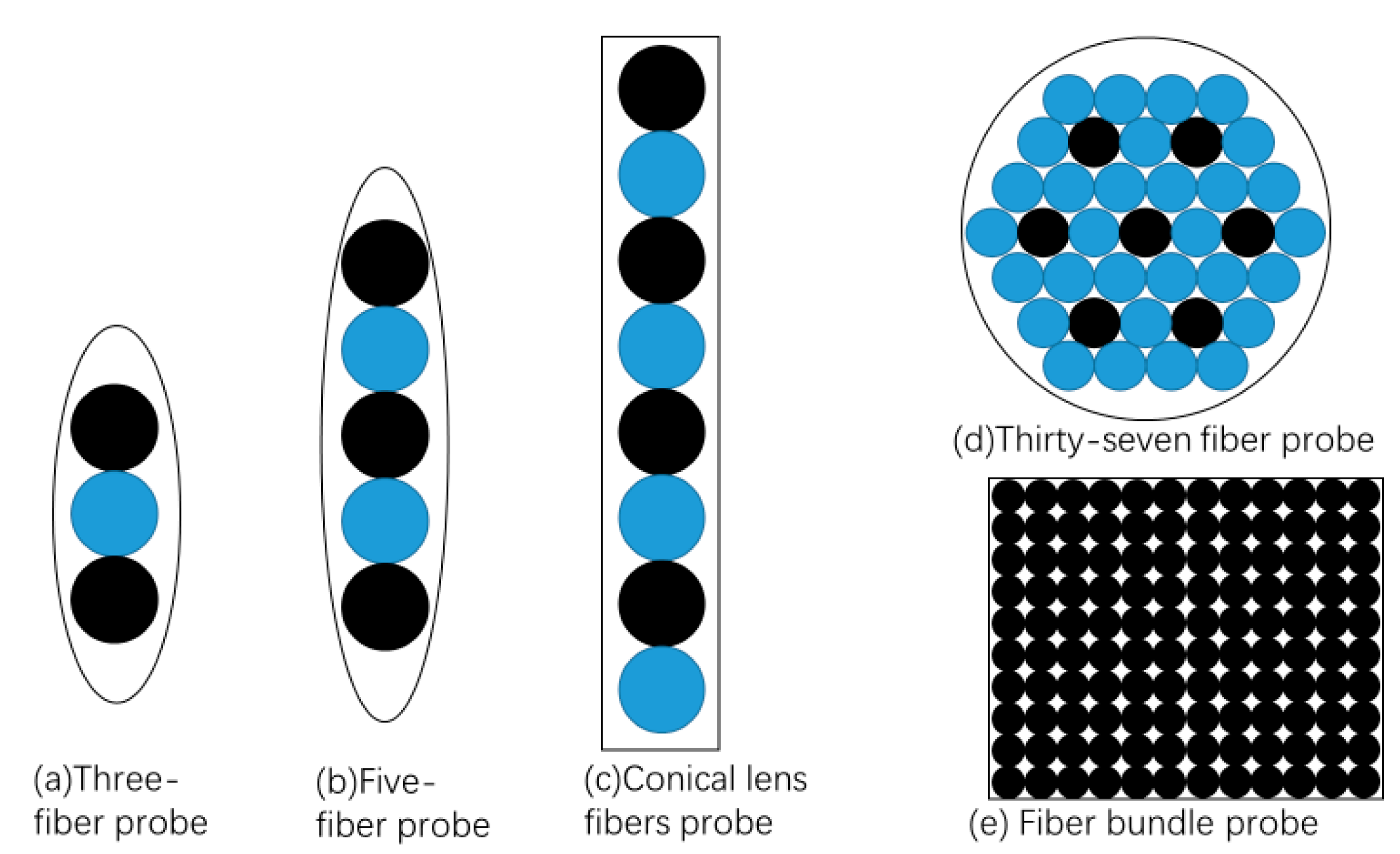
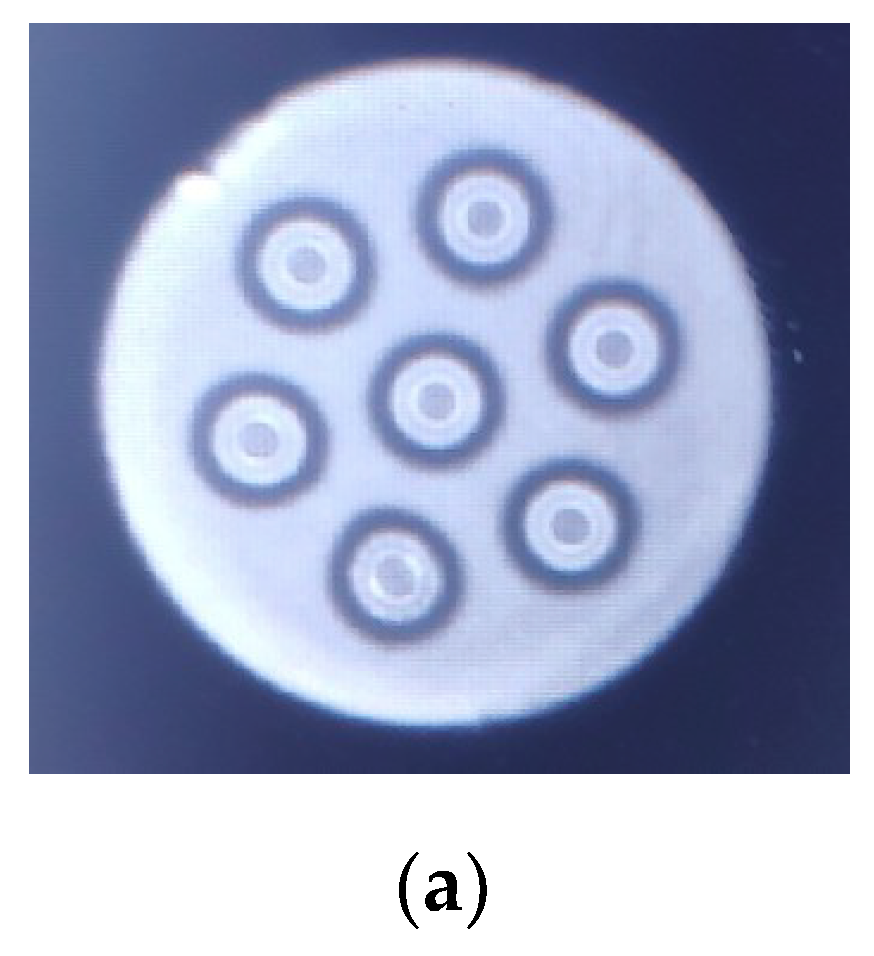
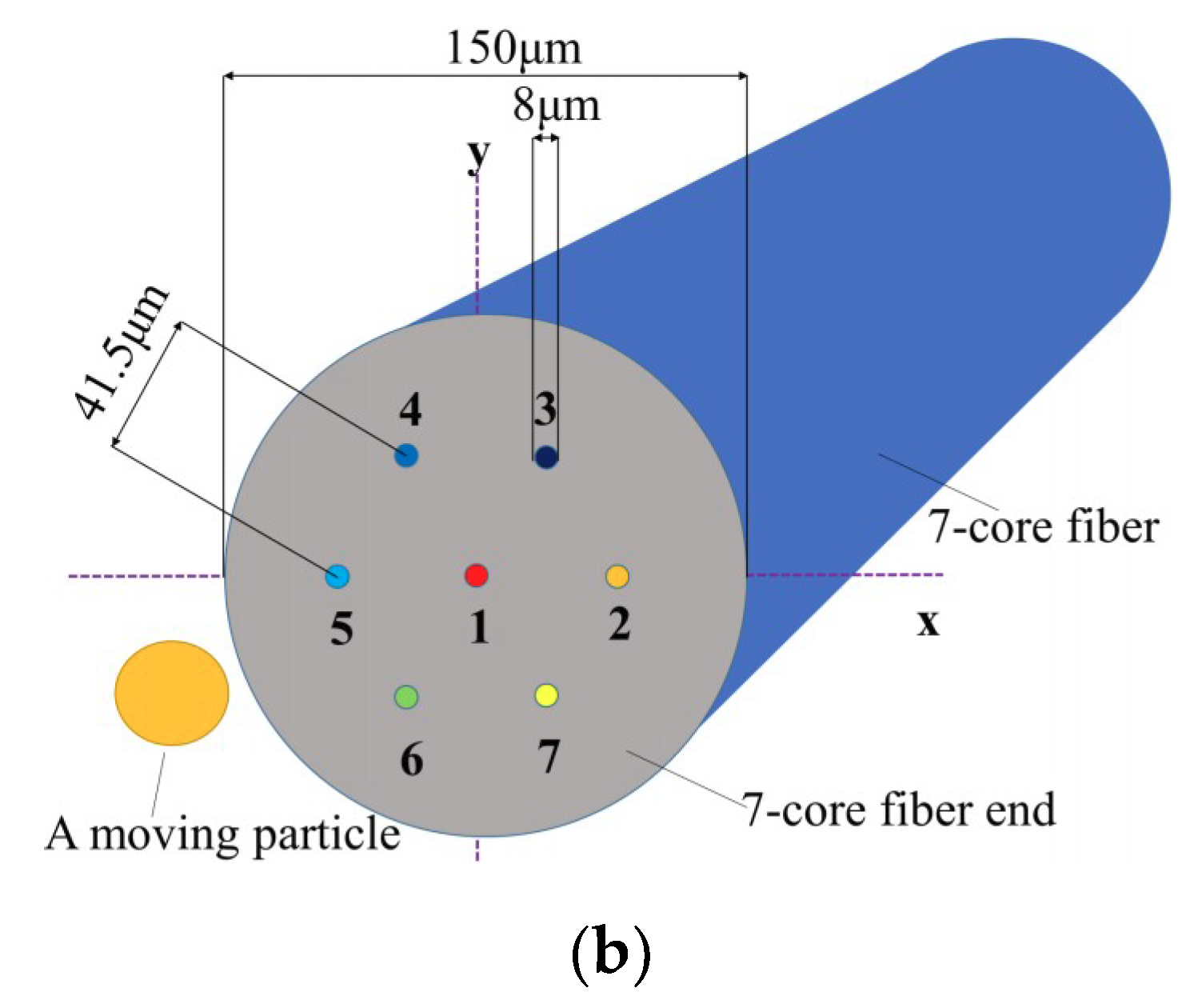
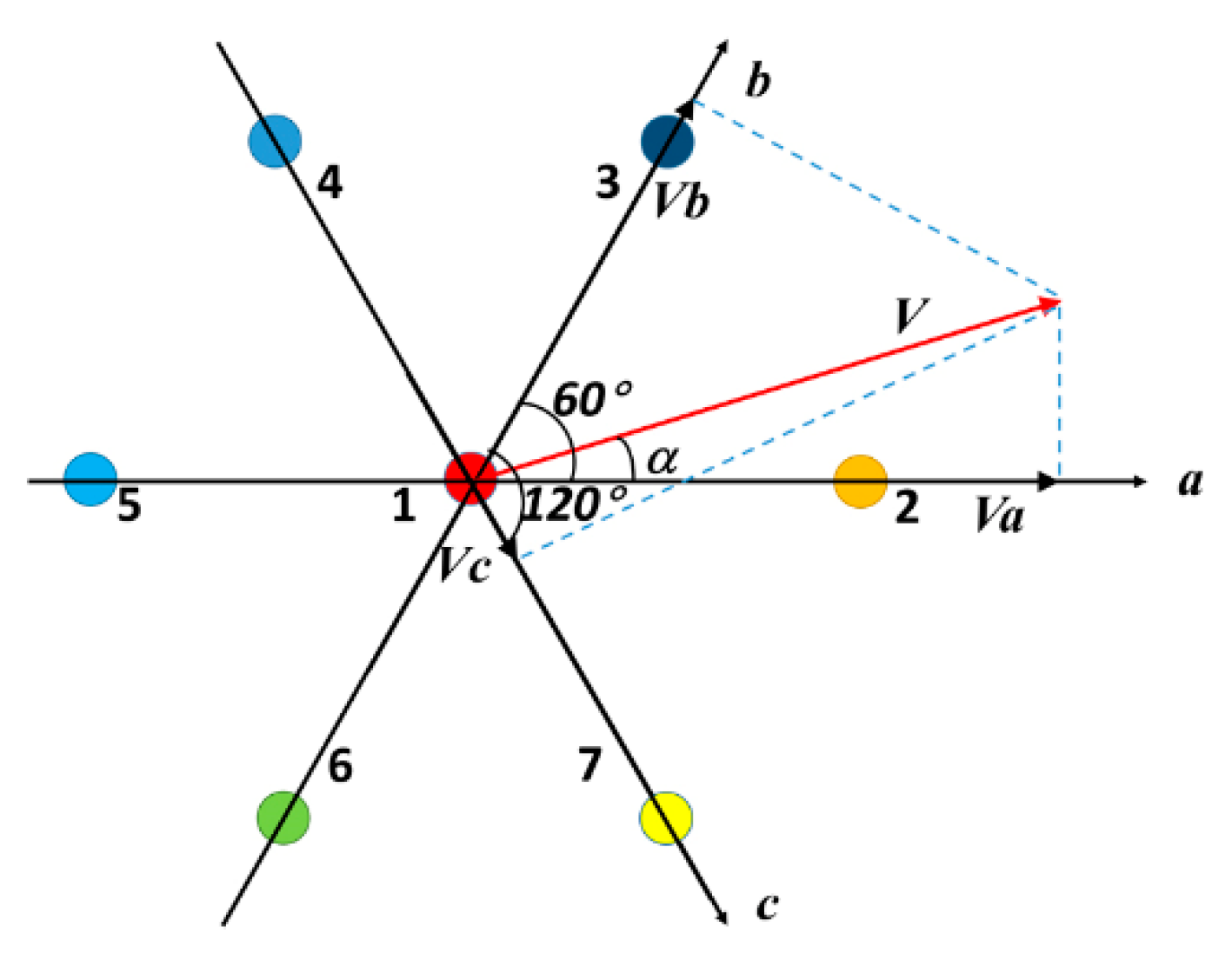
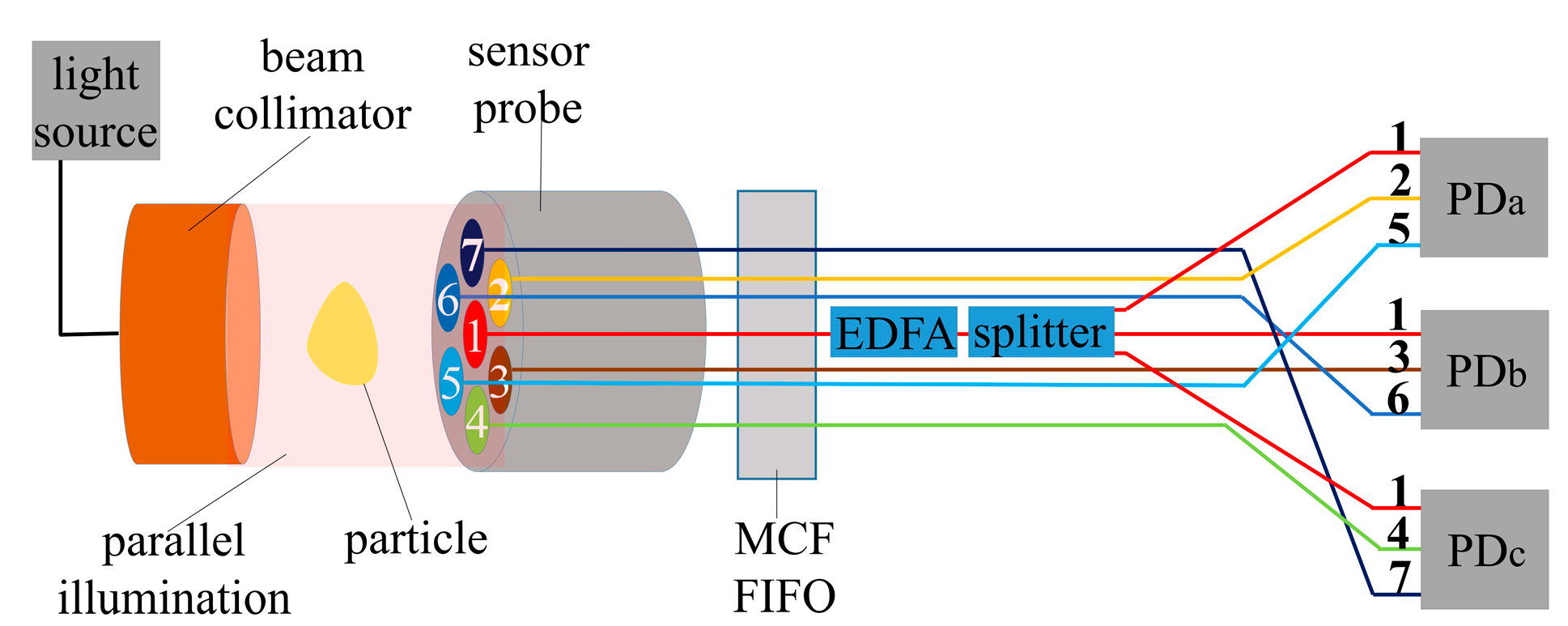
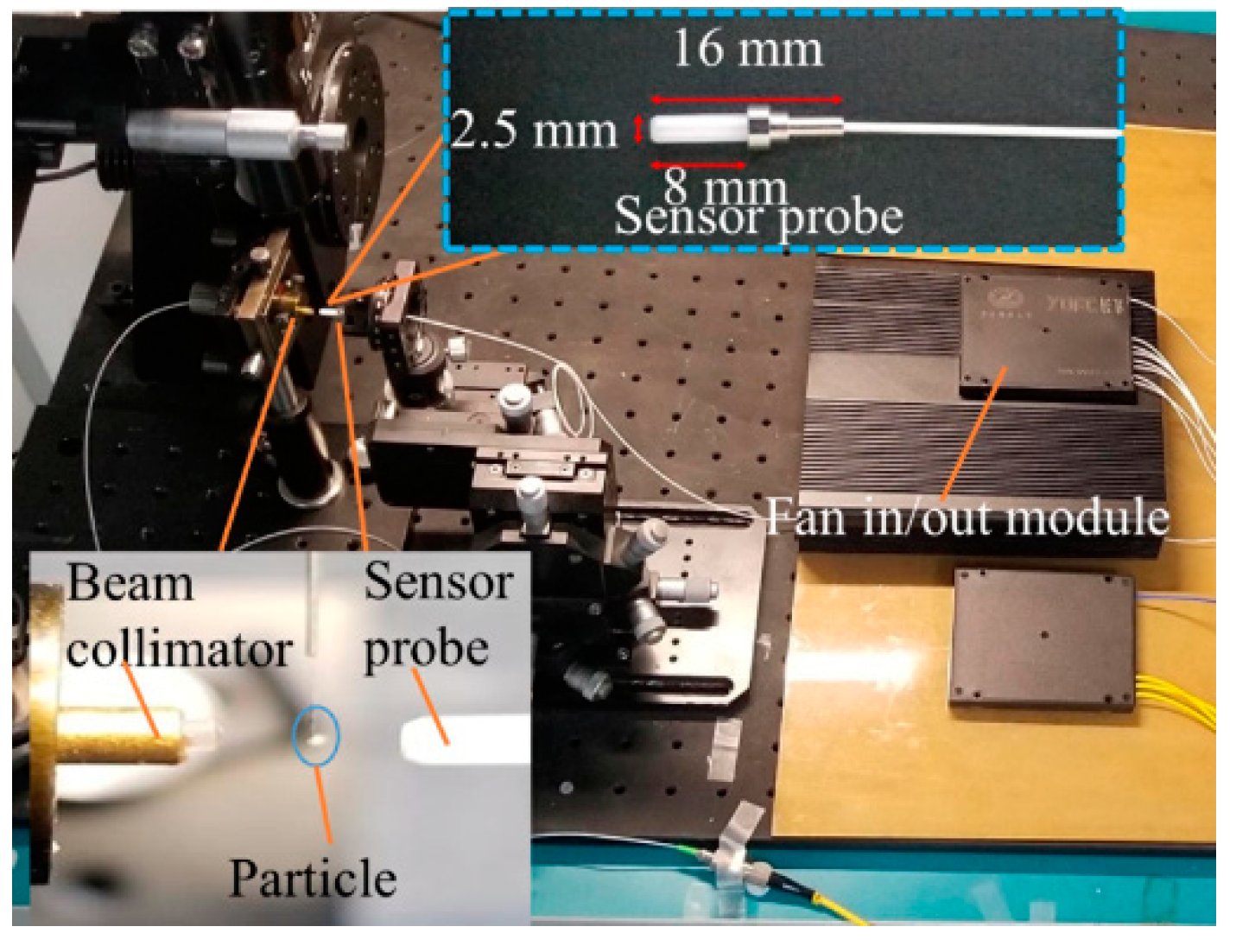
2. Materials and Methods
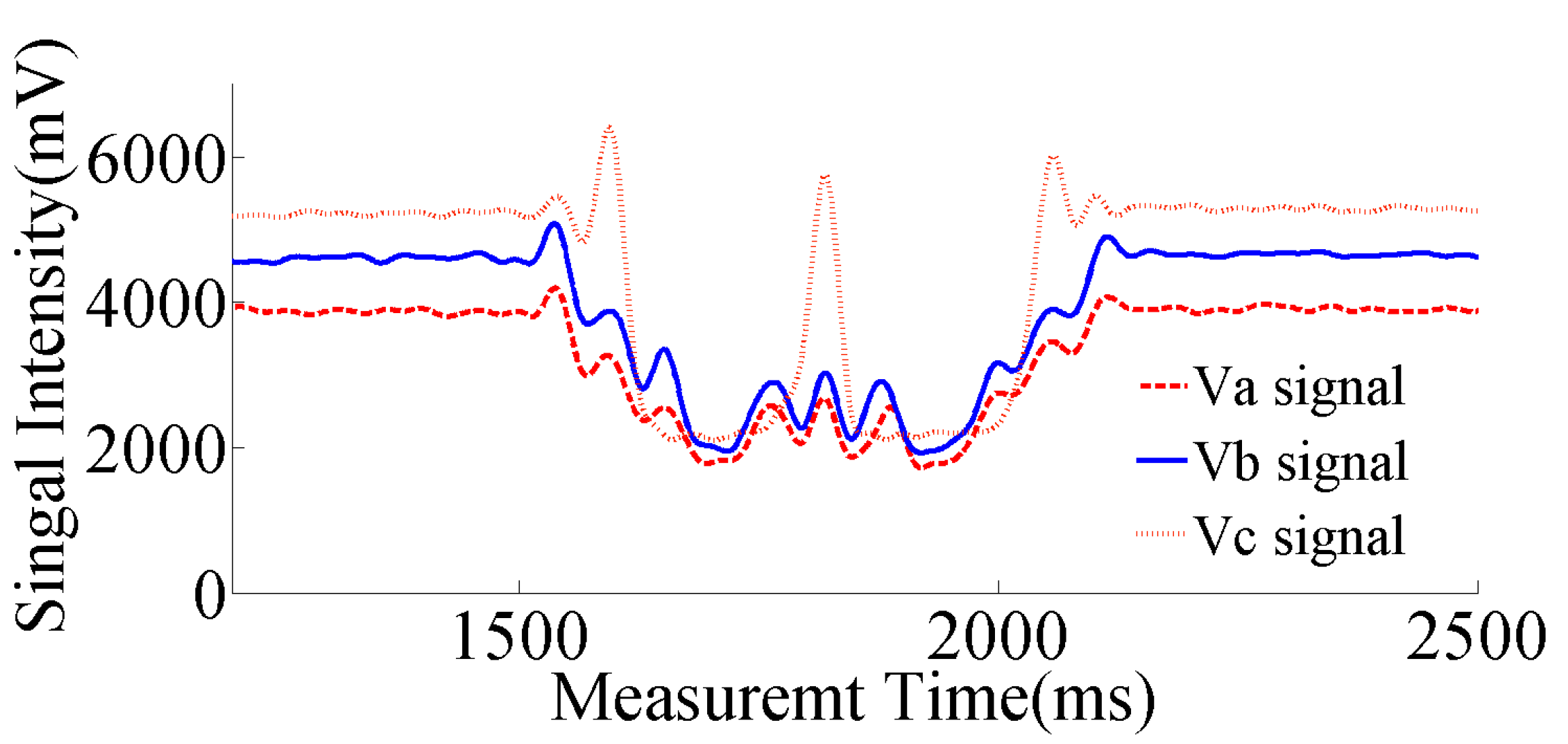
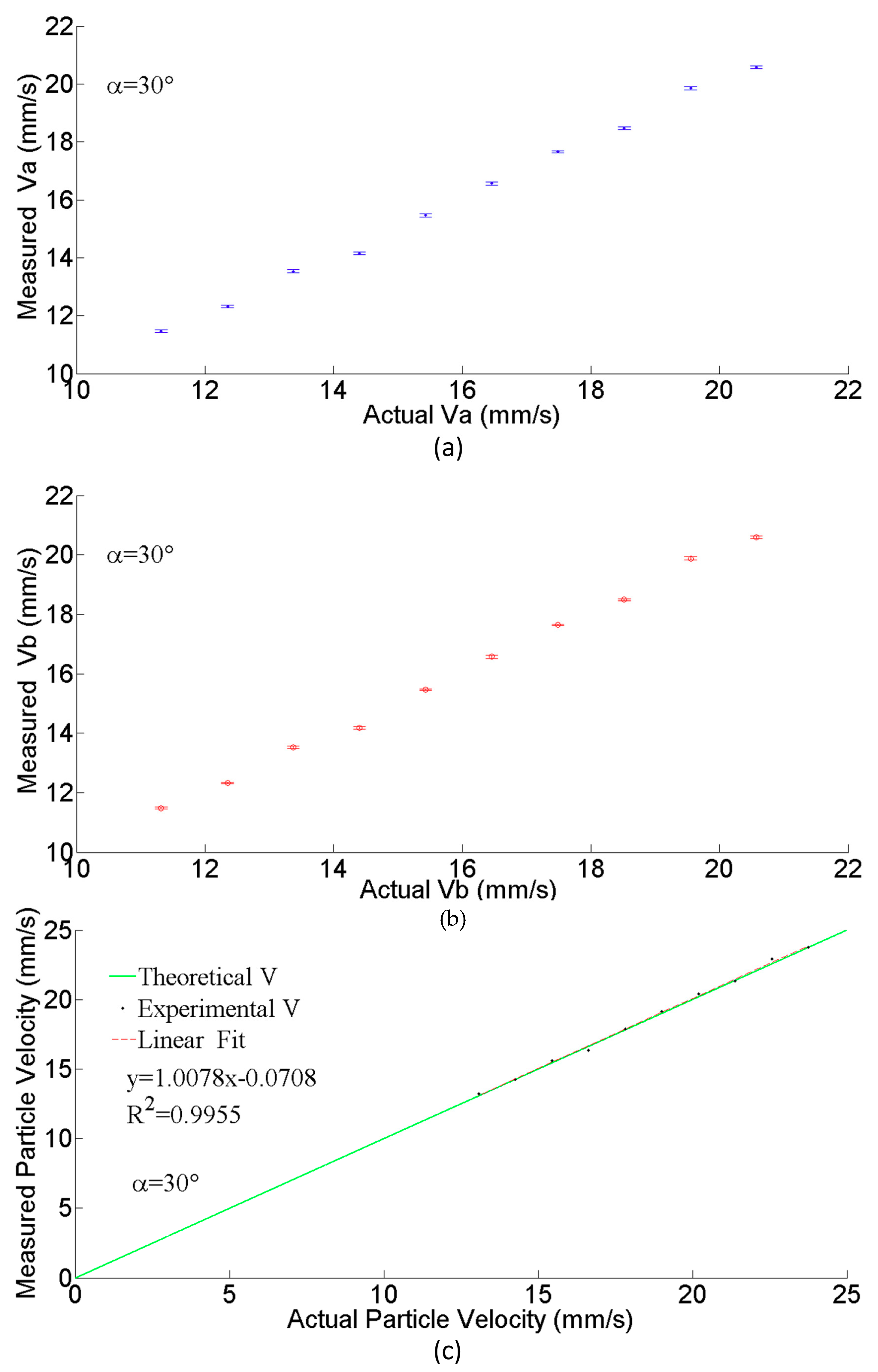
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shen, Z.; Cao, J.; Arimoto, R.; Han, Z.; Zhang, R.; Han, Y.; Liu, S.; Okuda, T.; Nakao, S.; Tanaka, S. Ionic composition of TSP and PM2.5 during dust storms and air pollution episodes at Xi’an, China. Atmos. Environ. 2009, 43, 2911–2918. [Google Scholar] [CrossRef]
- Dunn, A.K.; Bolay, H.; Moskowitz, M.A.; Boas, D.A. Dynamic imaging of cerebral blood flow using laser speckle. J. Cereb. Blood Flow Metab. 2001, 21, 195–201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ingolf, M.; Wild, W.; Aschemann, H. Real-time measurement of human blood flow with high temporal and spatial resolution. In Proceedings of the SPIE, San Jose, CA, USA, 14 February 2007; p. 644507. [Google Scholar] [CrossRef]
- Fan, L.; Gao, Y.; Hayakawa, A.; Hochgreb, S. Simultaneous, two-camera, 2d gas-phase temperature and velocity measurements by thermographic particle image velocimetry with ZnO tracers. Exp. Fluids 2017, 58, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Yang, X.; Fu, C.; Yang, Y.; Li, Z.; Zhang, H.; Qi, F. 10 kHz simultaneous PIV/PLIF study of the diffusion flame response to periodic acoustic forcing. Appl. Opt. 2019, 58, 112–120. [Google Scholar] [CrossRef] [PubMed]
- Ojo, A.O.; Fond, B.; Abram, C.; Van Wachem, B.G.; Heyes, A.L.; Beyrau, F. Thermographic laser Doppler velocimetry using the phase-shifted luminescence of BAM: Eu2+ phosphor particles for thermometry. Opt. Express 2017, 25, 11833–11843. [Google Scholar] [CrossRef] [PubMed]
- Fond, B.; Abram, C.; Heyes, A.L.; Kempf, A.M.; Beyrau, F. Simultaneous temperature, mixture fraction and velocity imaging in turbulent flows using thermographic phosphor tracer particles. Opt. Express 2012, 20, 22118–22133. [Google Scholar] [CrossRef] [PubMed]
- Ushizaka, T.; Asakura, T. Measurements of flow velocity in a microscopic region using a transmission grating. Appl. Opt. 1983, 22, 1870–1874. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Grace, J.R.; Bi, X. Novel multifunctional optical-fiber probe: I. Development and validation. AIChE J. 2003, 49, 1405–1420. [Google Scholar] [CrossRef]
- Zhou, J.; Grace, J.R.; Lim, C.J.; Brereton, C.M.H. Particle velocity profiles in a circulating fluidized bed riser of square cross-section. Chem. Eng. Sci. 1995, 50, 237–244. [Google Scholar] [CrossRef]
- Tayebi, D.; Svendsen, H.F.; Grislingas, A.; Mejdell, T.; Johannessen, K. Dynamics of fluidized-bed reactors. Development and application of a new multi-fiber optical probe. Chem. Eng. Sci. 1999, 54, 2113–2122. [Google Scholar] [CrossRef]
- Tani, N.; Kondo, H.; Mori, M.; Hishida, K.; Maeda, M. Development of fiberscope PIV system by controlling diode laser illumination. Exp. Fluids 2002, 33, 752–758. [Google Scholar] [CrossRef]
- Ma, X.; Deng, S.; Li, X. Microparticle velocity sensing using a conical lens fiber array. Appl. Opt. 2019, 58, 3742–3747. [Google Scholar] [CrossRef]
- Abe, Y.; Shikama, K.; Ono, H.; Yanagi, S.; Takahashi, T. Fan-in/fan-out device employing v-groove substrate for multicore fibre. Electron. Lett. 2015, 51, 1347–1348. [Google Scholar] [CrossRef]
- Li, F.; Zhong, H.; Wang, Y.; Kang, Y.; Huang, D.; Guo, Y. Performance Analysis of Continuous-Variable Quantum Key Distribution with Multi-Core Fiber. Appl. Sci. 2018, 8, 1951. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Qiu, S.; Xu, H.; Lin, T.; Meng, F.; Han, Y.; Qi, Y.; Wang, C.; Hou, L. Trench-Assisted Multicore Fiber with Single Supermode Transmission and Nearly Zero Flattened Dispersion. Appl. Sci. 2018, 8, 2483. [Google Scholar] [CrossRef] [Green Version]
- YOFC Company. Multi Core Fiber (MCF). Available online: https://en.yofc.com/index.php/view/2349.html (accessed on 30 November 2018).
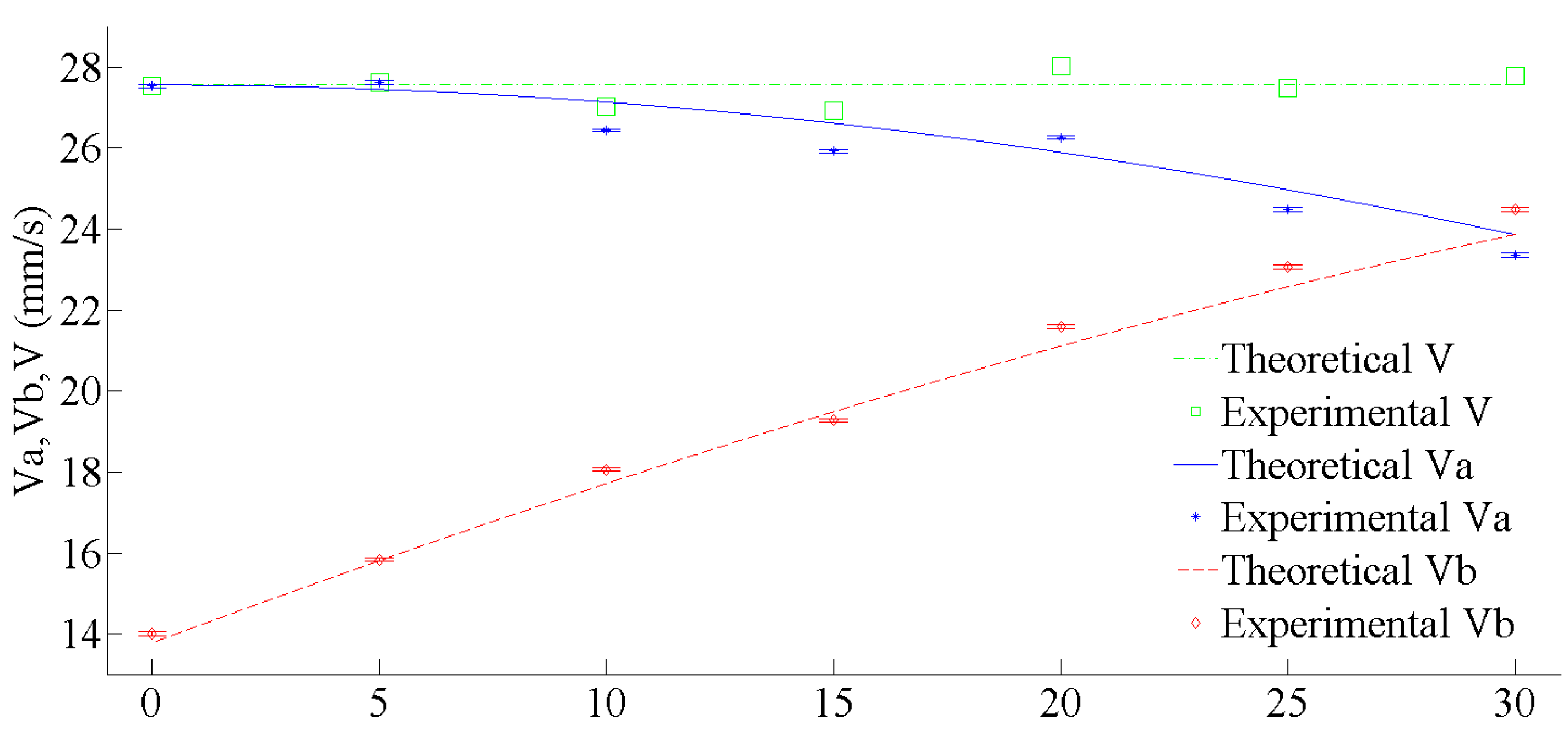

| α (°) | Va (mm/s) | Vb (mm/s) | V (mm/s) |
|---|---|---|---|
| 0 | 27.53 | 14.01 | 27.53 |
| 5 | 27.62 | 15.84 | 27.45 |
| 10 | 26.44 | 18.06 | 27.14 |
| 15 | 25.92 | 19.28 | 26.93 |
| 20 | 26.26 | 21.58 | 28.01 |
| 25 | 24.49 | 23.07 | 27.50 |
| 30 | 24.48 | 24.48 | 27.78 |
| Actual Velocity (mm/s) | Velocity Measured by MCF (mm/s) | Relative Error Measured by MCF (%) | Velocity Measured by Fiber Array (mm/s) | Relative Error Measured by Fiber Array (%) |
|---|---|---|---|---|
| 13.07 | 13.25 | 1.38 | 12.58 | 3.75 |
| 15.44 | 15.62 | 1.17 | 15.27 | 1.10 |
| 17.82 | 17.84 | 0.11 | 17.16 | 3.70 |
| 20.2 | 20.4 | 0.99 | 19.76 | 2.18 |
| 22.57 | 22.93 | 1.60 | 23.09 | 2.30 |
| 23.73 | 23.75 | 0.08 | 24.63 | 3.79 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Sun, Z.; Luo, H.; Li, X. A Novel Fiber Optic Sensor for Microparticle Velocity Measurement Using Multicore Fiber. Appl. Sci. 2020, 10, 4829. https://doi.org/10.3390/app10144829
Ma X, Sun Z, Luo H, Li X. A Novel Fiber Optic Sensor for Microparticle Velocity Measurement Using Multicore Fiber. Applied Sciences. 2020; 10(14):4829. https://doi.org/10.3390/app10144829
Chicago/Turabian StyleMa, Xin, Zhao Sun, Haimei Luo, and Xinwan Li. 2020. "A Novel Fiber Optic Sensor for Microparticle Velocity Measurement Using Multicore Fiber" Applied Sciences 10, no. 14: 4829. https://doi.org/10.3390/app10144829
APA StyleMa, X., Sun, Z., Luo, H., & Li, X. (2020). A Novel Fiber Optic Sensor for Microparticle Velocity Measurement Using Multicore Fiber. Applied Sciences, 10(14), 4829. https://doi.org/10.3390/app10144829





