Human Skeleton Data Augmentation for Person Identification over Deep Neural Network
Abstract
:1. Introduction
2. Related Work
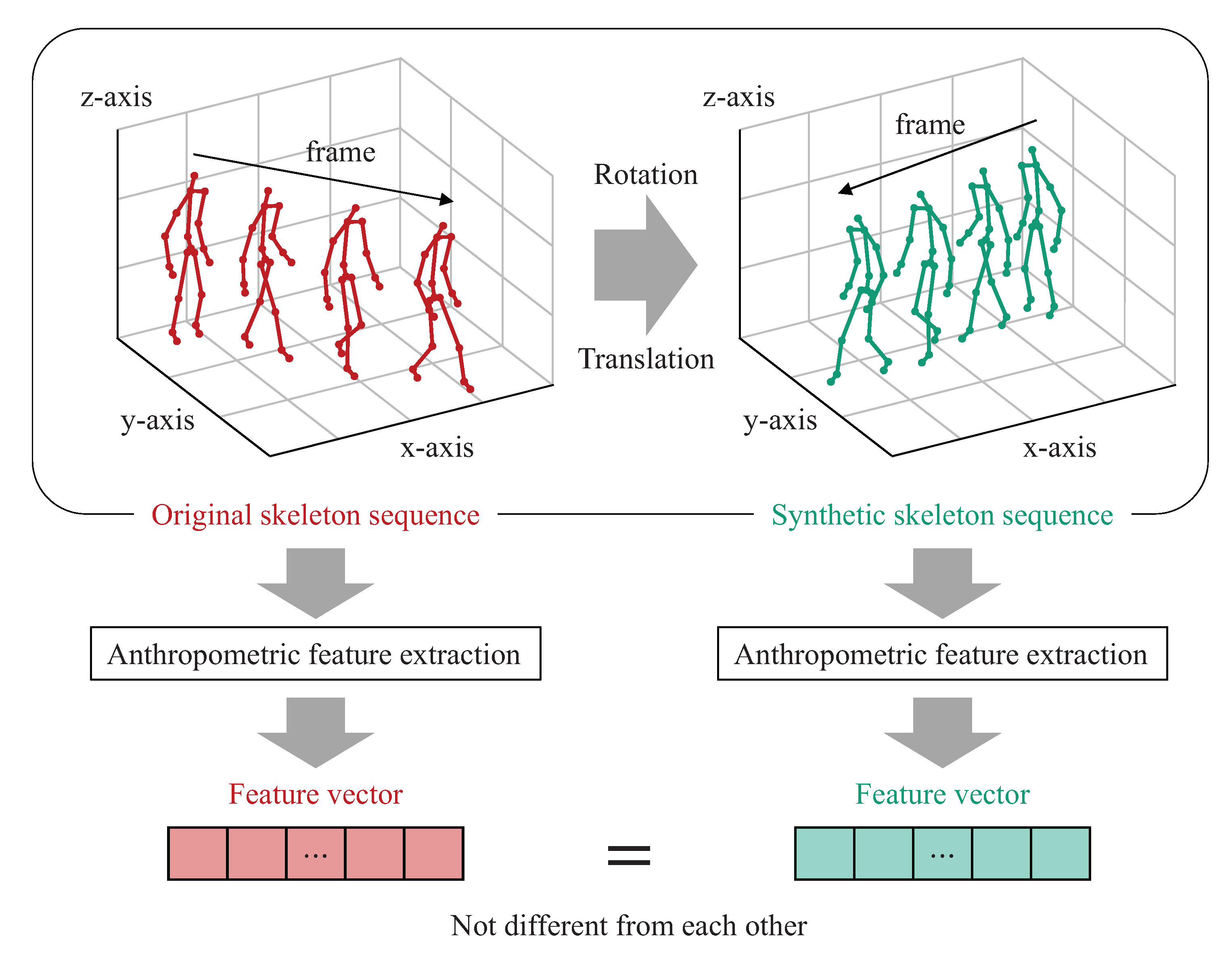
3. Motivation
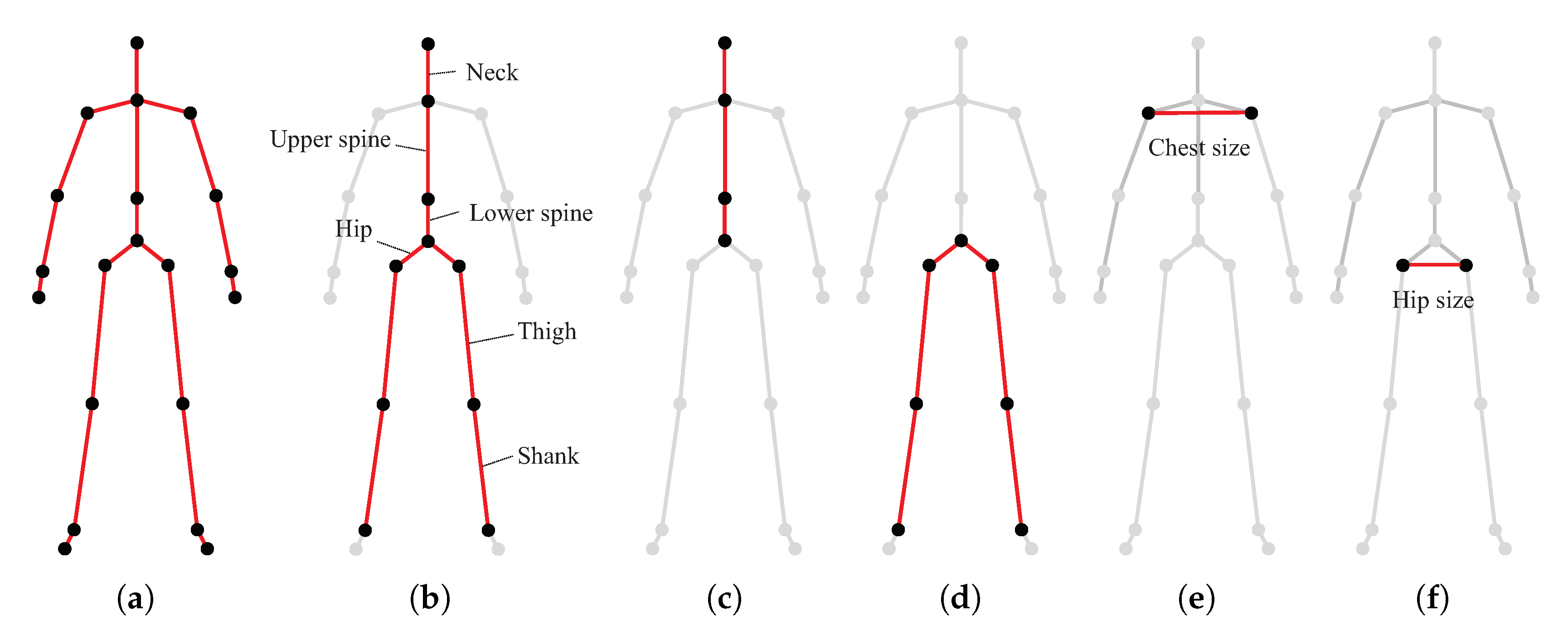
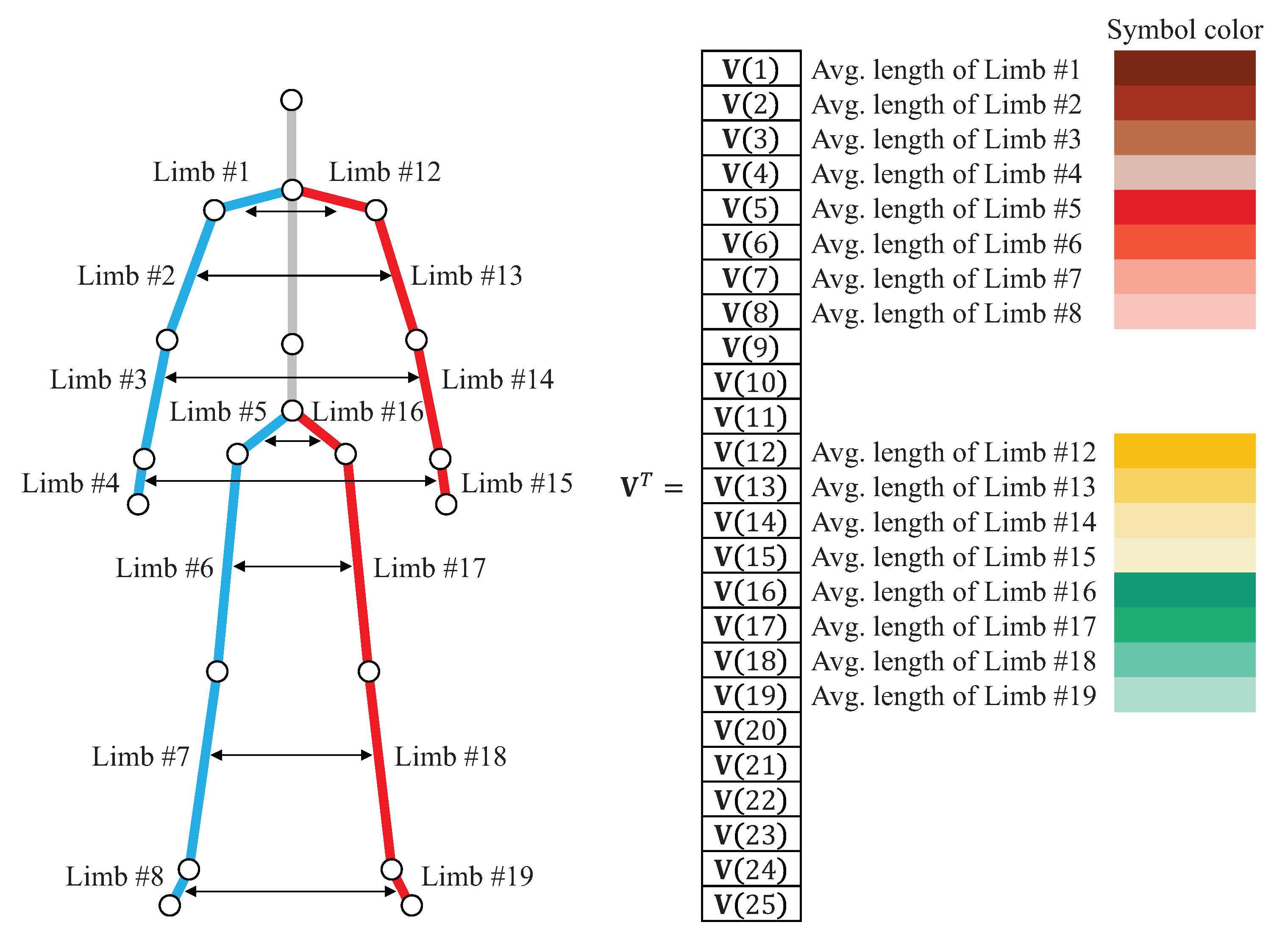
4. 3D Human Skeleton Model and Anthropometric Features
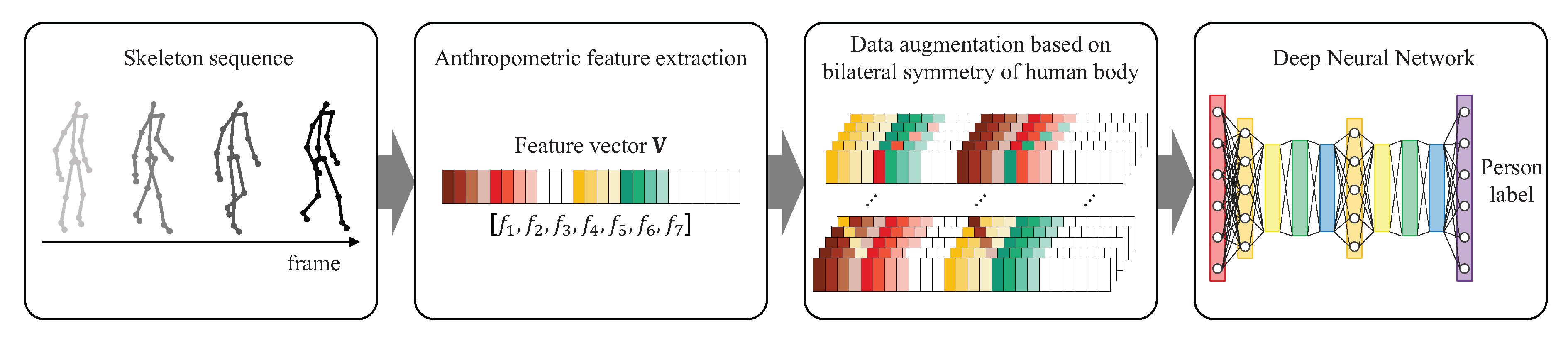
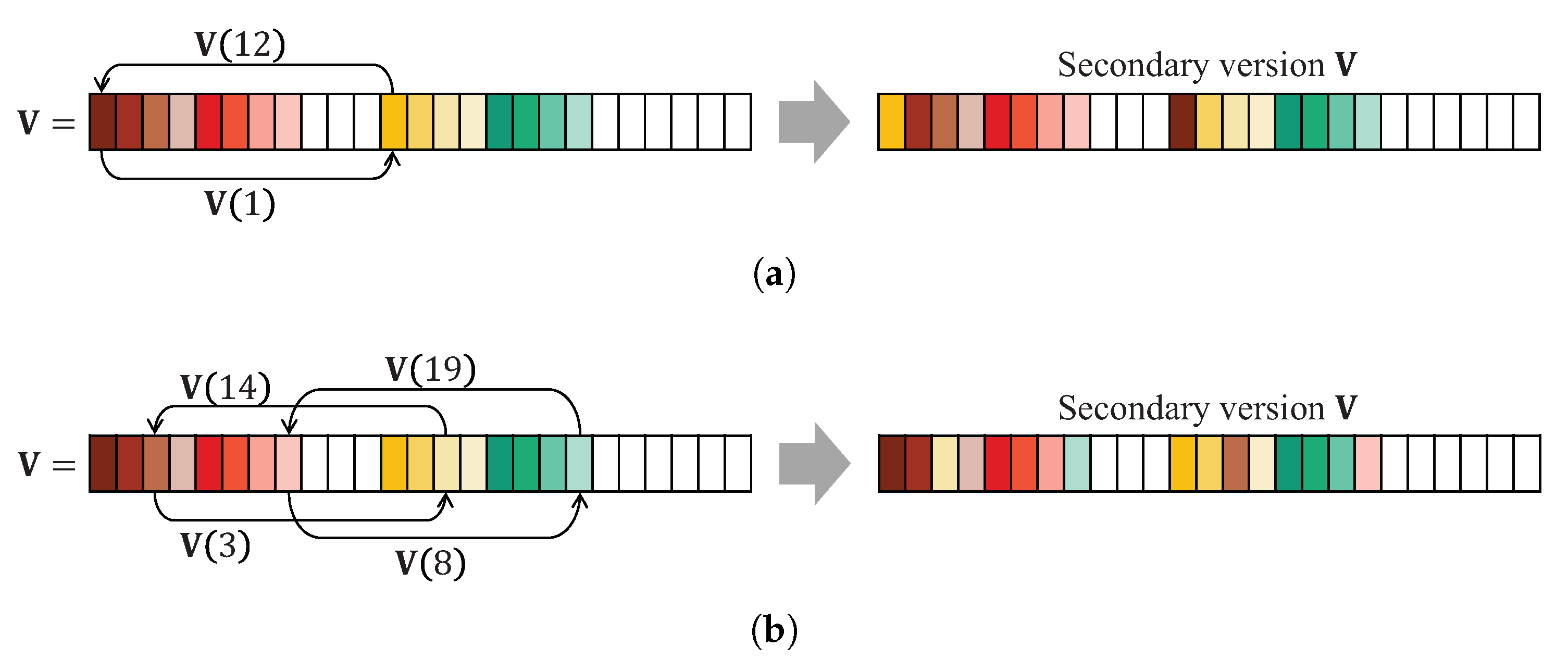
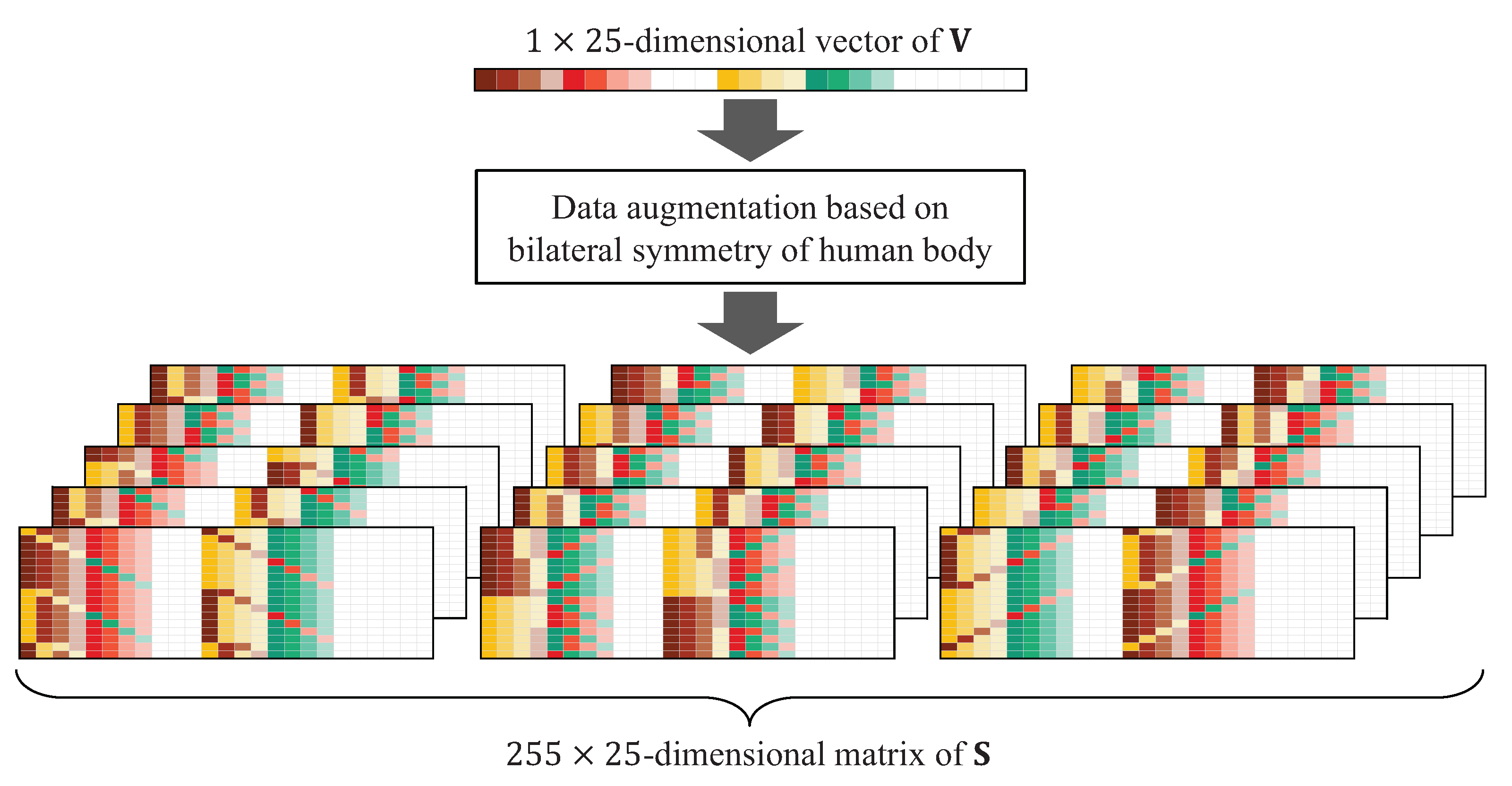
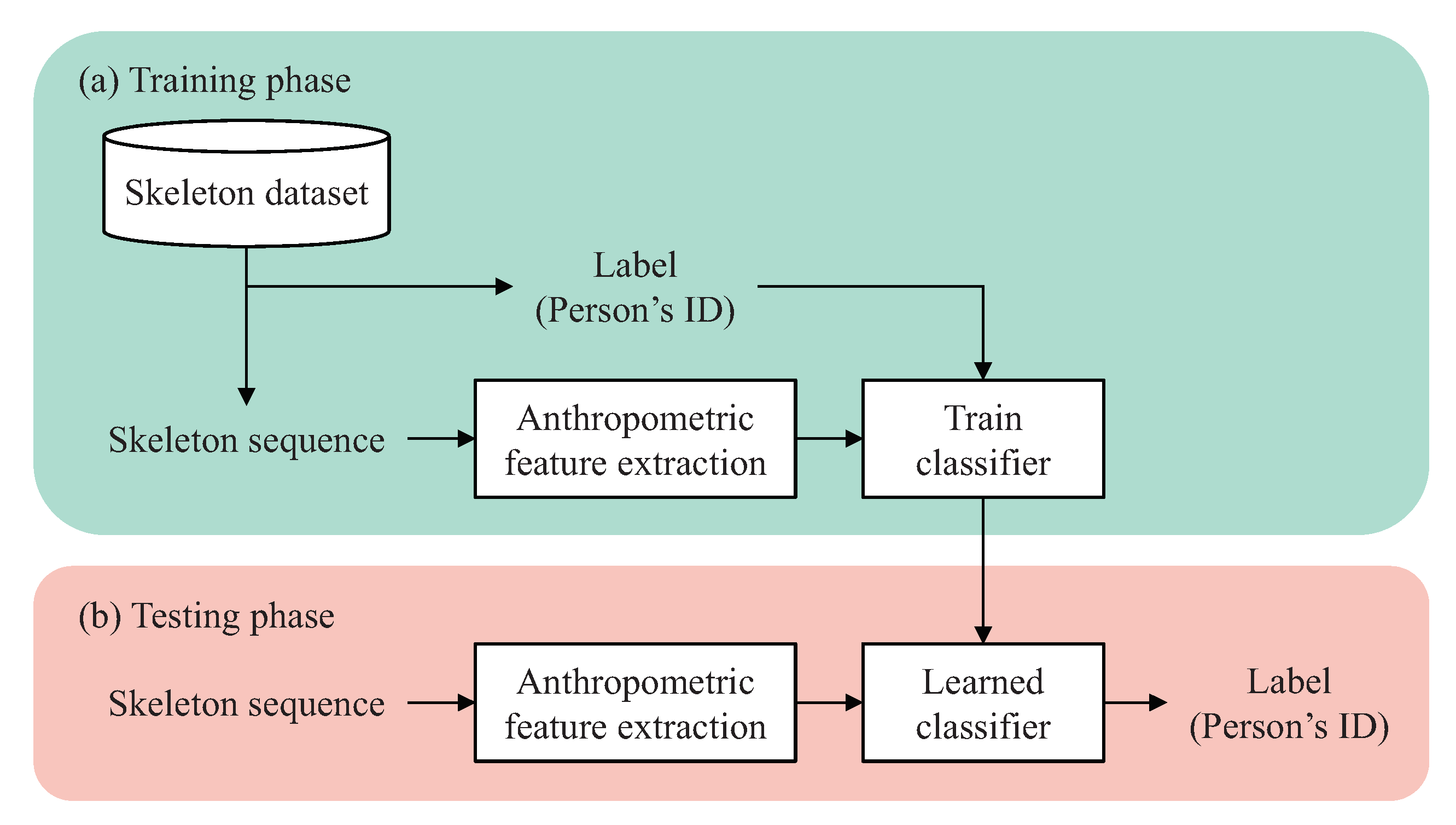
5. Data Augmentation for Person Identification
5.1. Human Bilateral Symmetry-Based Data Augmentation
| Algorithm 1 Pseudocode of the proposed data augmentation method |
Input:-dimensional feature vector of |
Output:-dimensional matrix of |
|
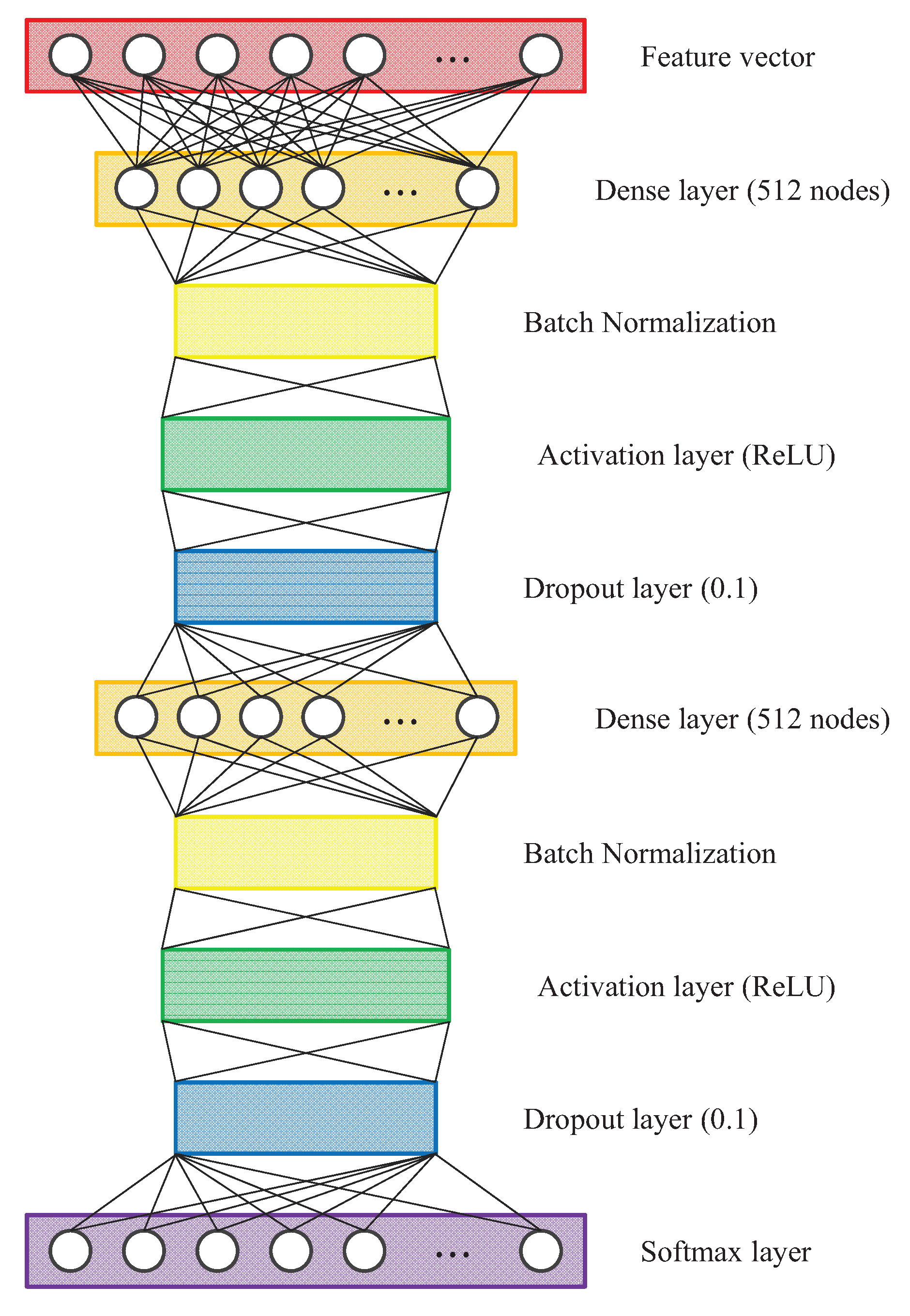
5.2. Deep Neural Network for Person Identification
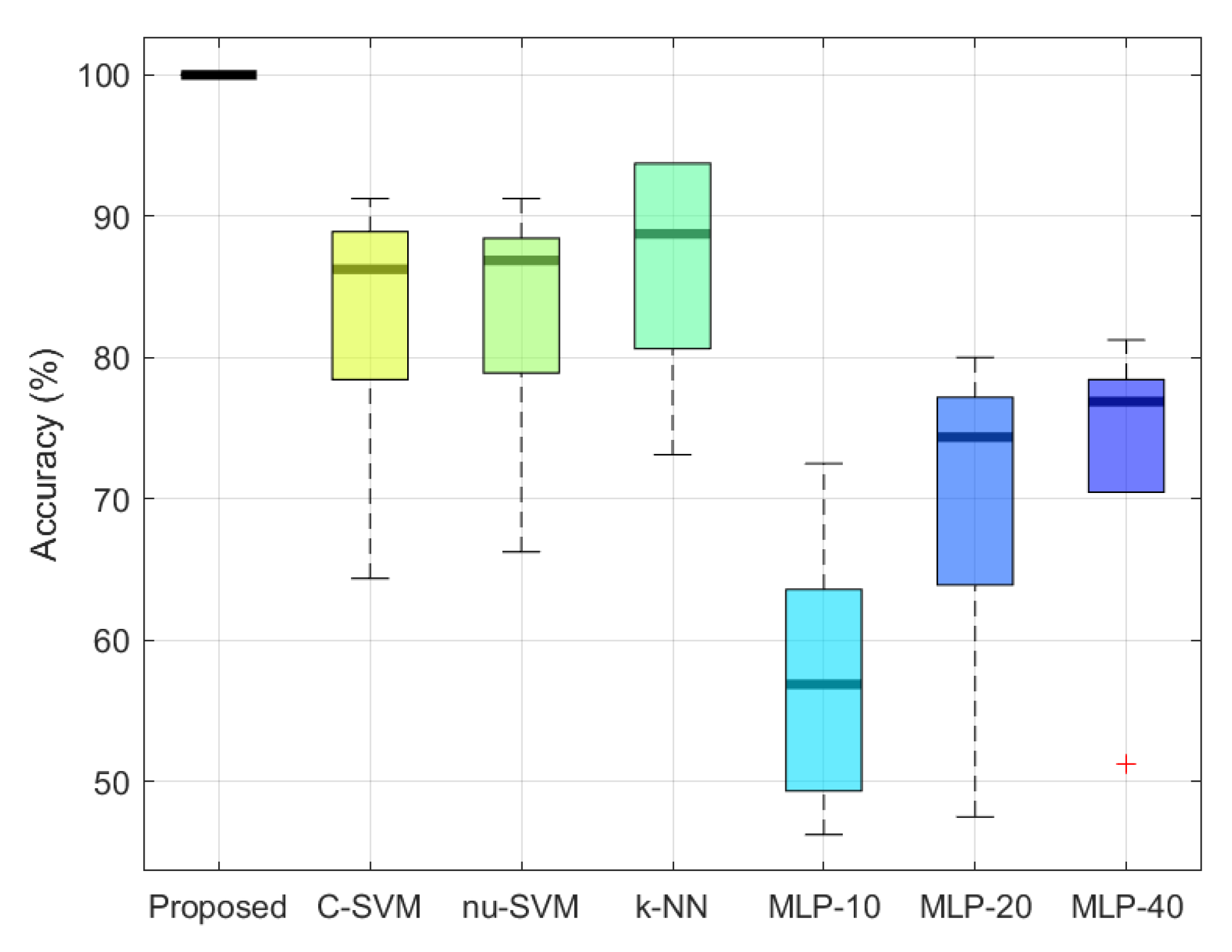
6. Experimental Evaluation and Results
6.1. Dataset and Evaluation Protocol
6.2. Four Benchmark Methods
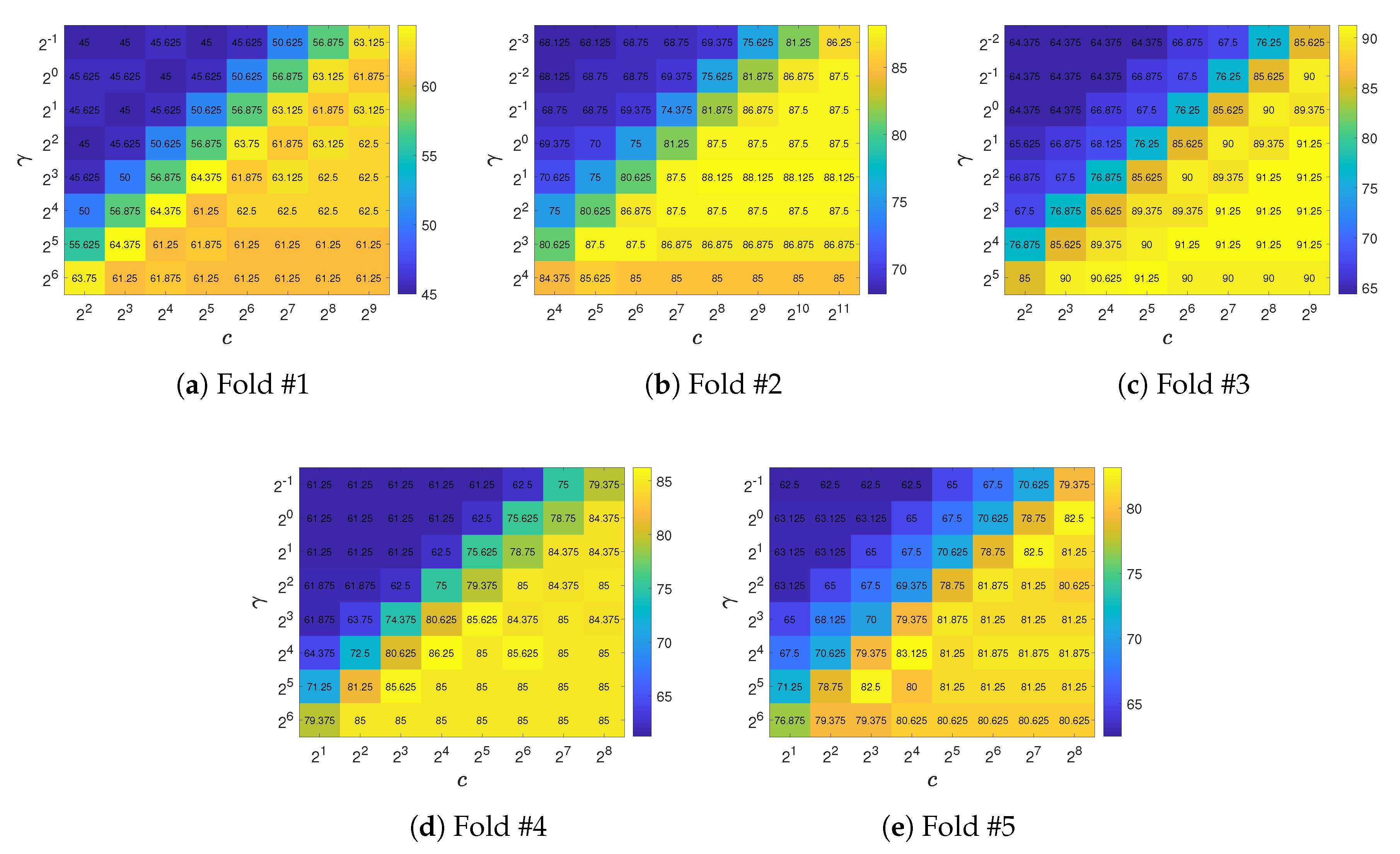
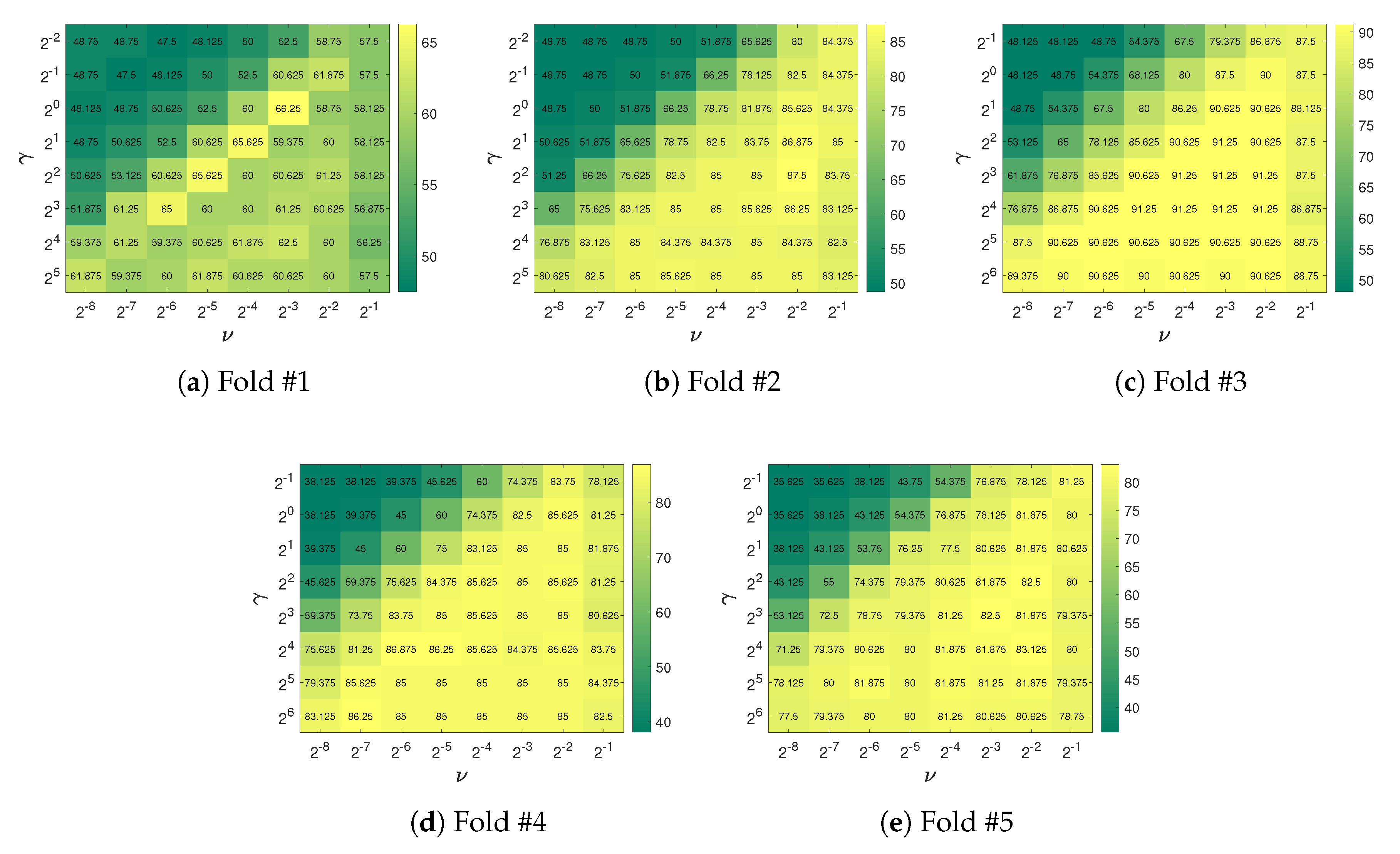
- C-SVM and nu-SVM: To implement C-SVM and nu-SVM that support multi-class classification, we used LIBSVM—an open-source library for SVMs [47]. According to the recommendation in [48], we used the radial basis function (RBF) kernel for C-SVM and nu-SVM. C-SVM has a cost parameter, denoted c, whose value ranges from 0 to ∞. The nu-SVM method has a regularization parameter, denoted g, with a value range . The RBF kernel has a gamma parameter, denoted . The grid search method was used to find the best parameter combination for both C-SVM and nu-SVM.
- k-NN: According to the results of the previous studies [22,23,24,25], k-NN achieved the best performance in the task of person identification. To implement k-NN, we used the MATLAB function fitcknn. To determine the best hyperparameter configuration, we performed hyperparameter optimization supported in the function fitcknn.
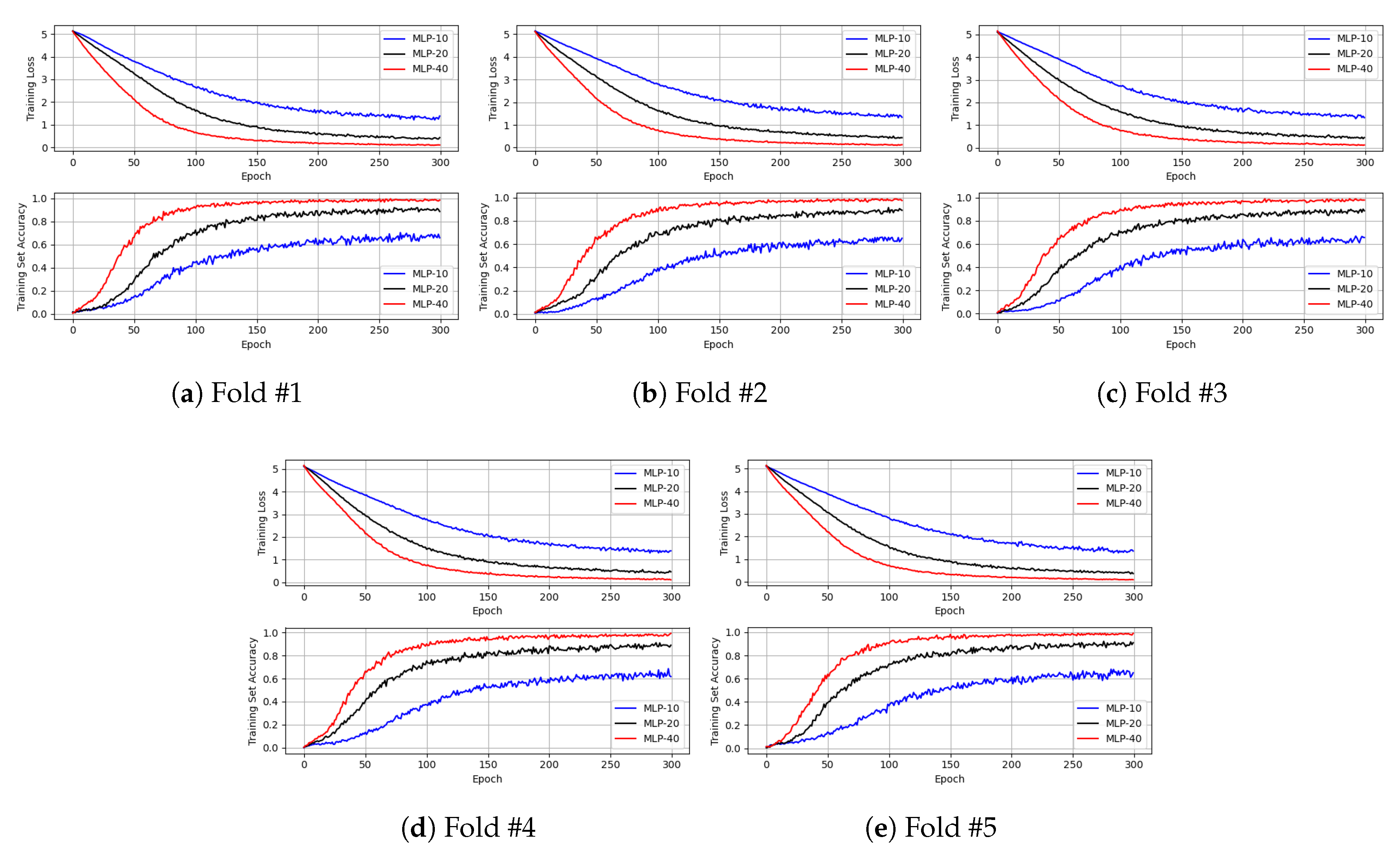
- MLP: According to the results of the previous studies [22,23,24,25], MLP showed the worst performance in the task of person identification. In [22], MLP had 10 hidden units. In [23], the number of hidden units was 20. Conversely, in [24,25], MLP, which had 40 hidden units, was used. For performance comparison, we implemented the three MLPs using TensorFlow [49]. However, as mentioned in Section 3, in the experiments, we observed that the training set accuracy of each MLP was lower than 10% when each MLP comprised only a single hidden layer. Therefore, to overcome this issue and to improve the training set accuracy, the batch normalization layer, activation layer, and dropout layer were successively added after the hidden layer of each MLP. For simplicity, we called the three MLPs: MLP-10, MLP-20, and MLP-40, respectively. Here, the suffix number denotes the number of hidden units in the hidden layer.
6.3. Results and Comparisons
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jain, A.K.; Ross, A.; Pankanti, S. Biometrics: A tool for information security. IEEE Trans. Inf. Forensics Secur. 2006, 1, 125–143. [Google Scholar] [CrossRef] [Green Version]
- Eastwood, S.C.; Shmerko, V.P.; Yanushkevich, S.N.; Drahansky, M.; Gorodnichy, D.O. Biometric-enabled authentication machines: A survey of open-set real-world applications. IEEE Trans. Hum.-Mach. Syst. 2016, 46, 231–242. [Google Scholar] [CrossRef]
- Park, K.; Park, J.; Lee, J. An IoT system for remote monitoring of patients at home. Appl. Sci. 2017, 7, 260. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Mu, Z.; Yuan, L.; Zeng, H.; Chen, L. 3D ear normalization and recognition based on local surface variation. Appl. Sci. 2017, 7, 104. [Google Scholar] [CrossRef] [Green Version]
- Shnain, N.A.; Hussain, Z.M.; Lu, S.F. A feature-based structural measure: An image similarity measure for face recognition. Appl. Sci. 2017, 7, 786. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Zhao, H.; Cao, Z.; Guo, F.; Pang, L. A Customized Semantic Segmentation Network for the Fingerprint Singular Point Detection. Appl. Sci. 2020, 10, 3868. [Google Scholar] [CrossRef]
- Li, C.; Min, X.; Sun, S.; Lin, W.; Tang, Z. DeepGait: A learning deep convolutional representation for view-invariant gait recognition using joint Bayesian. Appl. Sci. 2017, 7, 210. [Google Scholar] [CrossRef]
- Tobji, R.; Di, W.; Ayoub, N. FMnet: Iris Segmentation and Recognition by Using Fully and Multi-Scale CNN for Biometric Security. Appl. Sci. 2019, 9, 2042. [Google Scholar] [CrossRef] [Green Version]
- Izadpanahkakhk, M.; Razavi, S.M.; Taghipour-Gorjikolaie, M.; Zahiri, S.H.; Uncini, A. Deep region of interest and feature extraction models for palmprint verification using convolutional neural networks transfer learning. Appl. Sci. 2018, 8, 1210. [Google Scholar] [CrossRef] [Green Version]
- Galka, J.; Masior, M.; Salasa, M. Voice authentication embedded solution for secured access control. IEEE Trans. Consum. Electron. 2014, 60, 653–661. [Google Scholar] [CrossRef]
- Collins, R.T.; Gross, R.; Shi, J. Silhouette-based human identification from body shape and gait. In Proceedings of the IEEE International Conference on Automatic Face and Gesture Recognition (FG), Washington, DC, USA, 21 May 2002; pp. 366–371. [Google Scholar]
- Wang, L.; Tan, T.; Ning, H.; Hu, W. Silhouette analysis-based gait recognition for human identification. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1505–1518. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Malave, L.; Sarkar, S. Studies on silhouette quality and gait recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Washington, DC, USA, 27 June–2 July 2004; pp. 704–711. [Google Scholar]
- Liu, Z.; Sarkar, S. Simplest representation yet for gait recognition: Averaged silhouette. In Proceedings of the IEEE International Conference on Pattern Recognition (ICPR), Cambridge, UK, 26 August 2004; pp. 211–214. [Google Scholar]
- Liu, Z.; Sarkar, S. Effect of silhouette quality on hard problems in gait recognition. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2005, 35, 170–183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shotton, J.; Fitzgibbon, A.; Cook, M.; Sharp, T.; Finocchio, M.; Moore, R.; Kipman, A.; Blake, A. Real-time human pose recognition in parts from single depth images. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 1297–1304. [Google Scholar]
- Kwon, B.; Kim, D.; Kim, J.; Lee, I.; Kim, J.; Oh, H.; Kim, H.; Lee, S. Implementation of human action recognition system using multiple Kinect sensors. In Proceedings of the 16th Pacific Rim Conference on Multimedia (PCM), Gwangju, Korea, 16–18 September 2015; pp. 334–343. [Google Scholar]
- Kwon, B.; Kim, J.; Lee, S. An enhanced multi-view human action recognition system for virtual training simulator. In Proceedings of the Asia–Pacific Signal and Information Processing Association Annual Summit Conference (APSIPA ASC), Jeju, Korea, 13–16 December 2016; pp. 1–4. [Google Scholar]
- Kwon, B.; Kim, J.; Lee, K.; Lee, Y.K.; Park, S.; Lee, S. Implementation of a virtual training simulator based on 360° multi-view human action recognition. IEEE Access 2017, 5, 12496–12511. [Google Scholar] [CrossRef]
- Munsell, B.C.; Temlyakov, A.; Qu, C.; Wang, S. Person identification using full-body motion and anthropometric biometrics from Kinect videos. In Proceedings of the European Conference on Computer Vision (ECCV), Florence, Italy, 7–13 October 2012; pp. 91–100. [Google Scholar]
- Wu, J.; Konrad, J.; Ishwar, P. Dynamic time warping for gesture-based user identification and authentication with Kinect. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 2371–2375. [Google Scholar]
- Araujo, R.; Graña, G.; Andersson, V. Towards skeleton biometric identification using the Microsoft Kinect sensor. In Proceedings of the 28th Symposium on Applied Computing (SAC), Coimbra, Portugal, 18–22 March 2013; pp. 21–26. [Google Scholar]
- Andersson, V.; Dutra, R.; Araujo, R. Anthropometric and human gait identification using skeleton data from Kinect sensor. In Proceedings of the 29th Symposium on Applied Computing (SAC), Gyeongju, Korea, 24–28 March 2014; pp. 60–61. [Google Scholar]
- Andersson, V.; Araujo, R. Full body person identification using the Kinect sensor. In Proceedings of the 26th IEEE International Conference on Tools with Artificial Intelligence (ICTAI), Limassol, Cyprus, 10–12 November 2014; pp. 627–633. [Google Scholar]
- Andersson, V.; Araujo, R. Person identification using anthropometric and gait data from Kinect sensor. In Proceedings of the 29th Association for the Advancement of Artificial Intelligence (AAAI) Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 425–431. [Google Scholar]
- Yang, K.; Dou, Y.; Lv, S.; Zhang, F.; Lv, Q. Relative distance features for gait recognition with Kinect. J. Vis. Commun. Image Represent. 2016, 39, 209–217. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Wang, Y.; Li, J.; Wan, W.; Cheng, D.; Zhang, H. View-invariant gait recognition based on Kinect skeleton feature. Multimed. Tools Appl. 2018, 77, 24909–24935. [Google Scholar] [CrossRef]
- Huitzil, I.; Dranca, L.; Bernad, J.; Bobillo, F. Gait recognition using fuzzy ontologies and Kinect sensor data. Int. J. Approx. Reason. 2019, 113, 354–371. [Google Scholar] [CrossRef]
- Donati, L.; Iotti, E.; Mordonini, G.; Prati, A. Fashion Product Classification through Deep Learning and Computer Vision. Appl. Sci. 2019, 9, 1385. [Google Scholar] [CrossRef] [Green Version]
- Young, T.; Hazarika, D.; Poria, S.; Cambria, E. Recent trends in deep learning based natural language processing. IEEE Comput. Intell. Mag. 2018, 13, 55–75. [Google Scholar] [CrossRef]
- Song, H.; Kwon, B.; Lee, S.; Lee, S. Dictionary based compression type classification using a CNN architecture. In Proceedings of the Asia–Pacific Signal and Information Processing Association Annual Summit Conference (APSIPA ASC), Lanzhou, China, 18–21 November 2019; pp. 245–248. [Google Scholar]
- Kwon, B.; Song, H.; Lee, S. Accurate blind Lempel-Ziv-77 parameter estimation via 1-D to 2-D data conversion over convolutional neural network. IEEE Access 2020, 8, 43965–43979. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Nguyen, T.; Nahavandi, S. System design perspective for human-level agents using deep reinforcement learning: A survey. IEEE Access 2017, 5, 27091–27102. [Google Scholar] [CrossRef]
- Menger, V.; Scheepers, F.; Spruit, M. Comparing deep learning and classical machine learning approaches for predicting inpatient violence incidents from clinical text. Appl. Sci. 2018, 8, 981. [Google Scholar] [CrossRef] [Green Version]
- Kulyukin, V.; Mukherjee, S.; Amlathe, P. Toward audio beehive monitoring: Deep learning vs. standard machine learning in classifying beehive audio samples. Appl. Sci. 2018, 8, 1573. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Wang, Y.; Li, Y. A survey on deep learning-driven remote sensing image scene understanding: Scene classification, scene retrieval and scene-guided object detection. Appl. Sci. 2019, 9, 2110. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Lang, B. Machine learning and deep learning methods for intrusion detection systems: A survey. Appl. Sci. 2019, 9, 4396. [Google Scholar] [CrossRef] [Green Version]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Krogh, A.; Hertz, J.A. A simple weight decay can improve generalization. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Denver, CO, USA, 30 November–3 December 1992; pp. 950–957. [Google Scholar]
- Wang, H.; Wang, L. Modeling temporal dynamics and spatial configurations of actions using two-stream recurrent neural networks. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 499–508. [Google Scholar]
- Li, B.; Dai, Y.; Cheng, X.; Chen, H.; Lin, Y.; He, M. Skeleton based action recognition using translation-scale invariant image mapping and multi-scale deep CNN. In Proceedings of the IEEE International Conference on Multimedia and Expo Workshops (ICMEW), Hong Kong, China, 10–14 July 2017; pp. 601–604. [Google Scholar]
- Kwon, B.; Huh, J.; Lee, K.; Lee, S. Optimal camera point selection toward the most preferable view of 3D human pose. IEEE Trans. Syst. Man Cybern. Syst. 2020. [Google Scholar] [CrossRef]
- Nambiar, A.; Bernardino, A.; Nascimento, J.C.; Fred, A. Towards view-point invariant person re-identification via fusion of anthropometric and gait features from Kinect measurements. In Proceedings of the International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Porto, Portugal, 27 February–1 March 2017; pp. 108–119. [Google Scholar]
- Nambiar, A.; Bernardino, A.; Nascimento, J.C.; Fred, A. Context-aware person re-identification in the wild via fusion of gait and anthropometric features. In Proceedings of the 12th IEEE International Conference on Automatic Face and Gesture Recognition (FG), Washington, DC, USA, 30 May–3 June 2017; pp. 973–980. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Hsu, C.W.; Chang, C.C.; Lin, C.J. A Practical Guide to Support Vector Classification; National Taiwan University: Taipei, Taiwan, 2003. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-normalizing neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4 December–9 December 2017; pp. 971–980. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Kong, L.; Yuan, X.; Maharjan, A.M. A hybrid framework for automatic joint detection of human poses in depth frames. Pattern Recognit. 2018, 77, 216–225. [Google Scholar] [CrossRef]

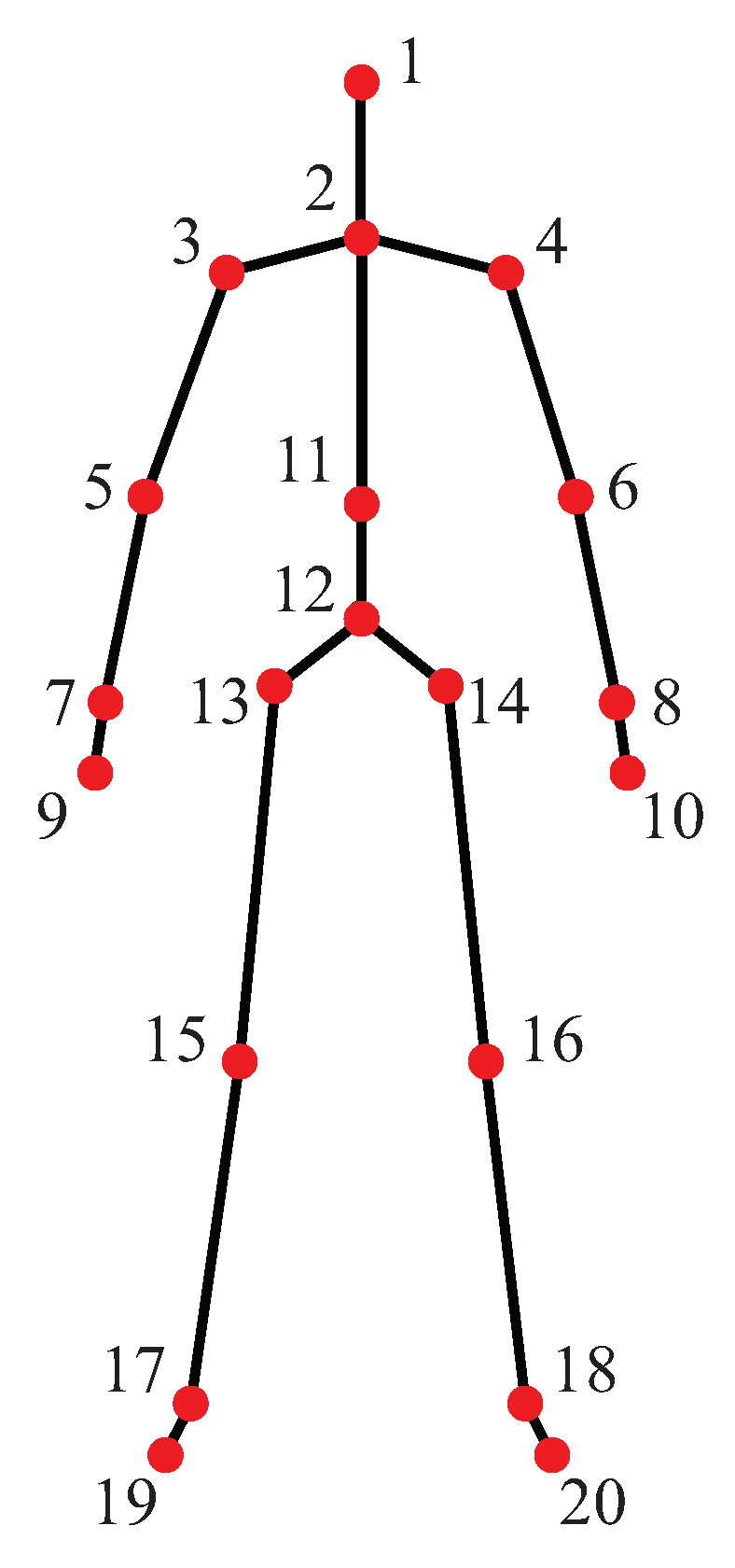

| Joint # | Joint Name | Joint # | Joint Name |
|---|---|---|---|
| 1 | head | 11 | spine |
| 2 | center of shoulder | 12 | center of hip |
| 3 | right shoulder | 13 | right hip |
| 4 | left shoulder | 14 | left hip |
| 5 | right elbow | 15 | right knee |
| 6 | left elbow | 16 | left knee |
| 7 | right wrist | 17 | right ankle |
| 8 | left wrist | 18 | left ankle |
| 9 | right hand | 19 | right foot |
| 10 | left hand | 20 | left foot |
| Limb # | Pair of Joints | |||
|---|---|---|---|---|
| 1 | center of shoulder | – | right shoulder | |
| 2 | right shoulder | – | right elbow | |
| 3 | right elbow | – | right wrist | |
| 4 | right wrist | – | right hand | |
| 5 | center of hip | – | right hip | |
| 6 | right hip | – | right knee | |
| 7 | right knee | – | right ankle | |
| 8 | right ankle | – | right foot | |
| 9 | head | – | center of shoulder | |
| 10 | center of shoulder | – | spine | |
| 11 | spine | – | center of hip | |
| 12 | center of shoulder | – | left shoulder | |
| 13 | left shoulder | – | left elbow | |
| 14 | left elbow | – | left wrist | |
| 15 | left wrist | – | left hand | |
| 16 | center of hip | – | left hip | |
| 17 | left hip | – | left knee | |
| 18 | left knee | – | left ankle | |
| 19 | left ankle | – | left foot | |
| Fold # | Hyperparameters | |||||
|---|---|---|---|---|---|---|
| k | Distance Metric | Distance Weighting Function | Exponent | Standardize | Accuracy (%) | |
| 1 | 1 | euclidean | inverse | - | true | 73.125 |
| 2 | 3 | cityblock | squaredinverse | - | true | 88.750 |
| 3 | 3 | minkowski | squaredinverse | 0.8615 | true | 93.750 |
| 4 | 1 | minkowski | equal | 0.8335 | true | 93.750 |
| 5 | 2 | minkowski | squaredinverse | 2.1445 | true | 83.125 |
| Fold # | MLP | ||
|---|---|---|---|
| MLP-10 | MLP-20 | MLP-40 | |
| 1 | 46.250 | 47.500 | 51.250 |
| 2 | 56.880 | 76.250 | 76.880 |
| 3 | 72.500 | 80.000 | 81.250 |
| 4 | 50.370 | 74.370 | 77.500 |
| 5 | 60.620 | 69.380 | 76.880 |
| Avg. | 57.324 | 69.500 | 72.752 |
| Method | Accuracy |
|---|---|
| C-SVM | 82.625 |
| nu-SVM | 83.000 |
| k-NN | 86.500 |
| MLP-10 | 57.324 |
| MLP-20 | 69.500 |
| MLP-40 | 72.752 |
| MLP-10 + Proposed DA | 75.528 |
| MLP-20 + Proposed DA | 93.752 |
| MLP-40 + Proposed DA | 98.372 |
| Proposed DNN + Proposed DA | 100.000 |
| Method | Fold #1 | Fold #2 | Fold #3 | Fold #4 | Fold #5 | Avg. |
|---|---|---|---|---|---|---|
| Proposed DA | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Benchmark DA #1 | 52.50 | 59.38 | 62.50 | 52.50 | 68.12 | 59.00 |
| Benchmark DA #2 | 68.12 | 63.75 | 86.87 | 61.25 | 73.12 | 70.62 |
| Benchmark DA #3 | 63.13 | 88.75 | 75.63 | 83.75 | 77.50 | 77.75 |
| Benchmark DA #4 | 64.38 | 87.50 | 90.00 | 84.38 | 76.25 | 80.50 |
| Parameter | Number of Dense Layers () | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Number of dense nodes per layer () | 2 | 14.876 | 9.372 | 8.998 | 8.124 | 5.874 |
| 4 | 44.126 | 28.876 | 27.624 | 21.498 | 16.378 | |
| 8 | 65.502 | 56.626 | 49.998 | 47.248 | 46.750 | |
| 16 | 84.674 | 82.548 | 81.500 | 78.752 | 75.626 | |
| 32 | 95.462 | 94.348 | 91.370 | 88.200 | 85.374 | |
| 64 | 97.498 | 98.700 | 94.670 | 92.266 | 89.736 | |
| 128 | 97.983 | 99.120 | 98.316 | 96.189 | 94.586 | |
| 256 | 98.500 | 99.874 | 99.374 | 98.626 | 97.876 | |
| 512 | 99.248 | 100.000 | 100.000 | 100.000 | 100.000 | |
| Activation Function | ReLU | Sigmoid | Softmax | Softplus | Softsign | Tanh | SELU | ELU | Exponential |
|---|---|---|---|---|---|---|---|---|---|
| Average accuracy | 100 | 100 | 20.88 | 100 | 100 | 99.87 | 100 | 100 | 67.34 |
| Dropout rate | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|---|
| Average accuracy | 100 | 100 | 96.126 | 76.872 | 53.872 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, B.; Lee, S. Human Skeleton Data Augmentation for Person Identification over Deep Neural Network. Appl. Sci. 2020, 10, 4849. https://doi.org/10.3390/app10144849
Kwon B, Lee S. Human Skeleton Data Augmentation for Person Identification over Deep Neural Network. Applied Sciences. 2020; 10(14):4849. https://doi.org/10.3390/app10144849
Chicago/Turabian StyleKwon, Beom, and Sanghoon Lee. 2020. "Human Skeleton Data Augmentation for Person Identification over Deep Neural Network" Applied Sciences 10, no. 14: 4849. https://doi.org/10.3390/app10144849
APA StyleKwon, B., & Lee, S. (2020). Human Skeleton Data Augmentation for Person Identification over Deep Neural Network. Applied Sciences, 10(14), 4849. https://doi.org/10.3390/app10144849





