Magneto-Rheological Elastomer Composites. A Review
Abstract
:1. Introduction
1.1. Physical Static Mechanism of MR Effect
1.2. Dynamic of MRE
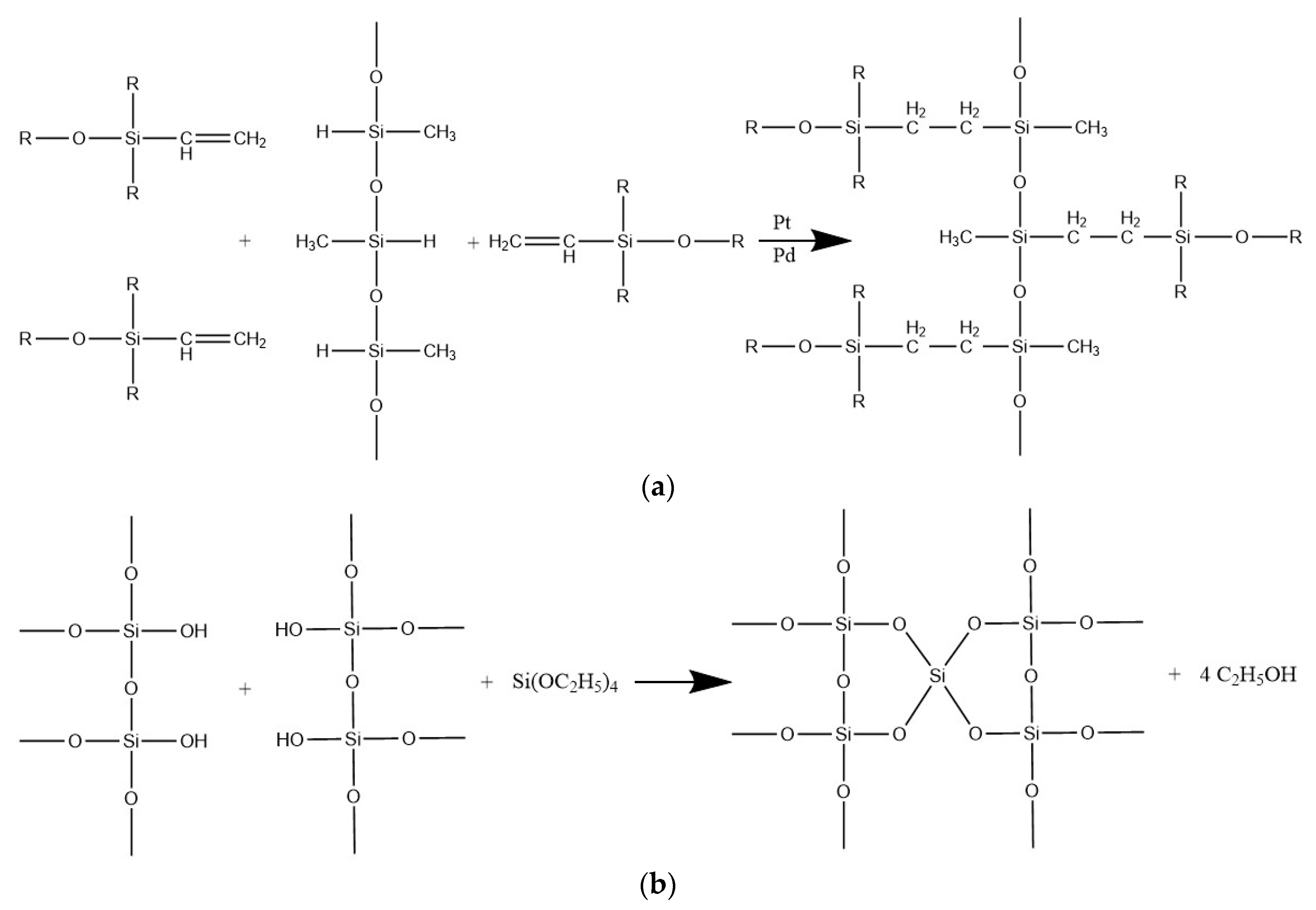
2. Materials and Methods
3. Results and Discussion
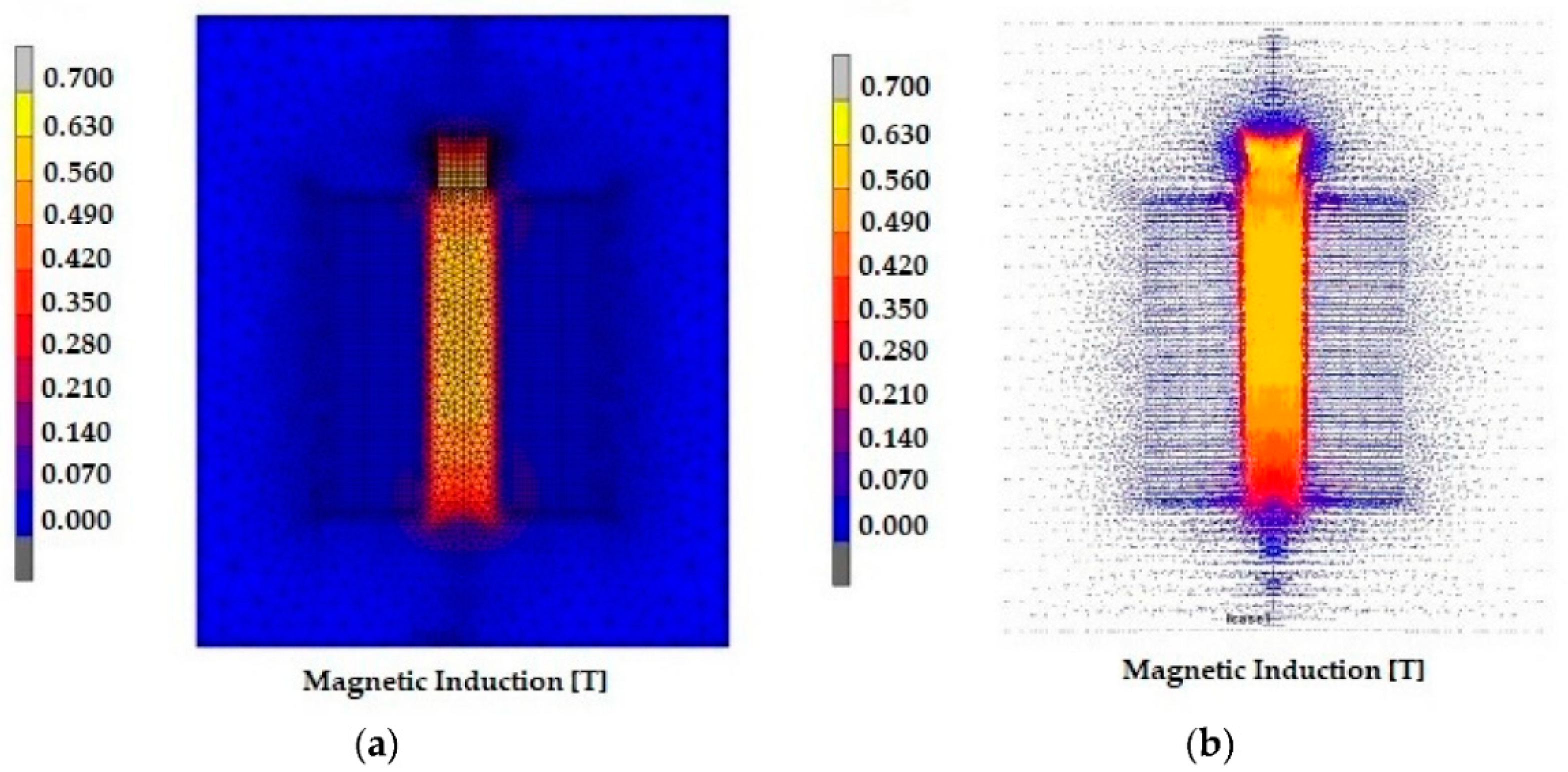
3.1. Simulation Mechanism of MRES Composite and Magnetic Flux Distribution
3.2. Surface Characterization Using SEM and µCT Technique
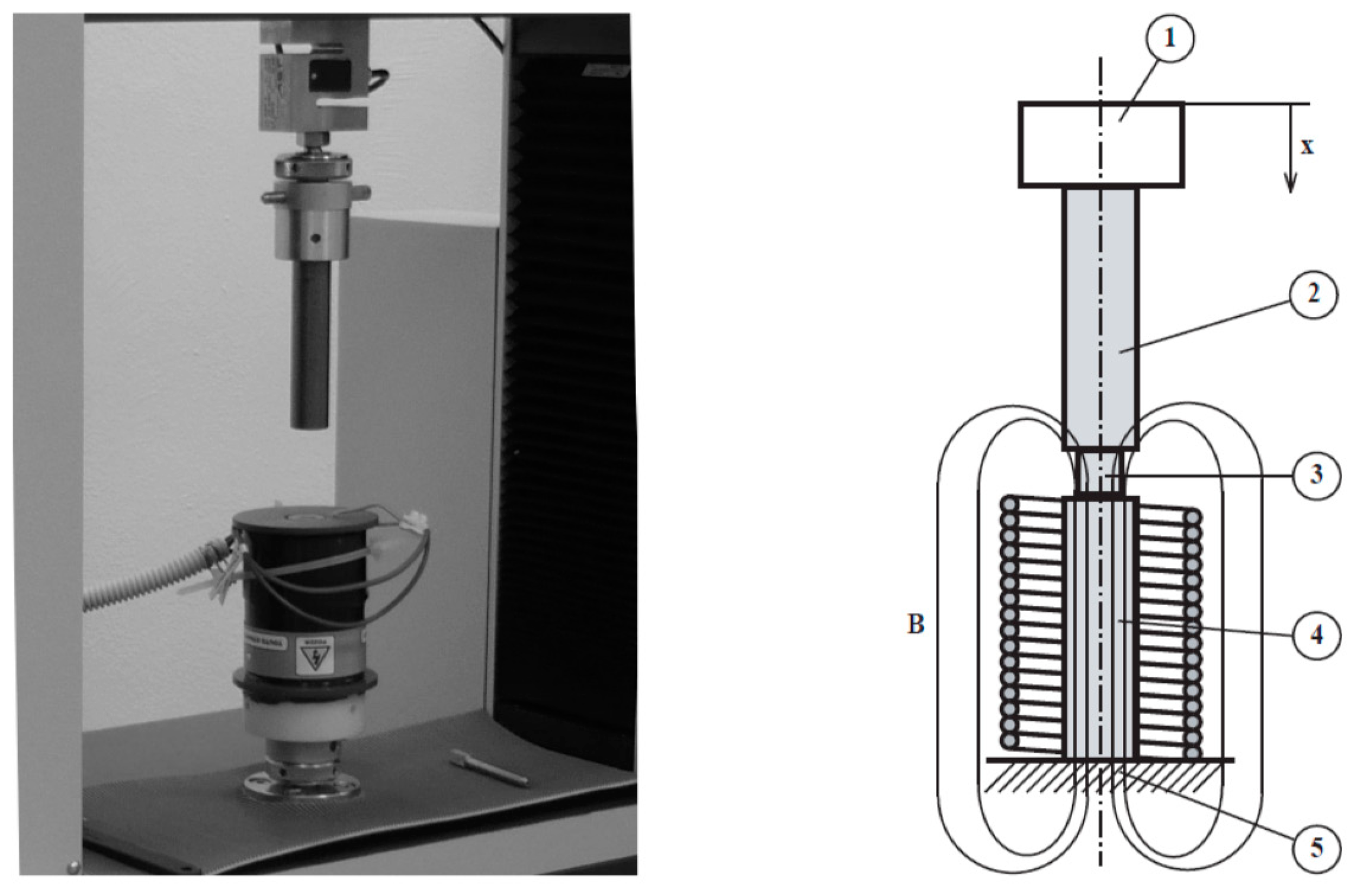
3.3. Static Characterization of MREs Composite, Single Field Active, Deformation (Squeeze) Mode
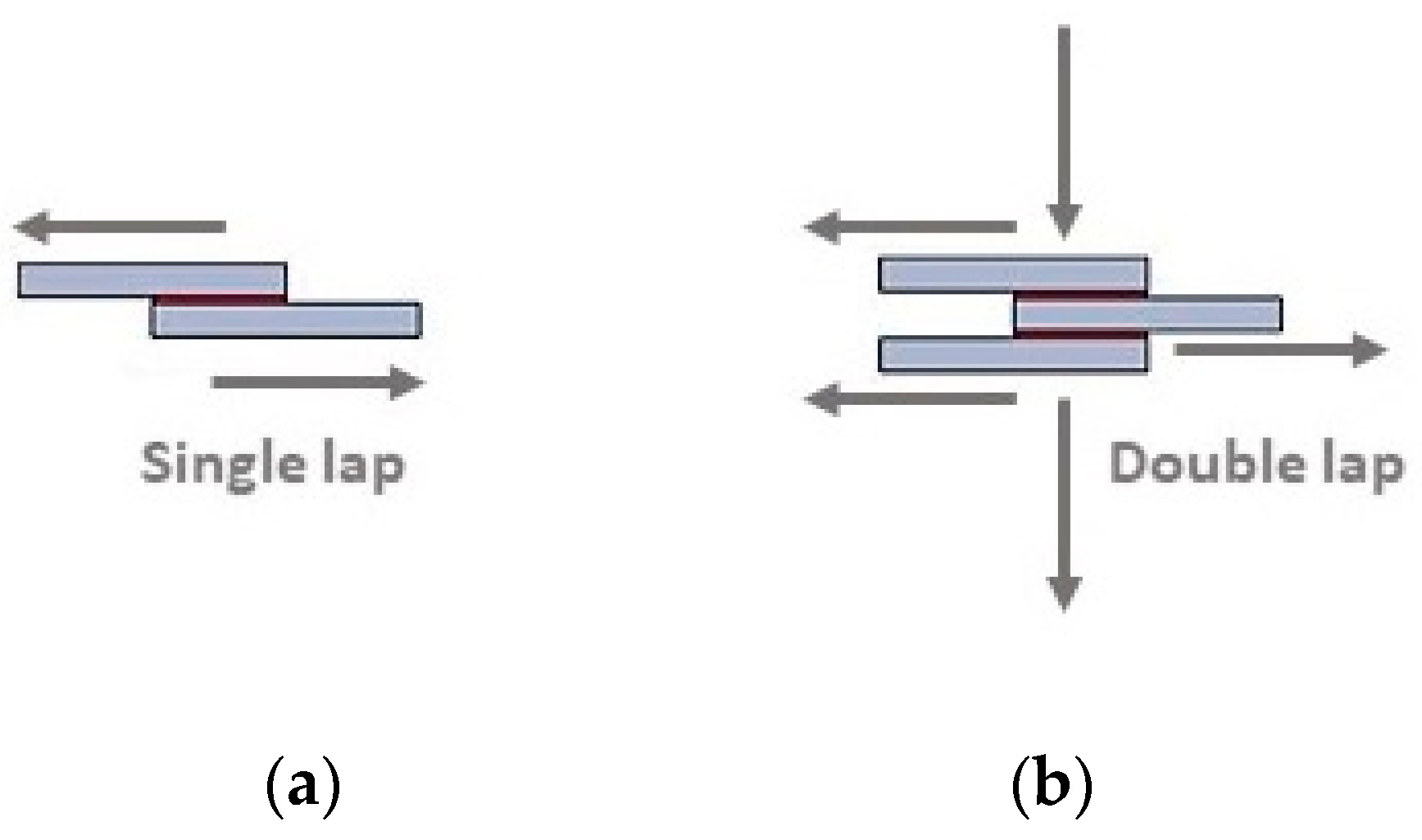
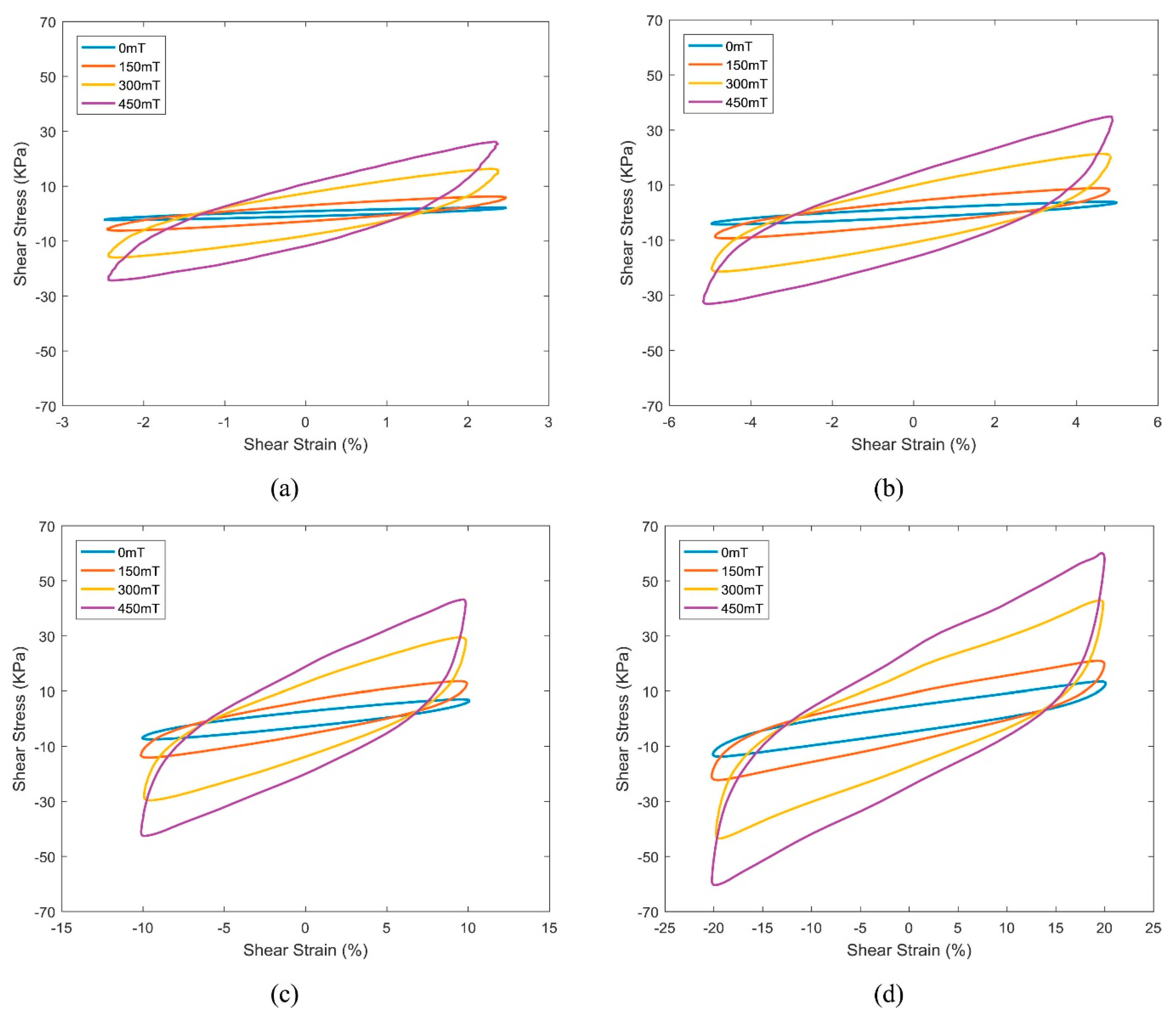
3.4. Dynamic Characterization (Shear Test, Single, and Double Mode)
4. Future Prospectus on the Applications of MREs Composite
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, Y.; Li, J.; Li, W.; Du, H. A state-of-the-art review on magnetorheological elastomer devices. Smart Mater. Struct. 2014, 23, 123001. [Google Scholar] [CrossRef]
- Zhang, J.; Pang, H.; Wang, Y.; Gong, X. The magneto-mechanical properties of off-axis anisotropic magnetorheological elastomers. Compos. Sci. Technol. 2020, 191, 108079. [Google Scholar] [CrossRef]
- Samal, S. Effect of shape and size of filler particle on the aggregation and sedimentation behavior of the polymer composite. Powder Technol. 2020, 366, 43–51. [Google Scholar] [CrossRef]
- Shahrivar, K.; de Vicente, J. Thermoresponsive polymer-based magneto-rheological (MR) composites as a bridge between MR fluids and MR elastomers. Soft Matter 2013, 48, 11451–11456. [Google Scholar] [CrossRef]
- Kim, Y.K.; Koo, J.H.; Kim, K.S.; Kim, S. Developing a real time controlled adaptive MRE-based tunable vibration absorber system for a linear cryogenic cooler. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Budapest, Hungary, 3–7 July 2011; pp. 287–290. [Google Scholar] [CrossRef]
- Ginder, J.M.; Scholotter, W.F.; Nichols, M.E. Magnetorheological elastomers in tunable vibration absorbers. In Proceedings of the SPIE’s 8th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 4–8 March 2001; Volume 4331. [Google Scholar] [CrossRef]
- Jolly, M.R.; Carlson, J.D.; Munoz, B.C. A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 1996, 5, 607–614. [Google Scholar] [CrossRef]
- Balasoiu, M.; Bica, I. Composite magnetorheological elastomers as dielectrics for plane capacitors: Effects of magnetic field intensity. Results Phys. 2016, 6, 199–202. [Google Scholar] [CrossRef] [Green Version]
- Flatau, A.B.; Dapino, M.J.; Calkins, F.T. High bandwidth tenability in a smart vibration absorber. J. Intell. Mater. Syst. Struct. 2000, 11, 923–929. [Google Scholar] [CrossRef]
- Thevenot, J.; de Oliveira, H.; Sandre, O.; Lecommandoux, S. Magnetic responsive polymer composite materials. Chem. Soc. Rev. 2013, 42, 7099–7116. [Google Scholar] [CrossRef] [Green Version]
- Chertovich, A.V.; Stepanov, G.V.; Kramarenko, E.Y.; Khokhlov, A.R. New Composite Elastomers with Giant Magnetic Response. Macromol. Mater. Eng. 2010, 295, 336–341. [Google Scholar] [CrossRef]
- Krautz, M.; Werner, D.; Schrödner, M.; Funk, A.; Jantz, A.; Popp, J.; Eckert, J.; Waske, A. Hysteretic behavior of soft magnetic elastomer composites. J. Magn. Magn. Mater. 2017, 426, 60–63. [Google Scholar] [CrossRef]
- Filipcsei, G.; Csetneki, I.; Szilágyi, A.; Zrínyi, M. Magnetic Field-Responsive Smart Polymer Composites. In Oligomers-Polymer Composites-Molecular Imprinting; Springer: Berlin/Heidelberg, Germany, 2007; Volume 206. [Google Scholar] [CrossRef]
- Farshad, M.; Benine, A. Magnetoactive elastomer composites. Polym. Test. 2004, 23, 347–353. [Google Scholar] [CrossRef]
- Mehnert, M.; Hossain, M.; Steinmann, P. Towards a thermo-magneto-mechanical framework for magneto-rheological elastomers. Int. J. Solids Struct. 2017, 128, 117–132. [Google Scholar] [CrossRef]
- de Vicente, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R. Magnetorheological fluids: A review. Soft Matter 2011, 8, 3701–3710. [Google Scholar] [CrossRef]
- Chen, L.; Jerrams, S. A rheological model of the dynamic behaviour of magnetorheological elastomers. Aip J. Appl. Phys. 2011, 110, 013513. [Google Scholar] [CrossRef]
- Samal, S.; Kolinova, M.; Blanco, I. The Magneto-Mechanical Behavior of Active Components in Iron-Elastomer Composite. J. Compos. Sci. 2018, 2, 54. [Google Scholar] [CrossRef] [Green Version]
- Kallio, M. The Elastic and Damping Properties of Magnetorheological Elastomers: Dissertation; VTT Technical Research Centre of Finland; VTT: Espoo, Finland, 2005; p. 146. Available online: http://www.vtt.fi/inf/pdf/publications/2005/P565.pdf (accessed on 27 June 2020).
- Samal, S.; Vlach, J.; Kavan, P. Improved mechanical properties of magneto rheological elastomeric composite with isotropic iron filler distribution. Ciência Tecnol. Dos Mater. 2016, 28, 155–161. [Google Scholar] [CrossRef]
- Samal, S.; Vlach, J.; Kolinova, M.; Kavan, P. Micro-computed tomography characterization of isotropic filler distribution in magnetorheological elastomeric composites. Adv. Process. Manuf. Technol. Nanostructured Multifunct. Mater. 2017, 7, 57–69. [Google Scholar] [CrossRef]
- Samal, S.; Kolinova, M.; Rahier, H.; Dal Poggetto, G.; Blanco, I. Investigation of the Internal Structure of Fiber Reinforced Geopolymer Composite under Mechanical Impact: A Micro Computed Tomography (µCT) Study. Appl. Sci. 2019, 9, 516. [Google Scholar] [CrossRef] [Green Version]
- Samal, S.; Škodová, M.; Blanco, I. Effects of Filler Distribution on Magnetorheological Silicon-Based Composites. Materials 2019, 12, 3017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dargahi, A.; Sedaghati, R.; Rakheja, S. On the properties of magnetorheological elastomers in shear mode: Design, fabrication and characterization. Compos. Part B Eng. 2019, 159, 269–283. [Google Scholar] [CrossRef]
- Asadi Khanouki, M.; Sedaghati, R.; Hemmatian, M. Multidisciplinary Design Optimization of a Novel Sandwich Beam-Based Adaptive Tuned Vibration Absorber Featuring Magnetorheological Elastomer. Materials 2020, 13, 2261. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 2015, 56–57, 55–80. [Google Scholar] [CrossRef]
- Kallio, M.; Lindroos, T.; Aalto, S.; Järvinen, E.; Kärnä, T.; Meinander, T. Dynamic compression testing of a tunable spring element consisting of a magnetorheological elastomer. Smart Mater. Struct. 2007, 16, 506–514. [Google Scholar] [CrossRef]
- Dong, X.-M.; Yu, M.; Liao, C.-R.; Chen, W.-M. A new variable stiffness absorber based on magneto-rheological elastomer. Trans. Nonferrous Met. Soc. China 2009, 19, s611–s615. [Google Scholar] [CrossRef]
- Samal, S.; Kolinova, M.; Blanco, I.; Dal Poggetto, G.; Catauro, M. Magnetorheological Elastomer Composites: The Influence of Iron Particle Distribution on the Surface Morphology. Macromol. Symp. 2020, 389, 1900053. [Google Scholar] [CrossRef]
- Seo, J.; Kim, S.; Samal, S.; Kim, H. Viscous behaviour of Bi2O3–B2O3–ZnO glass composites with ceramic fillers. Adv. Appl. Ceram. 2014, 113, 334–340. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Feng, X.-Q.; Lauke, B.; Mai, Y.-W. Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate–polymer composites. Compos. Part B 2008, 39, 933–961. [Google Scholar] [CrossRef]
- Nurul, A.Y.; Saiful, A.M.; Ubaidillah, S.A.; Salihah, T.S.; Nurul, A.A.W. Thermal Stability and Rheological Properties of Epoxidized Natural Rubber-Based Magnetorheological Elastomer. Int. J. Mol. Sci. 2019, 20, 746. [Google Scholar] [CrossRef] [Green Version]
- Samal, S.; Stuchlík, M.; Petrikova, I. Thermal behavior of flax and jute reinforced in matrix acrylic composite. J. Therm. Anal. Calorim. 2018, 131, 1035–1040. [Google Scholar] [CrossRef]
- Cantournet, S.; Desmorat, R.; Besson, J. Mullins effect and cyclic stress softening of filler elastomers by internal sliding and friction thermodynamics model. Int. J. Solids Struct. 2009, 46, 2255–2264. [Google Scholar] [CrossRef]
- Clough, J.; Creton, C.; Craig, S.; Sijbesma, R. Covalent bond scission in the Mullins effect of a filler elastomer: Real-time Visualization with Mechanoluminescence. Adv. Funct. Mater. 2016, 26, 9063–9074. [Google Scholar] [CrossRef] [Green Version]
- Chazeau, L.; Brown, J.D.; Yanyo, L.C.; Sternstein, S.S. Modulus recovery kinetics and other insights into the Payne effect for filled elastomers. Polym. Compos. 2000, 21, 202–223. [Google Scholar] [CrossRef]
- Frohlich, J.; Niedermeier, W.; Luginsland, H.-D. The effect of filler-filler and filler-elastomer interaction on rubber reinforcement. Compos. Part A Appl. Sci. Manuf. 2005, 36, 449–460. [Google Scholar] [CrossRef]
- Jolly, M.R.; Carlson, J.D.; Munoz, B.C.; Bullions, T.A. The magnetoviscoelastic effect of elastomer composites consisting of ferrous particles embedded in a polymer matrix. J. Intell. Mater. Syst. Struct. 1996, 7, 613–622. [Google Scholar] [CrossRef]
- Stepanov, G.V.; Borin, D.Y.; Raikher, L.Y.; Melenev, P.V.; Perov, N.S. Motion of ferroparticles inside the polymeric matrix in magnetoactive elastomers. J. Phys. Condens. Matter. 2008, 20, 204121. [Google Scholar] [CrossRef]
- Glavan, G.; Kettl, W.; Brunhuber, A.; Shamonin, M.; Drevenšek-Olenik, I. Effect of material composition on tunable surface roughness of magnetoactive elastomers. Polymers 2019, 11, 594. [Google Scholar] [CrossRef] [Green Version]
- Li, W.H.; Zhang, X.Z.; Du, H. Magnetorheological elastomers and their applications. In Advances in Elastomers I: Blends and Interpenetrating Networks; Visakh, P.M., Thomas, S., Chandra, A.K., Mathew, A.P., Eds.; Springer: Berlin, Germany, 2013; pp. 357–374. [Google Scholar]
- Boczkowska, A.; Awietjan, S. Microstructure and Properties of Magnetorheological Elastomers. Adv. Elastomers–Technol. Prop. Appl. 2012, 595. [Google Scholar] [CrossRef] [Green Version]












© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samal, S.; Škodová, M.; Abate, L.; Blanco, I. Magneto-Rheological Elastomer Composites. A Review. Appl. Sci. 2020, 10, 4899. https://doi.org/10.3390/app10144899
Samal S, Škodová M, Abate L, Blanco I. Magneto-Rheological Elastomer Composites. A Review. Applied Sciences. 2020; 10(14):4899. https://doi.org/10.3390/app10144899
Chicago/Turabian StyleSamal, Sneha, Marcela Škodová, Lorenzo Abate, and Ignazio Blanco. 2020. "Magneto-Rheological Elastomer Composites. A Review" Applied Sciences 10, no. 14: 4899. https://doi.org/10.3390/app10144899
APA StyleSamal, S., Škodová, M., Abate, L., & Blanco, I. (2020). Magneto-Rheological Elastomer Composites. A Review. Applied Sciences, 10(14), 4899. https://doi.org/10.3390/app10144899






