The Effects of Stress on Second Harmonics in Plate-Like Structures
Abstract
:1. Introduction
2. Theoretical Basis
2.1. Nonlinear Ultrasonic Guided Waves
2.2. Amplitude Coefficient of Second Harmonic Mode
- Phase matching: ;
- Non-zero power flux: .
3. Analytical Method of Second Harmonics Under Stress Change
3.1. Mode Shape Calculation
3.2. Analysis of Second Harmonics in Plate
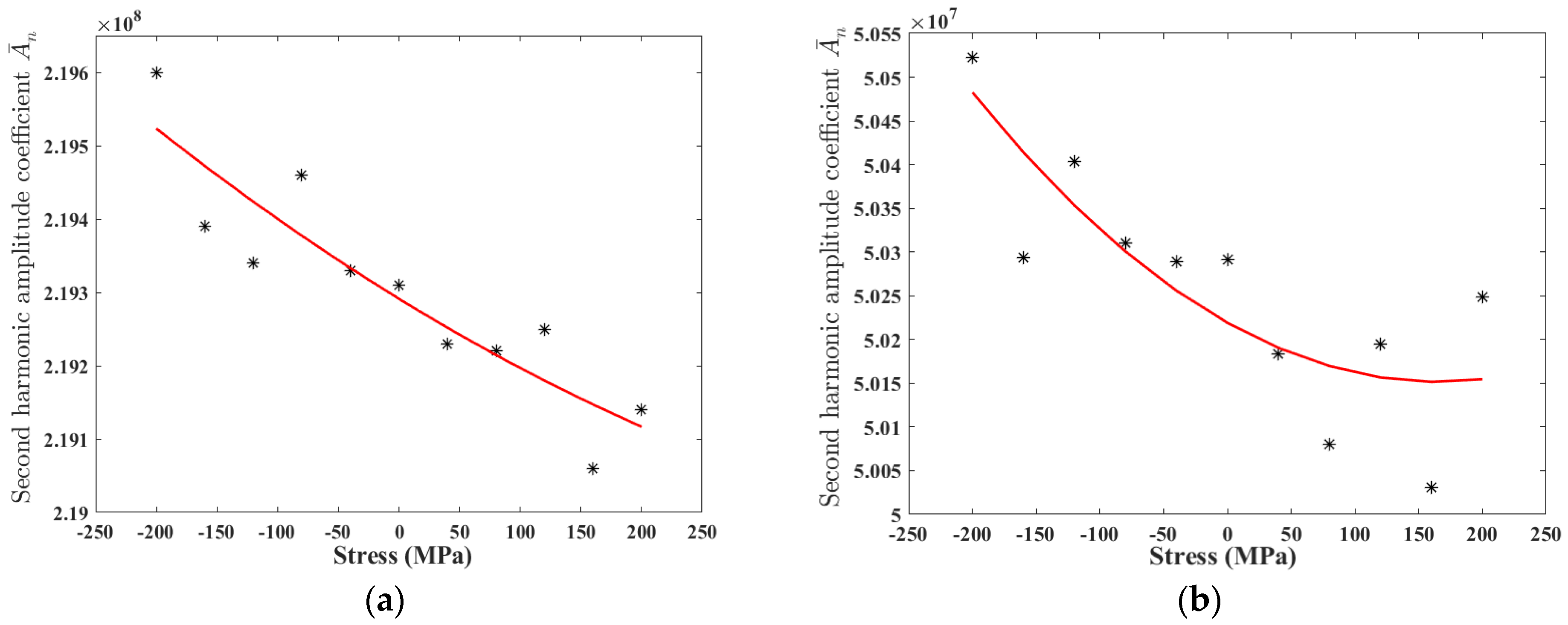
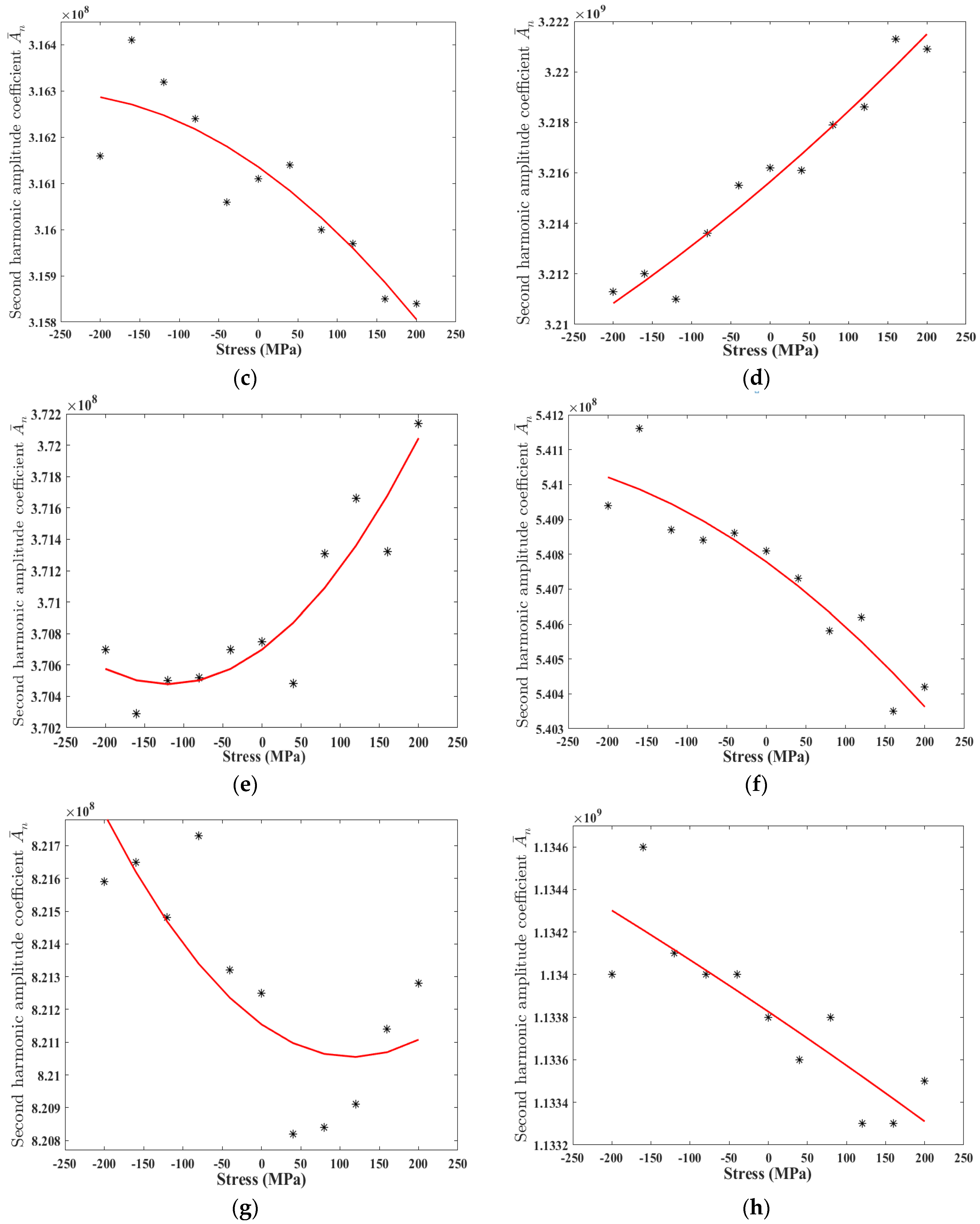
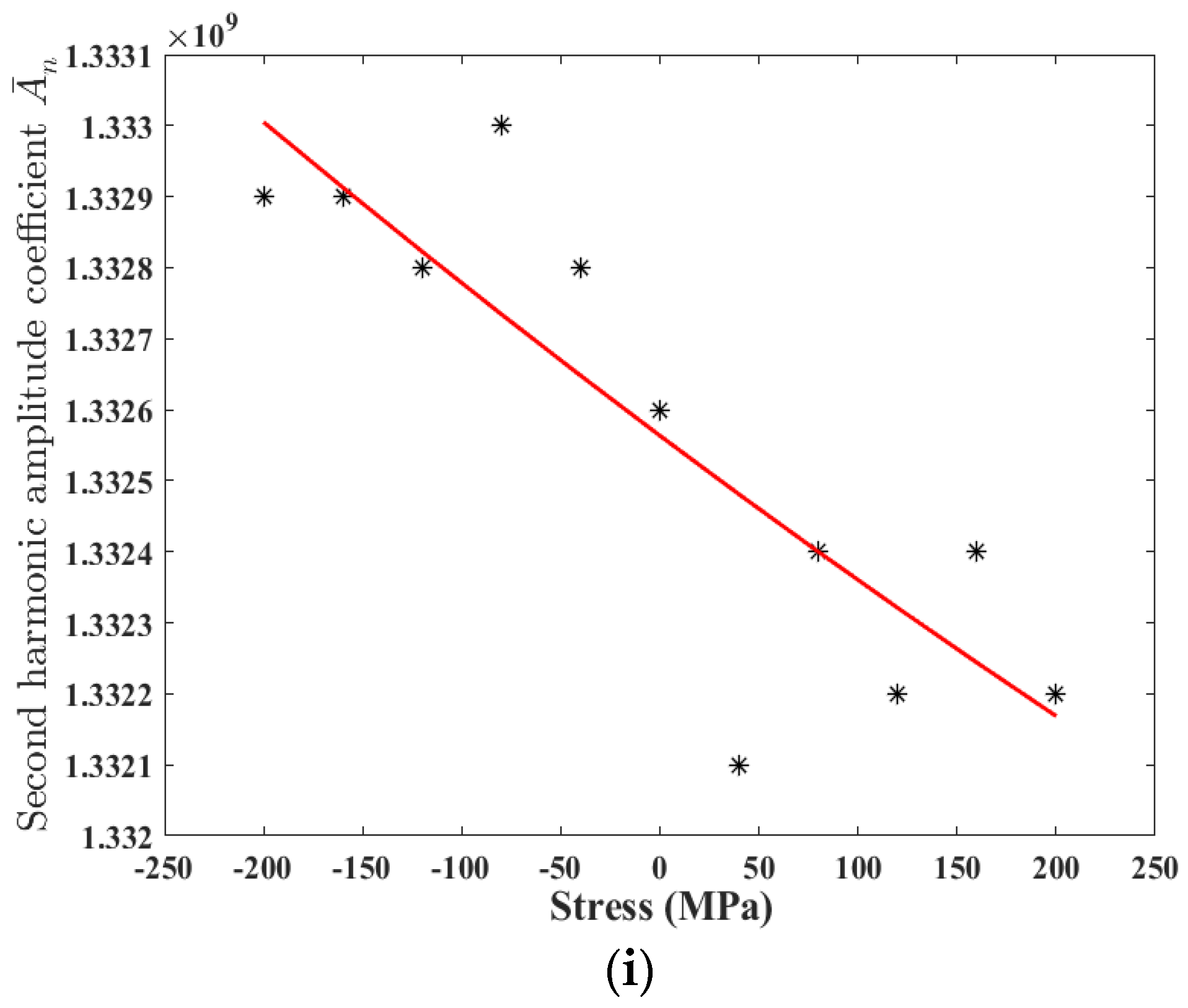
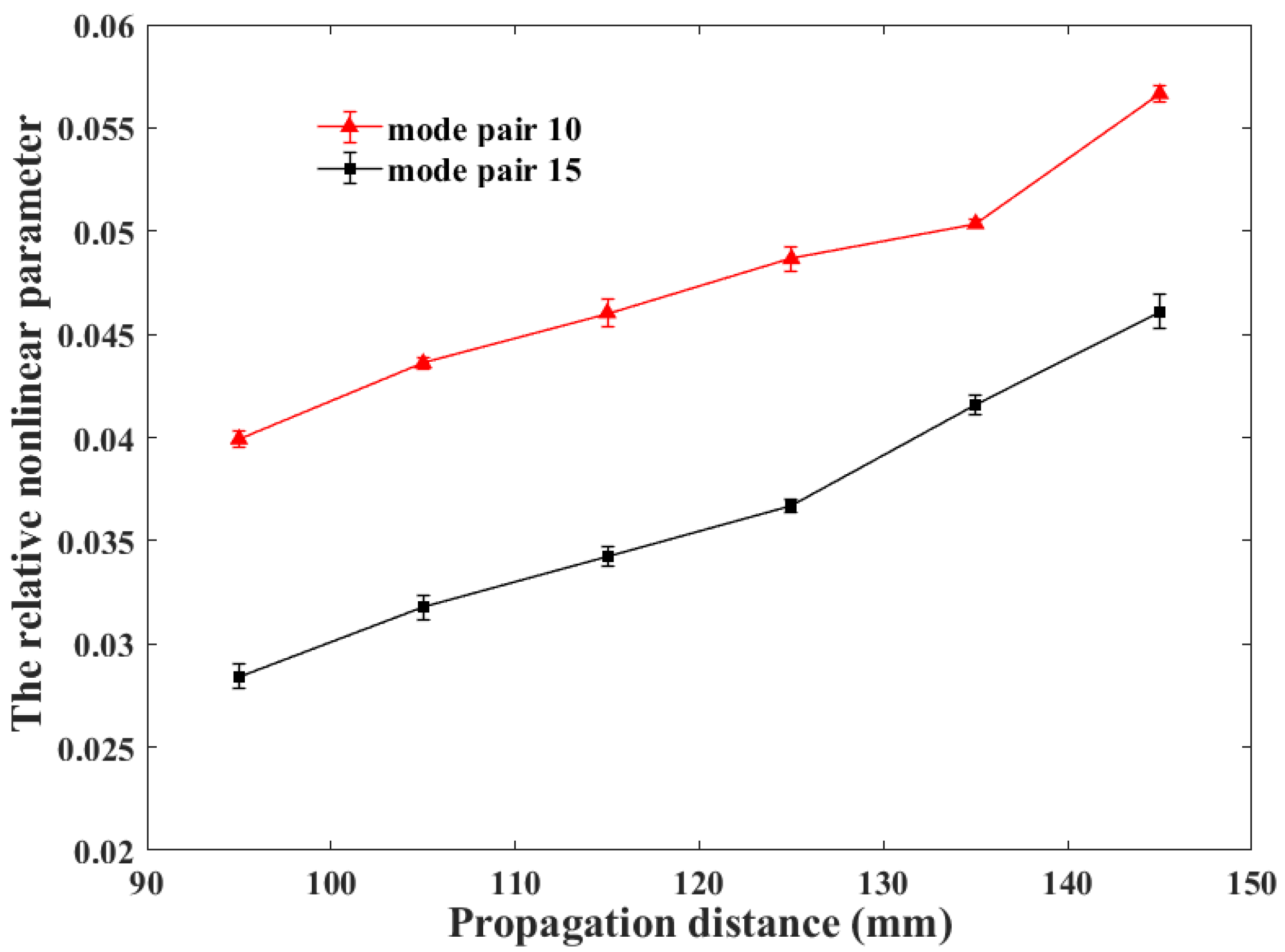
3.3. Response of Second Harmonics under Stress
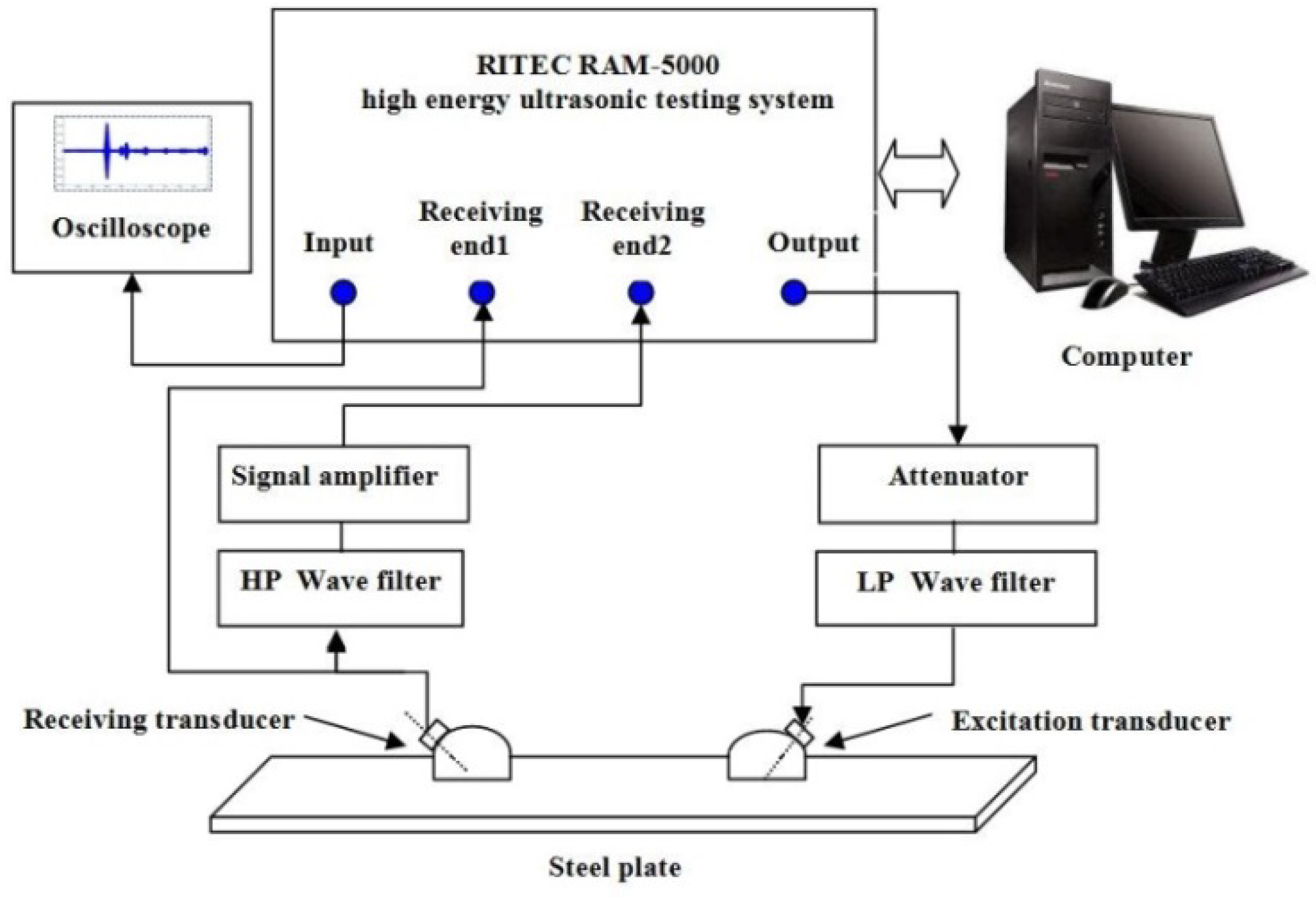
4. Experimental Verifications
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kawashima, K.; Omote, R.; Ito, T.; Fujita, H.; Shima, T. Nonlinear acoustic response through minute surface cracks: FEM simulation and experimentation. Ultrasonics 2002, 40, 611–615. [Google Scholar] [CrossRef]
- Brotherhood, C.J.; Drinkwater, B.W.; Dixon, S. The detectability of kissing bonds in adhesive joints using ultrasonic techniques. Ultrasonics 2003, 41, 521–529. [Google Scholar] [CrossRef]
- Bermes, C.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Experimental characterization of material nonlinearity using Lamb waves. Appl. Phys. Lett. 2007, 90, 2067–2073. [Google Scholar] [CrossRef]
- Walker, S.V.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Fatigue damage evaluation in A36 steel using nonlinear Rayleigh surface waves. NDT&E Int. 2012, 48, 10–15. [Google Scholar]
- Kim, G.; In, C.W.; Kim, J.Y.; Kurtis, K.E.; Jacobs, L.J. Air-coupled detection of nonlinear Rayleigh surface waves in concrete-application to microcracking detection. NDT&E Int. 2014, 67, 64–70. [Google Scholar]
- Thiele, S.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Air-coupled detection of nonlinear Rayleigh surface waves to assess material nonlinearity. Ultrasonics 2014, 54, 1470–1475. [Google Scholar] [CrossRef]
- Xiang, Y.X.; Deng, M.X.; Xuan, F.Z. Creep damage characterization using nonlinear ultrasonic guided wave method: A mesoscale model. J. Appl. Phys. 2014, 115, 044914. [Google Scholar] [CrossRef]
- Rose, J.L.; Avioli, M.J.; Mudgec, P.; Sanderson, R. Guided wave inspection potential of defects in rail. NDT&E Int. 2004, 37, 153–161. [Google Scholar]
- Mazzotti, M.; Marzani, A.; Bartoli, I.; Viola, E. Guided waves dispersion analysis for prestressed viscoelastic waveguides by means of the SAFE method. Int. J. Solids Struct. 2012, 49, 2359–2372. [Google Scholar] [CrossRef] [Green Version]
- Xing, B.; Yu, Z.J.; Xu, X.N.; Zhu, L.Q.; Shi, H.M. Research on a Rail Defect Location Method Based on a Single Mode Extraction Algorithm. Appl. Sci. 2019, 9, 1107. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.N.; Xing, B.; Zhuang, L.; Shi, H.M.; Zhu, L.Q. A Graphical Analysis Method of Guided Wave Modes in Rails. Appl. Sci. 2019, 9, 1529. [Google Scholar] [CrossRef] [Green Version]
- Shi, H.M.; Zhuang, L.; Xu, X.N.; Yu, Z.J.; Zhu, L.Q. An Ultrasonic Guided Wave Mode Selection and Excitation Method in Rail Defect Detection. Appl. Sci. 2019, 9, 1170. [Google Scholar] [CrossRef] [Green Version]
- Duan, X.Y.; Zhu, L.Q.; Yu, Z.J.; Xu, X.N. Estimating the Axial Load of In Service Continuously Welded Rail Under the Influences of Rail Wear and Temperature. IEEE Access 2019, 7, 143524–143538. [Google Scholar] [CrossRef]
- Bartoli, I.; Nucera, C.; Srivastava, A.; Salamone, S.; Phillips, R.; Di Scalea, F.; Coccia, S.; Sikorsky, C.S. Nonlinear ultrasonic guided waves for stress monitoring in prestressing tendons for post-tensioned concrete structures. Proc. SPIE 2009, 19, 230–235. [Google Scholar]
- Bartoli, I.; Coccia, S.; Phillips, R.; Srivastava, A.; Di Scalea, F.; Salamone, S. Stress dependence of guided waves in rails. Proc. SPIE 2010, 7650, 2101–2110. [Google Scholar]
- Liu, M.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Measuring residual stress using nonlinear ultrasound. API Conf. Proc. 2010, 1211, 1365–1372. [Google Scholar]
- Liu, M.; Kim, J.Y.; Jacobs, L.J.; Qu, J. Experimental study of nonlinear Rayleigh wave propagation in shot-peend aluminum plates—Feasibility of measuring residual stress. NDT&E Int. 2011, 44, 67–74. [Google Scholar]
- Yan, H.J.; Xu, C.G.; Xiao, D.G.; Cai, H.C. Research on Nonlinear Ultrasonic Properties of Tension Stess in Metal Materials. J. Mec. Eng. 2016, 52, 22–29. [Google Scholar] [CrossRef]
- Yan, H.J.; Liu, F.B.; Pan, Q.X. Nonlinear Ultrasonic Properties of Stress in 2024 Aluminum. Adv. Mat. Res. 2017, 1142, 371–377. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields and Waves in Solids; Robert E. Krieger Publishing Company: Malabar, FL, USA, 1990. [Google Scholar]
- Deng, M.X. Cumulative second-harmonic generation accompanying nonlinear shear horizontal mode propagation in a solid plate. J. Appl. Phys. 1998, 84, 3500–3505. [Google Scholar]
- Deng, M.X. Cumulative second-harmonic generation of Lamb-modes propagation in a solid plate. J. Appl. Phys. 1999, 85, 3051–3058. [Google Scholar] [CrossRef]
- Deng, M.X. Analysis of second-harmonic generation of Lamb modes using a modal analysis approach. J. Appl. Phys. 2003, 94, 4152–4159. [Google Scholar] [CrossRef]
- De Lima, W.J.N.; Hamilton, M.F. Finite-amplitude waves in isotropic elastic plates. J. Sound Vib. 2003, 265, 819–839. [Google Scholar] [CrossRef]
- De Lima, W.J.N.; Hamilton, M.F. Finite amplitude waves in isotropic elastic waveguides with arbitrary constant cross sectional area. Wave Motion 2005, 41, 1–11. [Google Scholar] [CrossRef]
- Chillara, V.K.; Lissenden, C.J. Interaction of guided wave modes in isotropic weakly nonlinear elastic plates: Higher harmonic generation. J. Appl. Phys. 2012, 111, 4909–4915. [Google Scholar]
- Srivastava, A.; Di Scalea, F. On the existence of antisymmetric or symmetric Lamb waves at nonlinear higher harmonics. J. Sound Vib. 2009, 323, 932–943. [Google Scholar] [CrossRef]
- Lee, T.H.; Choi, I.H. The nonlinearity of guided wave in an elastic plate. Mod. Phys. Lett. B 2008, 22, 1135–1140. [Google Scholar] [CrossRef]
- Pruell, C.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Evaluation of plasticity driven material damage using Lamb waves. Appl. Phys. Lett. 2007, 91, 231911. [Google Scholar] [CrossRef]
- Deng, M.X.; Xiang, Y.; Liu, L. Time-domain analysis and experimental examination of cumulative second-harmonic generation by primary Lamb wave propagation. J. Appl. Phys. 2011, 109, 113525. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Kim, J.Y.; Jacobs, L.J.; Qu, J.; Li, Z. Experimental investigation of symmetry properties of second harmonic Lamb waves. J. Appl. Phys. 2012, 111, 381–389. [Google Scholar] [CrossRef]
- Liu, Y.; Chillara, V.K.; Lissenden, C.J. On selection of primary modes for generation of strong internally resonant second harmonics in plates. J. Sound Vib. 2013, 33, 4517–4528. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity, 2nd ed.; Permagon Press: New York, NY, USA, 1970. [Google Scholar]
- Chillara, V.K.; Lissenden, C.J. Nonlinear guided waves in plates: A numerical perspective. Ultrasonics 2014, 54, 1553–1558. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, Z.A. Interaction of plane longitudinal and transverse elastic waves. Sov. Phys. Acoust. 1960, 6, 306–310. [Google Scholar]
- Nucera, C.; Di Scalea, F. Nonlinear Semianalytical Finite-Element Algorithm for the Analysis of Internal Resonance Conditions in Complex Waveguides. J. Eng. Mech. 2014, 140, 502–522. [Google Scholar] [CrossRef]
- Müller, M.F.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Characteristics of second harmonic generation of Lamb waves in nonlinear elastic plates. J. Acoust. Soc. Am. 2010, 127, 2141–2152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Loveday, P.W. Semi-analytical finite element analysis of elastic waveguides subjected to axial loads. Ultrasonics 2008, 49, 298–300. [Google Scholar] [CrossRef]
- Nucera, C.; Di Scalea, F. Nondestructive measurement of neutral temperature in continuous welded rails by nonlinear ultrasonic guided waves. J. Acoust. Soc. Am. 2014, 136, 2561–2574. [Google Scholar] [CrossRef]
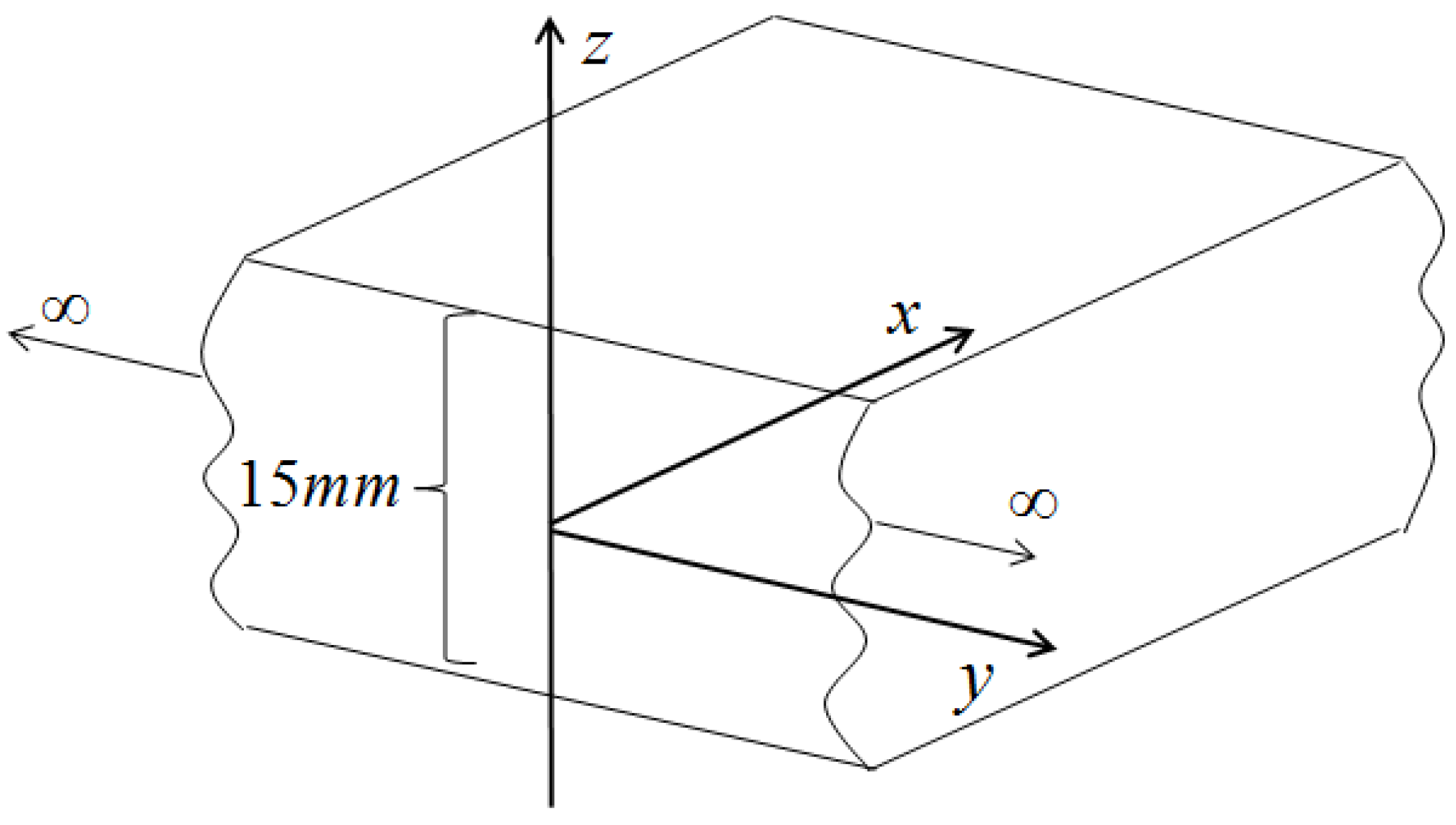

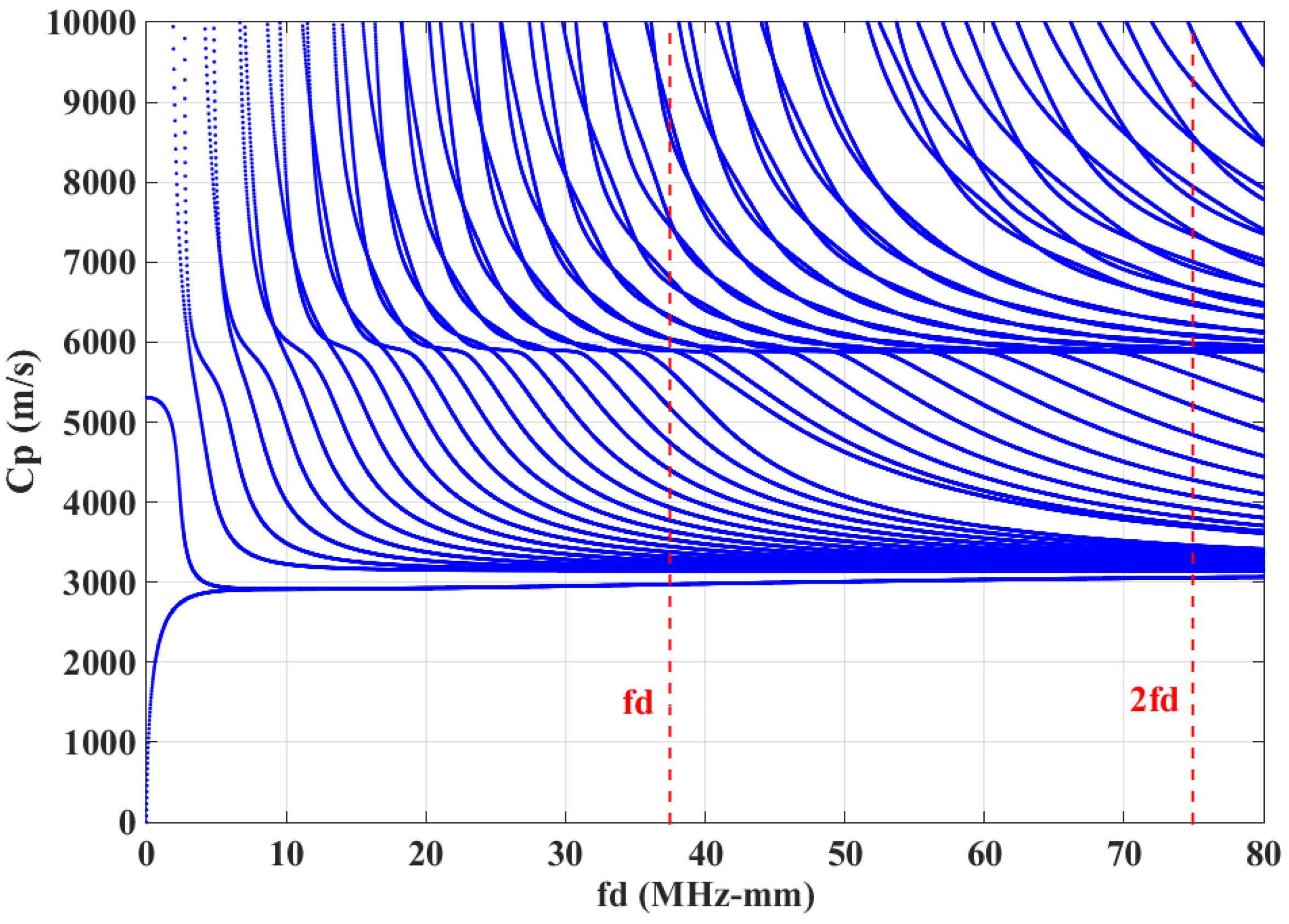
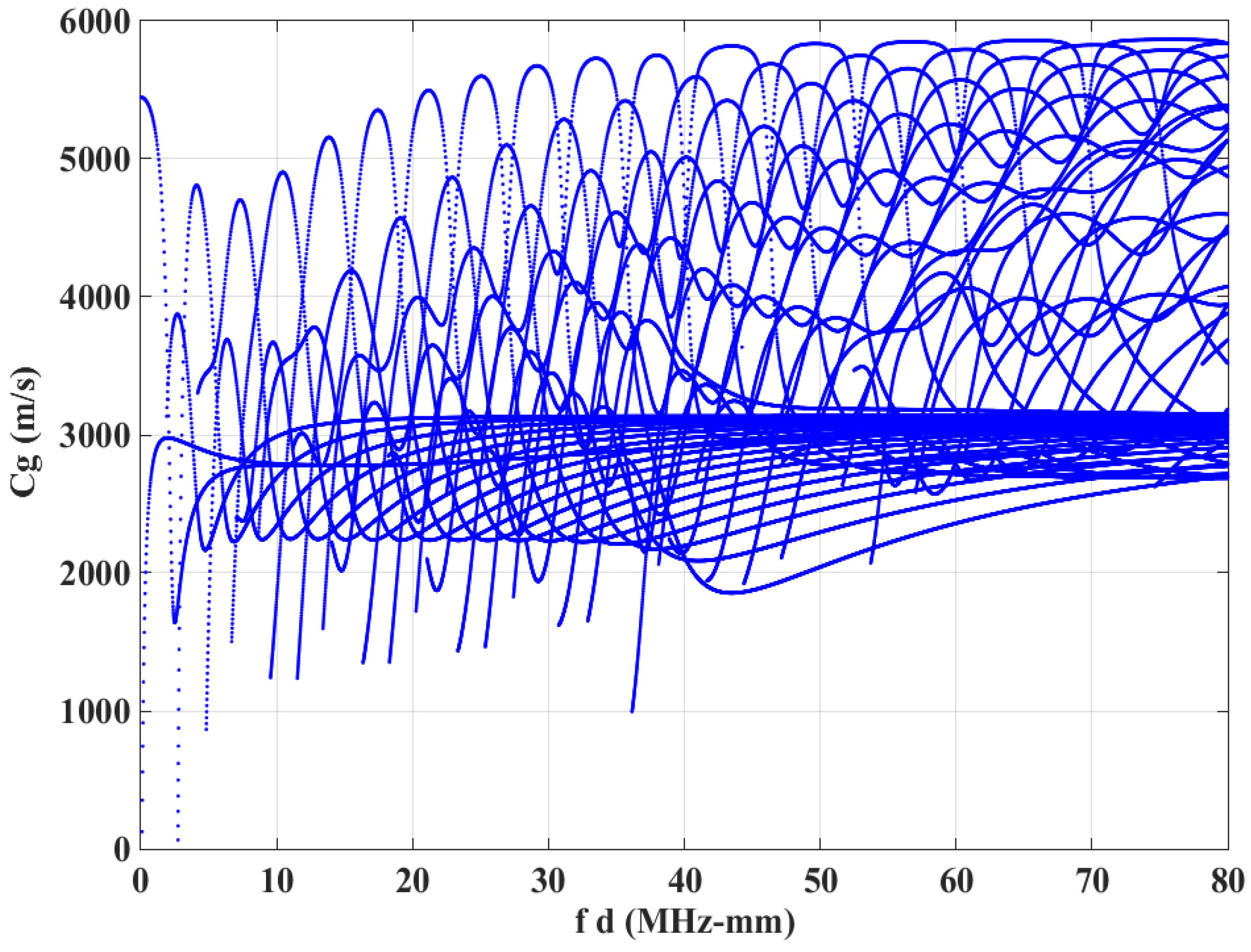

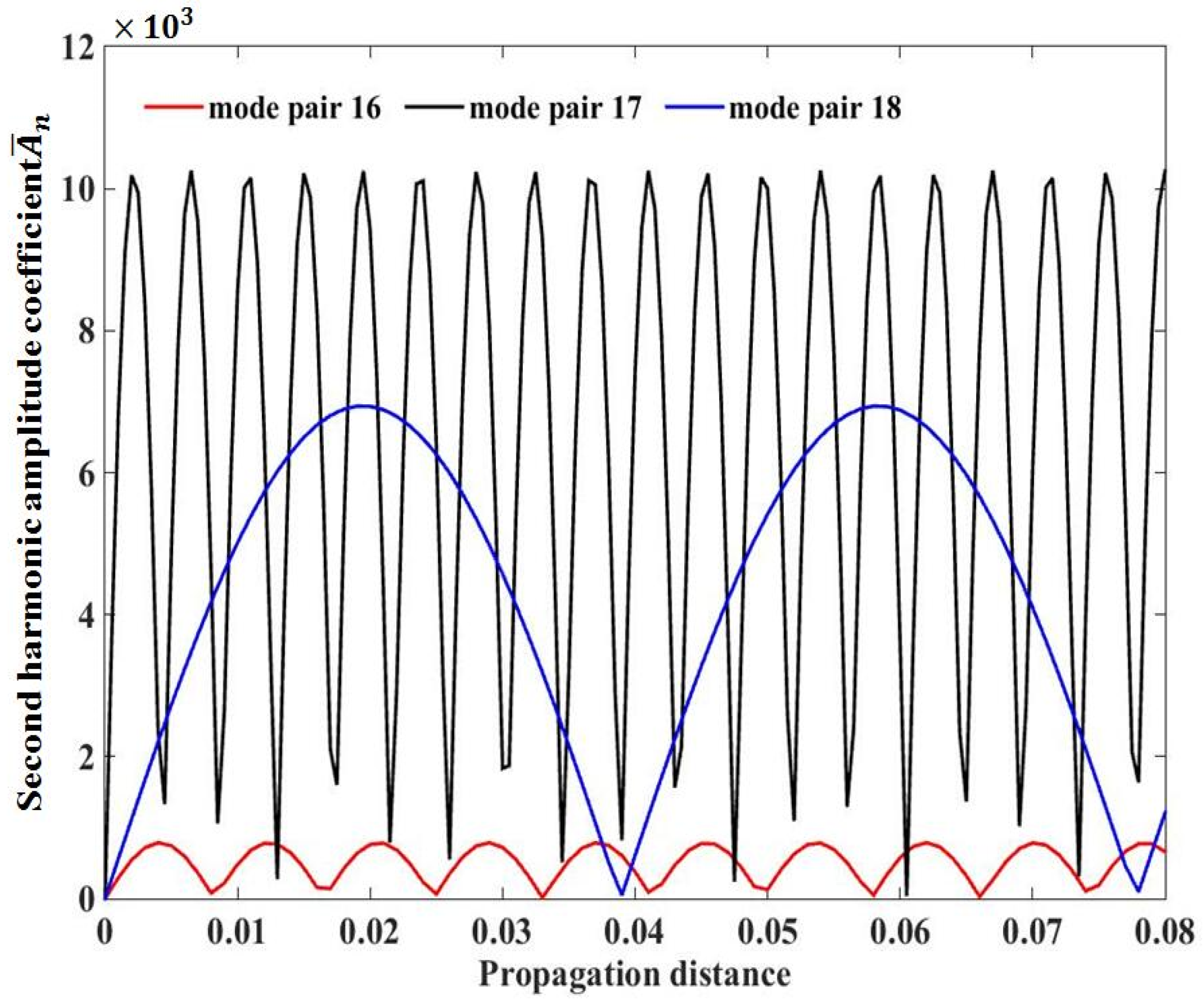



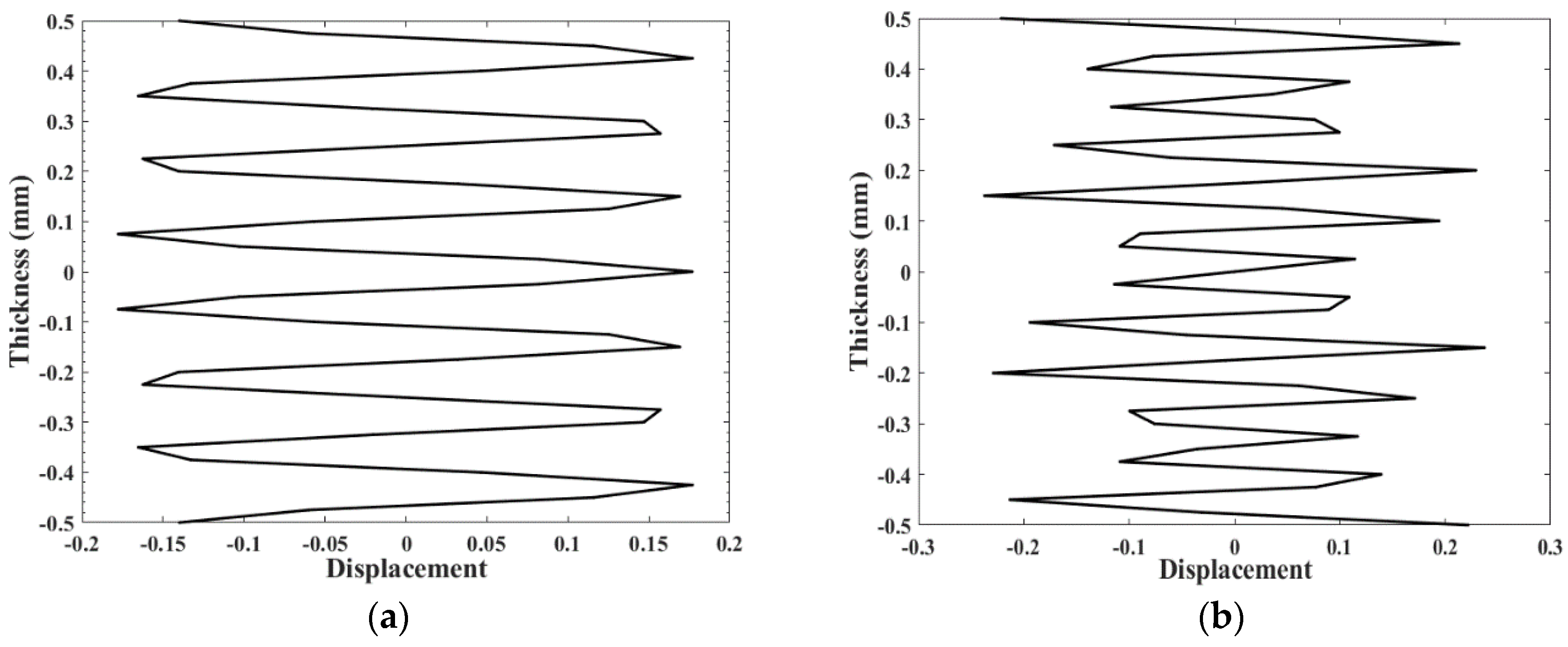
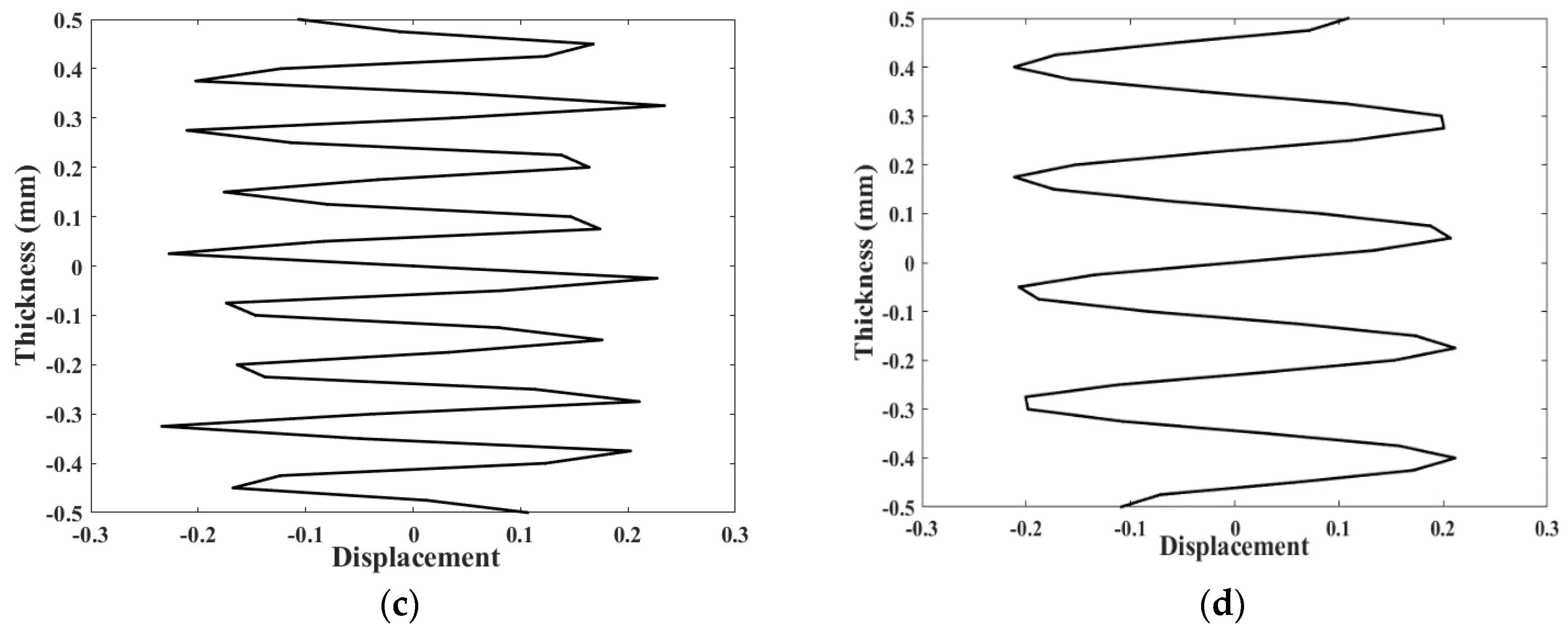


| 7932 | 116 | 83 | −340 | −647 | −17 |
| Number of Mode Pair | Frequency-Thickness | Phase Velocity (m/s) | Group Velocity (m/s) | Modal Shape | |
|---|---|---|---|---|---|
| 1 | 37.5 | 3144 | 3013 | S | 0 |
| 75 | 3141 | 2771 | A | ||
| 2 | 37.5 | 3144 | 3013 | S | 0 |
| 75 | 3144 | 3505 | A | ||
| 3 | 37.5 | 3154 | 1372 | A | 0 |
| 75 | 3160 | 2741 | A | ||
| 4 | 37.5 | 3171 | 1294 | S | 0 |
| 75 | 3180 | 2617 | A | ||
| 5 | 37.5 | 3195 | 1361 | S | 0 |
| 75 | 3206 | 2706 | A | ||
| 6 | 37.5 | 5904 | 2132 | A | 0 |
| 75 | 5908 | 4917 | A | ||
| 7 | 37.5 | 3171 | 1294 | S | 10.91 |
| 75 | 3169 | 2744 | S | ||
| 8 | 37.5 | 3144 | 3013 | S | 12.97 |
| 75 | 3147 | 2765 | S | ||
| 9 | 37.5 | 3195 | 1361 | S | 145.63 |
| 75 | 3192 | 3142 | S | ||
| 10 | 37.5 | 3933 | 1088 | A | 195.04 |
| 75 | 3920 | 2492 | S | ||
| 11 | 37.5 | 3448 | 1271 | A | 262.33 |
| 75 | 3458 | 2331 | S | ||
| 12 | 37.5 | 3227 | 1343 | A | 288.42 |
| 75 | 3223 | 2728 | S | ||
| 13 | 37.5 | 3267 | 3013 | S | 479.75 |
| 75 | 3263 | 2644 | S | ||
| 14 | 37.5 | 3316 | 1303 | A | 695.08 |
| 75 | 3315 | 2581 | S | ||
| 15 | 37.5 | 3376 | 1275 | S | 834.27 |
| 75 | 3382 | 2488 | S | ||
| 16 | 50 | 3170 | 1828 | S | 12.19 |
| 75 | 3169 | 2744 | S | ||
| 17 | 37.5 | 3535 | 1349 | S | 27.32 |
| 75 | 3263 | 2644 | S | ||
| 18 | 37.5 | 3641 | 1176 | A | 40.87 |
| 75 | 3315 | 2581 | S |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, X.; Zhu, L.; Yu, Z. The Effects of Stress on Second Harmonics in Plate-Like Structures. Appl. Sci. 2020, 10, 5124. https://doi.org/10.3390/app10155124
Niu X, Zhu L, Yu Z. The Effects of Stress on Second Harmonics in Plate-Like Structures. Applied Sciences. 2020; 10(15):5124. https://doi.org/10.3390/app10155124
Chicago/Turabian StyleNiu, Xiaochuan, Liqiang Zhu, and Zujun Yu. 2020. "The Effects of Stress on Second Harmonics in Plate-Like Structures" Applied Sciences 10, no. 15: 5124. https://doi.org/10.3390/app10155124
APA StyleNiu, X., Zhu, L., & Yu, Z. (2020). The Effects of Stress on Second Harmonics in Plate-Like Structures. Applied Sciences, 10(15), 5124. https://doi.org/10.3390/app10155124





