Field Monitoring of the Deformation and Internal Forces of the Surrounding Rock and Support Structures in the Construction of a Super-Span High-Speed Railway Tunnel—A Case Study
Abstract
:1. Introduction
2. Project Overview and In-Situ Monitoring
2.1. Badaling Great Wall Station
2.2. Geological Conditions
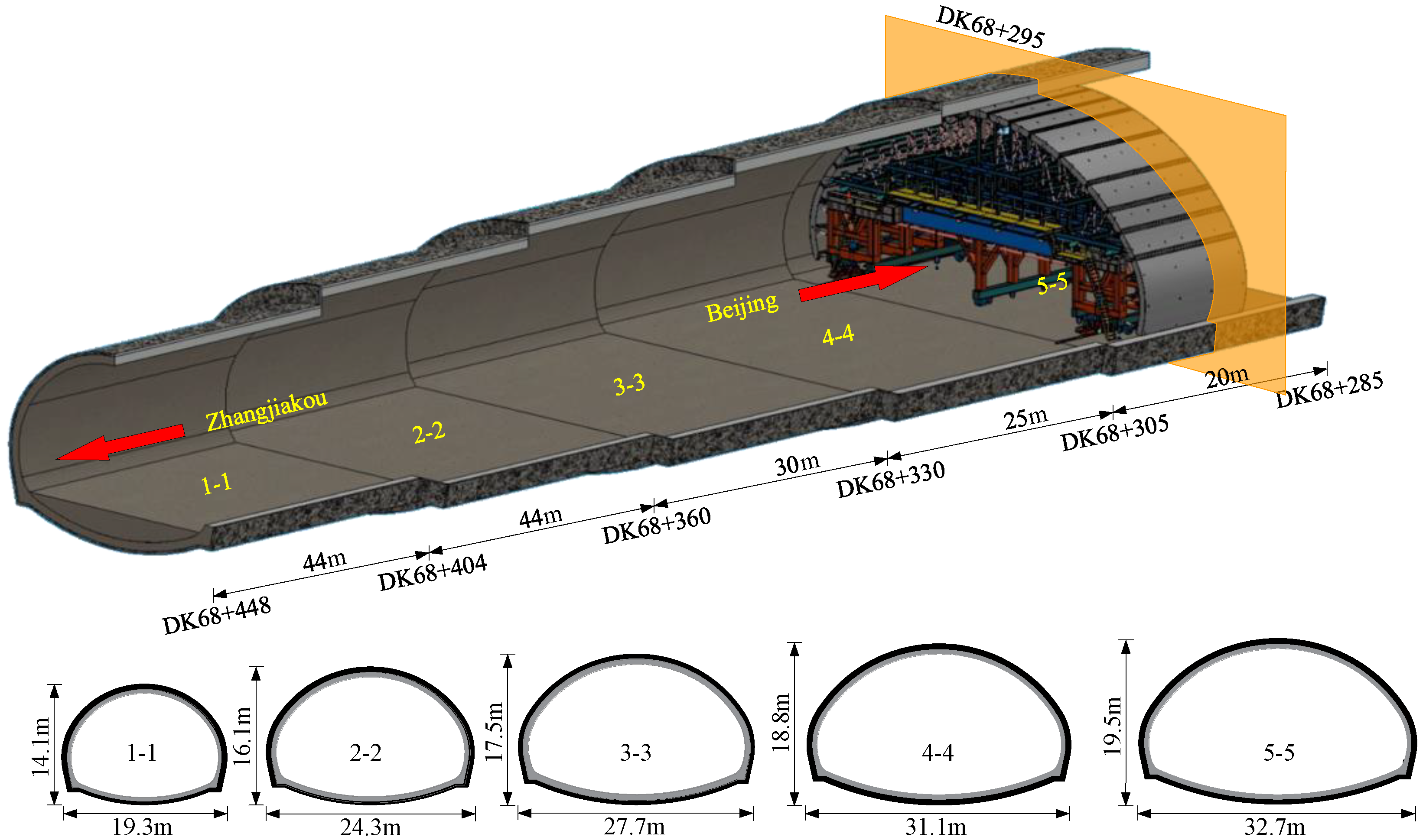
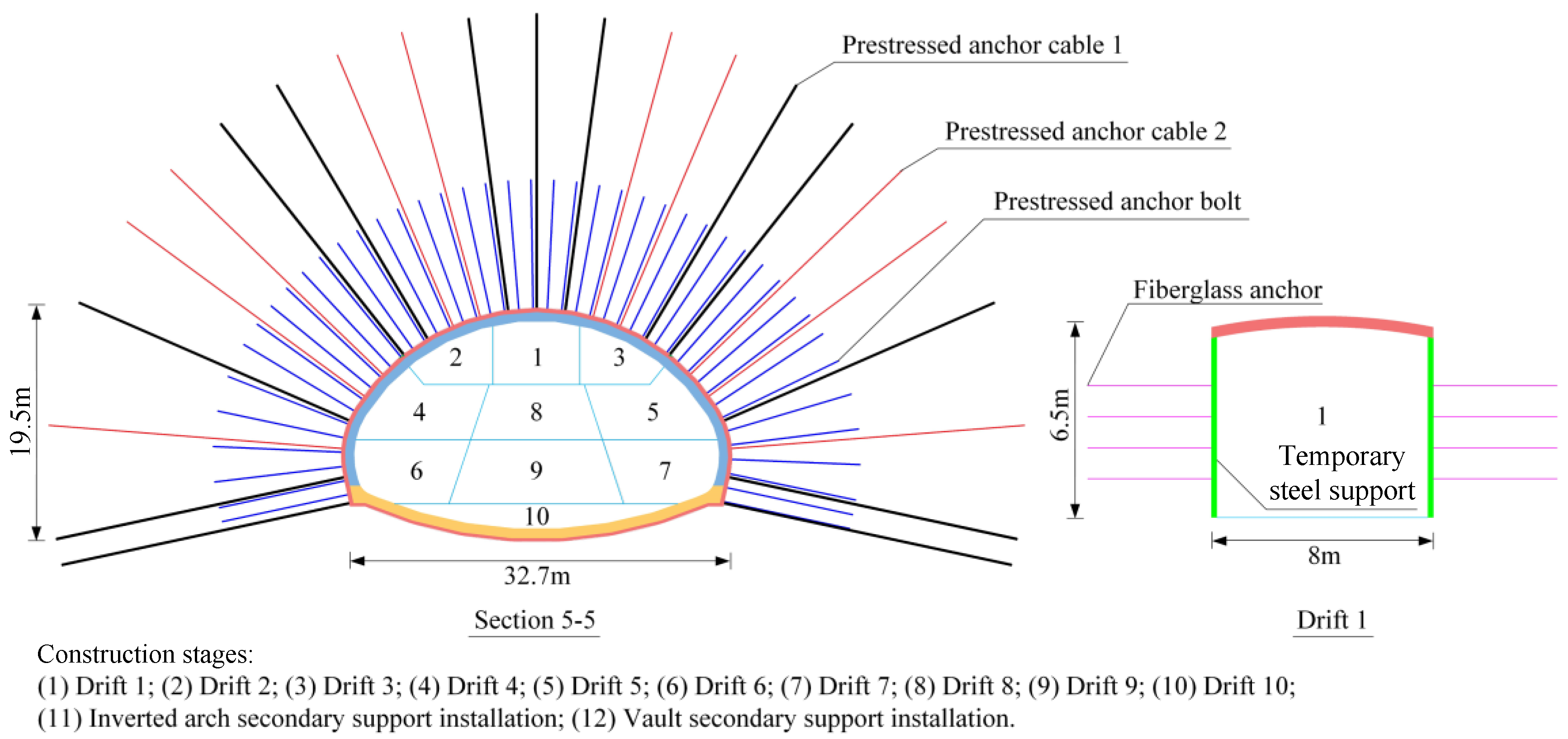
2.3. Structure of the Tunnel
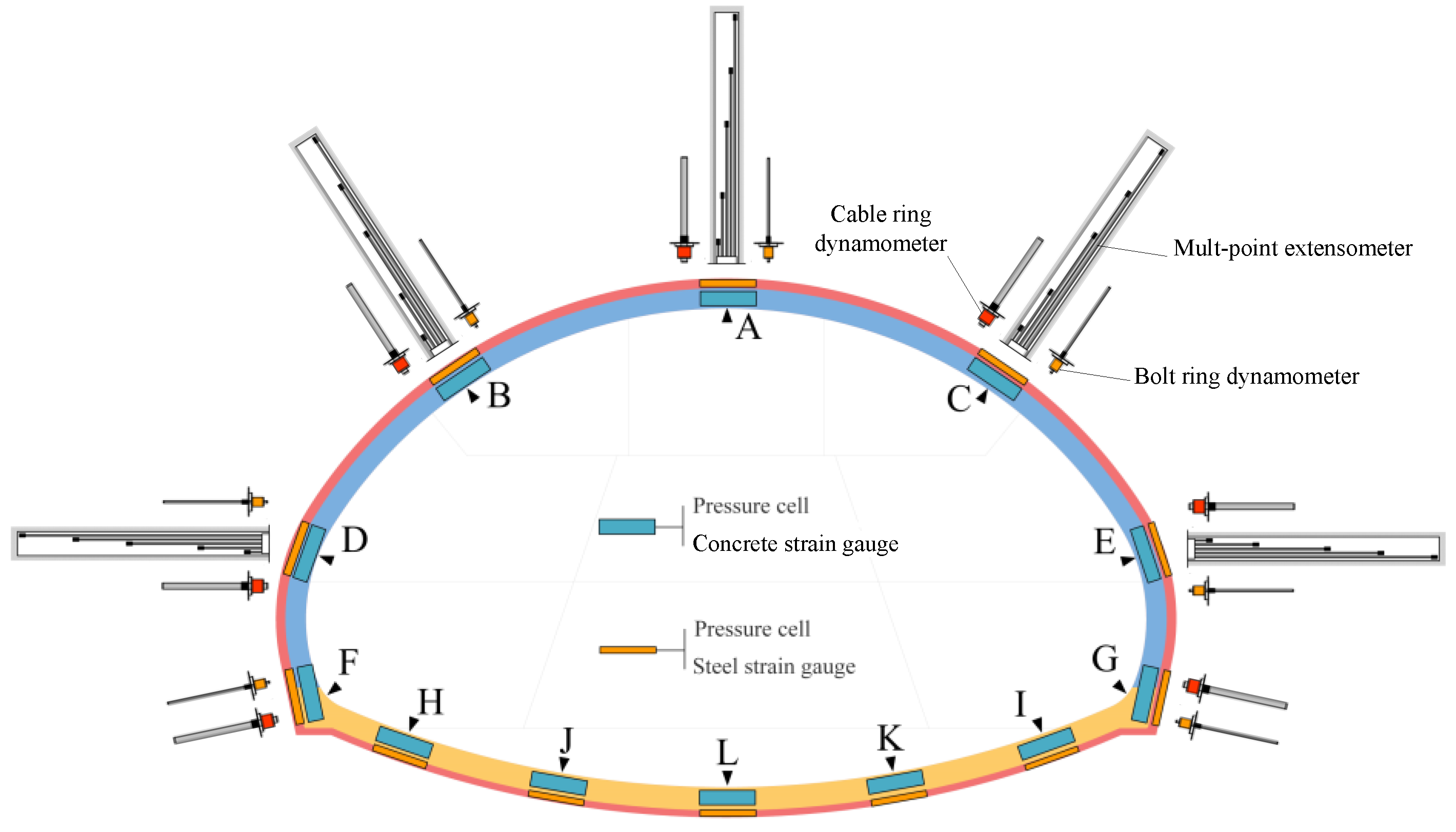
2.4. Monitoring Arrangement
3. Monitoring Results and Analysis
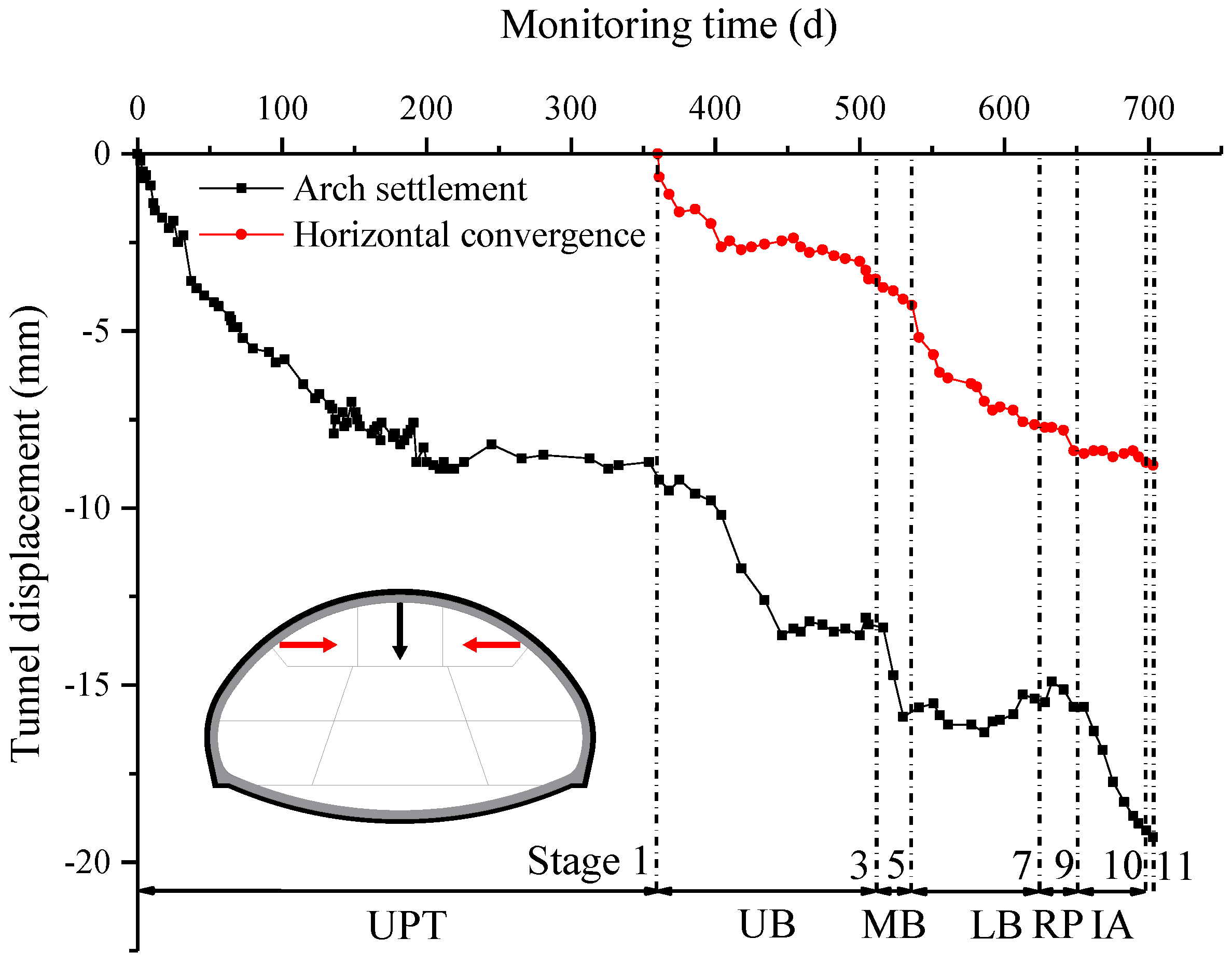
3.1. Tunnel Displacement
3.2. Internal Displacement of the Surrounding Rock
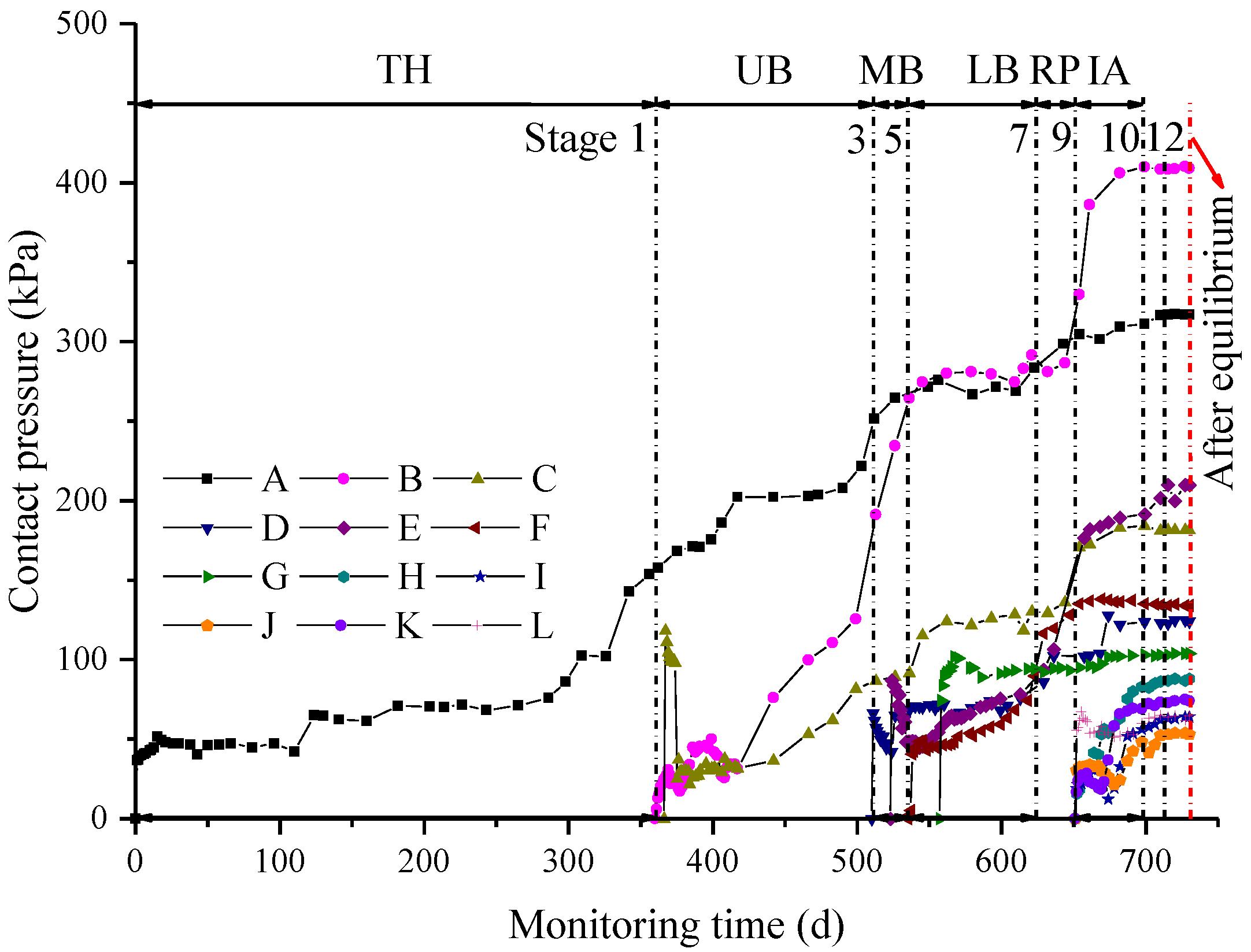
3.3. Contact Pressure between the Surrounding Rock and the Primary Supports
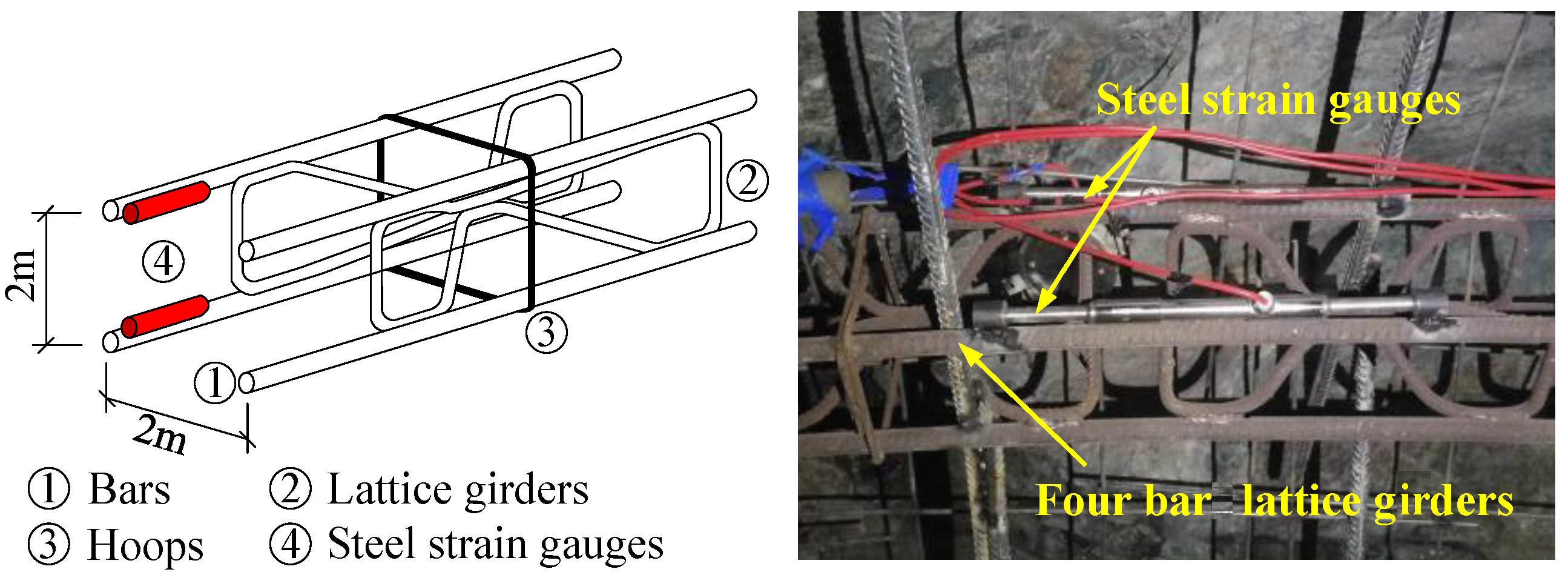
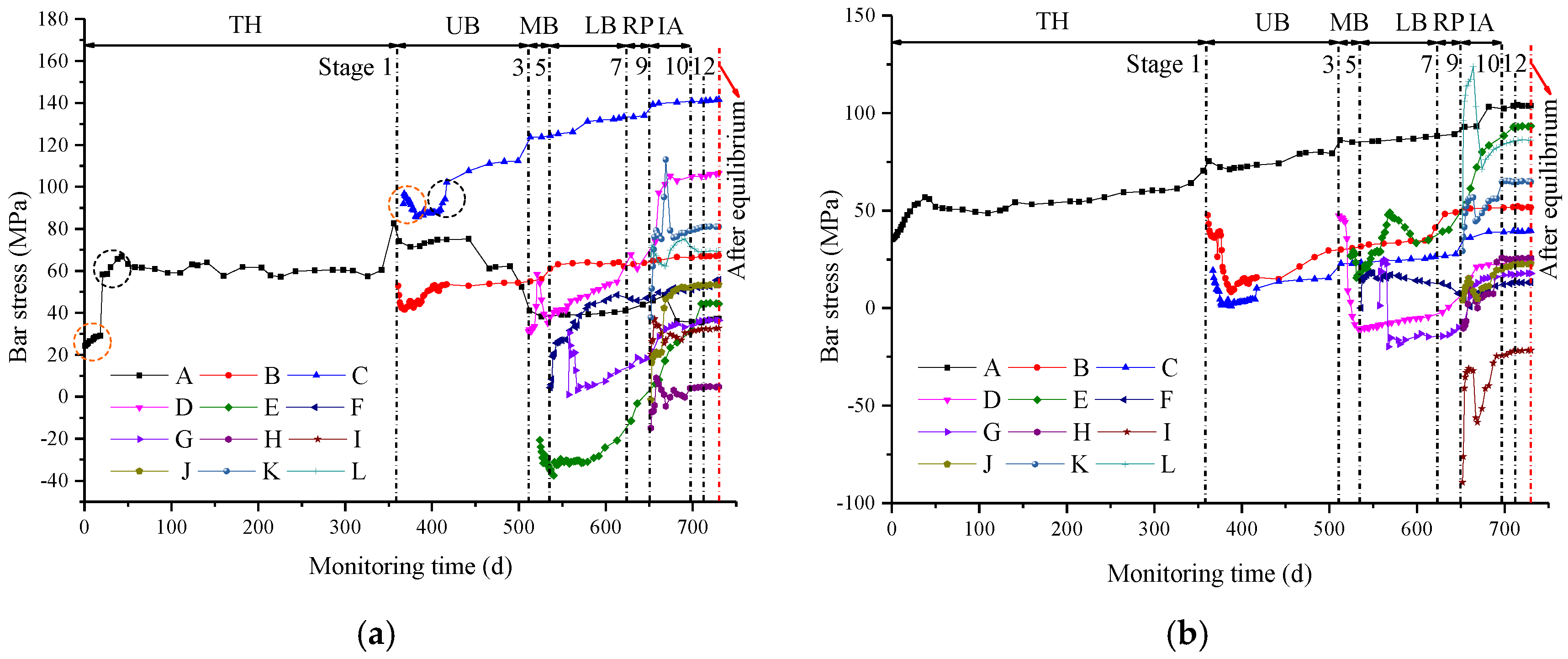
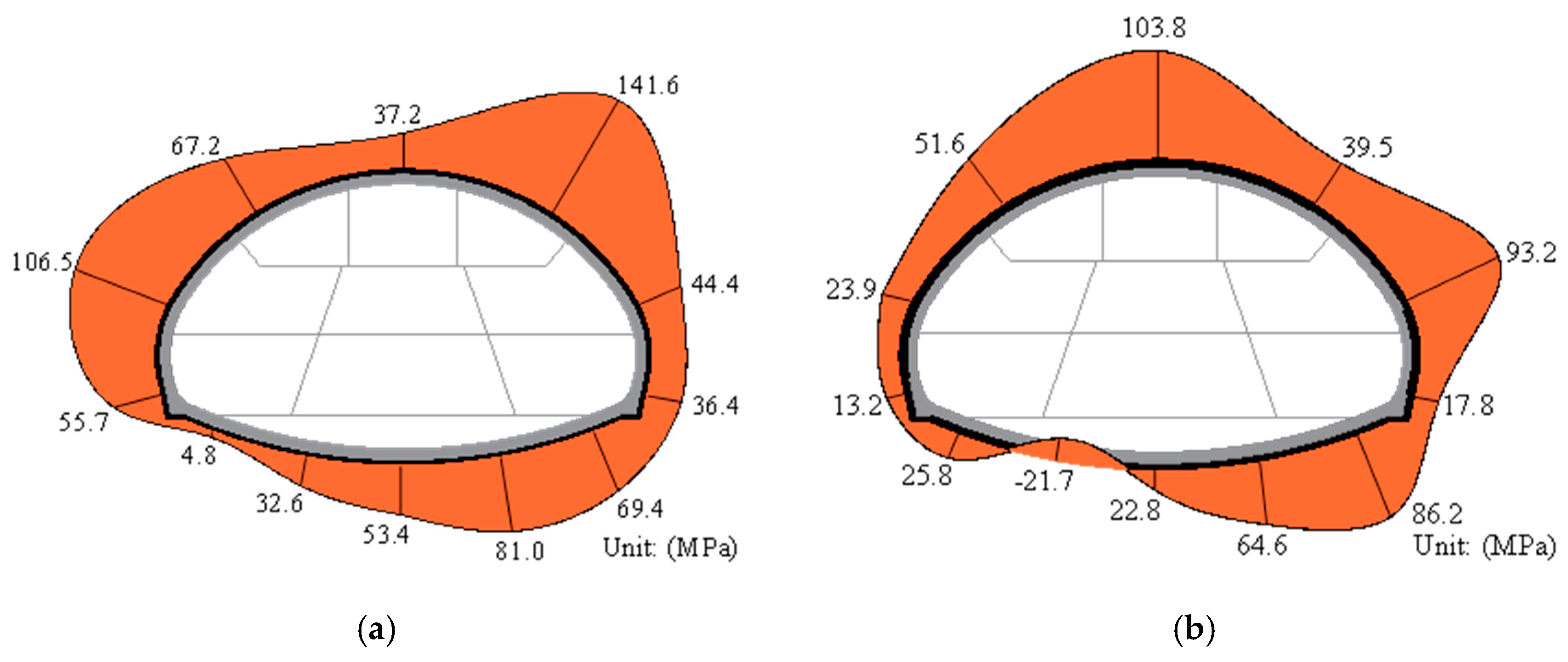
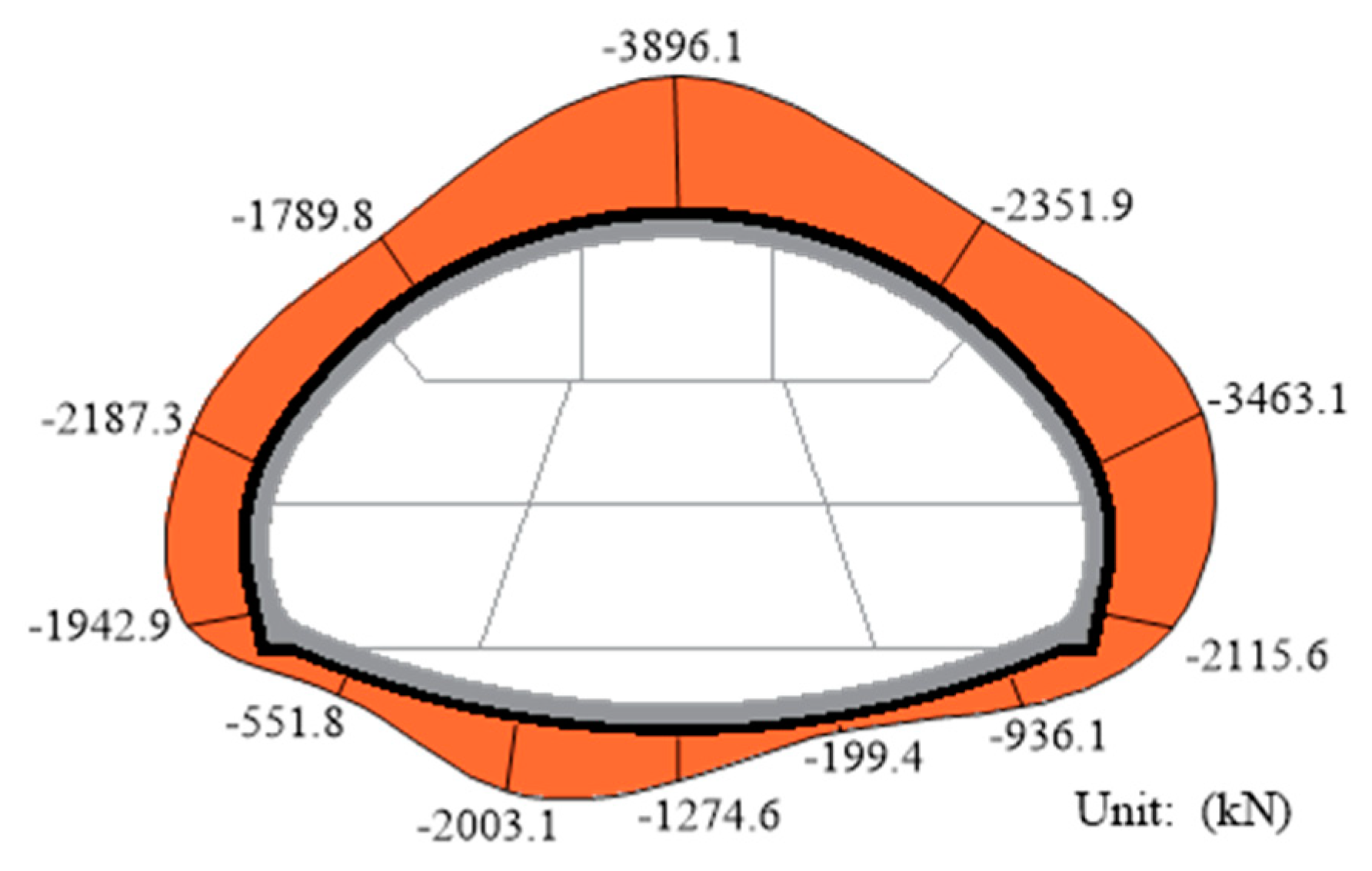
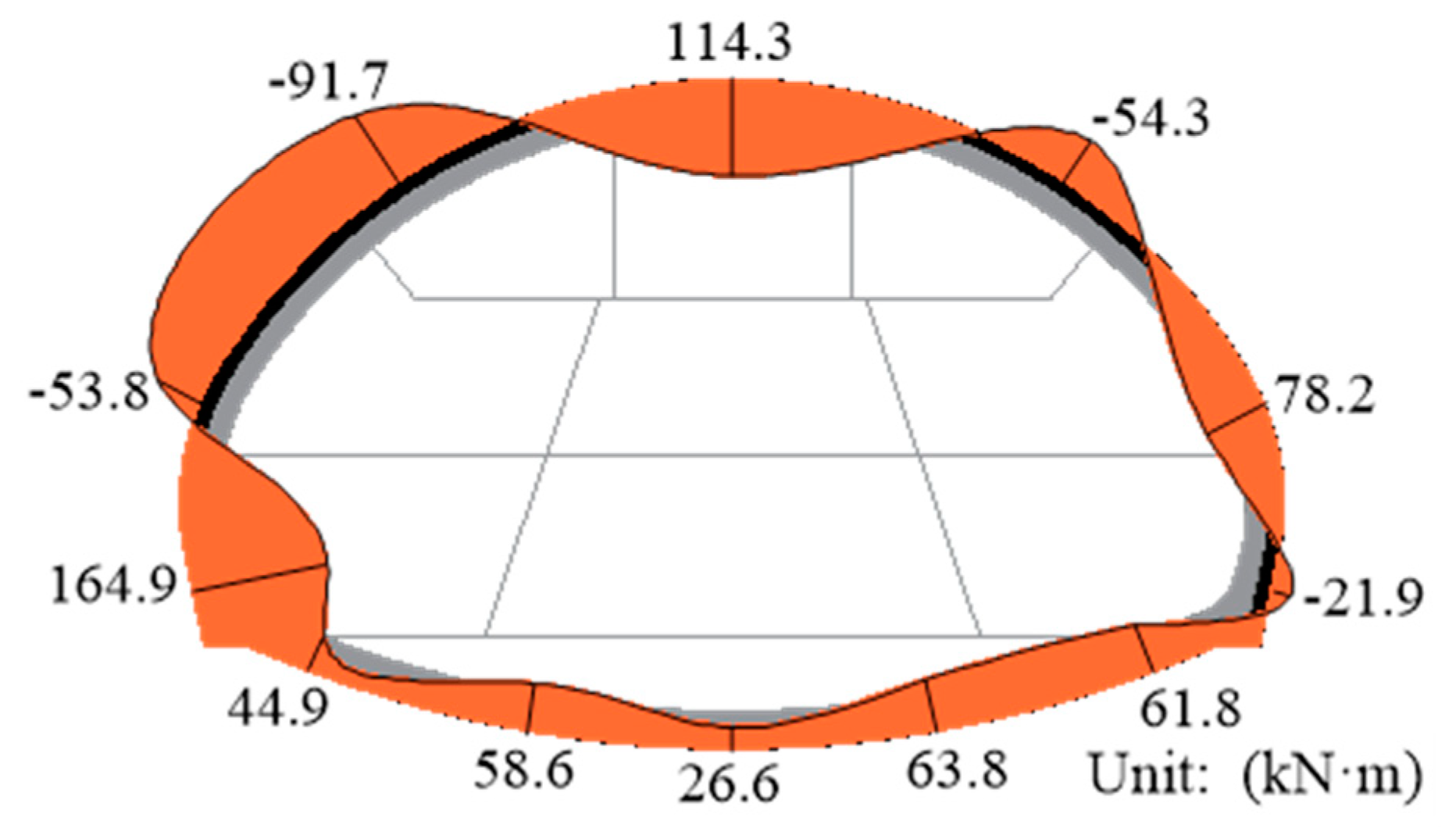
3.4. Internal Force in the Four Bar Lattice Girders
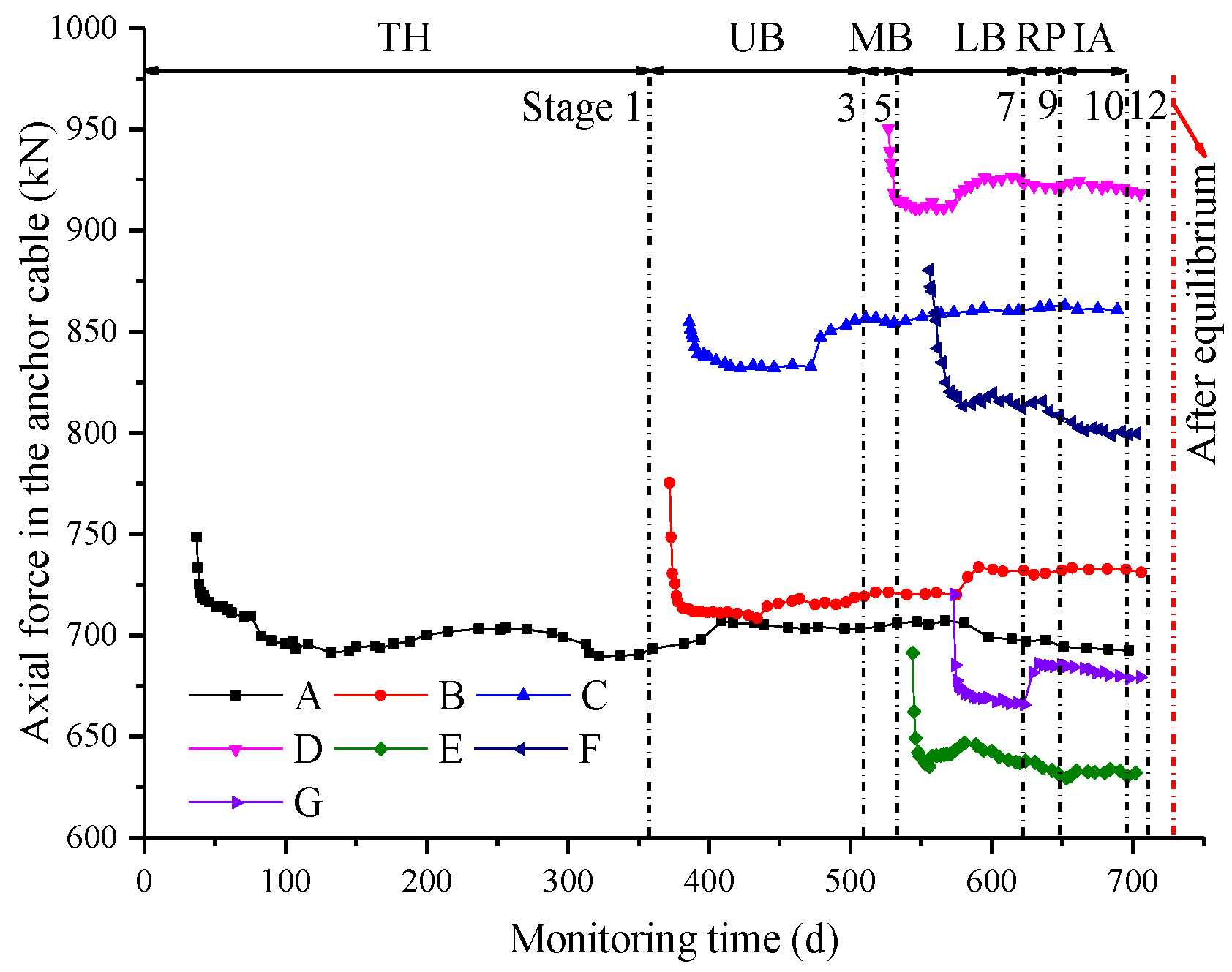
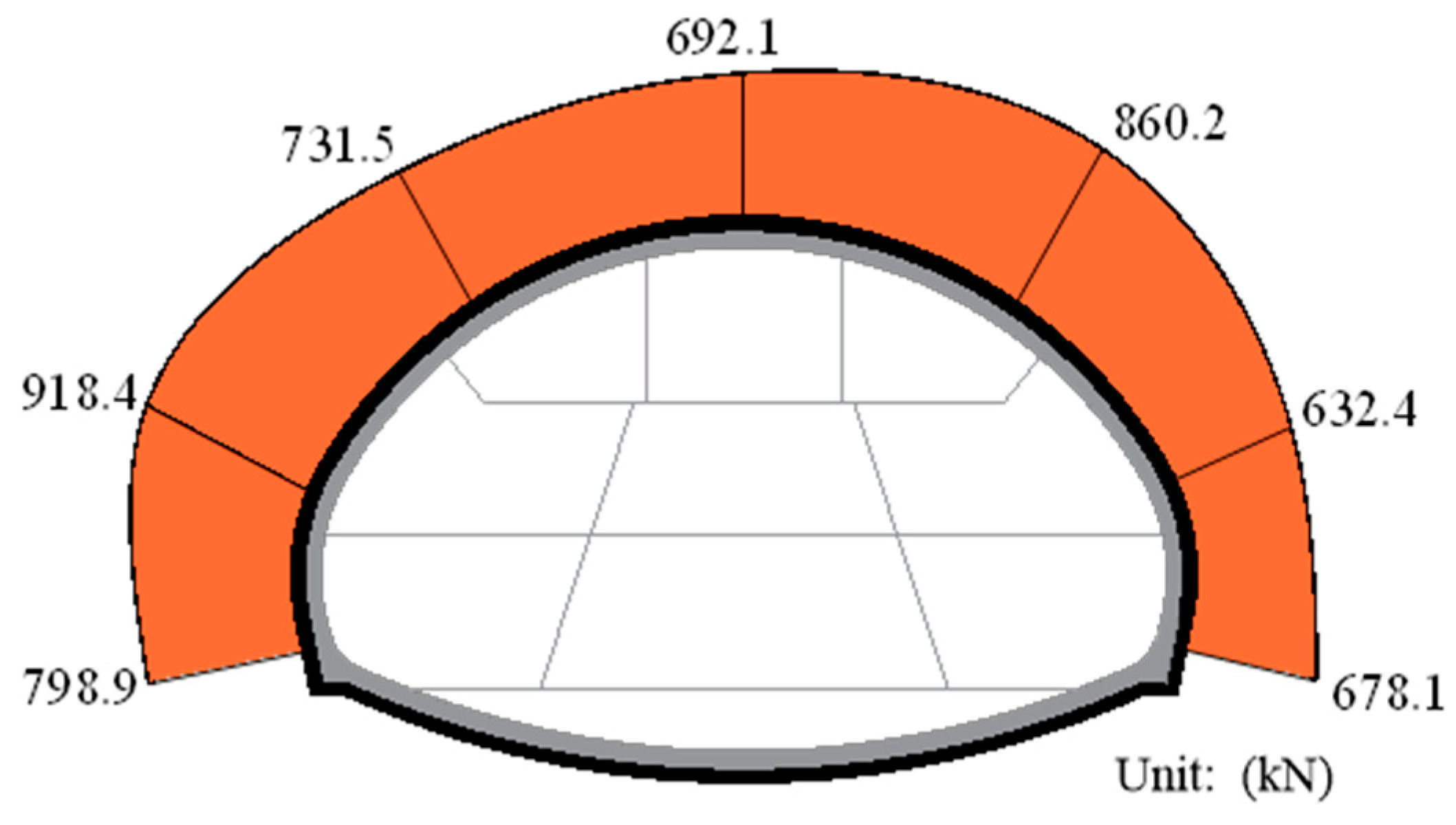
3.5. Axial Force in the Anchor Cables
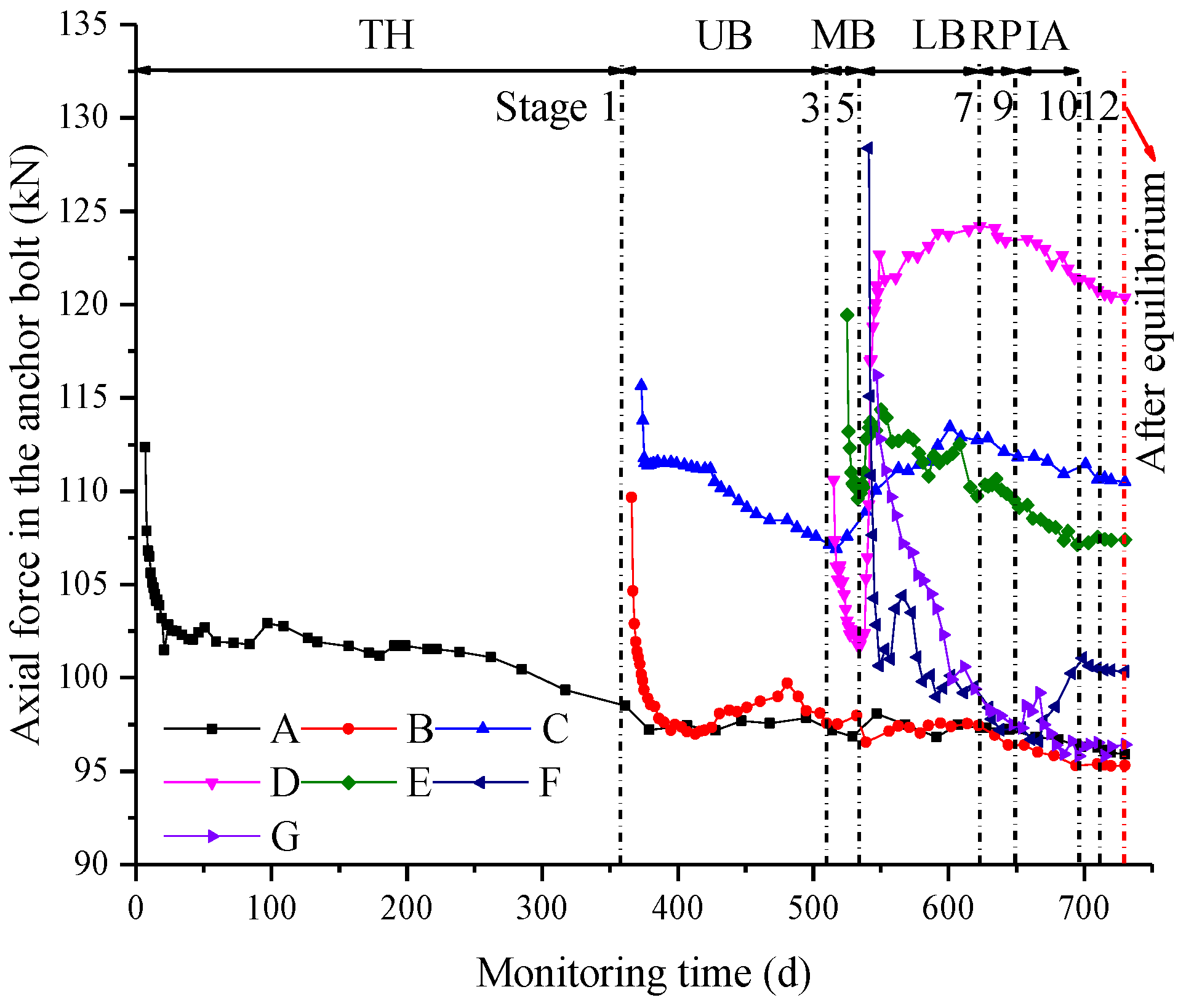
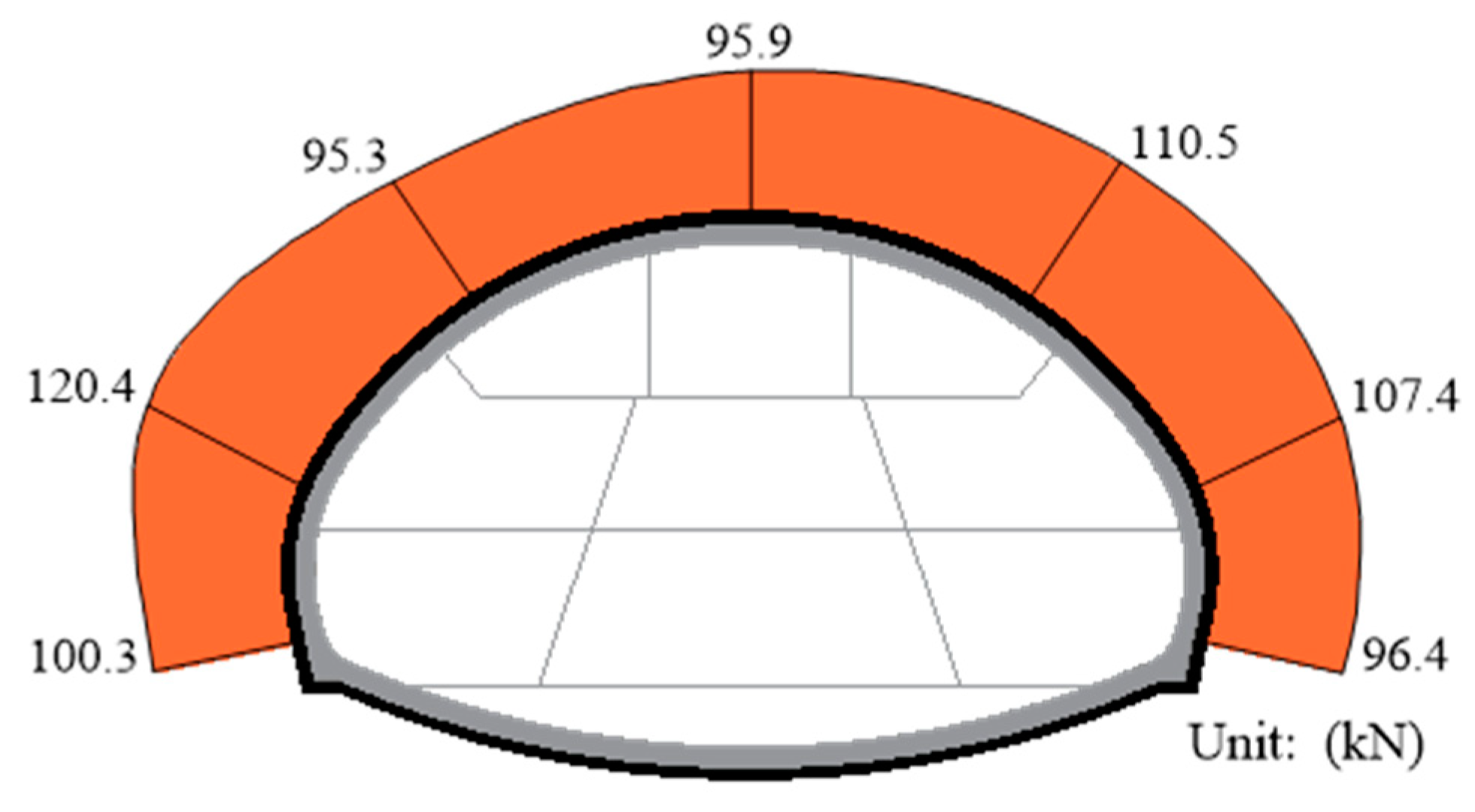
3.6. Axial Force in the Anchor Bolts
3.7. Contact Pressure between the Primary and Secondary Supports
3.8. Internal Force in the Secondary Supports
4. Conclusions
- (1)
- The internal displacement of the rock surrounding the tunnel increased greatly at the very beginning of the excavation. After stabilization, the internal displacements of the surrounding rock within 13 m from the orifice were significantly greater than that of the surrounding rock within 13–25 m from the orifice.
- (2)
- By using the analysis method of the special time points combined with the deformation increments at different depths, the critical range of damage of the surrounding rock was obtained. The ranges of the damage of the surrounding rock at different positions were controlled to within 9 m. The range of the damage of the surrounding rock at the tunnel’s crown was greater than that at the tunnel’s spandrel, which was even greater than that at the haunch of the tunnel.
- (3)
- For the larger range of the damage of the surrounding rock at the tunnel’s crown, anchor cables with larger prestresses were used to limit its development. The axial forces in the anchor bolts and the anchor cables showed a rapid drop at the beginning of the installation, which is 3.6–14.8% and 1.8–7.6% in this project, respectively. This needed to be considered during the tensioning process. The final axial forces in the anchor bolts and the anchor cables accounted for 60.0–75.7% and 41.6–60.4% of the corresponding yield loads, respectively, which not only exerted a load-bearing capacity but also retained a sufficient safety factor. The density of the anchor cables therefore could be reduced appropriately in order to coordinate the utilization of the anchor bolts and the anchor cables.
- (4)
- For the super-span tunnel constructed using the bench method, the excavation of the upper part of the tunnel was the main stage of the development of the contact pressures between the surrounding rock and the primary supports. In addition, the contact pressures between the surrounding rock and the primary supports at different locations were significantly different. In this project, the contact pressures between the surrounding rock and the primary supports at the crown, spandrel and haunch of the tunnel were obviously greater than that at the arch springing and the inverted arch, which means that the utilization rate of supports’ performance in different spatial positions was different. In order to ensure that the supporting structures were in uniform load-bearing conditions, they could be suitably strengthened in places where the loads were greater, and weakened where the loads were smaller.
- (5)
- The secondary supports not only served as a structure to provide a sufficient safety margin but also bear certain loads during construction as well as during long-term periods of operation of the super-span transition section. The contact pressures between the primary and secondary supports rapidly increased within one week after the construction of the secondary supports, which could reach more than 15% of the stable values. The distribution characteristics of the contact pressure between the primary and secondary supports was similar to that of the contact pressure between the surrounding rock and the primary supports, and the maximum value appeared at the tunnel crown, a value of only 135.1 kPa. By analyzing the axial forces and bending moments at the different positions of the secondary supports, it was found that the tunnel crown was the most unfavorable position.
Author Contributions
Funding
Conflicts of Interest
References
- Liu, D.P.; Zhang, D.L.; Fang, Q.; Sun, Z.Y.; Cao, L.Q.; Li, A. Displacement characteristics of shallow-buried large-section loess tunnel with different types of pre-supports: A case study of New Badaling tunnel. Appl. Sci. 2020, 10, 195. [Google Scholar] [CrossRef] [Green Version]
- Li, P.F.; Zhao, Y.; Zhou, X.J. Displacement characteristics of high-speed railway tunnel construction in loess ground by using multi-step excavation method. Tunn. Undergr. Space Technol. 2016, 51, 41–55. [Google Scholar] [CrossRef]
- Shi, C.H.; Cao, C.Y.; Lei, M.F. Construction technology for a shallow-buried underwater interchange tunnel with a large span. Tunn. Undergr. Space Technol. 2017, 70, 317–329. [Google Scholar] [CrossRef]
- Luo, Y.B.; Chen, J.X.; Gao, S.T.; Deng, X.H.; Diao, P.S. Stability analysis of super-large-section tunnel in loess ground considering water infiltration caused by irrigation. Environ. Earth Sci. 2017, 76, 763. [Google Scholar] [CrossRef]
- Shang, Y.L.; Du, S.J.; Han, T.Y.; Shao, B.A. Case study on deformation control of upper-soft and lower-hard large span tunnel station using combined control technology and monitoring demonstration. Sains Malays. 2017, 46, 2091–2099. [Google Scholar] [CrossRef]
- Warren, C.D.; Mortimore, R.N. Chalk engineering geology-Channel Tunnel Rail Link and North Downs Tunnel. Q. J. Eng. Geol. Hydrogeol. 2003, 36, 17–34. [Google Scholar] [CrossRef]
- Kunikane, Y.; Kawabata, N.; Yamada, T.; Shimoda, A. Influence of stationary vehicles on backlayering characteristics of fire plume in a large cross section tunnel. JSME Int. J. B -Fluid T. 2006, 49, 594–600. [Google Scholar] [CrossRef] [Green Version]
- Haruyama, K.; Teramoto, S.; Taira, K. Construction of large cross-section double-tier Metropolitan Inter-city Highway (Ken-O–Do) Ome Tunnel by NATM. Tunn. Undergr. Space Technol. 2005, 20, 111–119. [Google Scholar] [CrossRef]
- Salcher, M.; Bertuzzi, R. Results of pull tests of rock bolts and cable bolts in Sydney sandstone and shale. Tunn. Undergr. Space Technol. 2018, 74, 60–70. [Google Scholar] [CrossRef]
- Feng, J.M.; Yan, C.W.; Ye, L.; Ding, X.Q.; Zhang, J.R.; Li, Z.L. Evaluation of installation timing of initial ground support for large-span tunnel in hard rock. Tunn. Undergr. Space Technol. 2019, 93, 103087. [Google Scholar] [CrossRef]
- Wu, Y.X.; Lin, W.; Qi, A. Design and applications of a new supporting method for the small tunnel sheds. Ing. Sismica 2017, 34, 49–63. [Google Scholar]
- Jia, P.J.; Zhao, W.; Chen, Y.; Li, S.G.; Han, J.Y.; Dong, J.C. A case study on the application of the steel tube slab structure in construction of a subway station. Appl. Sci. 2018, 8, 1437. [Google Scholar] [CrossRef] [Green Version]
- Sadaghiani, M.H.; Dadizadeh, S. Study on the effect of a new construction method for a large span metro underground station in Tabriz-Iran. Tunn. Undergr. Space Technol. 2010, 25, 63–69. [Google Scholar] [CrossRef]
- Mori, K.; Abe, Y. Large rectangular cross-section tunneling by the multi-micro shield tunneling (MMST) method. Tunn. Undergr. Space Technol. 2005, 20, 129–141. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Kolivand, F.; Ghorbani, M.; Yasrobi, S. Design of sequential excavation method for large span urban tunnels in soft ground-Niayesh tunnel. Tunn. Undergr. Space Technol. 2013, 35, 178–188. [Google Scholar] [CrossRef]
- Tonon, F. Sequential excavation, NATM and ADECO: What they have in common and how they differ. Tunn. Undergr. Space Technol. 2010, 25, 245–265. [Google Scholar] [CrossRef]
- He, P.; Li, S.C.; Li, L.P.; Zhang, Q.Q.; Xu, F.; Chen, Y.J. Discontinuous deformation analysis of super section tunnel surrounding rock stability based on joint distribution simulation. Comput. Geotech. 2017, 91, 218–229. [Google Scholar] [CrossRef]
- Verma, H.K.; Samadhiya, N.K.; Singh, M.; Goel, R.K.; Singh, P.K. Blast induced rock mass damage around tunnels. Tunn. Undergr. Space Technol. 2018, 71, 149–158. [Google Scholar] [CrossRef]
- Molladavoodi, H. Study of ground response curve (GRC) based on a damage model. Arch. Min. Sci. 2013, 58, 655–672. [Google Scholar]
- Zhang, D.L.; Fang, Q.; Hou, Y.J.; Li, P.F.; Wong, L.N.Y. Protection of buildings against damages as a result of adjacent large-span tunneling in shallowly buried soft ground. J. Geotech. Geoenviron. Eng. 2013, 139, 903–913. [Google Scholar] [CrossRef]













| Name | Location | Span (m) | Height (m) | Excavation Area (m2) | Geological Condition | Excavation Method |
|---|---|---|---|---|---|---|
| Longtoushan tunnel | Guangdong province | 21.5 | 13.6 | 229.4 | weakly weathered granite | both side drift method |
| Zengjiaping No.1 tunnel | Yunnan province | 20.6 | 12.6 | 240.0 | limestone and marl | both side drift method |
| Hanjialing tunnel | Liaoning province | 22.5 | 15.5 | 273.3 | shale and limestone | bench method |
| Gongbei tunnel | Guangdong province | 18.7 | 50.8 | 330.2 | silt and sandy pebble | freeze-sealing pipe roofmethod |
| Fenghuangshan tunnel | Yunnan province | 26.1 | 17.3 | 363.5 | weakly weathered basalt and tuff | both side drift method |
| Hongtudi station of Chongqing metro line 6 | Chongqing municipality | 25.9 | 22.0 | 375.8 | moderately weathered sandy mudstone | both side drift method |
| Xinkaotang tunnel | Fujian province | 30.3 | 17.0 | 396.1 | completely weathered granite | both side drift method |
| Linjiangmen station of Chongqing Metro Line 2 | Chongqing municipality | 23.0 | 20.6 | 421.0 | sandstone and sandy mudstone | both side drift method |
| Liantang tunnel | Guangdong province | 30.01 | 18.41 | 428.5 | slightly weathered sandstone | both side drift method |
| Specific Weight (kN/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Cohesion (MPa) | Friction Angle (°) | |
|---|---|---|---|---|---|
| Tuff breccia | 27.0 | 11.3 | 0.30 | 0.8 | 40.2 |
| Granite | 26.3 | 25.9 | 0.24 | 1.7 | 51.3 |
| Monzonitic granite | 27.2 | 21.5 | 0.23 | 1.5 | 50.8 |
| Grade I | Grade II | Grade III | Grade IV | Grade V | |
|---|---|---|---|---|---|
| Value | (Very Good) | (Good) | (Fair) | (Poor) | (Very Poor) |
| BQ | >550 | 451–550 | 351–450 | 251–350 | <250 |
| Q | >40 | 10–40 | 4–10 | 1–4 | <1 |
| Tunnel Support Type | Specific Parameters | Installation Area | |
|---|---|---|---|
| temporary support | fiberglass anchor | Φ25 mm, L = 4 m, 1 m × 1 m (longitudinal and circumferential spaced) | sidewalls of Drift 1 |
| steel support | No.16 I-shaped steel, 0.8 m longitudinal spaced | sidewalls of Drift 1 | |
| shotcrete | thickness: 8 cm, concrete type: C30 | sidewalls of Drift 1 | |
| primary support | prestressed anchor bolt | Φ32 mm, L = 11 m, 0.8 m × 1.2 m (longitudinal and circumferential spacing), 100 kN pretension | vault |
| prestressed anchor cable 1 | Φ15.2 mm × 7 steel stranded wires, L = 25 m, 700 kN pretension | vault | |
| prestressed anchor cable 2 | Φ15.2 mm × 5 steel stranded wires, L = 25 m, 500 kN pretension | vault | |
| steel rib | Φ22 mm four bars lattice girders, 0.8 m longitudinal spaced | whole section | |
| shotcrete of vault | (1) thickness: 5 cm, concrete type: C30, containing nano-silica and fiber concrete (2) thickness: 18.2 cm, concrete type: C30, containing fiber concrete (3) thickness: 11.8 cm, concrete type: C30 | vault | |
| shotcrete of inverted arch | thickness: 25 cm, concrete type: C30 | inverted arch | |
| secondary support | form working concrete | thickness: 60 cm, concrete type: C35, Φ28 mm main reinforcement, 0.2 m longitudinal spaced | whole section |
| Displacement Parameter | Monitoring Section | Construction Stage | |||||
|---|---|---|---|---|---|---|---|
| Stage 1 | Stage 2–3 | Stage 4–5 | Stage 6–7 | Stage 8–9 | Stage 10–11 | ||
| Settlement Proportion (%) | DK68+290 | 35.1 | 29.9 | 11.6 | 9.3 | 3.8 | 10.3 |
| DK68+295 | 54.0 | 21.6 | 10.7 | 5.7 | 1.7 | 6.3 | |
| DK68+300 | 41.4 | 35.2 | 7.1 | 11.0 | 3.2 | 2.1 | |
| Convergence Proportion (%) | DK68+290 | — | 42.3 | 21.7 | 19.7 | 7.7 | 8.6 |
| DK68+295 | — | 38.6 | 17.8 | 26.8 | 8.9 | 7.9 | |
| DK68+300 | — | 30.6 | 31.5 | 14.3 | 4.1 | 19.5 | |
| Monitoring Position | |||||
|---|---|---|---|---|---|
| Crown | Left Spandrel | Right Spandrel | Left Haunch | Right Haunch | |
| Damage Range (m) | 8.1 | 7.4 | 7.2 | 6.5 | 6.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Zhang, D.; Fang, Q.; Sun, Z.; Luo, J.; Li, A. Field Monitoring of the Deformation and Internal Forces of the Surrounding Rock and Support Structures in the Construction of a Super-Span High-Speed Railway Tunnel—A Case Study. Appl. Sci. 2020, 10, 5182. https://doi.org/10.3390/app10155182
Liu D, Zhang D, Fang Q, Sun Z, Luo J, Li A. Field Monitoring of the Deformation and Internal Forces of the Surrounding Rock and Support Structures in the Construction of a Super-Span High-Speed Railway Tunnel—A Case Study. Applied Sciences. 2020; 10(15):5182. https://doi.org/10.3390/app10155182
Chicago/Turabian StyleLiu, Daoping, Dingli Zhang, Qian Fang, Zhenyu Sun, Jiwei Luo, and Ao Li. 2020. "Field Monitoring of the Deformation and Internal Forces of the Surrounding Rock and Support Structures in the Construction of a Super-Span High-Speed Railway Tunnel—A Case Study" Applied Sciences 10, no. 15: 5182. https://doi.org/10.3390/app10155182
APA StyleLiu, D., Zhang, D., Fang, Q., Sun, Z., Luo, J., & Li, A. (2020). Field Monitoring of the Deformation and Internal Forces of the Surrounding Rock and Support Structures in the Construction of a Super-Span High-Speed Railway Tunnel—A Case Study. Applied Sciences, 10(15), 5182. https://doi.org/10.3390/app10155182





