Comparison on Search Failure between Hash Tables and a Functional Bloom Filter

Abstract

Hash-based data structures have been widely used in many applications. An intrinsic problem of hashing is collision, in which two or more elements are hashed to the same value. If a hash table is heavily loaded, more collisions would occur. Elements that could not be stored in a hash table because of the collision cause search failures. Many variant structures have been studied to reduce the number of collisions, but none of the structures completely solves the collision problem. In this paper, we claim that a functional Bloom filter (FBF) provides a lower search failure rate than hash tables, when a hash table is heavily loaded. In other words, a hash table can be replaced with an FBF because the FBF is more effective than hash tables in the search failure rate in storing a large amount of data to a limited size of memory. While hash tables require to store each input key in addition to its return value, a functional Bloom filter stores return values without input keys, because different index combinations according to each input key can be used to identify the input key. In search failure rates, we theoretically compare the FBF with hash-based data structures, such as multi-hash table, cuckoo hash table, and d-left hash table. We also provide simulation results to prove the validity of our theoretical results. The simulation results show that the search failure rates of hash tables are larger than that of the functional Bloom filter when the load factor is larger than 0.6.

1. Introduction

A key-value data structure that returns a value corresponding to an input key has been used in many fields [1,2,3]. Various network applications, such as Internet Protocol (IP) address lookup, packet classification, name lookup in Named Data Networking (NDN), traffic classification in Software-Defined Networking (SDN), and cloud computing [4,5,6,7,8], use key-value structures for data storage. For example, in performing a Pending Interest Table (PIT) lookup in the NDN, a content name is used as a key, and the input faces of each Interest packet are returned as the value corresponding to the key [9,10,11,12].

As a representative key-value data structure, hashing has been popularly applied to various applications [13,14,15,16]. Hashing converts an input key string to an index, which can be used to point an entry in a hash table. The pointed entry stores both the key itself (or the signature of the key) and a return value. Collision in hash indexes is an intrinsic problem of hash-based data structures. Elements that could not be stored in a hash table because of hash collisions cause failures in search process. To reduce the number of hash collisions, several variant structures have been studied such as multi-hashing, cuckoo hashing, and d-left hashing [17,18,19]. In order to avoid an excessive number of hash collisions, the load factor of a hash table, which indicates the ratio of the number of stored elements compared to the number of entries in a hash table, should be small enough.

A functional Bloom filter satisfies the key-value operation required in various applications [20,21,22,23,24,25]. Unlike a hash table, a functional Bloom filter does not require to store input keys, as different combinations of Bloom filter indexes for each input key can work as the signature of the input key.

Even though modern hardware equipments have a sufficient amount of internal memory to accommodate large hash tables, an efficient use of the memory, which is a limited resource, is required to provide scalability. For example, according to Cisco’s annual Internet report [26], IoT devices will account for 50 percent of all networked devices by 2023, and a 5G connection will generate nearly three times more traffic than the 4G connection of 2018 because there will be 29.3 billion networked devices by 2023, up from 18.4 billion of 2018. In order to keep up with the ever-increasing network traffic, it is necessary to build effective data structures which utilize limited memory resources efficiently [27,28,29].

In this paper, we claim that a functional Bloom filter provides a lower search failure rate than hash-based data structures in storing a large amount of data to a limited size of memory. The search failure is the most important criterion for evaluating the performance of key-value structures. Therefore, as a key-value structure, the FBF can effectively replace hash tables. The basic idea of this paper was briefly introduced in [30], and we provide a thorough theoretical analysis and compare each data structure in their search failure probabilities in this paper. Our theoretical analysis is validated by simulation results for each structure.

The remainder of this paper is organized as follows. Section 2 describes the Bloom filter and hash table as related works. In Section 3, we explain and compare four data structures: a multi-hash table, a cuckoo hash table, a d-left hash table, and a functional Bloom filter. Section 4 theoretically analyzes the probability of signature collision and the probability of search failure for each structure. Section 5 evaluates and compares the performance of each data structure, and Section 6 concludes the paper.

2. Related Works

2.1. Bloom Filter Theory

A Bloom filter (BF) [31] is a bit-vector-based data structure used to represent the membership information for set $S=\{x_1,x_2,\dots ,x_n\}$ consisting of n elements in universe set U. We use key and element interchangeably to denote $x_p\in S$ for $1\le p\le n$. A Bloom filter is an array of m bits, which is initialized to zero. As each cell of a Bloom filter $c\left[j\right]$, for $0\le j<m$, is composed of a single bit, the value of each cell can have only 0 or 1. A Bloom filter uses k independent hash functions $\{h_1,h_2,\dots ,h_k\}$ in programming and querying. The optimal number of hash functions is as follows [32,33].

$$k=\frac{m}{n}ln2$$

(1)

For element $x_p\in S$, $h_i(x_p)$ can have any value in range $\{0,1,2,\dots ,m-1\}$ for $1\le i\le k$, and $h_1(x_p)$, $h_2(x_p)$, …, and $h_k(x_p)$ are cell indexes for $x_p$. In programming $x_p$, the $c\left[h_i(x_p)\right]$s are set to 1 for $1\le i\le k$. In querying a given input y to check its membership, the Bloom filter verifies whether all of the $c\left[h_i(y)\right]$s are set to 1 using the same k hash functions as programming. If at least one of $c\left[h_i(y)\right]$s is 0, it is obviously $y\notin S$, which is termed a negative. If all $c\left[h_i(y)\right]$s are 1, it would be $y\in S$, which is termed a positive. However, even in case of $y\notin S$, all $c\left[h_i(y)\right]$s may be set to 1 because of hash collision, and it is termed a false positive. The false positive rate can be reduced by increasing the size of the Bloom filter, but cannot be completely eliminated. However, negative results are always true. The false positive rate of the BF is obtained as follows [32,33].

$$f={\left(1-{(1-\frac{1}{m})}^{kn}\right)}^k\approx {\left(1-e^{-\frac{kn}{m}}\right)}^k$$

(2)

A Bloom filter and its variant structures have been popularly used for many applications due to their simple and space-efficient nature identifying non-members of a given set [34,35,36,37,38,39,40].

2.2. Hash Table

Each entry in a hash table stores an input key (or the signature of the key) and a return value corresponding to the key. A useful property of a hash-based data structure is that a search can be completed by a constant number of accesses. However, a hash table has the problem of collision, where multiple different keys are hashed into a single bucket. Two different methods are used in resolving hash collisions: chaining and open addressing [41,42]. The chaining stores the collided key in an additional bucket using a linked list pointer. In the open addressing, a hash collision is resolved by searching through alternative locations using a predetermined probe sequence, until an unused bucket is found. Thus, the linked list pointer is not required, but probing can lead to a large number of accesses in the worst case. In order to avoid an excessive number of hash collisions, a load factor does not exceed 0.7 in general [43]. Variant structures have been studied such as multiple hashing, cuckoo hashing, and d-left hashing to cope with the collision problem [17,18,19].

3. Hash-Based Key-Value Data Structures

A key-value data structure stores a key and a corresponding value in pairs, and returns the value when a given input matches the key. In other words, assuming that set $S=\{(x_1,v_1),(x_2,v_2),\dots ,(x_n,v_n)\}$ is stored in a hash table using hash function $h(·)$, $(x_p,v_p)$ (for $1\le p\le n$) is stored in $e\left[h(x_p)\right]$. In searching y, if $x_p$ in $e[h(y)]$ is equal to y, $v_p$ is returned. 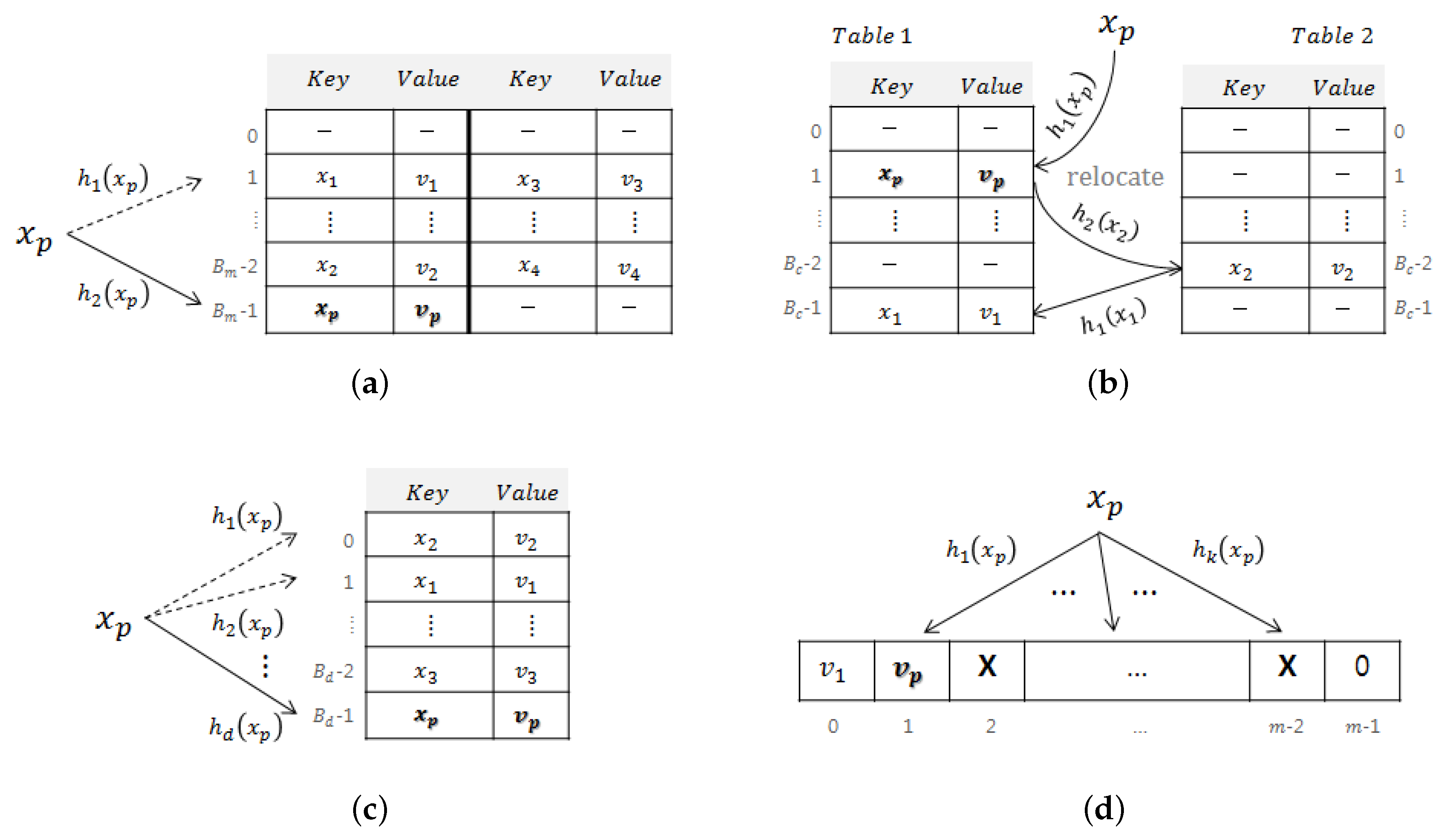Figure 1 shows the hash-based key-value data structures considered in this paper: a multi-hash table, a cuckoo hash table, a d-left hash table, and a functional Bloom filter. The basic idea of this paper was briefly introduced in [30]. This paper additionally provides theoretical analysis and compares each data structure in their search failure rates. We assume that hash tables store a fixed-length signature (instead of a variable-length key) and a value corresponding to each key.

Table 1. Notation and definition.

Symbol	Meaning
$M_h$	memory size of a hash table
n	number of elements in a given set
m	number of cells in a functional Bloom filter
k	number of hash functions for an FBF
d	number of hash functions for a d-left table
$\alpha$	load factor of a multi-hash table
$B_m$	number of buckets in a multi-hash table
$B_c$	number of buckets in a cuckoo hash table
$B_d$	number of buckets in a d-left hash table
L	number of bits for a return value in hash tables
	number of bits of a cell in an FBF
$2lo{g}_{2}n$	number of bits of the signature of an element
r	number of the available signatures ($2^{2lo{g}_{2}n}$)

represents notations and definitions used in key-value data structures.

3.1. Multi-Hash Table

A multi-hash table [17] uses multiple hash functions instead of a single hash function for each key to reduce the number of collisions. Figure 1a shows a multi-hash table with two hash functions and two entries per bucket. For given set $S=\{(x_1,v_1),(x_2,v_2),\dots ,(x_n,v_n)\}$, in inserting element $x_p\in S$ to the multi-hash table in Figure 1a, among the two buckets pointed by two hash indexes, the signature of $x_p$ and return value $v_p$ are stored in the bucket with a smaller number of loads. In this way, a multi-hash table distributes a number of loads more evenly. If there is no empty entry in both buckets, $x_p$ cannot be stored (i.e., overflow).

In searching, the first and second buckets are checked in turn, if there is no matching entry in the first bucket. If an element could not be stored because of hash collision, searching for this element causes a false negative. In this case, a search failure occurs for this specific input. Assuming that a bucket of a multi-hash table has two entries, where n is the number of elements in a given set and $\alpha$ is a load factor, the number of buckets ($B_m$) in the multi-hash table is $\frac{n}{2\alpha }$. The amount of the memory ($M_h$) is $2(2lo{g}_{2}n+L)B_m$, where the signature of a key has $2lo{g}_{2}n$ bits and a return value has L bits.

3.2. Cuckoo Hash Table

A cuckoo hash table shown in Figure 1b uses two hash tables, and each bucket of a cuckoo hash table stores a signature and a return value. Therefore, if the same amount of memory is used as a multi-hash table, the number of buckets ($B_c$) in a cuckoo hash table is the same as $B_m$.

Each element uses a single index per table. When a new element is inserted, cuckoo hashing [18] solves hash collision by pushing the preoccupied element to the other table. In Figure 1b, when inserting $x_p\in S$, if there is a collision in the bucket of the first table (i.e., $e_1\left[h_1(x_p)\right]$), $x_p$ is stored in the bucket and element $x_2$ (of which bucket is taken away) is pushed to the second table (i.e., $e_2\left[h_2(x_2)\right]$). If a collision also occurs in the second table, this procedure is repeated until the pushed element finds an empty bucket (i.e., $e_1\left[h_1(x_1)\right]$ in Figure 1b. Therefore, in inserting an element, even though each element uses only one hash index for each table, more entries can be examined in the cuckoo hashing by involving other elements already stored in the table. As will be shown in Section 4.2.2, if there occur two loops in inserting an element, the element cannot be saved. The unsaved element, due to an overflow in insertion procedure, causes a false negative in search procedure, and it is classified as a search failure.

In searching, only two buckets pointed by two hash indexes for each given input are checked. Therefore, the number of bucket accesses in searching an input is always two, even though the number of accesses in inserting a key can be large as the load factor increases.

3.3. d-Left Hash Table

In inserting $x_p\in S$, the d-left hash table [19] uses d hash functions and stores $x_p$ in the bucket with the smallest number of loads. Figure 1c shows a d-left hash table, where each bucket includes a single entry and the number of hash functions is d. As we assume the d-left hash table with a single entry per bucket, $x_p$ is stored in the topmost empty bucket (i.e., $e\left[h_d(x_p)\right]$ in Figure 1c. If collisions occur in all d entries, $x_p$ cannot be saved. The unsaved element, due to an overflow in insertion procedure, causes a false negative in the search procedure, and it is classified as a search failure.

In searching an input, each bucket is checked from the topmost bucket to the $d^{th}$ bucket until the input has a match. If the same amount of memory is used as a multi-hash table, the number of buckets ($B_d$) in a d-left hash table is equal to $\frac{M_h}{2lo{g}_{2}n+L}$, as each bucket stores a signature and a return value.

3.4. Functional Bloom Filter

A functional Bloom filter (FBF) [20,21,22] is a variant of a standard Bloom filter that returns a value corresponding to a key as well as its membership. Figure 1d shows a functional Bloom filter with m cells and k hash indexes. As each cell is composed of L bits, each cell can have a value with range $\{0,1,\dots ,2^L-1\}$. In a functional Bloom filter, the signature of each key is not stored and only a value corresponding to each key is stored in each cell, as various combinations of k hash indexes can serve as the signatures.

Every cell in an FBF is initialized to 0. To program set $S=\{(x_1,v_1),(x_2,v_2),$$\dots ,(x_n,v_n)\}$ to an FBF, in inserting element $x_p\in S$, k independent hash functions $\{h_1,h_2,\dots ,h_k\}$ are used. The FBF is programmed by setting return value $v_p$ of $x_p$ in all cells pointed by $h_i(x_p)$s for $1\le i\le k$. Key $x_p$ is used to obtain hash indexes to access k cells but not stored, and the return value $v_p$ is only stored.

An important issue when dealing with a functional Bloom filter is how to resolve collision because a cell cannot store two or more different return values. Collided cells are not used in returning a value in a functional Bloom filter. In other words, in storing an element, if a value different from the return value of the element is already stored in an accessed cell, the cell is set to the maximum value $2^L-1$ to represent the collision. Cells with the maximum value are named conflict cells, denoted with $\mathbf{X}$ in Figure 1d. Thus, each cell can represent $2^L-2$ return values in a functional Bloom filter, and values in conflict cells are not used in querying.

In querying, a functional Bloom filter returns three types of results: negative, positive, and indeterminable. For input y, if there exists at least one cell with $c\left[h_i(y)\right]=0$ for $1\le i\le k$, it obviously means $y\notin S$, which is termed negative. Additionally, for cells with values other than conflict, if there are any cells with $c\left[h_i(y)\right]\ne c\left[h_j(y)\right]$ for $1\le i,j\le k$, it is also $y\notin S$, as these cells are programmed by different keys other than y. For cells with values other than conflict, if all $c\left[h_i(y)\right]$s are the same, it would be $y\in S$ and the FBF returns $c\left[h_i(y)\right]$, which is termed positive. It should be noted that, as in a standard BF, an FBF can return a false positive. For $1\le i\le k$, if all $c\left[h_i(y)\right]$ = $2^L-1$, which means that conflicts occur in every cell, the FBF fails to return a value, and it is termed indeterminable. Search failure of a functional Bloom filter is defined by false positive and indeterminable results.

If the same amount of memory is used as a multi-hash table, the number of cells (m) in a functional Bloom filter is calculated by $\frac{M_h}{L}$, as each cell only stores a return value without the signature of a key. As described in the querying procedure, by comparing the values of multiple cells pointed by an input, a functional Bloom filter can determine the return value without storing key $x_p$ (or the signature of $x_p$).

4. Theoretical Analysis

A theoretical analysis of hash collisions inevitably occurring in hash-based structures has been studied [15,16,44,45]. We theoretically analyze signature collision and search failure probabilities for the hash-based key-value data structures described in Section 3.

4.1. Signature Collision

A key with a variable length needs to be converted to a fixed-length signature to be stored in a fixed-width hash entry. Since a signature is generated by hashing, signature collision can also occur, in which two or more different keys are mapped to the same signature. The number of bits for a signature is set as $2lo{g}_{2}n$ in this work, where n is the number of elements stored in a hash table.

In a hash table, a signature collision can cause two types of search failures: false result and false positive. A false result occurs for elements included in a given set if two or more different keys which have the same signature but different return values are mapped to the same entry in a hash table in insertion procedure. In this case, if the key which could not be stored because of entry collision is given as an input, a wrong value can be returned in search procedure, as the signature of the key matches the stored signature.

False positive occurs for an input not included in a given set if the input has the same signature as an element included in the set and the hash index of the input is mapped to the entry, where the signature of the element is stored. In search procedure, the input is recognized as the element that has been stored in insertion procedure.

The probabilities of false result and false positive caused by signature collision can be derived as follows. Let r represent the number of available signatures. If the number of bits of a signature is set as $2lo{g}_{2}n$, then $r=2^{2lo{g}_{2}n}=n^2$. Probability that a signature value is unused after one element is mapped to a signature by hashing is $1-\frac{1}{r}$. Thus, probability that a signature is unused after n elements are mapped by hashing is ${(1-\frac{1}{r})}^n$.

Let $E(N_{unused})$ be the expected number of unused signatures.

$$E(N_{unused})=\sum _{i=1}^r{(1-\frac{1}{r})}^n=r{(1-\frac{1}{r})}^n$$

(3)

Let $E(N_{used})$ be the expected number of used signatures.

$$E(N_{used})=r-E(N_{unused})=r-r{(1-\frac{1}{r})}^n$$

(4)

Each used signature would contain one key (element) that has not been collided in the process of signature mapping. Therefore, the number of collisions would be n minus the number of used signatures. Let $E(N_{collision})$ represent the expected number of collisions in signature mapping.

$$E(N_{collision})=n-E(N_{used})=n-r+r{(1-\frac{1}{r})}^n$$

(5)

If we set $r=n^2$, then

$$E(N_{collision})=n-n^2+n^2{(1-\frac{1}{n^2})}^n.$$

(6)

We can numerically show that $E(N_{collision})$ in Label (6) converges to 0.5 as n becomes large.

Let $P_{co}$ represent the probability that an element are collided in the process of signature mapping.

$$P_{co}=\frac{E(N_{collision})}{n}=1-n+n{(1-\frac{1}{n^2})}^n$$

(7)

If an element is mapped to a bucket, where another element with the same signature was already stored, the element that has been collided in signature mapping cannot be stored because the element is considered to be already stored. Therefore, when both signature collision and bucket collision occur in an insertion procedure, a false result occurs in the search procedure. Let B represent the number of buckets in a hash table and $P_{fr}$ represent the probability of false results. In other words, $P_{fr}$ represents the probability that an element is mapped to the bucket where another element with the same signature as itself is stored.

$$P_{fr}=P_{co}·\frac{1}{B}=\left(1-n+n{(1-\frac{1}{n^2})}^n\right)·\frac{1}{B}$$

(8)

Let $P_{us}$ represent the probability that a non-programmed input (which is not included in the insertion set) is mapped to a used signature. As there are r possible signatures,

$$P_{us}=\frac{E(N_{used})}{r}=1-{(1-\frac{1}{r})}^n=1-{(1-\frac{1}{n^2})}^n.$$

(9)

A false positive occurs in search procedure, when a non-programmed input is mapped to a specific used signature and its hash index is mapped to the bucket, where the specific used signature is stored. Let $P_{fp}$ represent the probability of false positives.

$$P_{fp}=P_{us}·\frac{1}{B}=\left(1-{(1-\frac{1}{n^2})}^n\right)·\frac{1}{B}$$

(10)

As shown in Labels (8) and (10), the probabilities of false result and false positive occurring in search procedure due to signature collision are very small, and therefore it proves that $2lo{g}_{2}n$ bits are enough for signature length. Therefore, signature collision is not considered when analyzing search failure probability in the next section. The functional Bloom filter does not have a signature collision problem because it stores return value only without storing signature at all.

4.2. Search Failure Probability

Search failure probability of a hash table is equal to false negative probability, which occurs when an element could not be inserted to a hash table because of index collision. Search failure probability of the functional Bloom filter is the summation of false positive and indeterminable probabilities. The false positive occurs when a value is returned for a non-programmed input. The indeterminable occurs when every cell pointed by an input has a conflict value. The indeterminable means that the result cannot be determined by the functional Bloom filter. For theoretical analysis, we assume that the number of inputs in searching set U is $3n$, i.e., $\left|S\right|=n$, $|S^c|=2n$, and $\left|U\right|=|S+S^c|=3n$.

4.2.1. Multi-Hash Table

In inserting an element to a multi-hash table shown in Figure 1a, if four entries in two buckets were already occupied, the element cannot be stored. When $i-1$ elements were stored, the number of buckets where both entries are occupied is $\lfloor \frac{i-1}{2}\rfloor$. The $i^{th}$ element cannot be inserted when each of the two hash indexes of the $i^{th}$ element is mapped to one of the $\lfloor \frac{i-1}{2}\rfloor$ occupied buckets. Let $P_{o_i}$ be the probability that an overflow occurs for the $i^{th}$ element. Then, $P_{o_i}$ has the upper bound as follows.

$$P_{o_i}\le {\left(\frac{\lfloor \frac{i-1}{2}\rfloor }{B_m}\right)}^2$$

(11)

Let $P_m$ be the probability that an element cannot be stored when n elements are inserted in a multi-hash table. Then, from Label (11), $P_m$ is derived as follows.

$$P_m=\frac{1}{n}\sum _{i=1}^n{P}_{o_i}\le \frac{1}{n}\sum _{i=1}^n{\left(\frac{\lfloor \frac{i-1}{2}\rfloor }{B_m}\right)}^2$$

(12)

Assuming that n is even,

$$\begin{array}{cc}\hfill P_m& \le \frac{1}{n}\sum _{i=1}^n{\left(\frac{\lfloor \frac{i-1}{2}\rfloor }{B_m}\right)}^2\hfill \\ \hfill & =\frac{1}{n{B_m}^2}\left(0^2+0^2+1^2+1^2+\dots +{(\frac{n-2}{2})}^2+{(\frac{n-2}{2})}^2\right)\hfill \\ \hfill & =\frac{2}{n{B_m}^2}\sum _{j=1}^{\frac{n-2}{2}}{j}^2.\hfill \end{array}$$

(13)

As $B_m=\frac{n}{2\alpha }$ in a multi-hash table, and assuming that n is very large, Label (13) can be formulated as follows,

$$\begin{array}{cc}\hfill P_m& \le \frac{2}{n{B_m}^2}\sum _{j=1}^{\frac{n-2}{2}}{j}^2=\frac{(n-2)(n-1)}{12{B_m}^2}\hfill \\ \hfill & =\frac{(n-2)(n-1)}{12{(\frac{n}{2\alpha })}^2}=\frac{{\alpha }^2(n^2-3n+2)}{3n^2}\hfill \\ \hfill & \approx \frac{{\alpha }^2}{3}\hfill \end{array}$$

(14)

where $\alpha$ is the load factor of a multi-hash table. When n is odd, the same result is obtained.

Let $P(F_m)$ represent the false negative probability of a multi-hash table. It can be formulated as

$$P(F_m)=P(S)P(F_m|S)+P(S^c)P(F_m|S^c)$$

(15)

where $P(S)$ and $P(S^c)$ represent the probability that input y is included in S and $S^c$, respectively, and $U=S\cup S^c$ and $S\cap S^c=\varnothing$. For $3n$ inputs, $P(S)=\frac{n}{3n}=\frac{1}{3}$ and $P(S^c)=\frac{2n}{3n}=\frac{2}{3}$. Among n elements in S, false negatives occur for the elements that could not be stored, and $P(F_m|S^c)=0$ as any element in $S^c$ does not produce false negatives. Therefore, $P(F_m)$ has the following upper bound.

$$P(F_m)=P(S)P(F_m|S)=\frac{1}{3}{P}_m\le \frac{{\alpha }^2}{9}$$

(16)

Labels (14) and (16) hold true when $\alpha \le 1$. In case of $\alpha >1$, the number of elements is more than the number of entries in a hash table (i.e., $n>2B_m$). Assuming that no empty entry exists in a hash table when the number of programmed elements is $2B_m$, the $i^{th}$ element cannot be inserted in the table for $2B_m<i\le n$. In other words, in calculating $P_m$ for $\alpha >1$, the probability that the $i^{th}$ element cannot be inserted is 1, which means that the collision unavoidably occurs. Thus, for $\alpha >1$, $P_m$ is derived as follows.

$$\begin{array}{cc}\hfill P_m& \le \frac{1}{n}\left(\frac{1}{{B_m}^2}·\left(0^2+0^2+1^2+1^2+\dots +{(\frac{2B_m-2}{2})}^2+{(\frac{2B_m-2}{2})}^2\right)+(n-2B_m)\right)\hfill \\ \hfill & =\frac{1}{n}\left(\frac{2}{{B_m}^2}\sum _{j=1}^{B_m-1}{j}^2+(n-2B_m)\right)\hfill \\ \hfill & \approx 1-\frac{2}{3\alpha }\hfill \end{array}$$

(17)

Therefore, $P(F_m)$ for $\alpha >1$ has the following upper bound.

$$P(F_m)=P(S)P(F_m|S)=\frac{1}{3}{P}_m\le \frac{1}{3}\left(1-\frac{2}{3\alpha }\right)$$

(18)

4.2.2. Cuckoo Hash Table

A false negative that results in search failure in a cuckoo hash table also occurs when searching an element that could not be inserted. Figure 2 shows a case where an element cannot be stored in a cuckoo hash table. In inserting 3 elements, $x_1$, $x_2$, and $x_3$, in sequence, if $h_1(x_1)$ = $h_1(x_2)$ = $h_1(x_3)$ and $h_2(x_1)$ = $h_2(x_2)$ = $h_2(x_3)$, element $x_3$ cannot be stored, as two loops occur. The insertion procedure should stop; otherwise, the insertion procedure will repeat infinitely.

To find the upper bound of probability that an element cannot be stored in a cuckoo hash table because of two loops, assume that the $2(i-1)$ indexes of $i-1$ elements are mapped to only $i-1$ buckets and elements are evenly distributed to both tables (the difference between the number of occupied buckets in the first table and the second table is equal to 0 or 1). When the $i^{th}$ element needs to be inserted, if the $i^{th}$ element selects two (one in each table) of the $i-1$ buckets, two loops occur. Let $P_c$ represent the probability that an element cannot be stored in a cuckoo hash table because of two loops. Assuming that n is even, then $P_c$ is formulated as follows.

$$\begin{array}{cc}{P}_c\hfill & \le \frac{1}{n}\left(0^2+0^2+(\frac{1}{B_c}·\frac{1}{B_c})+(\frac{2}{B_c}·\frac{1}{B_c})+\dots +(\frac{\frac{n-2}{2}}{B_c}·\frac{\frac{n-2}{2}}{B_c})+(\frac{\frac{n}{2}}{B_c}·\frac{\frac{n-2}{2}}{B_c})\right)\hfill \\ \hfill & =\frac{1}{n{B_c}^2}\left(\sum _{j=1}^{\frac{n-2}{2}}{j}^2+\sum _{j=1}^{\frac{n}{2}}j(j-1)\right)\hfill \end{array}$$

(19)

As $P_c$ has to be handled depending on whether the $i^{th}$ element is an odd-numbered or an even-numbered element, the summation in Label (19) consists of two types of sequences for j. Because $B_c=B_m$, and assuming that n is very large, Label (19) can be formulated as follows.

$$\begin{array}{cc}{P}_c\hfill & \le \frac{1}{n{B_c}^2}\left(\sum _{j=1}^{\frac{n-2}{2}}{j}^2+\sum _{j=1}^{\frac{n}{2}}j(j-1)\right)=\frac{1}{24{B_c}^2}(2n^2-3n-2)\hfill \\ \hfill & =\frac{{\alpha }^2(2n^2-3n-2)}{6n^2}\approx \frac{{\alpha }^2}{3}\hfill \end{array}$$

(20)

where $\alpha$ is the load factor of a multi-hash table. When n is odd, the same result is also obtained.

Let $P(F_c)$ represent the false negative probability of a cuckoo hash table. For $3n$ inputs, as $P(F_c|S^c)=0$, the $P(F_c)$ has the following upper bound.

$$\begin{array}{cc}\hfill P(F_c)& =P(S)P(F_c|S)+P(S^c)P(F_c|S^c)\hfill \end{array}$$

$$\begin{array}{c}\hfill =P(S)P(F_c|S)=\frac{1}{3}{P}_c\le \frac{{\alpha }^2}{9}\end{array}$$

(21)

Labels (20) and (21) hold true when $\alpha \le 1$. In case of $\alpha >1$, the number of elements is more than the number of entries in a hash table (i.e., $n>2B_c$). Assuming that no empty entry exists in a hash table when the number of programmed elements is $2B_c$, the $i^{th}$ element cannot be inserted in the table for $2B_c<i\le n$. In other words, in calculating $P_c$ for $\alpha >1$, the probability that the $i^{th}$ element cannot be inserted is 1, which means collision unavoidably occurs. Thus, for $\alpha >1$, $P_c$ is derived as follows.

$$\begin{array}{cc}\hfill P_c& \le \frac{1}{n}\left(0^2+0^2+(\frac{1}{B_c}·\frac{1}{B_c})+(\frac{2}{B_c}·\frac{1}{B_c})+\dots +(\frac{\frac{2B_c-2}{2}}{B_c}·\frac{\frac{2B_c-2}{2}}{B_c})+(\frac{\frac{2B_c}{2}}{B_c}·\frac{\frac{2B_c-2}{2}}{B_c})+(n-2B_c)\right)\hfill \\ \hfill & =\frac{1}{n}\left(\frac{1}{{B_c}^2}\left(\sum _{j=1}^{B_c-1}{j}^2+\sum _{j=1}^{B_c}j(j-1)\right)+(n-2B_c)\right)\hfill \\ \hfill & \approx 1-\frac{2}{3\alpha }\hfill \end{array}$$

(22)

Therefore, $P(F_c)$ for $\alpha >1$ has the following upper bound.

$$\begin{array}{c}\hfill P(F_c)=P(S)P(F_c|S)=\frac{1}{3}{P}_c\le \frac{1}{3}\left(1-\frac{2}{3\alpha }\right)\end{array}$$

(23)

4.2.3. d-Left Hash Table

The d-left hash table is assumed to have only one entry per bucket in this work. If collisions occur in all d buckets, an element cannot be stored. When searching an element that could not be inserted, search failure occurs due to false negative. Let $P_d$ represent the probability that an element cannot be stored in a d-left hash table because of collisions in all d buckets. Then, $P_d$ is formulated as follows.

$$\begin{array}{cc}{P}_d\hfill & =\frac{1}{n}\left(0^d+{(\frac{1}{B_d})}^d+{(\frac{2}{B_d})}^d+\dots +{(\frac{n-1}{B_d})}^d\right)\hfill \\ \hfill & =\frac{1}{n{B_d}^d}\sum _{j=1}^{n-1}{j}^d\hfill \end{array}$$

(24)

Let $P(F_d)$ represent the false negative probability of a d-left hash table. For $3n$ inputs, since $P(F_d|S^c)=0$, $P(F_d)$ is as follows.

$$\begin{array}{cc}P(F_d)\hfill & =P(S)P(F_d|S)+P(S^c)P(F_d|S^c)\hfill \\ \hfill & =P(S)P(F_d|S)=\frac{1}{3}{P}_d=\frac{1}{3n{B_d}^d}\sum _{j=1}^{n-1}{j}^d\hfill \end{array}$$

(25)

Labels (24) and (25) hold true when $\alpha \le 1$. In case of $\alpha >1$, the number of elements is more than the number of entries in a hash table (i.e., $n>B_d$). Assuming that no empty entry exists in a hash table when the number of programmed elements is $B_d$, the $i^{th}$ element cannot be inserted in the table for $B_d<i\le n$. In other words, in calculating $P_d$ for $\alpha >1$, the probability that the $i^{th}$ element cannot be inserted is 1, which means collision unavoidably occurs. Thus, for $\alpha >1$, $P_d$ is formulated as follows.

$$\begin{array}{cc}{P}_d\hfill & =\frac{1}{n}\left(0^d+{(\frac{1}{B_d})}^d+{(\frac{2}{B_d})}^d+\dots +{(\frac{B_d-1}{B_d})}^d+(n-B_d)\right)\hfill \\ \hfill & =\frac{1}{n}\left(\frac{1}{{B_d}^d}\sum _{j=1}^{B_d-1}{j}^d+(n-B_d)\right)\hfill \end{array}$$

(26)

Therefore, $P(F_d)$ for $\alpha >1$ is as follows.

$$\begin{array}{cc}\hfill P(F_d)& =P(S)P(F_d|S)=\frac{1}{3}{P}_d\hfill \\ \hfill & =\frac{1}{3n}\left(\frac{1}{{B_d}^d}\sum _{j=1}^{B_d-1}{j}^d+(n-B_d)\right)\hfill \end{array}$$

(27)

4.2.4. Functional Bloom Filter

Based on the analysis of a functional Bloom filter (FBF) in [22], we compare search failure probability with other hash-based data structures in this paper. Let $P(F_b)$ represent the search failure probability of a functional Bloom filter. As the search failure of an FBF is caused by indeterminable or false positive, $P(F_b)$ can be formulated as follows.

$$\begin{array}{c}\hfill P(F_b)=P(I)+P(F_P)\end{array}$$

(28)

where $P(I)$ represents the probability of indeterminables and $P(F_P)$ represents the probability of false positives in a functional Bloom filter.

Let L represent the number of bits in a cell of an FBF. Among $2^L$ possible values in a cell, value $2^L-1$ is reserved to represent conflict. Value 0 is reserved for the initial before programming. Therefore, a functional Bloom filter can have $2^L-2$ return values. Let $S_q$ represent the set of elements whose return value is q with $S_q\subset S$ ($1\le q\le Q$), where $Q=2^L-2$. Assuming that return values are uniformly distributed, let $n^{\prime }=\frac{n}{Q}$ be the number of elements in $S_q$ for $1\le q\le Q$.

• Indeterminable Probability

In the querying procedure, if all the return values of k cells for input y are set as $2^L-1$, i.e., conflict, then the functional Bloom filter cannot return a value, termed an indeterminable. Conflict occurs when a specific cell that was hashed by any element in $S_q$ is hashed at least once by any other element in $S-S_q$.

The probability of indeterminable, $P(I)$, can be formulated as

$$P(I)=P(S)P(I|S)+P(S^c)P(I|S^c).$$

(29)

In Label (29), $P(S)$ and $P(S^c)$ represent the probability that an input y is included in S and $S^c$, respectively, where $U=S\cup S^c$ and $S\cap S^c=\varnothing$.

Consider $P(I|S)$ first. If input y is included in S ($y\in S$), input y would be included in one of $S_q$ among $q=1,\dots ,Q$. Consider a specific cell that is hashed by $y\in S_q$. If the specific cell is hashed at least once by any other element in $S-S_q$, then the cell would set conflict. The probability that the specific cell is not selected (hashed) by $n-n^{\prime }$ elements in $S-S_q$ with k hash functions is ${(1-\frac{1}{m})}^{k(n-n^{\prime })}$. Let $P_{c,i}$ represent the probability of conflict for an element in set S, which is the event that the specific cell is hashed at least once by $n-n^{\prime }$ elements with k hash functions.

$$P_{c,i}=1-{(1-\frac{1}{m})}^{k(n-n^{\prime })}$$

(30)

There would be k cells that are hashed by the specific input y with k hash functions. An indeterminable event occurs when all k cells hashed by y get conflict.

$$P(I|S)={(P_{c,i})}^k=({1-{(1-\frac{1}{m})}^{k(n-n^{\prime })})}^k$$

(31)

Now we consider $P(I|S^c)$. Let $P_{c,n}$ represent the probability of conflict for input y which is not in set S ($y\notin S$). Consider a specific cell that is hashed by y. If the specific cell was hashed by any element in $S_q$ and it was also hashed at least once by any other element in $S-S_q$ in programming, then the specific cell is in conflict. The numbers of elements in $S_q$ and $S-S_q$ are $n^{\prime }$ and $n-n^{\prime }$, respectively. $P_{c,n}$ is calculated as follows.

$$P_{c,n}=\left(1-{(1-\frac{1}{m})}^{k{n}^{\prime }}\right)\sum _{q=1}^{Q-1}\left(1-{(1-\frac{1}{m})}^{k(n-q{n}^{\prime })}\right)$$

(32)

$P_{c,n}$ is calculated avoiding duplications for $q=1,\dots ,Q$. An indeterminable event occurs when all k cells hashed by y with k hash functions get conflict.

$$P(I|S^c)={(P_{c,n})}^k$$

(33)

For $3n$ inputs (with n elements in S and with $2n$ elements in $S^c$), then $P(S)=\frac{n}{3n}=\frac{1}{3}$ and $P(S^c)=\frac{2n}{3n}=\frac{2}{3}$. Therefore, from Label (29)

$$P(I)=\frac{1}{3}{(P_{c,i})}^k+\frac{2}{3}{(P_{c,n})}^k.$$

(34)

• False Positive Probability

A false positive that results in a search failure can occur for input $y\notin S$ only. In other words, $P(F_P|S)=0$, which means that inputs included in set S do not cause false positives. Therefore, the probability of false positives in a functional Bloom filter, $P(F_P)$, can be formulated as

$$P(F_P)=P(S^c)P(F_P|S^c).$$

(35)

We need to consider $P(F_P|S^c)$. Let $P_{p,n}$ represent the positive probability for input y which is not in set S ($y\notin S$). Consider a specific cell that is hashed by y. If the specific cell was hashed by any element in $S_q$ and it was not hashed by any other element in $S-S_q$ in programming, then the specific cell has value q for $1\le q\le Q$. The probability that the specific cell is not hashed by $n-n^{\prime }$ elements in $S-S_q$ with k hash functions is ${(1-\frac{1}{m})}^{k(n-n^{\prime })}$.

$$P_{p,n}=\left(1-{(1-\frac{1}{m})}^{k{n}^{\prime }}\right){(1-\frac{1}{m})}^{k(n-n^{\prime })}$$

(36)

The false positive event occurs when all of the cells other than conflict cells among k cells hashed by y have the same value. Note that there can be Q cases with equal probability for $q=1,\dots ,Q$.

$$P(F_P|S^c)=Q\sum _{j=1}^k\left(\genfrac{}{}{0pt}{}{k}{j}\right){(P_{p,n})}^j·{(P_{c,n})}^{k-j}$$

(37)

For $3n$ inputs, as $P(S^c)=\frac{2n}{3n}=\frac{2}{3}$, $P(F_P)$ is as follows.

$$P(F_P)=\frac{2}{3}Q\sum _{j=1}^k\left(\genfrac{}{}{0pt}{}{k}{j}\right){(P_{p,n})}^j·{(P_{c,n})}^{k-j}$$

(38)

From Labels (28), (29), and (35), the search failure probability of a functional Bloom filter, $P(F_b)$, can be formulated as follows.

$$\begin{array}{cc}\hfill P(F_b)& =P(I)+P(F_P)\hfill \end{array}$$

$$\begin{array}{c}=\left(P(S)P(I|S)+P(S^c)P(I|S^c)\right)+P(S^c)P(F_P|S^c)\hfill \end{array}$$

(39)

$$\begin{array}{c}=P(S)P(I|S)+P(S^c)\left(P(I|S^c)+P(F_P|S^c)\right)\hfill \end{array}$$

(40)

$$\begin{array}{c}\hfill =\frac{1}{3}{(P_{c,i})}^k+\frac{2}{3}\left({(P_{c,n})}^k+Q\sum _{j=1}^k\left(\genfrac{}{}{0pt}{}{k}{j}\right){(P_{p,n})}^j·{(P_{c,n})}^{k-j}\right)\end{array}$$

(41)

We have an interesting question here of whether false positive or indeterminable is more harmful to raise search failure. While some of the indeterminables are caused by positive inputs, which are the elements included in the programming set, every false positive is caused by negative inputs, which are not included in the programming set. It has been recently shown that the indeterminables caused by positive inputs can be identified and resolved in the programming procedure by constructing an additional functional Bloom filter [46]. Therefore, false positives are more harmful to raise the search failures.

5. Performance Evaluation

In this section, we evaluate and compare the performance of four hash-based data structures described in the previous section using a specific example of name lookup in Named Data Networking (NDN), which uses a key-value data structure. In this application, keys are URLs and values are their output faces. As an FBF stores values only, the number of bits in an FBF cell is allocated according to the number of output faces; however, hash tables store the signature of a key and a corresponding value in pairs. Simulations are carried out using random URLs provided by Web Information Company ALEXA [47]. For simulation, we have randomly selected and made three experimental sets.

Table 2. Number of elements in experimental data sets.

Set	$\mathit{n}(\mathit{S})$	$\mathit{n}(\mathit{U})$
8k	$2^{13}$	$2^{13}+2^{13}\times 2$
32k	$2^{15}$	$2^{15}+2^{15}\times 2$
130k	$2^{17}$	$2^{17}+2^{17}\times 2$

shows experimental data sets. Set S is stored to hash tables and to a functional Bloom filter. The number of URLs in input set U used in searching is three times the number of URLs of set S. One-third of set U is the same as set S, which means that these inputs should have a match from hash tables and from the functional Bloom filter. The remaining two-thirds is included in set $S^c$, which means that these inputs do not have a match. We assume 14 kinds of return values, and therefore the size of a return value is 4 bits.

In our simulation, search failure performance is evaluated in various load factors, and load factors are controlled by adjusting the size of a hash table instead of the number of stored elements. In other words, the number of elements to be inserted in a hash table is fixed, and the load factor is increased by reducing hash table sizes. We first construct a multi-hash table with load factors ($\alpha$) of 0.6, 0.8, 1, 1.2, and 1.4, and then measure the required amount of memory for each multi-hash table according to $\alpha$. We then construct a cuckoo hash table, a d-left hash table, and a functional Bloom filter, using the same amount of memory as the multi-hash table. We assume that the number of hash functions d in a d-left hash table is equal to k, which is the optimal number of hash indexes of a functional Bloom filter.

A 64-bit cyclic redundancy check (CRC) generator is used as a hash function for our simulation. A number of hash indexes were extracted by combining a variable number of bits of a CRC code generated by a key or an input. Therefore, even if multiple hash indexes are required, there is almost no difference in the amount of computational overhead, once a CRC code is obtained.

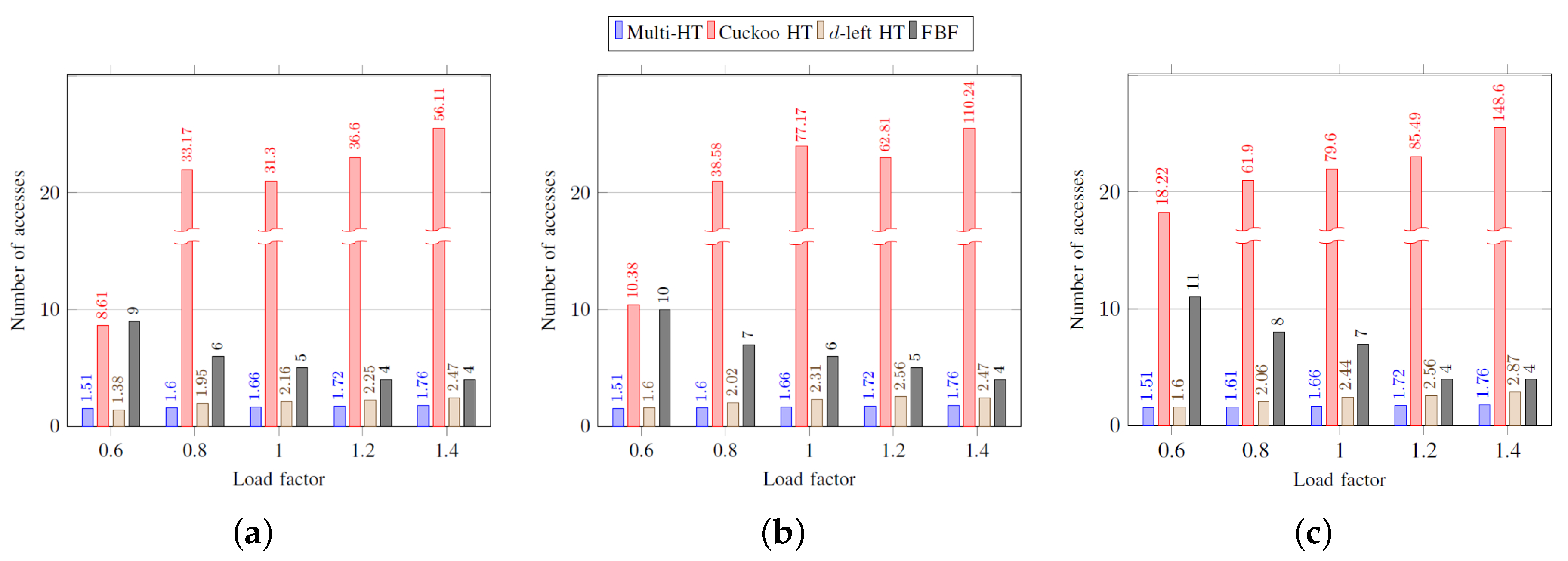
Figure 3 shows the average number of memory accesses in inserting an element according to load factors. As the load factor increases, the cuckoo hash table requires a large number of accesses because many buckets are affected until an empty entry is found. The multi-hash table shows the best performance in most cases, as elements can be inserted if an empty entry is found even before two accesses. However, it is worth noting that the multi-hash table, the d-left hash table, and the functional Bloom filter have the performance proportional to $O(1)$. The average number of memory accesses for the functional Bloom filter is always k obtained from Label (1). As the load factor increases, k decreases, as $\frac{m}{n}$ in Label (1) decreases.

Figure 4 shows the worst-case number of memory accesses in inserting an element according to load factors. As shown, the multi-hash table, the d-left hash table, and the functional Bloom filter show better performance than the cuckoo hash table, and these structures have a performance proportional to $O(1)$. The worst-case performance of the cuckoo hash table is not acceptable as shown. For the functional Bloom filter, the average and the worst-case number of accesses are the same as the number of memory accesses is always equal to k.

Figure 5 and Figure 6 show the average and the worst-case number of memory accesses during search procedure, respectively. Unlike insertion performance, the cuckoo hash table practically has the same performance as the multi-hash table because two hash functions for each element are used, and therefore each of the search procedure is completed within two accesses. In case of the d-left hash table, as the number of hash functions d is equal to k, the search procedure is completed within k accesses. The search performance of the functional Bloom filter is also k accesses as the same as insertion performance.

Figure 7 shows the comparison on search failure rates between theoretical and simulation results as the load factor increases. It is shown that the theoretical and simulation results become similar as the load factor increases. For the theoretical results of hash tables, Labels (16), (21), and (25) are used for $\alpha \le 1$, and Labels (18), (23), and (27) are used for $\alpha >1$. In cases of the multi-hash table and the cuckoo hash table, parameters determining the performance of a data structure, such as the number of buckets and the number of hash functions, are the same, and therefore these tables have almost the same theoretical upper bounds. In evaluating the performance of data structures, the worst-case performance is the most critical, and thus the upper bound is important. It is shown that simulation results are less than the upper bound, as the worst case was assumed in calculating the upper bounds for these structures. Because a cuckoo hash table can access more buckets in inserting an element than a multi-hashing table, it has a better search failure rate when the load factor is 0.6, but no meaningful difference when the load factor is larger than 0.6.

In cases of the d-left hash table and the functional Bloom filter, simulation results show very similar patterns to their theoretical results. As shown in Figure 7, the functional Bloom filter shows the best search failure rate when $\alpha$ increases. More specifically, in terms of the simulation result for 130k at $\alpha =1$ shown in Figure 7c, the search failure rate of the Multi-HT is 5%, and it is ten times larger than that of the FBF, which is 0.5%. Note that the search failure rate of the FBF decreases slightly as the number of elements increases, as $\frac{m}{n}$ for the FBF increases as the number of elements increases. Therefore, the functional Bloom filter is the most efficient structure which can replace hash tables, when the search failure rate is the most concern in storing a large set of elements to a limited size of memory.

6. Conclusions

In this paper, we claim that a functional Bloom filter as a key-value structure is better than hash tables, especially in search failure probability, when a vast amount of information is required to be processed and retrieved in a restricted memory. While hash tables require storing each key in addition to its return value, a functional Bloom filter stores return values without keys, because different index combinations according to each key can be used to identify the key. In order to prove that the functional Bloom filter has a lower search failure probability than a multi-hash table, a cuckoo hash table, and a d-left hash table as the load factor increases, the search failure probabilities of the key-value data structures are theoretically analyzed. The theoretical analysis has been validated through simulations. Simulation results show that the search failure rates of the hash tables are larger than that of the functional Bloom filter, when the load factor is larger than 0.6.