The Hemodynamics of Aneurysms Treated with Flow-Diverting Stents Considering both Stent and Aneurysm/Artery Geometries
Abstract
1. Introduction
2. Materials and Methods
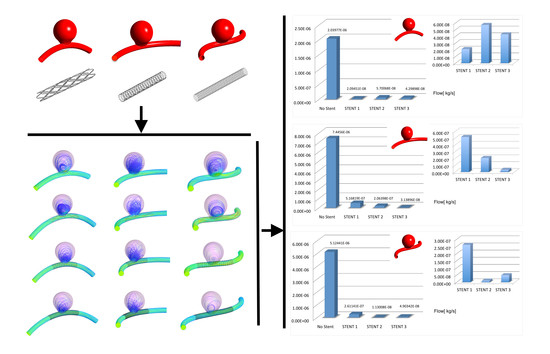
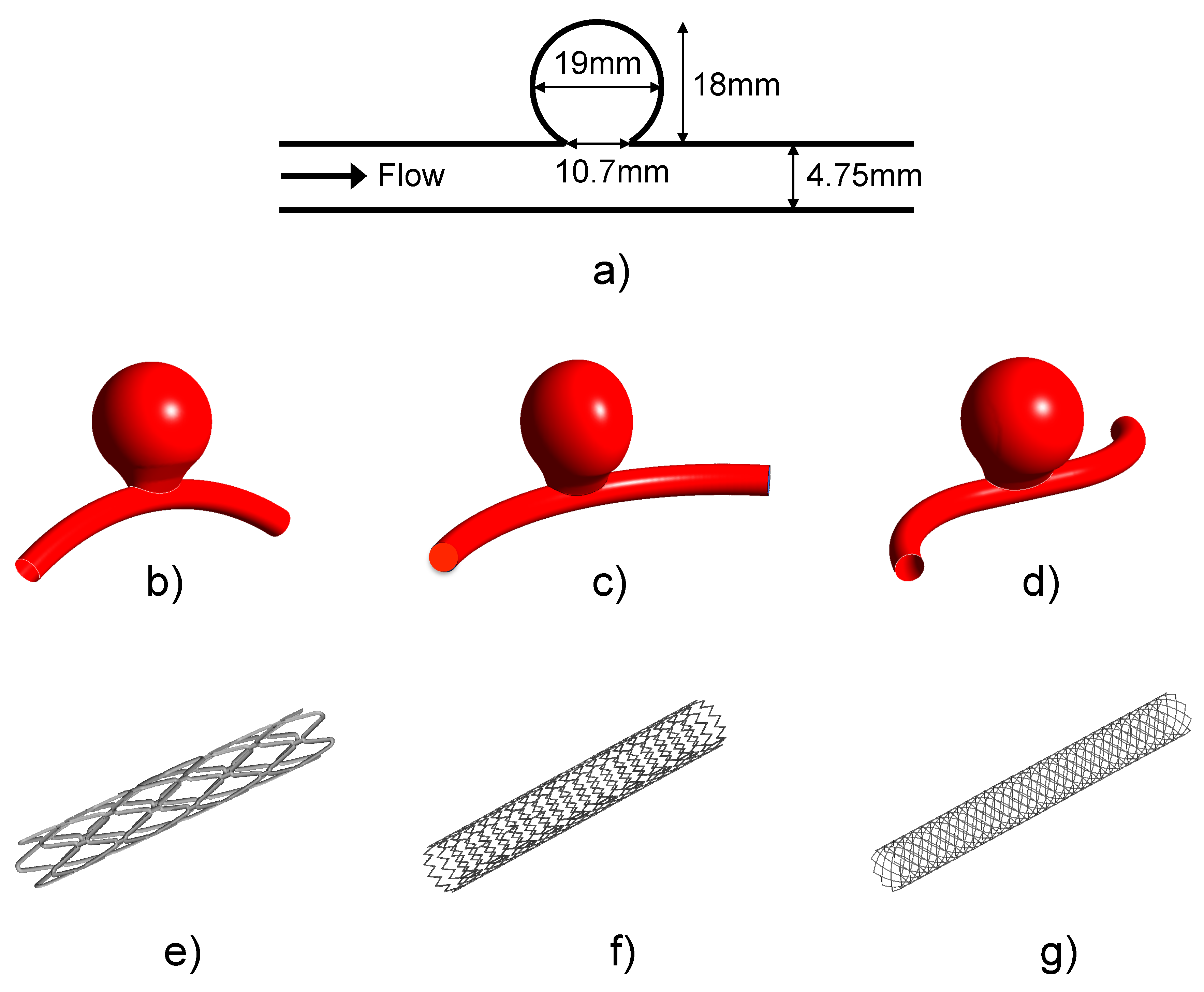
2.1. Idealized Aneurysm Model under Different Geometrical Configurations
2.2. FDS Geometries
2.3. Summary of the Considered Cases
2.4. Numerical Discretization, Blood Rheology and Boundary Conditions
2.5. Numerical Modeling
2.6. Hemodynamics Indices
3. Results
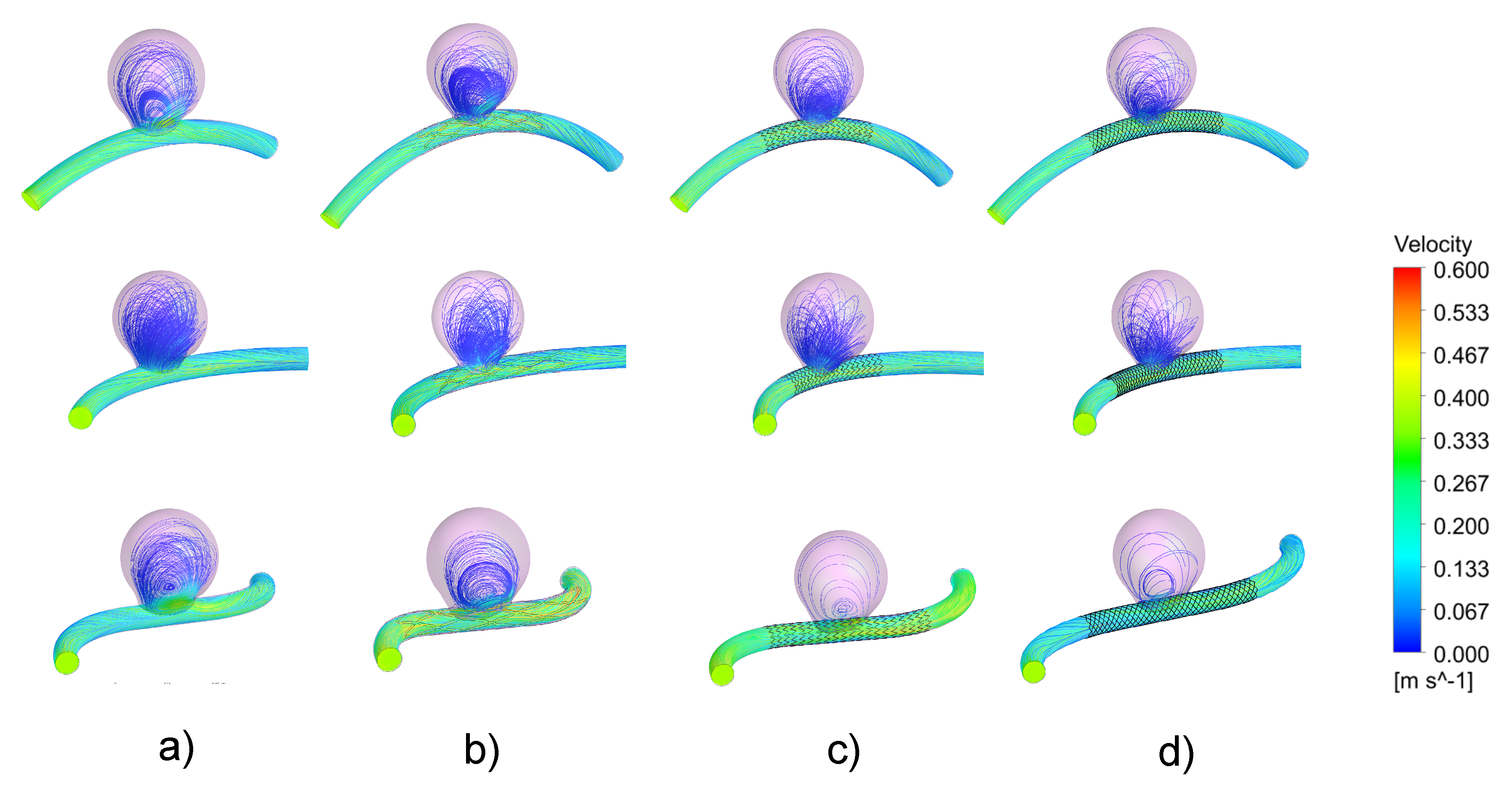
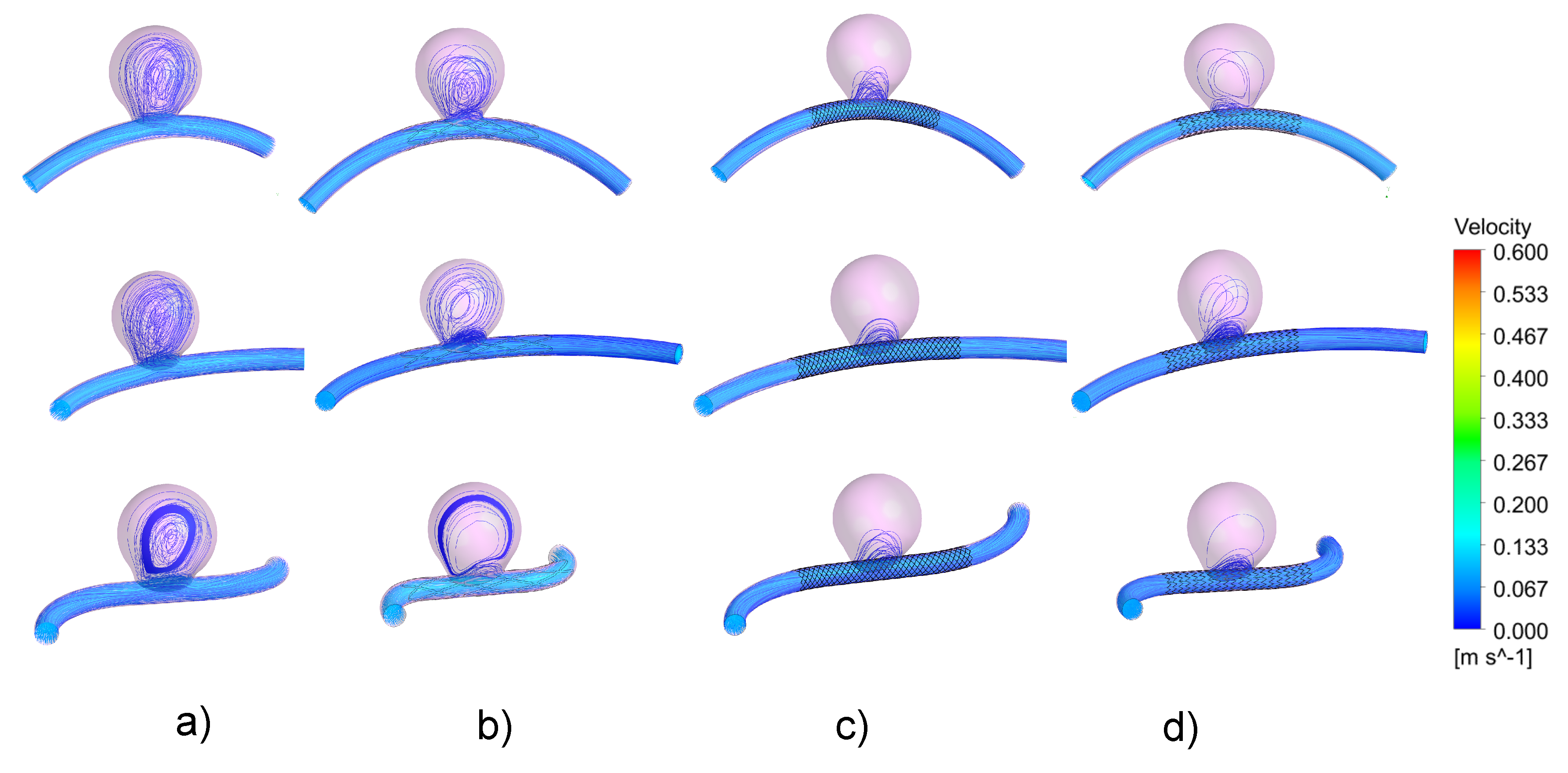
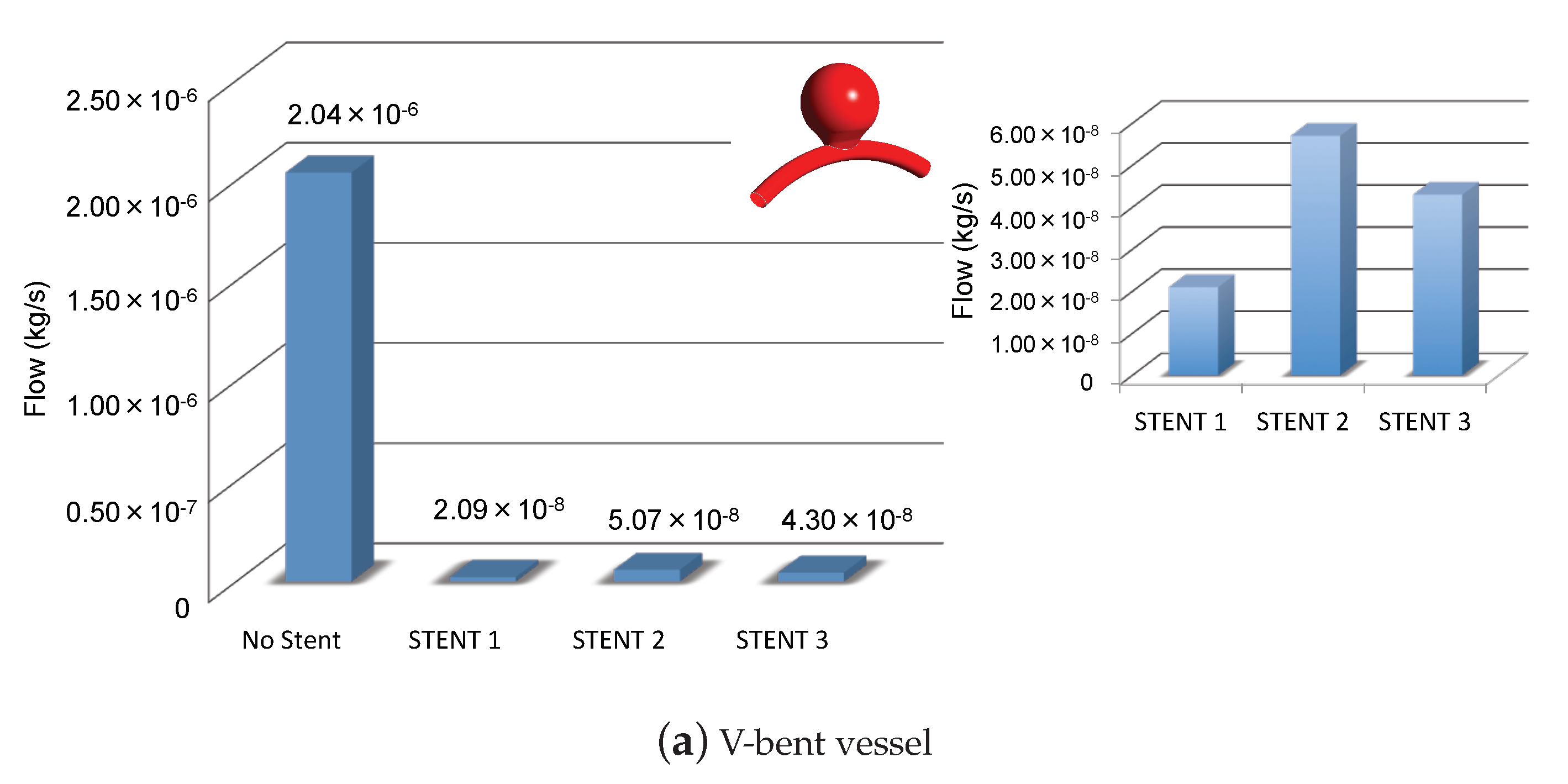
3.1. Impacts of the Stents on the Velocity Field and on Intra-Aneurysmal Flow
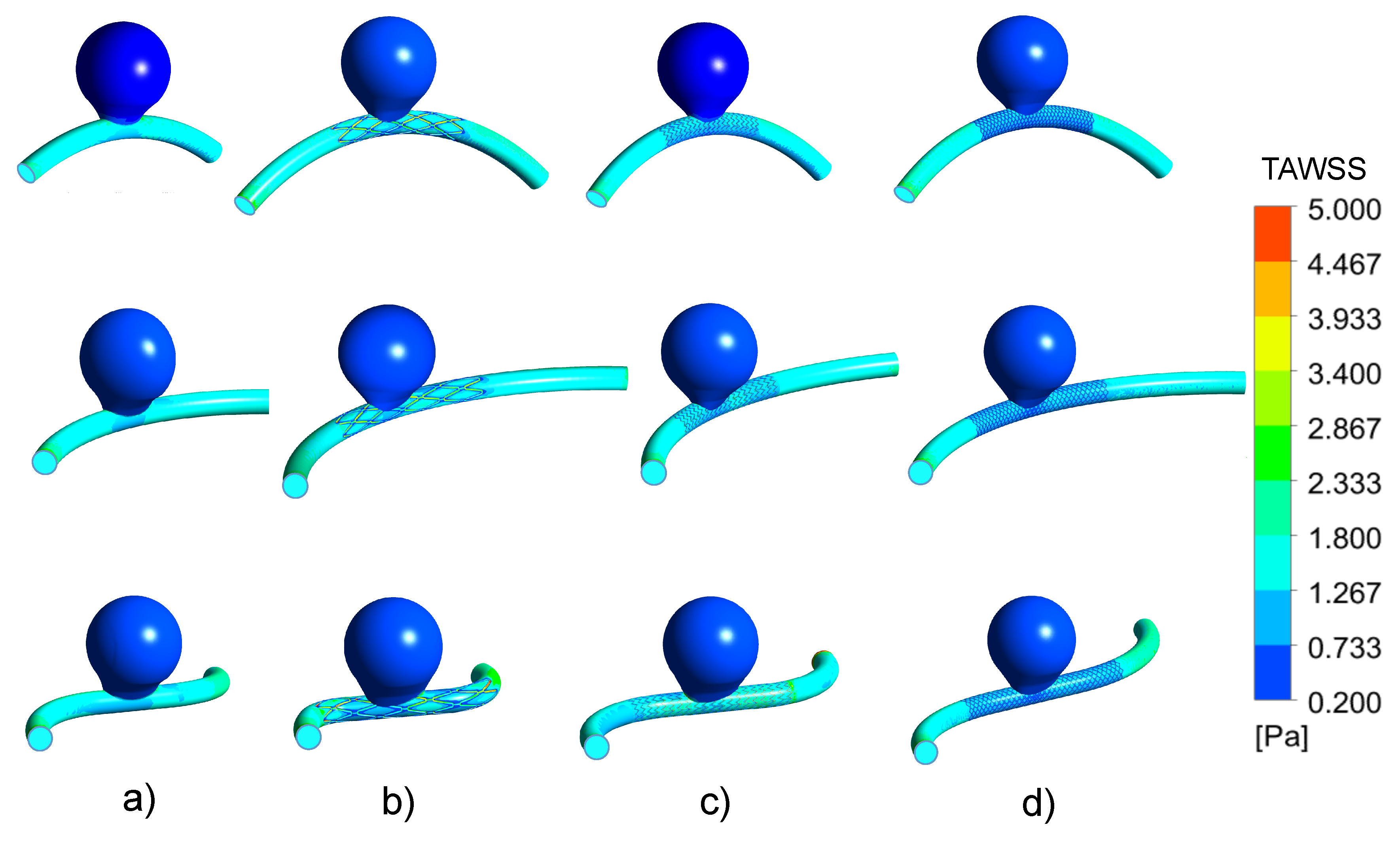
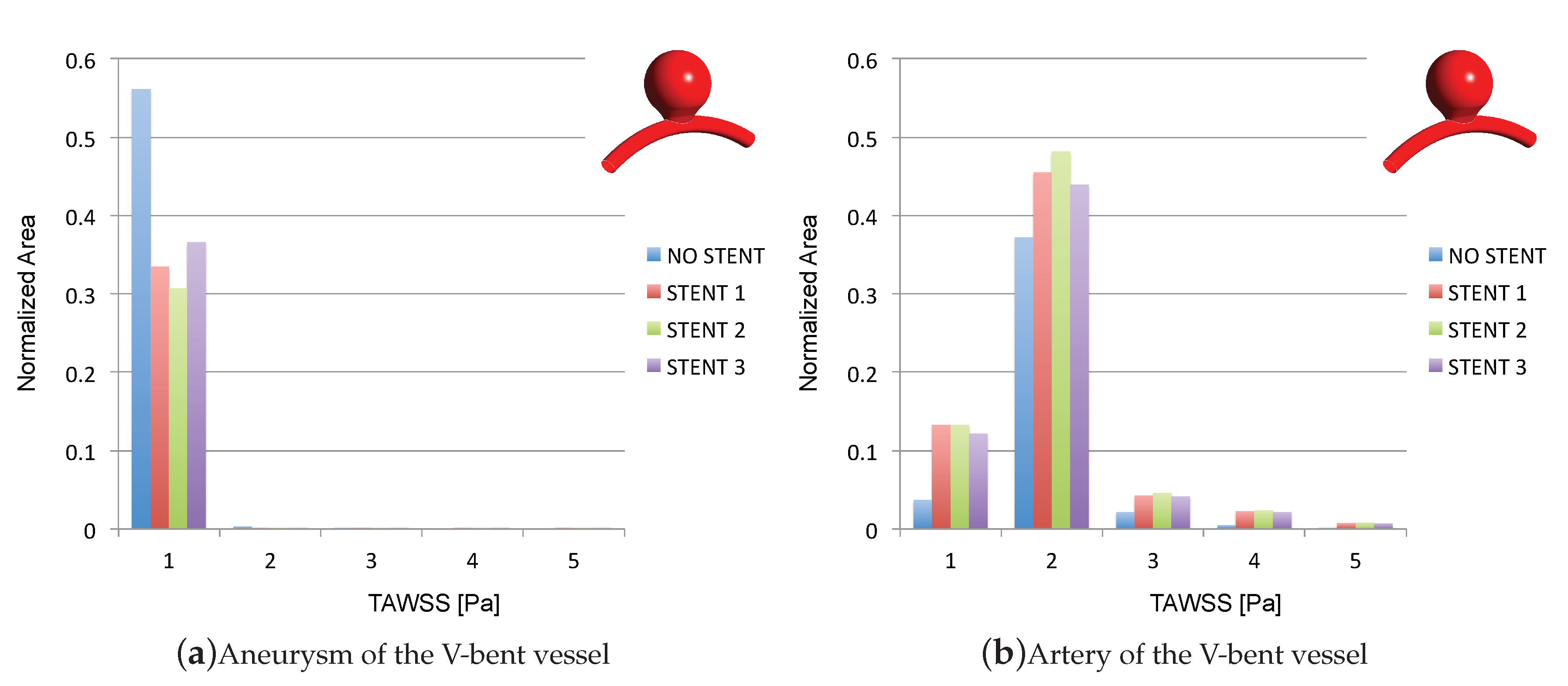
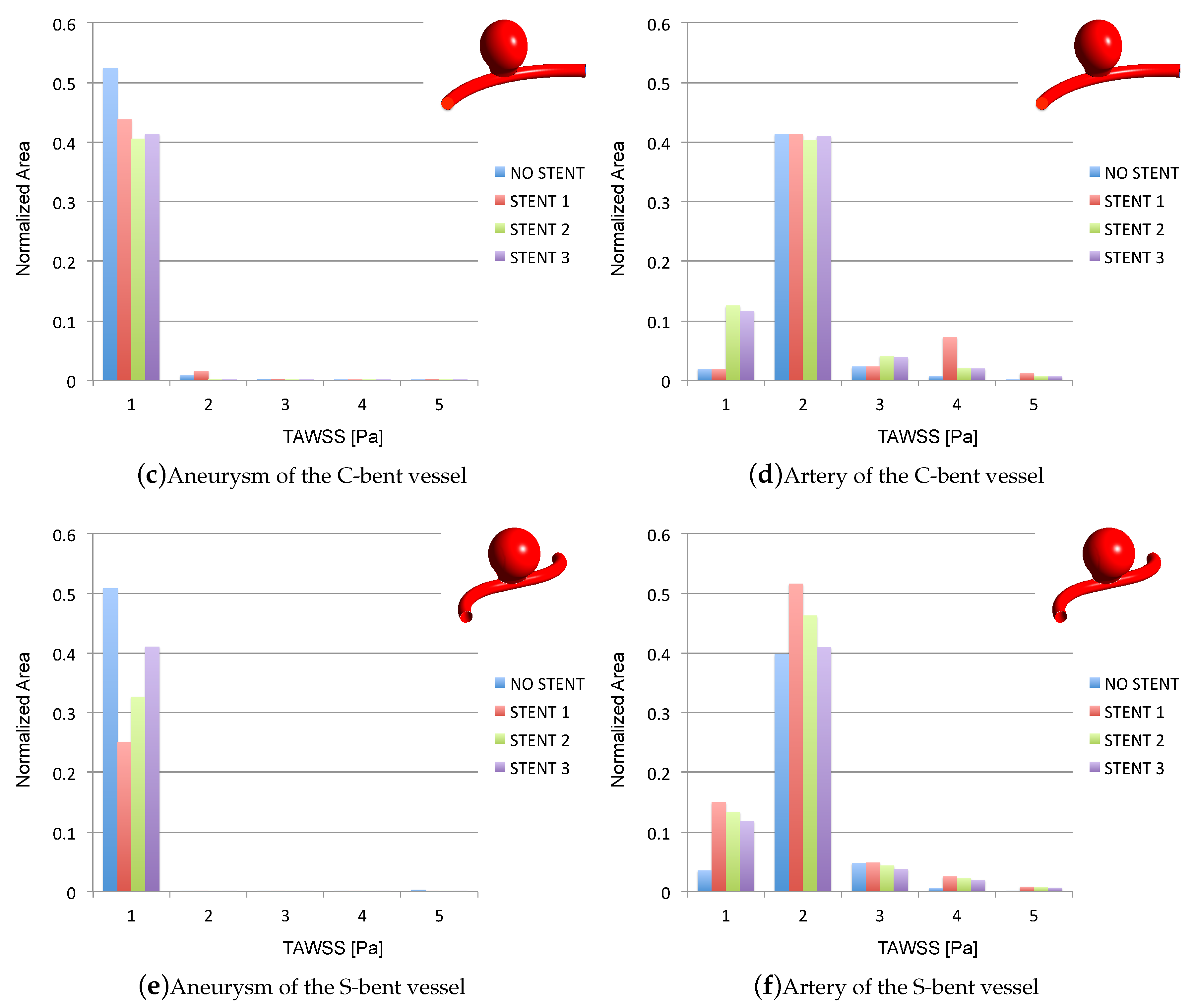
3.2. Impacts of the Stents on the WSS-Related Indices: TAWSS
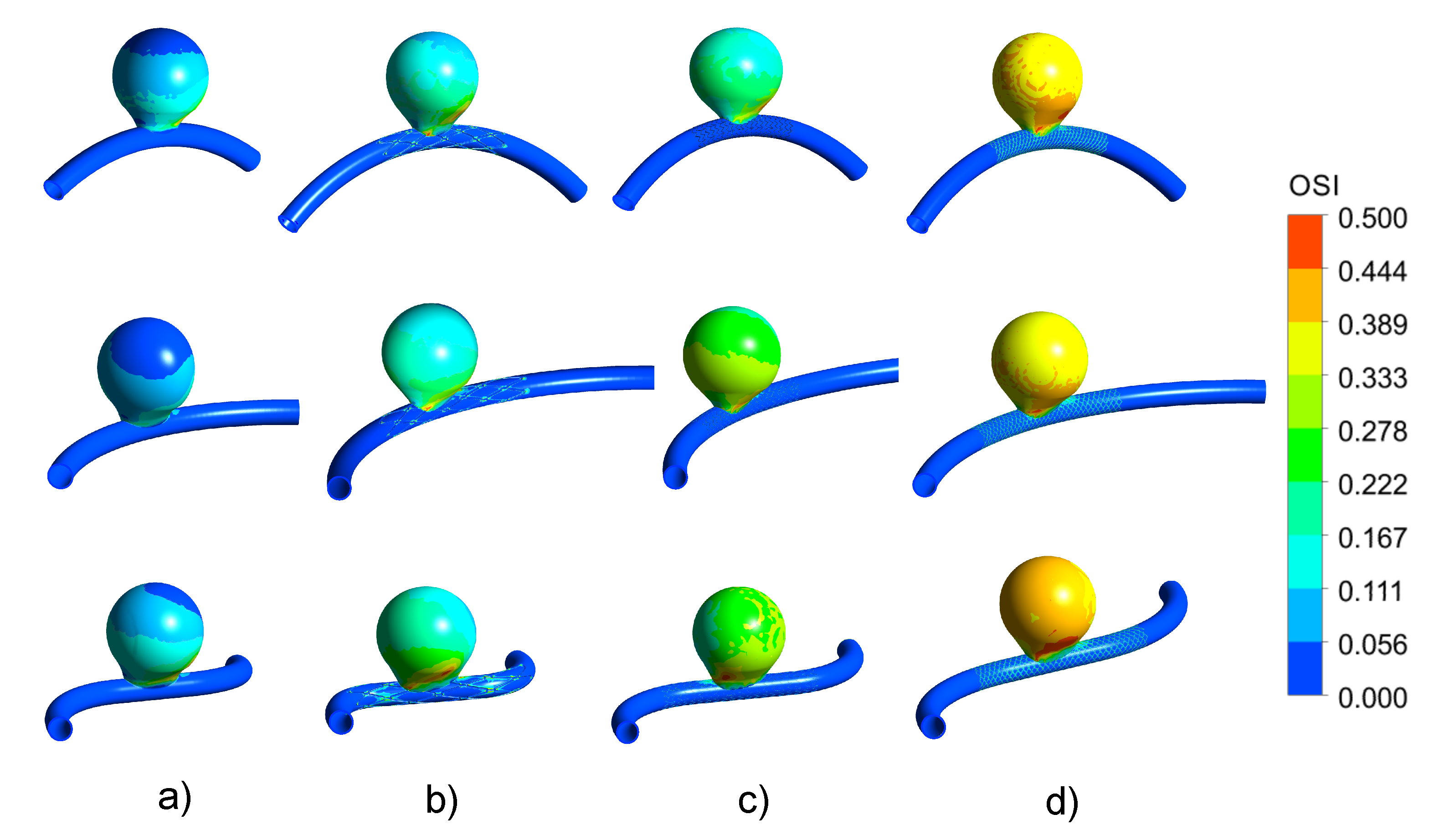
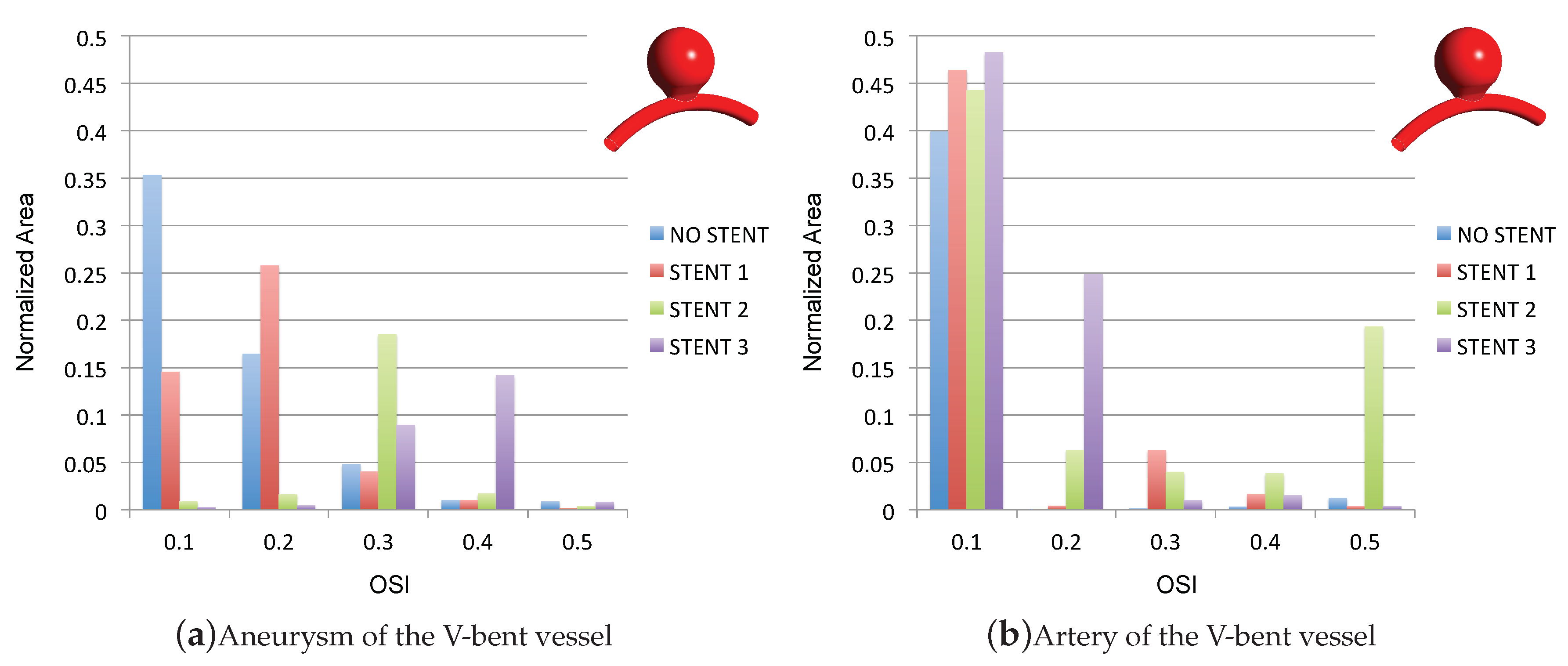
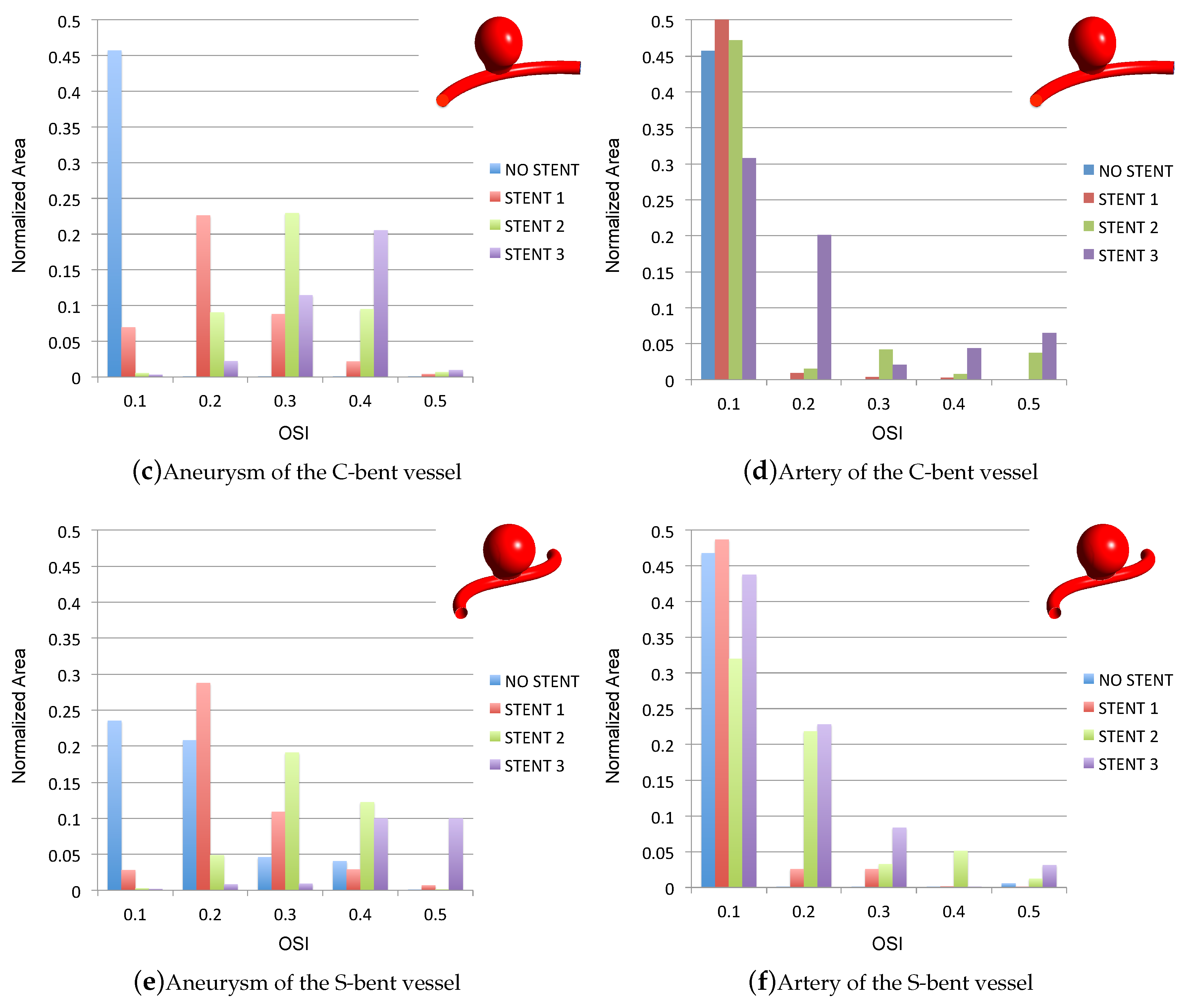
3.3. Impact of the Stents on the WSS-Related Indices: OSI
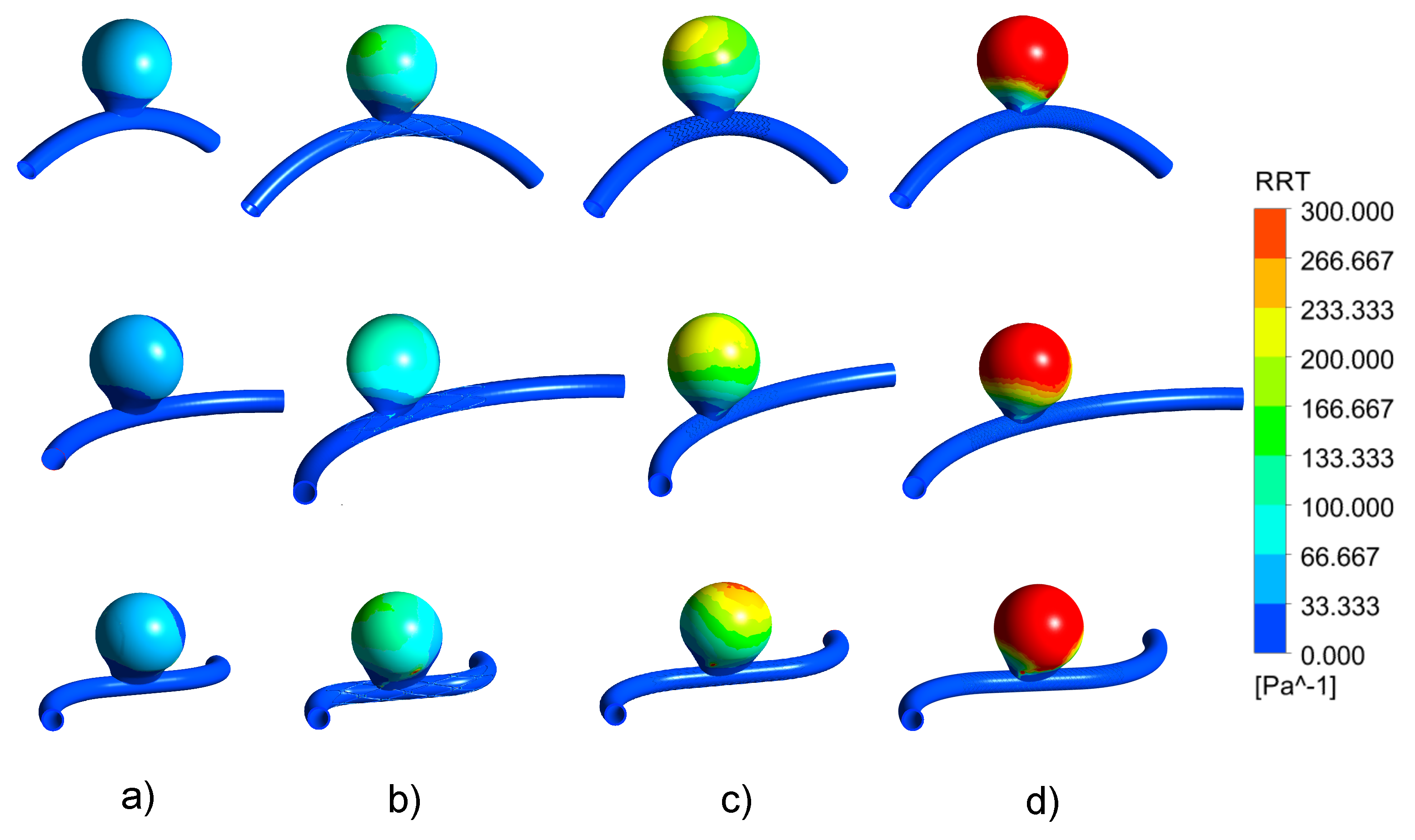
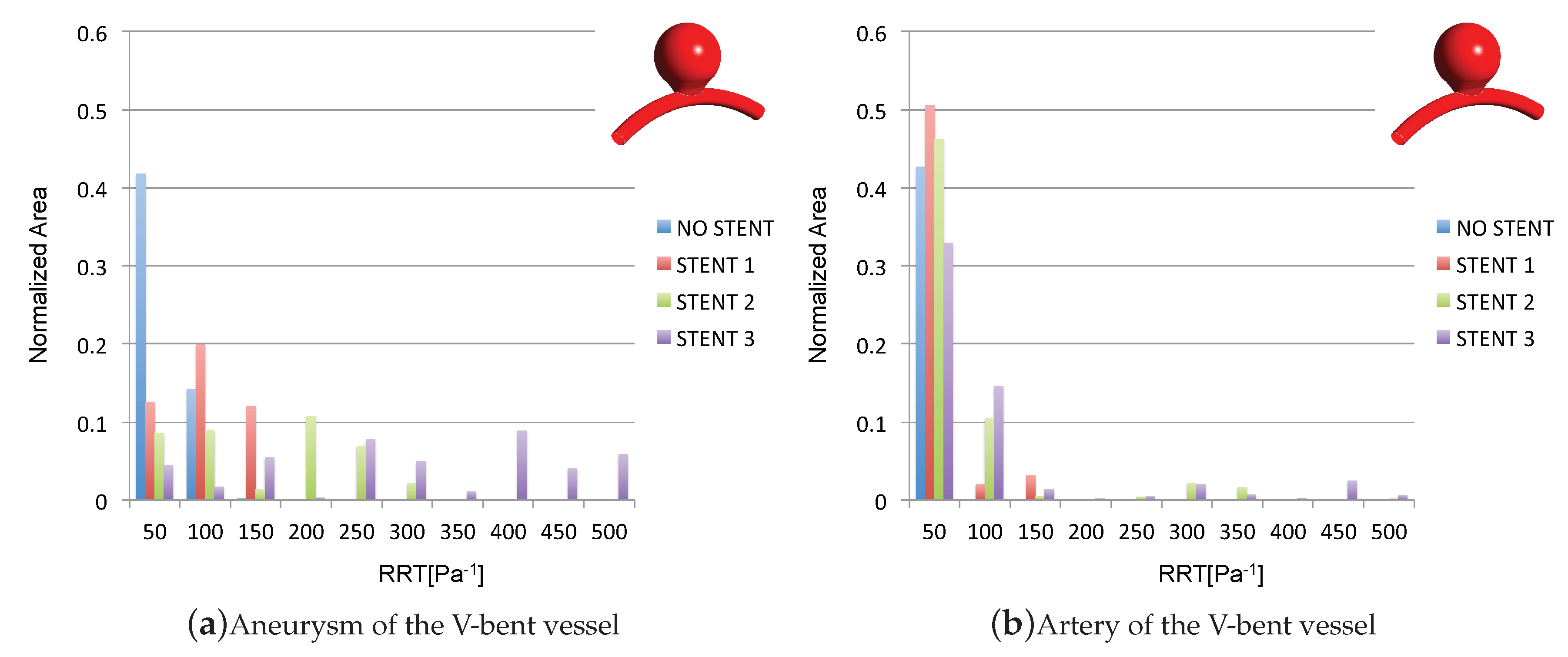
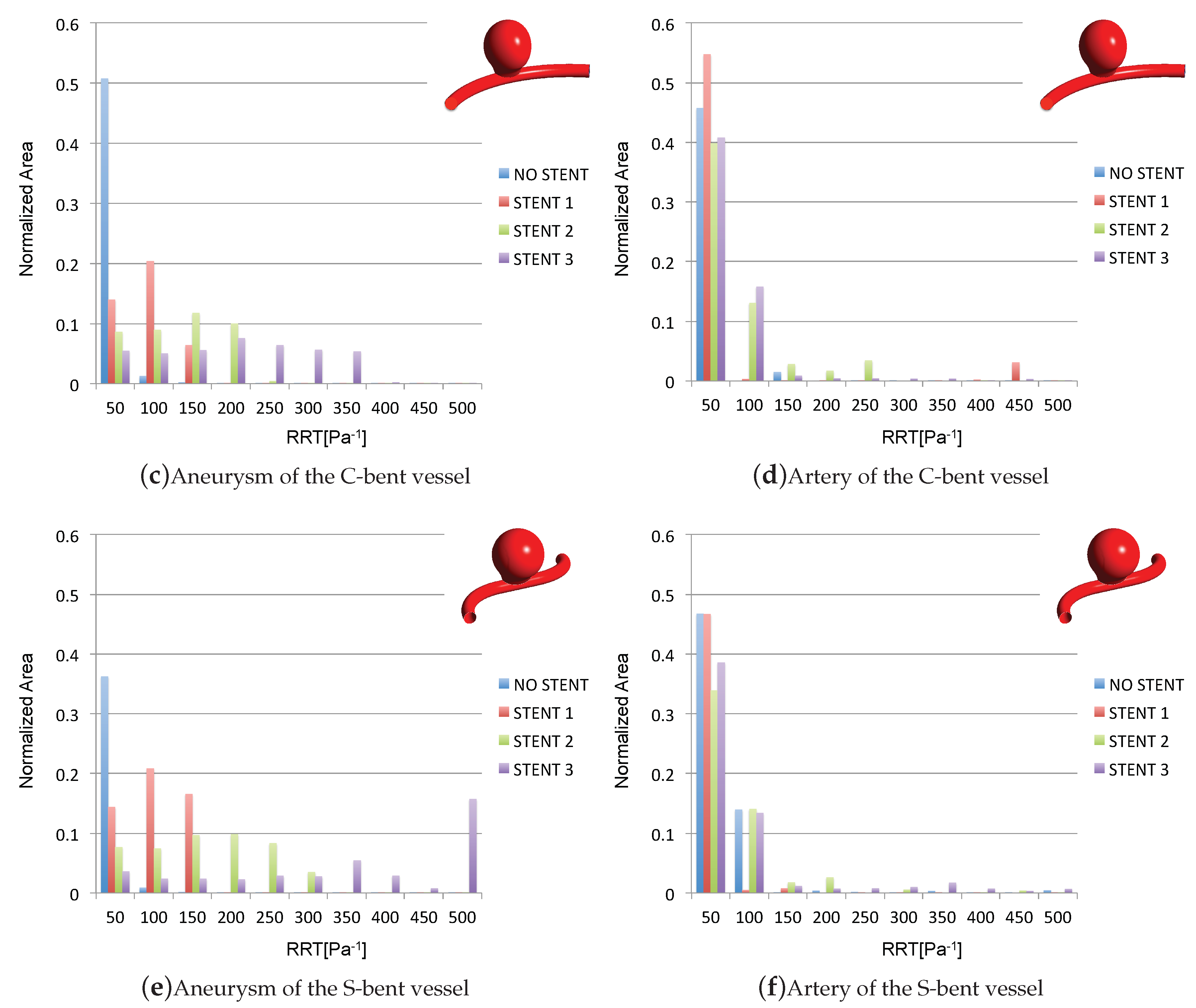
3.4. Impact of the Stents on the WSS-Related Indices: RRT
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Valencia, A.; Morales, H.; Rivera, R.; Bravo, E.; Galvez, M. Blood flow dynamics in patient-specific cerebral aneurysm models: The relationship between wall shear stress and aneurysm area index. Med. Eng. Phys. 2008, 30, 329–340. [Google Scholar] [CrossRef]
- Kim, Y.H.; Xu, X.; Lee, J.S. The Effect of Stent Porosity and Strut Shape on Saccular Aneurysm and its Numerical Analysis with Lattice Boltzmann Method. Ann. Biomed. Eng. 2010, 38, 2274–2292. [Google Scholar] [CrossRef]
- Roloff, C.; Bordás, R.; Nickl, R.; Mátrai, Z.; Szilárd, N.S.S.; Thévenin, D. Investigation of the velocity field in a full-scale model of a cerebral aneurysm. Int. J. Heat Fluid Flow 2013, 43, 212–219. [Google Scholar] [CrossRef]
- Csippa, B.; Závodszky, G.; Paál, G.; Szikora, I. A new hypothesis on the role of vessel topology in cerebral aneurysm initiation. Comput. Biol. Med. 2018, 103, 244–251. [Google Scholar] [CrossRef]
- Weibers, D.O.; Whisnant, J.P.; Houston, J., III; Meissner, I.; Brown, R.D., Jr.; Piepgras, D.G.; Forbes, G.S.; Thielen, K.; Nichols, D.; O’ Fallon, W.M.; et al. International Study of Unruptured Intracranial Aneurysms Investigators. Unruptured intracranial aneurysm: Natural history, clinical outcome, and risks of surgical and endovascular treatment. Lancet 2003, 362, 103–110. [Google Scholar]
- Seshadhri, S.; Janiga, G.; Beuing, O.; Skalej, M.; Thevenin, D. Impact of stents and flow diverters on hemodynamics in idealized aneurysm models. J. Biomech. Eng. 2011, 133, 071005. [Google Scholar] [CrossRef]
- Kulcsár, Z.; Augsburger, L.; Reymond, P.; Pereira, V.M.; Hirsch, S.; Mallik, A.S.; Millar, J.; Wetzel, S.G.; Wanke, I.; Rufenacht, D.A. Flow diversion treatment: Intra-aneurismal blood flow velocity and WSS reduction are parameters to predict aneurysm thrombosis. Acta Neurochir. (Wien) 2012, 154, 1827–1834. [Google Scholar] [CrossRef]
- Anzai, H.; Ohta, M.; Falcone, J.L.; Chopard, B. Optimization of flow diverters for cerebral aneurysms. J. Comput. Sci. 2012, 3, 1–7. [Google Scholar] [CrossRef]
- Mut, F.; Raschi, M.; Scrivano, E.; Bleise, C.; Chudyk, J.; Ceratto, R.; Lylyk, P.; Cebral, J.R. Association between hemodynamic conditions and occlusion times after flow diversion in cerebral aneurysms. J. Neurointerv. Surg. 2015, 7, 286–290. [Google Scholar] [CrossRef]
- Ouared, R.; Larrabide, I.; Brina, O.; Bouillot, P.; Erceg, G.; Yilmaz, H.; Lovblad, K.O.; Mendes Pereira, V. Computational fluid dynamics analysis of flow reduction induced by flow-diverting stents in intracranial aneurysms: A patient-unspecific hemodynamics change perspective. J. NeuroInterv. Surg. 2016, 8, 1–6. [Google Scholar] [CrossRef]
- Lylyk, P.; Miranda, C.; Ceratto, R.; Ferrario, A.; Scrivano, E.; Luna, H.R.; Berez, A.L.; Tran, Q.; Nelson, P.K.; Fiorella, D. Curative endovascular reconstruction of cerebral aneurysms with the pipeline embolization device: The Buenos Aires experience. Neurosurgery 2009, 64, 632–642. [Google Scholar] [CrossRef]
- Becske, T.; Kallmes, D.F.; Saatci, I.; McDougall, C.G.; Szikora, I.; Lanzino, G.; Moran, C.J.; Woo, H.H.; Lopes, D.K.; Berez, A.L.; et al. Pipeline for uncoilable or failed aneurysms: Results from a multicenter clinical trial. Radiology 2013, 267, 858–868. [Google Scholar] [CrossRef]
- Kim, M.; Taulbee, D.B.; Tremmel, M.; Meng, H. Comparison of Two Stents in Modifying Cerebral Aneurysm Hemodynamics. Ann. Biomed. Eng. 2008, 36, 726–741. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Tian, Z.; Liu, J.; Jing, L.; Paliwal, N.; Wang, S.; Zhang, Y.; Xiang, J.; Siddiqui, A.H.; Meng, H.; et al. Flow diverter effect of LVIS stent on cerebral aneurysm hemodynamics: A comparison with Enterprise stents and the Pipeline device. J. Transl. Med. 2016, 14, 199. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Wang, Y.; Kao, E.; Flórez-Valencia, L.; Courbebaisse, G. Towards optimal flow diverter porosity for the treatment of intracranial aneurysm. J. Biomech. 2016, 82, 20–27. [Google Scholar]
- Dholakia, R.; Sadasivan, C.; Fiorella, D.J.; Woo, H.H.; Lieber, B.B. Hemodynamics of Flow Diverters. J. Biomech. Eng. 2017, 139, 021002-10. [Google Scholar] [CrossRef] [PubMed]
- Lieber, B.B.; Stancampiano, A.P.; Wakhloo, A.K. Alteration of hemodynamics in aneurism models by stenting: Influence on stent porosity. Ann. Biomed. Eng. 1997, 25, 460–469. [Google Scholar] [CrossRef] [PubMed]
- Lieber, B.B.; Livescu, V.; Hopkins, L.N.; Wakhloo, A.K. Particle image velocimetry assessment of stent design influence on intra-aneurysmal flow. Ann. Biomed. Eng. 2002, 30, 768–777. [Google Scholar] [CrossRef] [PubMed]
- Cebral, J.R.; Mut, F.; Raschi, M.; Scrivano, E.; Ceratto, R.; Lylyk, P.; Putman, C.M. Aneurysm rupture following treatment with flow-diverting stents: Computational hemodynamics analysis of treatment. Am. J. Neuroradiol. 2011, 32, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Mut, F.; Cebral, J.R. Effects of flow-diverting device oversizing on hemodynamics alteration in cerebral aneurysms. Am. J. Neuroradiol. 2012, 33, 2010–2016. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chong, W.; Qian, Y. Investigation of intracranial aneurysm hemodynamcs following flow diverter stent treatment. Med. Eng. Phys. 2013, 35, 608–615. [Google Scholar] [CrossRef]
- Larrabide, I.; Aguilar, M.L.; Morales, H.G.; Geers, A.J.; Kulcsár, Z.; Rufenacht, D.; Frangi, A.F. Intra-aneurysmal pressure and flow changes induced by flow diverters: Relation to aneurysm size and shape. Am. J. Neuroradiol. 2013, 34, 816–822. [Google Scholar] [CrossRef] [PubMed]
- Levitt, M.R.; McGah, P.M.; Aliseda, A.; Mourad, P.D.; Nerva, J.D.; Vaidya, S.S.; Morton, R.P.; Ghodke, B.V.; Kim, L.J. Cerebral aneurysms treated with flow-diverting stents: Computational models with intravascular blood flow measurements. Am. J. Neuroradiol. 2014, 35, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Larrabide, I.; Geers, A.J.; Morales, H.G.; Aguilar, M.L.; Rufenacht, D.A. Effect of Aneurysm and ICA Morphology on Hemodynamics Before and After Flow Diverter Treatment. J. Neurointerv. Surg. 2015, 7, 272–280. [Google Scholar] [CrossRef] [PubMed]
- Larrabide, I.; Geers, A.J.; Morales, H.G.; Bijlenga, P.; Rufenacht, D.A. Change in aneurysmal flow pulsatility after flow diverter treatment. Comput. Med. Imaging Graph. 2016, 50, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.T.; Li, Y.; Aubry, N.; Massoudi, M.; Antaki, J.F. Numerical Simulation of Red Blood Cell-Induced Platelet Transport in Saccular Aneurysms. Appl. Sci. 2017, 7, 484. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, M.; Verrelli, D.I.; Chong, W.; Ohta, M.; Qian, Y. Numerical simulation of aneurysmal haemodynamics with calibratedporous-medium models of flow-diverting stents. J. Biomech. 2018, 80, 88–94. [Google Scholar] [CrossRef]
- Catalán-Echeverría, B.; Kelly, M.E.; Peeling, L.; Bergstrom, D.; Chen, X.; Malvè, M. CFD-based Comparison Study of a New Flow Diverting Stent and Commercially-Available Ones for the Treatment of Cerebral Aneurysms. Appl. Sci. 2019, 9, 1341. [Google Scholar] [CrossRef]
- Sarrami-Foroushani, A.; Lassila, T.; Hejazi, S.M.; Nagaraja, S.; Bacon, A.; Frangi, A.F. A computational model for prediction of clot platelet content in flow-diverted intracranial aneurysm. J. Biomech. 2019, 91, 7–13. [Google Scholar] [CrossRef]
- Pereira, V.M.; Bonnefous, O.; Ouared, R.; Brina, O.; Stawiaski, J.H.; Aerts, H.; Ruijters, D.; Narata, A.P.; Bijlenga, P.; Schaller, K.; et al. A DSA-based method using contrast-motion estimation for the assessment of the intra-aneurysmal flow changes induced by flow-diverter stents. Am. J. Neuroradiol. 2013, 34, 808–815. [Google Scholar] [CrossRef]
- Seibert, B.; Tummala, R.P.; Chow, R.; Faridar, A.; Moudavi, S.A.; Divani, A.A. Intracranial aneurysm: Review of current treatment options and outcomes. Front. Neurol. 2011, 2, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Jeong, W.; Han, M.H.; Rhee, K. The hemodynamic alterations induced by the vascular angular deformation in stent-assisted coiling of bifurcation aneurysms. Comput. Biol. Med. 2014, 53, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Voss, S.; Beuing, O.; Janiga, G.; Berg, P. Stent-induced vessel deformation after intracranial aneurysm treatment—A hemodynamic pilot study. Comput. Biol. Med. 2019, 11, 103338. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, S.; Shimogonya, Y.; Yonemoto, N. Differences in Cerebral Aneurysm Rupture Rate According to Anatomies Depend on the Hemodynamics Environment. Am. J. Neuroradiol. 2019, 40, 834–839. [Google Scholar] [CrossRef]
- Li, W.; Liu, J.; Zhang, Y.; Wang, K.; Wang, Y. Flow Diversion and Outcomes of Vertebral Fusiform Aneurysms After Stent-Only Treatment: A Hemodynamic Study. World Neurosurg. 2017, 107, 202–210. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Feng, J.; Huang, Y.; Tokgoz, A.; Gillard, J.; Lu, Q.; Teng, Z. Influence of overlapping pattern of multiple overlapping uncovered stents on the local mechanical environment: A patient-specific parameter study. J. Biomech. 2017, 188–196, 202–210. [Google Scholar]
- Wang, S.; Zhang, Y.; Feng, J.; Huang, Y.; Hui, P.; Gillard, J.H.; Lu, Q.; Teng, Z. The role of porosity and 3D cross-stent configuration of multiple overlapping uncovered stents in the management of complex aortic aneurysms—Insights from haemodynamics. Med. Nov. Technol. Devices 2019, 3, 100020. [Google Scholar] [CrossRef]
- Han, X.; Wu, X.; Kelly, M.; Chen, X.B. Fabrication and Optimal Design of Biodegradable Polymeric Stents for Aneurysms Treatments. J. Funct. Biomater. 2017, 8, 8. [Google Scholar] [CrossRef]
- Torii, R.; Oshima, M.; Kobayashi, T.; Takagi, K.; Tezduyar, T.E. Fluid-structure interaction modeling of blood flow and cerebral aneurysm: Significance of artery and aneurysm shapes. Comput. Methods Appl. Mech. Eng. 2009, 198, 3613–3621. [Google Scholar] [CrossRef]
- Ansys Inc. Ansys CFX Theory Manual v.16; Ansys Software: Canonsburg, PA, USA, 2016. [Google Scholar]
- Jou, L.D.; Lee, D.H.; Morsi, H.; Mawad, M.E. Wall shear stress on ruptured and unruptured intracranial aneurysms at the internal carotid artery. Am. J. Neuroradiol. 2008, 29, 1761–1767. [Google Scholar] [CrossRef]
- He, X.; Ku, D.N. Pulsatile flow in the human left coronary artery bifurcation: Average conditions. J. Biomech. Eng. 1996, 118, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Himburg, H.A.; Grzybowski, D.M.; Hazel, A.L.; LaMack, J.A.; Li, X.M.; Friedman, M.H. Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. Am. J. Physiol. Heart Circ. Physiol. 2004, 286, H1916–H1922. [Google Scholar] [CrossRef] [PubMed]
- Xiang, J.; Natarajan, S.K.; Tremmel, M.; Ma, D.; Mocco, J.; Hopkins, L.N.; Siddiqui, A.H.; Levy, E.I.; Meng, H. Hemodynamic-Morphologic Discriminants for Intracranial Aneurysm Rupture. Stroke 2011, 42, 144–152. [Google Scholar] [CrossRef]
- Anzai, H.; Falcone, J.L.; Chopard, B.; Hayase, T.; Ohta, M. Optimization of Strut Placement in Flow Diverter Stents for Four Different Aneurysm Configurations. J. Biomech. Eng. 2014, 136, 061006. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.Y.; Wei, Y.; Su, Y.L.; Yuan, Q.; Yang, C.F. Impacts of Internal Carotid Artery Revascularization on Flow in Anterior Communicating Artery Aneurysm: A Preliminary Multiscale Numerical Investigation. Appl. Sci. 2019, 9, 4143. [Google Scholar] [CrossRef]
- Chiastra, C.; Migliavacca, F.; Martínez, M.A.; Malvè, M. On the necessity of modelling fluid-structure interaction for stented coronary arteries. J. Mech. Behav. Biomed. Mater. 2014, 34, 217–230. [Google Scholar] [CrossRef]
- Wu, Y.F.; Yang, P.F.; Shen, J.; Huang, Q.H.; Zhang, X.; Qian, Y.; Liu, J.M. A comparison of the hemodynamic effects of flow diverters on wide-necked and narrow- necked cerebral aneurysms. J. Clin. Neurosci. 2012, 19, 1520–1524. [Google Scholar] [CrossRef]

| Thickness [mm] | Length [mm] | Diameter [mm] | Porosity | |
|---|---|---|---|---|
| STENT 1 | 0.4 | 40 | 4.75 | |
| STENT 2 | 0.1 | 40 | 4.75 | |
| STENT 3 | 0.1 | 40 | 4.75 |
| Vessel | Diameter [mm] | Aspect Ratio [mm] | Stent |
|---|---|---|---|
| V-bent, C-bent, S-bent | 4.75 | 1.68 | No stent, STENT 1, 2, 3 |
| No Stent | STENT 1 | STENT 2 | STENT 3 | |
|---|---|---|---|---|
| 3D elements | 329,286 | 10,949,532 | 14,403,306 | 18,358,866 |
| 2D elements | 94,830 | 1,143,257 | 1,040,456 | 1,440,800 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cillo-Velasco, P.R.; Luciano, R.D.; Kelly, M.E.; Peeling, L.; Bergstrom, D.J.; Chen, X.; Malvè, M. The Hemodynamics of Aneurysms Treated with Flow-Diverting Stents Considering both Stent and Aneurysm/Artery Geometries. Appl. Sci. 2020, 10, 5239. https://doi.org/10.3390/app10155239
Cillo-Velasco PR, Luciano RD, Kelly ME, Peeling L, Bergstrom DJ, Chen X, Malvè M. The Hemodynamics of Aneurysms Treated with Flow-Diverting Stents Considering both Stent and Aneurysm/Artery Geometries. Applied Sciences. 2020; 10(15):5239. https://doi.org/10.3390/app10155239
Chicago/Turabian StyleCillo-Velasco, Paulo R., Rafaello D. Luciano, Michael E. Kelly, Lissa Peeling, Donald J. Bergstrom, Xiongbiao Chen, and Mauro Malvè. 2020. "The Hemodynamics of Aneurysms Treated with Flow-Diverting Stents Considering both Stent and Aneurysm/Artery Geometries" Applied Sciences 10, no. 15: 5239. https://doi.org/10.3390/app10155239
APA StyleCillo-Velasco, P. R., Luciano, R. D., Kelly, M. E., Peeling, L., Bergstrom, D. J., Chen, X., & Malvè, M. (2020). The Hemodynamics of Aneurysms Treated with Flow-Diverting Stents Considering both Stent and Aneurysm/Artery Geometries. Applied Sciences, 10(15), 5239. https://doi.org/10.3390/app10155239