A Challenge: Support of Standing Balance in Assistive Robotic Devices
Abstract
:1. Introduction
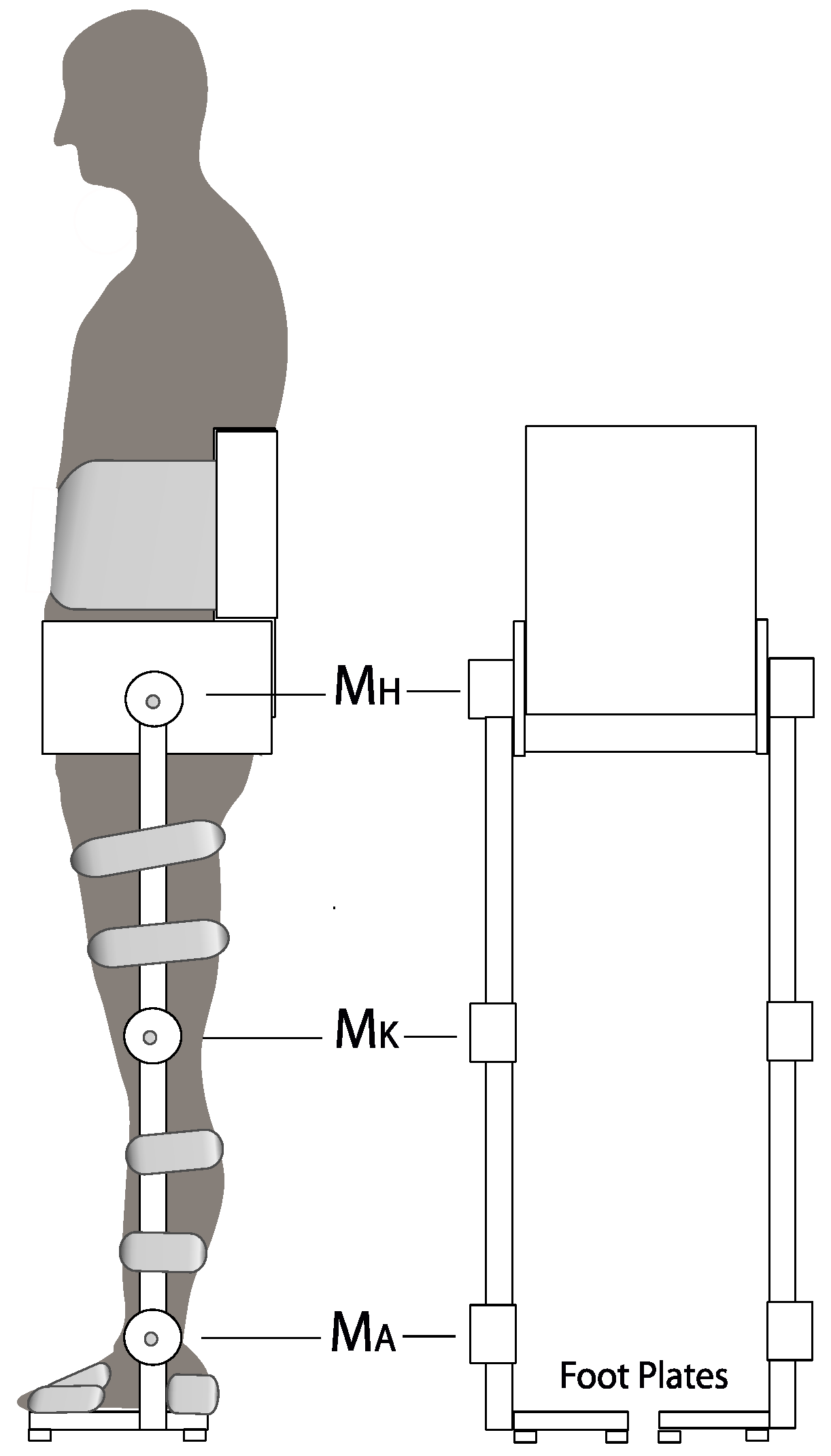
2. Functionality of Exoskeleton
3. Human Derived Self-Balancing Control
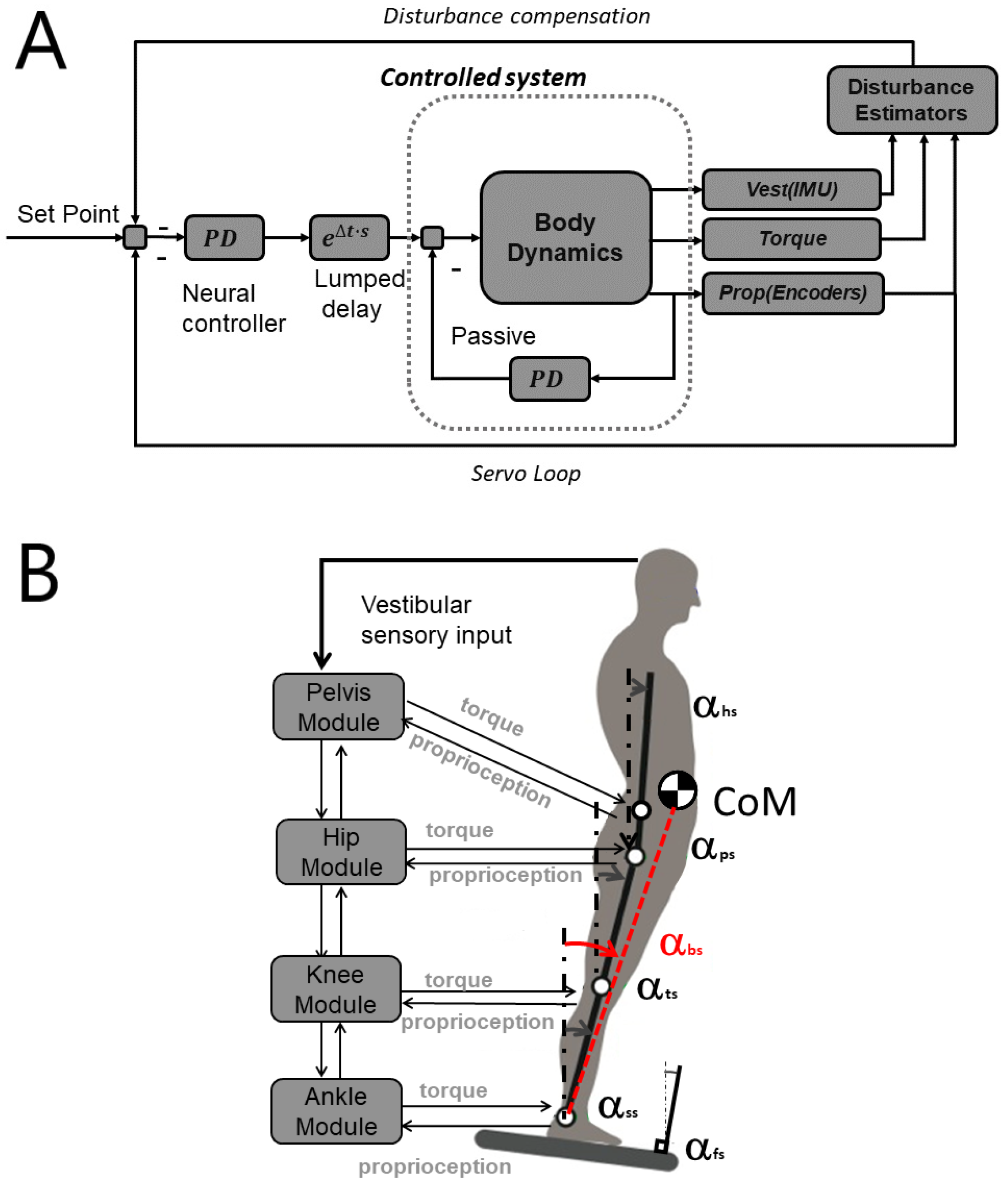
3.1. The Human-Derived Disturbance Estimation and Compensation (DEC) Control
- (a)
- Provides multisensory disturbances estimates of the four basic physical joint impacts: (i) rotation and (ii) translation of supporting links as well as (iii) contact forces and (iv) field forces affecting supported links;
- (b)
- Compensates the impacts using long-latency feedback (reflex) loops in a servo control, with
- (c)
- Low loop gain that tolerates biologic feedback time delays and makes the actuation compliant and the energy consumption low.
3.2. Human-Inspired Control System in Robotic Platform
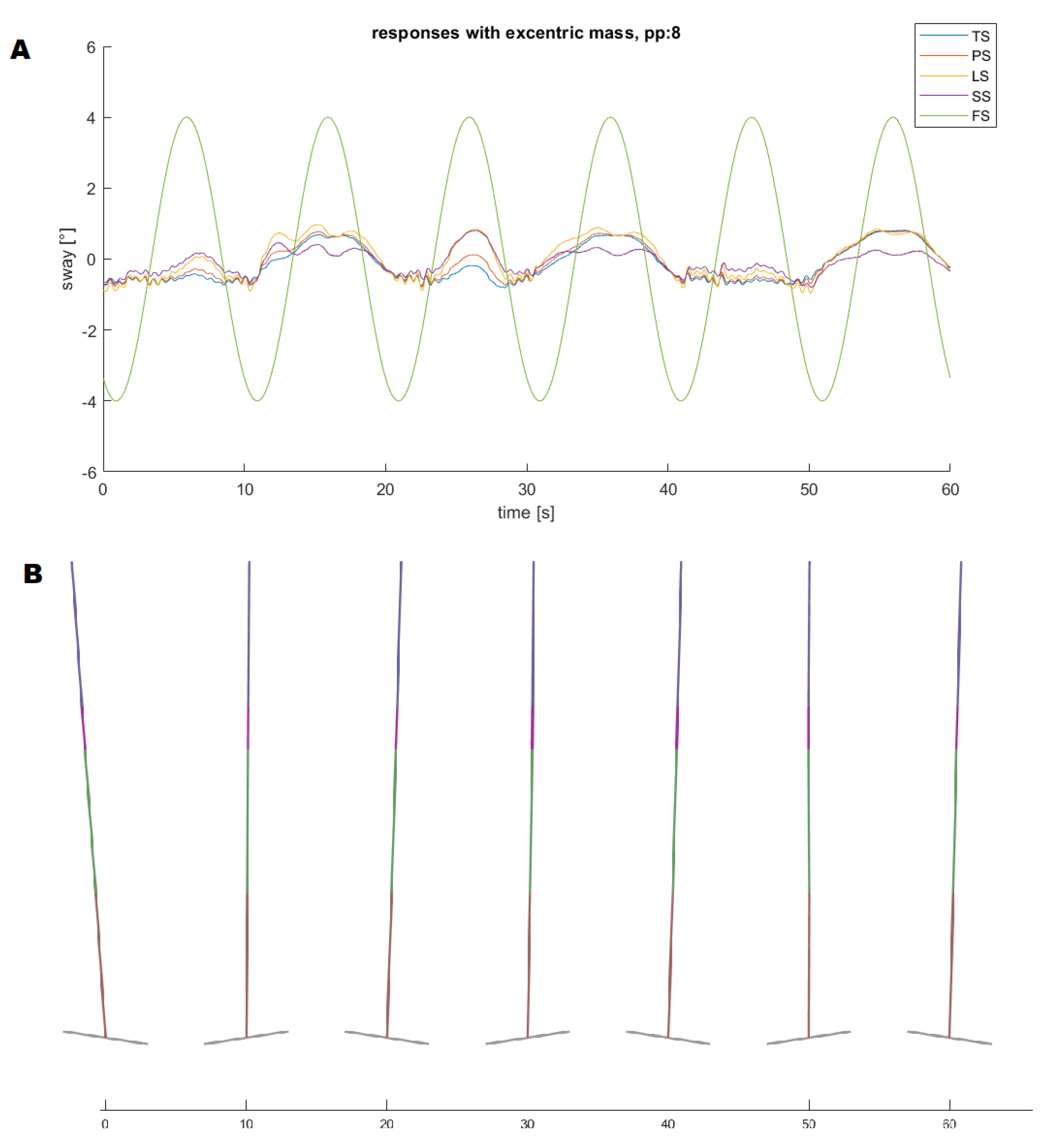
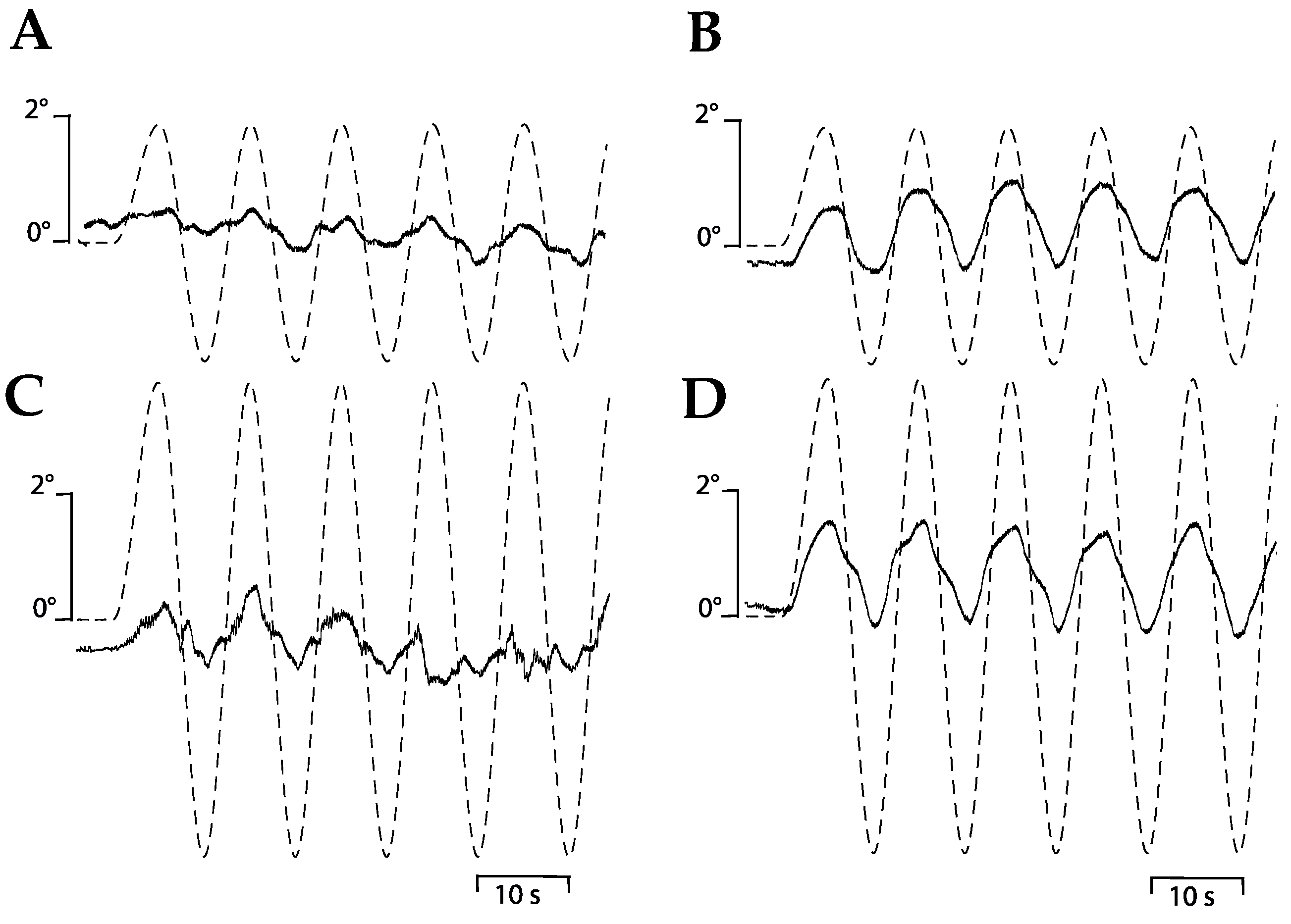
3.3. Balancing Experiment
4. Potential Extensions of the Balancing Tests
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Chang, S.-H.; Afzal, T.; Berliner, J.; Francisco, G.E.; Kern, M.; TIRR SCI Clinical Exoskeleton Group. Exoskeleton-assisted gait training to improve gait in individuals with spinal cord injury: a pilot randomized study. Pilot Feasibility Stud. 2018, 4, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, T.; Cempini, M.; Oddo, C.M.; Vitiello, N. Review of assistive strategies in powered lower-limb orthoses and exoskeletons. Robot. Auton. Syst. 2015, 64, 120–136. [Google Scholar] [CrossRef]
- Lajeunesse, V.; Vincent, C.; Routhier, F.; Careau, E.; Michaud, F. Exoskeletons’ design and usefulness evidence according to a systematic review of lower limb exoskeletons used for functional mobility by people with spinal cord injury. Disabil. Rehabilitation: Assist. Technol. 2015, 11, 535–547. [Google Scholar] [CrossRef] [PubMed]
- Lal, S. Premature degenerative shoulder changes in spinal cord injury patients. Spinal Cord 1998, 36, 186–189. [Google Scholar] [CrossRef] [Green Version]
- Louie, D.R.; Eng, J.J.; Lam, T. Spinal Cord Injury Research Evidence (SCIRE) Research Team Gait speed using powered robotic exoskeletons after spinal cord injury: a systematic review and correlational study. J. Neuroeng. Rehabilitation 2015, 12, 82. [Google Scholar] [CrossRef] [Green Version]
- Talaty, M.; Esquenazi, A.; Briceno, J.E. Differentiating ability in users of the ReWalkTM powered exoskeleton: An analysis of walking kinematics. In Proceedings of the 2013 IEEE International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 20–24 June 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Mergner, T. A neurological view on reactive human stance control. Annu. Rev. Control. 2010, 34, 177–198. [Google Scholar] [CrossRef]
- Rajasekaran, V.; Aranda, J.; Casals, A.; Pons, J.L.; Aranda-Lopez, J. An adaptive control strategy for postural stability using a wearable robot. Robot. Auton. Syst. 2015, 73, 16–23. [Google Scholar] [CrossRef] [Green Version]
- Emmens, A.R.; Van Asseldonk, E.H.F.; Van Der Kooij, H. Effects of a powered ankle-foot orthosis on perturbed standing balance. J. Neuroeng. Rehabilitation 2018, 15, 50. [Google Scholar] [CrossRef]
- Emmens, A.; Van Asseldonk, E.; Masciullo, M.; Aquila, M.; Pisotta, I.; Tagliamonte, N.L.; Tamburella, F.; Molinari, M.; Van Der Kooij, H. Improving the Standing Balance of Paraplegics through the Use of a Wearable Exoskeleton. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), Enschede, The Netherlands, 26–29 August 2018; pp. 707–712. [Google Scholar] [CrossRef]
- Khalili, M.; Machiel Van der Loos, H.; Borisoff, J. Studies on Practical Applications of Safe-Fall Control Strategies for Lower Limb Exoskeletons. In Proceedings of the 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), Toronto, ON, Canada, 24–28 June 2019; pp. 536–541. [Google Scholar] [CrossRef]
- Tokur, D.; Grimmer, M.; Seyfarth, A. Review of balance recovery in response to external perturbations during daily activities. Hum. Mov. Sci. 2019, 69, 102546. [Google Scholar] [CrossRef]
- Robotic Exoskeleton Exo-H3|Technaid—Leading Motion. Available online: https://www.technaid.com/products/robotic-exoskeleton-exo-exoesqueleto-h3/ (accessed on 6 July 2020).
- Hyon, S.; Morimoto, J.; Matsubara, T.; Noda, T.; Kawato, M. XoR: Hybrid drive exoskeleton robot that can balance. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; 2011; pp. 3975–3981. [Google Scholar]
- Chang, M.; Kim, Y.; Lee, Y.; Jeon, D. A research on the postural stability of a person wearing the lower limb exoskeletal robot by the HAT model. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017. [Google Scholar] [CrossRef]
- Khalili, M.; Borisoff, J.; Van der Loos, H. Developing safe fall strategies for lower limb exoskeletons. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 314–319. [Google Scholar] [CrossRef]
- Mergner, T.; Schweigart, G.; Fennell, L. Vestibular humanoid postural control. J. Physiol. 2009, 103, 178–194. [Google Scholar] [CrossRef]
- Mergner, T.; Glasauer, S. A simple model of vestibular canal-otolith signal fusion. Ann. N. Y. Acad. Sci. 1999, 871, 430–434. [Google Scholar] [CrossRef] [PubMed]
- Atkenson, C.; Stephens, B. Multiple balance strategies from one optimization criterion. In Proceedings of the 2007 7th IEEE-RAS International Conference on Humanoid Robots, Pittsburgh, PA, USA, 29 November–1 December 2007; pp. 57–64. [Google Scholar] [CrossRef]
- Padois, V.; Ivaldi, S.; Babič, J.; Mistry, M.; Peters, J.; Nori, F. Whole-body multi-contact motion in humans and humanoids: Advances of the CoDyCo European project. Robot. Auton. Syst. 2017, 90, 97–117. [Google Scholar] [CrossRef]
- Torricelli, D.; Gonzalez-Vargas, J.; Veneman, J.F.; Mombaur, K.; Tsagarakis, N.; Del-Ama, A.J.; Gil-Agudo, Á.; Moreno, J.C.; Pons, J.L. Benchmarking Bipedal Locomotion: A Unified Scheme for Humanoids, Wearable Robots, and Humans. IEEE Robot. Autom. Mag. 2015, 22, 103–115. [Google Scholar] [CrossRef] [Green Version]
- Mergner, T.; Lippi, V. Posture Control—Human-Inspired Approaches for Humanoid Robot Benchmarking: Conceptualizing Tests, Protocols and Analyses. Front. Neurorobotics 2018, 12, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schweigart, G.; Mergner, T. Human stance control beyond steady state response and inverted pendulum simplification. Exp. Brain Res. 2007, 185, 635–653. [Google Scholar] [CrossRef]
- Horak, F.B.; Nashner, L.M. Central programming of postural movements: adaptation to altered support-surface configurations. J. Neurophysiol. 1986, 55, 1369–1381. [Google Scholar] [CrossRef]
- Assländer, L.; Hettich, G.; Mergner, T. Visual contribution to human standing balance during support surface tilts. Hum. Mov. Sci. 2015, 41, 147–164. [Google Scholar] [CrossRef] [Green Version]
- Mergner, T.; Schweigart, G.; Fennell, L.; Maurer, C. Posture Control in Vestibular-Loss Patients. Ann. N. Y. Acad. Sci. 2009, 1164, 206–215. [Google Scholar] [CrossRef]
- Lippi, V. Prediction in the context of a human-inspired posture control model. Robot. Auton. Syst. 2018, 107, 63–70. [Google Scholar] [CrossRef]
- Hettich, G.; Assländer, L.; Gollhofer, A.; Mergner, T. Human hip–ankle coordination emerging from multisensory feedback control. Hum. Mov. Sci. 2014, 37, 123–146. [Google Scholar] [CrossRef] [Green Version]
- Mergner, T. The matryoshka dolls principle in human dynamic behavior in space: A theory of linked references for multisensory perception and control of action. Cah. Psychol. Cogn. 2002, 21, 129–212. [Google Scholar]
- Lippi, V.; Mergner, T.; Szumowski, M.; Zurawska, M.S.; Zielińska, T. Human-inspired humanoid balancing and posture control in frontal plane. Symposium on Robot Design, Dynamics and Control; Springer: Cham, Switzerland, 2016; pp. 285–292. [Google Scholar] [CrossRef]
- Lippi, V.; Mergner, T.; Hettich, G. A bio-inspired modular system for humanoid posture control. In Proceedings of IROS 2013 Workshop on Neuroscience and Robotics, Tokyo, Japan, 3 November 2013; Ugur, E., Oztop, E., Morimoto, J., Ishii, S., Eds.; Towards a Robot-Enabled, Neuroscience-Guided Healthy Society: Tokyo, Japan, 2013; pp. 16–21. [Google Scholar]
- Lippi, V.; Mergner, T. Human-Derived Disturbance Estimation and Compensation (DEC) Method Lends Itself to a Modular Sensorimotor Control in a Humanoid Robot. Front. Neurorobotics 2017, 11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lippi, V.; Molinari, F. Lyapunov Stability of a Nonlinear Bio-inspired System for the Control of Humanoid Balance. In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics, Online Streaming, 7–9 July 2020; Volume 1, pp. 726–733, ISBN 978-989-758-442-8. [Google Scholar] [CrossRef]
- Hettich, G.; Lippi, V.; Mergner, T. Human-like Sensor Fusion Mechanisms in a Postural Control Robot. In Proceedings of the NEUROTECHNIX, Vilamoura, Portugal, 18–20 September 2013; pp. 152–160. [Google Scholar] [CrossRef]
- Hettich, G.; Lippi, V.; Mergner, T. Human-like sensor fusion implemented in the posture control of a bipedal robot. Neurotechnology, Electronics, and Informatics; Springer: Cham, Switzerland, 2015; pp. 29–45. [Google Scholar] [CrossRef]
- Zielinska, T.; Gao, Z.; Zurawska, M.; Zheng, Q.; Mergner, T.; Lippi, V. Postural balance using a disturbance rejection method. In Proceedings of the 2017 11th International Workshop on Robot Motion and Control (RoMoCo), Wąsowo Palace, Poland, 3–5 July 2017; pp. 23–28. [Google Scholar] [CrossRef]
- Manuelli, L.; Tedrake, R. Localizing external contact using proprioceptive sensors: The Contact Particle Filter. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; Volume 47, pp. 5062–5069. [Google Scholar] [CrossRef] [Green Version]
- Veale, A.J.; Xie, S.Q. Towards compliant and wearable robotic orthoses: A review of current and emerging actuator technologies. Med Eng. Phys. 2016, 38, 317–325. [Google Scholar] [CrossRef]
- Kazerooni, H.; Racine, J.; Huang, L.; Stenger, R. On the control of the berkeley lower extremity exoskeleton (BLEEX). In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 4353–4360. [Google Scholar]
- Fleischer, C.; Hommel, G. A Human--Exoskeleton Interface Utilizing Electromyography. IEEE Trans. Robot. 2008, 24, 872–882. [Google Scholar] [CrossRef]
- Marcheschi, S.; Salsedo, F.; Fontana, M.; Bergamasco, M. Body extender: Whole body exoskeleton for human power augmentation. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 611–616. [Google Scholar] [CrossRef]
- Fritz, H.; Patzer, D.; Galen, S.S. Robotic exoskeletons for reengaging in everyday activities: promises, pitfalls, and opportunities. Disabil. Rehabil. 2017, 41, 560–563. [Google Scholar] [CrossRef]


| Body mass | 15.30 | kg |
| Upper body mass (including pelvis) | 9.50 | kg |
| Thighs mass | 2.80 | kg |
| Shanks mass | 3.00 | kg |
| Total height (from ankle joints) | 1.52 | m |
| Body COM height (from ankle joints) | 0.68 | m |
| Shank COM height | 0.32 | m |
| Thigh COM height | 0.31 | m |
| Symbol | Quantity | Value | |
|---|---|---|---|
| ANKLE | |||
| Kp | proportional gain | 119.57 | Nm/rad |
| Kd | derivative gain | 11.95 | Nms/rad |
| Gext | external torque gain | 0.5 | |
| ωext | External torque filter cutoff frequency | 5 | rad/s |
| KNEE | |||
| Kp | proportional gain | 55.72 | Nm/rad |
| Kd | derivative gain | 0.4458 | Nms/rad |
| Gext | external torque gain | 0.5 | |
| ωext | External torque filter cutoff frequency | 5 | rad/s |
| HIP | |||
| Kp | proportional gain | 22.71 | Nm/rad |
| Kd | derivative gain | 5.67 | Nms/rad |
| Gext | external torque gain | 0.5 | |
| ωext | External torque filter cutoff frequency | 5 | rad/s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lippi, V.; Mergner, T. A Challenge: Support of Standing Balance in Assistive Robotic Devices. Appl. Sci. 2020, 10, 5240. https://doi.org/10.3390/app10155240
Lippi V, Mergner T. A Challenge: Support of Standing Balance in Assistive Robotic Devices. Applied Sciences. 2020; 10(15):5240. https://doi.org/10.3390/app10155240
Chicago/Turabian StyleLippi, Vittorio, and Thomas Mergner. 2020. "A Challenge: Support of Standing Balance in Assistive Robotic Devices" Applied Sciences 10, no. 15: 5240. https://doi.org/10.3390/app10155240




