Contribution to the Physical Modelling of Single Charged Defects Causing the Random Telegraph Noise in Junctionless FinFET
Abstract
:1. Introduction
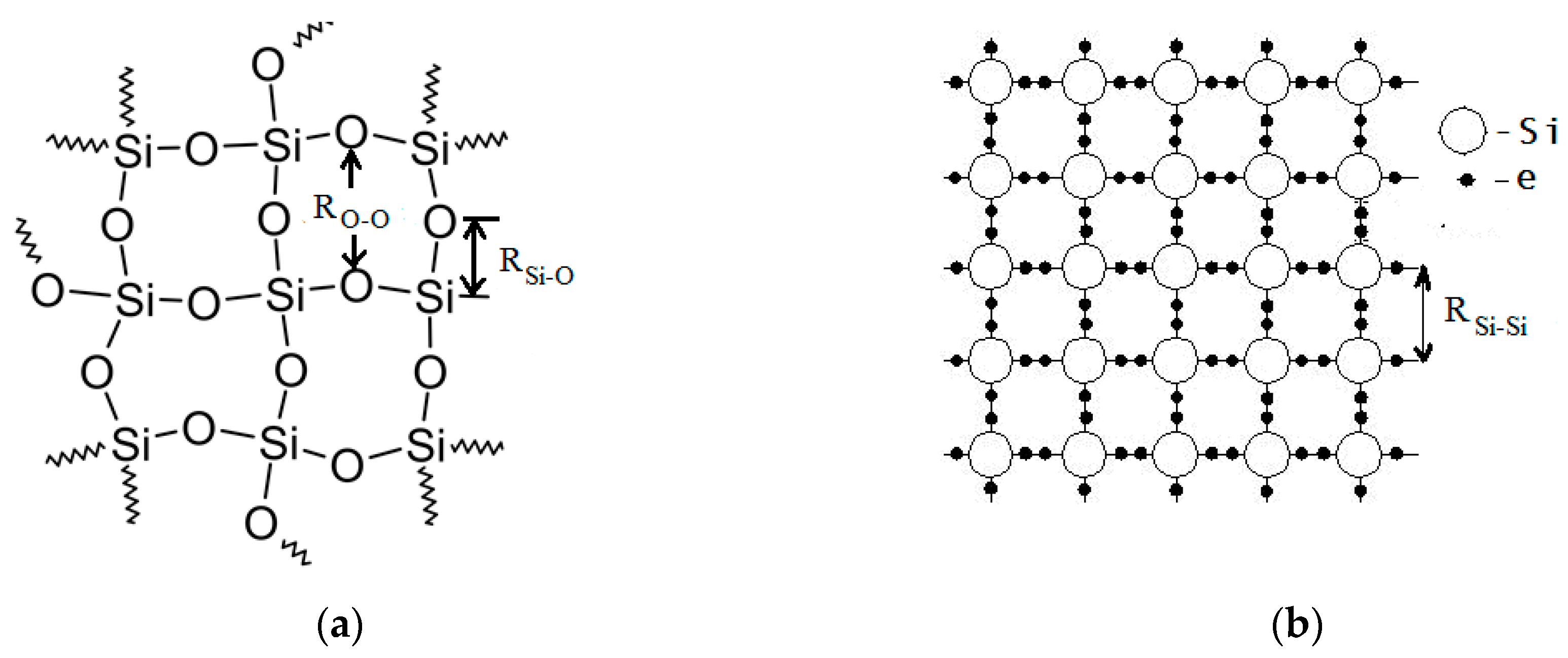
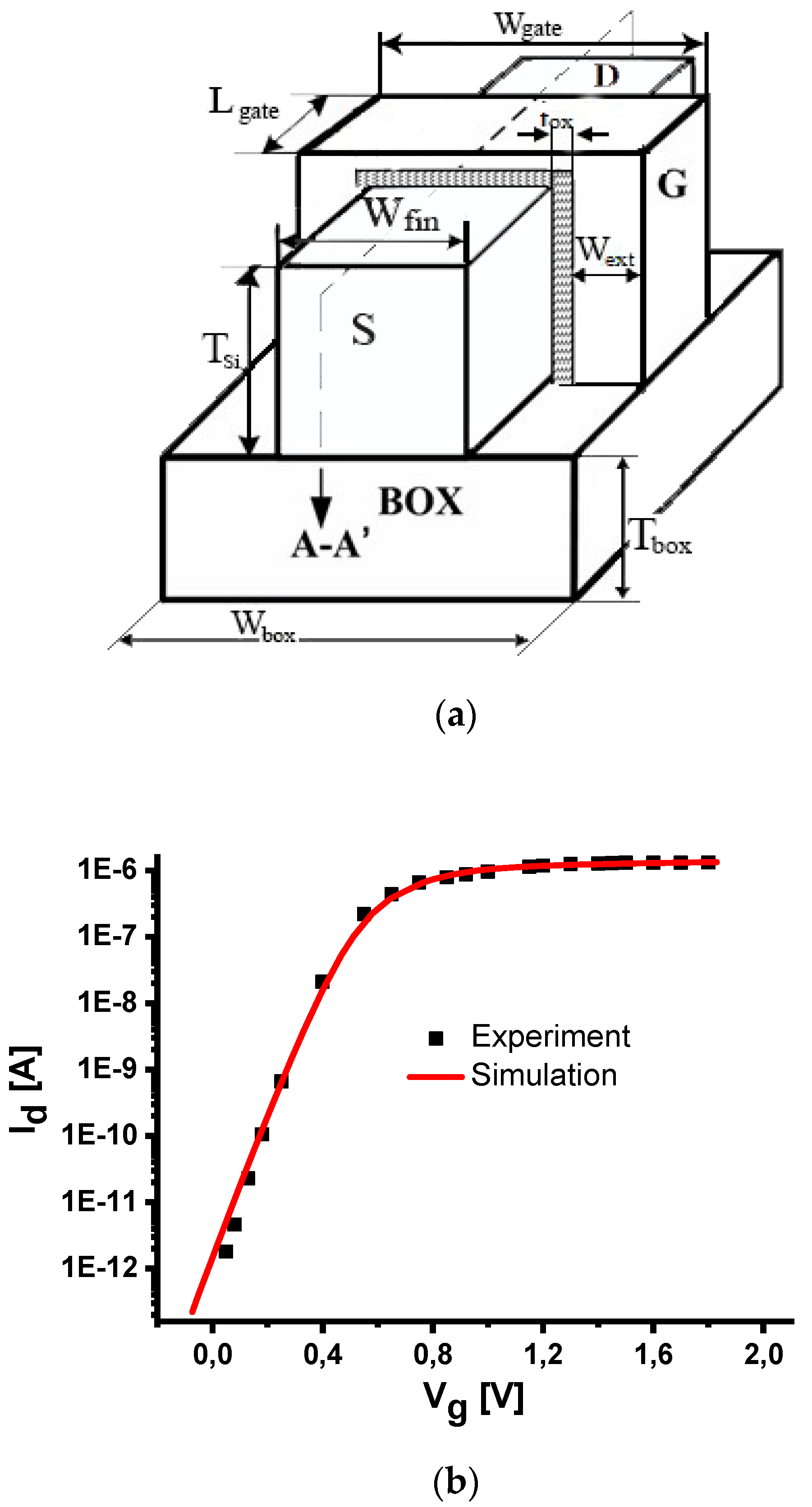
2. Modeling and Simulation Procedure
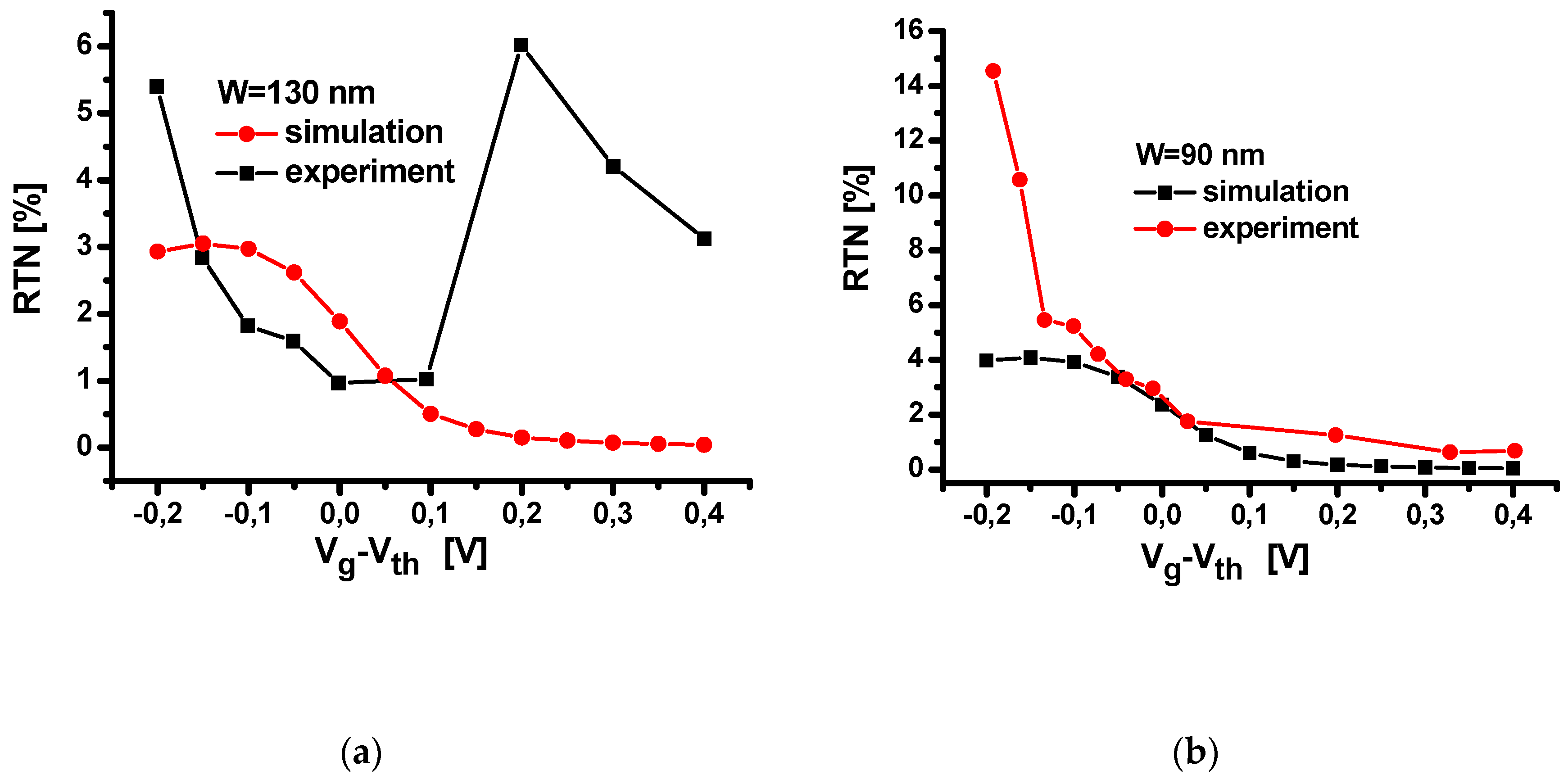
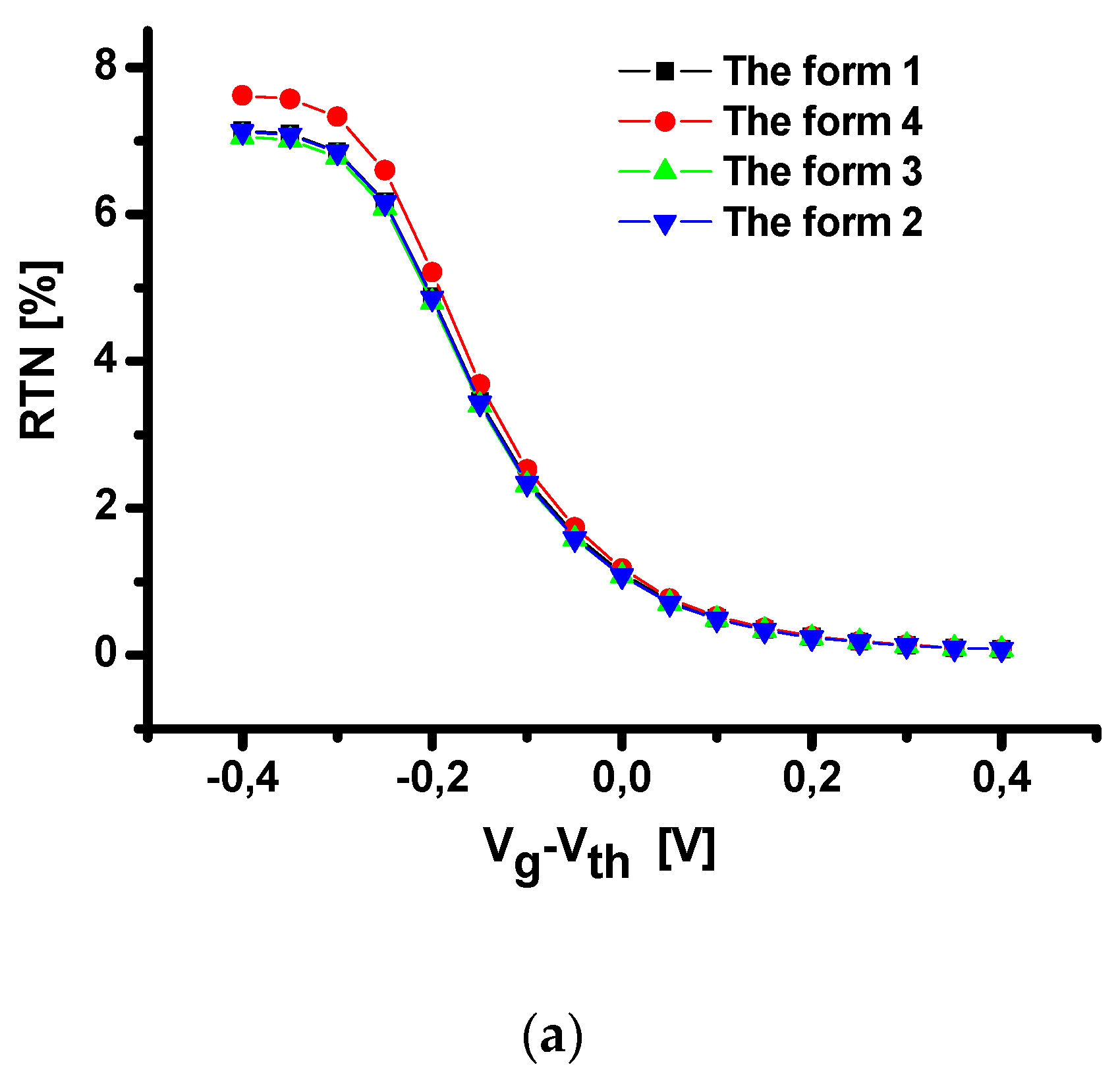
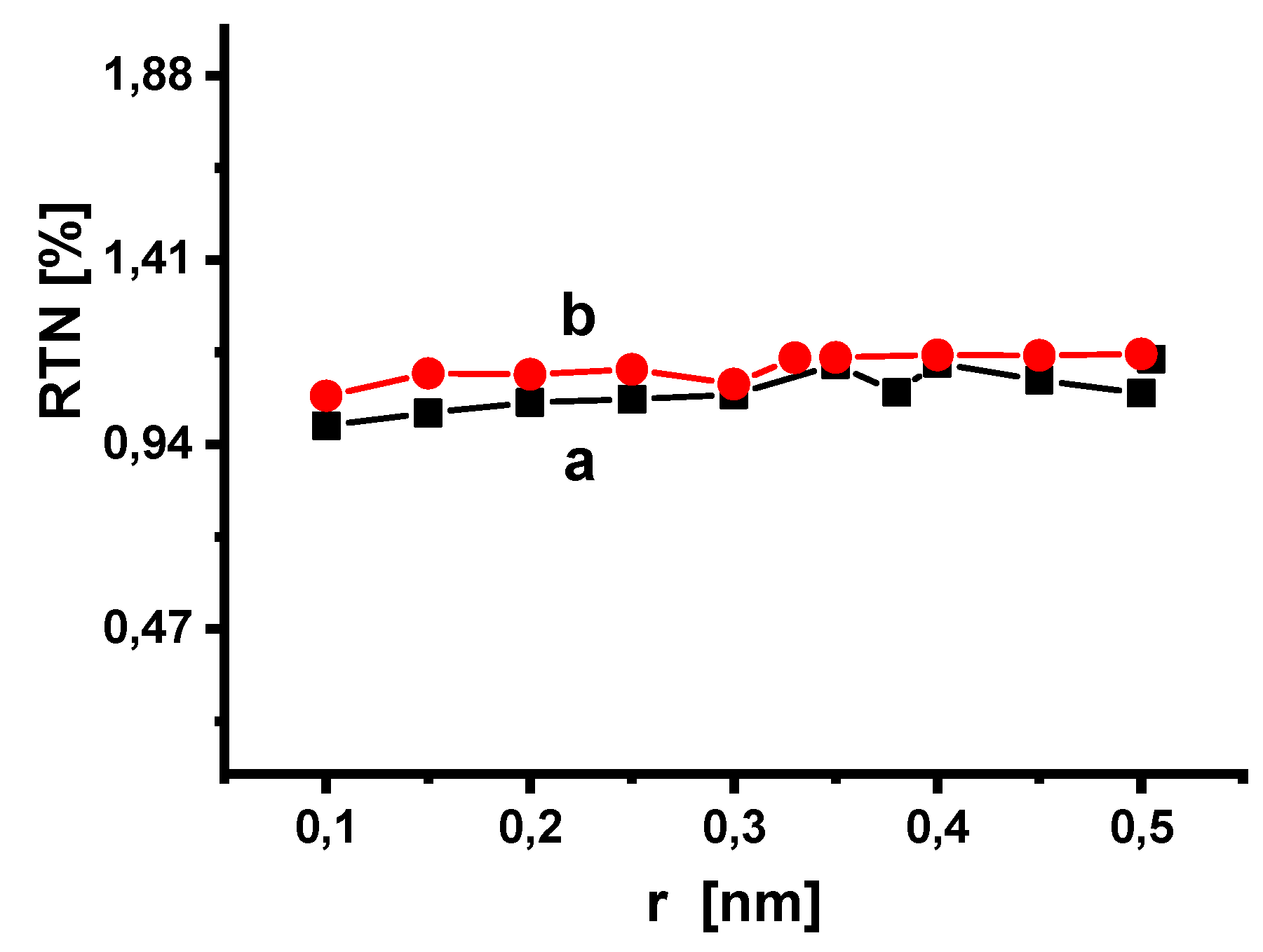
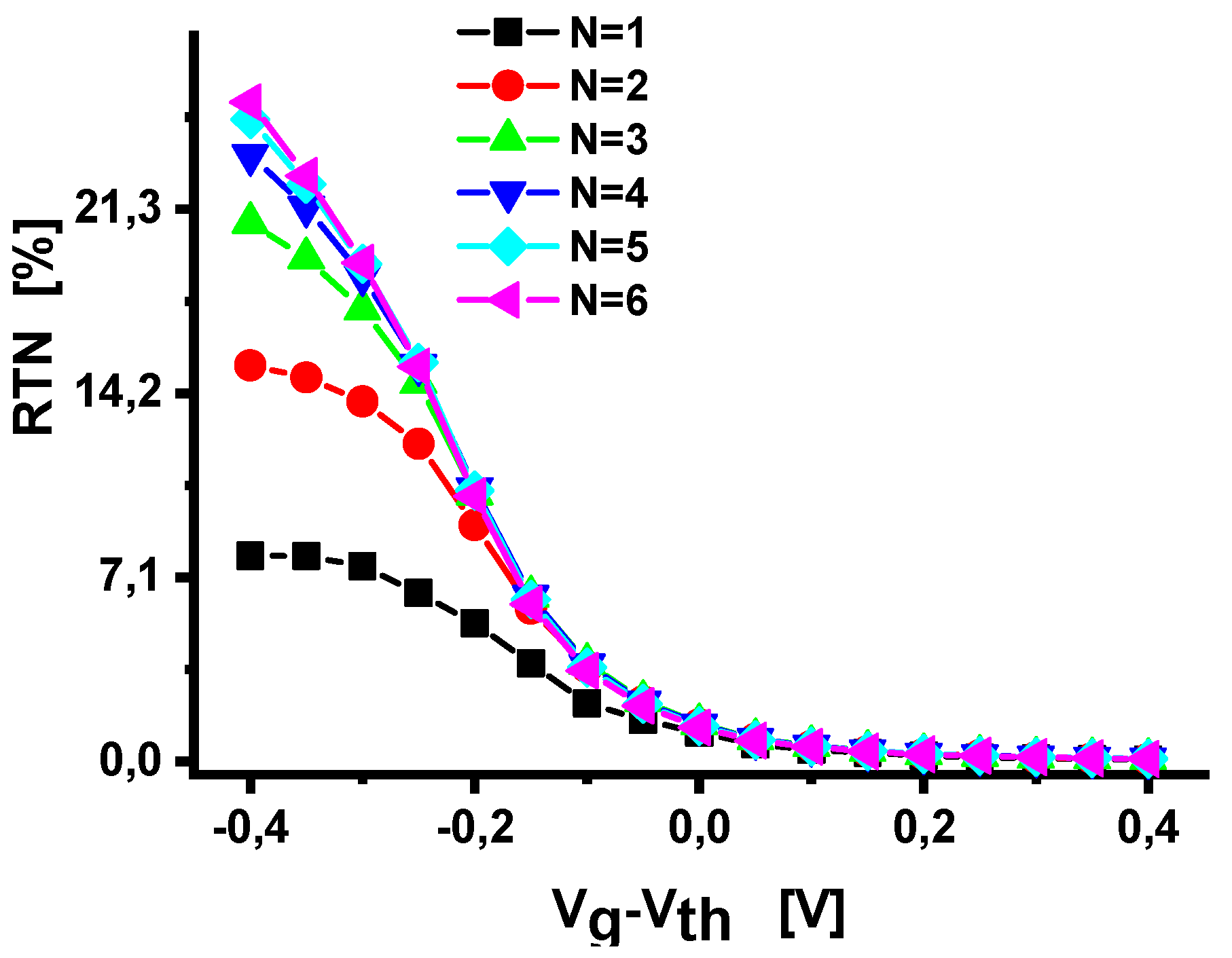
3. Simulation Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kaczer, B.; Franco, J.; Weckx, P.; Roussel, P.J.; Putcha, V.; Bury, E.; Simicic, M.; Chasin, A.; Linten, D.; Parvais, B.; et al. A brief overview of gate oxide defect properties and their relation to MOSFET instabilities and device and circuit time-dependent variability. Microelectron. Reliab. 2018, 81, 186–194. [Google Scholar] [CrossRef]
- Kang, C.J.; Buh, G.H.; Lee, S.; Kim, C.K.; Mang, K.M.; Im, C.; Kuka, Y. Charge trap dynamics in a SiO2 layer on Si by scanning capacitance Microscopy. Appl. Phys. Lett. 1999, 74, 1815–1817. [Google Scholar] [CrossRef]
- Sriram, S.R.; Bindu, B. Analytical modeling of random discrete traps induced threshold voltage fluctuations in double-gate MOSFET with HfO2/SiO2 gate dielectric stack. Microelectron. Reliab. 2019, 99, 87–95. [Google Scholar]
- Toh, S.O.; Liu, T.J.K.; Nikolic, B. Impact of Random Telegraph Signaling Noise on SRAM Stability. In Proceedings of the 2011 Symposium on VLSI Technology—Digest of Technical Papers, Honolulu, HI, USA, 14–16 June 2011; pp. 204–205. [Google Scholar]
- Kao, T.H.; Chang, S.J.; Fang, Y.K.; Huang, P.C.; Wang, B.C.; Wu, C.Y.; Wu, S.L. Investigation of low-frequency noise of 28-nm technology process, of high-k/metal gate p-MOSFETs with fluorine incorporation. Solid-State Electron. 2016, 115, 7–11. [Google Scholar] [CrossRef]
- Javier, D.; Javier, M.; Rosana, R.; Rafael, C.; Elisenda, R.; Francisco, V.; Fernandez, M.N. A smart noise- and RTN-removal method for parameter extraction of CMOS aging compact models. Solid-State Electron. 2019, 159, 99–105. [Google Scholar]
- Asenov, A.; Balasubramaniam, R.; Brown, A.R.; Davies, J.H.; Saini, S. Random Telegraph Signal Amplitudes in Sub-100 nm (Decanano) MOSFETs: A 3D “Atomistic” Simulation Study. In Proceedings of the International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2000; pp. 279–282. [Google Scholar]
- Velayudhan, V.; Gamiz, F.; Martin-Martinez, J.; Rodriguez, R.; Nafria, M.; Aymerich, X. Influence of the interface trap location on the performance and variability of ultra-scaled MOSFETs. Microelectron. Reliab. 2013, 53, 1243–1246. [Google Scholar] [CrossRef]
- Contoyiannis, Y.; Potirakis, S.M.; Stavrinides, S.G.; Hanias, M.P.; Tassis, D.; Theodorou, C.G. Intermittency-induced criticality in the random telegraph noise of nanoscale UTBB FD-SOI MOSFETs. Microelectron. Eng. 2019, 216, 111027. [Google Scholar] [CrossRef]
- Shamsur, A.S.M.; Rouf, Z.Ç. Channel hot carrier induced volatile oxide traps responsible for random telegraph signals in submicron pMOSFETs. Solid-State Electron. 2020, 164, 107745. [Google Scholar] [CrossRef]
- Carlos, M.; Noel, R.; Francisco, G.; Akiko, O. Systematic method for electrical characterization of random telegraph noise in MOSFETs. Solid-State Electron. 2017, 128, 115–120. [Google Scholar]
- Angelica, L.; Andrew, R.; Brown, A.A.; Scott, R. Random telegraph signal noise simulation of decanano MOSFETs subject to atomic scale structure variation. Superlattices Microstruct. 2003, 34, 293–300. [Google Scholar]
- Gerrer, L.; Amoroso, S.M.; Hussin, R.; Asenov, A. RTN distribution comparison for bulk, FDSOI and FinFETs devices. Microelectron. Reliab. 2014, 54, 1749–1752. [Google Scholar] [CrossRef]
- Fan, M.L.; Yang, S.Y.; Hu, V.P.H.; Chen, Y.N.; Su, P.; Chuang, C.T. Single-trap-induced random telegraph noise for FinFET, Si/Ge Nanowire FET, Tunnel FET, SRAM and logic circuits. Microelectron. Reliab. 2014, 54, 698–711. [Google Scholar] [CrossRef]
- Rudenko, T.; Nazarov, A.; Barraud, S.; Kilchytska, V.; Flandre, D. A method for threshold voltage extraction in junctionless MOSFETs using the derivative of transconductance-to-current ratio. Solid-State Electron. 2019, 161, 107723. [Google Scholar] [CrossRef]
- Lee, C.W.; Ferain, I.; Afzalian, A.; Yan, R.; Akhavan, N.D.; Razavi, P.; Colinge, J.P. Performance estimation of junctionless multigate transistors. Solid-State Electron. 2010, 54, 97–103. [Google Scholar] [CrossRef]
- Miura, K.; Ino, T.; Tada, M.; Ohsaki, H. Shrinkage of atomic distances in ultrathin a-SiO2 film. Philos. Mag. 1992, 66, 25–36. [Google Scholar] [CrossRef]
- Hössinger, A. Simulation of Ion Implantation for ULSI Technology. Ph.D. Thesis, Technische Universität Wien, Wien, Austria, July 2000. [Google Scholar]
- Beltrán, J.I.; Muñoz, M.C.; Hafner, J. Structural, electronic and magnetic properties of the surfaces of tetragonal and cubic HfO2. New J. Phys. 2008, 10, 063031. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.; Ramprasad, R. Oxygen defect accumulation at Si:HfO2 interfaces. Appl. Phys. Lett. 2008, 92, 182908. [Google Scholar] [CrossRef] [Green Version]
- Benthem, K.V.; Rashkeev, S.N.; Pennycook, S.J. Atomic and Electronic Structure Investigations of HfO2/SiO2/Si Gate Stacks Using Aberration-Corrected STEM. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2005; Volume 788, pp. 79–84. [Google Scholar] [CrossRef]
- DiMaria, D.J. The Physics of SiO2 and its Interfaces; Pantelides, S.T., Ed.; Pergamon: New York, NY, USA, 1978; pp. 160–178. [Google Scholar]
- Lax, M. Cascade capture of electrons in solids. Phys. Rev. 1960, 119, 1502. [Google Scholar] [CrossRef]
- Tzou, J.J.; Sun, J.Y.; Sah, C.T. Field dependence of two large hole capture cross sections in thermal oxide on silicon. Appl. Phys. Lett. 1983, 43, 861. [Google Scholar] [CrossRef]
- McWhorter, A.L. 1/f Noise and Germanium Surface Properties. In Semiconductor Surface Physics; Kingston, R.H., Ed.; University of Pennsylvania Press: Philadelphia, PA, USA, 1957; pp. 207–228. [Google Scholar]
- Goes, W.; Schanovsky, F.; Grasser, T.; Reisinger, H.; Kaczer, B. Advanced Modeling of Oxide Defects for Random Telegraph Noise. In Proceedings of the 21st International Conference on Noise and Fluctuations, Toronto, ON, Canada, 12–16 June 2011; pp. 204–207. [Google Scholar]
- Campbell, J.P.; Yu, L.C.; Cheung, K.P.; Qin, J.; Suehle, J.S.; Oates, A.; Sheng, K. Large Random Telegraph Noise in Sub-Threshold Operation of Nano-Scale nMOSFETs. In Proceedings of the 2009 IEEE International Conference on IC Design and Technology, Austin, TX, USA, 18–20 May 2009; pp. 17–20. [Google Scholar]
- Sentaurus™ Device User Guide; Version 2018; Synopsys: Mountain View, CA, USA, 2018.
- García-Loureiro, A.J.; Seoane, N.; Aldegunde, M.; Valín, R.; Asenov, A.; Martinez, A.; Kalna, K. Implementation of the density gradient quantum corrections for 3-D simulations of multigate nanoscaled transistors. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2011, 30, 841. [Google Scholar]
- Asenov, A.; Brown, A.; Watling, J. Quantum Corrections in the Simulation of Decanano MOSFETs. Solid-State Electron. 2003, 47, 1141. [Google Scholar] [CrossRef] [Green Version]
- Barraud, S.; Berthomé, M.; Coquand, R.; Cassé, M.; Ernst, T.; Samson, M.P.; Perreau, P.; Bourdelle, K.K.; Faynot, O.; Poiroux, T. Scaling of Trigate Junctionless Nanowire MOSFET with Gate Length Down to 13 nm. Electron. Device Lett. 2012, 33, 9. [Google Scholar] [CrossRef]


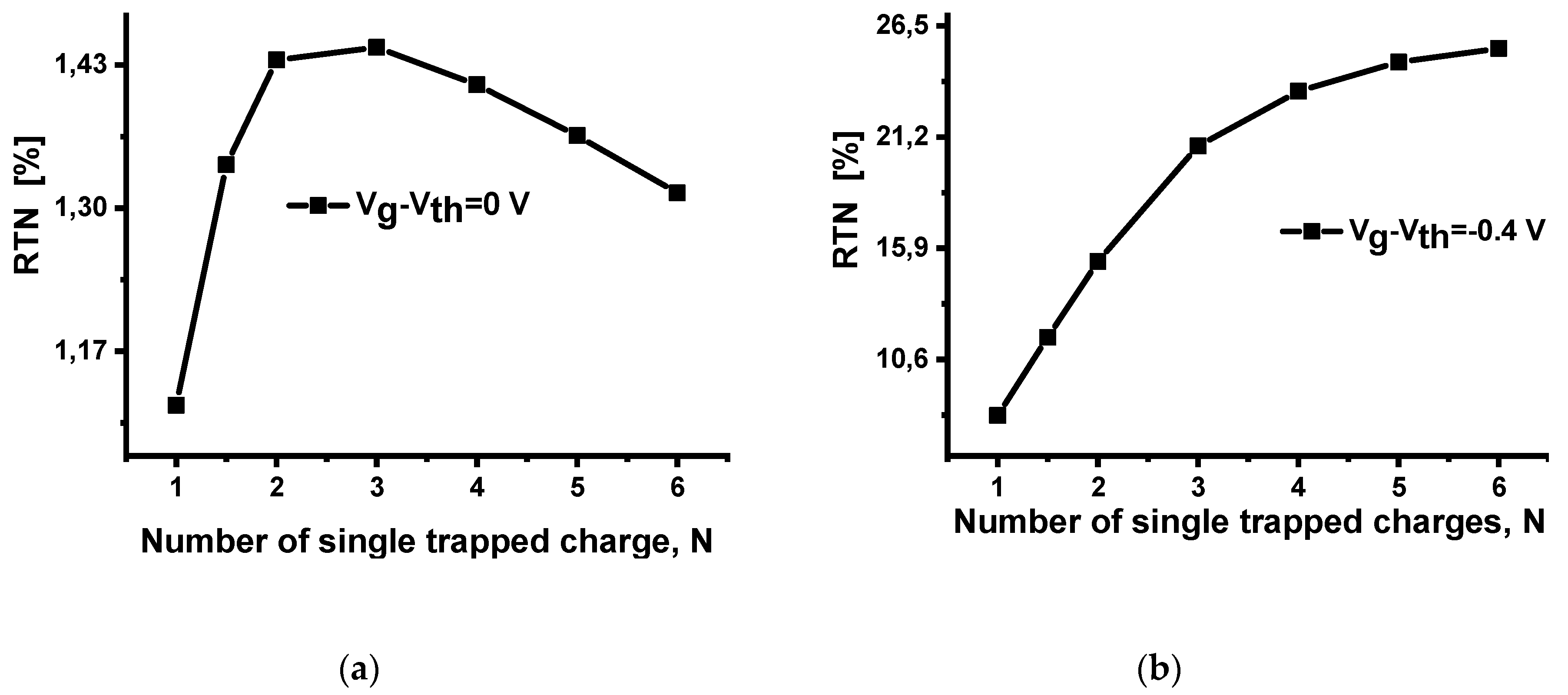
| Parameters | Designation | Value of the Parameters |
|---|---|---|
| The channel doping concentration | Nch | 2 × 1016 cm−3 |
| Gate oxide thickness | tox | 1.4 nm |
| Gate width | Wgate | 90, 130 nm |
| Gate length | Lgate | 55 nm |
| Parameters | Designation | Value of the Parameters |
|---|---|---|
| The channel doping concentration | Nch | 5 × 1018 cm−3 |
| Equivalent gate oxide thickness (HfO2) | teff | 1.2 nm |
| Channel thickness | Tsi | 9 nm |
| Channel width | Wfin | 22 nm |
| Gate width | Wgate | 55 nm |
| Gate length | Lgate | 13 nm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atamuratov, A.E.; Khalilloev, M.M.; Yusupov, A.; García-Loureiro, A.J.; Chedjou, J.C.; Kyandoghere, K. Contribution to the Physical Modelling of Single Charged Defects Causing the Random Telegraph Noise in Junctionless FinFET. Appl. Sci. 2020, 10, 5327. https://doi.org/10.3390/app10155327
Atamuratov AE, Khalilloev MM, Yusupov A, García-Loureiro AJ, Chedjou JC, Kyandoghere K. Contribution to the Physical Modelling of Single Charged Defects Causing the Random Telegraph Noise in Junctionless FinFET. Applied Sciences. 2020; 10(15):5327. https://doi.org/10.3390/app10155327
Chicago/Turabian StyleAtamuratov, Atabek E., Mahkam M. Khalilloev, Ahmed Yusupov, A. J. García-Loureiro, Jean Chamberlain Chedjou, and Kyamakya Kyandoghere. 2020. "Contribution to the Physical Modelling of Single Charged Defects Causing the Random Telegraph Noise in Junctionless FinFET" Applied Sciences 10, no. 15: 5327. https://doi.org/10.3390/app10155327
APA StyleAtamuratov, A. E., Khalilloev, M. M., Yusupov, A., García-Loureiro, A. J., Chedjou, J. C., & Kyandoghere, K. (2020). Contribution to the Physical Modelling of Single Charged Defects Causing the Random Telegraph Noise in Junctionless FinFET. Applied Sciences, 10(15), 5327. https://doi.org/10.3390/app10155327







