Assessment of Pohang Earthquake-Induced Liquefaction at Youngil-Man Port Using the UBCSAND2 Model
Abstract
:1. Introduction
2. Methodology
2.1. UBCSAND2 Constitutive Model
2.1.1. Elastic Response
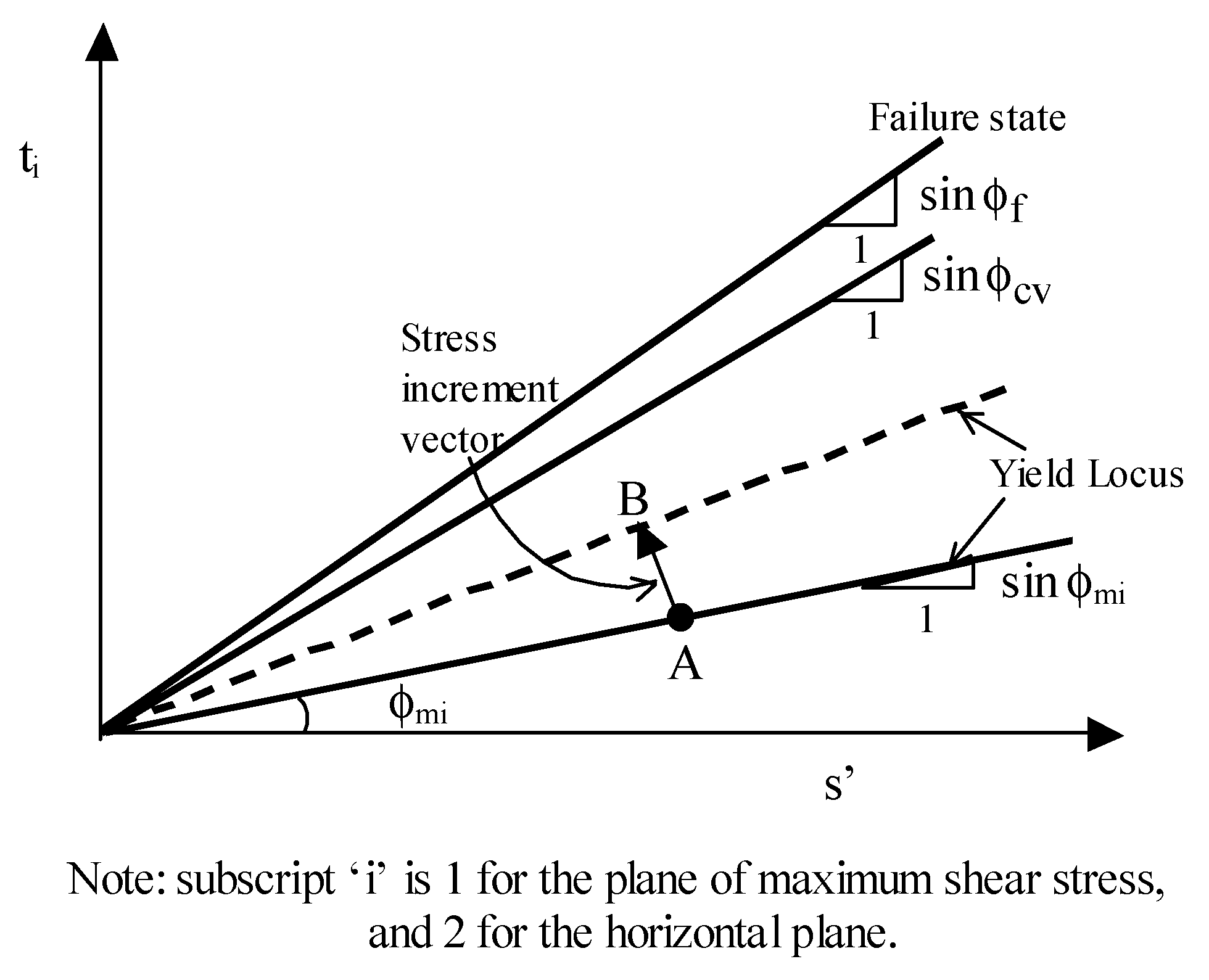
2.1.2. Yield Surface
2.1.3. Hardening and Flow Rule on Maximum Shear Stress Plane
2.1.4. Hardening Rule and Flow Rule on the Horizontal Plane
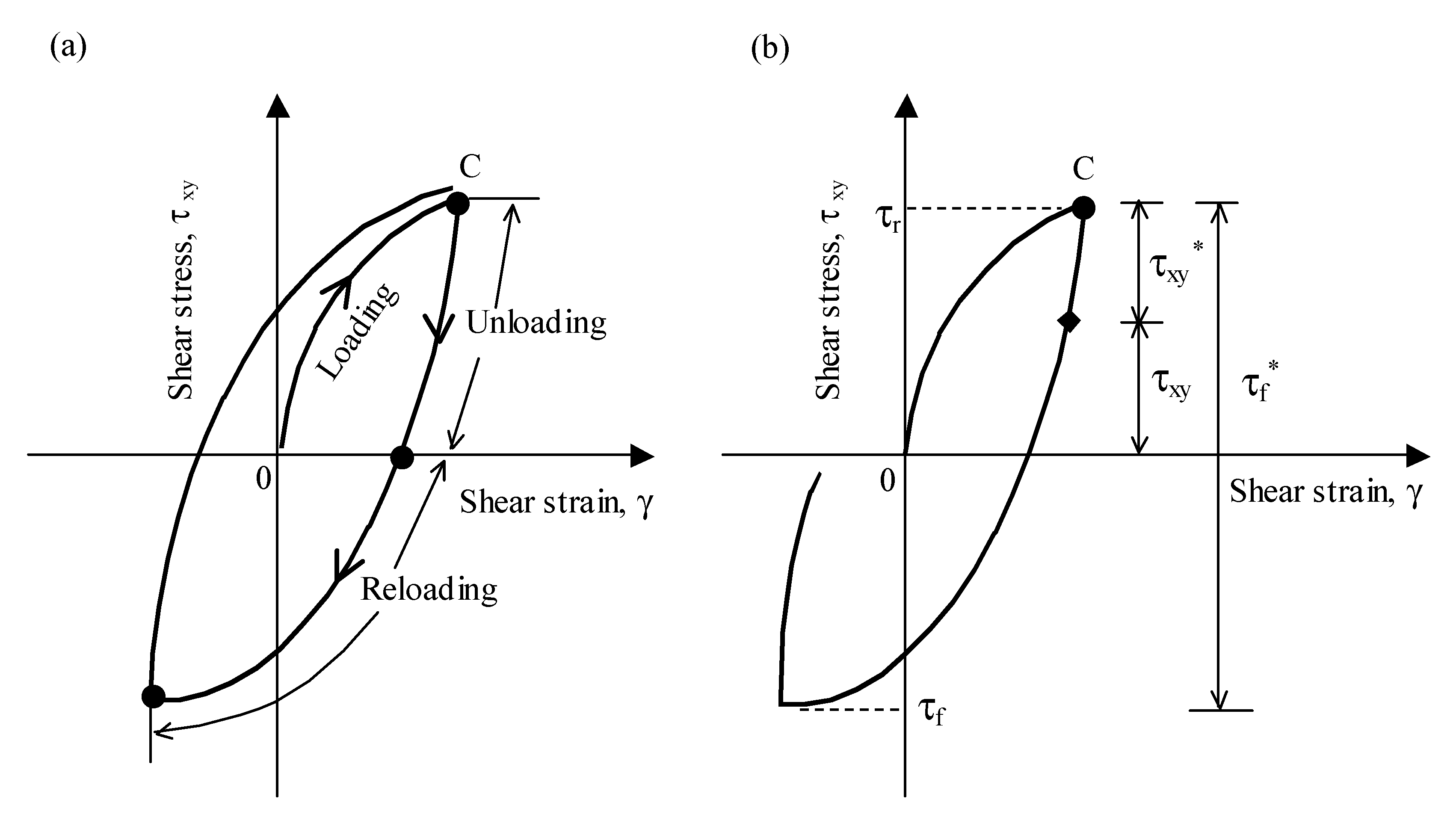
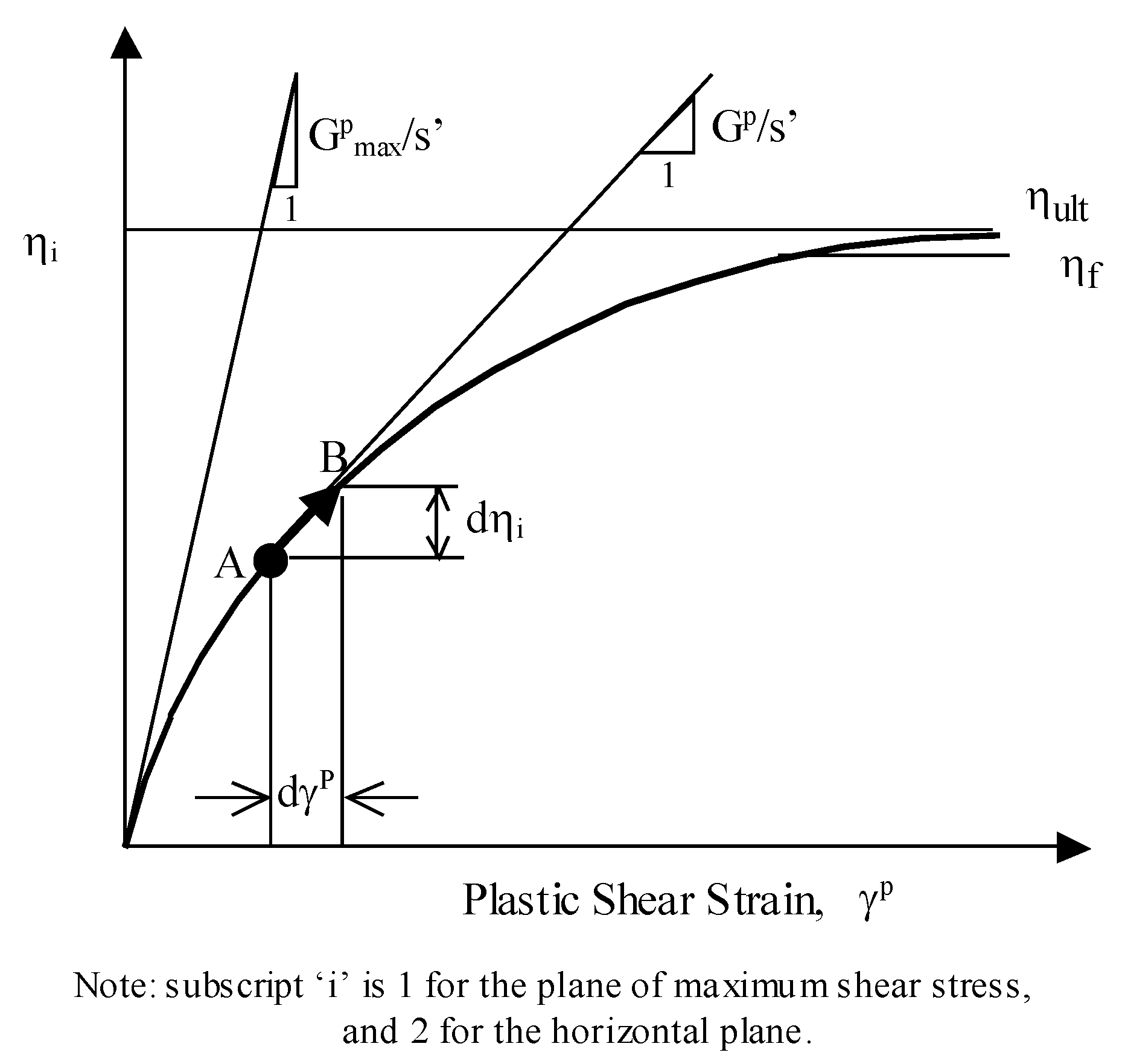
2.1.5. Hardening of Stress-Dilatancy
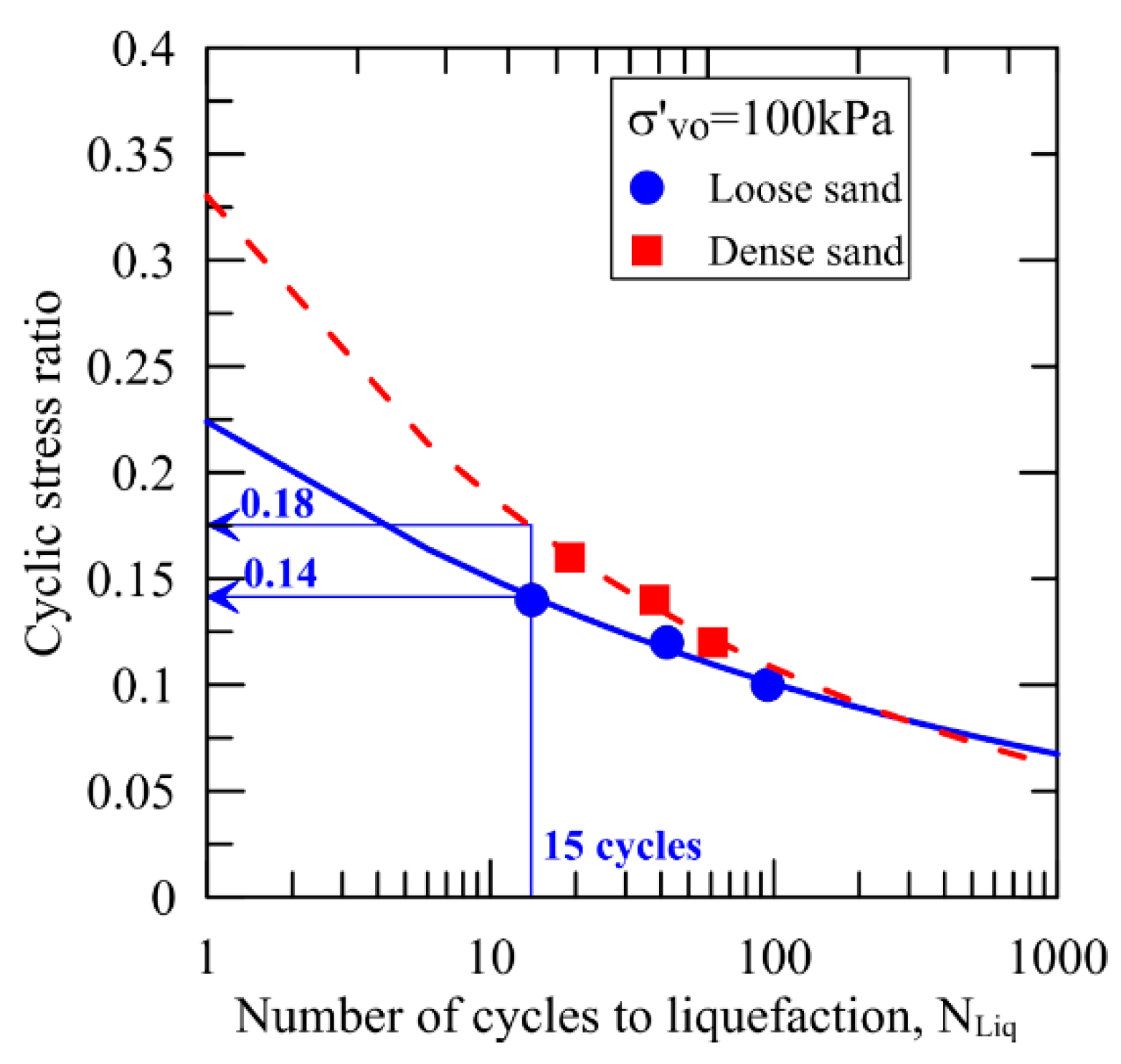
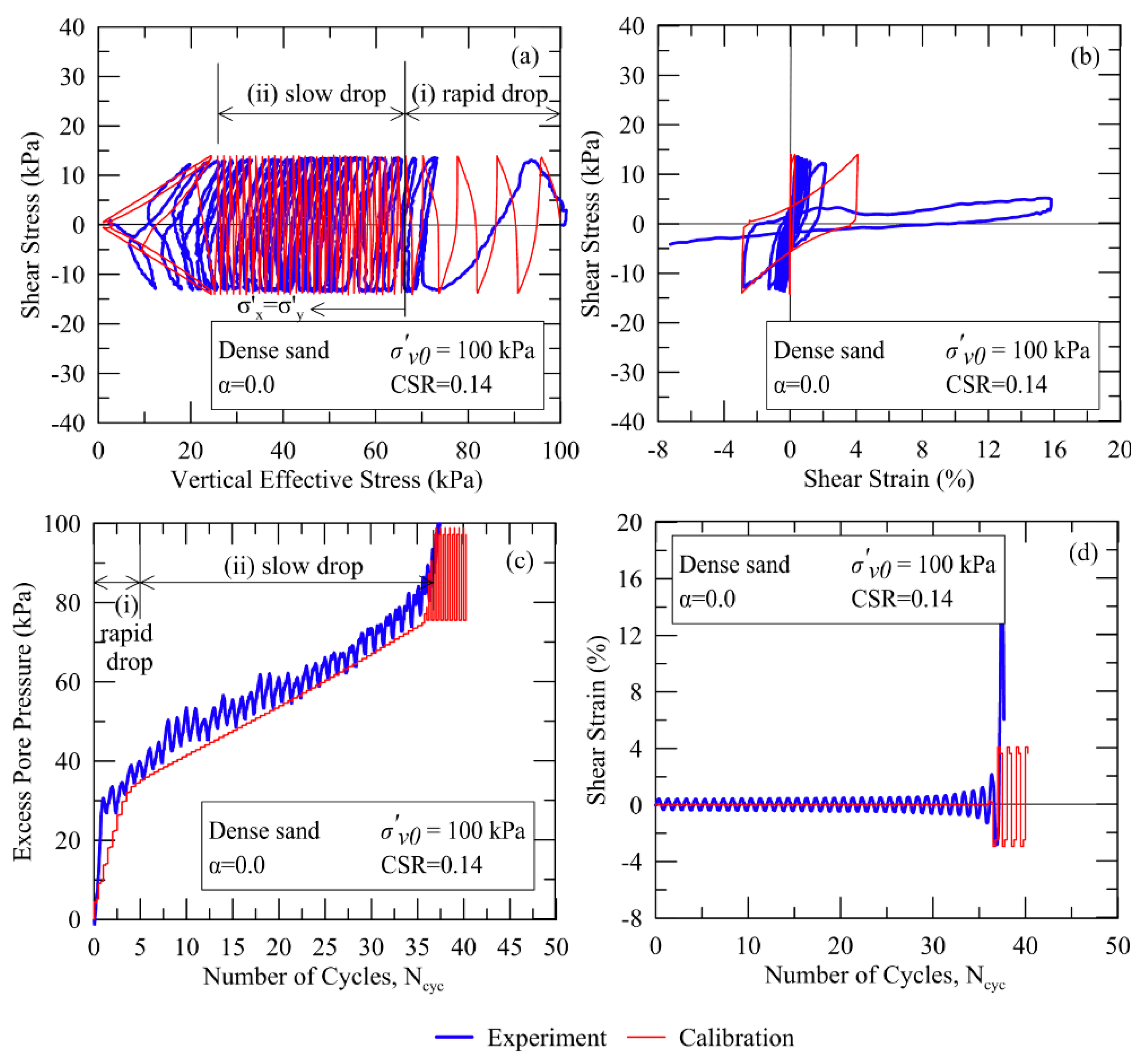
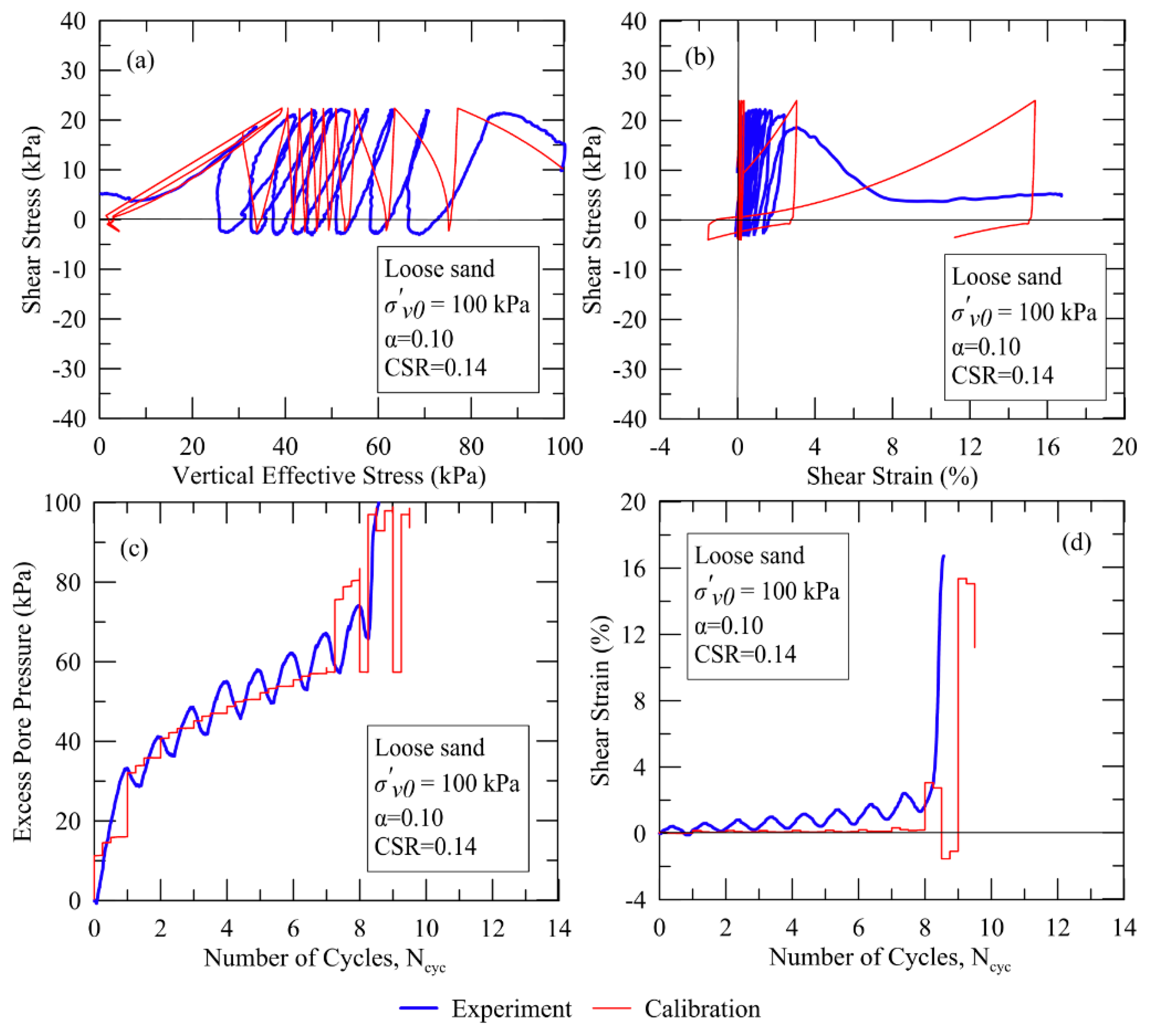
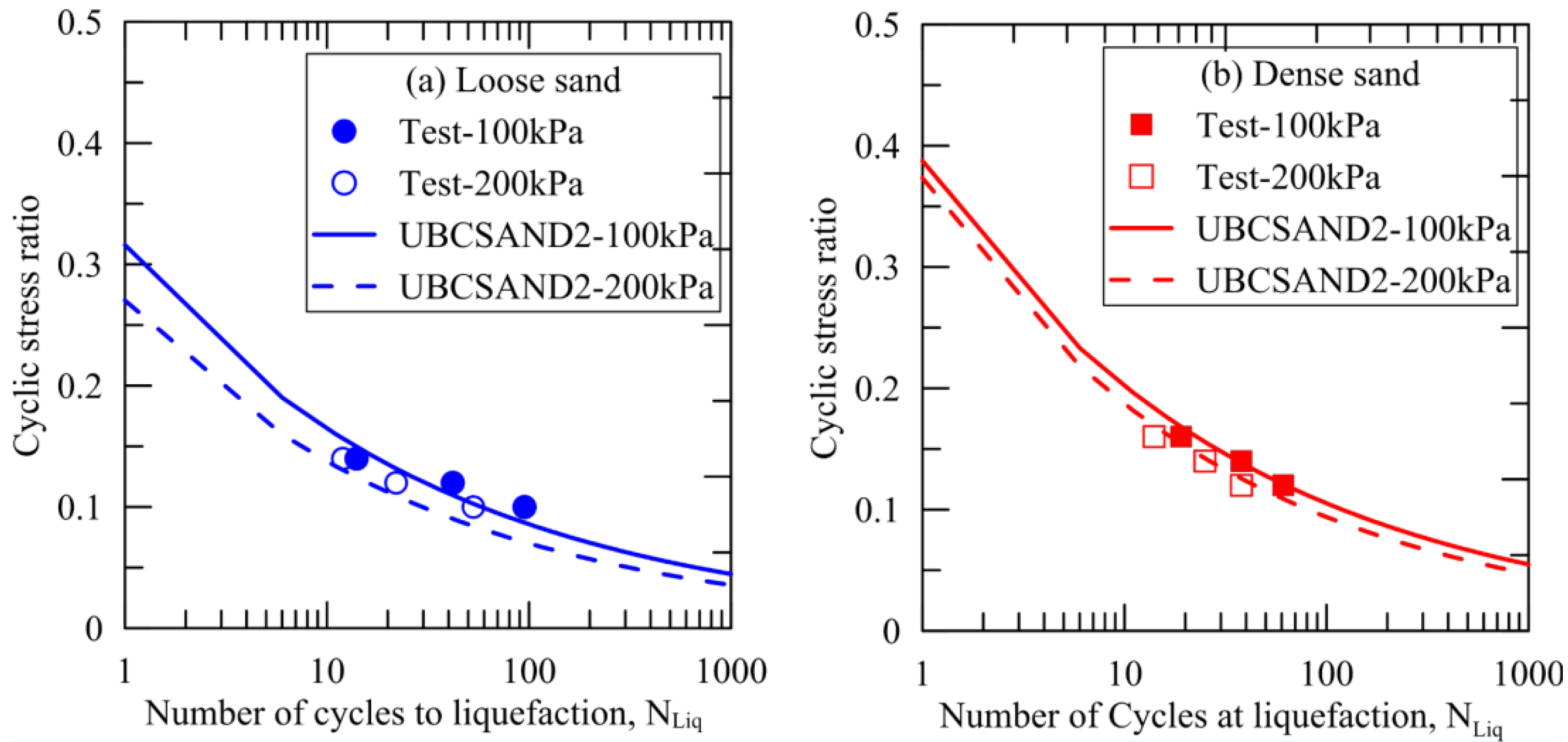
2.2. UBCSAND2 Calibration for Undrained CDSS Tests on Pohang Sand
2.3. Assessment of Pohang Earthquake-Induced Liquefaction at Youngil-Man Port Using the UBCSAND2 Model
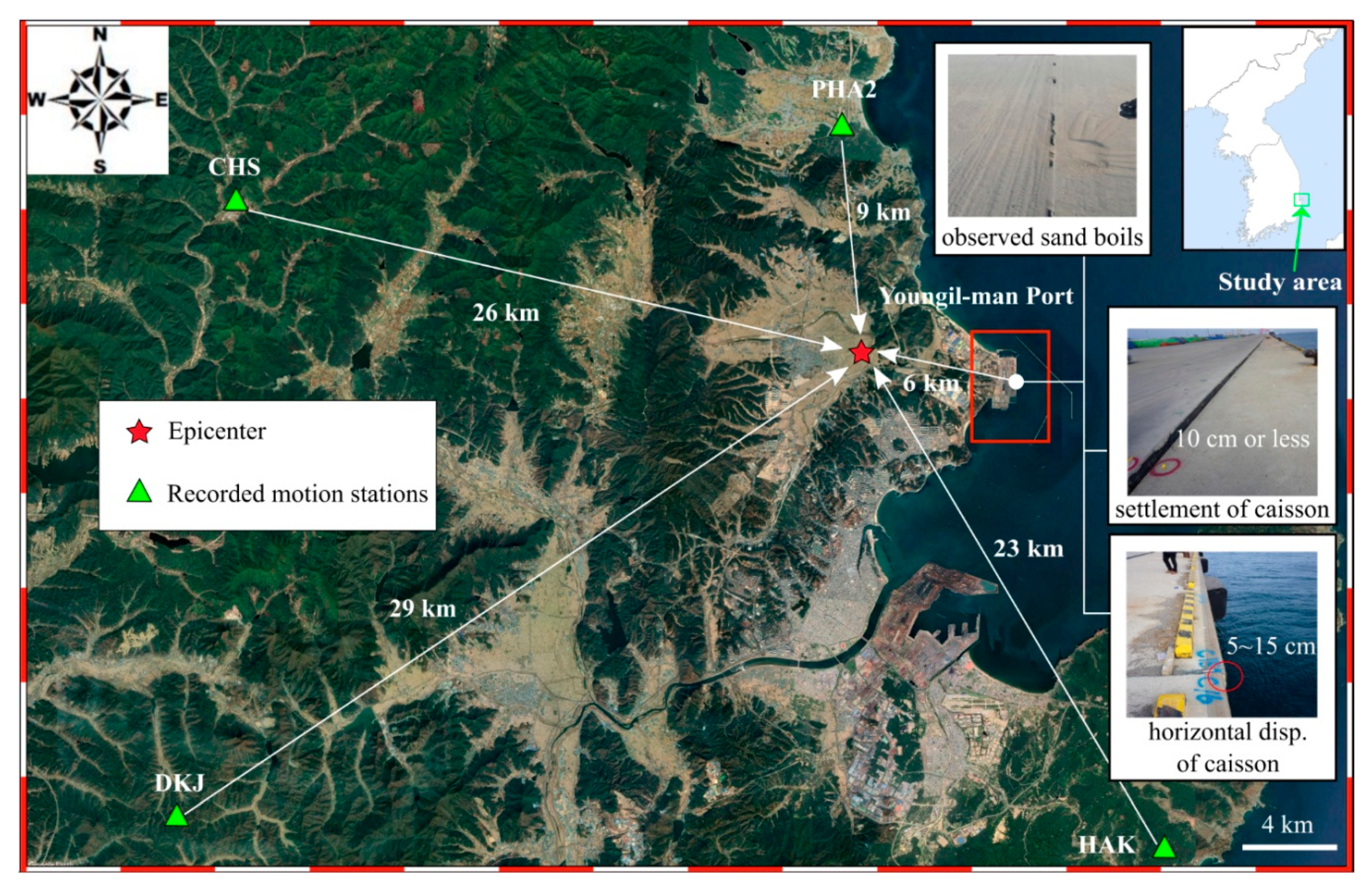
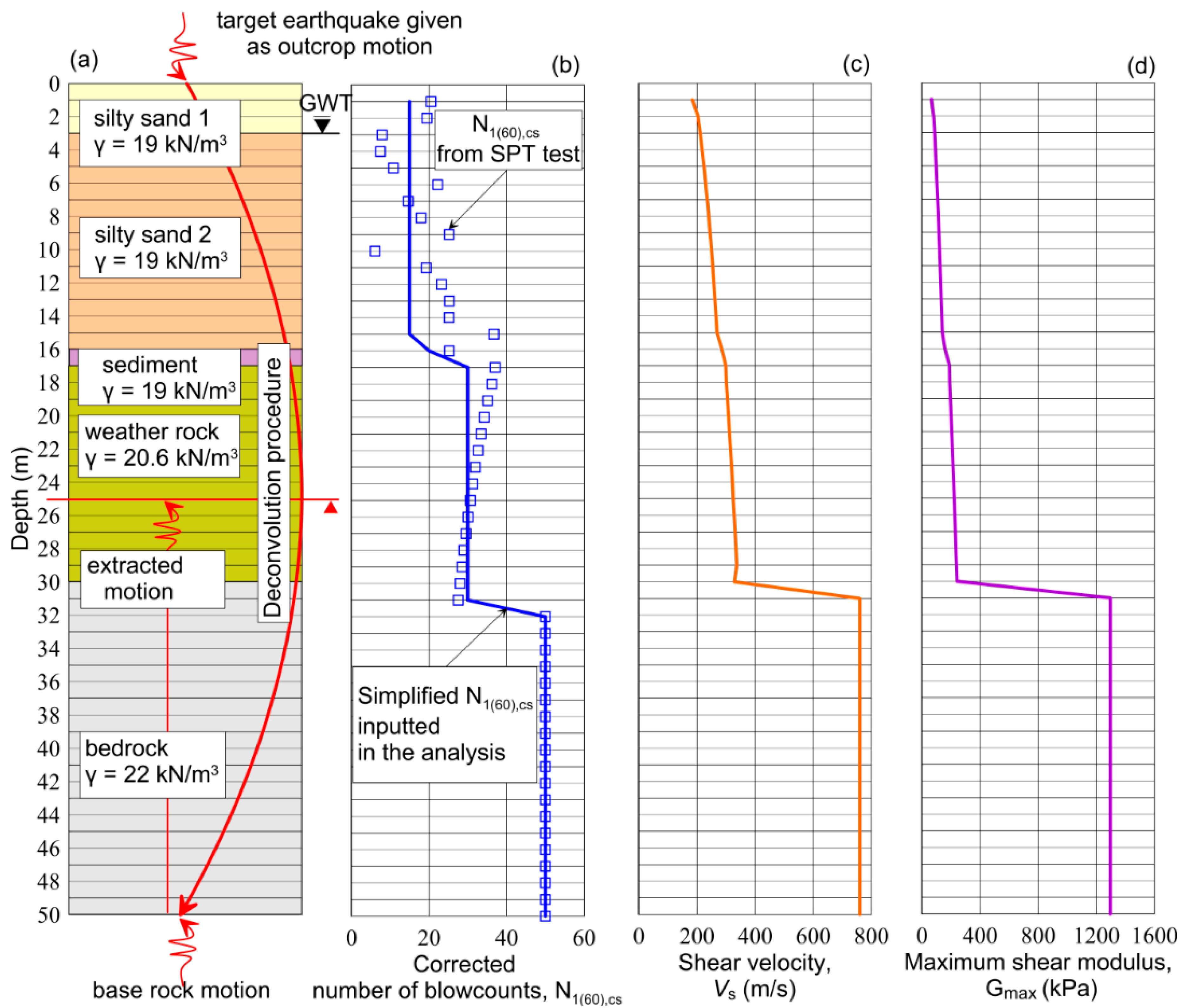
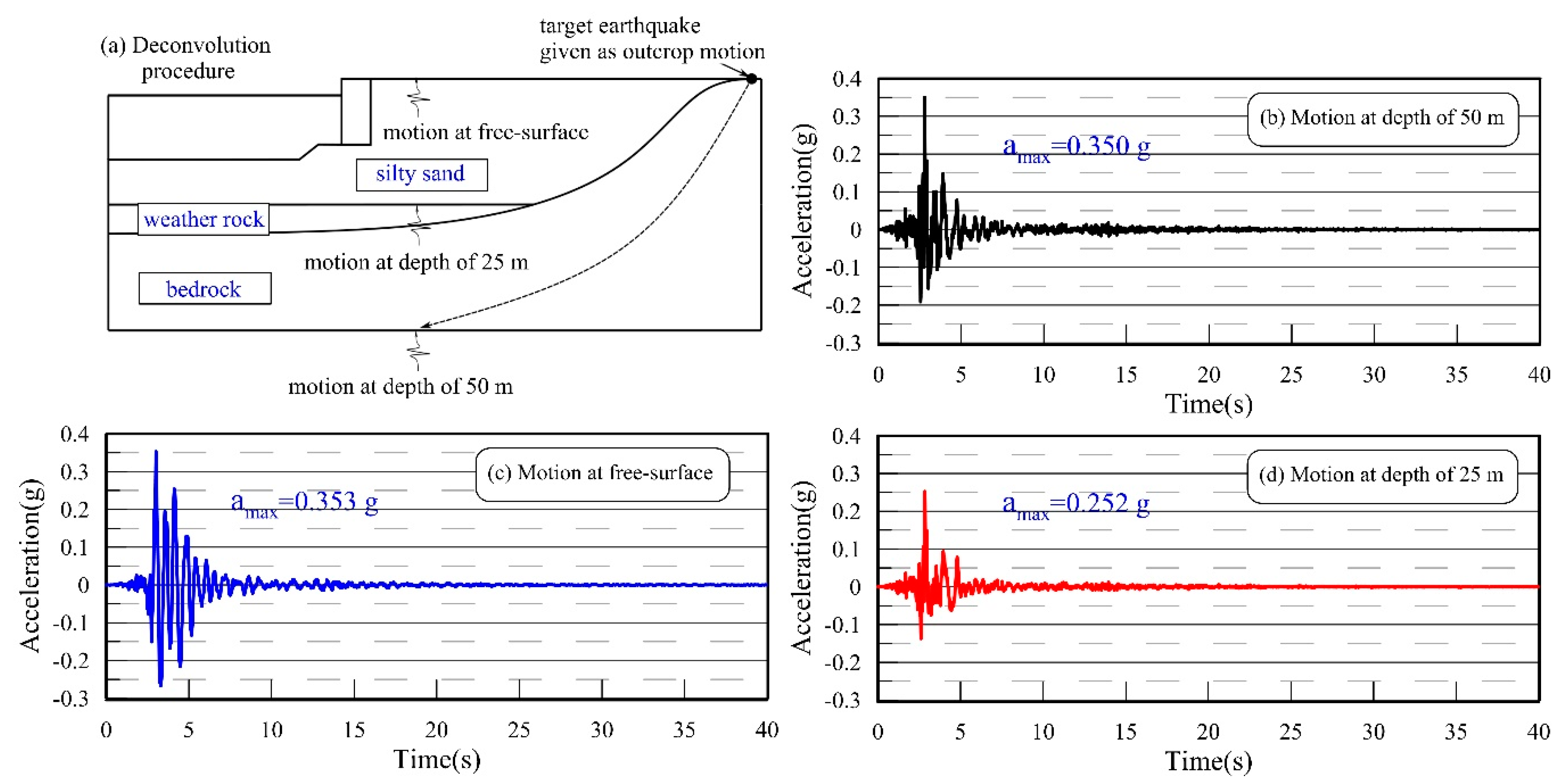
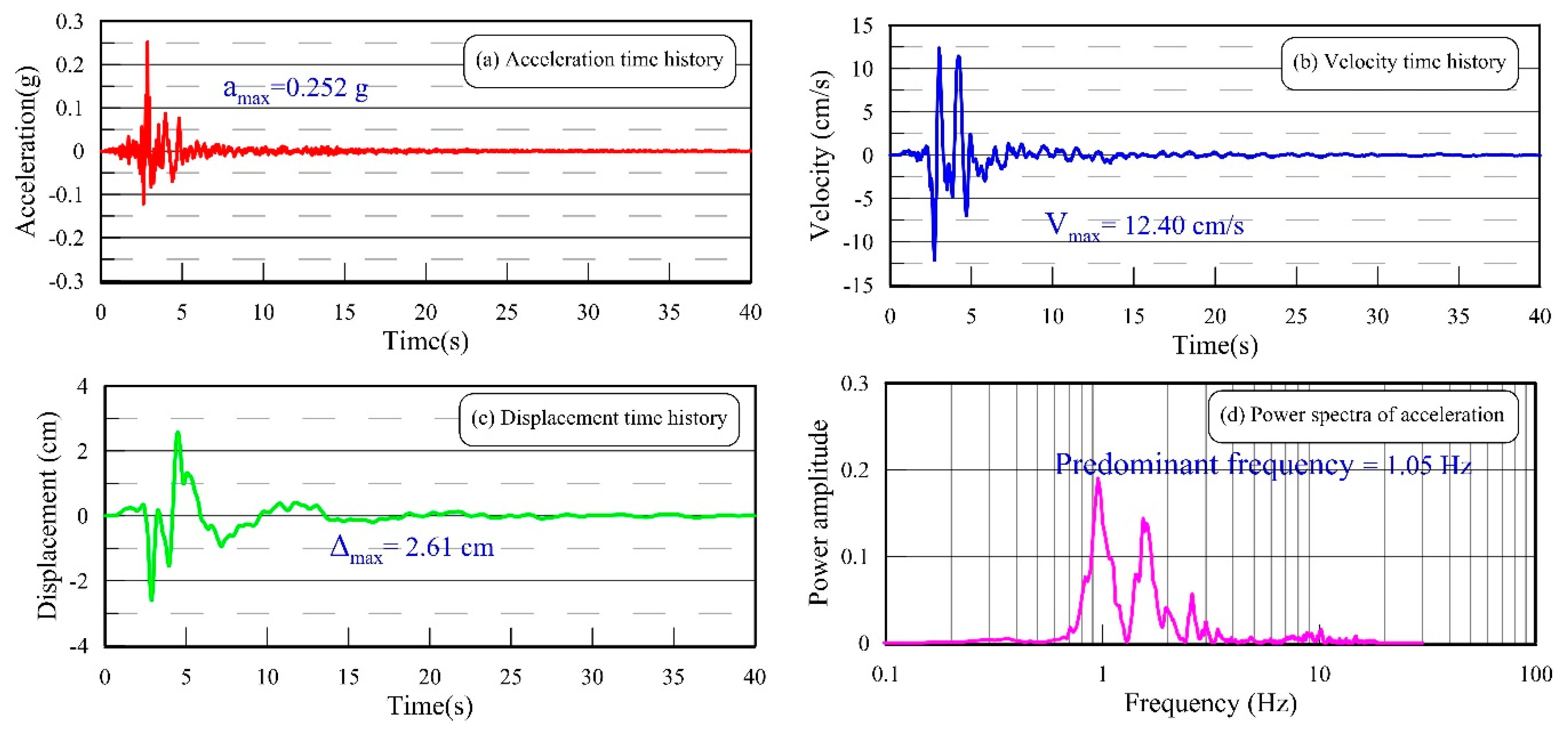
2.3.1. Study Area and Ground Motion of the Pohang Earthquake
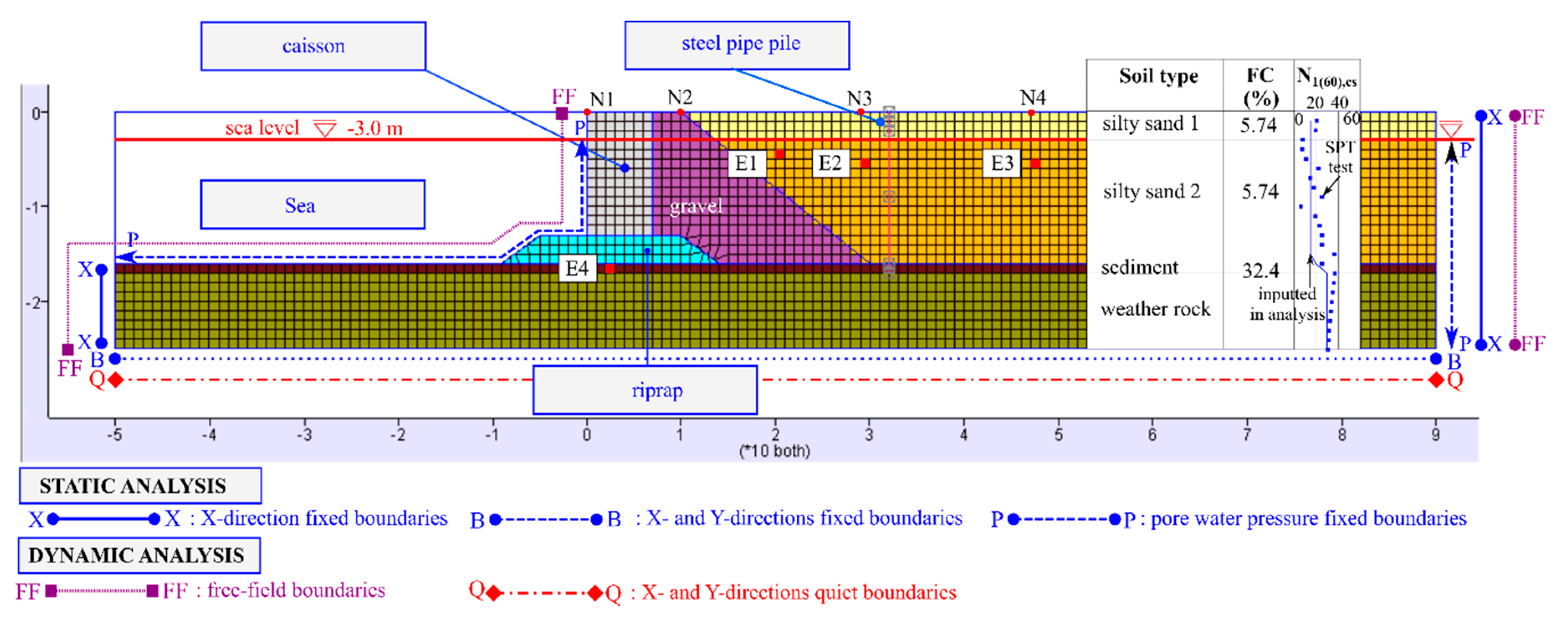
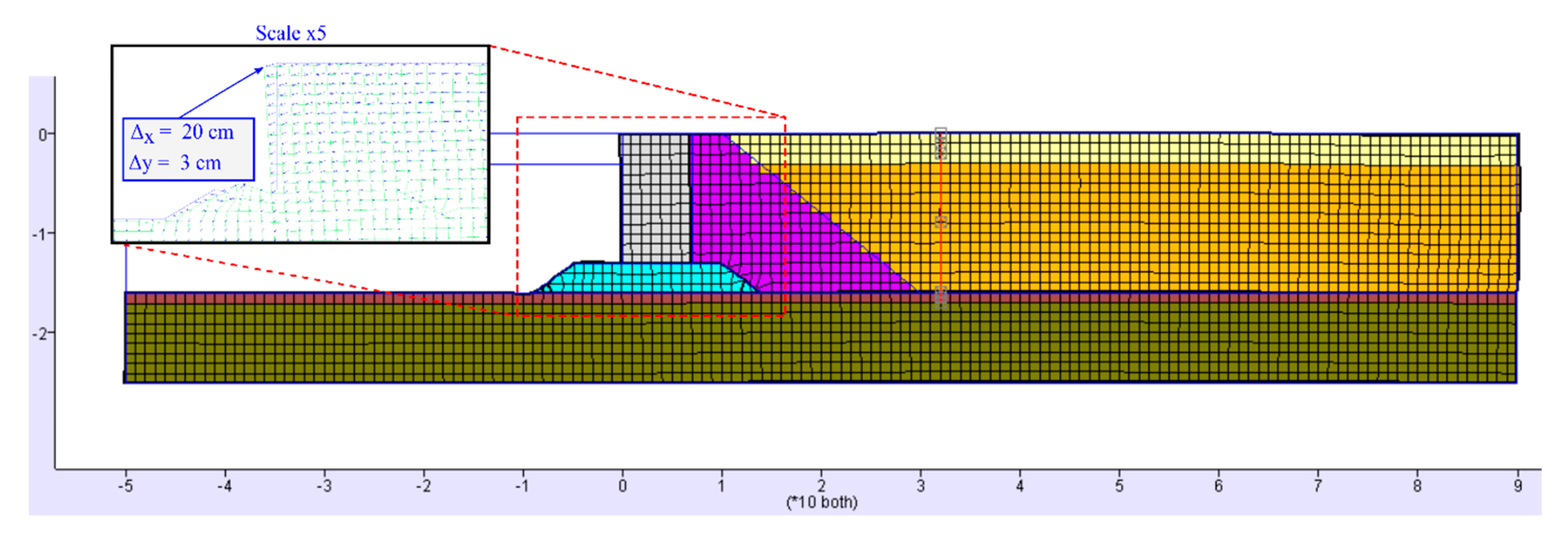
2.3.2. Numerical Modeling
3. Results and Discussion
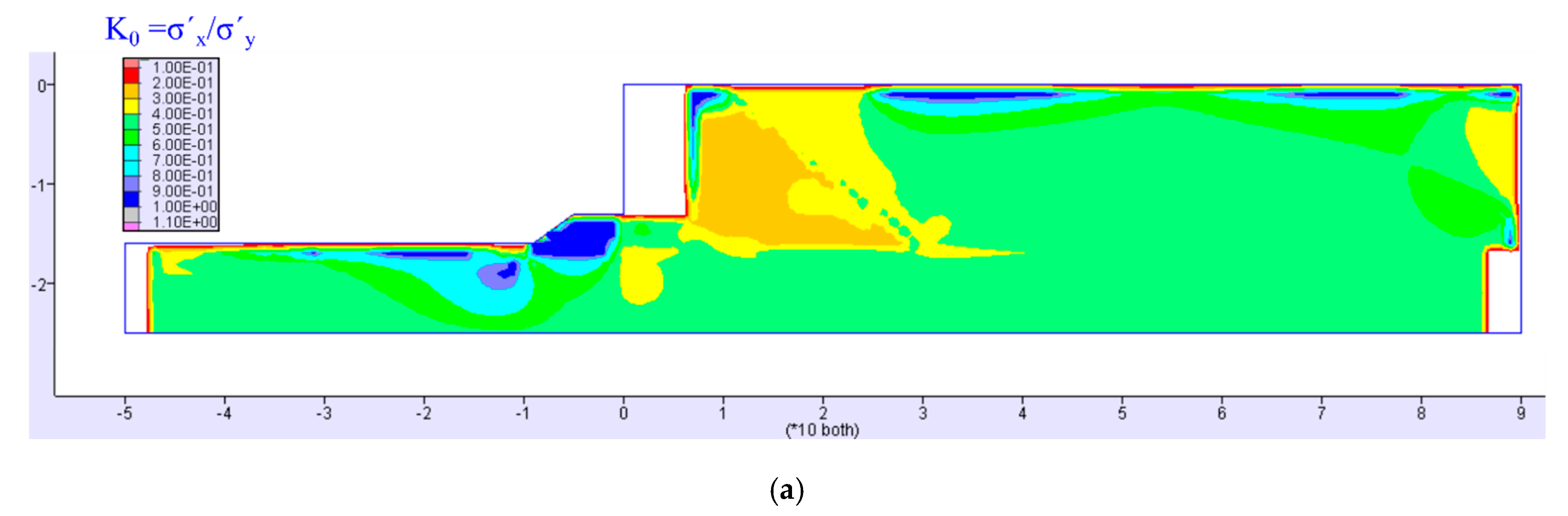
3.1. Pre-Earthquake Stress Conditions
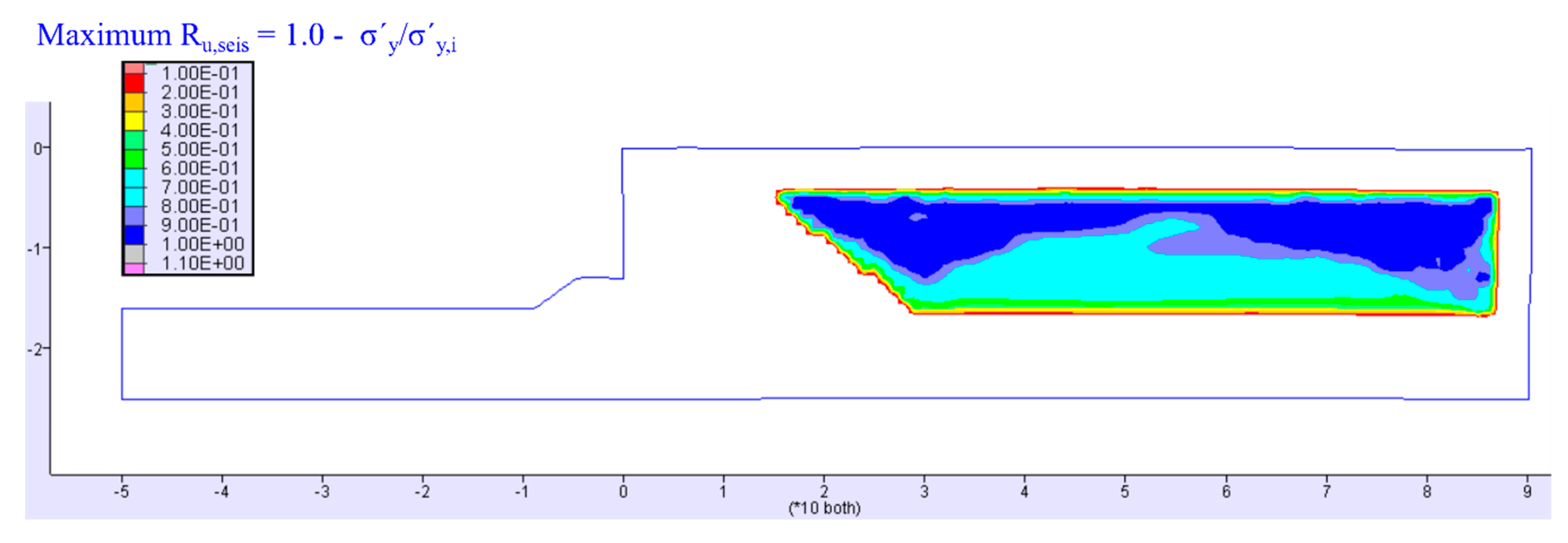
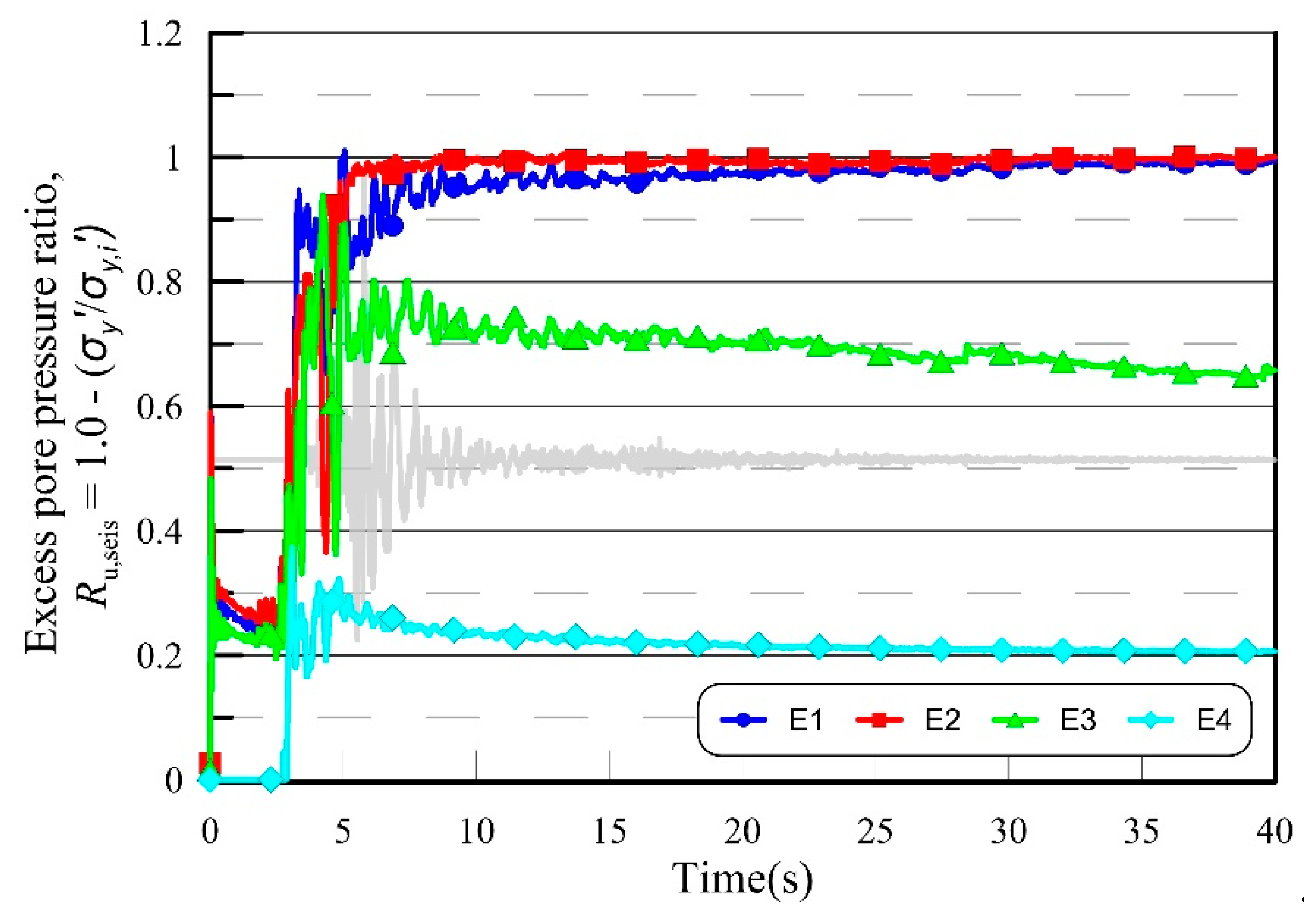
3.2. Excess Pore Water Pressure
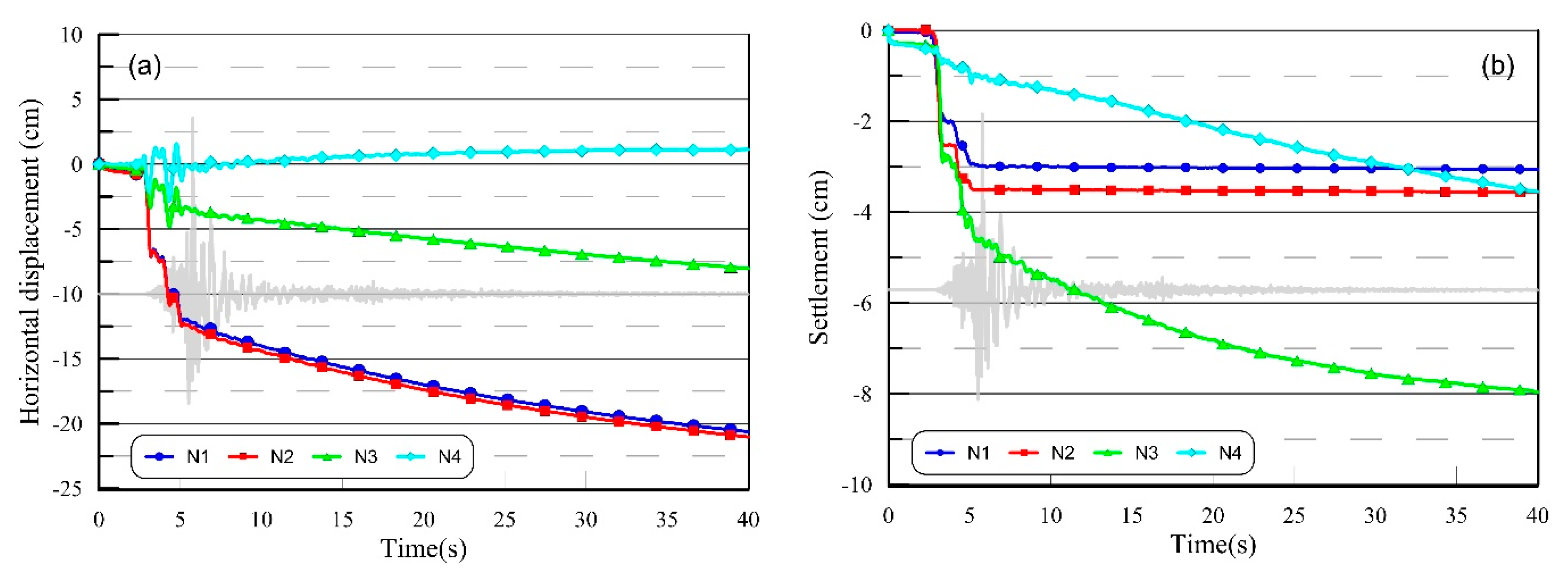
3.3. Displacements
3.4. Shear Stress–Strain and Acceleration
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Aubry, D.; Modaresi, H. Seismic wave propagation in soils including non-linear and pore pressure effects. In Recent Advances in Earthquake Engineering and Structural Dynamics; Ouest éditions: Nantes, France, 1992; pp. 209–224. [Google Scholar]
- Beaty, M.H.; Perlea, V.G. Several observations on advanced analyses with liquefiable materials. In Proceedings of the 31st Annual USSD Conference and 21st Conference on Century Dam Design-Advances and Adaptations, San Diego, CA, USA, 11–15 April 2011; pp. 1369–1397. [Google Scholar]
- Beaty, M.H.; Byrne, P.M. UBCSAND constitutive model version 904aR. Itasca UDM Web Site 2011, 1–69. [Google Scholar]
- Byrne, P.M.; Park, S.S.; Beaty, M.; Sharp, M.; Gonzalez, L.; Abdoun, T. Numerical modeling of liquefaction and comparison with centrifuge tests. Can. Geotech. J. 2004, 41, 193–211. [Google Scholar] [CrossRef]
- Beaty, M.H. Application of UBCSAND to the LEAP centrifuge experiments. Soil Dyn. Earthq. Eng. 2018, 104, 143–153. [Google Scholar] [CrossRef]
- Yang, D.; Naesgaard, E.; Byrne, P.M.; Adalier, K.; Abdoun, T. Numerical model verification calibration of George Massey Tunnel using centrifuge models. Can. Geotech. J. 2004, 41, 921–942. [Google Scholar] [CrossRef] [Green Version]
- Seid-Karbasi, M.; Byrne, P.M. Seismic liquefaction, lateral spreading, and flow slides: A numerical investigation into void redistribution. Can. Geotech. J. 2007, 44, 873–890. [Google Scholar] [CrossRef]
- Park, S.S. A Two Mobilized-Plane Model and Its Application for Soil Liquefaction Analysis. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2005. Available online: https://open.library.ubc.ca/cIRcle/collections/ubctheses/831/items/1.0063362 (accessed on 20 April 2020).
- Kang, S.; Kim, B.; Bae, S.; Lee, H.; Kim, M. Earthquake-induced ground deformations in the low-seismicity region: A case of the 2017 M5.4 Pohang, South Korea, earthquake. Earthq. Spectra 2019, 35, 1235–1260. [Google Scholar] [CrossRef]
- Choi, J.H.; Ko, K.; Gihm, Y.S.; Cho, C.S.; Lee, H.; Song, S.G.; Bang, E.S.; Lee, H.J.; Bae, H.K.; Kim, S.W.; et al. Surface Deformations and Rupture Processes Associated with the 2017 Mw 5.4 Pohang, Korea, Earthquake. Bull. Seismol. Soc. Am. 2019, 109, 756–769. [Google Scholar] [CrossRef]
- Kim, S.; Hwang, W.K.; Kim, T.H.; Kang, G.C. A case study on earthquake-induced deformation of quay wall and backfill in Pohang by 2D-effective stress analysis. J. Korean Geotech. Soc. 2019, 35, 15–27. (In Korean) [Google Scholar] [CrossRef]
- Lee, H.J.; Kang, G.C.; Hwang, W.K.; Lee, M.S.; Kim, T.H. Behavior Analysis on Earthquake-Induced Deformation of Quay Wall and Apron in Ground at Youngilman Port Considering Drainage Condition Using FEM Analysis. J. Korean Soc. Coast. Ocean Eng. 2019, 31, 386–394. (In Korean) [Google Scholar] [CrossRef] [Green Version]
- Baek, W.H.; Choi, J.S.; Ahn, J.K. Liquefaction Hazard Map Based on in Pohang Under Based on Earthquake Scenarios. J. Earthq. Eng. Soc. Korea 2018, 22, 219–224. (In Korean) [Google Scholar] [CrossRef]
- Jeong, M.S. Investigation and analysis of Pohang earthquake in relation to geotechnical earthquake engineering. In Proceedings of the Symposium on characteristics of Pohang Earthquake and Countermeasures for Geotechnical Structure, Seoul, Korea, 7 February 2018; Available online: http://www.ksce.or.kr/not/Default.asp?page=1&bidx=48219&sfield=>xt=&gbn=13&bcat=&ctop=MN0099&htop=MN0031&ptop=MN0031&idx=&bgbn=R (accessed on 23 September 2019). (In Korean).
- Ahn, J.K.; Baek, W.H.; Choi, J.S.; Kwak, D.Y. Investigation of Pohang Earthquake Liquefaction Using 1D Effective-Stress Site Response Analysis. J. Korean Geotech. Soc. 2018, 34, 37–49. (In Korean) [Google Scholar] [CrossRef]
- Iai, S.; Matsunaga, Y.; Kameoka, T. Strain Space Plasticity Model for Cyclic Mobility. Soils Found. 1992, 32, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Iai, S.; Matsunaga, Y.; Kameoka, T. Analysis of Undrained Cyclic behavior of Sand under Anisotropic Consolidation. Soils Found. 1992, 32, 16–20. [Google Scholar] [CrossRef]
- Puebla, H.; Byrne, P.M.; Phillips, R. Analysis of CANLEX liquefaction embankments: Prototype and centrifuge models. Can. Geotech. J. 1997, 34, 641–657. [Google Scholar] [CrossRef]
- Beaty, M.; Byrne, P.M. An Effective Stress Model for Predicting Liquefaction Behaviour of Sand. Geotechnical Earthquake Engineering and Soil Dynamics III; Dakoulas, P., Yegian, M., Holtz, R., Eds.; ASCE, Geotechnical Special Publication: Seattle, DC, USA, 1998; pp. 766–777. [Google Scholar]
- Park, S.S.; Byrne, P.M. Practical constitutive model for soil liquefaction. In Proceedings of the 9th International Symposium on Numerical Models in Geomechanics (NUMOG IX), Ottawa, ON, Canada, 25–27 August 2004; pp. 181–186. [Google Scholar]
- Rowe, P.W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. Proc. R. Soc. Lond. Math. Phys. Sci. Ser. A 1962, 269, 500–557. [Google Scholar]
- Silver, M.L.; Seed, H.B. Volume changes in sands during cyclic loading. J. Soil Mech. Found. Div. 1971, 97, 1171–1182. [Google Scholar]
- Sriskandakumar, S. Cyclic Loading Response of Fraser River Sand for Validation of Numerical Models Simulating Centrifuge Tests. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2004. Available online: https://open.library.ubc.ca/cIRcle/collections/ubctheses/831/items/1.0063399 (accessed on 15 April 2020).
- Nong, Z. Liquefaction Characteristics of Nakdong River Sand Using Cyclic Triaxial and Simple Shear Tests. Ph.D. Thesis, Kyungpook National University, Daegu, South Korea, 2020. Available online: https://dcollection.knu.ac.kr (accessed on 3 June 2020).
- Youd, T.L.; Idriss, I.M. Liquefaction resistance of soils: Summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils. J. Geotech. Geoenvironmental Eng. 2001, 127, 297–313. [Google Scholar] [CrossRef] [Green Version]
- National Earthquake Comprehensive Information System (NECIS). Available online: http://necis.kma.go.kr/ (accessed on 23 September 2019). (In Korean).
- Korea Building Code; Architectural Institute of Korea: Seoul, Korea, 2016; Available online: http://aikkbc.or.kr (accessed on 6 May 2020).
- Dreger, D.; Beroza, G.C.; Day, S.M.; Goulet, C.A.; Jordan, T.H.; Spudich, P.A.; Stewart, J.P. Validation of the SCEC Broadband Platform V14.2 Simulation Methods Using Pseudospectral Acceleration Data. Seismol. Res. Lett. 2015, 86, 1. [Google Scholar] [CrossRef]
- Chowdhury, K.H. Evaluation of the State of Practice Regarding Nonlinear Seismic Deformation Analyses of Embankment Dams Subject to Soil Liquefaction Based on Case Histories. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2018. Available online: https://escholarship.org/uc/item/4515d2j1 (accessed on 20 May 2020).
- Itasca Consulting Group Inc. Minneapolis, Minnesota. FLAC–Fast Lagrangian Analysis of Continua, Version 7.0, Software. 2011. Available online: https://www.itascacg.com/software/flac (accessed on 30 March 2020).
- EduPro Civil Systems, Inc. Sammamish, Washington DC, 2018. ProShake, Version 2.0, Software. Available online: http://www.proshake.com/PS2.0Educational.html (accessed on 8 June 2020).
- Lee, J.; Hwang, J.; Son, M.; Son, B.S.; Oh, J.; Lee, H. Mineral Compositions and Distribution in the Drilling Cores from the Miocene Pohang Basin, Korea. J. Miner. Soc. Korea 2017, 30, 113–126. [Google Scholar] [CrossRef]
- Integrated DB Center of National Geotechnical Information. 2015, SPT Database. Available online: http://www.geoinfo.or.kr (accessed on 15 May 2015).
- Mun, G.Y. A Study on the Effect of Relative Density and Particle Size Distribution on the Liquefaction Resistance Strength of Sand in Pohang Liquefaction Region. Master’s Thesis, Pusan National University, Pusan, Korea, 2018. [Google Scholar]
- Park, S.S.; Nong, Z.; Choi, S.G.; Moon, H.D. Liquefaction Resistance of Pohang Sand. J. Korean Geotech. Soc. 2018, 34, 5–17. (In Korean) [Google Scholar] [CrossRef]
- Morita, T.; Iai, S.; Liu, H.; Ichii, K.; Sato, Y. Simplified Method to Determine Parameter of FLIP. In Technical Note of the Port and Harbor Research Institutive; Japan Ministry of Transport: Chiyoda, Tokyo, Japan, 1997. [Google Scholar]
- Iai, S. Seismic Design Guidelines for Port Structures; A.A. Balkema Publishers: Lisse, The Netherlands; Abingdon, UK; Exton, PA, USA; Tokyo, Japan, 2000. [Google Scholar]
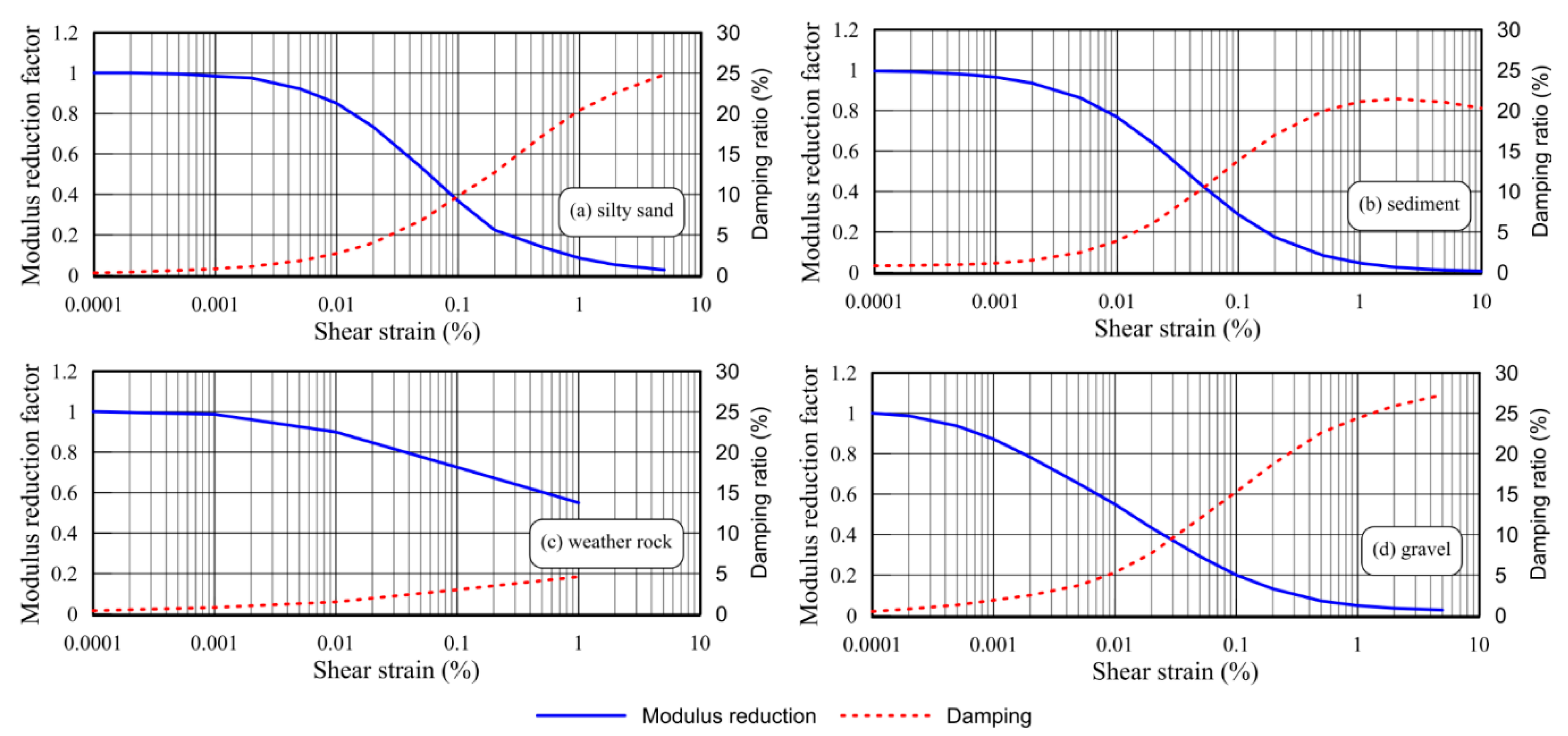
- Seed, H.B.; Wong, R.T.; Idriss, I.M.; Tokimatsu, K. Moduli and damping factors for dynamic analyses of cohesionless soils. J. Geotech. Eng. 1986, 112, 1016–1032. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–878. [Google Scholar]
- Roesset, J.M.; Ettouney, M.M. Transmitting boundaries: A comparison. Int. J. Numer. Anal. Methods Geomech. 1977, 1, 151–176. [Google Scholar] [CrossRef]
- Jaky, J. The coefficient of earth pressure at rest. J. Soc. Hung. Archit. Eng. 1993, 30, 647–666. [Google Scholar]







| Parameters | Generic Parameters | Calibration | ||
|---|---|---|---|---|
| Function | Values | Loose | Dense | |
| (N1)60 | Normalized, corrected SPT blow counts | Varies | 12.50 | 16.50 |
| CDr | Correlation factor between (N1)60 and Dr | Constant | 46 | 46 |
| Dr | Relative density | [(N1)60/CDr]0.5 | 0.53 | 0.61 |
| ϕcv | Constant volume friction angle | 33° | 33.00 | 33.00 |
| ϕf | Peak friction angle | ϕcv + (N1)60/10 + max(0, ((N1)60 − 15)/5) | 34.25 | 34.95 |
| kGe | Elastic shear modulus number | 21.7 × 20 × (N1)600.333 | 1006 | 1104 |
| kBe | Elastic bulk modulus number | 0.7 × kGe | 704 | 773 |
| kGp | Plastic shear modulus number | kGe (N1)602 × 0.003 + 100 | 572 | 1002 |
| me | Elastic shear exponent | 0.5 | 0.50 | 0.50 |
| ne | Elastic bulk exponent | 0.5 | 0.50 | 0.50 |
| np | Plastic shear exponent | 0.4 | 0.40 | 0.40 |
| Rf | Failure ratio | min(1.1 × (N1)60−0.15, 0.99) | 0.75 | 0.72 |
| a | Factor for hfac1 calculation | 1.05 − 0.03 × (N1)60 + 0.04 × [(N1)60]2 − 0.000185 × [(N1)60]3 + 2.92E − 6 × [(N1)60]4 | 1.01 | 1.03 |
| b | Factor for hfac1 calculation | 1.0/{−0.424 − 0.259 × (N1)60 + 0.00763 × [(N1)60]2} | −0.4 | −0.38 |
| hfac1 | Factor of primary hardener | A × (σ′v0/Patm)b | 1.01/0.77 (*) | 1.03/0.79 (*) |
| hfac2 | Factor of secondary hardener | 1.0 | 1.00 | 1.00 |
| hfac3 | Factor of dilation hardener | 1.0 | 1.00 | 1.00 |
| anisofac | Factor of anisotropic plastic response | 1.0 | 1.00 | 1.00 |
| Ch | Cyclic hardening | 8.33 × (Dr)2 − 5.0 × Dr + 2.2292 | 1.89 | 2.22 |
| Station | Location | Distance from Epicenter (km) | Site Classification | PGA (g) | |||
|---|---|---|---|---|---|---|---|
| E | N | NS | EW | UD | |||
| PHA2 | 129.37080° | 36.19290° | 9 | SB | 0.271200 | 0.243283 | 0.140000 |
| CHS | 129.08811° | 36.18113° | 26 | SB | 0.027800 | 0.021200 | 0.01900 |
| DKJ | 129.10892° | 35.94675° | 29 | SB | 0.048300 | 0.02500 | 0.042800 |
| HAK | 129.50037° | 35.92955° | 23 | SB | 0.036400 | 0.026700 | 0.030300 |
| Materials | γd (kN/m3) | N1(60) | Model | Parameters for Non-Liquefied Soils | Remarks | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| G (kPa) | B (kPa) | c (kPa) | ϕ (deg) | k (m/s) | ν | |||||
| Silty sand 1 | 19.00 | 15.00 | UBC2 | - | - | - | - | - | - | Liquefied |
| Silty sand 2 | 19.00 | 15.00 | UBC2 | - | - | - | - | - | - | Liquefied |
| Sediment | 19.00 | 20.00 | M-C | 1.43 × 105 | 3.72 × 105 | 0.00 | 30.0 | 1 × 10−5 | 0.33 | Non-liquefied |
| Weathered rock | 20.60 | 50.00 | M-C | 2.85 × 105 | 7.43 × 105 | 0.00 | 30.0 | 1 × 10−4 | 0.25 | Non-liquefied |
| Riprap | 18.00 | 50.00 | M-C | 2.49 × 105 | 6.49 × 105 | 0.00 | 40.0 | 1 × 10−1 | 0.33 | Non-liquefied |
| Gravel | 20.00 | 50.00 | M-C | 7.22 × 105 | 7.22 × 105 | 0.00 | 33.0 | 1 × 10−4 | 0.33 | Non-liquefied |
| Concrete | 23.00 | - | elastic | 1.00 × 107 | 1.67 × 107 | - | - | - | 0.25 | Elastic |
| Steel pipe pile | 78.5 | - | elastic | E = 2.1 × 108 kPa, ν = 0.2, A = 0.01671 m2, I = 7.3 × 10−5 m4, D = 1.884 m | Elastic | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doan, N.-P.; Park, S.-S.; Lee, D.-E. Assessment of Pohang Earthquake-Induced Liquefaction at Youngil-Man Port Using the UBCSAND2 Model. Appl. Sci. 2020, 10, 5424. https://doi.org/10.3390/app10165424
Doan N-P, Park S-S, Lee D-E. Assessment of Pohang Earthquake-Induced Liquefaction at Youngil-Man Port Using the UBCSAND2 Model. Applied Sciences. 2020; 10(16):5424. https://doi.org/10.3390/app10165424
Chicago/Turabian StyleDoan, Nhat-Phi, Sung-Sik Park, and Dong-Eun Lee. 2020. "Assessment of Pohang Earthquake-Induced Liquefaction at Youngil-Man Port Using the UBCSAND2 Model" Applied Sciences 10, no. 16: 5424. https://doi.org/10.3390/app10165424






