1. Introduction
Gas–liquid two-phase flow is a common phenomenon occurring in petroleum, chemical, refrigeration and power generation industries [
1,
2,
3]. Due to the unstable flow, heat and mass transfer process, the flow pattern and interface structure of two-phase flow are usually complex [
4,
5,
6]. Therefore, the two-phase flow parameters are difficult to measure quickly and accurately [
7]. However, the knowledge of local parameters of two-phase flow plays a critical role in the studies of the heat and mass transfer characteristics and mechanism of the gas–liquid two-phase, the development of two-phase modeling research, the optimization of two-phase flow patterns and the safety and stability of equipment operation [
8,
9,
10]. The theoretical models, including the two-fluid model and interfacial area transportation model, rely heavily on the advanced measurement techniques to provide benchmark database and possibility of inspecting new phenomenon and physical laws. The flow parameters including phase distribution, void fraction, interfacial area concentration (IAC), bubble size, velocity, etc. of two-phase flow have great impacts on the heat and mass transfer characteristics, the reaction efficiency and operation safety of multiple chemical applications [
11,
12,
13,
14,
15]. Hence, it is particularly necessary to develop and utilize accurate, fast and convenient methods to explore the two-phase flow details.
Currently, the measurement methods of local two-phase flow parameters can be divided into the following two categories: (1) the photography and image process techniques, having the advantage of lack influence on the flow, usually called visual measurement [
16,
17,
18] and (2) the point by point measurement [
3,
19,
20], in which optical or electrical signal that can be altered by involved phases. However, the first kind of methods is only applied to systems where the flow channel or vessel is transparent, unless the photography employs high energy ray to penetrate metal walls [
21,
22]. Besides, it is hard for visual measurements to distinguish bubbles at different depths when bubbles are overlapped in complex two-phase flow [
23]. Nevertheless, this method has contributed greatly in the identification of flow regimes, track of simple bubbly flow and determination of bubble condensation rate in phase changing flows [
23,
24,
25,
26,
27,
28]. For the second category of methods, one of its important kinds is the wire-sensor mesh [
29,
30,
31,
32,
33] where a matrix of measurement points is created at the cross points of two arrays of parallel mesh wires. Electrical signals from the wire-sensor mesh are collected and then analyzed by a program to get void fraction, bubble size, bubble velocity and so on across the whole flow field. Another kind is the sensor probe including single-sensor probe, double-sensor probe, four-sensor probe and other multiple-sensor probes [
34,
35,
36,
37,
38,
39,
40,
41,
42]. Moving the probe across the two-phase flow field, local flow parameters at different positions can be measured. Although both the wire-sensor mesh and sensor probe interfere measurements affect the original two-phase flow field, this intrusion can be limited by a great extent with very thin wires or probes. Moreover, compared with the visual measurement, the point-to-point sensors are easier to be adopted online for practical opaque tube and vessel and more complex two-phase flow.
In the above-mentioned method, only two sensors apart from the probe shell are used in the double-sensor probe, and thus two series of signals can be collected. In the simple measurement theorem of double-sensor probe, it is assumed that the direction of interface and velocity of bubbles (or interface) are both in parallel to the connection between the two sensors’ tips. As a result, the double-sensor probe can be applied to measure local flow void fraction, IAC and magnitude of velocity when the two-phase flow is very consistently stable bubbly flow, and the accuracy can be very high without too much care to the signal process and correction algorithm [
34]. However, more assumptions and more complicated signal processing and correction algorithms are necessary if the flow becomes complicated or more parameters, e.g., bubble size and interface direction, have to be detected. Inevitably, more uncertainties would be produced in the application of single-sensor probe or double-sensor probe if employing these assumptions [
43,
44,
45,
46]. As uncertain assumptions must be incorporated, it is hard for the double-sensor probe to obtain real local flow parameters in multi-dimensional two-phase flow.
Meanwhile, the typical multiple-sensor probe, namely the four-sensor probe, as a promising alternative compared with single-sensor probe and double-sensor probe, is developed by a few researchers to omit the involvement of so many assumptions. According to measurement theorem of four-sensor probe, it is unnecessary to coordinate the connections of the sensors’ tips to the direction of interface or direction of interface displacement velocity, while the void fraction, IAC and chord length can still be calculated. In addition, the interface direction can be obtained by the proper processing and trigonometric operation of the four series of signals from the four sensors [
47,
48,
49,
50,
51]. However, the bubble velocity or interface displacement velocity is still unknown, except its component in the normal direction of interface [
36]. It has been proved that this problem can be compensated by employing several four-sensor probes or multiple-sensor probe, five-sensor probe, six-sensor probe, etc. [
52,
53]. With a much simpler assumption of the two-phase flow, obtaining the full velocity vector by using merely one four-sensor probe can also be realized. For instance, assuming a spherical or symmetric bubble shape and a bubble velocity perpendicular to the symmetric plane has been demonstrated to be a concise way to get the full components of bubble velocity [
54,
55,
56]. The above simplifications when calculating the total interface velocity vector only apply to special cases. Considering this fact, the local interface velocity directions can be practically provided by prior measurement, flow simulation and even other legitimate assumption in many two-phase flows. It is necessary and significant for obtaining interface details to propose a new method to get the total interface velocity vector based on the known interface velocity directions.
Besides the development of algorithm for four-sensor probe, the miniaturization of the probe and sensors are essential to guarantee the accuracy of measurement. According to the published literature [
47,
50], both the diameter of sensor wire and the total front area formed by all four sensors have great influence on the bubbles’ behavior. Thus, it is recommended to use as small as possible sensors and probe of cross-sectional area. With the assumption of a much smaller probe than the size of bubble, the error produced during the application of the probe stems mainly from the bouncing away of bubble from the probe and the slipping away of interface through the gap between sensors. Their errors or uncertainties are acceptable [
36,
47,
49]. Therefore, with the solution of the many issues of four-sensor probe, including its fabrication and further miniaturization, the correction for its disturbance to original flow and the improvement of signal process algorithm, it is promising to be widely applied in multiphase flow measurement inside chemical reactor, oil piping, power generation facility and heat exchanger. In addition, the method will be easy to be adopted for different combinations of fluid components. Even if the flow were experiencing phase changing, including boiling and condensation, the method would still be applicable with proper algorithm improvement and correction.
However, the bubbles in two-phase flow keep deforming and are hard to be taken as sphere or symmetric, resulting in few studies on the accurate, convenient and efficient measurement of local flow parameters having been published thus far. Therefore, a new signal processing method for four-sensor probe to get the bubble velocity vector was developed in this study and the vector-based calculation was used for the first time to deduct the local flow parameters. Besides, the interface direction obtained from the probe were for the first time validated against a visual experiment that was also performed. The void fraction, IAC, bubble velocity, bubble chord length and interface direction resulting from the probe measurement were compared with the visual measurement. The application perspectives of this method in the field of mass and heat transfer of gas–liquid two-phase flow is discussed. The proposed methods in the present paper are expected to be useful in the heat and mass transfer characteristics and mechanism studies of the gas–liquid two-phase and the direct measurement of two-phase flow. Meanwhile, it can able provide significant database for the improvement of two-phase models.
2. Measurement Principles of Four-Sensor Probe
2.1. Electrical Circuit of Four-Sensor Probe
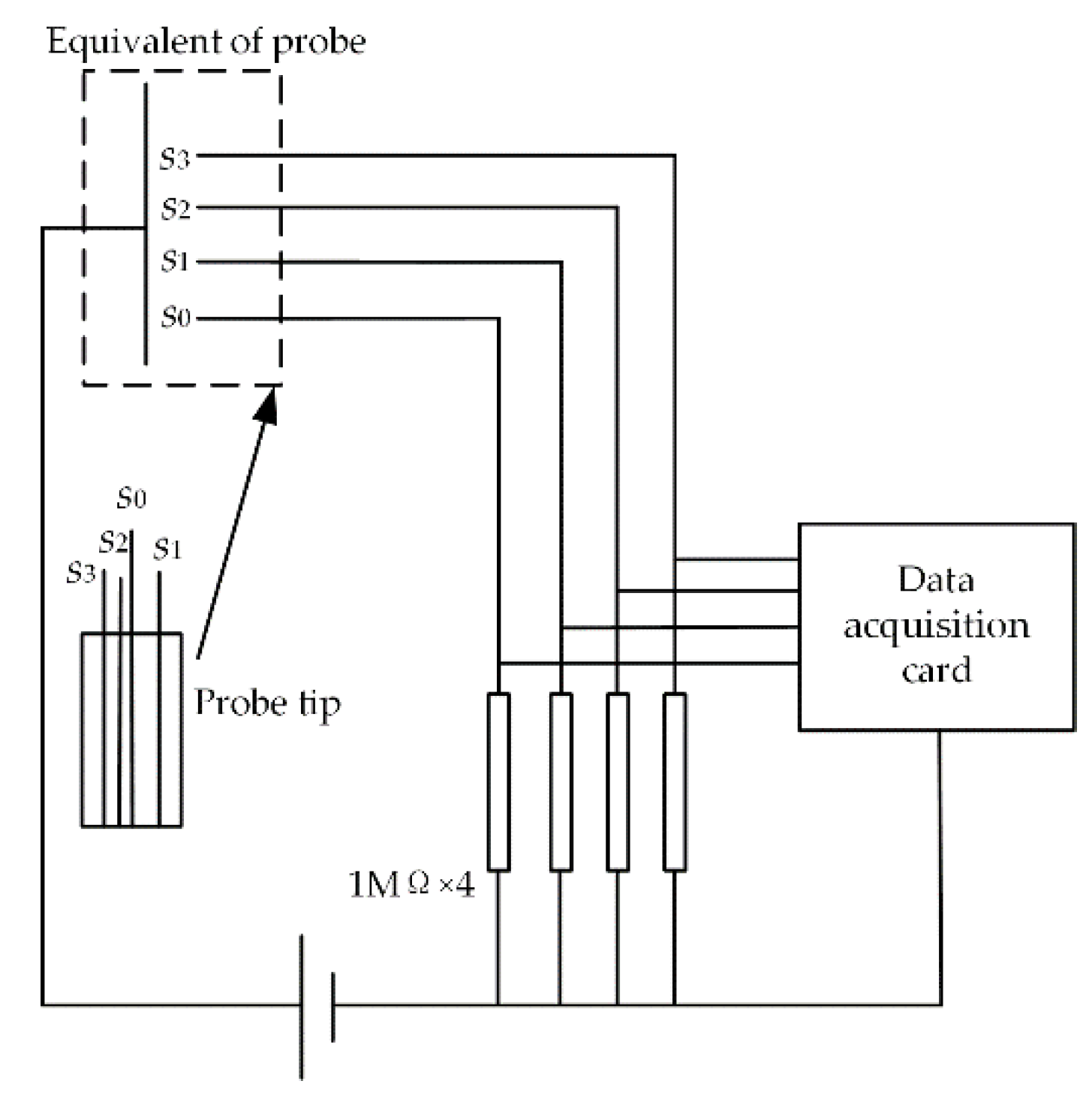
As shown in
Figure 1, an electrical circuit can be adopted in the four-sensor probe measurement. Since signal filtering and noise reduction can be easily realized by the appropriate signal pre-processing MATLAB codes (MATLAB 2017b, MathWorks, Inc., Natic, MA, USA), the circuit elements responsible for these functions were not necessary and thereby only four electrical resistances were employed in the circuit. The probe contains four sensors denoted
s0,
s1,
s2 and
s3, which connect to the negative electrode of the DC power supply through their respective resistance. The four sensors are covered by a rigid stainless-steel shell, which connects to the positive electrode of the DC power and functions as the common high voltage pole.
The shell of the probe made of metal was not insulated and thus always in contact with water. The four sensors are well insulated except at their very ends where the sensors can contact the water and thus get through to the positive pole of DC supplier. The signals from s0 to s3 are either high level or low level, depending on whether the sensor tips are submerged into water or exposed to the bubble air. A high voltage level indicates that a particular sensor is submerged in water and a low voltage level indicates that a particular sensor is exposed to air. Finally, the signals of high or low voltage from four sensors were transmitted to data collection system composed by a data acquisition unit (Art Technology, Beijing, China) and a PC. It is worth noting that the sensors have to be connected to the negative electrode of the DC power to avoid electrochemical corrosion and expand the probe’s lifespan.
For the data acquisition system, it is suggested in the literature that a sample frequency higher than 10 kHz is required to guarantee resolution. Therefore, a sample frequency of 10 kHz for each of the four sensors was employed in this study.
2.2. Fabrication of the Probe
As the impact of probe on bubble only becomes negligible with small probe size, the accuracy of the measurement improves with the downsizing of the four-sensor probe, thus the size of the probe should be miniaturized as much as possible. The four-sensor probe used in the present study was hand-made using stainless steel tube with internal diameter 1.2 mm and outer diameter 1.5 mm as the positive electrode and four copper wires of diameter 0.1 mm as the negative electrodes. The specific dimensions of the probe and its picture in reality are shown in
Figure 2.
The dimensions of the four-sensor probe and the relative position of sensor tips are shown in
Figure 2a,b, respectively. As shown in
Figure 2c, to provide support for the probe, the four sensors made of copper wire were fixed inside a stainless tube by epoxy resin, and the stainless tube with a length of 300 mm was then fixed by its end inside a short tube of internal dimeter of 5 mm with resin, before mounting it in a slide module, as shown in
Section 3.1. Each copper wire was covered by electrically insulation material except the tip was polished by sandpaper for electrical contact with water. Choosing the wire tip as coordinate center and the axis of
s0 as the
y-coordinate, the three vectors formed by the probe are
S1 (0, 1.75, 0.5),
S2 (0.5, 1.5, 0.5) and
S3 (0.5, 1.5, 0), which are used in
Section 2.4.
2.3. Signal Pre-Processing
After data collection, the signals were processed by a MATLAB program consisting of mainly two functions, the pre-processing and deduction of local flow parameters. The signal pre-processing was designed to obtain the time instants when each of the four sensors penetrate or recede a bubble.
In an ideal case, the signals should be square wave (see
Figure 3d) with the high-level representing sensor contact with water and the low-level representing passing-by of a particular bubble. However, mainly due to the delaying of data collection system and electromagnetic interference, the practically collected signal demonstrates noising inclining and fluctuating features, as shown in
Figure 3a. Average filtering was applied to attenuate the noise signal firstly, with the result shown in
Figure 3b. Then, a threshold voltage was chosen for signal binarization, as shown in
Figure 3c. The signal inversion so that the high level corresponds to air is shown in
Figure 3d. The threshold value adopted should be slightly higher than the noise voltage, to avoid the influence of noise while ensuring the accuracy of instants when sensor penetrates or recedes a bubble. After that, the resulted square wave was extracted to separate the rising edge corresponding to bubble approaching a sensor and falling edge corresponding to bubble leaving a senor, as shown in
Figure 3e.
The above procedures shown in
Figure 3a–e are the same for
s0 to
s3, and thus eight sets of signal are obtained. Since one bubble has two interfaces passing-by one sensor, eight rising and falling instants are produced in total (four rising edges and four falling edges), as shown in
Figure 4, where the eight instants produced by one bubble are noted by
ti ׳ and
ti ״ (
i = 0, 1, 2, 3) with ׳ noting rising instant and ״ noting falling instant. To make sure each of the eight-instant group belong to the same bubble (effective bubble), the collected signals are screened by cross-checking every bubble using the method described by Equation (1):
which guarantees the time delay when bubble approaches (or leaves) one sensor and another must be smaller than the retaining duration of one bubble. This is in the first place required by the assumption that the four-sensor probe is much smaller than the measured bubbles.
The above procedures allow omitting two kinds of ineffective bubbles. The first kind is those bubbles for which eight-instant signal is incomplete, which means that only part of the four sensors penetrate them. This means bubbles that slide or bounce off the probe. Another kind of ineffective bubbles are those whose eight-edge group does not fit the conditions of Equation (1). These bubbles can be either very small or highly deformed and are also considered as ineffective bubble. Neglecting ineffective bubbles when calculating the local flow parameters might cause error because these bubbles still have contribution to IAC. To counteract the error, the ineffective bubbles were kept counted in the program and the IAC was corrected using the average contribution of effective bubbles. The details are discussed in
Section 2.4.
2.4. Deduction of Local Flow Parameters from Electrical Signals
Before calculation of the local flow parameters, the following assumptions should be made: (1) The probe containing the four sensors is very small in size in comparison to the bubble diameter, indicating that all measured bubbles are so-called large bubbles. Small bubbles can be detectable by one or a few sensors of the four-sensor probe, but they are neglected during the signal pre-processing based on the fact that a few rising or falling edges are missing, or no edge is missing but the eight-instant does not fit Equation (1). (2) The magnitudes of interface velocity and its direction remain unchanged when an interface passes by the sensors of probe. This is true as long as the probe size is small compared to the bubbles.
The void fraction equals the ratio of the duration of the sensor contact with air to the total measurement duration. It should be noted that as there are four sensors in the probe, thus the final void fraction can be determined by their average value, as shown by Equation (2).
where
ttotal denotes the total measurement time.
With the eight-instant (edge) of each effective bubble and known size and positions of the four sensors in the probe, the local flow parameters contributed by each effective bubble can be obtained. The measurement principles of other local flow parameters are schematically presented in
Figure 5, which shows the relationships between different vectors.
Local time-averaged IAC was predicted by Ishii [
57] to be related to the interface velocity projected in the normal direction of particular plane:
where
l,
Vl and
nl denote the
lth interface, the vector of interface velocity and the unitary vector normal to the
lth interface, respectively, at a particular measurement point. The short line above
a indicates a time-averaged value.
It is worth noting that, as mentioned in
Section 2.3, since the neglected ineffective bubbles also contribute the IAC, Equation (3) must be corrected by multiplication factor, as shown in Equation (4):
where
Neff and
Nineff are the number of effective and ineffective bubbles, respectively. This correction to IAC has taken the contribution of each ineffective bubbles to be equal to the average contribution of effective bubbles. A bubble is treated as ineffective mainly due to its small size and continually deforming feature. However, because of its higher surface to volume ratio, its contribution to IAC is usually larger than a bubble of large size and regular shape. Therefore, the result from Equation (4) is still expected to be lower than the true IAC.
As the methods proposed by previous researchers who have employed trigonometric functions to determine the direction of interface are not conducive to comprehensible and fast calculation, a distinct and brief vector-based calculation is proposed and performed to obtain the interface direction here in this section. The cross-product of two vectors is also a vector and its direction is perpendicular to the plane formed by the original two vectors, hence the normal vector of one interface can be determined by three velocities measurable by the probe, as shown in
Figure 5c and mathematically by Equation (5):
where
V1,
V2 and
V3 are the three measured velocities of a particular interface, respectively. They, respectively, have the same directions with the three position vectors formed by the probe,
S1,
S2 and
S3, and their magnitudes are obtained by dividing each position vector by the time delay from the probe signals. Mathematically, it can be expressed by:
where
ti (
i = 1, 2, 3) and
t0 denote the time-instant of rising or falling edges of
si and
s0, respectively. (
ti −
t0) are the time-instant delays between
si and
s0. When
ti and
t0 correspond to rising edges,
nl and
Vi are the unitary normal vector and measured velocities of the front interface of a bubble, respectively; and, when
ti and
t0 corresponds to falling edges,
nl and
Vi are the unitary normal vector and measured velocities of the rear interface of a bubble, respectively.
The interfacial measurement theorem proposed by Shen [
36] indicates the projections on the
nl of the interface displacement velocity vector
Vl and the measured velocities
Vi are the same, and the theorem can be expressed as:
from which the velocity component into the normal direction of interface can be easily obtained. In contrast, obtaining the three components of
Vl requires more assumptions or measuring parameters, for instance a further assumption of sphere-shape bubble [
51] or symmetric bubble [
56]. However, the application of these assumptions is only suitable when bubbles encountered in two-phase are not highly distorted or deforming.
A new method to get the whole components of
Vl is proposed in this study by using the known or legitimately assumed velocity direction, i.e., the unit vector of
Vl. Although the shape and size of bubbles keep changing in two-phase flow, the direction of bubbles velocity is usually constant and thus the direction of
Vl often remains constant or constant on an averaged level at one fixed position of the flow field. As a result, by a known or assumed interface velocity direction
nv (
Figure 5), the magnitude of
Vl can be obtained as follows:
The above equation applies well when the two-phase flow is limited internal flow, where the direction of the interface velocity can be regarded as parallel to the channel axis. For arbitrary multi-dimensional two-phase flow, the equation and the resulted method still apply, as long as the local flow direction can be provided by legitimate assumption, flow simulation or prior measurement. For a fixed location, the local time-averaged magnitude of interface velocity can be obtained by averaging through numerous bubbles and denoted by Vl.
As shown by Equation (9), the local time-averaged chord length of a bubble at a fixed position is an averaged product of the
Vl and the averaged time duration of the four signals at high voltage.
where
N denotes the number of bubbles during the measurement duration.
The direction of interface
nl can be shown more explicitly by the angle between
nl and the axis of the flow by Equation (10).
where
naxis is the direction of the channel axis.
2.5. Innovations of the Present Probe Algorithm
In the pioneering literature related to four-sensor probe, the interfacial velocity can only be obtained for the component that is vertical to the interface itself. If the full interfacial velocity vector is intended to be obtained, assumptions must be made. For instance, bubbles formed in the flow field in [
51] were so small that they were assumed to be spherical. In [
53], the authors made an assumption that the interface is very large and it moves only in its normal direction. In [
56], the flattened bubbles were regarded as symmetrical to a center plane. Although these assumptions help ascertain the full components of the interfacial velocity, they only apply in special cases since the interface in practical gas–liquid flow is usually quite complicated.
Considering the fact that the explicit expression of bubble or interfacial velocity for four-sensor probe has not been completely developed, this paper proposes that, if the moving direction of interface can be ascertained prior to probe measurement, then the above assumptions will be unnecessary and the full interfacial velocity can be acquired. Fortunately, the fields of averaged moving directions of the interface, for so many quasi-steady two-phase flows, are actually the flow fields for the two-phase mixture and are easy to make certain through methods of prior measurement, simulation or even legitimate assumptions. These are the primary innovations of the present algorithm for four-sensor probe, as shown in
Section 2.4.
Besides, the signal deduction process is all vector-based, which is different from the complex matrix, trigonometric functions and tensors. Although the basic rules are the same in essence and the results are expected to be same, no matter vector-based or trigonometric function-based algorithms are used, the method proposed in this paper has the merits of easy to read, clear and efficient to modify or improve.
3. Experimental Facilities
To validate the availability and correctness of the probe measurement methods, an experiment was performed to compare the local flow parameters obtained by the four-sensor probe and visual measurement, including void fraction, IAC, velocity, chord length and interface direction. An air–water two-phase flow with bubbles approximately the same size injected vertically up in a transparent tube was adopted. There is no doubt that such flow properties can be easily determined by senor probe or visual techniques with high accuracy. Therefore, it was chosen as a validation case for the proposed four-sensor probe measurement method.
Although the proposed probe and algorithm have not yet been validated, the existing fundamental measurement principles described in
Section 2 can also apply to micro and conventional large systems. For fierce two-phase flow scenarios, corrosive fluid, high pressure system, high flow rate and cases of flow experiencing heat and mass transfer, the measurement methods still apply as long as the probe is fixed strongly and prevented from damage. The experiment in this study was only designed for the purpose of primary method validation, considering that it is convenient to be measured by visual technique and easy to be replicated.
3.1. Bubbly Flow in Vertical Pipe
An air–water two-phase bubbly flow system in a vertical tube was built to get the local flow parameter by both four-sensor probe and visual techniques. The test facility and flow rate were chosen for obtaining a simple and steady two-phase flow pattern. As shown in
Figure 6, a transparent glass tube with the length of 0.5 m and internal diameter of 8 mm was used as the test section, and water was filled up to a height of 0.4 m during the experiment. Air produced by air compressor and regulated by surge tank and control valve was injected from the bottom of the tube. The air flow rate was maintained at 0.1 L/min during the test. As a result, it was found that a steady series of cap bubbles was produced inside the tube.
The top of the transparent tube was open to the atmosphere, and the four-sensor probe was vertically mounted in a one-dimensional sliding module with its tip pointing downside, so the probe could move horizontally to measure parameters across the tube diameter transversely. Only the 4.5 mm in the middle part of the 8-mm-diameter tube was accessible for measurement, resulting in a range from −2.5 to 2 mm with the interval of 0.5 mm.
The DC power supply of the probe was from a 9-V battery to avoid voltage fluctuation characterizing AC power supplier. The probe was connected to a data acquisition card which then transferred the collected data to a laptop. The data collection system was able to collect and transform the analog electrical signal to digital form at frequency of 10 kHz for each of the four sensors. For every transverse position of the probe in the tube, the data collecting persisted for 80 s and thus 800,000 data points were obtained for each sensor.
A high-speed camera was employed to record the images of bubble in a system without a probe. Images of 1262-pixel vertically and 710-pixel horizontally with a frequency of 50 fps were shot for 80 s. Through the image processing and analysis, the local flow parameters of the two-phase flow could be obtained, which is typical for the so-called visual measurement.
3.2. Visual Measurement Techniques
Besides the probe measurement described in
Section 2, the flow parameters can also be obtained by the visual measurement which contains image recording and processing.
A series of continuous captured images is shown in
Figure 7, with time intervals between each of 20 ms. It can be seen that the recorded bubbles are roughly in cap shape, and the space intervals between bubbles are roughly constant. When a bubble reached the location where the four-sensor probe was located, as shown by the red frame of
Figure 7, the image was taken as one of the images constituting the visual measurement.
For each of the chosen images, the subsequent bubble image processing is shown in
Figure 8 and
Figure 9. For the first step of image processing (
Figure 8a as an example), each bubble was cropped out, according to marked edges and converted into binary black and white image (matrix), as shown in
Figure 8b–d, respectively. Five successive chosen bubbles are shown in
Figure 9a, and it can be seen that, although the flow conditions remain unchanged during the test, the shape of cap bubbles change continuously. To obtain the interface direction and bubble chord length, the images of bubble were added up in MATLAB code and divided by the number of bubbles to get the averaged bubble shape. The resulted image (matrix) shown in
Figure 9b stands for the probability of a pixel occupied by gas phase (void fraction). As the number of images
n increases, the difference of the resulted images reduces to minor, and it was found that
n = 100 is enough in this research. By binarization of the last image of
Figure 9b taken with 0.5 as the threshold value, the averaged bubble and its edge are shown in
Figure 9c,d, respectively. Based on
Figure 9d, the time-averaged bubble interface direction θ and bubble chord length
C at different radial location can be read by MATLAB.
Assuming the averaged bubble in
Figure 9c is axisymmetric, the bubble volume can be obtained by integrating the bubble’s cross area at each horizontal layer throughout the bottom to top of the bubble, as shown in Equation (11). The total area of the interface can be obtained by integrating the bubble’s interface area at each horizontal layer throughout the bottom to top of the bubble, as shown in Equation (12):
where
r, a function of vertical location, is the radius of bubble at each horizontal layer.
The time-averaged void fraction across the whole diameter can be obtained through dividing
BV by the average interval volume between two successive bubbles, as shown in Equation (13):
where the two short lines above
Vf indicate time-averaged and space-averaged value for the same time, A is the cross area of the test tube and
L is the average distance between two successive bubbles.
In a similar manner, the time-averaged IAC across the whole diameter can be obtained through dividing
Ba by the average interval volume between two successive bubbles, as shown in Equation (14):
The time-averaged bubble velocity equals the bubble production frequency multiplied by the averaged bubble distance and can be expressed by:
where
N and
ttotal are the total number of bubbles produced and the total measurement time, respectively.
4. Results and Discussion
It is worth noting that the four-sensor probe can only give out local flow parameters of two-phase flow. It is unable to discriminate different two-phase flow regimes of stratified, slug, wavy, etc. Extra correlation research is required to make connections between local flow parameters to global flow regimes. Measuring local flow parameters at multiple locations is the purpose of the four-sensor probe and the validations against visual measurement are hence extended below.
For cap bubble occupying almost the tube diameter from −4 to 4 mm, ten radial locations ranging from −2.5 to 2 mm are measured by the four-sensor probe. The numbers of total detectable bubbles and the numbers and ratios of the effective bubbles in the 80-s measurement duration at each radial location are given in
Table 1. It can be seen that 350 bubbles on average are produced in 80 s, resulting in a bubble frequency of 4.375 per second. The uncertainty of the counted bubble number changes between −5 to 6, indicating that the steady and uniform features of the bubbly flow, which is necessary for this verification test.
As expected, the effective number of bubbles recognized by the MATLAB code is lower than their total number. Meanwhile, both the effective number and the ratio of the effective number to the total number decrease, and this decrease becomes faster toward the ends of the test range. For the test location beyond 2 mm, the ratio can be well below 0.5. This is because, as the probe moves away from tube axis, the bubble interfaces become more inclined and it becomes easy for the bubble to slip away from the probe. It should be noted that the errors of the obtained local flow parameters increase with the decrease of ratio of number of effective bubbles to their total number.
The void fraction from four-sensor probe by Equation (2) and visual measurement by Equation (13) are compared in
Figure 10. Since the void fraction from Equation (13) is an average void fraction across the whole tube diameter, it appears as a horizontal straight line in
Figure 10. In view of the bubble shape shown in
Figure 9c, the bubbly flow should produce a void fraction distribution with a peak value in the tube axis and decrease towards the tube wall. This trend was successfully reflected by the probe measurement, as shown by the black square dots in
Figure 10. Its arithmetic mean value shown by the dashed line agrees well with the visual measurement, with an overestimation of 8.4%.
The IAC from four-sensor probe by Equation (4) and visual measurement by Equation (14) are compared in
Figure 11. Since the IAC from Equation (14) is an average void fraction across the whole tube diameter, it appears as a horizontal straight line in
Figure 11. In view of the bubble shape shown in
Figure 9c, the normal vector of bubble interface changes from vertical near the tube axis to pointing right-upwards near the tube wall, thus the angle between bubble velocity which is parallel to the tube and the normal vector of interface increase and the denominator of Equation (3) decreases. As a result, a larger IAC should be observed near the tube wall, with a minimum value emerging at the tube axis. This trend was successfully captured by the probe measurement, as shown by the black square dots in
Figure 11. Its arithmetic mean value shown by the dashed line agrees well with the visual measurement, with an underestimation of 1.7%.
The bubble velocity from four-sensor probe by Equation (8) and visual measurement by Equation (15) are compared in
Figure 12. Because bubble moves as an entity, it is worth noting that the bubble velocity measured at different radial locations should remain constant when the probe moves from tube axis to tube wall. However, the black square dots in
Figure 12 representing probe measured velocity demonstrate fluctuation feature. This is mainly caused by error and it can be seen the error increases towards the tube wall. Nevertheless, its arithmetic mean value shown by the dashed line agrees well with the visual measurement, with an overestimation of 9.3%.
The chord length from four-sensor probe by Equation (9) and visual measurement are compared in
Figure 13. Both the probe measurement and visual measurement show the same trend with the chord length emerging in the middle with maximum value and decreasing towards both sides. The largest deviation between them is 8.7% at −2.5 mm, and the deviation decreases towards the pipe axis.
Although the interface direction is required to calculate the interface displacement velocity in the interfacial measurement theorem expressed by Equation (7), it is rarely verified against other measurement techniques in the accessible literature. Instead of directly using of the interface normal vector, the interface direction can be represented more conveniently by the angle between the interface normal vector and the tube axis. The angle from four-sensor probe by Equation (10) and visual measurement are compared, as shown in
Figure 14.
Figure 14a,b shows the comparisons at front interface and rear interface, respectively. As can be seen, both measurement methods show very close results with the deviation between them growing distinct towards the tube wall, and the largest errors are 22.4% and 3.1% for the front and rear interfaces, respectively.
The quantitative comparisons of the measured parameters, the deviation of the probe measurement from the visual measurement are shown in
Table 2 and
Table 3. From the above, it is demonstrated that the measurement of bubbly flow by the four-sensor probe can give agreeable flow parameters with visual measurement techniques in aspects of void fraction, IAC, bubble velocity, bubble chord length and interface direction. Thereby, it also proves the correctness of the proposed method.
It is common knowledge that the bubble condensation is a kind of typical enhanced heat and mass transfer method encountered in numerous industrial processes such as steam–air mixture injected into subcooled zone, subcooled flow boiling and direct contact condensation [
27]. Further knowledge of the bubble interface phenomena and the accurate measurement of the local flow parameters at the multi-scale interfaces, such as the void fraction, IAC, bubble velocity, bubble chord length and interface direction, are important parameters to study the process and mechanism of heat and mass transfer in gas–liquid two-phase flow. As previously reported in the literature [
27,
45,
46,
58], during the gas–liquid two-phase heat and mass transfer, the interface structure, void fraction, IAC, bubble equivalent diameter, their velocity, etc. show nonlinear variations, resulting in that they are difficult to be measured quickly and accurately. Although the double-sensor probe with multiple assumptions can also be employed to measure these parameters, it is hard to obtain realistic local data in multi-dimensional two-phase flow. As a result, the method proposed in the present study is expected to promote the solution of this problem.
The interface velocity and its direction obtained using the brief vector-based calculation method proposed in this study are beneficial to further master the heat and mass transfer process at the interface from a macro viewpoint. Meanwhile, the IAC is an important parameter to characterizing the interface transfer phenomenon (heat and mass transfer). Compared with the double-sensor probe, the four-sensor probe is used to measure the IAC to be able to solve the detection error caused by the escape and retreat of bubbles. On this basis, by combining the proposed vector-based signal processing method, a variety of assumptions can be avoided, which will be of great significance to further study the internal relationship between IAC and bubble size, bubble deformation and condensation effect, as well as to modify the calculation model of IAC. This shows that the proposed method can be widely applied in the future research of heat and mass transfer characteristics.
Combined with several groups of four-sensor probes and the new vector-based signal processing method, the variation laws of the void fraction, the bubble size and number of bubbles in the condensation area can be measured accurately, quickly and conveniently, and thereby the phase distribution characteristics in the condensation area can be known. Especially during the air–steam mixture bubble condensation, the phase distribution characteristics, the interface velocity and direction can reveal the mechanism affecting the interface heat and mass transfer. Furthermore, some small bubbles with high non-condensable gas concentration appear at the later stage of the air–steam mixture bubbles condensation [
58]. According to the previous study [
59], when the content of non-condensable air is constant, the volume change rate of bubble increases with the decrease of bubble diameter. This means that the process of small bubble condensation is of great significance for studying the enhancement of condensation heat transfer of air–steam mixture bubbles. Therefore, the proposed method in this study will also be promising for investigating the influence mechanism of non-condensable air at the interface on the tiny steam bubble condensation enhancement.
5. Conclusions
The void fraction, IAC, bubble size, velocity, etc. of two-phase flow have great influences on the heat and mass transfer characteristics, the reaction efficiency and the operation safety of multiple chemical applications. To obtain detailed knowledge of two-phase flow, a miniaturized four-sensor probe was made firstly in this study. Then, a new method based on vector calculation to get the interface direction and a new method to get the bubble velocity magnitude were proposed, by which other local flow parameters can be obtained from the signals produced by four-sensor probe. For the purpose of verification of the probe made and the elaboration algorithm developed, an experimental facility was also built and air–water two-phase bubbly flow was tested. Besides the measurement by probe, the flow parameters were also obtained by video recording and image process techniques. For the first time, the direction of bubble interface was compared with visual image of bubble.
The calculation of interface velocity vector was shown to be realizable using legitimate interface velocity direction. The comparison between the results obtained from probe measurement and visual measurement indicates their good agreement. However, since the number of ineffective bubbles increases moving towards tube wall, the measurement error by probe also increases while the probe moves away from tube axis. The averaged values across the tube are over predicted by 8.4%, under predicted by 1.7% and over predicted by 9.3% with probe measurement for void fraction, IAC and bubble velocity, respectively, in comparison to the visual measurement counterpart. The chord length and angle between tube axis and normal to the interface show great consistency with visual results, with maximum deviations of 8.7% and 22.4%, respectively.
After more validation tests against multiple kinds of two-phase flow parameters, it can be concluded that the methods proposed in this study are promising in the characteristics and mechanism studies of the gas–liquid heat and mass transfer, the direct measurement of gas–liquid two-phase flow and providing significant database for the improvement of two-phase flow models.