Understanding Time-Evolving Citation Dynamics across Fields of Sciences
Abstract
:1. Introduction
2. Related Work
3. Background
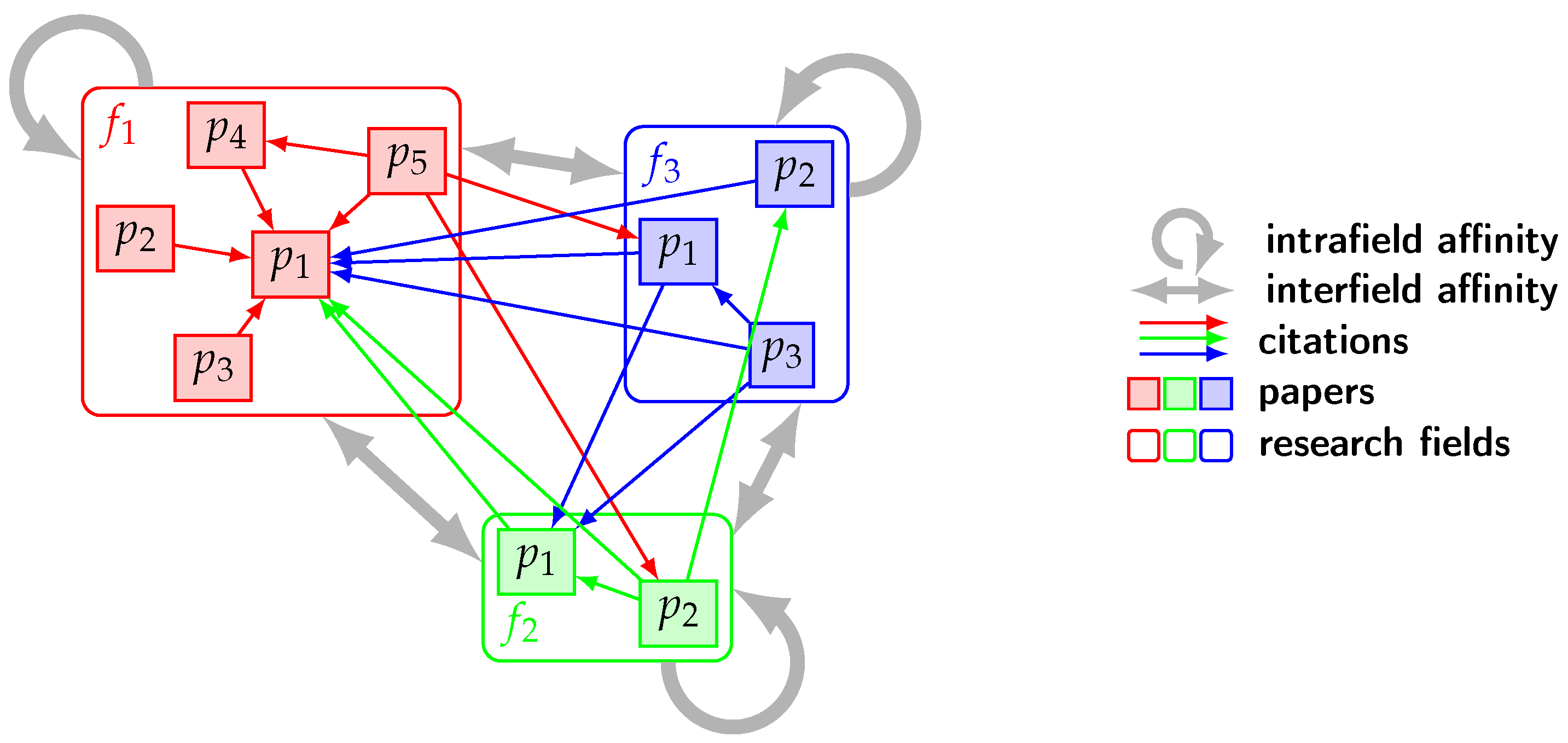
3.1. Interdisciplinary Citation Flow
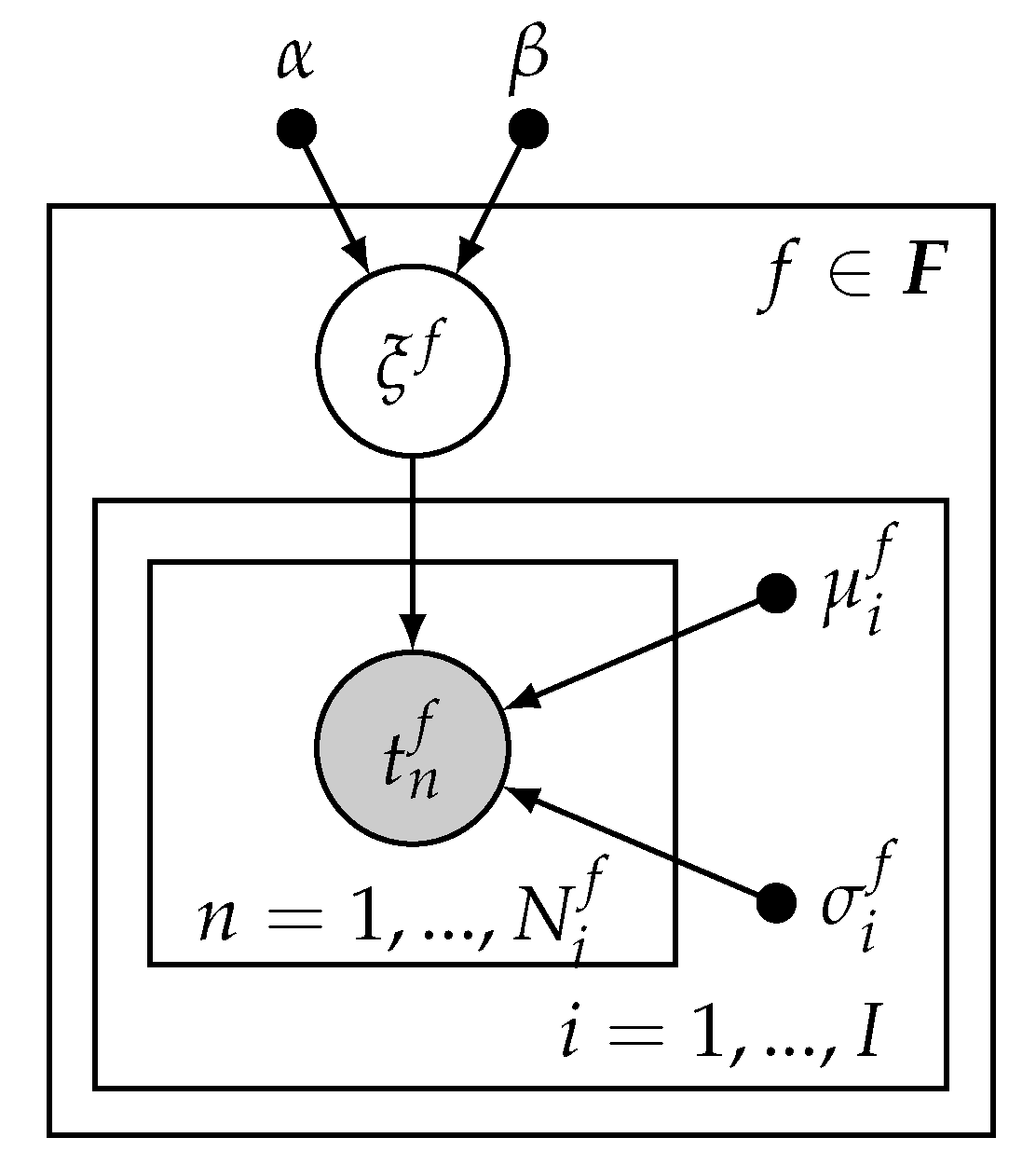
3.2. Affinity Poisson Process
4. Popularity Prediction
4.1. Data Statistics
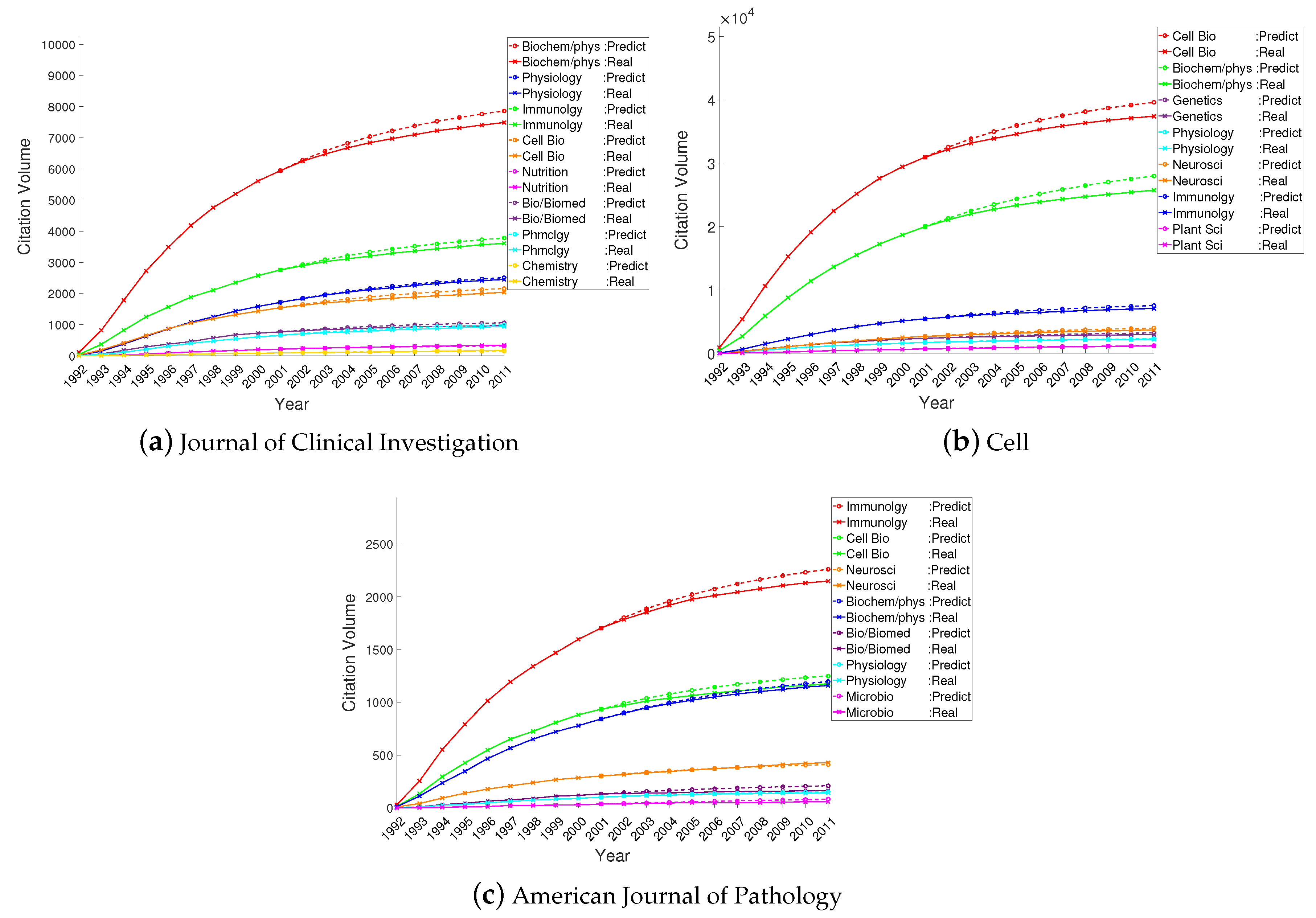
4.2. Prediction of Interdisciplinary Citation Volumes
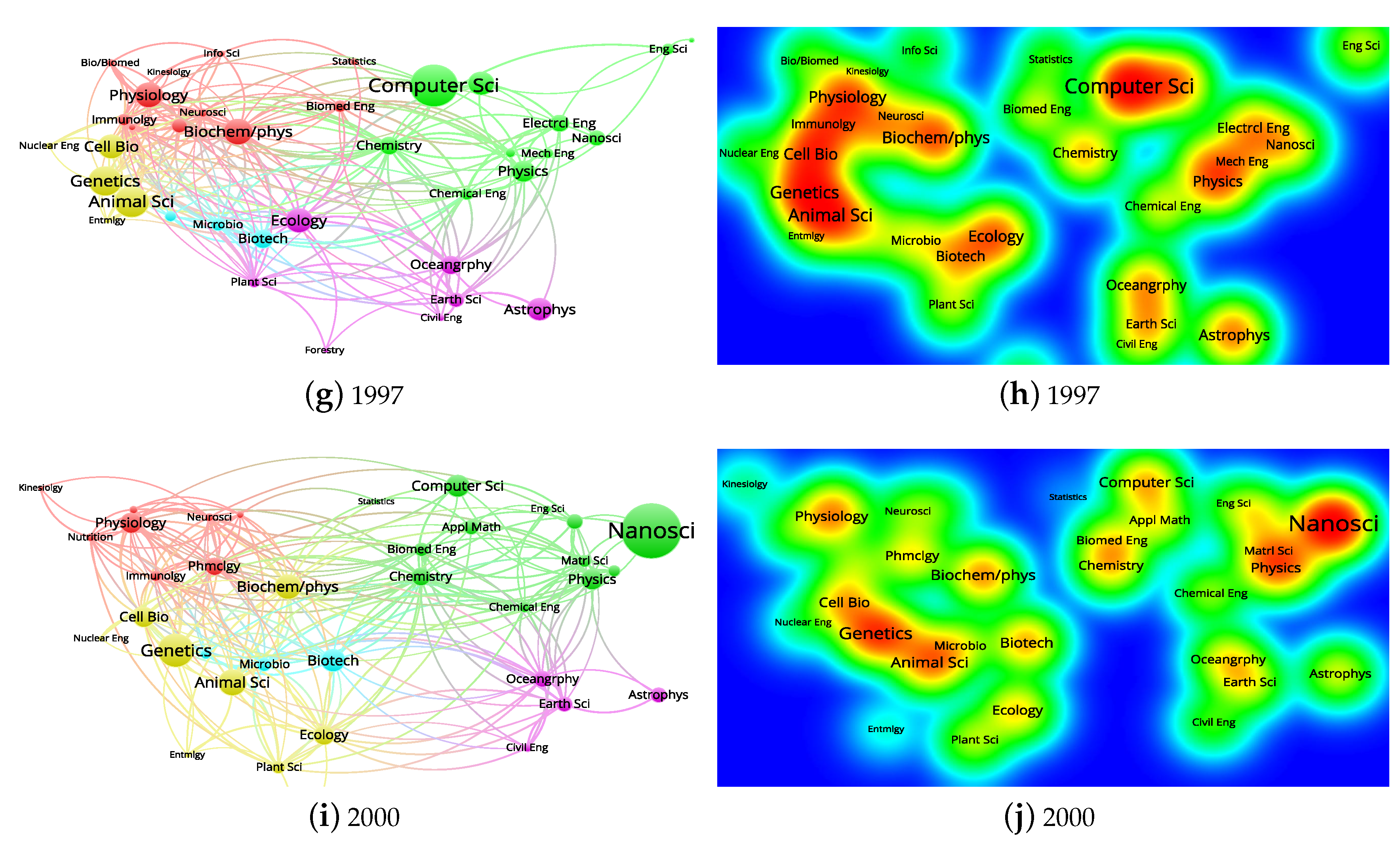
5. Affinity Map
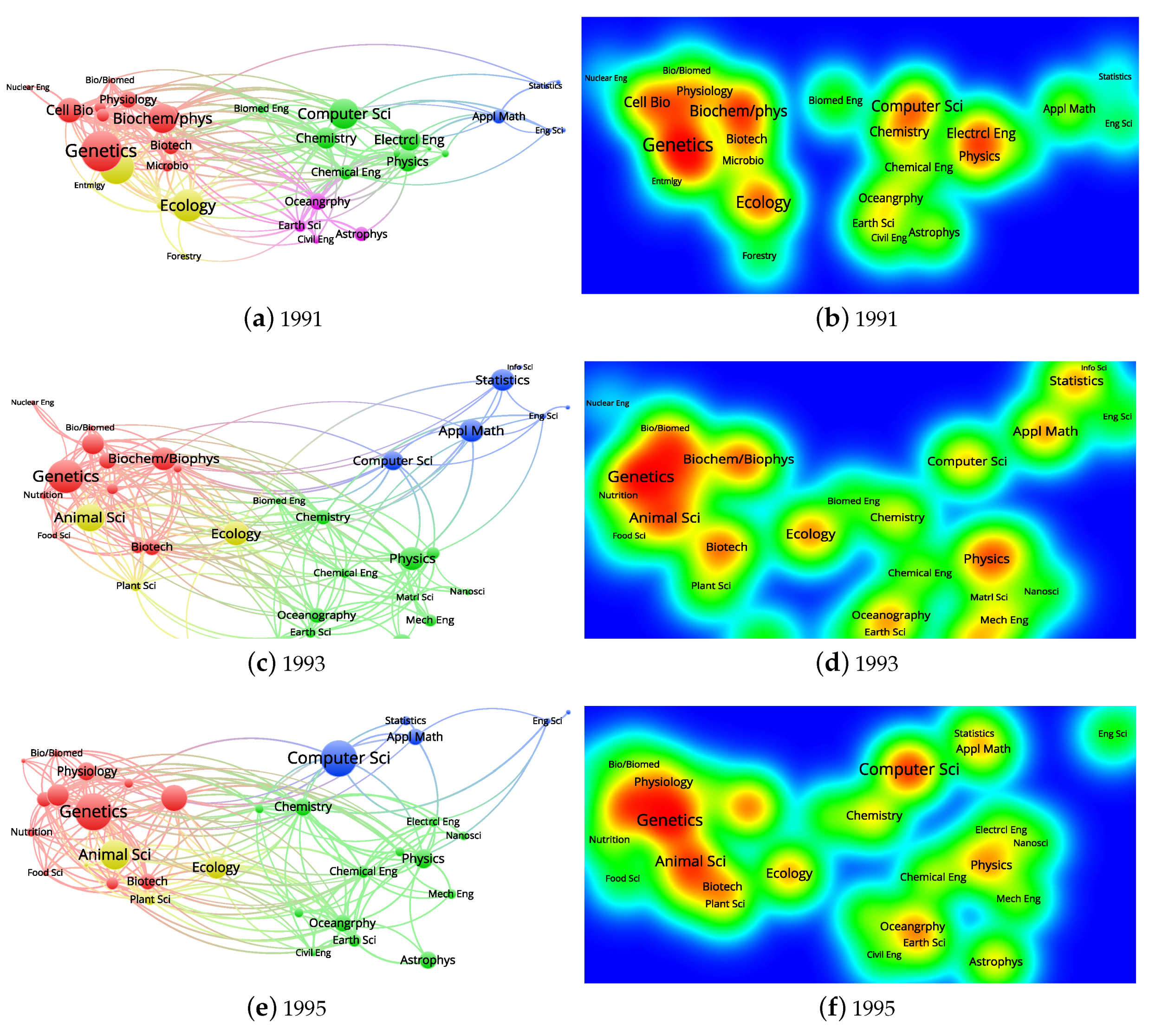
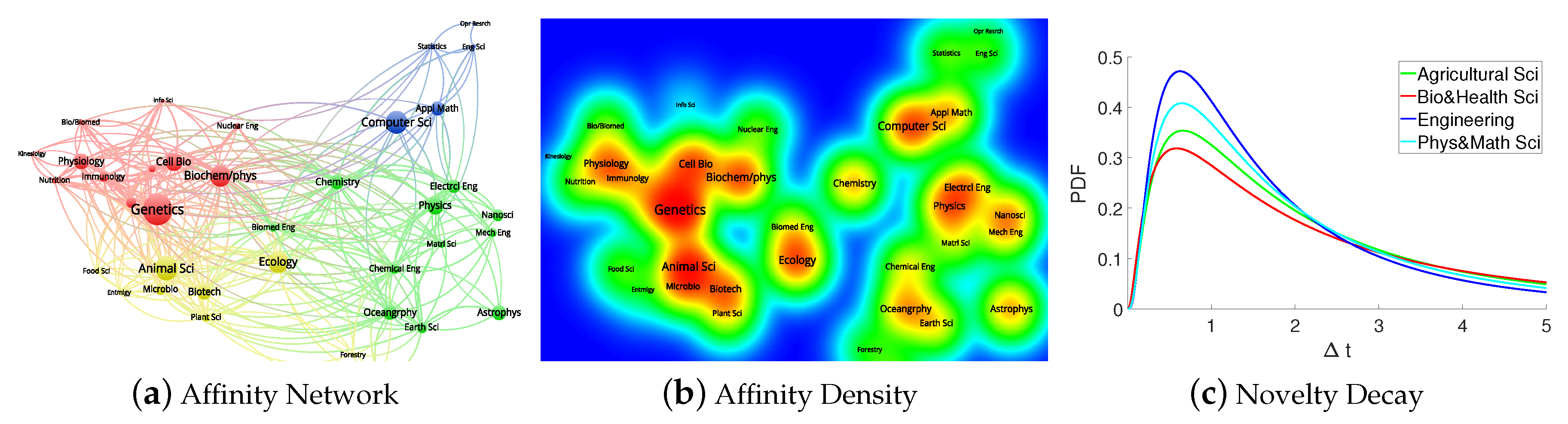
5.1. Affinity Network
5.2. Affinity Density
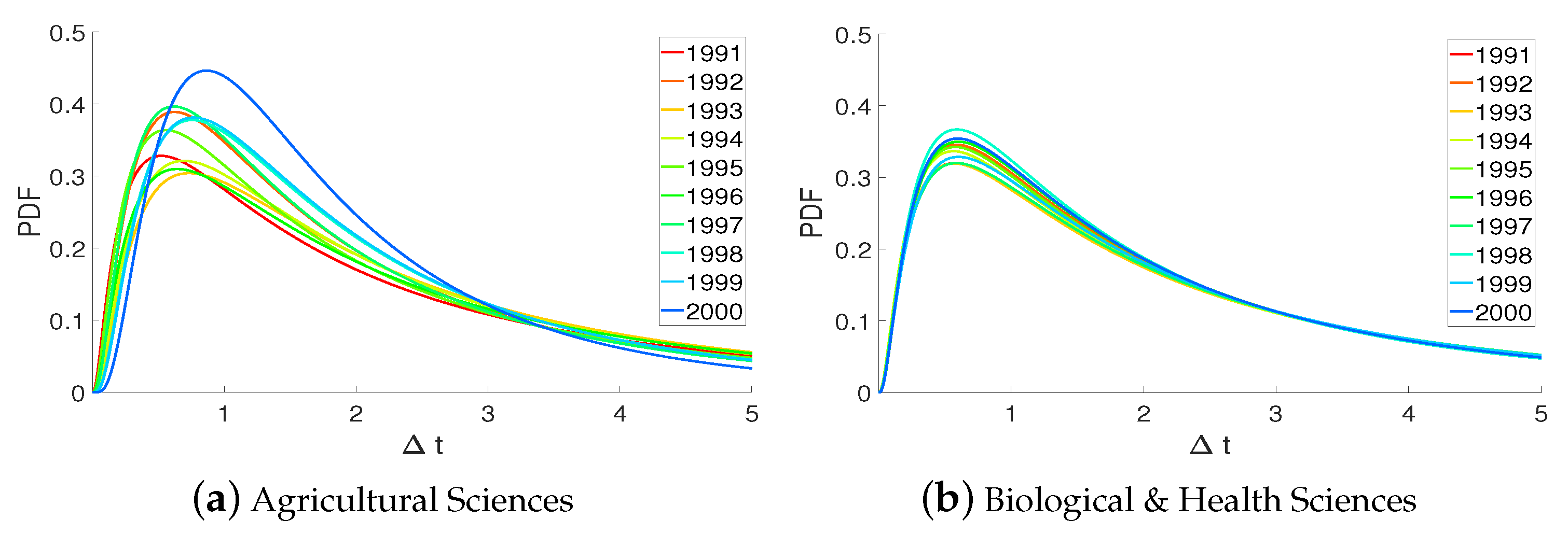
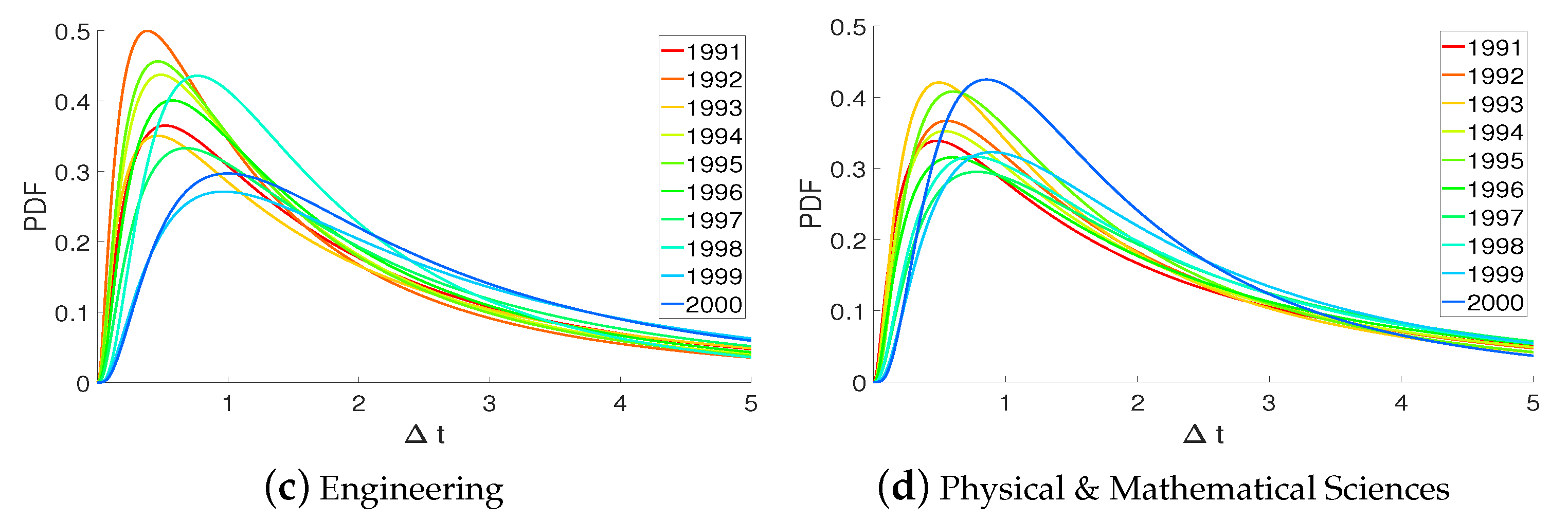
5.3. Novelty Decay
5.4. Holistic View
6. Conclusions
- Affinity between subfields is time-evolving, and overall NRC subfields become more interdisciplinary across the four NRC fields over time; affinity between the BH subfields becomes more distant but closer to other NRC field over time, while affinity between the PM subfields is locally clustered earlier but becomes closer to other fields over time.
- In terms of novelty decay, the AS and PM fields exhibit slower aging for earlier publications, while the EG field shows the opposite, i.e., faster decay of earlier publications. The BH field shows a consistent aging for different year publications and the slowest time decay among the four NRC fields.
- Overall, 37 NRC subfields are not only locally clustered but also globally interrelated with each other beyond disciplines and NRC fields. Highly interdisciplinary subfields for each NRC field are: biochemistry/biophysics, genetics, and ecology in the BH field, animal science in the AS field, physics, chemistry, computer science, and applied mathematics in the PM field, electrical engineering, oceanography, and nanoscience in the EG field. In terms of novelty decay, the EG, PM, AS, and BH fields are aging in that order.
Funding
Conflicts of Interest
Abbreviations
| APP | Affinity Poisson Process |
| RPP | Reinforcement Poisson Process |
| STEM | Science, technology, engineering, and mathematics |
| NRC | National Research Council |
| AS | Agricultural Sciences |
| BH | Biological and Health Sciences |
| EG | Engineering |
| PM | Physical and Mathematical Sciences |
Appendix A. Lognormal Distributions
Appendix A.1. Integral of Lognormal Distributions
Appendix A.2. Logarithm of Lognormal Distributions
Appendix B. Bayesian Inference
Appendix C. Learning Parameters
Appendix D. Partial Derivatives of Log Marginal Likelihood
Appendix D.1. Partial Derivatives with Respect to Hyperparameters
Appendix D.2. Partial Derivatives with Respect to Aging Parameters
Appendix E. Experimental Results
| Cited NRC Subfield | Citing NRC Subfield | Example Common Keyword |
|---|---|---|
| Genetics & Genomics | Biochem/Biophysics & Structural Biology | acid, genome, amplification, ycleotide sequence, escherichia coli, enzyme, transcription factor, etc. |
| Ecology & Evolutionary Biology | growth, selection, conservation, temperature, evolution, resistance, accumulation, etc. | |
| Cell & Developmental Biology | cell line, phenotype, embryo, p53, transformation, receptor, tumor, differentiation, induction, etc. | |
| Computer Sciences | Physics | equation, simulation, flow, approximation, noise, generation, energy, interface, transition, etc. |
| Biochem/Biophysics & Structural Biology | cell, program, domain, sequence, resolution, stability, plasma, ligand, conformation, etc. | |
| Neuroscience & Neurobiology | information, neuron, network, sequence, recognition, movement, sensitivity, protein, etc. | |
| Nanoscience & Nanotechnology | Chemistry | polymer, spectroscopy, crystal, spectra, morphology, protein, binding, oxygen, gold, etc. |
| Materials Science & Engineering | molecular beam epitaxy, atomic force microscopy, chemical vapor deposition, photoluminescence, etc. | |
| Electrical & Computer Engineering | fabrication, interface, array, sensor, biosensor, electrode, diode, wavelength, gaas, etc. |
Appendix F. Metadata
| Subject Area (WOS) | NRC Subfield | NRC Field |
|---|---|---|
| Agricult, Dairy & Animal Sci | Animal Sciences | Agricultural Sciences |
| Fisheries | ||
| Reproductive Biology | ||
| Zoology | ||
| Entomology | Entomology | |
| Food Science & Technology | Food Science | |
| Forestry | Forestry & Forest Sciences | |
| Nutrition & Dietetics | Nutrition | |
| Agronomy | Plant Sciences | |
| Horticulture | ||
| Plant Sciences | ||
| Biochem. Research Methods | Biochemistry, Biophysics, and Structural Biology | Biological and Health Sciences |
| Biochem. & Molecular Bio. | ||
| Biology | ||
| Biophysics | ||
| Med., Research & Exprmtl | ||
| Cardiac & Cardiovasclr Sys. | Bio/Integrated Biomed Sci | |
| Biotech. & Appl. Microbio. | Biotechnology | |
| Anatomy & Morphology | Cell and Developmental Biology | |
| Cell Biology | ||
| Developmental Biology | ||
| Oncology | ||
| Biodiversity Conservation | Ecology and Evolutionary Biology | |
| Ecology | ||
| Environmental Sciences | ||
| Evolutionary Biology | ||
| Marine & Freshwater Biology | ||
| Genetics & Heredity | Genetics and Genomics | |
| Immunology | Immunology and Infectious Disease | |
| Infectious Diseases | ||
| Pathology | ||
| Veterinary Sciences | ||
| Sport Sciences | Kinesiology | |
| Microbiology | Microbiology | |
| Virology | ||
| Neurosciences | Neuroscience and Neurobiology | |
| Pharmacology & Pharmacy | Pharmacology, Toxicology and Environmental Health | |
| Toxicology | ||
| Endocrinology & Metabolism | Physiology | |
| Physiology |
| Subject Area (WOS) | NRC Subfield | NRC Field |
|---|---|---|
| Agricultural Engineering | Biomedical Engineering and Bioengineering | Engineering |
| Engineering, Biomedical | ||
| Engineering, Chemical | Chemical Engineering | |
| Engineering, Environmental | ||
| Engineering, Petroleum | ||
| Imaging Sci & Photographic Technology | ||
| Constr. & Building Tech. | Civil and Environmental Engineering | |
| Engineering, Civil | ||
| Engineering, Geological | ||
| Transportation Sci & Tech | ||
| Eng, Electrical & Electronic | Electrical& Computer Eng | |
| Automation & Control Systems | Eng. Science & Materials | |
| Medical Informatics | Information Science | |
| Materials Science, Biomaterials | Materials Science and Engineering | |
| Materials Science, Ceramics | ||
| Materials Science, Characterization, Testing | ||
| Matrls Sci, Coatings & Films | ||
| Materials Sci, Composites | ||
| Matrls Sci, Multidisciplinary | ||
| Matrls Sc, Paper & Wood | ||
| Materials Science, Textiles | ||
| Metallurgy & Metallugcl Eng | ||
| Engineering, Mechanical | Mechanical Engineering | |
| Engineering, Ocean | ||
| Nanosci & Nanotechnology | Nanosci & Nanotech | |
| Nuclear Sci & Technology | Nuclear Engineering | |
| Engineering, Industrial | Operations Research, Systems Engineering and Industrial Engineering | |
| Engineering, Manufacturing | ||
| Opr Research & Mgmt Sci |
| Subject Area (WOS) | NRC Subfield | NRC Field |
|---|---|---|
| Mathematics | Applied Mathematics | Physical and Mathematical Sciences |
| Mathematics, Applied | ||
| Math, Intrdisciplnry Applied | ||
| Astronomy & Astrophysics | Astrophysics and Astronomy | |
| Chemistry, Analytical | Chemistry | |
| Chemistry, Applied | ||
| Chem, Inorganic & Nuclear | ||
| Chemistry, Medicinal | ||
| Chemistry, Multidisciplinary | ||
| Chemistry, Organic | ||
| Chemistry, Physical | ||
| Electrochemistry | ||
| Polymer Science | ||
| Computer Science, AI | Computer Sciences | |
| Computer Sci, Cybernetics | ||
| Computer Sci, HW & Arch. | ||
| Computer Sci, Info. Systems | ||
| Computer Sci, Interdisc Appl | ||
| Computer Sci, SW Eng | ||
| Computer Sci, Thry & Mthds | ||
| Geochemistry & Geophysics | Earth Sciences | |
| Geology | ||
| Geosci, Multidisciplinary | ||
| Soil Science | ||
| Limnology | Oceanography, Atmospheric Sciences and Meteorology | |
| Meteorlgy & Atmospheric Sci | ||
| Oceanography | ||
| Water Resources | ||
| Acoustics | Physics | |
| Optics | ||
| Physics, Applied | ||
| Phys, Atomic, Molclr&Chem | ||
| Physics, Condensed Matter | ||
| Physics, Fluids & Plasmas | ||
| Physics, Mathematical | ||
| Physics, Multidisciplinary | ||
| Physics, Nuclear | ||
| Physics, Particles & Fields | ||
| Statistics & Probability | Statistics and Probability |
References
- Kim, M.; Paini, D.; Jurdak, R. Real-world diffusion dynamics based on point process approaches: A review. Artif. Intell. Rev. 2020, 53, 321–350. [Google Scholar]
- Farajtabar, M.; Wang, Y.; Gomez-Rodriguez, M.; Li, S.; Zha, H.; Song, L. Coevolve: A joint point process model for information diffusion and network co-evolution. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 1954–1962. [Google Scholar]
- Gao, S.; Ma, J.; Chen, Z. Modeling and Predicting Retweeting Dynamics on Microblogging Platforms. In Proceedings of the ACM International Conference on Web Search and Data Mining, Florence, Italy, 18–22 May 2015; pp. 107–116. [Google Scholar]
- Zhao, Q.; Erdogdu, M.A.; He, H.Y.; Rajaraman, A.; Leskovec, J. SEISMIC: A Self-Exciting Point Process Model for Predicting Tweet Popularity. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Melbourne, Australia, 19–23 October 2015; pp. 1513–1522. [Google Scholar]
- Kim, M.; Xie, L.; Christen, P. Event diffusion patterns in social media. In Proceedings of the International Conference on Weblogs and Social Media, Dublin, Ireland, 4–7 June 2012; pp. 178–185. [Google Scholar]
- Shen, H.; Wang, D.; Song, C.; Barabási, A.L. Modeling and Predicting Popularity Dynamics via Reinforced Poisson Processes. In Proceedings of the AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; pp. 291–297. [Google Scholar]
- Wang, D.; Song, C.; Barabási, A.L. Quantifying long-term scientific impact. Science 2013, 342, 127–132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, M.; Paini, D.; Jurdak, R. Modeling stochastic processes in disease spread across a heterogeneous social system. Proc. Natl. Acad. Sci. USA 2019, 116, 401–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, M.; McFarland, D.A.; Leskovec, J. Modeling affinity based popularity dynamics. In Proceedings of the ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 477–486. [Google Scholar]
- Web of Science. Available online: https://www.webofscience.com/.
- Ostriker, J.P.; Kuh, C.V.; Voytuk, J.A. A Data-Based Assessment of Research-Doctorate Programs in the United States; National Academies Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Shen, H.W.; Barabási, A.L. Collective credit allocation in science. Proc. Natl. Acad. Sci. USA 2014, 111, 12325–12330. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Redner, S. Citation statistics from 110 years of physical review. Phys. Today 2005, 58, 49–54. [Google Scholar] [CrossRef] [Green Version]
- Sinatra, R.; Deville, P.; Szell, M.; Wang, D.; Barabási, A.L. A century of physics. Nat. Phys. 2015, 11, 791–796. [Google Scholar] [CrossRef]
- Wuchty, S.; Jones, B.F.; Uzzi, B. The increasing dominance of teams in production of knowledge. Science 2007, 316, 1036–1039. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milojević, S. Modes of collaboration in modern science: Beyond power laws and preferential attachment. J. Assoc. Inf. Sci. Technol. 2010, 61, 1410–1423. [Google Scholar] [CrossRef] [Green Version]
- Powell, W.W.; White, D.R.; Koput, K.W.; Owen-Smith, J. Network dynamics and field evolution: The growth of interorganizational collaboration in the life sciences. Am. J. Sociol. 2005, 110, 1132–1205. [Google Scholar] [CrossRef] [Green Version]
- Jones, B.F.; Wuchty, S.; Uzzi, B. Multi-university research teams: Shifting impact, geography, and stratification in science. Science 2008, 322, 1259–1262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ver Steeg, G.; Galstyan, A. Information transfer in social media. In Proceedings of the International Conference on World Wide Web, Lyon, France, 16–20 April 2012; pp. 509–518. [Google Scholar]
- Kim, M.; Newth, D.; Christen, P. Macro-level information transfer in social media: Reflections of crowd phenomena. Neurocomputing 2016, 172, 84–99. [Google Scholar] [CrossRef]
- Kim, M.; Newth, D.; Christen, P. Modeling dynamics of diffusion across heterogeneous social networks: News diffusion in social media. Entropy 2013, 15, 4215–4242. [Google Scholar] [CrossRef] [Green Version]
- Myers, S.A.; Zhu, C.; Leskovec, J. Information diffusion and external influence in networks. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 33–41. [Google Scholar]
- Kim, M.; Newth, D.; Christen, P. Uncovering diffusion in academic publications using model-driven and model-free approaches. In Proceedings of the 2014 IEEE Fourth International Conference on Big Data and Cloud Computing, Sydney, Australia, 3–5 December 2014; pp. 564–571. [Google Scholar]
- Wu, F.; Huberman, B.A. Novelty and collective attention. Proc. Natl. Acad. Sci. USA 2007, 104, 17599–17601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, M.; Newth, D.; Christen, P. Modeling Dynamics of Meta-Populations with a Probabilistic Approach: Global Diffusion in Social Media. In Proceedings of the International Conference on Information and Knowledge Management, San Francisco, CA, USA, 27 October–1 November 2013; pp. 489–498. [Google Scholar]
- Rodriguez, M.G.; Leskovec, J.; Schölkopf, B. Modeling Information Propagation with Survival Theory. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 666–674. [Google Scholar]
- Kouritzin, M.A.; Zeng, Y. Bayesian model selection via filtering for a class of micro-movement models of asset price. Int. J. Theor. Appl. Financ. 2005, 8, 97–121. [Google Scholar] [CrossRef]
- Kouritzin, M.A.; Zeng, Y. Weak convergence for a type of conditional expectation: Application to the inference for a class of asset price models. Nonlinear Anal. Methods Appl. 2005, 60, 231–239. [Google Scholar]
- Brémaud, P. Point Processes and Queues: Martingale Dynamics; Springer: New York, NY, USA, 1981; Volume 50. [Google Scholar]
- Iwata, T.; Shah, A.; Ghahramani, Z. Discovering latent influence in online social activities via shared cascade poisson processes. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; pp. 266–274. [Google Scholar]
- Van Noorden, R. Interdisciplinary research by the numbers. Nature 2015, 525, 306–307. [Google Scholar] [CrossRef] [PubMed]
- Cinlar, E. Introduction to Stochastic Processes; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Eck, N.J.v.; Waltman, L. How to normalize cooccurrence data? An analysis of some well-known similarity measures. J. Assoc. Inf. Sci. Technol. 2009, 60, 1635–1651. [Google Scholar] [CrossRef] [Green Version]



| Sym. | Descriptions |
|---|---|
| set of all research fields in science | |
| research field of the cited paper, (usually ommited for brevity) | |
| f | research field of the citing paper, |
| I | total number of papers in the cited field |
| i | i-th paper in the cited field, |
| citation count of paper i, received from the citing field f | |
| n-th citation timestamp of paper i, received from the citing field f, | |
| citation timestamps of paper i, received from f such that | |
| citation timestamps of the cited field, received from f such that | |
| all citation timestamps of the cited field such that | |
| citation intensity of paper i at time t for the citations received from the citing field f | |
| citation intensity of paper i at time t such that | |
| affinity of the citing field f towards the cited field | |
| citation count of paper i, received from the citing field f up to time t | |
| citation count of paper i in the cited field up to time t such that | |
| aging effect of paper i in the citing field f after time t since its publication | |
| lognormal distribution parameters such that |
| NRC Field | #Subfield | #Subject | #Journal | #Paper | #Citation |
|---|---|---|---|---|---|
| Agricultural Sci | 6 | 11 | 104 | 128,685 | 518,434 |
| Bio & Health Sci | 12 | 29 | 362 | 832,805 | 4,201,683 |
| Engineering | 11 | 29 | 145 | 228,397 | 943,834 |
| Phys & Math Sci | 8 | 39 | 267 | 537,658 | 1,914,953 |
| Total | 37 | 108 | 878 | 1,727,545 | 7,578,904 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M. Understanding Time-Evolving Citation Dynamics across Fields of Sciences. Appl. Sci. 2020, 10, 5846. https://doi.org/10.3390/app10175846
Kim M. Understanding Time-Evolving Citation Dynamics across Fields of Sciences. Applied Sciences. 2020; 10(17):5846. https://doi.org/10.3390/app10175846
Chicago/Turabian StyleKim, Minkyoung. 2020. "Understanding Time-Evolving Citation Dynamics across Fields of Sciences" Applied Sciences 10, no. 17: 5846. https://doi.org/10.3390/app10175846
APA StyleKim, M. (2020). Understanding Time-Evolving Citation Dynamics across Fields of Sciences. Applied Sciences, 10(17), 5846. https://doi.org/10.3390/app10175846





