Energy Commitment for a Power System Supplied by Multiple Energy Carriers System using Following Optimization Algorithm

Abstract

In today’s world, the development and continuation of life require energy. Supplying this energy demand requires careful and scientific planning of the energy provided by a variety of products, such as oil, gas, coal, electricity, etc. A new study on the operation of energy carriers called Energy Commitment (EC) is proposed. The purpose of the EC is to set a pattern for the use of energy carriers to supply energy demand, considering technical and economic constraints. EC is a constrained optimization problem that can be solved by using optimization methods. This study suggests the Following Optimization Algorithm (FOA) to solve the EC problem to achieve technical and economic benefits. Minimizing energy supply costs for the total study period is considered as an objective function. The FOA simulates social relationships among the community members who try to improve their community by following each other. Simulation is carried out on a 10-unit energy system supplied by various types of energy carriers that includes transportation, agriculture, industrial, residential, commercial, and public sectors. The results show that the optimal energy supply for a grid with 0.15447 Millions of Barrels of Oil Equivalent (MBOE) of energy demand costs 9.0922 millions dollar for a 24-h study period. However, if the energy supply is not optimal, the costs of operating energy carriers will increase and move away from the optimal economic situation. The economic distribution of electrical demand between 10 power plants and the amount of production units per hour of the study period is determined. The EC outputs are presented, which include an appropriate pattern of energy carrier utilization, energy demand supply costs, appropriate combination of units, and power plant production. The behavior and process of achieving the answer in the convergence curve for the implementation of FOA on EC indicates the exploration and exploitation capacity of FOA. Based on the simulated results, EC provides more information than Unit Commitment (UC) and analyzes the network more efficiently and deeply.

1. Introduction

An energy carrier is a substance—for example, fuel, or sometimes a phenomenon (energy system)—that contains energy, which can be later converted to other forms, such as mechanical work or heat, or operate chemical or physical processes. Today’s societies use several energy carriers in the industry, service, residential, and transportation sectors. Among the various energy carriers, oil is of paramount importance, since its price has a considerable effect on economic growth. Besides, neither oil nor any of the fossil fuels such as coal and natural gas have endless sources. The growing demand on the one hand and declining fossil resources, on the other hand, necessitate full consideration for the operation of energy. Therefore, the operation of energy carriers to supply the energy demand, called the Energy Commitment (EC) problem, is studied, in particular from the perspective of an electric power system.

Unit Commitment (UC) is a significant study carried out in the operation of the electricity grid. An essential criterion in UC is the supply of power demand with the least fuel cost and optimal combination of different power plants [1]. It forms the basis of energy carrier commitment.

The UC issue has been of great interest to researchers as evident from the following representative literature. In [2], uncertainty in the production of virtual power plants is investigated, and transmission line constraints in solving the UC problem for large-scale networks are studied in [3]. The UC problem in the presence of Flexible AC Transmission System (FACTS) devices and energy storage devices is investigated in [4]. To solve the UC problem, a novel annual analysis is proposed for the thermal power generator and pumped storages under a massive introduction of renewable energy sources [5]. Ref. [6], the authors proposed the implementation of the UC in the presence of energy storage systems and its optimal size for a region in northern Chile. Solving the UC problem in the presence of wind, nuclear, and thermal power plants has been studied by considering the security constraints of the transmission line and the influence of wind power uncertainty on the spinning reserve capacity of the system in China [7]. A new method based on the Particle Swarm Optimization (PSO) algorithm, [8], and the solution of the UC problem using genetic algorithm was proposed in [9]. Other algorithms, such as the Gray Wolf Optimizer (GWO) [10], Whale Optimization Algorithm (WOA) [11], simulated annealing [12], and shuffled frog-leaping algorithm [13] have also been suggested to find the solution to the UC problem.

In recent years, Multi-Carrier Energy (MCE) systems that improve energy efficiency and reliability have received much attention. Each of the gas, electrical, and heat networks consists of energy sources, several loads, and a set of transmission lines or pipes that supply energy demand through the resources of the system. The flow value of the supply lines of each of these grids can be calculated mathematically by the quantities of those lines [14].

A mathematical model for intelligent loads participation in load response programs in an MCE system management is proposed, [15]. In this model, the optimal operation is performed using an energy storage system. The effects of load response programs on the efficiency and operating costs of MCE systems in the presence and absence of wind energy and energy storage are evaluated and analyzed in [16]. The teaching and learning-based optimization algorithm is applied to optimize the operation of MCE systems in [17].

In general, an Energy Hub (EH) is an interface between the production, consumption, and transmission of different forms of energy. EHs are connected to electric power grids and perform energy conversion operations from one state to another or improve the quality of energy delivered to the load. Thus, the inputs of an EH consist of different forms of energy, and its outputs are system loads. The purpose of the EH is to provide the required energy for load demand through its input and internal equipment [18].

The concept of EH has been introduced in various residential, commercial, and other applications. In this regard, economy and energy savings in a hospital have been studied [19], and linear integer programming is presented to improve the performance of an electric micro-grid in the presence of cooling, thermal, and electrical loads [20]. The optimal operation of a residential house as an EH using the PSO algorithm is proposed in [21]. The optimal operation of an EH has been studied considering the energy storage systems in [22]. The EH has also been proposed for economic and reliability purposes in [23] with the aim of proper selection of the internal EH equipment. Furthermore, the energy management of smart hubs is discussed in [24].

As mentioned in the previous subsections, in UC, the goal is to determine the appropriate pattern of power plant production to supply the electrical demand. In an MCE system, gas, electrical, and heat networks are examined, and the purpose of the EH is to supply the required energy demand through its input and internal equipment. Although very valuable studies have been conducted by researchers in the operation of power systems, the operation of an integrated grid called the energy grid and determining the appropriate pattern of use of energy carriers to supply energy demand in this network has been less studied. Therefore, a new study named the Energy Commitment (EC) problem that determines a suitable pattern of energy carriers utilization to supply the energy demand in particular from the perspective of an electric power system is proposed. In the proposed EC study, more details of the network such as the simulation of oil refining and the impact of the imports and exports of energy carriers are considered.

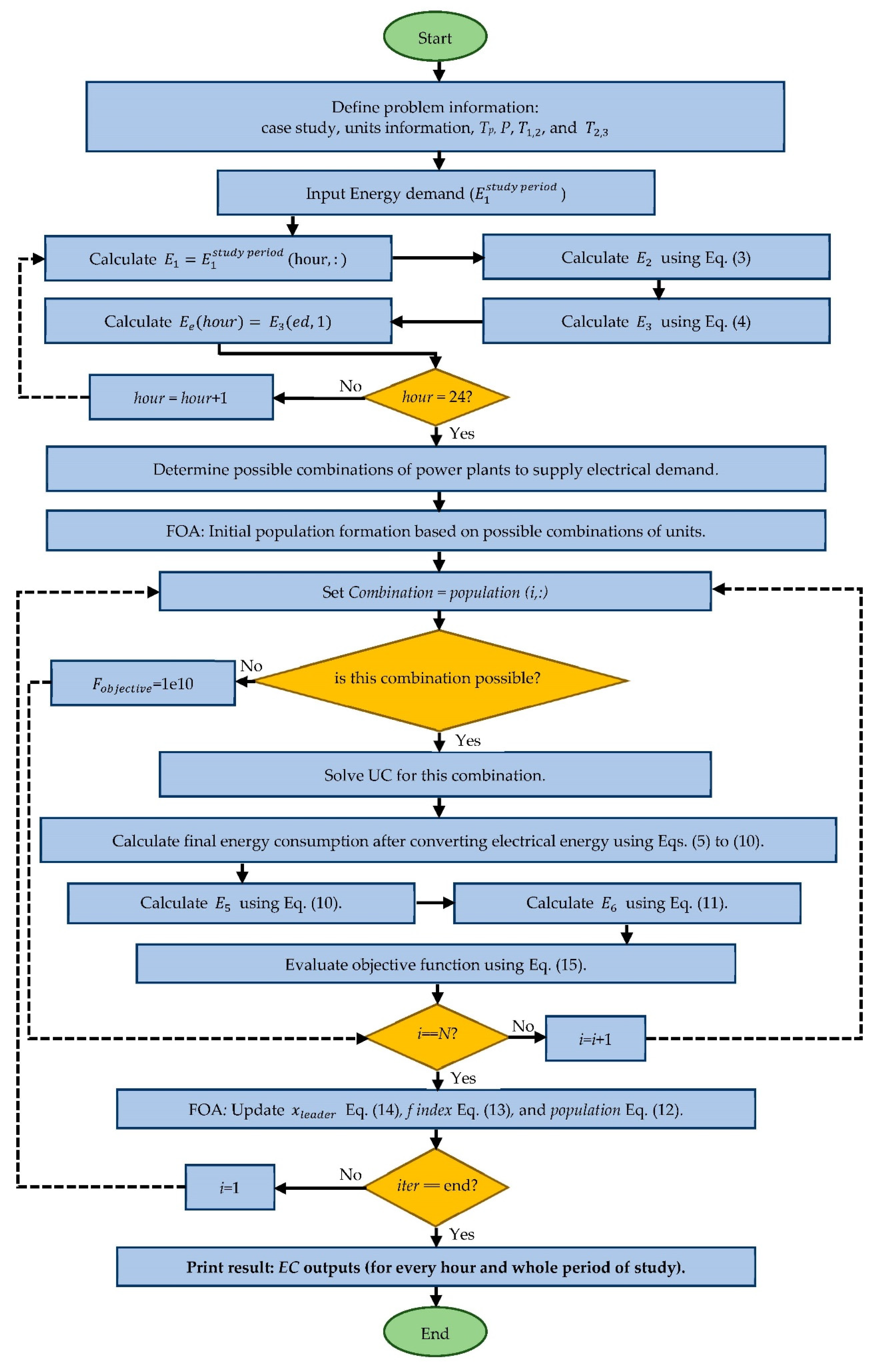
The EC problem in a multi-carrier energy system is proposed to be studied using the Following Optimization Algorithm (FOA). Therefore, the optimal operation of energy carriers can be obtained. The proposed study aims to realize the following:

• Mathematical modeling and formulation for an EC problem.
• Objective function is considered as minimizing energy supply costs for the total study period.
• The FOA is used to solve the EC problem, which is a constrained optimization problem.
• Study the technical aspect of supply energy demand in various sections (with different types of energy carriers).
• Applying the proposed study to a standard energy grid that includes different sectors of energy consumption (transportation, agriculture, industrial, residential, commercial, and public).
• Studying the simulation of refinery and oil-refining process.
• Studying the impact of import and export of energy carriers on EC.
• Determining the appropriate pattern for the use of energy carriers to supply energy demand, considering technical and economic constraints.
• Increasing the awareness of the importance of an EC study to enhance the operation of energy systems.

The introduction and background of the topic are presented in Section 1. The problem definition and problem formulation are described, respectively, in Section 2 and Section 3. Application of the proposed study is investigated and discussed in Section 4, while the conclusions are presented in Section 5.

2. Problem Definition

2.1. Energy Commitment

Researchers have provided valuable studies on energy and energy management [25,26,27,28,29]. A significant issue in energy studies is the operation of energy carriers. The primary energy carriers are those that are directly extracted from natural sources such as crude oil, hard coal, and natural gas. All carriers of energy, not primary but produced from primary energy, are called secondary energy carriers [30].

Table 1. Terminology for Energy Commodities [30].

	Primary		Secondary
		Combustible
Non-renewable	nuclear	Coals Crude oil Liquid Gas Natural gas Oil shale	Petroleum products Manufactured solid fuels Gases	Heat and electricity
Renewable	heat and non-thermal electricity	Biofuels	Any fuels derived from renewables

shows an overview of renewable versus non-renewable energy and primary versus secondary energy.

Researchers over time have conducted wide research into the operation of power systems and power supply to consumers. In the unit commitment study, the on or off status of the units and the optimal production of each unit are determined for a specific period of study based on the predicted electric demand. Although resolving the UC provides valuable information, dependencies between energy carriers are not considered.

Therefore, the following can be mentioned:

• The UC focuses solely on the study of the electrical grid and the supply of electrical demand.
• In the UC, only the forecast of electricity demand is available.
• Independent optimization of energy networks does not necessarily lead to the optimization of the entire energy network.
• In the UC, possible substitutions between energy carriers are not considered.

The study of EC is introduced with the attitude of operation of energy carriers in an integrated energy network, considering the possibility of possible substitutions between energy carriers. In the proposed EC study, instead of forecasting electricity consumption, forecasting energy demand for other energy carriers is also available, and based on this, the optimal operation of energy carriers is presented simultaneously.

EC determines the most appropriate pattern of using energy carriers wherein first technical problems and then economic issues are adequately addressed. If the energy carriers are used according to the peak demand, it will cost a lot. In fact, energy carriers should be optimally utilized, as managing energy resources properly can save a considerable amount of money. In the EC issue, first, the energy demand (actually the energy demand curve) must be determined. This energy demand curve, similar to the UC problem, can be a 24-h curve. In the UC problem, for every hour of the study, there is an electricity demand that must be met by the appropriate combination of units. However, in the EC, for every hour of the study, there is an energy demand of different types, including electricity, gas, car fuel, aircraft fuel, etc., which must be met using the appropriate combination of energy carriers.

2.2. Energy Grid

The EC study should be done in a proper space called the energy grid. The various sectors of the proposed energy grid are transportation, agriculture, industrial, residential, commercial, and public sectors.

In the energy grid, the energy demand is calculated as the sum of the demand in the various subdivisions of the grid using (1):

$$E{C}_f=E{C}_1+E{C}_2+\dots +E{C}_N= {\displaystyle \sum }_{i=1}^{N}E{C}_i$$

(1)

where $E{C}_f$ is the total energy demand, $E{C}_i$ is the energy demand of the i-th sector of the grid, and $N$ is the number of different sectors of the energy grid.

The primary constraint on the EC problem is to supply the total energy demand. The energy consumption in different parts is (2):

$$E_1= {\left[E{C}_1 E{C}_2\dots E{C}_i\dots E{C}_N\right]}^T$$

(2)

where $E_1$ is the energy demand matrix in the various energy sectors. This energy demand can include a variety of energy carriers such as natural gas, electricity, coal, etc. For the energy grid proposed, the energy demand is considered to be as below:

$$E_1=\left[\begin{array}{cc}E{C}_1& \mathrm{total}\mathrm{energy}\mathrm{demand}\mathrm{in}\mathrm{residential},\mathrm{commercial},\mathrm{and}\mathrm{public}\mathrm{sector}\hfill \\ E{C}_2& \mathrm{total}\mathrm{energy}\mathrm{demand}\mathrm{in}\mathrm{industrial}\mathrm{sector}\hfill \\ E{C}_3& \mathrm{total}\mathrm{energy}\mathrm{demand}\mathrm{in}\mathrm{transportation}\mathrm{sector}\hfill \\ E{C}_4& \mathrm{total}\mathrm{energy}\mathrm{demand}\mathrm{in}\mathrm{agriculture}\mathrm{sector}\hfill \\ E{C}_5& \mathrm{total}\mathrm{energy}\mathrm{demand}\mathrm{in}\mathrm{other}\mathrm{sector}\hfill \\ E{C}_6& \mathrm{total}\mathrm{energy}\mathrm{demand}\mathrm{in}\mathrm{non}-\mathrm{energy}\mathrm{sector}\hfill \end{array}\right]$$

3. Problem Formulation

Energy network matrix modeling is presented. This modeling is performed in several steps, from the lowest energy level (final energy consumption) to the highest energy level (primary energy carriers).

Final energy consumption based on different energy carriers is specified as:

$$E_2= T_{1,2} \times E_1$$

(3)

where $E_2$ is the final energy consumption based on different energy carriers and $T_{1,2}$ is the transform matrix of different sectors to different energy carriers. The values of $T_{1,2}$ are determined based on the simulation of experimental and practical data.

Energy loss is modeled using (4).

$$E_3= T_{2,3} \times E_2$$

(4)

where $E_3$ is the final energy consumption based on different energy carriers considering losses and $T_{2,3}$ is the efficiency matrix. The values of $T_{2,3}$ are determined based on the simulation of experimental and practical data.

At this stage, the electrical energy is proportioned to the energy carriers. In fact, at this point, the UC problem must be resolved. The electrical energy of different power plants is determined as shown in (5):

$$E_u= T_u \times E_e$$

(5)

where $E_u$ is the electrical energy of different power plants, $T_u$ is the separation matrix of electricity generated by various power plants that is calculated based on solving UC, and $E_e$ is the total electricity demand.

Input fuel for different power plants is determined by (6):

$$E_{e_1}= T_{u,f} \times E_u$$

(6)

where $E_{e_1}$ is the input fuel for different power plants and $T_{u,f}$ is the power plant efficiency matrix.

The source energy carrier for electricity generation is determined using (7).

$$E_{e_2}= T_{f,c} \times E_{e_1}$$

(7)

where $E_{e_2}$ is the source energy carrier for electricity generation and $T_{f,c}$ is the conversion matrix of input fuel to energy carriers.

After the calculation of electrical energy, the final energy consumption is calculated using (8).

$$E_4= E_3+E_{e_2}-E_e$$

(8)

where $E_4$ is the final energy consumption after converting electrical energy to input carriers to units.

At this stage, the process of refining crude oil is simulated using (9).

$$E_{p_1}= T_p \times E_p$$

(9)

where $E_{p_1}$ represents the energy carriers produced by refining, $T_p$ is the separation matrix of products created from refining crude oil, and $E_p$ is the maximum capacity of refineries.

After simulation of the refining crude oil process, the final energy consumption is calculated using (10).

$$E_5= E_4+E_p-E_{p_1}$$

(10)

where $E_5$ is the final energy consumption after refining crude oil. Actually, $E_5$ determines the energy carriers that supply the energy demand.

Import and export of energy carriers are determined by (11):

$$E_6= E_5-P$$

(11)

where P is the domestic production of energy carriers, and $E_{6 }$ is the import and/or export of energy carriers. In $E_6$, the positive sign means import and negative sign means export of energy carriers.

4. Simulation Studies

Optimization algorithms have the ability to solve complex problems. In this regard, various optimization algorithms have been introduced by researchers [31,32,33,34,35,36,37,38,39,40] and have been applied by scientists in various fields such as energy [41], protection [42], electrical engineering [43,44,45,46], and energy carriers [47,48] to achieve the optimal solution. The EC problem is simulated on an MCE system, and the Following Optimization Algorithm (FOA) [49] as an optimization method is used in the simulations to find the best solution of the EC problem.

4.1. Case Study

The EC problem is tested on an energy grid with 10 generating plants. The final energy consumption for a 24-hour period is presented in

Table A8. Final energy consumption (BOE).

Hour	1	2	3	4	5	6	7	8
Residential, commercial, and public	1640.43	1757.603	1991.95	2226.297	2343.471	2577.818	2694.992	2812.165
Industrial	772.0152	827.1591	937.447	1047.735	1102.879	1213.167	1268.311	1323.455
Transportation	1043.164	1117.676	1266.699	1415.723	1490.234	1639.258	1713.769	1788.281
Agriculture	137.0101	146.7966	166.3694	185.9423	195.7288	215.3016	225.0881	234.8745
Other	10.25525	10.98777	12.4528	13.91784	14.65036	16.11539	16.84791	17.58043
Non-energy	349.9091	374.9026	424.8896	474.8766	499.8702	549.8572	574.8507	599.8442
Hour	9	10	11	12	13	14	15	16
Residential, commercial, and public	3046.512	3398.033	3632.38	3878.444	3515.206	3280.859	2812.165	2460.645
Industrial	1433.742	1599.174	1709.462	1825.264	1654.318	1544.03	1323.455	1158.023
Transportation	1937.305	2160.84	2309.863	2466.338	2235.351	2086.328	1788.281	1564.746
Agriculture	254.4474	283.8067	303.3796	323.9311	293.5931	274.0203	234.8745	205.5152
Other	19.04546	21.24302	22.70805	24.24634	21.97553	20.5105	17.58043	15.38287
Non-energy	649.8312	724.8117	774.7987	827.2851	749.8052	699.8182	599.8442	524.8637
Hour	17	18	19	20	21	22	23	24
Residential, commercial, and public	2343.471	2812.165	3280.859	3046.512	2577.818	2109.124	1991.95	1874.777
Industrial	1102.879	1323.455	1544.03	1433.742	1213.167	992.5909	937.447	882.3031
Transportation	1490.234	1788.281	2086.328	1937.305	1639.258	1341.211	1266.699	1192.187
Agriculture	195.7288	234.8745	274.0203	254.4474	215.3016	176.1559	166.3694	156.583
Other	14.65036	17.58043	20.5105	19.04546	16.11539	13.18532	12.4528	11.72028
Non-energy	499.8702	599.8442	699.8182	649.8312	549.8572	449.8831	424.8896	399.8961

. The transform matrix of different sectors to different energy carriers ($T_{1,2}$) is specified in

Table A9. $T_{1,2}$ Matrix.

	Residential, Commercial and Public	Industrial	Transportation	Agriculture	Other	Non-Energy
Petroleum	0	0	0	0	0	0
Liquid gas	0.051	0.013	0.01	0	0	0
Fuel oil	0.023	0.212	0.014	0	0	0
Gas oil	0.055	0.087	0.363	0.689	0	0
Kerosene	0.141	0.002	0	0.018	0	0
Gasoline	0.002	0.002	0.573	0.003	0	0
Plane fuel	0	0	0.031	0	0	0
Other products	0	0	0	0	0	0.402
Natural gas	0.564	0.521	0.007	0	0	0.497
Coke gas	0	0.021	0	0	0	0
Coal	0.0003	0	0	0	0	0.101
Non-commercial fuels	0.064	0	0	0	0	0
Electricity (power)	0.102	0.142	0.0004	0.29	1	0

. The energy unit used in this article is Millions of Barrels of Oil Equivalent (MBOE).

4.2. Simulation Studies and Discussion

4.2.1. Electrical Energy

A network with 10 electric power plants is used. Information on these plants is provided in Appendix A. According to Algorithm 1, at each hour of the study, the economic distribution of electrical energy is solved for all possible combinations of power plants.

4.2.2. Following Optimization Algorithm (FOA)

In FOA, [49], which is a swarm-based algorithm, search factors are indeed members of the community that try to improve the community by ‘following’ each other. (12) to (14) are the main equations of the FOA.

$$x_i^d=\left(1-fr\right)x_{i,0}^d+fr x_{leader}^d$$

(12)

$$f=1-exp \left(\frac{-t^{1.5}}{T}\right)$$

(13)

$$x_{leader}=\{\begin{array}{c}for minimization problem: location of \min \left(fi{t}_j\right) j∊\left\{1:N\right\}\\ for maximization problem:location of \max \left(fi{t}_j\right) j∊\left\{1:N\right\}\end{array}$$

(14)

In the above equations, $x_{i,0}^d$ refers to the initial balance point along with the d dimension of member i, and r represents a random number with a uniform distribution within the [0–1] span used to preserve the search random state. $x_{leader}$ shows the values of the problem variables for the best member of the community, which is named the leader. Moreover, $x_{leader}^d$ is the d-th dimension of the position of the mentioned leader. Symbol ‘f’ represents the ‘following’ co-efficient, t is the iteration count, T is the maximum number of iterations, and fit is the community fitness vector.

4.2.3. Objective Function and Constraints

The objective function for the EC problem is defined in (15). The constraints on start-up costs and production range of units are specified in (16) and (18), respectively.

$$F_{objective}=min\left\{{\displaystyle \sum }_{t=1}^T\left[{\displaystyle \sum }_{i=1}^{N_c}carrie{r}_i^t\times pric{e}_i+{\displaystyle \sum }_{i=1}^{N_g}S{C}_i^t+{\displaystyle \sum }_{i=1}^{N_g}{C}_i{u}_i^t\right] \right\}$$

(15)

$$S{C}_i^t=\{\begin{array}{cc}\hfill S{C}_i,& u_i^t>u_i^{t-1}\hfill \\ \hfill 0,& else\hfill \end{array}$$

(16)

$$P_{g_i}^{min}\le P_{g_i}\le P_{g_i}^{max}$$

(17)

$${\displaystyle \sum }_{i=1}^{N_g}{P}_{g_i}^t=loa{d}^t$$

(18)

where T is the study period, $N_c$ is the number of various carriers, $carrie{r}_i^t$ in the need for the i-th carrier at the t-th hour, and $pric{e}_i$ is its price, $N_g$ is the number of units, $S{C}_i^t$ is the start-up cost for the i-th unit in the t-th hour, $C_i$ is the fixed cost for the i-th unit and $u_i^t$ is the status (on or off) of it in the t-th hour, $P_{g_i}$ is the production of the i-th unit, and $loa{d}^t$ is the electricity demand in the t-th hour.

The EC problem solution steps are shown in Algorithm 1. The flowchart of the EC solution method using the FOA algorithm is also shown in Figure 1.

Algorithm 1. EC algorithm.

START EC

1:

Problem information.

2:

Inputs data: $E_1^{study period }$, $T_{1,2}$

3:

hour = 1: Study period (24 h)

4:

$E_1=E_1^{study period }\left(\mathrm{hour},:\right)$.

5:

$E_2$

$\leftarrow$

Equation (3): $E_2= T_{1,2} \times E_1$

# calculate final energy consumption

6:

$E_3$

$\leftarrow$

Equation (4):$E_3= T_{2,3} \times E_2$

# calculate final energy consumption considering losses

7:

$E_e=E_3\left(ed,1\right)$ and $ed$ = row number of electrical demand in $E_3$.

8:

END hour

9:

Determine possible combinations of power plants to supply electrical demand.

10:

FOA

11:

Initial population formation based on possible combinations of units.

12:

ITER = 1:T

13:

For i=1:Npopulatio

14:

Combination = population (i,:).

15:

IF is this combination possible?

16:

UC Problem solving.

17:

input energy calculation to power plants.

18:

END UC solving.

19:

$E_4$

$\leftarrow$

Equation (5):$E_u= T_u \times E_e$

# calculate final energy consumption after converting electrical energy

Equation (6):$E_{e_1}= T_{u,f} \times E_u$

Equation (7):$E_{e_2}= T_{f,c} \times E_{e_1}$

Equation (8):$E_4= E_3+E_{e_2}-E_e$

20:

$E_{p_1}$

$\leftarrow$

Equation $\left(9\right):E_{p_1}= T_p \times E_p$

# calculate refining crude oil process

21:

$E_5$

$\leftarrow$

Equation (10): $E_5= E_4+E_p-E_{p_1}$

# calculate final energy consumption after refining crude oil

22:

$E_6$

$\leftarrow$

Equation (11): $E_6= E_5-P$

# calculate import and export of energy carriers

# calculate objective function

23:

$F_{objective}$

$\leftarrow$

$F_{objective}=min\left\{{\displaystyle {\displaystyle \sum }_{t=1}^T}\left[\begin{array}{c}{\displaystyle {\displaystyle \sum }_{i=1}^{N_c}}carrie{r}_i^t\times pric{e}_i\\ +{\displaystyle {\displaystyle \sum }_{i=1}^{N_g}}S{C}_i^t+{\displaystyle {\displaystyle \sum }_{i=1}^{N_g}}{C}_i{u}_i^t\end{array}\right]\right\}$

24:

Else if the combination is impossible.

25:

Fitness = 1e10.

26:

END if

27:

${\mathit{x}}_{\mathit{l}\mathit{e}\mathit{a}\mathit{d}\mathit{e}r}$

$\leftarrow$

Equation (14): $location of \min \left(fi{t}_j\right) j∊\left\{1:N\right\}$

# update leader

28:

f index

$\leftarrow$

Equation (13): $f=1-exp \left(\frac{-t^{1.5}}{T}\right)$

# update ‘following’ co-efficient

29:

population

$\leftarrow$

Equation (12): $x_i^d=\left(1-fr\right)x_{i,0}^d+fr x_{leader}^d$

# update population

30:

END FOR

31:

END ITER

32:

# EC outputs (for every hour and whole period of study).

33:

Determining the most appropriate pattern of using energy carriers.

34:

Import and export of energy carriers.

35:

Cost of energy supply.

36:

Convergence curve.

END EC

4.2.4. Results and Finding

The proposed EC operation is simulated on the mentioned energy grid with 10 power plants and energy demand in different sectors of transportation, agriculture, industrial, residential, commercial, and public. The EC problem is coded in MATLAB and executed on a system with a quad-core 3.3 GHz processor and 8 GB of RAM.

Table 2. The appropriate combination of units and total cost for energy supply.

Hour	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	Cost (Millions Dollar)
Combination	2	2	3	3	4	5	6	7	8	9	10	10	9	6	5	5	5	5	7	7	7	3	3	3	9.0922

presents one of the most important outputs of EC i.e., determining the appropriate combination of power plant units to meet the electricity demand. For each hour of operation, different combinations of power plant units are available to meet the electricity demand. However, a combination of units must be chosen that is also economical. According to Table 2, the appropriate combination for the entire 24-h study period is the combination: (2,2,3,3,4,5,6,7,8,9,10,10,9,6,5,5,5,5,7,7,7,3,3,3). The value of the objective function based on this combination is 9.0922 million dollars.

Table 3. The need for energy carriers (BOE) to supply the energy demand. BOE: Barrels of Oil Equivalent.

Hour	1	2	3	4	5	6	7	8
Liquid gas	104.1298	111.5676	126.4433	141.3189	148.7568	163.6325	171.0703	178.5081
Fuel oil	520.0702	558.1365	625.2257	691.7656	717.0365	755.9679	786.1914	826.9545
Gas oil	634.0488	679.3489	772.0559	864.8909	913.3675	1020.223	1067.949	1113.281
Kerosene	235.3108	252.1187	285.7345	319.3504	336.1583	369.7741	386.582	403.3899
Gasoline	602.9689	646.0381	732.1765	818.3149	861.3841	947.5225	990.5917	1033.661
Plane fuel	32.33808	34.64795	39.26767	43.8874	46.19726	50.81699	53.12685	55.43671
Natural gas	2639.622	2830.853	3211.644	3592.334	3783.39	4181.017	4377.497	4576.617
Coke gas	16.21232	17.37034	19.68639	22.00243	23.16046	25.4765	26.63452	27.79255
Coal	35.83295	38.39245	43.51144	48.63043	51.18993	56.30892	58.86842	61.42791
hour	9	10	11	12	13	14	15	16
Liquid gas	193.3838	215.6973	230.573	246.1925	223.1352	208.2595	178.5081	156.1946
Fuel oil	881.7413	928.0273	1002.576	1044.985	966.8135	894.5986	832.8839	732.4652
Gas oil	1224.697	1402.697	1497.324	1611.015	1448.653	1355.62	1113.497	971.3697
Kerosene	437.0058	487.4295	521.0453	556.342	504.2374	470.6216	403.3899	352.9662
Gasoline	1119.799	1249.007	1335.145	1425.591	1292.076	1205.938	1033.661	904.4533
Plane fuel	60.05644	66.98603	71.60575	76.45647	69.29589	64.67617	55.43671	48.50712
Natural gas	5002.489	5643.05	6045.205	6465.625	5843.64	5444.886	4579.159	3990.681
Coke gas	30.10859	33.58266	35.89871	38.33055	34.74068	32.42464	27.79255	24.31848
Coal	66.5469	74.22539	79.34439	84.71933	76.78489	71.6659	61.42791	53.74942
hour	17	18	19	20	21	22	23	24
Liquid gas	148.7568	178.5081	208.2595	193.3838	163.6325	133.8811	126.4433	119.0054
Fuel oil	717.0365	832.8839	907.5986	876.7413	760.8939	663.2921	625.2257	587.1594
Gas oil	920.7956	1113.497	1352.626	1228.716	1019.635	817.3559	772.0559	726.7558
Kerosene	336.1583	403.3899	470.6216	437.0058	369.7741	302.5425	285.7345	268.9266
Gasoline	861.3841	1033.661	1205.938	1119.799	947.5225	775.2457	732.1765	689.1073
Plane fuel	46.19726	55.43671	64.67617	60.05644	50.81699	41.57754	39.26767	36.95781
Natural gas	3803.633	4579.159	5447.676	5008.352	4188.186	3402.875	3211.644	3020.413
Coke gas	23.16046	27.79255	32.42464	30.10859	25.4765	20.84441	19.68639	18.52836
Coal	51.18993	61.42791	71.6659	66.5469	56.30892	46.07093	43.51144	40.95194

presents the need for energy carriers to meet the total energy demand as another important output of EC. In this table, for each hour of operation, the optimal amount of energy carriers is determined, which also includes the losses of the energy network. For example, in the network studied, 104.1298 BOE of liquid gas, 520.0702 BOE of fuel oil, 634.0488 BOE of gas oil, 235.3108 BOE of kerosene, 602.9689 BOE of gasoline, 32.33808 BOE of plane fuel, 2639.622 BOE of natural gas, 16.21232 BOE of coke gas, and 35.83295 BOE coal are needed to meet the energy demand in the first hour of operation.

Moreover, according to domestic production, the results of the import and export of energy carriers are shown in

Table 4. Import and export of carriers (BOE).

Hour	Import	Export
Petroleum	0	171,897
Liquid gas	1055.61	0
Fuel oil	0	8857.3
Gas oil	0	1952.09
Kerosene	0	127.814
Gasoline	8777.53	0
Plane fuel	1263.726	0
Natural gas	2964.269	0
Coke gas	0	39.7234
Coal	390.384	0

. According to this table, petroleum (171,897), fuel oil (8857.3), gas oil (1952.09), kerosene (127.814), and coke gas (39.72) are in the export section, and liquid gas (1055.61), gasoline (8777.53), plane fuel (1263.726), natural gas (2964.27), and coal (390.38) are in the import section.

Table 5. Unit Commitment (UC) result (MW).

Unit 1	Unit 2	Unit 3	Hour	Unit 4	Unit 5	Unit 6	Unit 7	Unit 8	Unit 9	Unit 10
1	455	245.8952	0	0	0	0	0	0	0	0
2	455	295.9591	0	0	0	0	0	0	0	0
3	455	376.087	20	0	0	0	0	0	0	0
4	455	455	41.21486	0	0	0	0	0	0	0
5	455	455	71.2788	20	0	0	0	0	0	0
6	455	455	130	36.40668	25	0	0	0	0	0
7	455	455	130	66.47061	25	20	0	0	0	0
8	455	455	130	91.53455	25	20	25	0	0	0
9	455	455	130	130	76.66243	20	25	10	0	0
10	455	455	130	130	162	74.85425	25	10	10	0
11	455	455	130	130	162	80	85	34.98213	10	10
12	455	455	130	130	162	80	85	55	55	50.11641
13	455	455	130	130	162	80	69.91819	10	10	0
14	455	455	130	130	162	69.79031	0	0	0	0
15	455	455	130	130	31.53455	0	0	0	0	0
16	455	455	96.34274	20	25	0	0	0	0	0
17	455	455	46.2788	20	25	0	0	0	0	0
18	455	455	130	130	31.53455	0	0	0	0	0
19	455	455	130	130	162	44.79031	25	0	0	0
20	455	455	130	130	86.66243	20	25	0	0	0
21	455	455	101.4067	20	25	20	25	0	0	0
22	455	426.1509	20	0	0	0	0	0	0	0
23	455	376.087	20	0	0	0	0	0	0	0
24	455	326.023	20	0	0	0	0	0	0	0

presents the optimal combination and amount of production of power plant units for each hour of the study period. In fact, this table contains information about the two important outputs of the energy commitment i.e., ED and UC. ED is to determine the most appropriate production pattern of units according to economic and technical constraints.According to this table, it is clear that the mentioned energy network has the peak of energy demand in the 12th hour of operation. In addition, at the 11th hour of operation, the amount of electricity demand is such that all units are turned on to supply it.

The convergence curve of the performance of FOA in solving the EC problem is shown in Figure 2. This curve is plotted based on the best solution obtained until each iteration in terms of algorithm iteration. As shown in this figure, FOA converged in iteration number 115 and provided the optimal solution of 9.0922 million dollars.

Based on the outputs presented from the implementation of the EC, as well as the mentioned topics, the following findings are identified.

• EC is a constrained optimization problem that can be solved using various methods, especially optimization algorithms.
• The goal in EC is determination of the most appropriate pattern of using energy carriers to supply energy demand, wherein first technical problems and then economic issues are adequately addressed.
• In the EC study, various sectors of energy consumption including transportation, agriculture, industrial, residential, commercial, and public sectors are considered.
• EC is a more accurate and in-depth study than UC, as UC and ED are part of the outputs of energy commitment.
• EC study provides more details and information about the grid than UC studies.
• UC focuses only on the operation of electrical energy demand, while the EC also considers other energy carriers.
• By implementing the EC on an energy grid, important outputs are obtained, including the need to differentiate energy carriers, ED and UC information, and the import and export of energy carriers.
• FOA algorithm has a good performance in solving the EC problem by presenting a smooth convergent curve and achieving the optimal solution in the appropriate number of iterations.

5. Conclusions and Future Works

Energy consumption is one of the criteria for determining the level of development and quality of life in a country. The continuity of energy supply and ensuring long-term access to resources have required a comprehensive energy plan. Energy carriers are one of the critical topics in the field of energy operation. Thus, this paper presents a methodology called Energy Commitment (EC) for the optimized operation of energy carriers using the Following Optimization Algorithm (FOA).

The goal in EC is determination of the most appropriate pattern of using energy carriers to supply energy demand considering technical and economic issues. EC is a constrained optimization problem that can be solved using various methods, especially the optimization algorithms. In this paper, the FOA algorithm has been applied to solve the EC problem.

EC has been implemented on an energy grid with 10 power plants and including different consumption sectors of transportation, agriculture, industrial, residential, commercial, and general. Important outputs and information have been obtained by the implementation of an EC study on this energy network. This information and output signify the need for different energy carriers to meet the energy demand, the optimal combination and production of units (UC and EC outputs), and the amount of imports and exports of energy carriers.

Various combinations of power plants are available to supply the electricity demand for every hour of operation. According to the different fuel inputs to each power plant, different combinations of energy carriers are obtained. The appropriate combination of power plants and proper energy combination carriers to supply the energy consumption has been determined using the FOA. The FOA has a good performance in solving the EC problem by presenting a smooth convergent curve and achieving the optimal solution in the appropriate number of iterations.

The simulation results of the proposed study on the energy grid show that the EC analyzes the energy grid more efficiently and accurately than the UC. UC only studies the electrical energy network, while the EC operates energy carriers in an integrated energy network with energy demand for different energy carriers. Therefore, UC is one of the important outputs of the EC study and in fact, UC is a subset of the EC study.

The authors suggest implementing EC on various energy networks and scenarios, as well as using other optimization techniques for future studies. Ideas for further studies and future research include the introduction of new objective functions with new constraints such as the impact of CO₂ and EC solving considering the response time required by each energy storage/carrier.