Investigations of Adhesion under Different Slider-Lube/Disk Contact States at the Head–Disk Interface
Abstract
:1. Introduction
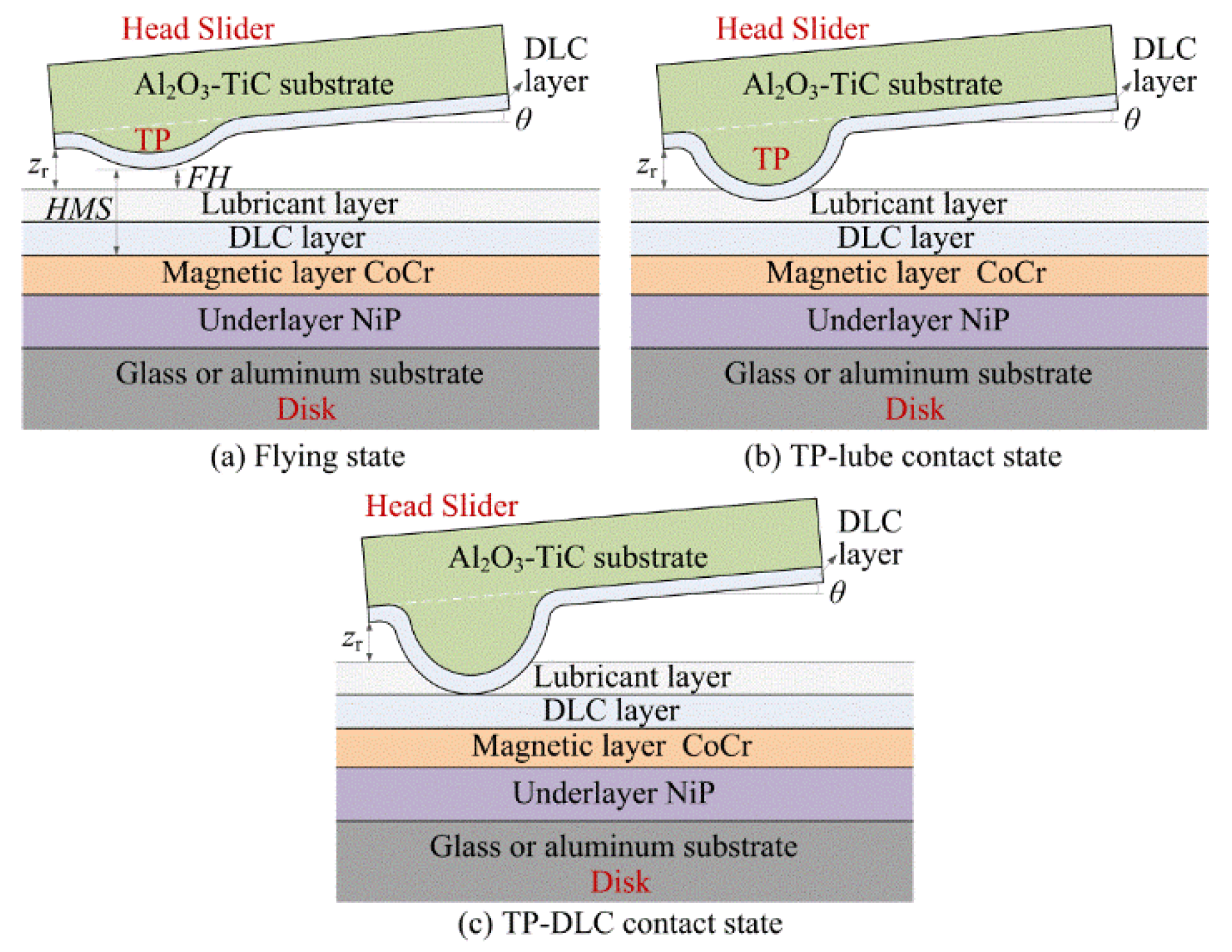
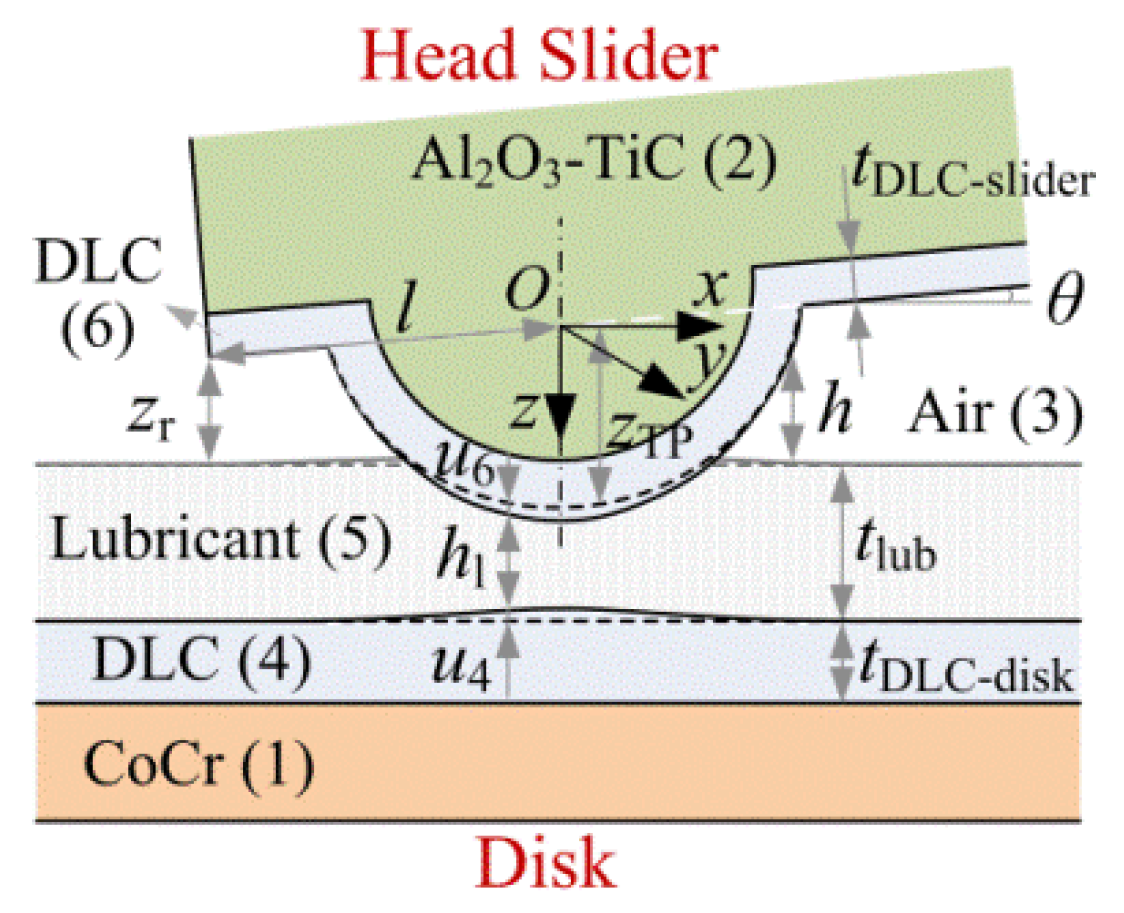
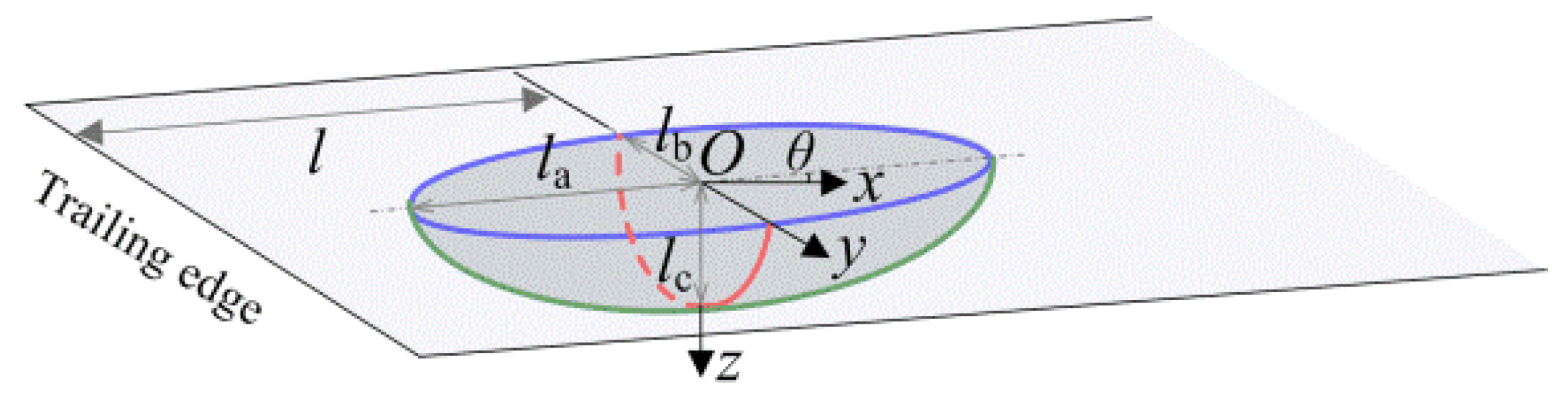
2. Methods
2.1. Theoretical Model
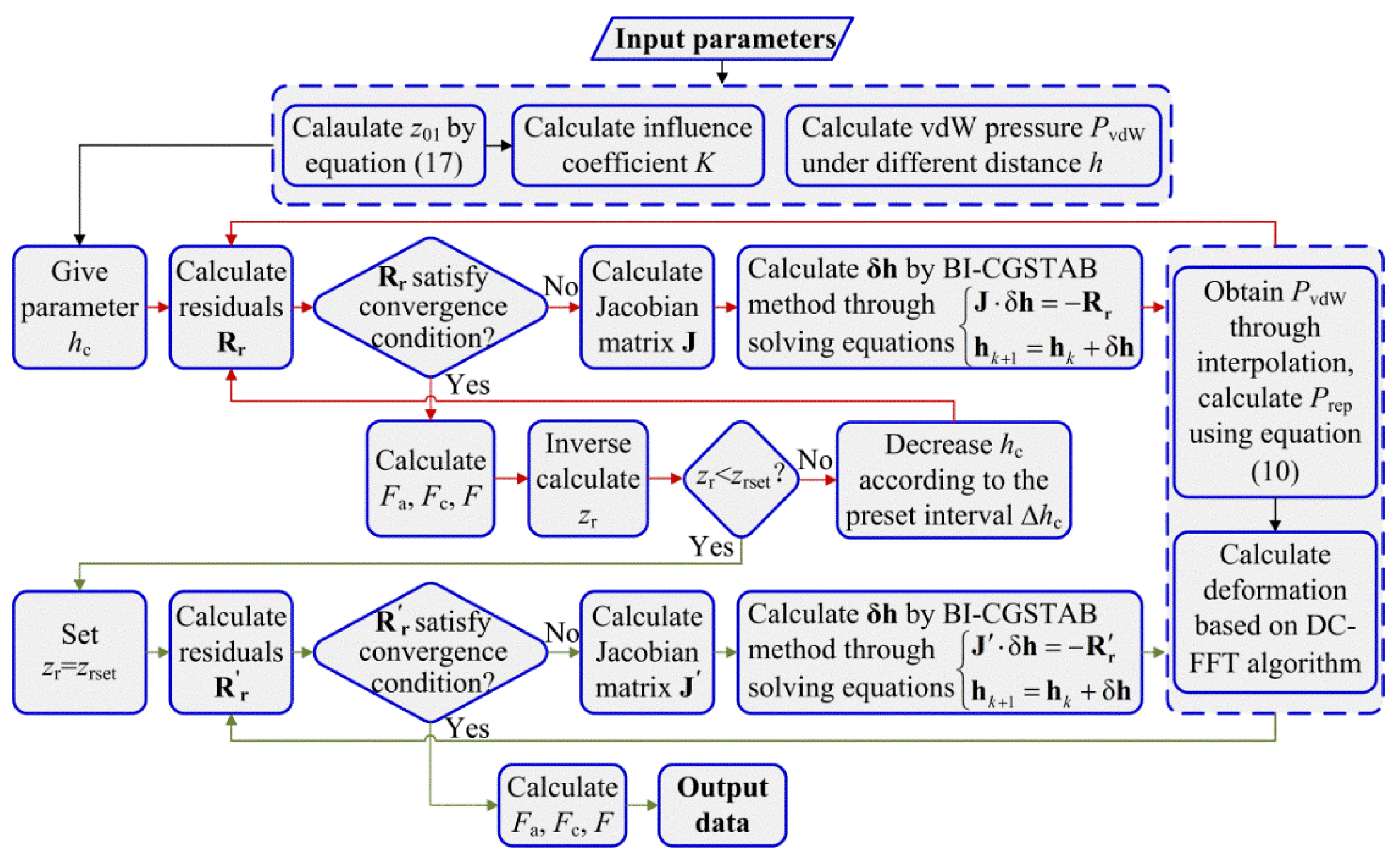
2.2. Numerical Method
3. Results and Discussions
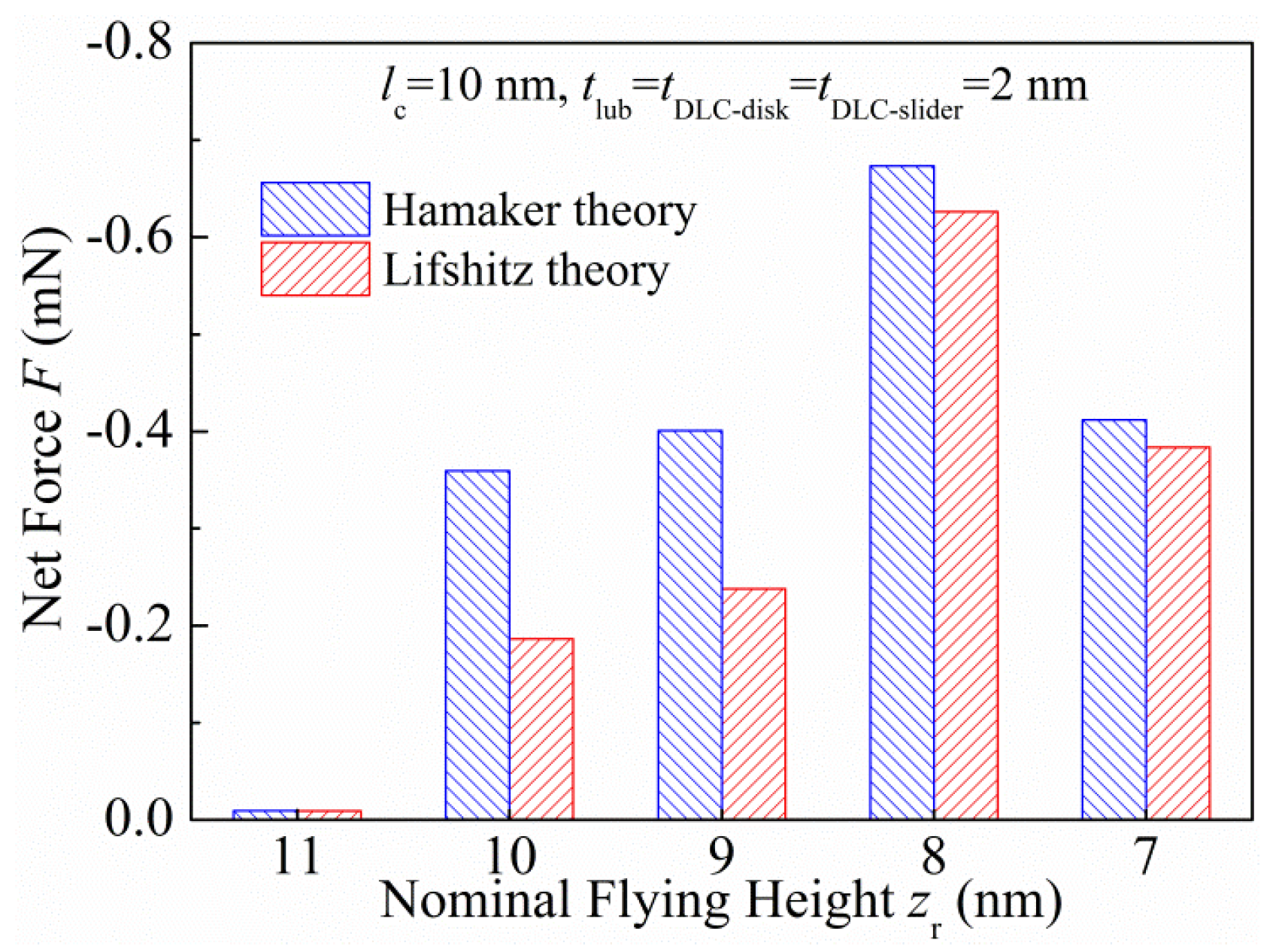
3.1. Comparisons of Results Between Hamaker Theory and Lifshitz Theory
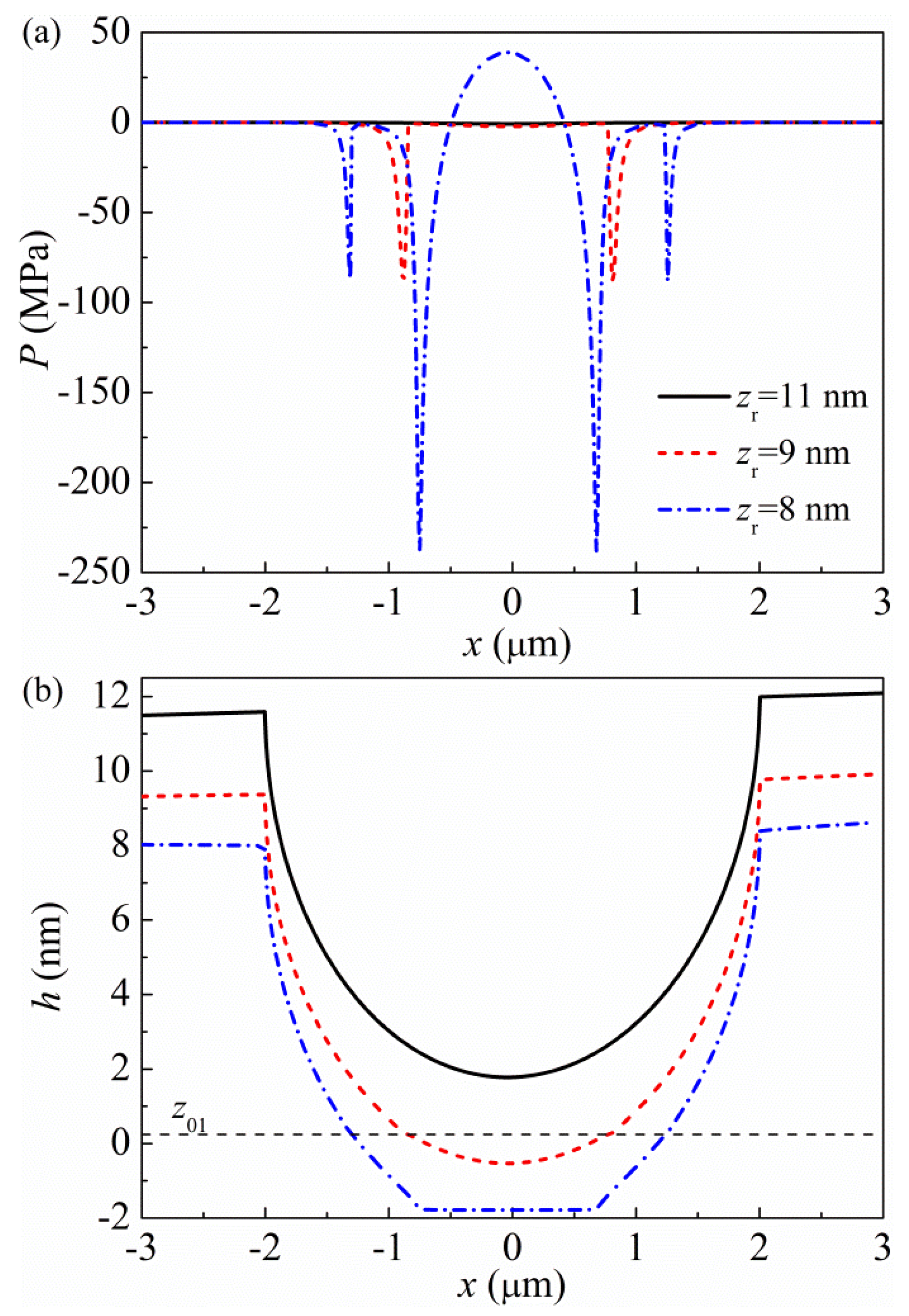
3.2. Analysis of The Adhesive Contact Characteristics at The HDI
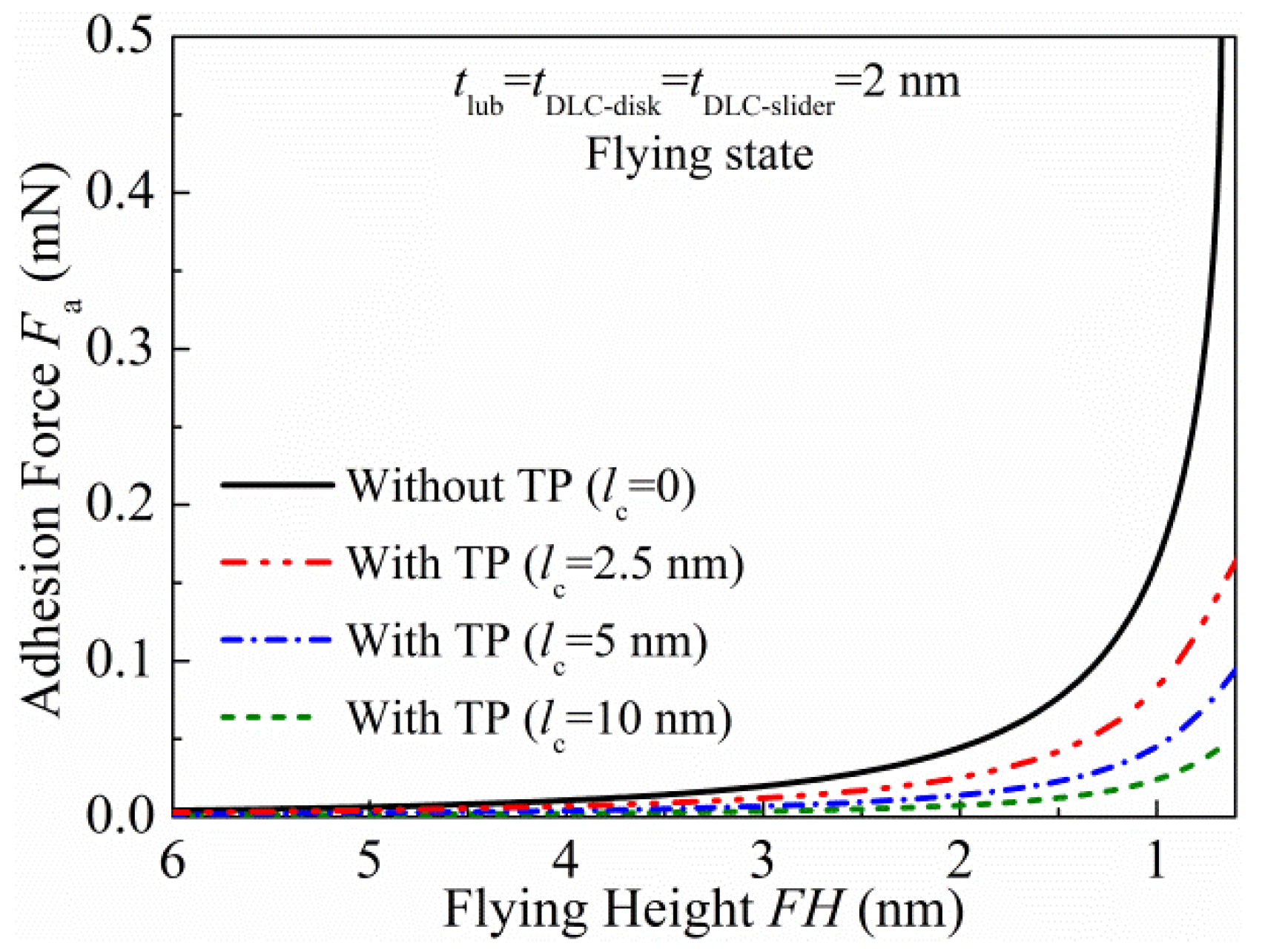
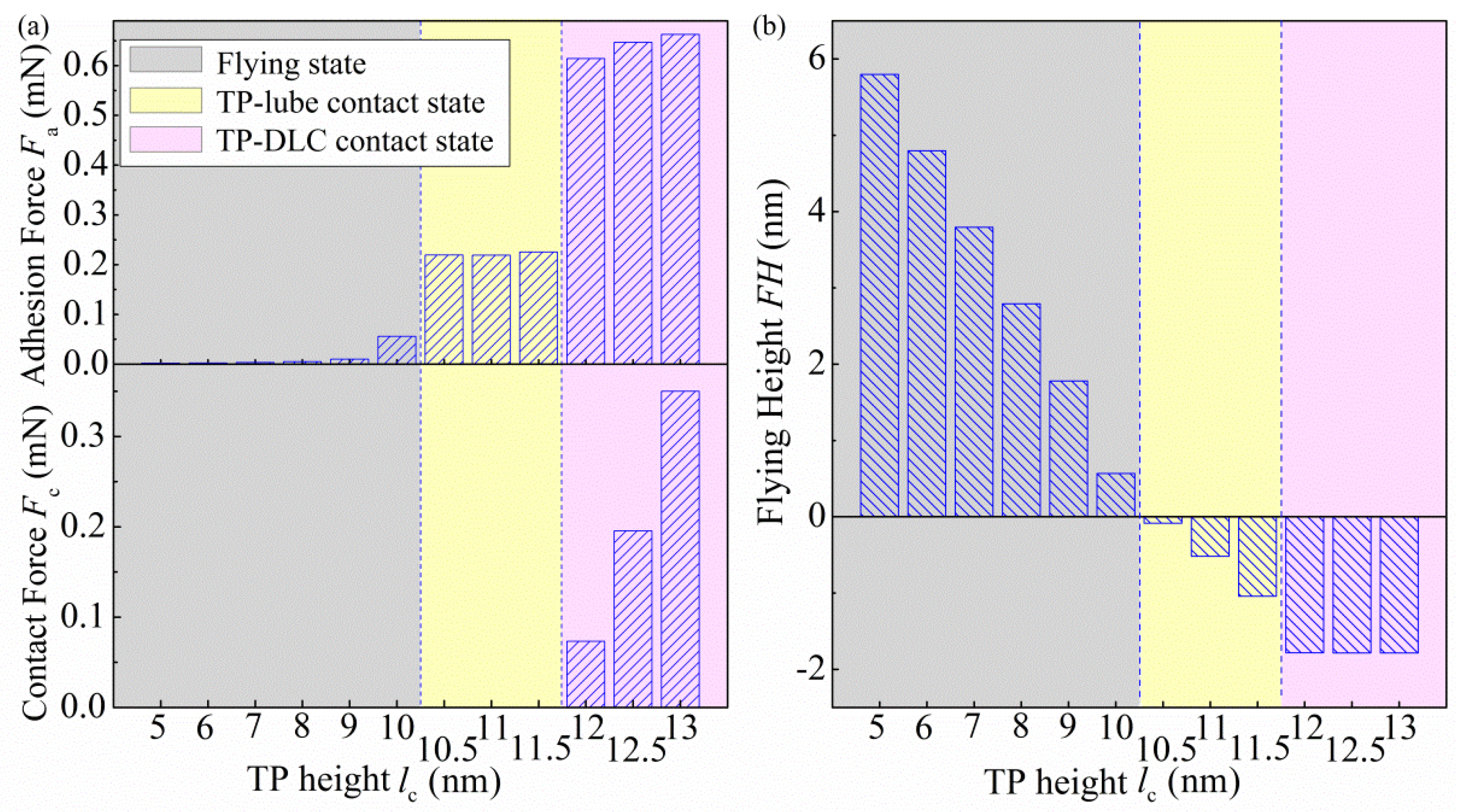
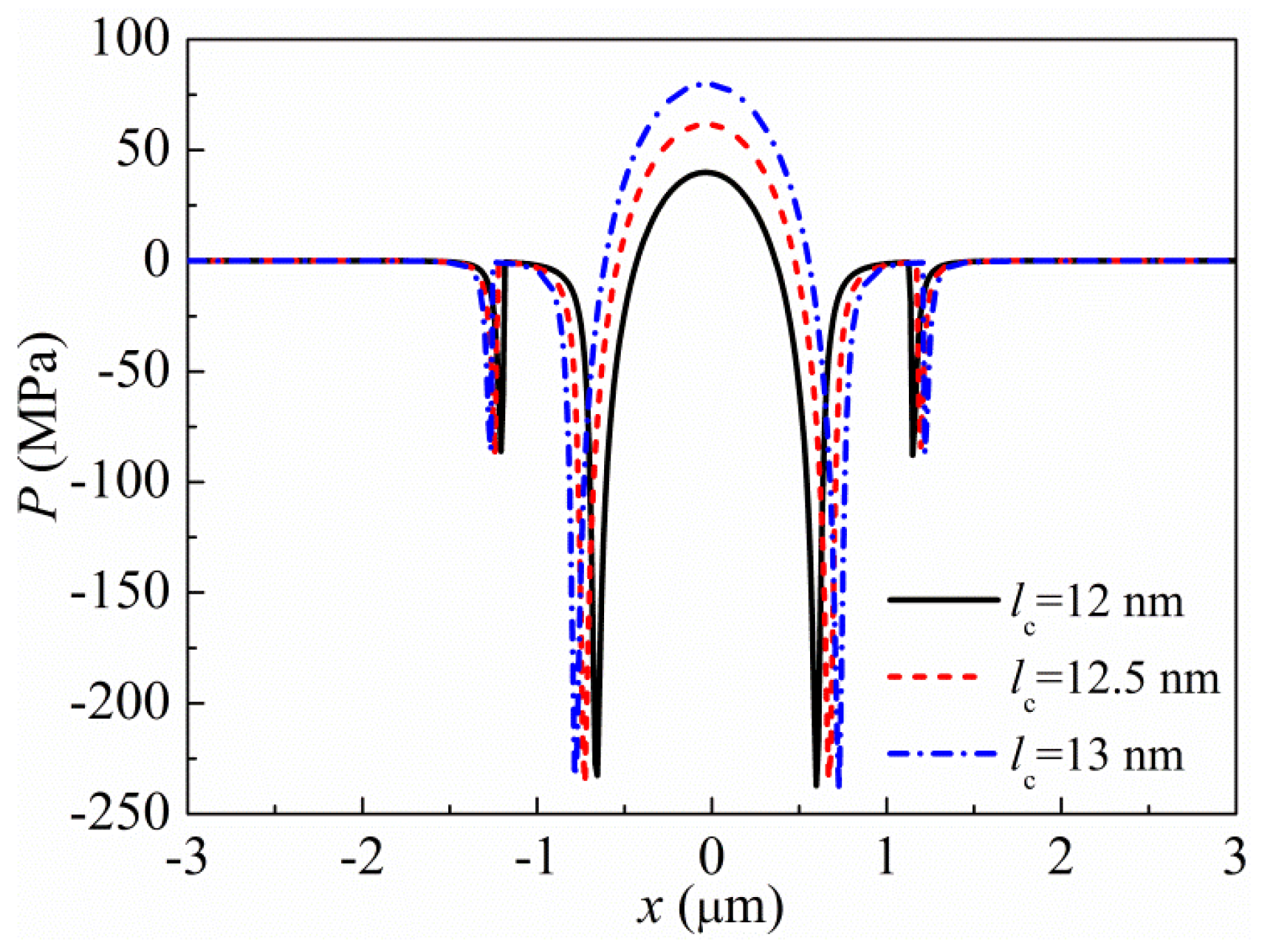
3.3. Effects of TP Height on the Interaction Force and FH at the HDI
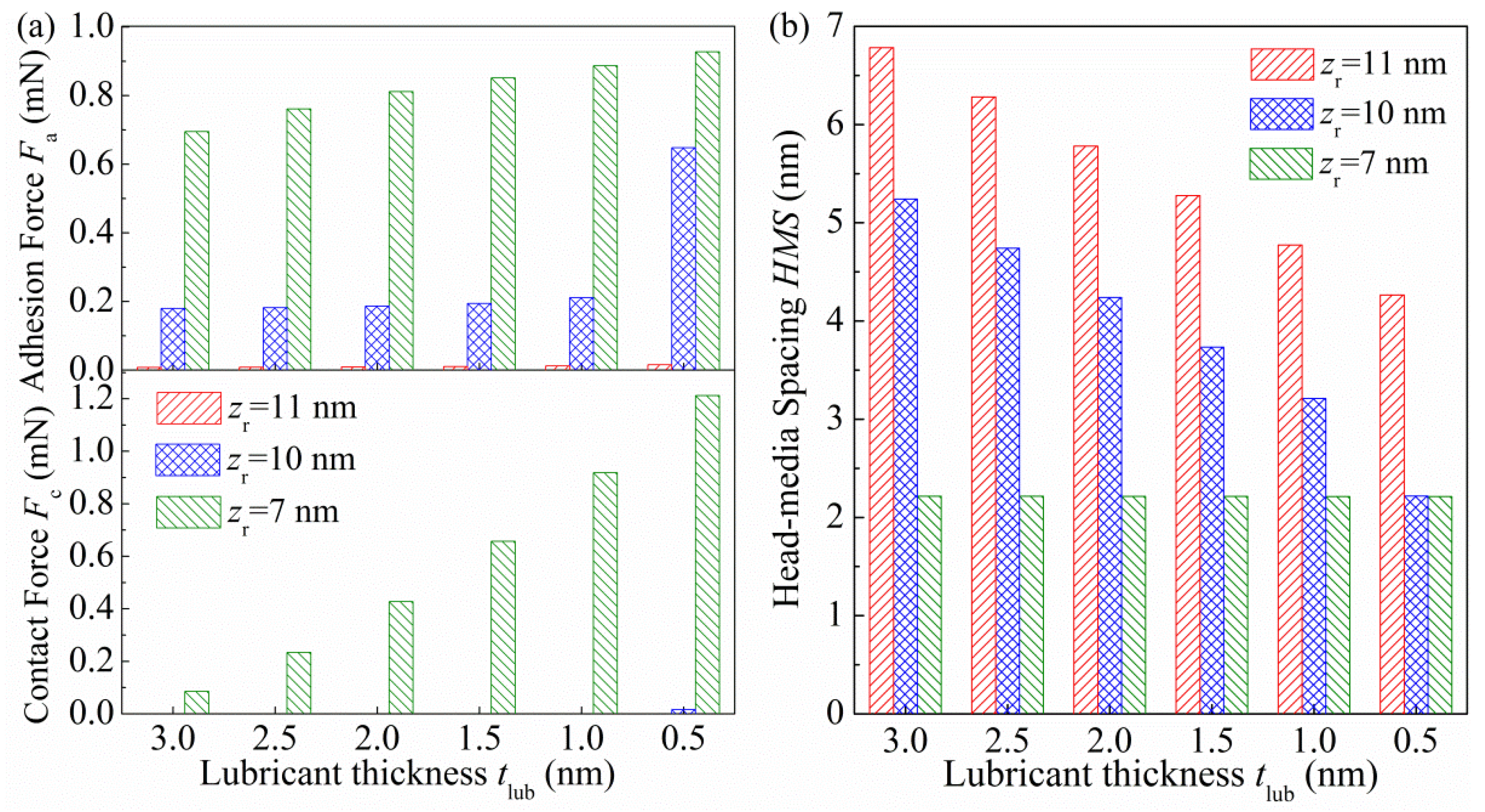
3.4. Effects of Lubricant Thickness on the Interaction Force and HMS at the HDI
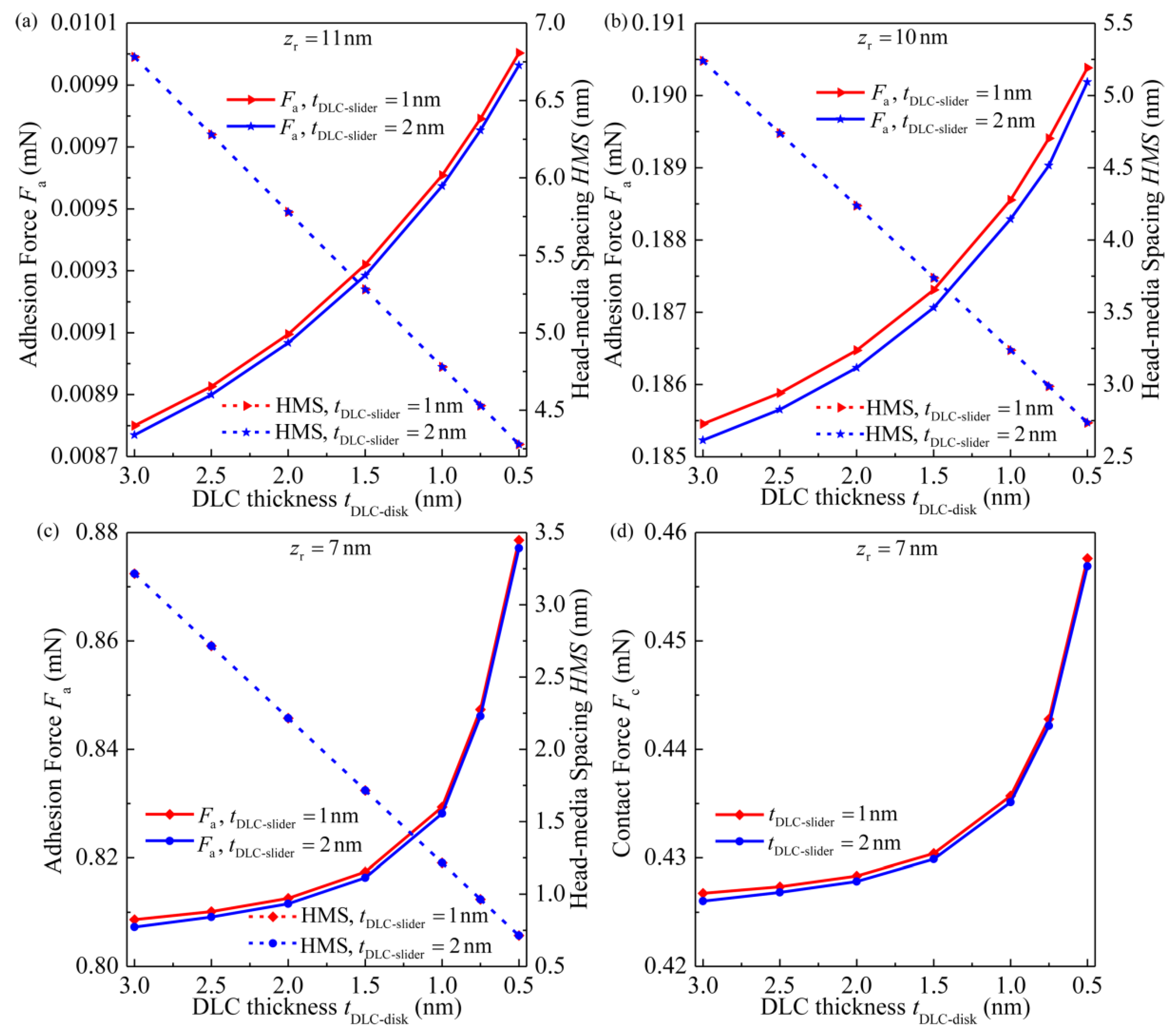
3.5. Effects of DLC Thickness on the Interaction Force and HMS at the HDI
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dawit, Z.S.; Polina, V.K.; Pyung, H. Experimental and direct numerical analysis of hard-disk drive. J. Mech. Sci. Technol. 2018, 32, 3507–3513. [Google Scholar]
- Samad, M.A.; Rismani, E.; Yang, H.; Sinha, S.K.; Bhatia, C.S. Overcoat Free Magnetic Media for Lower Magnetic Spacing and Improved Tribological Properties for Higher Areal Densities. Tribol. Lett. 2011, 43, 247–256. [Google Scholar] [CrossRef]
- Marchon, B.; Pitchford, T.; Hsia, Y.-T.; Gangopadhyay, S. The Head-Disk Interface Roadmap to an Areal Density of Tbit/in2. Adv. Tribol. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Katta, R.R.; Polycarpou, A.A. Microtribodynamics of Magnetic Storage Hard Disk Drives; Springer Science and Business Media LLC: New York, NY, USA, 2013; pp. 2244–2256. [Google Scholar]
- Vakis, A.I.; Polycarpou, A.A. Head-disk interface nanotribology for Tbit/inch2recording densities: Near-contact and contact recording. J. Phys. D Appl. Phys. 2010, 43, 225301. [Google Scholar] [CrossRef]
- Schultz, B.E. Thermal fly-height control (TFC) technology in Hitachi hard disk drives. Hitachi Glob. Storage Technol. San Jose 2007, 1–4. [Google Scholar]
- Hua, W.; Liu, B.; Yu, S.; Zhou, W. Contact recording review. Microsyst. Technol. 2010, 16, 493–503. [Google Scholar] [CrossRef]
- Vakis, A.I.; Polycarpou, A.A. Optimization of thermal fly-height control slider geometry for Tbit/in2 recording. Microsyst. Technol. 2010, 16, 1021–1034. [Google Scholar] [CrossRef]
- Ono, K. Effect of van der Waals Forces in a Near Contact Head-Disk Interface. IEEE Trans. Magn. 2008, 44, 3675–3678. [Google Scholar] [CrossRef]
- Suh, A.Y.; Polycarpou, A.A. Adhesive contact modeling for sub-5-nm ultralow flying magnetic storage head-disk interfaces including roughness effects. J. Appl. Phys. 2005, 97, 104328. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, M.; Yu, S.; Hua, W.; Wong, C.H.; Zhou, W.; Man, Y.; Gonzaga, L.; Ma, Y. Towards fly- and lubricant-contact recording. J. Magn. Magn. Mater. 2008, 320, 3183–3188. [Google Scholar] [CrossRef]
- Man, Y.; Liu, B.; Ng, K.K.; Yu, S.; Sinha, S.K.; Lim, S.C. Investigations of Light Contact and Lube-Surfing State with Electrical Current. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Elsevier: Santa Barbara, CA, USA, 2011. [Google Scholar]
- Hamaker, H. The London—van der Waals attraction between spherical particles. Physica 1937, 4, 1058–1072. [Google Scholar] [CrossRef]
- Wu, L.; Bogy, D.B. Effect of the Intermolecular Forces on the Flying Attitude of Sub-5 NM Flying Height Air Bearing Sliders in Hard Disk Drives. J. Tribol. 2002, 124, 562–567. [Google Scholar] [CrossRef]
- Trinh, T.D. Tribological Performance of the Head-Disk Interface in Perpendicular Magnetic Recording and Heat-Assisted Magnetic Recording. Ph.D. Thesis, University of California, San Diego, CA, USA, 2019. [Google Scholar]
- Yu, N.; Polycarpou, A.A. Adhesive contact based on the Lennard–Jones potential: A correction to the value of the equilibrium distance as used in the potential. J. Colloid Interface Sci. 2004, 278, 428–435. [Google Scholar] [CrossRef] [PubMed]
- Prokopovich, P.; Starov, V. Adhesion models: From single to multiple asperity contacts. Adv. Colloid Interface Sci. 2011, 168, 210–222. [Google Scholar] [CrossRef]
- Matthes, L.M.; Brunner, R.; Knigge, B.; Talke, F.E. Head Wear of Thermal Flying Height Control Sliders as a Function of Bonded Lubricant Ratio, Temperature, and Relative Humidity. Tribol. Lett. 2015, 60, 1–10. [Google Scholar] [CrossRef]
- Brunner, R.; Tyndall, G.W.; Waltman, R.J.; Talke, F.E. Adhesion Between Surfaces Separated by Molecularly Thin Perfluoropolyether Films. Tribol. Lett. 2010, 40, 41–48. [Google Scholar] [CrossRef] [Green Version]
- Lai, T.; Huang, P.; Cai, Y. Adhesion Reduction of Diamond-Like Carbon Films Based on Different Contact Geometries by Using an AFM. J. Adhes. 2014, 92, 18–38. [Google Scholar] [CrossRef]
- Lifshitz, E.; Hamermesh, M. The theory of molecular attractive forces between solids. Perspect. Theor. Phys. 1992, 2, 329–349. [Google Scholar] [CrossRef]
- Ninham, B.W.; Parsegian, V.A. van der Waals Interactions in Multilayer Systems. J. Chem. Phys. 1970, 53, 3398–3402. [Google Scholar] [CrossRef]
- White, L.R.; Dagastine, R.R.; Jones, P.M.; Hsia, Y.-T. van der Waals force calculation between laminated media, pertinent to the magnetic storage head-disk interface. J. Appl. Phys. 2005, 97, 104503. [Google Scholar] [CrossRef]
- Peng, W.; Crone, R.M.; Jones, P.M.; Hsia, Y.T. Effect of van der Waals force on air-bearing flying characteristics at ultra-low fly heigh. IEEE Trans. Magn. 2006, 42, 2483–2485. [Google Scholar] [CrossRef]
- Dagastine, R.R.; Bevan, M.; White, L.R.; Prieve, D.C. Calculation of van der Waals Forces with Diffuse Coatings: Applications to Roughness and Adsorbed Polymers. J. Adhes. 2004, 80, 365–394. [Google Scholar] [CrossRef]
- Derjaguin, V.B. Theorie des Anhaftens kleiner Teilchen. Prog. Surf. Sci. 1992, 40, 6–15. [Google Scholar] [CrossRef]
- Stanley, H.M.; Etsion, I.; Bogy, D.B. Adhesion of Contacting Rough Surfaces in the Presence of Sub-Boundary Lubrication. J. Tribol. 1990, 112, 98–104. [Google Scholar] [CrossRef]
- Wu, J.-J. Numerical analyses on elliptical adhesive contact. J. Phys. D Appl. Phys. 2006, 39, 1899–1907. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Q. Studying Contact Stress Fields Caused by Surface Tractions with a Discrete Convolution and Fast Fourier Transform Algorithm. J. Tribol. 2001, 124, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Yu, N.; Polycarpou, A.A.; Hanchi, J.V. Elastic contact mechanics-based contact and flash temperature analysis of impact-induced head disk interface damage. Microsyst. Technol. 2007, 14, 215–227. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Jiang, L.; Yang, W.; Ma, C.; Yu, Q. Investigations of Adhesion under Different Slider-Lube/Disk Contact States at the Head–Disk Interface. Appl. Sci. 2020, 10, 5899. https://doi.org/10.3390/app10175899
Zhang Y, Jiang L, Yang W, Ma C, Yu Q. Investigations of Adhesion under Different Slider-Lube/Disk Contact States at the Head–Disk Interface. Applied Sciences. 2020; 10(17):5899. https://doi.org/10.3390/app10175899
Chicago/Turabian StyleZhang, Yuyan, Ling Jiang, Weixu Yang, Chenbo Ma, and Qiuping Yu. 2020. "Investigations of Adhesion under Different Slider-Lube/Disk Contact States at the Head–Disk Interface" Applied Sciences 10, no. 17: 5899. https://doi.org/10.3390/app10175899
APA StyleZhang, Y., Jiang, L., Yang, W., Ma, C., & Yu, Q. (2020). Investigations of Adhesion under Different Slider-Lube/Disk Contact States at the Head–Disk Interface. Applied Sciences, 10(17), 5899. https://doi.org/10.3390/app10175899





