An Overview of Progressive Collapse Behavior of Steel Beam-to-Column Connections
Abstract
:1. Introduction
2. Ri Effects on Progressive Collapse
3. Development of Data Bank
4. Test Results
5. Discussions of Test Results
5.1. Catenary Mechanism
- i.
- The beam has an I-shaped section with elastic/perfectly plastic material.
- ii.
- Plastic hinges only appear at the mid-span and both ends, and hinges follow the rigid-plastic model.
- iii.
- The beam has symmetric restraint with the elastic response.
- iv.
- The restraint of the steel beam is symmetric and in elastic response.
- v.
- Once the whole I-section experiences yielding, the correlation between axial force and bending moment controls the behavior of the catenary mechanism.
5.2. Maximum Rotation and Ductility Capacity
5.3. Stiffness Degradation
5.4. Evaluation of Catenary and Flexural Mechanisms Under Different Ri
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pantidis, P.; Cao, L.; Gerasimidis, S. Partial Damage Distribution and Progressive Collapse of Buildings. In Structures Congress 2020; American Society of Civil Engineers: Reston, VA, USA, 2020. [Google Scholar]
- Brunesi, E.; Nascimbene, R.; Parisi, F.; Augenti, N. Progressive collapse fragility of reinforced concrete framed structures through incremental dynamic analysis. Eng. Struct. 2015, 104, 65–79. [Google Scholar] [CrossRef]
- Masoero, E.; Wittel, F.K.; Herrmann, H.J.; Chiaia, B.M. Progressive collapse mechanisms of brittle and ductile framed structures. J. Eng. Mech. 2010, 136, 987–995. [Google Scholar] [CrossRef]
- Agarwal, A.; Varma, A.H. Fire induced progressive collapse of steel building structures: The role of interior gravity columns. Eng. Struct. 2014, 58, 129–140. [Google Scholar] [CrossRef]
- Kim, J.; Park, J. Design of steel moment frames considering progressive collapse. Steel Compos. Struct. 2008, 8, 85–98. [Google Scholar] [CrossRef] [Green Version]
- Cassiano1a, D.; D’Aniello, M.; Rebelo, C.; Landolfo, R.; da Silva, L.S. Influence of seismic design rules on the robustness of steel moment resisting frames. Steel Compos. Struct. 2016, 21, 479–500. [Google Scholar] [CrossRef]
- Zhu, F.Y.; Chen, C.H.; Yao, Y.; Keer, L.M.; Huang, Y. Dynamic increase factor for progressive collapse analysis of semi-rigid steel frames. Steel Compos. Struct. 2018, 28, 209–221. [Google Scholar]
- Byfield, M.; Mudalige, W.; Morison, C.; Stoddart, E. A review of progressive collapse research and regulations. Proc. ICE Struct. Build. 2014, 167, 447–456. [Google Scholar] [CrossRef] [Green Version]
- Gsa, U. Progressive Collapse Analysis and Design Guidelines for New Federaloffice Buildings and Major Modernization Projects; The US General ServicesAdministration: Washington, DC, USA, 2003. [Google Scholar]
- Department of Defense. Design of Buildings to Resist Progressive Collapse; Unified Facilities Criteria (UFC)-DoD. 2005. Available online: https://www.wbdg.org/FFC/DOD/UFC/ARCHIVES/ufc_4_023_03_2009_c2.pdf (accessed on 18 July 2020).
- Wang, F.; Yang, J.; Pan, Z. Progressive collapse behaviour of steel framed substructures with various beam-column connections. Eng. Fail. Anal. 2020, 109, 104399. [Google Scholar] [CrossRef]
- Wang, H.; Tan, K.H.; Yang, B. Experimental Tests of Steel Frames with Different Beam–Column Connections under Falling Debris Impact. J. Struct. Eng. 2020, 146, 04019183. [Google Scholar] [CrossRef]
- Alrubaidi, M.; Elsanadedy, H.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Investigation of different steel intermediate moment frame connections under column-loss scenario. Thin Walled Struct. 2020, 154, 106875. [Google Scholar] [CrossRef]
- Guo, L.; Gao, S.; Fu, F. Structural performance of semi-rigid composite frame under column loss. Eng. Struct. 2015, 95, 112–126. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, J.; Xu, S.; Wang, Z. An investigation of the effect of semi-rigid connections on sudden column removal in steel frames. In Structures; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Xu, G.; Ellingwood, B.R. Disproportionate collapse performance of partially restrained steel frames with bolted T-stub connections. Eng. Struct. 2011, 33, 32–43. [Google Scholar] [CrossRef]
- Dinu, F.; Marginean, I.; Dubina, D. Experimental testing and numerical modelling of steel moment-frame connections under column loss. Eng. Struct. 2017, 151, 861–878. [Google Scholar] [CrossRef]
- Zahrai, S.M.; Ezoddin, A. Cap truss and steel strut to resist progressive collapse in RC frame structures. Steel Compos. Struct. 2018, 26, 635–647. [Google Scholar]
- Liu, C.; Tan, K.H.; Fung, T.C. Component-based steel beam–column connections modelling for dynamic progressive collapse analysis. J. Constr. Steel Res. 2015, 107, 24–36. [Google Scholar] [CrossRef]
- Tay, C.G.; Koh, C.G.; Liew, J. Efficient progressive collapse analysis for robustness evaluation of buildings experiencing column removal. J. Constr. Steel Res. 2016, 122, 395–408. [Google Scholar] [CrossRef]
- Qin, X.; Wang, W.; Chen, Y.; Bao, Y. Experimental study of through diaphragm connection types under a column removal scenario. J. Constr. Steel Res. 2015, 112, 293–304. [Google Scholar] [CrossRef]
- Faridmehr, I.; Osman, M.H.; Nejad, A.F.; Tahir, M.M.; Azimi, M. Seismic and Progressive Collapse Assessment of New Proposed Steel Connection. Adv. Struct. Eng. 2015, 18, 439–452. [Google Scholar] [CrossRef]
- Li, L.; Wang, W.; Chen, Y.; Teh, L.H. A basis for comparing progressive collapse resistance of moment frames and connections. J. Constr. Steel Res. 2017, 139, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Stylianidis, P.; Nethercot, D.; Izzuddin, B.; Elghazouli, A.Y. Study of the mechanics of progressive collapse with simplified beam models. Eng. Struct. 2016, 117, 287–304. [Google Scholar] [CrossRef]
- Li, L.; Wang, W.; Teh, L.H.; Chen, Y. Effects of span-to-depth ratios on moment connection damage evolution under catenary action. J. Constr. Steel Res. 2017, 139, 18–29. [Google Scholar] [CrossRef] [Green Version]
- Rezvani, F.H.; Yousefi, A.M.; Ronagh, H.R. Effect of span length on progressive collapse behaviour of steel moment resisting frames. In Structures; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Sun, R.R.; Burgess, I.W.; Huang, Z.; Dong, G. Progressive failure modelling and ductility demand of steel beam-to-column connections in fire. Eng. Struct. 2015, 89, 66–78. [Google Scholar] [CrossRef]
- Kuhlmann, U.; Rölle, L.; Izzuddin, B.A.; Pereira, M.F. Resistance and Response of Steel and Steel–Concrete Composite Structures in Progressive Collapse Assessment. Struct. Eng. Int. 2012, 22, 86–92. [Google Scholar] [CrossRef]
- Liu, Y.; Málaga-Chuquitaype, C.; Elghazouli, A.Y. Behaviour of open beam-to-tubular column angle connections under combined loading conditions. Steel Compos. Struct. 2014, 16, 157–185. [Google Scholar] [CrossRef]
- Goldaran, R.; Turer, A. Application of acoustic emission for damage classification and assessment of corrosion in pre-stressed concrete pipes. Measurement 2020, 160, 107855. [Google Scholar] [CrossRef]
- Hadidi, A.; Jasour, R.; Rafiee, A. On the progressive collapse resistant optimal seismic design of steel frames. Struct. Eng. Mech. 2016, 60, 761–779. [Google Scholar] [CrossRef]
- Kordbagh, B.; Mohammadi, M. Influence of seismicity level and height of the building on progressive collapse resistance of steel frames. Struct. Des. Tall Spec. Build. 2017, 26, e1305. [Google Scholar] [CrossRef]
- Chen, J.; Shu, W.; Huang, H. Rate-Dependent Progressive Collapse Resistance of Beam-to-Column Connections with Different Seismic Details. J. Perform. Constr. Facil. 2017, 31, 04016086. [Google Scholar] [CrossRef]
- Yang, B.; Tan, K.H. Robustness of Bolted-Angle Connections against Progressive Collapse: Experimental Tests of Beam-Column Joints and Development of Component-Based Models. J. Struct. Eng. 2013, 139, 1498–1514. [Google Scholar] [CrossRef]
- Jamshidi, A.; Koduru, S.; Driver, R.G. Reliability Analysis of Shear Tab Connections under Progressive Collapse Scenario. In Structures Congress 2014; ASCE: Reston, VA, USA, 2014. [Google Scholar]
- Qin, C.B.; Chian, S.C.; Yang, X.L. 3D Limit Analysis of Progressive Collapse in Partly Weathered Hoek–Brown Rock Banks. Int. J. Geomech. 2017, 17, 04017011. [Google Scholar] [CrossRef]
- Oosterhof, S.A.; Driver, R.G. Shear connection modelling for column removal analysis. J. Constr. Steel Res. 2016, 117, 227–242. [Google Scholar] [CrossRef]
- Shen, J.; Astaneh-Asl, A. Hysteresis model of bolted-angle connections. J. Constr. Steel Res. 2000, 54, 317–343. [Google Scholar] [CrossRef]
- Stylianidis, P.M.; Nethercot, D.A.; Izzuddin, B.A.; Elghazouli, A.Y. Progressive collapse: Failure criteria used in engineering analysis. In Structures Congress 2009: Don’t Mess with Structural Engineers: Expanding Our Role; ASCE: Reston, VA, USA, 2009. [Google Scholar]
- Seismic Provisions for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2010.
- Zhong, W.; Meng, B.; Hao, J. Performance of different stiffness connections against progressive collapse. J. Constr. Steel Res. 2017, 135, 162–175. [Google Scholar] [CrossRef]
- Faridmehr, I.; Osman, M.H.; Tahir, M.B.M.; Nejad, A.F.; Hodjati, R. Seismic and progressive collapse assessment of SidePlate moment connection system. Struct. Eng. Mech. 2015, 54, 35–54. [Google Scholar] [CrossRef]
- Wang, W.; Fang, C.; Qin, X.; Chen, Y.; Li, L. Performance of practical beam-to-SHS column connections against progressive collapse. Eng. Struct. 2016, 106, 332–347. [Google Scholar] [CrossRef]
- Yang, B.; Tan, K.H. Experimental tests of different types of bolted steel beam–column joints under a central-column-removal scenario. Eng. Struct. 2013, 54, 112–130. [Google Scholar] [CrossRef]
- Mckay, A.; Gomez, M.; Marchand, K. Non-Linear Dynamic Alternate Path Analysis for Progressive Collapse: Detailed Procedures Using UFC 4-023-03; Protection Engineering Consultants: Castle Hills, TX, USA, 2010; (Revised July 2009). [Google Scholar]
- Pekelnicky, R.; Engineers, S.D.; Poland, S.C.; Engineers, N.D. Seismic Evaluation and Retrofit Rehabilitation of Existing Buildings. In Proceedings of the SEAOC, Santa Fe, NM, USA, 12–15 September 2012. [Google Scholar]
- Daneshvar, H.; Driver, R.G. Behaviour of shear tab connections in column removal scenario. J. Constr. Steel Res. 2017, 138, 580–593. [Google Scholar] [CrossRef]
- Liu, X.C.; Cui, F.Y.; Zhan, X.X.; Yu, C.; Jiang, Z.Q. Seismic performance of bolted connection of H-beam to HSS-column with web end-plate. J. Constr. Steel Res. 2019, 156, 167–181. [Google Scholar] [CrossRef]
- Kermajani, M.; Ghaini, F.M.; Miresmaeili, R.; AghaKouchak, A.; Shadmand, M. Effect of weld metal toughness on fracture behavior under ultra-low cycle fatigue loading (earthquake). Mater. Sci. Eng. A 2016, 668, 30–37. [Google Scholar] [CrossRef]


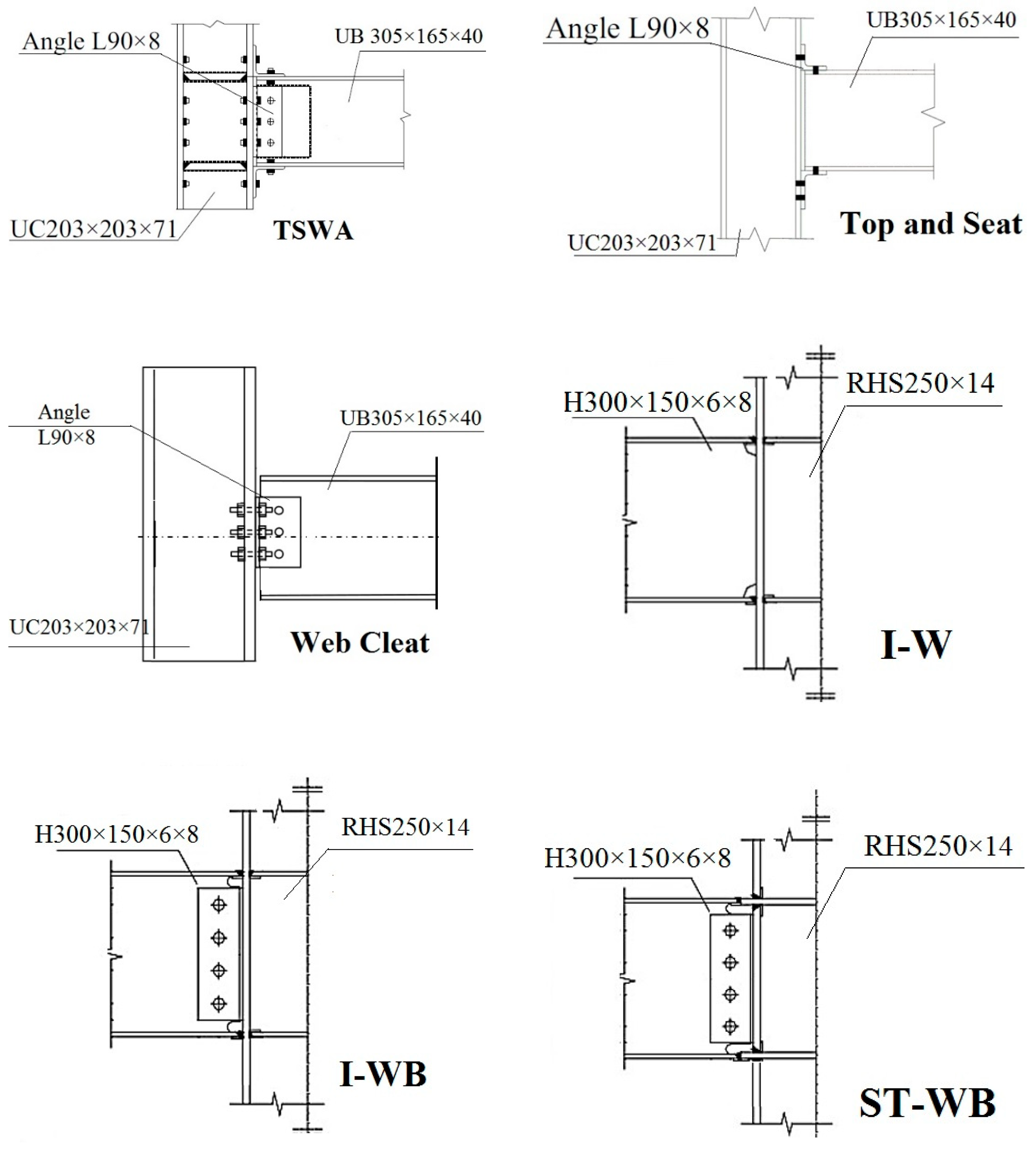

















| Span-to-Depth Ratio, Ri | Beam Section | Column Section |
|---|---|---|
| 5 | W 40 × 149 | W 40 × 531 |
| 10 | W 21 × 50 | W 21 × 248 |
| 15 | W 12 × 35 | W 12 × 50 |
| Specimen | Connection Type | Connection Category | Span-to-Depth Ratio Ri | Reference |
|---|---|---|---|---|
| WUF | Welded Unreinforced Flange-Welded Web | Fully rigid | 10 | W Zhong et al. [41] |
| SidePlate | SidePlate | 20 | Faridmehr et al. [42] | |
| I-W | Welded Flange-Weld Web Connection | 7.5 | W Wang et al. [43] | |
| I-WB | Welded Flange-Bolted Web Connection | 7.5 | W Wang et al. [43] | |
| ST-WB | Welded Flange-Bolted Web Connection with Shear Diaphragm | 7.5 | W Wang et al. [43] | |
| DWA | Double Web Angle | Flexible | 10 | W Zhong et al. [41] |
| TSWA (L = 8 mm) | Top and Seat-Web Angle | 7.9 | B Yang et al. [44] | |
| Web Cleat | Web Cleat | 7.9 | B Yang et al. [44] | |
| Top and Seat angle | Top and Seat Angle | 7.9 | B Yang et al. [44] | |
| Fine Plate | Fine Plate | 7.9 | B Yang et al. [44] | |
| TSWA (L = 10 mm) | Top and Seat-Web Angle | Semi-rigid | 10 | W Zhong et al. [41] |
| TSWA (L = 12 mm) | Top and Seat-Web Angle | 9.5 | B Yang et al. [44] | |
| Extended End-Plate | Extended End-Plate | 9.5 | B Yang et al. [44] | |
| Flush End-Plate | Flush End-Plate | 9.5 | B Yang et al. [44] |
| Specimen | Failure Mode | ||
|---|---|---|---|
| Fully rigid | |||
| WUF | 1.45 | 11.77 | Fracture at the flange |
| SidePlate | 6.38 | 8.3 | Beam failure |
| I-W | 1.25 | 7.27 | Bottom flange and beam web fractured, weld fracture |
| I-WB | 1.25 | 16 | Fracture of shear plate and bottom flange |
| ST-WB | 1.25 | 15.4 | Fracture of shear plate and bottom flange |
| Semi-rigid | |||
| TSWA (L = 10 mm) | 2.24 | 21.3 | Fracture at the angle and failure of the web bolt |
| TSWA (L = 12 mm) | 1.72 | 17.3 | Fracture bolt |
| Extended end-plate | 0.91 | 14.22 | Fracture of weld |
| Flush end-plate | 1.17 | 12.6 | Bolt thread stripping |
| Flexible | |||
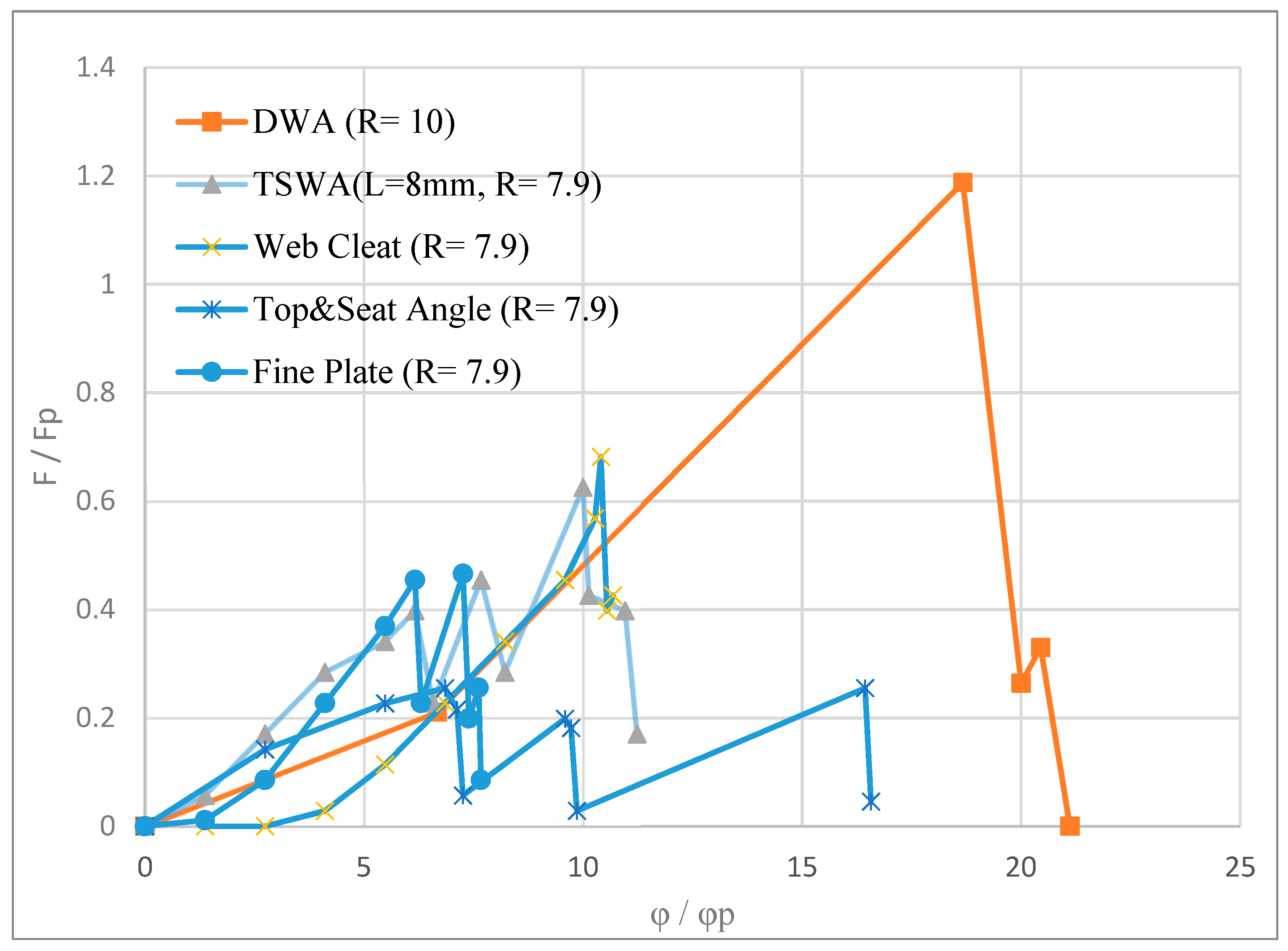
| DWA | 1.2 | 20.4 | Fracture at the shear angles |
| TSWA (L = 8 mm) | 0.62 | 10.9 | Fractured web angle |
| Web Cleat | 0.68 | 10.54 | Fractured angle |
| Top and Seat angle | 0.25 | 16.4 | Fractured bottom angle |
| Fine Plate | 0.46 | 7.6 | Bolt fractured in shear |
| Connection Type | Nonlinear Modeling Parameters | Nonlinear Acceptance Criteria | ||
|---|---|---|---|---|
| Plastic Rotation Angle (Rad) | Residual Strength Ratio | Plastic Rotation Angle (Rad) | ||
| Primary Component | ||||
| Fully Restrained Moment Connections | ||||
| WUF | ||||
| SidePlate® | ||||
| Partially Restrained Moment Connections (Relatively Stiff) | ||||
| Shear in Bolt | ||||
| Tension in Bolt | ||||
| Tension in Tee | 0.012 | 0.018 | 0.8 | 0.010 |
| Flexure in Tee | 0.042 | 0.084 | 0.2 | 0.035 |
| Partially Restrained Simple Connections (Flexible) | ||||
| Flexure in Angles | ||||
| Simple Shear Tab | ||||
| Specimen | |||
|---|---|---|---|
| WUF | 0.023 | 0.176 | 7.6 |
| SidePlate | 0.02 | 0.19 | 9.5 |
| I-W | 0.018 | 0.067 | 3.7 |
| I-WB | 0.02 | 0.168 | 8.4 |
| ST-WB | 0.019 | 0.17 | 8.9 |
| TSWA (L = 10 mm) | 0.033 | 0.32 | 9.6 |
| TSWA (L = 12 mm) | 0.025 | 0.23 | 9.2 |
| Extended end-plate | 0.02 | 0.184 | 8.9 |
| Flush end-plate | 0.02 | 0.143 | 7.1 |
| DWA | 0.065 | 0.36 | 5.53 |
| TSWA (L = 8 mm) | 0.061 | 0.149 | 2.44 |
| Web Cleat | 0.041 | 0.156 | 3.8 |
| Top and Seat angle | 0.041 | 0.246 | 6 |
| Fine Plate | 0.03 | 0.108 | 3.6 |
| Average | 6.73 |
| Specimen | |||
|---|---|---|---|
| WUF | 1295.3 | 3.02 | 0.35 |
| SidePlate | 20.2 | 17.3 | 4.95 |
| I-W | 5457.6 | 1.37 | 0.36 |
| I-WB | 5457.6 | 2.02 | 0.19 |
| ST-WB | 5457.6 | 2.55 | 0.24 |
| TSWA (L = 10 mm) | 1295.3 | 0.93 | 0.26 |
| TSWA (L = 12 mm) | 4420 | 0.35 | 0.16 |
| Extended end-plate | 4420 | 1.08 | 0.09 |
| Flush end-plate | 4420 | 0.79 | 0.27 |
| DWA | 1295.3 | 0.12 | 0.06 |
| TSWA (L = 8 mm) | 6787.7 | 0.07 | 0.06 |
| Web Cleat | 6787.7 | 0.019 | 0.06 |
| Top and Seat angle | 6787.7 | 0.09 | 0.02 |
| Fine Plate | 6787.7 | 0.014 | 0.06 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faridmehr, I.; Hajmohammadian Baghban, M. An Overview of Progressive Collapse Behavior of Steel Beam-to-Column Connections. Appl. Sci. 2020, 10, 6003. https://doi.org/10.3390/app10176003
Faridmehr I, Hajmohammadian Baghban M. An Overview of Progressive Collapse Behavior of Steel Beam-to-Column Connections. Applied Sciences. 2020; 10(17):6003. https://doi.org/10.3390/app10176003
Chicago/Turabian StyleFaridmehr, Iman, and Mohammad Hajmohammadian Baghban. 2020. "An Overview of Progressive Collapse Behavior of Steel Beam-to-Column Connections" Applied Sciences 10, no. 17: 6003. https://doi.org/10.3390/app10176003
APA StyleFaridmehr, I., & Hajmohammadian Baghban, M. (2020). An Overview of Progressive Collapse Behavior of Steel Beam-to-Column Connections. Applied Sciences, 10(17), 6003. https://doi.org/10.3390/app10176003






